Amorphization evolution study of CrCoFeNiMn high entropy alloy for mechanical performance optimization by deep potential molecular dynamics

Abstract

In the study, we explore the structural evolution of Cantor high-entropy alloy (HEA) under different super-cooling rates and its correlation with mechanical property variations by the developed machine learning-driven deep potential molecular dynamics (DPMD) simulation. Our results reveal the critical super-cooling rate of amorphization-crystallization transition of Cantor alloy and the local structure constitutions at different temperatures during the super-cooling process. The associated mechanical property studies demonstrate the glassy Cantor alloy amorphized at high super-cooling rate exhibits a superior capability of ductility but this capability is unrelated to the amorphization cooling rates. While the high strength of Cantor alloy requires a lower super-cooling rate which might result in the crystallization, amorphizing the Cantor alloy at the critical super-cooling rate of amorphization-crystallization transition could compatibilize both ductility and strength capabilities. Such a discovery sheds new lights on the material development and its mechanical performance optimization for industrial applications.

Introduction

HEA is a new class of metallic materials composing of multiple principal elements mixing at near equi-atomic proportions^1,2,3. Generally, the atomic percentage of each principal element in HEA is between 5 at% and 35 at%. Due to the unique design concept, HEAs generally possess high configurational entropy, heavy lattice distortion and sluggish diffusion, which enable them to exhibit promising properties including enhanced mechanical performance, corrosion resistance, and irradiation resistance^4,5,6. Among the extensive range of HEAs, the CrCoFeNiMn HEA, also called the Cantor, is one of the most studied alloys due to its excellent mechanical properties of strength, ductility, and toughness^7,8,9,10.

The superior combination of strength, ductility, and toughness for Cantor alloy can be achieved by inducing phase transformation and local stacking fault energy variation¹¹, adding tiny amount of new elements^12,13, and amorphizing the alloy itself^14,15,16,17, etc. Among which, the amorphization is one of the most promising ways to achieve the superior combination of different mechanical properties, which has been demonstrated in other alloys^{14,15,16,17,18,19,20,21}. Currently, there are two main routes for obtaining the amorphous structure of Cantor alloy. One is destabilization of a crystalline solid phase into a disordered one, also known as solid-state amorphization^14,15. Through the synergy of several deformation mechanisms in the Cantor alloy, including dislocation slip and twinning at early stages^22,23 and crack bridging at late stages of deformation^24,25, the Cantor alloy has demonstrated excellent mechanical performance at both room temperature and cryogenic temperature, with a high tensile strength of approximately 1 GPa, an elongation of around 60–70%, and a fracture toughness exceeding 200 MPa$\sqrt{m}$¹⁵. However, this amorphization only occurs at the local dislocation area such as crack tip field. Super-cooling is another main route for amorphization by retaining dynamic disorder in a fast-cooling liquid phase and can be employed to produce bulk amorphous alloy^26,27. Based on this method, quite a few alloys including Ti-based²⁸, Co-based²⁹, and Fe-based³⁰ amorphous alloys have been successfully synthesized. Thus, super-cooling can serve as a promising way to amorphize the bulk Cantor alloy and improve its mechanical properties.

The evolution of Cantor alloy’s microstructure during super-cooling is crucial to understand its amorphization process and the associated material properties, which is of great importance for the material development and engineering applications. Despite its importance, due to the lack of adequate rapid quenching techniques, the study on the microstructure evolution of Cantor alloy and the material properties at amorphous state has been very limited. As a computational tool with high accuracy, ab initio molecular dynamics (AIMD), has been widely used in many disciplines^31,32,33 including physics, chemistry, biology, and materials science, and could be a practical strategy for the amorphization study of Cantor alloy. However, AIMD simulation is computationally intensive, limiting its typical applications to hundreds of atoms and time scales of $\sim$100 ps³⁴. To address the dilemma of accuracy versus efficiency in AIMD simulation, a deep potential molecular dynamics (DPMD) model integrating AIMD simulation and machine learning (ML) method was developed in the present study. The developed DPMD takes advantages of the accuracy of first-principle calculations and the efficiency of using traditional empirical potentials^35,36,37. By using this method, the solidification process of Cantor alloy across a temperature range of 300 K to 3000 K under different super-cooling rates was comprehensively studied through structural analysis techniques including radial distribution function and Voronoi tessellation. Mechanical properties of solid Cantor alloys at 300 K with different microstructures were also examined. Combining with the local structure study, the relationship between the microstructure of glassy Cantor alloy and mechanical properties has been unveiled, and a new material design strategy to compatibilize ductility and strength capabilities was proposed. Although Cantor alloy was the focus of this study, the material design strategy reported herein can be extended to other materials for their mechanical performance optimizations in engineering applications.

Results

Validation of the developed DP

In DPMD, it uses the density functional theory (DFT) based AIMD datasets for the training of potentials. To validate the developed DP, the root-mean-square error (RMSE) of energy and force obtained from DPMD and DFT is calculated as below to evaluate the deviation degree of the results predicted by DPMD and DFT simulations,

$${RMSE}=\sqrt{\frac{1}{m}\mathop{\sum }\limits_{i=1}^{m}{\left({x}_{{Dp}}-{x}_{{DFT}}\right)}^{2}}$$

(1)

where ${x}_{{Dp}}$ is the energy (or force) estimated by DP method, ${x}_{{DFT}}$ is the energy (or force) estimated by DFT method, m refers to the number of structures used for calculating the RMSE. The smaller RMSE indicates a closer computational accuracy of these two methods.

Figure 1a, b display the RMSE for energy and force as a function of training steps in the study of the Cantor alloy, which reaches stable after the training step of 3 × 10⁵. Therefore, the ML training step of 4 × 10⁵ implemented in this study is sufficient to train the DP model. For validation, 200 different structures of Cantor alloy are randomly selected from the training and validation datasets, respectively. The energy and force of these structures were calculated by using DFT and the trained DP model. Figure 1c–f shows the performance of the DP model for Cantor alloy across the temperature range of 300 to 3000 K in the training and validation datasets. The RMSE for energy and force derived from the training dataset using DFT and DP model are 6.13 meV/atom and 41.9 meV/Å, respectively. For the validation dataset, the RMSE values for energy and force are 6.17 meV/atom and 42.3 meV/Å, which are close to those obtained from the training dataset. The calculated RMSE values in this study are close or even lower than the ones reported in previous literatures^38,39, indicating that the trained DP model has achieved a level of accuracy comparable to that of DFT and can be utilized for the subsequent study of the Cantor alloy.

Fig. 1: The training of DP model.

Errors in the training process of DP model for Cantor alloy in a energy and b force. The comparisons of c energy and d force in x, y, and z directions predicted by DP with DFT calculations from the training dataset for Cantor alloy in the temperature range of 300 to 3000 K. The comparisons of f energy and g force in x, y, and z directions predicted by DP with DFT calculations from the validation dataset for Cantor alloy in the temperature range of 300 to 3000 K.

Microstructure evolution of Cantor alloy

The radial distribution function (RDF) is a pair correlation that describes how, on average, the atoms in a system are radially packed around each other, and has been proved to be a particularly effective way of characterizing the average microstructure of disordered molecular systems⁴⁰. The microstructure information can be reflected by the peak position, peak shape, intensity, etc. The partial radial distribution function (PRDF) of atom pair i-j is described by Eq. (2)

$${g}_{{ij}}\left(r\right)=\frac{V}{{N}_{i}{N}_{j}}\left\langle \mathop{\sum }\limits_{\alpha =1}^{{N}_{i}}\frac{{n}_{\alpha j}\left(r,\,\Delta r\right)}{4\pi {r}^{2}\Delta r}\right\rangle$$

(2)

where V is the volume of the supercell, i is the central atom, j is the coordination atom, ${N}_{i}$ and ${N}_{j}$ are the numbers of i and j atom in the supercell, respectively, ${n}_{\alpha j}\left(r,\,\Delta r\right)$ is the number of j atom in the sphere shell from r to r + Δr, and the symbol $\left\langle \cdots \right\rangle$ represents the time average. While the total radial distribution function (TRDF) is evaluated by Eq. (3)

$$g\left(r\right)=\sum _{i}\sum _{j}{c}_{i}{c}_{j}{b}_{i}{b}_{j}\left[{g}_{{ij}}\left(r\right)-1\right]$$

(3)

where ${c}_{i}$ (or ${c}_{j}$) is the atomic fraction of species i (or j) in the system and ${b}_{i}$ (or ${b}_{j}$) is its coherent scattering length.

Figure 2a shows the comparison of the TRDF of different structures (body-centered cube (BCC), face-centered cube (FCC), icosahedral (ICOS), and melt) acquired by AIMD and DPMD for Cantor alloy, from which a very good agreement can be observed. This further validated the DPMD model developed in this study. Figure 2b–e display the temperature-dependent TRDF of the Cantor alloy from 3000 K to 300 K under four different super-cooling rates obtained by DPMD simulations. In Fig. 2b–e, all TRDFs display three main peaks: P1, P2, and P3 within the temperature range of 1700–3000 K, which are the typical characteristics of liquid phase³⁶. As the temperature decreases, the amplitudes of these three main peaks gradually increase, implying that the ordered arrangement of atoms is enhanced⁴¹. In Fig. 2b, c, the P2 of TRDFs splits into two sub-peaks (P2_1 and P2_2) as the temperature drops to 1000 K under the cooling rates of 100 K/ps and 10 K/ps, and the sub-peak P2_1 at ~4.1 Å is slightly higher than the P2_2 at ~4.8 Å. This is a typical indicator of liquid–glass transition (amorphous transition)⁴², implying the Cantor melt experiences amorphous transition during the cooling rates of 100 K/ps and 10 K/ps. The liquid-glass transition temperature of 1000 K is close to the melting temperature identified by the temperature dependence of volume variation as shown in Supplementary Fig. 1.

Fig. 2: The RDF analysis.

a A comparison of TRDFs of the Cantor alloy with different structures from AIMD and DPMD at 300 K and 3000 K. The temperature-dependent TRDFs of the Cantor alloy under four cooling rates of 100 K/ps (b), 10 K/ps (c), 1 K/ps (d) and 0.1 K/ps (e). f The TRDFs of glassy Cantor alloy (formed under 100 K/ps) at 300 K scaled by the first peak position R₁; the solid and dashed vertical lines denote the characteristic constants in the corresponding FCC and BCC crystalline lattice structures, respectively.

While in Fig. 2d, e, a small peak appears out between P1 and P2, at around 3.3 Å. This peak is close to the position of the second peak of Cantor alloy with FCC structure as shown in Fig. 2a. It is conjectured that the FCC-like cluster is formed during the cooling process under the super-cooling rates of 1 K/ps and 0.1 K/ps. In addition, a few new small peaks resembling the characteristic peaks of BCC structure of Cantor alloy as shown in Fig. 2a appear out during the cooling process. Taking these observations into account, it is inferred that, unlike the glassy Cantor alloy formed under the high super-cooling rates of 100 K/ps and 10 K/ps, a dual-phase crystalline Cantor alloy with BCC and FCC structures is formed under the lower super-cooling rates of 1 K/ps and 0.1 K/ps. Further study on the temperature dependence of volume variation under different super-cooling rates (Supplementary Fig. 1) indicates that the critical super-cooling rate of amorphization-crystallization transition of Cantor alloy is between 1 K/ps and 2 K/ps.

The arrangement of peak positions R_i in RDFs scaled by the first peak position R₁ can be used to analyze the inherent atomic packing modes of the formed glassy Cantor alloy under super-cooling⁴³. It has been demonstrated that the constants associated with the values of R_i/R₁ correspond to some relative atomic positions in a lattice structure³⁹. For different lattice structures, the values of R_i/R₁ are unique and thereby reflect the characteristic atomic packing and structural feature, such that they can be regarded as the characteristic constants in the corresponding lattice structures. By evaluating the TRDF of glassy Cantor alloy formed at 300 K under the super-cooling rate of 100 K/ps (see Fig. 2b), the structure of the glassy Cantor alloy was analyzed. Figure 2f shows the scaled TRDF of the glassy Cantor alloy by the first peak position R₁ with the characteristic constants of FCC and BCC lattice structures (the exact values of the characteristic constants of FCC and BCC are listed in Supplementary Table 1). The values of R_i/R₁ (i = 1, 2, 3, 4, and 5) for the glassy Cantor alloy are 1, 1.701, 1.990, 2.567, and 3.412 as listed in Table 1. Among which, the values of R_i/R₁ (i = 3, 4, and 5) are quite close to the constants of $\sqrt{4}$, $\sqrt{20/3}$, and $\sqrt{35/3}$, the characteristic constants of BCC lattice structure. While the value of R₂/R₁ is close to FCC lattice structure characteristic constant, $\sqrt{3}$. Thus, it means that the Cantor alloy at glassy state may share a similar atomic packing order nature with its crystalline counterpart, and the atomic packing order does not strictly conform to either FCC or BCC arrangements but instead shows a hybridization of FCC and BCC orders. It should be noted that this specific atomic packing order formulated in glassy Cantor alloy are hidden in their broad distributions of TRDFs or structure factors and cannot be directly detected in diffraction experiments. The values of the scaled R_i/R₁ for the TRDFs of glassy Cantor alloy at other temperatures in Fig. 2b were also examined (see Supplementary Table 2) and the hybridization of FCC and BCC orders for Cantor alloy at glassy state was found not to change with the temperature.

Table 1 The first peak position R₁ (Å) and the relative atomic positions scaled by R₁ in the RDFs of glassy Cantor alloy at 300 K under the super-cooling rate of 100 K/ps obtained from DPMD simulations

Inspired by the hidden order obtained from TRDFs, the hidden order of each element in glassy Cantor alloy at 300 K formed under the super-cooling rate of 100 K/ps was also investigated. The scaled peak positions of R_i/R₁ are listed in Table 1. The hidden order of each element for the glassy Cantor alloy can be classified into three types: pure BCC structure, pure FCC structure, and a hybridization of BCC and FCC structures. As shown in Table 1, the scaled peak positions of R_i/R₁ (i = 2, 3, 4, and 5) in Cr-Cr, Cr-Mn, Co-Mn, and Fe-Fe PRDFs follow BCC order, but select different characteristic constants of BCC lattice structure. This means that while these atomic pairs exhibit a similar structural motif in terms of BCC arrangement, the specific arrangements of atoms may differ. Similarly, the examinations of Co-Fe, Fe-Mn, and Ni-Ni PRDFs show they follow FCC order, but close to different characteristic constants of FCC as well. For the remaining atom pairs, they do not exactly follow the order of either FCC or BCC, but rather exhibit a hybridization of both FCC and BCC orders.

Based on the analysis of radial distribution function above, the Cantor melt forms different structures under different super-cooling rates, with high super-cooling rate (e.g., 10 K/ps) leading to amorphous formation while low cooling rate (e.g., 0.1 K/ps) leading to crystalline structure. However, it should be noted that radial distribution function only provides the mean structural information. To determine the local structure evolution of Cantor alloy during the super-cooling process under these four different cooling rates, Voronoi tessellation capable of studying the detailed local environment of each atom was induced. According to this method of analysis, Voronoi polyhedron (VP) is defined by Schläfli’s notation, 〈n₃, n₄, n₅, n₆〉, where n_i is the number of i-edged faces of a polyhedron^44,45. As an example, the Voronoi indices of standard BCC, FCC, and ICOS are 〈0, 6, 0, 8〉, 〈0, 12, 0, 0〉, and 〈0, 0, 12, 0〉, respectively⁴⁶.

Figure 3a–d show the calculated populations of the top 15 VP types of the Cantor alloy during four different super-cooling rates from which a few certain dominant polyhedrons can be observed. The topological structures of these 15 VPs of the Cantor alloy are displayed in Fig. 3e. In Fig. 3a–d, the predominant VP types for liquid phase (1600 and 3000 K) under the four different cooling rates are 〈0, 2, 8, 4〉, 〈0, 3, 6, 4〉, 〈0, 3, 6, 5〉, suggesting the structural uniformity of Cantor melt above the melting temperature⁴⁷. For solid phase (1000 K and 300 K), the predominant VPs are 〈0, 1, 10, 2〉, 〈0, 2, 8, 4〉, and 〈0, 3, 6, 4〉 under the cooling rates of 100 K/ps and 10 K/ps, while the dominant VPs are 〈0, 4, 4, 6〉 and 〈0, 6, 0, 8〉 under the cooling rates of 0.1 K/ps and 1 K/ps.

Fig. 3: The Voronoi index analysis.

Temperature dependences of main Voronoi indices of Cantor alloy during the four super-cooling rates of a 100 K/ps, b 10 K/ps, c 1 K/ps, and d 0.1 K/ps; (e) representative snapshots of the most common VP types in glassy and crystalline Cantor alloy. Cr atoms in red, Co atoms in blue, Fe atoms in yellow, Ni atoms in pink, and Mn atoms in green, respectively.

To clarify the structure evolution of the Cantor alloy during the four cooling rates in detail, the 15 dominant VPs discussed above are classified into three categories⁴²: (a) ICOS-like clusters including 〈0, 0, 12, 0〉, 〈0, 2, 8, x〉, 〈0, 1, 10, x〉, and 〈1, 0, 9, 3〉, $x=\mathrm{1,2}\cdots 4$; (b) BCC-like clusters with 〈0, 6, 0, 8〉; (c) FCC-like clusters including 〈0, 3, 6, 4〉, 〈0, 3, 6, 5〉, 〈0, 4, 4, 6〉, 〈0, 4, 4, 7〉, and 〈0, 12, 0, 0〉. Based on this classification, the fraction variations of ICOS-like, FCC-like, and BCC-like clusters of the Cantor alloy during the super-cooling process under the four cooling rates are plotted in Fig. 4a–d. The fraction variations of these three different clusters for the cooling rates (100 K/ps and 10 K/ps) under which the glassy Cantor alloy formed follow a similar trend. As shown in Fig. 4a, b, the ICOS-like cluster dominates during the whole super-cooling process, and its fraction increases with the decrease of temperature. The fraction of FCC-like clusters increases with the decreasing temperature until the temperature drops to around 1000 K. The presence of BCC-like clusters is minimal, less than 1%, throughout the entire cooling process. In comparison of Fig. 4a, b, it is found the fractions of ICOS-like cluster and FCC-like cluster at 300 K under the two different cooling rates are quite close. The structure composition of glassy Cantor alloy at 300 K formed under other cooling rates was also analyzed (see Supplementary Fig. 2) and the same phenomenon was observed, indicating that cooling rate hardly affects the local structure composition of glassy Cantor alloy.

Fig. 4: The structural evolution of Cantor alloy under different cooling rates.

The fractions of ICOS-like, FCC-like, and BCC-like clusters versus temperature under the four different super-cooling rates of a 100 K/ps, b 10 K/ps, c 1 K/ps, and d 0.1 K/ps.

The fraction variations of ICOS-like, FCC-like, and BCC-like clusters of the Cantor alloy during the cooling process for the cooling rates of 1 K/ps and 0.1 K/ps under which the crystalline Cantor alloy formed follow another variation trend. As shown in Fig. 4c, d, the ICOS-like cluster and FCC-like cluster dominate in the liquid state while the fraction of BCC-like cluster is negligible. On the other hand, the fractions of FCC-like and BCC-like clusters increase while that of ICOS-like cluster drops sharply when the crystallization occurs (~1500 K for 1 K/ps and ~1600 K for 0.1 K/ps). The higher initial crystallization temperature at lower super-cooling rate (~1500 K for 1 K/ps and ~1600 K for 0.1 K/ps) is ascribed to that the ICOS-like cluster has sufficient activation energy and relaxation to escape from its position surrounded by adjacent atoms at lower cooling rate, breaking the “cage trapping” effect⁴³. The fraction of BCC-like cluster continuingly increases while that of FCC-like cluster remains almost unchanged during the super-cooling process after crystallization occurring. BCC-like cluster becomes dominated at the room temperature of 300 K and the proportion of BCC-like clusters is higher at the lower cooling rate, indicating that slower cooling rates favor the formation of BCC-like clusters.

Overall, Cantor melt experiences different phase transitions under different super-cooling rates. It undergoes amorphous transition at higher super-cooling rates of 100 K/ps and 10 K/ps, but a complicated crystalline transition at lower super-cooling rates of 1 K/ps and 0.1 K/ps, which forms a dual-phase alloy with both BCC and FCC structures at room temperature. This can be attributed to the sufficient relaxation of central atoms in ICOS-like clusters when applying a lower super-cooling rate. The relaxation process reduces the nucleation free energy barrier for BCC-like and FCC-like clusters, which thus become more prevalent comparing to other cluster types. A conclusion can be drawn that the transition from a melt to a crystalline or a glassy state is a result of competition between crystal-like and ICOS-like clusters.

Discussions

Based on the above structure study, the Cantor melt forms different microstructures depending on the cooling rates applied, with higher super-cooling rate leading to amorphous formation while lower super-cooling rate leading to mixed FCC and BCC structure. Amorphous solids have the potential to exhibit excellent mechanical performance with high strength, high hardness, and excellent ductility. On the other hand, the BCC structure typically offers high strength across various temperatures and large strain states. Therefore, it is of interest to explore the mechanical properties of Cantor alloy with different structures and reveal the connections between structure and mechanical properties. In this study, 19 Cantor alloys with different structures were prepared by different super-cooling rates (0.1 K/ps, 1 K/ps, 2 K/ps, 3 K/ps, 4 K/ps, 5 K/ps, 10 K/ps, 15 K/ps, 18 K/ps, 20 K/ps, 30 K/ps, 40 K/ps, 50 K/ps, 60 K/ps, 70 K/ps, 80 K/ps, 90 K/ps, and 100 K/ps) or purposely built as polycrystal FCC structure. The local structure constitutions for these Cantor alloys are listed in Supplementary Table 3.

To evaluate the mechanical properties of these 19 Cantor alloys with different structures, the elastic constants and stress-strain curve were investigated. The stress-strain curves were obtained by applying tensile loading along the x-axis of the supercell at a strain rate of 5 × 10⁸ s⁻¹ in the NPT ensemble. The calculated stress-strain curves for the 19 cantor alloys with different structures, including 18 Cantor alloys prepared by different super-cooling rates and one Cantor alloy with polycrystal FCC structure, are shown in Fig. 5a. To validate the simulated stress-strain curves of the Cantor alloys in this study, the simulated stress-strain curve of the Cantor alloy with polycrystal FCC structure (the most common structure of Cantor alloy manufactured by traditional alloy processing) was compared with the one reported by Zhang et al.⁴⁸ and shown in Fig. 5b. From Fig. 5b, a good agreement between the stress-strain curve in this study and the previous literature can be observed, implying the accuracy of the simulated stress-strain curves in this study.

Fig. 5: The simulated stress-strain curves by DPMD simulation.

a The simulated stress-strain curves of Cantor alloys with different structures; b the comparison of the simulated stress-strain curve of the polycrystal FCC cantor alloy with the previous literature.

The tensile strength was extracted from the stress strain curve for Cantor alloy as displayed in Fig. 5a for studying the relationship between the alloy’s structure and mechanical performance. Figure 6a–c show the tensile strength of Cantor alloy at 300 K as functions of ICOS-like cluster, FCC-like cluster, and BCC-like cluster, in which no relationships between the tensile strength and the alloy structure constitutions were observed. It means the strength of Cantor alloy is not determined by its local structure constitution. The tensile strength of Cantor alloys solidified under different super-cooling rates as shown in Fig. 6d exhibits that the tensile strength increases with the decreasing super-cooling rates at lower cooling rates (0.1 K/ps, 1 K/ps, and 2 K/ps in this study). However, the strength of Cantor alloy is not affected by the super-cooling rates when it exceeds 2 K/ps (cooling rate for amorphous transition). In comparison with polycrystal FCC Cantor alloy with the calculated tensile strength of 4.28 GPa, only the Cantor alloy formed under the super-cooling rates of 0.1 K/ps, 1 K/ps, and 2 K/ps has a higher strength. It indicates that the strength of Cantor alloy might not be improved through the amorphous transition unless the Cantor alloy is amorphized at a relatively low super-cooling rate, that is, the critical cooling rate (or close to) of amorphization-crystallization transition.

Fig. 6: The exploration of affecting factors of mechanical properties of Cantor alloy.

The tensile strength as functions of ICOS-like cluster (a), FCC-like cluster (b), BCC-like cluster (c), and super-cooling rate (d).

On the other hand, the elastic constants were calculated through NVT ensembles at 300 K by applying a series of ±2% deformations. For cubic Cantor alloys, there are three independent elastic constants c₁₁, c₁₂, and c₄₄⁴⁹, which were calculated and listed in Supplementary Table 4. The bulk modulus B and shear modulus G were derived by Voigt-Reuss-Hill (VRH) approximation^50,51,52 as follows once the elastic constants were obtained

$${B}_{V}={B}_{R}=\frac{{c}_{11}+2{c}_{12}}{3}$$

(4)

$${G}_{V}=\frac{{c}_{11}-{c}_{12}+3{c}_{44}}{5}$$

(5)

$${G}_{R}=\frac{5\left({c}_{11}-{c}_{12}\right){c}_{44}}{4{c}_{44}+3{c}_{11}-3{c}_{12}}$$

(6)

The Voigt approximation ${B}_{V}$, ${G}_{V}$ and Reuss approximation ${B}_{R}$, ${G}_{R}$ represent the upper and lower bounds of B and G. Therefore, the arithmetic means ${B}_{H}=\left({B}_{V}+{B}_{R}\right)/2$, ${G}_{H}=\left({G}_{V}+{G}_{R}\right)/2$ were suggested to estimate B and G⁴⁸. Then, the kinetic fragility index m⁵³ and Poisson’s ratio ν⁵⁴ expressed in Eqs. (7) and (8) were calculated to characterize the material’s ductility.

$$m=12\left(\frac{B}{G}+0.67\right)$$

(7)

$$\nu =\frac{3{B}_{H}-2{G}_{H}}{2\left(3{B}_{H}+{G}_{H}\right)}$$

(8)

The calculated results of B, G, m, and ν for the 23 Cantor alloys with different structures are listed in Supplementary Table 5.

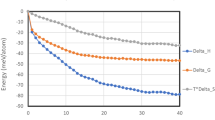
Figure 7 shows the calculated kinetic fragility index m and Poisson’s ratio ν for Cantor alloys with different structures. Typically, higher m and larger ν values are regarded as indicators of better ductility in compression^55,56,57,58. From Fig. 7, it is clear that the Cantor alloys at amorphous states have larger values of m and ν than it being at crystalline states. However, at (or close to) the critical cooling rate of amorphization-crystallization transition, for instance, 1 K/ps or 2 K/ps, the solidified Cantor alloy shows better ductility even being at crystalline state. In addition, the m and ν of glassy Cantor alloys amorphized under different super-cooling rates do not exhibit a high discrepancy, which is consistent with the close structure constitutions of glassy Cantor alloys amorphized at different super-cooling rates (see Supplementary Fig. 2). This means the ductility of Cantor alloy might not be affected by the super-cooling rate once the amorphization occurs.

Fig. 7: The exploration of ductility of Cantor alloy.

The calculated kinetic fragility index m (a) and Poisson’s ratio ν (b) of Cantor alloys with different structures.

The above discussion tells the amorphization of Cantor alloy can indeed improve its ductility. However, unlike what was reported in previous studies^14,15, amorphous Cantor alloy might not necessarily have a superior strength capability. The strength of amorphous Cantor alloy can be enhanced by applying a relatively low super-cooling rate. To unveil this phenomenon, the element distributions of the high-strength Cantor alloys solidified at the relatively low super-cooling rates of 0.1, 1, and 2 K/ps were simulated and shown in Fig. 8a from which the segregation of Co can be clearly observed. In contrast, the element distribution of Cantor alloy solidified under high super-cooling rate of 100 K/ps does not show up Co segregation. This indicates the Co segregation could be the main factor contributing to the high strength. Indeed, the diffusivity of Co is much lower compared with other constituent elements of Cantor alloy at low super-cooling rate of 0.1 K/ps (Fig. 8b) while the diffusivities of all constituent elements are essentially the same at high super-cooling rate of 100 K/ps (Fig. 8c). The low super-cooling rate could cause a decrease in the movement of Co atoms, leading to their segregation in the alloy and bringing a high strength capability of the material itself.

Fig. 8: The relationship between structure and kinetic.

a The element distribution of Cantor alloys with different structures at 300 K solidified under different super-cooling rates; the self-diffusivity of each element in Cantor alloys under two different super-cooling rates: 0.1 K/ps (b) and 100 K/ps (c).

This study was devoted to optimize the mechanical performance of Cantor alloy such that it can compatibilize both ductility and strength capabilities for industrial applications. Our results show that the Cantor alloy can be amorphized at high super-cooling rate and the amorphous Cantor alloy exhibits a good capability of ductility. The strength capability of Cantor alloy is mainly dependent on the Co segregation which requires a relatively low super-cooling rate. Fortunately, the local structure constitutions of Cantor alloy barely change with cooling rates and the ductility will not be affected as well once the amorphization or crystallization occurs. Therefore, amorphizing the Cantor alloy at the the critical cooling rate of amorphization-crystallization transition, can serve a way to obtain the superior combination of strength and ductility capabilities. This strategy can also be extended to other materials for their mechanical performance optimizations for industrial applications.

Methodology

DP-GEN for Cantor structures

In this study, the DP generator (DP-GEN) was used to generate a set of training data that covers a sufficient wide range of relevant configurational space. DP-GEN is a concurrent learning procedure, and each iteration includes three main steps: training, exploration, and labeling⁵⁹ (see Supplementary Fig. 3). In the first iteration, 1000 different structures of liquid and amorphous cells were selected as the initial training dataset. With this density functional theory (DFT) training dataset, four deep potential (DP) models were trained. Afterwards, the exploration process utilized one of the DP models for MD simulations to explore configuration spaces at varying temperatures and pressures while the other three DP models were taken to predict the corresponding energies and atomic forces. The maximum deviation of the DP model prediction of forces defined in Eq. (9) was used to formulate the criterion for labeling

$${\sigma }_{f}^{\max }={\max }_{i}\sqrt{\left\langle {\left|{F}_{i}-\left\langle {F}_{i}\right\rangle \right|}^{2}\right\rangle }$$

(9)

where $\left\langle \cdots \right\rangle$ denotes the average of the DP model ensemble. Only configurations with ${\sigma }_{{low}} < {\sigma }_{f}^{\max } < {\sigma }_{{high}}$ (see Supplementary Fig. 3) were labeled as candidates for the further DFT calculations and added to the training dataset for next iteration. Here, ${\sigma }_{{low}}$ and ${\sigma }_{{high}}$ were set to 0.05 and 0.20 eV/Å, respectively, as suggested in the previous study⁶⁰. The exploration of each system was considered converged when the percentage of accurate configurations exceeded 99.5%⁶¹. The exploration setting parameters of DP-GEN iterations were detailly listed in Supplementary Table 6 while the percentage of candidate, accurate and failed configurations for each iteration were listed in Supplementary Table 7. Five iterations were performed for data training in this study. In each iteration, 600 structures were randomly selected for self-consistent calculation of the DFT. Combining with the 1000 initial datasets, there were 4000 different structures included in total in the dataset. Utilizing this data, 99.63% of accuracy was achieved in the sixth round.

DFT calculation setting

The initial training dataset was generated by conducting 10,000 steps of AIMD at ten temperatures of 3000, 2700, 2400, 2100, 1800, 1500, 1200, 900, 600, and 300 K. 100 different structures were selected for each temperature, which results in a total of 1000 structures in dataset. The AIMD simulations of Cantor alloy were implemented by the Vienna Ab-Initio Simulation Package (VASP)^62,63. The exchange-correction energy of the electrons was treated by the generalized gradient approximation (GGA) in the form of Perdew-Burke-Ernzerhof (PBE) functional⁶⁴. The electron-ion interaction was approximated by Projector-Augmented-Wave (PAW) pseudopotentials⁶⁵. The wave function of valent electrons was expanded in plane wave basis set with an energy cutoff of 400 eV. According to the VASP manual, the convergence of VASP simulation requires the cutoff energy to exceed 1.3 times the maximum ENMAX⁶⁶. For the Cantor alloy, the maximum ENMAX is 270 eV. The cutoff energy of 400 eV in this study is higher than 1.3 times the maximum ENMAX and is large enough to ensure an accurate calculation. The energy convergence criterion of the electronic self-consistency was set to 10⁻⁶ eV per atom. Newton’s equation of motion was solved through Verlet’s algorithm with a time step of 3 fs. The spin polarization was utilized in the simulation since the elements of Cr, Co, Fe, Ni, and Mn have unpaired electrons in their valent shells.

The simulated CrCoFeNiMn alloy is composed of 20 Cr, 20 Co, 20 Fe, 20 Ni, and 20 Mn with a molar percentage of 20% for each element, as shown in Supplementary Fig. 4a. Only Γ point was considered to sample the supercell Brillouin zone. All dynamical simulations were performed in the NVT ensemble by means of a Nosé-Hoover thermostat to control temperature⁶⁷. The equation of motion was solved through Verlet’s algorithm with a time step of 3 fs. To avoid the memory effect from the initial random structure, the initial configurations were heated to 3000 K, and then step-wise cooled down to 2700, 2400, 2100, 1800, 1500, 1200, 900, 600, and 300 K. After quenching down to the desired temperature, the equilibrium volume of supercells was obtained by adjusting the internal pressure close to 0⁶⁸. At each target temperature, the equilibrium volume was used as input configuration in the following 10000 steps of NVT ensemble simulation.

DP training and testing

For the training of DPs of Cantor alloy, the DeepMD-kit package⁶⁹ was selected. The DeepMD-kit provides a machine learning-based approach for training and evaluating atomic energies and forces using neural networks. The theory of DPMD is detailed in the previous literatures^30,35. During the training of DPs, the embedding network and fitting network employed have sizes of {25, 50, 100} and {240, 240, 240}, respectively. The radial cutoff (r_c) was set to 7.0 Å, which allows for capturing atoms within the first coordination shell of atom i. Additionally, a smooth cutoff parameter of 2.5 Å was utilized. As regards the prefactors of the energy, force and virial terms in the loss function, which were changed from 0.002 to 1 and 1000 to 1, respectively.

DPMD simulations

Once the testing stage is complete, the trained DPs are seamlessly integrated into the large-scale atomic/molecular massively parallel simulator (LAMMPS)⁷⁰ through the interface provided by DeePMD-kit. This enables the utilization of the DPs within the LAMMPS framework for further simulations and analysis. The periodic boundary condition was employed in all DPMD simulations to address boundary effects. Newton’s equations of motion were numerically solved using the Verlet algorithm with a time step of 1 fs. The size of supercell for DPMD simulations, as depicted in Supplementary Fig. 4b–f, was tested by expanding the equilibrium configuration from the AIMD simulation by a factor of 2 × 2 × 2, 3 × 3 × 3, 4 × 4 × 4, 5 × 5 × 5, and 6 × 6 × 6, under five super-cooling rates R: 1 K/ps, 5 K/ps, 10 K/ps, 50 K/ps, and 100 Kps. The temperature-dependent internal energy of Cantor alloy is shown in Supplementary Fig. 5a–f. It was found that convergence was achieved until the 5 × 5 × 5 supercell. Therefore, a supercell with the size of 5 × 5 × 5 × 100 atoms was ultimately selected for the simulation. At the temperature of 3000 K, this supercell undergoes a 500 ps simulation under the NPT ensemble, followed by a 500 ps simulation under the NVT ensemble with a Nosé-Hoover thermostat to achieve temperature equilibrium. The balanced structure was cooled to 300 K with 18 cooling rates R: 0.1 K/ps, 1 K/ps, 2 K/ps, 3 K/ps, 4 K/ps, 5 K/ps, 10 K/ps, 15 K/ps, 18 K/ps, 20 K/ps, 30 K/ps, 40 K/ps, 50 K/ps, 60 K/ps, 70 K/ps, 80 K/ps, 90 K/ps, and 100 K/ps.

To systematically investigate the structural changes during the cooling process, four cooling rates of 0.1 K/ps, 1 K/ps, and 10 K/ps and 100 K/ps were chosen. The equilibrium structure at 3000 K was gradually cooled down to the temperature of 300 K with these four chosen cooling rates. For each target temperature, the system was optimized using the same method employed at 3000 K. Subsequently, the last 300 ps of the NVT simulation was utilized for analyzing the structural characteristics. To evaluate the mechanical properties, the elastic constants were calculated based on the final structure obtained from the NVT ensemble simulation at 300 K, considering 18 different cooling rates.

The validation of the developed DP model in this study was achieved by the comparisons of melting point and diffusivity with the results reported in previous literature. The melting point was obtained by two methods, single-phase and two-phase method⁷¹, as shown in Supplementary Fig. 1c. For the single-phase method, the temperature-dependent internal energy of Cantor alloy under the super-cooling rates of 0.1 K/ps in Supplementary Fig. 1a shows the melting point (the temperature at which the density changes sharply) of crystalline Cantor alloy is about 1500 K. For the two-phase method, the melting point versus simulation time is depicted in Supplementary Fig. 1b, where the melting point reaches equilibrium after 10 ps. The averaged melting point is about 1500 K when it reaches equilibrium. The melting points obtained by the two methods were almost the same, which is also close to the experimental value of 1543 K reported by Owen et al.⁷². In addition, the diffusivity of each element in Cantor alloy was also calculated (see Supplementary Table 8) and a very good agreement was observed with the values reported by Ding et al.³¹ and Hou et al.⁷³.