Introduction

Emerging as a powerful technology of the data-driven paradigm in materials science, machine learning (ML) has considerably accelerated the design and discovery of promising materials in recent years1,2,3,4, including ML interatomic potentials5, inverse design of materials6, efficient property predictions7,8,9. Simultaneously, the advancements in high-performance computing greatly facilitate the establishment of diverse material-related databases utilizing density functional theory (DFT)-based high-throughput calculations (HTC), such as the Materials Project (MP)10, Open Quantum Materials Database (OQMD)11,12, Automatic-FLOW for materials discovery (AFLOW)13, Joint Automated Repository for Various Integrated Simulations (JARVIS)14, etc. These continuously expanding databases also lay a solid foundation for the application of cutting-edge ML technology in the field of materials science.

As the two main categories of ML, namely supervised and unsupervised learning strategies, both have achieved remarkable success in different ways. On the one hand, supervised learning enables the efficient predictions of material properties by-passing solving the complex equations of quantum mechanics based on expensive DFT calculations, which emphasizes the requirement of large human-labeled datasets for model training to ensure accuracy. Ridge regression15, decision tree16, support vector machine17, random forest18, gradient boosting decision tree19, etc., are widely employed in designing and screening potential materials with desired properties, which also elucidate the close relationships between the structure and target property20. On the other hand, as a technology operates without the necessity of well-labeled training data, unsupervised learning possesses the capability to infer the underlying patterns among varieties of materials within a feature space. Predominantly employed methods in unsupervised learning encompass clustering, dimensionality reduction, and anomaly detection, in which clustering can categorize different materials into the corresponding clusters by assessing their similarities between each other, thereby identifying candidates resembling the anticipated data points21,22,23. In this context, combining HTC and ML technologies can not only efficiently explore novel materials in the vast chemical space but also gain insights into the structure-property relationships at a quantitative level. However, a significant challenge lies in labeling data for materials with intrinsically complex properties in the vast chemical space, especially the lattice thermal conductivity (κL), due to the complexities involved in experimental measurements and the unbearable computational costs associated with accurate DFT calculations. Is there an effective approach to reduce the cost of labeling, while enabling the efficient prediction of complex properties and elucidation of structure-property relationships?

Functional materials exhibiting ultralow κL possess vital significance across various fields, such as power generation24, heat conduction25, thermal barrier coatings26 and so on27,28,29, which greatly advance the development of industry. Particularly, owing to the key role in directly converting heat energy into electricity based on the thermoelectric (TE) effect, TE materials have become the focal point of considerable interest in academic and industrial research. Indeed, the conversion efficiency of a TE material is theoretically quantified by its figure of merit zT: zT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the absolute temperature, respectively. Moreover, κ can be expressed in two parts: κ = κe + κL, where κe and κL are the electronic thermal conductivity and lattice thermal conductivity, respectively, indicating that they all contribute to heat conduction. For metallic materials, κe plays a dominant role in heat conduction due to the presence of a large number of free electrons. On the contrary, in semiconductors or insulators, thermal energy is predominantly transferred through lattice vibrations, with κL making the primary contribution. In this process, the quanta of such lattice vibrations in a solid are the so-called phonons.

As clearly noticed, toward the goal of seeking TE materials with optimal zT values, it requires not only maximizing the power factor (S2σ) but also minimizing the thermal conductivity (κe + κL) simultaneously30. Notably, the distinct and separate scale of the mean free paths for electrons and phonons contributes to the independence of κL as a parameter in zT, which makes decreasing κL become a significant avenue to realize the ideal concept of “phonon-glass and electron-crystal”31,32, ultimately leading to excellent TE performance. For the past decades, unremitting efforts have been made to discover a series of materials with κL, for instance, Tl3VSe433, TlInTe234, InTe35, CsAg5Te336, AgSbSe237, etc. However, the conversion efficiency of TE materials has persistently been a significant challenge in the efficient recovery of waste heat, that is to say, useful materials featuring ultralow κL are still in urgent demand. Despite the few successes of traditional trial-and-error experiments and case-by-case DFT calculations in the exploration of desired materials, efficient and robust material design oriented towards κL in the vast chemical space is hindered by the complex structure–property relationships and size-limited resources.

In the present work, we propose a novel hierarchy-boosted funnel learning (HiBoFL) framework that integrates unsupervised learning and supervised learning to efficiently achieve the predictions of costly-labeled complex properties, which is successfully applied to identify semiconductors with ultralow κL. Unsupervised learning is used to uncover underlying patterns among different materials, facilitating the identification of problem-specific clusters with a high likelihood of exhibiting ultralow κL. Based the low-cost HTC on this significantly reduced space of specific clusters, we establish a local database and discover a series of semiconductors with ultralow κL, in which Cs2SnSe3 and Cs2GeSe3 are screened out for in-depth mechanism analysis. Furthermore, a supervised classification model for directly predicting ultralow κL is trained to refine the coarse result of unsupervised learning. With resolved important descriptors that govern ultralow κL, we are capable of investigating the κL modulation mechanisms and uncovering a new factor that governs structural anharmonicity. We expect that this HiBoFL framework can also be widely applied in the discovery of other functional materials with excellent performances.

Results

HiBoFL framework for accelerating the discovery of functional materials

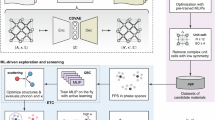
Our proposed novel HiBoFL framework for accelerating the discovery of functional materials with complex properties is shown in Fig. 1a, which exhibits a funnel-like structure driven by a hierarchical framework, effectively narrowing the search space while boosting model performances. This framework mainly includes four parts: (I) Data preparation. An initial theoretical or experimental dataset of the target material system is required, potentially involving preliminary high-throughput screening, data cleaning, and other preprocessing operations. (II) Unsupervised learning. Relevant features are extracted from the initial dataset, encompassing aspects such as experimental process parameters, intrinsic material attributes, etc. By employing clustering algorithms, distinct classes of data points with potentially similar properties can be identified, in which problem-specific clusters are selected to narrow the search space. (III) Data annotation. Data from the problem-specific clusters can be assigned corresponding property labels through further relatively low-cost experimental characterizations or HTC. This facilitates the establishment of a local database, enabling the extraction of prior domain knowledge through statistical data analysis. (IV) Supervised learning. The labeled dataset within the established local database can be used to further train supervised learning models, which helps refine the coarse result from unsupervised learning, ultimately enabling direct and rapid predictions of the target properties. Such a HiBoFL framework can not only reduce the expensive cost of labeling data for training supervised models, but also efficiently predict the complex properties.

Fig. 1: Hierarchy-boosted funnel learning (HiBoFL) framework for accelerating the discovery of functional materials.
figure 1

a Schematic of the HiBoFL framework, including data preparation, unsupervised learning, data annotation and supervised learning. b Workflow of applying the HiBoFL framework to efficiently identify semiconductors with ultralow κL.

Full size image

We then apply this HiBoFL framework to efficiently identify semiconductors with ultralow κL as shown in Fig. 1b. In the first step, we obtain the material dataset from the MP database based on its application programming interface (API) and then apply a series of screening criteria to derive the first-level dataset for subsequent research. In the second step, chemical composition descriptors based on Magpie38 and crystal structure descriptors derived from Voronoi tessellations39 are used to featurize the materials in the first-level dataset. We use principal component analysis (PCA)40, for dimensionality reduction thereby obtaining pivotal components. K-means clustering41,42 is then employed to identify materials with similar κL, which is visualized in a low-dimensional space using t-distributed stochastic neighbor embedding (t-SNE)43, and problem-specific clusters are selected based on similarity design rules to form the second-level dataset. In the third step, we use the phonon-elasticity-thermal (PET) model44 to perform low-cost HTC on the materials in the second-level dataset, establishing a local database based on the HTC results. On the one hand, a list of candidates for potential TE applications can be recommended and their statistical analysis can help us to summarize several domain knowledge of ultralow κL. On the other hand, we can directly screen out candidate materials with ultralow κL for in-depth mechanism analysis, where the results are verified by accurately solving the phonon Boltzmann transport equation (BTE) and the phonon thermal transport mechanisms are further revealed. In the fourth step, we perform ensemble learning on the labeled local database for directly classifying ultralow κL, training a robust CatBoost classifier45. The interpretable analysis of the pre-trained model based on the SHapley Additive exPlanations (SHAP) method46,47,48 further reveals the influence of important descriptors on ultralow κL. A new factor capable of significantly reducing κL via enhancing structural anharmonicity is discovered, eventually building a bridge between the ML model interpretability and first-principles analysis.

Preliminary high-throughput screening

The process of preliminary high-throughput screening to select materials for subsequent ML investigations is illustrated in Fig. 2a. Initially, we start by acquiring all the materials from the MP database based on its API, resulting in a total of 1,54,718 entries saved in a JSON file as the Python dictionary object. Of these, several specific criteria are set to narrow down the range of exploration. The first screening criterion focuses on the assessment of thermodynamic stability, in which the materials with energy above the convex hull (Ehull, the formation energy difference between the target compound and its competing phases) no more than 0.05 eV/atom are considered to show a high likelihood of being synthesized in experiments. Further, the band gap (Eg) can be directly retrieved from the MP database, set within the range of 0.1–2 eV for assessing electrical conductivity. This specific interval is highly characteristic of semiconductors, demonstrating the inherent capacity of these screened materials for favorable electrical conductivity. Additionally, taking into account of the computational cost associated with κL, our constraints on the material system involve ensuring that the number of atoms (Natoms) is less than 20 in the unit cell of a crystal structure and the number of elements (Nelements) is below four in one compound, respectively. Ultimately, through excluding the materials containing hydrogen, lanthanides, and actinides, and conducting structural analysis, we further obtain 2675 three-dimensional (3D) crystal structures without calculation errors. These materials constitute the first-level dataset for our in-depth investigations.

Fig. 2: Dataset preparation and unsupervised learning optimization.
figure 2

a Flowchart of preliminary high-throughput screening from the Materials Project database. b Optimization of the number of clusters k for the k-means algorithm based on the elbow method and silhouette coefficient (inset).

Full size image

Unsupervised learning for identifying materials with similar κ L

We next carry out unsupervised learning to identify materials with a high likelihood of exhibiting relatively low κL based on similarity design rules. Following the generation of the first-level dataset as input, the materials should be transformed into the length-fixed vectors as the so-called descriptors, which are the key point to distinguish different materials. Herein, we use two distinct types of descriptors to featurize these materials, namely, composition-based features and structure-based features, to account for the mapping relationships between different categories of descriptors and κL from the perspectives of chemical composition and crystal structure. Among them, composition-based features are generated based on Magpie data and denoted by {E}, including electronegativity, atomic number, fraction of electrons, etc., which are comprehensive enough to capture the characteristics of chemical compositions with different constituent elements and proportions. Through partitioning the crystal structures into Wigner-Seitz cells of each atom, a series of structure-based features can be derived from Voronoi tessellations based on the characteristics of the local environment of each atom in the unit cell, which are denoted by {S}. In this manner, each material can generate a total of 273 descriptors automatically without any time-consuming DFT calculations based on its corresponding composition and structure, jointly denoted by {E, S}. Notably, these descriptors have been successfully applied to the ML predictions of κL at various temperatures49, indicating their significant potential for mapping the property of κL. After feature generation, it is crucial to preprocess all the data thereby enhancing the performances of clustering model. To address the large variations among different feature values and transform them to follow a normal distribution, both standardization and quantile transformer are employed for preprocessing these descriptors. Further, we perform PCA based on singular value decomposition to project the preprocessed features to a lower dimensional space. PCA linearly combines original features into principal components (PCs), ensuring the hierarchical order based on their contributions, in which the first PC captures the largest explainable variance, followed by the second one and so forth. From the curve of total explainable variance changing with the number of PCs as shown in Figure S1, we can conclude that 83 PCs suffice to account for 99% of the variance among all 2675 materials in the first-level dataset. Hence, these 83 PCs are extracted as the pivotal components for input into the following clustering algorithm.

Subsequently, the k-means algorithm is utilized to identify the underlying associations with κL from these unlabeled materials, in which only one critical parameter is required to be pre-defined, i.e., the number of clusters k50. Based on the analysis of the elbow method51 and the silhouette coefficient52 as depicted in Fig. 2b, the elbow-like point of inflection on the curve emerges at a value of k = 7, indicating the location where inertia or distortion starts decreasing significantly at a very slow rate, represents the optimal k value for the k-means clustering. At this stage, a relatively high silhouette coefficient also illustrates that each material exhibits strong similarity within its respective cluster, while different clusters are well-separated as much as possible. As a result, we partition the first-level dataset into seven clusters (from C1, C2, …, to C7), on the basis of similarities of these feature vectors derived from chemical compositions and crystal structures, in which the materials in the same cluster are considered to show a high likelihood of possessing similar κL. Since the first two PCs only capture about 35% of the variance within entire data, it is insufficient for the clustering result to be intuitively visualized in a two-dimensional (2D) mapping. Unlike PCA, which emphasizes preserving large pairwise distances to maximize variance, t-SNE is a powerful non-linear dimensionality reduction technology for the visualization of high-dimensional data, aiming to maintain pairwise similarities among data points in a lower-dimensional space. We strictly use t-SNE only for the visualization of the resulting seven clusters of k-means algorithm as shown in Fig. 3, projecting the 83 PCs into a 2D latent space comprised of two t-SNE components. The result intuitively demonstrates the high-quality clustering with distinct separation between each cluster, where each point represents a material and its color relates to the corresponding category of cluster.

Fig. 3: Unsupervised learning result in the first-level dataset.
figure 3

Using t-SNE visualization for the seven clusters generated by the k-means algorithm, where each point represents a compound and is colored with the corresponding cluster. Eight represented materials in C1 and C2 with low experiment-measured κL are marked in the enlarged region.

Full size image

Since we have obtained seven clusters through k-means clustering, it is necessary to conduct the similarity analysis of these clusters. Materials within the same cluster are considered to show similar structures thereby likely sharing similar properties, which facilitates a deep comprehension of underlying patterns and relationships among the 2675 materials. To evaluate the similarity criteria of these materials, the reported κL values at 300 K for several known materials included in each cluster are collected from the previous studies (most are experimentally measured), which are all listed in Table S1 along with some other basic information. As we expected, materials within the same cluster exhibit closely similar κL values, while there is a comparatively significant difference in κL among materials from different clusters. Particularly, the known materials with relatively low κL are clustered into C1 and C2 through k-means clustering, including eight structures of Tl3AsSe3 (0.23 W/mK)53, Tl2Te3 (0.40 W/mK)54, Tl3SbS3 (0.42 W/mK)55, TlBiS2 (0.80 W/mK)56, CuBr (1.30 W/mK)57, Cu2GeS3 (1.20 W/mK)54, RbSbS2 (1.60 W/mK)55 and AgGaS2 (1.50 W/mK)58, which are all clearly shown in the enlarged part of Fig. 3. On the contrary, C7 contains materials with apparently large κL, including four structures of GaN (130 W/mK)59, BP (350 W/mK)60,61, SiC (490 W/mK)62, and Si (156 W/mK)63. Thus, as confirmed by the good distinction between low and high κL among each cluster, our proposed unsupervised learning model demonstrates great potential to identify compositional and structural information about the κL of these materials, leading to the successful clustering into different categories according to this property. Since the materials with a high likelihood of possessing relatively low κL tend to group into the two clusters of C1 and C2, the exploration scope for finding materials with low κL is reduced from 2675 materials to 704 materials, narrowing by approximately three-quarters. As a result, these two problem-specific clusters (C1 and C2) further constitute our second-level dataset.

HTC of problem-specific clusters for statistical analysis and material discovery

Given the success of unsupervised learning in significantly reducing the broad material search space, it has become feasible to further extend the second-level dataset into a labeled repository of thermal conductivity through HTC at affordable computational costs. Based on the PET empirical equation within the high-throughput framework, we derive the κPET values at 300 K ignoring the anisotropy for materials in the second-level dataset, while excluding structures that do not satisfy the mechanical stability criteria. The basic information and corresponding κPET values of the resulting 661 materials are then stored in a local database using MongoDB64, serving as a valuable repository to retrieve data and prioritize detailed theoretical and experimental investigations. Of particular note is that nearly 70% of these semiconductors exhibit the κPET values no greater than 2 W/mK (left panel in Fig. 4a), with a considerable portion of these materials remaining unreported to date. These materials also constitute a list of candidate materials with potential applications in the TE field (Table S2), which undoubtedly prove that the problem-specific clusters we identified through unsupervised learning indeed contain a significant number of materials with low thermal conductivity.

Fig. 4: HTC-based data annotation for statistical analysis and material discovery in the second-level dataset.
figure 4

a Pie chart of κPET separated by a threshold of 2 W/mK and distribution of different formula types with counts exceeding 20. b Heat map over the periodic table of elements for the visualization of element counts for materials with κPET ≤ 2 W/mK. c Box plot of different crystal systems for materials with κPET ≤ 2 W/mK. d Density scatter plot of shear modulus and bulk modulus for materials with κPET ≤ 2 W/mK. e Calculated κL as the function of temperature at different axes in Cs2SnSe3 and Cs2GeSe3 by solving the phonon BTE.

Full size image

In addition, we also count the distribution of different formula types with counts exceeding 20 in these materials with κPET ≤ 2 W/mK (right panel in Fig. 4a). Apparently, the structures represented by the two types of formula anonymous dominate in quantity, namely the ABC2 type characterized by the diamond-like structure, and the ABC3 type represented by the perovskite-type structure. To gain a more intuitive insight into the distribution patterns of materials with low thermal conductivity, we plot a heat map over the periodic table of elements in Fig. 4b, illustrating the count of elements present in these compounds with κPET no greater than 2 W/mK. Sulfur, selenium, tellurium, and oxygen belonging to the chalcogens consecutively occupy the largest counts among the anion elements, in which sulfur is the most abundant with a count of 102. As for the cation elements, silver, cesium, potassium, copper, and rubidium occupy the highest abundance, respectively. This can be explained by the fact that materials composed of heavy elements or characterized by weak chemical bonding typically exhibit lower κL. Notably, a few previous studies have constrained the search space of materials within the above-mentioned characteristics to investigate those with low thermal conductivity, such as high-throughput screening in chalcogenide ABC3 perovskites65 or diamond-like ABC2 compounds66, detailed analysis in the IV-VI chalcogenides67 and so forth37,68,69,70. The box plot of different crystal systems indicates that the κPET values of materials in each crystal system primarily cluster around 0.5 W/mK, with the monoclinic system exhibiting the largest quantity (Fig. 4c). We also show the density distributions of the shear modulus and bulk modulus obtained by the Voigt–Reuss–Hill (VRH) method as shown in Fig. 4d, which are primarily concentrated within the relatively small range of ~50 GPa. This suggests that materials with lower shear and bulk moduli might be more likely to exhibit lower thermal conductivity. These statistical analyses provide deep insights into the regulation of κL, which can offer prior domain knowledge for researchers in selecting specific systems to obtain ultralow κL.

To further validate the results and conduct in-depth analysis of the phonon thermal transport mechanisms, we calculate more precise κL values according to first-principles derived force constants and Boltzmann transport theory for the unreported materials Cs2SnSe3 and Cs2GeSe3, which are screened out based on the formula type ranking among the materials with the lowest κPET values. Figure 4e depicts the calculated κL as the function of temperature ranging from 100 to 500 K at different axes in the discussed two semiconductors, in which all the intrinsic κL values show obvious anisotropy and gradually decrease following the T-1 manner with the temperature increasing just as the hallmark of Umklapp scattering. The rise in temperature results in an elevation in the equilibrium phonon population, consequently leading to intense phonon-phonon collisions, as delineated by \(\overline{n}\approx {k}_{{\rm{B}}}T/\hslash \omega (T\gg {\Theta }_{{\rm{D}}})\), where \(\overline{n}\) is the average number of phonons, kB is the Boltzmann constant, T is the temperature, ω is the phonon frequency, ℏ is the reduced Planck constant, and ΘD is the Debye temperature. Moreover, these materials all exhibit intrinsically ultralow κL, with values all below 0.25 W/mK in any direction at 300 K, significantly lower than the κL (~2.3 W/mK) of the traditional TE material PbTe71. The results indicate the potential application of Cs2SnSe3 and Cs2GeSe3 in the TE field, further substantiating the effectiveness of our previously adopted approach–combining unsupervised learning with HTC to discover semiconductors with ultralow κL.

Mechanisms of phonon thermal transport properties

Generally speaking, compounds with heavier atoms tend to exhibit lower group velocities due to the reduced phonon frequency. As a result, a lower κL of Cs2SnSe3 was expected given the relatively heavy nature of Sn. However, it is noteworthy that the κL of Cs2SnSe3 is obviously higher than that of Cs2GeSe3 (i.e., ~3 times in the a-axis, ~1.7 times in the b-axis, ~2 times in the c-axis at 300 K), which presents an interesting unusual phenomenon. Next, we would like to discuss the microscopic mechanisms responsible for the ultralow κL and unusual difference observed among the two materials.

Cs2SnSe3 and Cs2GeSe3 both crystallize in the same space group C2/m (No. 12) of the monoclinic crystal system, with the fully optimized crystallographic parameters listed in Table S3. Their crystal structures are shown in Fig. 5a, b. Sn/Ge atoms are coordinated by four Se atoms in a tetrahedral geometry [SnSe4]/[GeSe4] at distances in 2.504–2.643 Å/2.336–2.477 Å, and these tetrahedra further share a common edge to form dimeric [Sn2Se6]/[Ge2Se6] building units, respectively, which form the four-membered [Sn2Se2]/[Ge2Se2] rings and are charge compensated by Cs cations. The phase diagrams for Cs–Sn–Se and Cs–Ge–Se systems based on the calculated energies in the MP database show that Cs2SnSe3 and Cs2GeSe3 possess similar thermodynamical stability with equal (zero) convex hull distances (Fig. S2). Simultaneously, the phonon dispersion curves along high-symmetry directions in Brillouin zone indicate that they are dynamically stable due to the absence of imaginary phonon modes (left panels in Fig. 5c, d). Thus, the results demonstrate the feasibility of experimentally synthesizing these two materials. To identify the bonding characteristics in Cs2SnSe3 and Cs2GeSe3, we employ the electron localization function (ELF) to quantify the extent of spatial localization of the reference electron with values ranging from 0 to 1 (Fig. 5a, b). The localization of electrons in the Sn/Ge–Se bonding region illustrates the covalent nature of the Sn/Ge–Se bonds, in which a polar covalent bond between Sn and Se (ELF ≈0.5) is observed due to the smaller electronegativity and larger atomic radius of Sn, leading to a significant difference among the two compounds. On the contrary, there is no overlapping of charge clouds between Cs atoms and other atoms, indicating the presence of strong ionic bonding which aligns with the fact that a relatively large electronegativity (on the pauling scale) difference (1.76) between Cs (0.79) and Se (2.55) results in strong ionic characteristics. Therefore, Cs2SnSe3 and Cs2GeSe3 both contain multiple types of bonds, i.e., ionic Cs–Se and covalent Sn/Ge–Se, resulting in complex crystal structures with bonding hierarchy. These complex structures, comprising heavy atoms, weakly bound and rigid distorted units with a significant bonding hierarchy, are anticipated to exhibit large lattice anharmonicity72.

Fig. 5: Mechanisms of phonon thermal transport properties based on first-principles calculations.
figure 5

Crystal structures and the projected 2D ELF diagrams of a Cs2SnSe3 and b Cs2GeSe3. Phonon dispersion (left panels), atom-projected PDOS (middle panels) and spectral κL(ω) (right panels) of c Cs2SnSe3 and d Cs2GeSe3. e Group velocity along the b-axis and f phonon lifetime as a function of frequency at 300 K for Cs2SnSe3 and Cs2GeSe3. g COHP and ICOHP projected on Sn-Se bonds in Cs2SnSe3 and Ge–Se bonds in Cs2GeSe3.

Full size image

The phonon dispersion reveals that there are 3 acoustic branches and 33 optical branches at each phonon wave vector q due to the 12 atoms in the primitive cell of both Cs2SnSe3 and Cs2GeSe3, in which three acoustic branches are composed of one longitudinal acoustic mode (LA) and two transverse acoustic modes (TA and TA’). A striking common feature of their phonon dispersion is that a waterfall-like low-lying optical branch (LLO) exhibits the avoided crossing behavior with acoustic modes around the Brillouin zone center, resulting in strong acoustic-optical coupling as one of the potential signals of the rattling model73. These characteristics can not only lead to a softening of the acoustic modes thereby yielding low phonon group velocities, but also greatly enhance the scattering rates of heat-carrying acoustic phonons, all of which contribute to the suppression of κL for Cs2SnSe3 and Cs2GeSe3. Analysis of the atom-projected PDOS and spectral κL(ω) (middle and right panels in Fig. 5c, d) indicate that acoustic and LLO phonon modes in the low-frequency range (0–2 THz) are primarily dictated by Cs and Se vibrations followed by Sn/Ge vibrations, which also make predominant contributions to the ultralow κL. A localized region mostly contributed by Cs atoms within a narrow energy window centered around 1 THz is observed in both compounds, indicating the anharmonic rattling-like motion of the weakly bonded Cs atoms, which is responsible for the presence of the soft LLO modes. This can also be confirmed in the potential energy curves obtained by shifting the atoms with respect to their static equilibrium positions along different axes as depicted in Fig. S3. Sn/Ge and Se atoms are both confined within the comparatively steep potential wells, whereas Cs atoms with heavier mass can vibrate easily with larger amplitude due to the shallowest potential energy surface in all the directions. These atoms exhibit nearly identical displacement magnitudes in their respective compounds. Therefore, the loosely bound Cs atoms are surrounded by [Sn2Se6]/[Ge2Se6] units thereby exhibiting the same rattling-like effect, which can result in a common strong anharmonicity in both compounds74,75.

Figures 5e and S4 show the frequency dependence of the group velocity υ from all the q points in different axes at 300 K for Cs2SnSe3 and Cs2GeSe3, as given by υλ = ∂ωλ/∂q. Most of the phonon modes possess ultralow υ values less than 2 km/s, confirming the lattice softening induced by the weak interatomic bonding, which is also consistent with the flat phonon bands observed in the phonon dispersion. Figure 5f depicts the overall short τ values mainly ranging from 0.2 to 20 ps, with low-frequency phonons exhibiting a gradual shortening trend in both compounds. This can be attributed to the presence of LLO modes, which facilitate more scattering paths and impede the heat flow, significantly enhancing the scattering rates thereby reducing τ for both acoustic and LLO modes, ultimately reducing κL. It is noteworthy that in the low-frequency phonon region, particularly within the acoustic phonon range, the phonon group velocities of these two compounds show little difference, yet the phonon lifetime of Cs2SnSe3 is significantly longer than that of Cs2GeSe3. Therefore, we conclude that the relatively lower anomalous κL of Cs2GeSe3 is attributed to its shorter phonon lifetime.

We speculate that the difference in the phonon lifetime between Cs2SnSe3 and Cs2GeSe3 might be related to the strength of Sn–Se and Ge–Se covalent bonding. This covalent bonding may induce anisotropic motion, involving the collective movement of Sn/Ge and Se atoms, thereby leading to a strong lattice anharmonicity within the system76. To investigate this effect on the phonon lifetime, we perform crystal orbital Hamilton population (COHP) calculations77 to analyze the energy-resolved local bonding information of Cs2SnSe3 and Cs2GeSe3. Figure 5g shows that anti-bonding states persist down to −3 eV below the Fermi level (EF) in Sn–Se bonding, which can weaken the corresponding bonding strength thereby forming a polar covalent bond as observed in ELF. This can be demonstrated by the integral of COHP (\({\rm{ICOHP}}=\mathop{\int}\nolimits_{-\infty }^{E}{\rm{COHP}}(E){\rm{d}}E\)) at the EF, which represents all occupied orbitals, serving as an indicator of bond strength. Since the average ICOHP values for Sn–Se and Ge–Se bonds are −0.72 eV and −4.49 eV, respectively, indicating the obviously weaker Sn–Se bonding in Cs2SnSe3. The stronger bonding strength of Ge–Se is also evident from its larger force constant \(\left\vert {\Phi }_{ij}\right\vert\) in comparison to that of Sn–Se (Fig. S5). Hence, the shorter phonon lifetime of Cs2GeSe3 relative to Cs2SnSe3 may be attributed to their significant difference in Ge–Se and Sn–Se covalent bonding, which can be further quantified at the structural descriptor level through subsequent interpretable ML approaches.

Interpretable supervised learning for predicting ultralow κ L

After labeling the materials in the second-level dataset based on our HTC framework to obtain the local database, we develop interpretable supervised classification models to predict ultralow κL for efficiently by-passing the complex ab initio calculations, which can further refine the coarse result of unsupervised learning and provide greater robustness. Here, materials with κPET not exceeding 2 W/mK are labeled as 1, which are considered to possess ultralow κL; otherwise, they are labeled as 0, signifying non-ultralow κL.

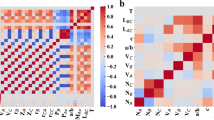
Beyond the input dataset itself, identifying the most relevant features and appropriate algorithms can significantly enhance the generalization and accuracy of ML models, which are also quite strongly intertwined. The chemical compositions and crystal structures of these compounds are also featurized into 273 descriptors based on the aforementioned Magpie data and Voronoi tessellations. As for the ML models, we compare eight widely-used classification algorithms for predicting material properties according to the indicators of area under the receiver operating characteristic curve (ROC AUC) and accuracy based on stratified tenfold cross-validation (Fig. S6): decision tree (DT)78, extra trees (ET)79, random forest (RF)80, gradient boosting classifier (GBC)81, adaptive boosting (AdaBoost)82, eXtreme Gradient Boosting (XGBoost)83, Light Gradient Boosting Machine (LightGBM)84, Categorical Boosting (CatBoost)45. Most algorithms demonstrate good performances, with the CatBoost algorithm achieving the best results, which is chosen to build the follow-up classification model. To avoid the curse of dimensionality, we perform feature selection using the model-based wrapper method and Pearson correlation method. Descriptors are iteratively removed based on the feature importance scores obtained from the CatBoost algorithm, and an ML model is subsequently trained using the remaining descriptors at each step. This process yields the curve depicting the model performance as a function of the number of features (Fig. S7), indicating that optimal performance is achieved when utilizing the top 11 features. To reduce the correlation between features, the Pearson correlation coefficients (p) of these 11 features are calculated, which are defined as: \(p={\rm{cov}}({x}_{i},{x}_{j})/{\sigma }_{{x}_{i}}{\sigma }_{{x}_{j}}\), where cov(xi, xj) is the covariance of features xi and \({x}_{j},{\sigma }_{{x}_{i/j}}\) is the standard deviation of the feature xi/j. For pairs of features with \(\left\vert p\right\vert \,>\,\) 0.8, we retain the one with the higher feature importance score. Figure 6a displays the heatmap of the Pearson correlation coefficient matrix among the selected nine features and illustrates the specific meanings of these features based on elemental attributes and Wigner–Seitz cells, indicating that we have successfully eliminated redundant descriptors. We adjust the hyperparameters of the ML model based on Bayesian optimization over 200 random trials, obtaining the best hyperparameters as listed in Table S4. As a result, the performances of the optimal CatBoost classification model are characterized by the ROC curve and the confusion matrix (Fig. 6b), showing its great ability in classifying semiconductors with ultralow κL due to the high ROC AUC (0.94), accuracy (0.90), precision (0.89), recall (0.90) and F1-score (0.89).

Fig. 6: Supervised learning in the local database and interpretable analysis.
figure 6

a Heat map of the Pearson correlation coefficient matrix among the selected descriptors and their definitions, which are classified into elemental and structural features. b ROC curve and confusion matrix of the optimal CatBoost classification model for predicting ultralow/non-ultralow κL. c Hierarchical clustering of the descriptors based on their SHAP values. d Global interpretability into κL classification using SHAP, including the feature importance and the impact of different features on ultralow κL. e Using t-SNE visualization for the overall contributions of all descriptors of each material to the model output based on their SHAP values. f Local interpretability into κL classification using SHAP, including the force plots of Cs2GeSe3 and Cs2SnSe3. g Discovered special descriptor \({L}^{\min }\) and its trend in influencing the phonon lifetime of Cs2GeSe3 and Cs2SnSe3.

Full size image

To establish the bridge between material descriptors and thermal transport mechanisms thereby demystifying the black-box nature of ML, we perform interpretable analysis for the pre-trained κL classification model based on the SHAP method46,47. Figure 6c shows the dendrogram of the optimal nine descriptors via using the hierarchical clustering based on their SHAP values, where a partition line classifies these features into three groups. Interestingly, beyond the minimum relative bond length \({L}^{\min }\), two classes of descriptors based on chemical compositions and crystal structures are identified as we expected. This indicates that \({L}^{\min }\) may possess a unique influence on ultralow κL.

The feature importance and the impact of different features on ultralow κL are shown in Fig. 6d, which make a global interpretation for the classification model. We here take the most important feature in the three classes as an example to detailedly explain the corresponding hierarchical influence on κL combining the SHAP values. For the most important feature \({W}_{{\rm{A}}}^{\min }\), defined as:

$${W}_{{\rm{A}}}^{\min }=\min \left\{{W}_{{\rm{A}}}^{{\rm{1}}},\ldots ,{W}_{{\rm{A}}}^{i},\ldots ,{W}_{{\rm{A}}}^{n}\right\}$$
(1)

Where \({W}_{{\rm{A}}}^{i}\) is the atomic weight of element i and n is the number of elements, respectively. Semiconductors with larger \({W}_{{\rm{A}}}^{\min }\) values tend to exhibit low κL since the corresponding positive SHAP values, whereas those with smaller \({W}_{{\rm{A}}}^{\min }\) values show the opposite trend. This can be explained by the dispersion relation for the frequency, just as \(\omega =2\sqrt{\beta /M}\left\vert \sin qa/2\right\vert\) in a one-dimensional crystal lattice, where β, M, and a are the bond force constant, atomic mass, and the distance between two neighboring atoms, respectively. Large M (W) can reduce the frequency ω and thus the group velocity υ, resulting in a low κL. For the feature α, defined as:

$$\alpha =\frac{N{V}_{\max }}{V}\times 100$$
(2)

Where N is the number of atoms, \({V}_{\max }\) is the largest sphere volume occupied by one atom that can fit inside its Voronoi cell, V is the cell volume. It is obvious that low α tends to have a positive effect on ultralow κL since its positive SHAP values, which can be explained by its direct effect on the bond length. α helps in understanding how closely the atoms are bonded, with lower values often signifying larger void space with longer bond lengths in a crystal structure. Longer bond lengths typically result in softer lattices characterized by lower group velocity υ, thereby reducing κL. As for the special feature \({L}^{\min }\), defined as:

$${L}^{\min }=\frac{\min \{{L}_{i}\}}{{\rm{mean}}\{{L}_{i}\}}$$
(3)

Where Li is the weighted average bond length of atom i in a crystal structure, defined as:

$${L}_{i}=\frac{{\sum }_{n}{A}_{n}\cdot {\left\Vert \vec{{r}_{n}}-\vec{{r}_{i}}\right\Vert }_{2}}{{\sum }_{n}{A}_{n}}$$
(4)

Where \(\vec{{r}_{i}}\) is the position of atom i, \(\vec{{r}_{n}}\) and An is the position and the area of the nth neighbor of atom i, respectively. Li provides a comprehensive description of the interactions between each atom and its nearest neighboring atoms in the crystal structure, with the result influenced by two components: the distance term \({\left\Vert \vec{{r}_{n}}-\vec{{r}_{i}}\right\Vert }_{2}\) and the weighted term An. The distance term \({\left\Vert \vec{{r}_{n}}-\vec{{r}_{i}}\right\Vert }_{2}\) directly governs the bond length between the nearest neighboring atoms, with shorter distances implying stronger bonding, thus leading to a lower Li. The weighted term An assigns varying weights to different nearest neighboring atoms, where the bond lengths corresponding to the nearest neighboring atoms with greater weights show a higher effect on Li. Therefore, \(\min \{{L}_{i}\}\) captures the local information within the structure, which may correspond to covalent bonds due to their typical shorter bond lengths. In contrast, mean{Li} captures the global information of a structure, encompassing both short covalent bonds, long ionic bonds, etc. We propose that the ratio of these two terms, i.e., \({L}^{\min }\), might potentially reflect the anharmonicity of materials. Lower \({L}^{\min }\) values exhibit positive SHAP values, which favor the emergence of ultralow κL. This implies that when a structure features lower \(\min \{{L}_{i}\}\) and higher mean{Li}, it may possess rigidly distorted and weakly bound units with a significant bonding hierarchy, typically leading to stronger anharmonicity, as previously analyzed.

The overall contributions of all descriptors of each material to the model output based on their SHAP values are visualized by the t-SNE method (Fig. 6e), showing that ultralow κL (dark blue) and non-ultralow κL (light blue) are clearly clustered into the corresponding groups. Cs2GeSe3 and Cs2SnSe3 are then marked out together to reveal the local interpretability using the SHAP force plots (Fig. 6f), thereby exploring their previously discussed unusual difference of κL. Among the features that have the most significant impact on these two materials, \({L}^{\min }\) surprisingly reaches a level of importance in Cs2GeSe3 comparable to that of \({W}_{{\rm{A}}}^{\min }\). Although \({W}_{{\rm{A}}}^{\min }\) in Cs2GeSe3 is lower than in Cs2SnSe3, the crucial role of \({L}^{\min }\) in anharmonicity drives the predicted κL of Cs2GeSe3 to be much lower. Given the significant difference in phonon lifetime τ between these two materials, as indicated by previous phonon thermal transport analysis, we speculate that \({L}^{\min }\) might have a great influence on τ, which can be supported by two perspectives. On the one hand, the trend between \({L}^{\min }\) and τ in Cs2GeSe3 and Cs2SnSe3 indicates that the former not only exhibits a lower \({L}^{\min }\) but also has a significantly shorter τ (Fig. 6g). This aligns with the impact of \({L}^{\min }\) on anharmonicity revealed by the SHAP analysis. On the other hand, Table S5 indicates that the \(\min \{{L}_{i}\}\) values in Cs2GeSe3 and Cs2SnSe3 correspond to the L values derived from the Voronoi polyhedra centered on Ge and Sn, respectively. Although Cs2GeSe3 has a lower mean{Li} compared to Cs2SnSe3, its much lower \(\min \{{L}_{i}\}\) (i.e., LGe) eventually results in a much lower \({L}^{\min }\). This is consistent with the results based on first-principles analysis, which attributes the difference in phonon lifetime to the stronger bonding strength (shorter bond length) of Ge–Se covalent bonding compared to that of Sn–Se covalent bonding.

Discussion

We propose a novel HiBoFL framework via integrating unsupervised learning and supervised learning to efficiently predict costly-labeled complex properties and uncover structure-property relationships. As a compelling demonstration, this framework has been successfully applied to identify semiconductors with ultralow κL, which circumvents large-scale brute-force ab initio calculations without clear objectives. By employing unsupervised learning for the materials from the MP database, we successfully group them into seven clusters. A few hundred materials in the problem-specific clusters C1 and C2 with a high likelihood of possessing low κL are selected from a pool of hundreds of thousands based on similarity design rules. We further conduct low-cost HTC on materials belonging to the two clusters, establishing a local database for researchers to retrieve and providing a list of candidate materials with potential applications in the TE field. Additionally, statistical analysis of these candidates offers valuable domain knowledge to guide the design of materials with ultralow κL. Cs2GeSe3 and Cs2SnSe3 with ultralow κL (~0.25 W/mK) are screened out, in which the anomalous ultralow κL of Cs2GeSe3 is attributed to the lower τ caused by the difference in covalent bonding. Based on the established local database, we train a robust supervised classification model to refine unsupervised learning, achieving a high ROC AUC of 0.94 on the test set, which can enable the efficient predictions of ultralow κL materials. The interpretable analysis of the classification model reveals the mechanisms of key descriptors on κL modulation, such as \({W}_{{\rm{A}}}^{\min },\alpha\) and \({L}^{\min }\), etc. The special factor \({L}^{\min }\) is discovered to show a unique influence on structural anharmonicity, leading to the difference of phonon lifetime in Cs2GeSe3 and Cs2SnSe3, in agreement with the first-principles analysis. We believe that this work provides a novel feasible way for efficiently seeking promising TE materials, in which the proposed HiBoFL framework is also expected to be applied in other material fields.

Methods

First-principles calculations

All the involved DFT-based first-principles calculations were carried out by using the projector-augmented wave (PAW) method85 to deal with ion-electron interactions as implemented in the Vienna Ab initio Simulation Package (VASP)86, in which the processing of data was conducted using VASPKIT87. The electronic exchange-correlation energy was described by the Perdew–Burke–Ernzerhof (PBE) functional under the generalized gradient approximation (GGA)88. Our automatic HTC workflow conducted on the candidate structures identified by unsupervised learning was accomplished within the framework of Python Materials Genomics (Pymatgen)89. With a plane-wave kinetic energy cutoff of 520 eV and a Γ-centered k-point grid of 2π × 0.04 Å−1 to sample the Brillouin zone, the structure optimization was terminated when the total energy convergence reached below 10−6 eV and the norms of all the forces were less than 0.01 eV/Å. The elastic properties of each material were calculated by applying a 1% change to the volume of the optimized conventional cell. To evaluate the dynamic stability and extract the second-order interaction-force constants (2nd-order IFCs) of Cs2SnSe3 and Cs2GeSe3, we used the finite displacement method90 for calculations as implemented in the Phonopy package91,92. The obtained 2nd-order IFCs were utilized to construct the dynamic matrix and compute the corresponding harmonic properties. Additionally, we utilized the script thirdorder.py93 to generate the 2 × 2 × 1 and 2 × 2 × 1 supercells in consideration of the 10th nearest neighbors for Cs2SnSe3 and Cs2GeSe3, thereby resulting in 1504 and 1500 supercells with displaced atoms for self-consistent calculations, respectively. The third-order interaction force constants (3rd-order IFCs) were further extracted to obtain the three-phonon scattering matrix elements, facilitating the calculations of anharmonic properties. Ultimately, we obtained the convergent κL values of these selected materials as implemented in the ShengBTE package94 within a 20 × 20 × 20 q-point grid in reciprocal space. The crystal structures and ELF diagrams were visualized using the Crystal Toolkit95 and VESTA96. Moreover, we calculated the COHP as implemented in the LOBSTER code77 to identify the bonding characteristics as bonding, anti-bonding, or non-bonding.

Theoretical framework

Taking into account the extremely high cost of precisely calculating κL, we employed the PET model proposed in our previous work44 within the HTC framework to obtain the corresponding values at 300 K for materials identified by unsupervised learning. The PET model has established the relationship between intrinsic κL and elastic properties, considering both acoustic phonon and optical phonon contributions, which achieves a certain balance between accuracy and efficiency. The empirical equation of κPET based on the PET model is expressed as:

$$\,{\kappa }_{{\rm{PET}}}=\frac{{(6{\pi }^{2})}^{2/3}}{3{\pi }^{3}}\cdot \frac{\overline{M}}{T{(\overline{V}N)}^{2/3}}\frac{{\overline{\upsilon }}^{3}}{{\overline{\gamma }}^{2}}+\frac{3{k}_{{\rm{B}}}\overline{\upsilon }}{2{\overline{V}}^{2/3}}{\left(\frac{\pi }{6}\right)}^{1/3}(1-{N}^{-2/3})$$
(5)

Where \(\overline{M}\) is the average atomic mass, T is the temperature, \(\overline{V}\) is the average atomic volume, N is the number of atoms in the primitive cell, kB is the Boltzmann constant, \(\overline{\upsilon }\) and \(\overline{\gamma }\) are the average sound velocity and average Grüneisen parameter, respectively. Among them, we can obtain \(\overline{\upsilon }\) as given by:

$$\begin{array}{ll}\overline{\upsilon }\;=\;{\left[\frac{1}{3}\left({\overline{\upsilon }}_{{\rm{L}}}^{-3}+2{\overline{\upsilon }}_{{\rm{T}}}^{-3}\right)\right]}^{-1/3}\\\quad\,=\;{\left\{\frac{1}{3}{\left(\frac{\overline{M}}{\overline{V}}\right)}^{3/2}\left[{\left(B+\frac{4}{3}G\right)}^{-3/2}+2{G}^{-3/2}\right]\right\}}^{-1/3}\end{array}$$
(6)

And \(\overline{\gamma }\) can be expressed as:

$$\begin{array}{lll}\overline{\gamma }\;=\;\sqrt{\frac{1}{3}({\overline{\gamma }}_{{\rm{L}}}^{2}+2{\overline{\gamma }}_{{\rm{T}}}^{2})}\\\quad\, =\sqrt{\frac{1}{3}\left\{{\left[\frac{1}{2}\frac{\partial {{\ln }}\,\left(B\,+\,\frac{4}{3}G\right)}{\partial {{\ln }}V}+\frac{1}{6}\right]}^{2}+2{\left(\frac{1}{2}\frac{\partial {{\ln }}\,G}{\partial {{\ln }}\,V}+\frac{1}{6}\right)}^{2}\right\}}\end{array}$$
(7)

Where \({\overline{\upsilon }}_{{\rm{L}}},{\overline{\upsilon }}_{{\rm{T}}},{\overline{\gamma }}_{{\rm{L}}}\) and \({\overline{\gamma }}_{{\rm{T}}}\) are the longitudinal sound velocity, transverse sound velocity, longitudinal Grüneisen parameter, and transverse Grüneisen parameter, respectively. B and G are bulk moduli and shear moduli, respectively. In this manner, we can calculate the κPET for different materials derived from their elastic properties within the HTC framework.

To further validate κPET from the PET empirical equation and investigate the phonon thermal transport mechanisms, we calculated more accurate κL values for Cs2SnSe3 and Cs2SnSe3 by iteratively solving the phonon BTE94,97:

$${\kappa }_{{\rm{L}}}^{\alpha \beta }=\frac{1}{{k}_{{\rm{B}}}{T}^{2}\Omega N}\mathop{\sum }\limits_{\lambda }{f}_{0}\left({f}_{0}+1\right){\left(\hslash {\omega }_{\lambda }\right)}^{2}{\upsilon }_{\lambda }^{\alpha }{F}_{\lambda }^{\beta }$$
(8)

Where α and β are the Cartesian indexes. kB, T, Ω, N are the Boltzmann constant, temperature, volume of the unit cell, and regular grid of q points, respectively. λ is a phonon mode including the branch index p and wave vector q, and f0 is the phonon distribution function based on Bose–Einstein statistics. \(\hslash ,{\omega }_{\lambda },{\upsilon }_{\lambda }^{\alpha }\) are the reduced Planck constant, phonon frequency, and phonon group velocity along the α direction, respectively. When only considering two- and three-phonon processes that contribute to scattering, the linearized BTE Fλ takes the form:

$${F}_{\lambda }={\tau }_{\lambda }^{0}({\upsilon }_{\lambda }+{\Delta }_{\lambda })$$
(9)

Where \({\tau }_{\lambda }^{0}\) and Δλ are the phonon lifetime of mode λ and corrective term from iteration, respectively.

Machine learning

The chemical compositions and crystal structures of materials were featurized into different descriptors using the Matminer package98. All parts related to ML were carried out using the Scikit-learn package99. To achieve the automation and acceleration of hyperparameter optimization in supervised learning, we employed the powerful Optuna package100 for efficiently finding the best hyperparameters. And to provide the interpretable analysis of the black-box ML model, a game-theoretic approach as implemented in the SHAP package46,47,48 was employed.

For unsupervised learning, the elbow method and the silhouette coefficient method are utilized to determine the optimal k value in k-means clustering. In the elbow method, the sum of squared errors (SSE) is defined as:

$$SSE=\mathop{\sum }\limits_{i=1}^{k}\sum _{x\in {C}_{i}}\parallel\!\! x-{\mu }_{i}{\parallel }^{2}$$
(10)

Where Ci represents the set of data points in cluster i, x is a data point in Ci, μi is the centroid of Ci. The silhouette coefficient is defined as:

$$s(x)=\frac{b(x)-a(x)}{\max (a(x),b(x))}$$
(11)

Where b(x) is the average intra-cluster distance and measures how close the data point x is to other points in Ci, a(x) is the average nearest-cluster distance and measures how far data point x is from the closest other cluster. After calculating the silhouette coefficient for all data points, the average value is then taken to obtain the mean silhouette coefficient for different values of k.

For supervised learning, accuracy, precision, recall, F1-score, and ROC AUC are utilized to evaluate the performance metrics of classification models, which are defined as:

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
(12)
$$Precision=\frac{TP}{TP+FP}$$
(13)
$$Recall=\frac{TP}{TP+FN}$$
(14)
$$F1\,\text{-}\,socre=\frac{2TP}{2TP+FP+FN}$$
(15)
$$ROC\,AUC=\mathop{\int}\nolimits_{0}^{1}TPR\,d(FPR)$$
(16)

Where TP is the number of true positives, FP is the number of false positives, TN is the number of true negatives, and FN is the number of false negatives. Moreover, TPR and FPR are the true positive rate and false positive rate, respectively, which are defined as:

$$TPR=\frac{TP}{TP+FN}$$
(17)
$$FPR=\frac{FP}{TN+FP}$$
(18)

For interpretable analysis, the SHAP value of a material descriptor is given by:

$${\varphi }_{i}(p)=\sum _{S\subseteq F\setminus \{i\}}\frac{| S| !(| F| -| S| -1)!}{| F| !}\left(p(S\cup \{i\})-p(S)\right)$$
(19)

Where p is the prediction model, F represents the set of all material descriptors, S represents the subset of all descriptors excluding the feature i, p(S) is the model prediction when only descriptors in S are considered, and p(S ∪ {i}) is the model prediction when feature i is also included.