Machine learning enabled accurate prediction of structural and magnetic properties of cobalt ferrite

Abstract

A machine learning enabled computational approach has been developed to accurately predict the equilibrium degree of inversion in spinel lattice and some magnetic properties of cobalt ferrite (CoFe₂O₄) crystal. The computational approach is composed of construction of a database from density functional theory calculations, training of machine learning models, and atomistic simulations. Support vector regression was employed to derive the relation between system energy and atomic structures of CoFe₂O₄. Using this trained machine learning model, atomistic Monte Carlo simulations predicted the equilibrium degree of inversion of CoFe₂O₄ to be 0.755 at 1237 K. The strength of twenty-three types of superexchange interactions were determined using the linear regression model and further applied in magnetic Monte Carlo simulations to predict the Curie temperature of CoFe₂O₄ to be 914 K. The predictions from the presented computational approach are well validated by the results from neutron diffraction measurement on CoFe₂O₄.

Introduction

Excellent structural, mechanical, optical and magnetic properties of spinel ferrites enable their applications in various fields, including high frequency transformers^1,2, microwave materials³, catalysts⁴, gas sensors⁵ and biomedical devices⁶. Cobalt ferrite (CoFe₂O₄) is a unique material that exhibits “semi-hard” behavior, possessing magnetic properties that include coercivity of ~5000 Oe⁷, saturation magnetization of ~78 emu/g⁸, and high Curie temperature of about 793 K^9,10, and hence is used in high-density recording media¹¹, spintronic devices¹⁰ and magnetic fluids¹².

Within a AB₂O₄ spinel crystal, two types of metal cations could have different distribution at the tetrahedral and octahedral sublattices¹³. Prior studies show that magnetic properties of spinel ferrites would vary with a change in cation distribution, which is quantified by degree of inversion (i.e., the ratio of the tetrahedral sites occupied by cation B)^14,15. For instance, Concas et al. reported that saturation magnetization of CoFe₂O₄ decreases from 99.4 emu/g to 76.3 emu/g as the degree of inversion increases from 0.71 to 0.95¹⁴. From the first principles density functional theory (DFT) calculations, Hou et al. demonstrated that the magnetization of spinel CoFe₂O₄ decreases from 7 µB to 3 µB per formular unit (f.u.) as the degree of inversion increases from 0.0 to 1.0¹⁶. Additionally, Venturini et al. observed that coercivity of CoFe₂O₄ decreases, whereas magnetic remanence and Curie temperature increases, with increasing degree of inversion¹⁵. While these prior observations consistently indicate an inverse relationship between the degree of inversion and magnetic properties, the theoretical understanding of the relationship between cation distribution and magnetic properties of spinel ferrites remain to be fully elucidated at this time.

The magnetic properties of spinel ferrites are described in terms of superexchange interactions, in which the interaction between two localized cation spins is mediated indirectly by orbital overlaps through a common O anion¹⁷. The strength of superexchange interaction is affected by the length and angle of such Metal-Oxygen-Metal (denoted as M₁-O-M₂) bonds^13,17. Goodenough-Kanamori rules summarize that when the angle of an M₁-O-M₂ bond approaches 180°, virtual electron transfer would occur between overlapping half-filled orbitals and lead to strong antiferromagnetic coupling. By contrast, when the bond angle is close to 90°, electron exchange would yield weak ferromagnetic coupling^18,19,20,21. For CoFe₂O_4, Bercoff et al. showed that the strength of superexchange interactions could be determined by fitting the experimental magnetization against temperature into a collinear two-sublattice model²². Moreover, Ansari et al. have predicted the strength of superexchange interactions by expressing the calculated energies of spinel CoFe₂O₄ with non-ground state spin configurations using the Heisenberg model²³. The results from both studies indicated that the superexchange interaction constant (i.e., strength) J_AB, across tetrahedral and octahedral sublattices, is significantly stronger than J_AA and J_BB, within respective tetrahedral and octahedral sublattice. As a result, dominantly negative J_AB leads to anti-parallel alignment of the magnetic moments at the tetrahedral and octahedral sublattices in spinel ferrites. Moreover, Ansari et al. used the predicted superexchange constants to calculate the Curie temperature of CoFe₂O₄ to be 480 K, which was found significantly lower than the experimental value of ~790 K²³. In a similar study, Morgan et al. applied the computationally predicted superexchange constants in Monte Carlo simulations to predict magnetic properties of spinel MnO₂. They also found the predicted Curie temperature of 62 K and Weiss constant of −210 K displayed pronounced discrepancy as compared to experimental values (Curie temperature of 32 K and Weiss constant of −104 K)²⁴. Hence, these current models clearly overlook important physics and it is desirable to develop a reliable computational approach to derive the superexchange strengths and predict the relevant magnetic properties of spinel ferrites in a fully atomistic model.

In the present study, we have developed a DFT data informed, machine learning enabled computational approach to extract the energy-structure relationship and predict twenty-three superexchange interaction constants associated to all the possible types of M₁-O-M₂ bonds for CoFe₂O₄ crystal. Furthermore, we employed these well-trained machine learning models in atomistic Monte Carlo simulations to predict the equilibrium degree of inversion as well as the magnetization of CoFe₂O₄ as a function of temperature. The model predictions, including equilibrium degree of inversion, total magnetization, magnetization at two sublattices, and Curie temperature, were well validated by our experimental data from neutron diffraction measurement.

Results

Structure and property database of CoFe₂O₄

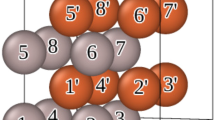
For training the machine learning models, we constructed a database consisting of the DFT-predicted structures, energies, and magnetic moments of spinel CoFe₂O₄ crystal with various distinct cation distributions and spin configurations. Cations can occupy either the tetrahedral sites enclosed by four oxygen ions, or the octahedral sites enclosed by six oxygen ions in a spinel crystal. In a normal spinel structure cell of CoFe₂O₄ crystal (Fig. 1a), eight Co cations occupy the tetrahedral sites, and 16 Fe cations are at the octahedral sites. By contrast, in an inverse spinel structure cell (Fig. 1b), eight Fe cations are at the tetrahedral sites whereas the other eight Fe cations and eight Co cations occupy the octahedral sites. Quantifying the cation distribution in a spinel crystal, the degree of inversion (denoted as x) of CoFe₂O₄ crystal is defined as the fraction of the tetrahedral sites occupied by Fe cations, ranging between 0.0 for a normal structure and 1.0 for an inverse structure. Illustrating the accuracy of the DFT predictions, we present the predicted lattice parameters of the CoFe₂O₄ oxide structures in Table 1. It is noticeable that the lattice parameter of the spinel CoFe₂O₄ crystal with a degree of inversion of 0.75 was predicted to be 8.46 Å, which is quite close to previous computational values of 8.462 Ų⁵ and 8.49 Ų⁶ and agrees well with experimental value of 8.38 Å from the literature²⁷ and 8.407 Å from our neutron scattering measurement at 4 K (Table S1). Moreover, the DFT calculations predict that the CoFe₂O₄ crystal with an inverse structure would have a system energy 0.04 eV/f.u. lower than that of a normal structure. This prediction is consistent with the value of 0.05 eV/f.u from a previous computational study²⁶.

Fig. 1: Atomistic structures of CoFe₂O₄ crystal.

a Normal spinel structure, b inverse spinel structure. In the figure, the red, blue, and gray balls represent O ions, Co cations and Fe cations, respectively. The tetrahedral and octahedral sites occupied by metal cations are enclosed by the tetrahedrons and octahedrons formed by O ions, respectively.

Table 1 Comparison of the DFT-predicted lattice parameters (in units of Å) of spinel CoFe₂O₄ with various degrees of inversion in this work with the results from prior work

For training different machine learning models, our database contains three datasets as in Table 2: Dataset A contains distinct CoFe₂O₄ structures with various cation distributions and their corresponding DFT-predicted system energies; Dataset B includes DFT-predicted atomic magnetic moments at different cations and the local environment of the metal cations in the spinel CoFe₂O₄ crystal; Dataset C comprises DFT-predicted system energies and atomic magnetic moments for the same crystal configurations used in Dataset B.

Table 2 Summary of machine learning datasets (A, B, C) constructed in this study

To predict the equilibrium cation distribution as a function of processing temperature, we organized Dataset A in our database to have both DFT-predicted system energies and structures of 62 distinct spinel CoFe₂O₄ crystal. Sampling various possible degree of inversion (x), Dataset A includes specifically one structure with x = 0.00, one structure with x = 0.25, 15 distinct structures with x = 0.50, 30 distinct structures with x = 0.75, and 15 distinct structure with x = 1.00. In the DFT calculations, cations at the octahedral sites were set to have majority spin whereas the cations at the tetrahedral sites have minority spin, consistent with the ground state magnetic ordering of spinel ferrites^25,28. In the dataset, a high-dimensional vector containing the numbers of different types of M₁-O-M₂ bonds is used to represent the different structures of CoFe₂O₄. In our prior study, 23 distinct types of M₁-O-M₂ bonds were identified in total and the numbers of each distinct type of M₁-O-M₂ bonds were found to be related to degree of inversion of a spinel crystal²⁹.

To predict the magnetic moment of any specified individual cation in CoFe₂O₄ as a function of its local environment, we organized Dataset B to have both DFT-predicted atomic magnetic moments and list of M₁-O-M₂ bonds connected to the metal cation in spinel CoFe₂O₄ crystal. We included the predicted magnetic moments from 16 distinct spinel structures covering 150 different cases of magnetic ordering. It should be noted that a M₁-O-M₂ bond could have two possible magnetic configurations with M₁ and M₂ having the same or opposite spins. Consequently, the local environment of a cation is expressed with a 46-dimensional vector, in which each component represents the number of a distinct type of M₁-O-M₂ bond with either parallel or antiparallel spin alignment of M₁ and M₂. In our computational model, each spinel CoFe₂O₄ crystal contains eight Co and 16 Fe cations. This leads to a total of 1200 data points for atomic magnetic moment of Co and 2400 data points for atomic magnetic moment of Fe in Dataset B.

To predict the superexchange constants between all possible pairs of cations, we further organized Dataset C to have both DFT-predicted system energies and atomic magnetic moments in the same 150 configurations used in Dataset B. For every M₁-O-M₂ bond, we recorded the magnetic moments of both cations M₁ and M₂ into Dataset C. As a result, there are in total 91,200 entries for the pairs of atomic magnetic moments. For each distinct structure, we calculated the energies of the ground-state magnetic ordering as well as five different non-ground state magnetic configurations. Some non-ground-state magnetic configurations were obtained by reversing the spin of one Co (or Fe) at the tetrahedral (or octahedral) site, respectively. Moreover, we included ferromagnetic ordering and example magnetic configurations sampled at finite temperature. The energy of each non-ground state spin configuration was recorded as the energy relative to that of the ground state spin configuration with the same structure and cation distribution.

Equilibrium cation distribution in spinel CoFe₂O₄

The energy-structure relation of CoFe₂O₄ was derived from Dataset A using the support vector regression (SVR) machine learning model implemented in scikit learn³⁰, which performs non-linear regression analysis by transforming the input data into higher dimensions using kernel functions. SVR model was previously used to predict the formation energies, lattice parameters and band gap of spinel oxides³¹ and found to have the best performance for prediction of cation distribution in spinel crystal³². In this study, the performance of SVR was evaluated using a four-fold cross-validation approach, in which the data was randomly split so that 75% of the data served as training input whereas the remaining 25% was used for testing the accuracy of the model predictions. The SVR model, employing a polynomial function as kernel function and a regularization parameter of 1.16, was found to have a root mean square error (RMSE) of 0.0058 eV/atom and a coefficient of determination (R²) of 0.9362 when comparing the predicted values with DFT-calculated results in the test set. Figure 2a shows the direct comparison between the predicted energies from SVR and those from DFT. The data points are found to be distributed closely around the reference line, indicating the satisfactory predictive accuracy of the SVR model. To quantify the risk of extrapolation in our test data, we computed the extrapolation grade γ(x), a metric based on maxvol algorithm^33,34. The average value of 0.78 across cross-validated test sets, smaller than the threshold value of 1.0, indicates that these configurations predominantly reside within the convex hull of the training data, consistent with the observed interpolation performance in Fig. 2a. Moreover, Fig. 2b shows the reduction in test RMSE with increasing number of distinct structures in the dataset. For each designated dataset size, we randomly selected data points from the full dataset and conducted a four-fold cross-validation on each selection. The test RMSE values shown in Fig. 2b are the average outcomes of 100 such cross-validation exercises, providing a thorough and reliable assessment across varying dataset sizes. Notably, Fig. 2b reveals that both values of test RMSE and its standard deviation reach desirable convergence when the dataset contains more than 50 distinct structures. Therefore, Dataset A, which comprises of 62 structures of CoFe₂O₄, is shown to be sufficiently large and comprehensive for SVR model to achieve good prediction accuracy.

Fig. 2: Performance of support vector regression model.

a DFT-calculated energies as compared to the energies predicted from SVR model for CoFe₂O₄. In this plot, the black and red dots represent training and test data. b Variation in the test set RMSE of SVR model as a function of the number of different structures in the dataset.

Furthermore, the well-trained SVR model was applied in atomistic Monte Carlo simulations to predict the equilibrium degree of inversion of spinel CoFe₂O₄ as a function of processing temperature. At the beginning of the Monte Carlo simulation, the crystal structure of CoFe₂O₄ was set to be a normal spinel structure comprising of eight formula units. In each iteration, an attempt was made to exchange the positions of two randomly selected cations of different types, and the associated energy change for this structural change was calculated using the trained SVR. A Boltzmann distribution-based probability (p) was used to determine the acceptance or rejection of the attempted structural change. Specifically, probability ${{p}}=\min [1,\exp \left(-\frac{\Delta {{E}}}{{{{k}}}_{{{B}}}{{T}}}\right)]$, where ΔE is the energy change, k_B is the Boltzmann constant, and T is system temperature. Each Monte Carlo simulation ran for 100,000 iterations. The convergence of these atomistic MC simulations was confirmed by ensuring a negligible difference in the average system energy of the sampled CoFe₂O₄ crystal after 30,000 MC steps. The degree of inversion was computed as the average over 500 structures sampled every 100 iterations in the last 50,000 iterations. Some representative atomistic structures generated from the MC simulations are shown in Fig. S1. The simulation temperature varied from 873 K to 1473 K, increasing in each step of 100 K. Figure 3 shows the equilibrium degree of inversion of CoFe₂O₄ predicted from the SVR enabled Monte Carlo simulations. The degree of inversion of CoFe₂O₄ was predicted to be 0.802 at 873 K, decreasing gradually to 0.743 at 1473 K. Our results show good agreement with available experimental results. For example, the predicted degree of inversion at 873 K is 0.802 close to the experimental value of 0.800 ± 0.06 at 873 K³⁵. At 1173 K, the predicted degree of inversion is 0.763, in good agreement with the value of 0.76 ± 0.02 reported by Ferreira et al.²⁷. It should be mentioned that we have tested that the MC simulations using a large crystal model containing 512 formula units do not change our prediction on degree of inversion by much (less than 1.7%), as shown in Table S2.

Fig. 3: Variation of predicted degree of inversion of spinel CoFe₂O₄ as a function of temperature.

Experimental data from Sawatzky et al.⁶⁶, Uzunova et al.³⁵, Waseda et al.⁶⁷, Ferreira et al.²⁷, as well our experimental result from neutron diffraction are included for comparison. In the figure, the dashed line depicts a smooth curve fitted with the Monte Carlo simulation data to guide the eye.

Validation of computational prediction was carried against degrees of inversion measured using neutron diffraction. To extract the degree of inversion, Co and Fe occupancies at A and B sites were constrained by the inversion relationship and the total stoichiometry allowing for the inversion parameter to be refined directly in our models with no additional refinable occupancy. The degree of inversion was found to be x = 0.7495 ± 0.00768 across the measured temperature range for a CoFe₂O₄ sample annealed at 1273 K, as fitted using the structural parameters presented in Table S1. Hence, this experimental result provides solid validation for the computational degree of inversion of 0.755 predicted from the MC simulation of CoFe₂O₄ crystal at 1273 K. Although CoFe₂O₄ becomes paramagnetic at high temperature, our SVR model was trained only on DFT data from the fully optimized ground-state (ferrimagnetic). The close agreement between MC-predicted degree of inversion and experimental data suggests that the ferrimagnetic-based training dataset effectively captures the energetic trends governing cation distribution in CoFe₂O₄. In the future, the training data will be supplemented with paramagnetic-state calculations to further improve the accuracy of high-temperature cation distribution predictions.

Magnetization of spinel CoFe₂O₄

The ground state magnetic ordering of CoFe₂O₄ crystal was found to be one in which all the cations at the octahedral sites have majority spin (i.e., spin up) whereas all the cations at the tetrahedral sites have minority spin (i.e., spin down). In Table 3, we present the DFT-calculated magnetic moments of the cations in spinel CoFe₂O₄ crystal with the ground state magnetic ordering. For CoFe₂O₄ with a degree of inversion of 0.75, we predicted the magnetic moments of 2.574 μ_B for Co at the tetrahedral sites and 2.649 μ_B for Co at the octahedral sites, as well as 4.071 μ_B for Fe at the tetrahedral sites and 4.195 μ_B for Fe at the octahedral sites. These values are found to agree well with previous computational results for CoFe₂O₄ (x = 0.75), which reported 2.43 μ_B for the tetrahedral Co, 2.64 μ_B for the octahedral Co, 3.95 μ_B for the tetrahedral Fe, and 4.12 μ_B for the octahedral Fe ions¹⁶. The average magnetic moments at the tetrahedral and octahedral sites of spinel CoFe₂O₄ (x = 0.75) were calculated to be 3.697 μ_B and 3.615 μ_B, respectively, which are consistent with the magnetic moments 3.921 ± 0.042 μ_B at the tetrahedral sites and 3.745 ± 0.081 μ_B at the octahedral sites measured from the neutron diffraction at 4 K³⁶. Furthermore, the results in Table 3 show that the total magnetic moment per unit formula of CoFe₂O₄ decreases with the degree of inversion, varying from 6.867 μ_B/f.u. in the normal structure to 2.974 μ_B/f.u in the inverse structure, in line with previous computational prediction¹⁶.

Table 3 Number and calculated magnetic moment of cations at the tetrahedral (T) and octahedral (O) sites in a spinel crystal containing eight CoFe₂O₄ formula and having different degree of inversion

It should be noted that the magnitude of the magnetic moment of a cation would change when its own spin direction is reversed. For instance, following a change from minority to majority spin, our DFT calculation results show that the magnitude of the magnetic moment of a Co at a tetrahedral site increases from 2.549 μB to 2.762 μB whereas that of a Fe at a tetrahedral site rises from 4.063 μ_B to 4.245 μ_B. Hence, our dataset contains both ground and non-ground state magnetic moments of Co and Fe and thus enables the trained machine learning model to accurately predict non-ground state magnetic moments in arbitrary spin configurations.

It is recognized that the local chemical environment could affect the magnetic moments of the cations in magnetic spinel crystal³⁷. In this study, we employed the Gaussian Process Regression (GPR) machine learning model implemented in scikit learn to establish the relationship between the magnetic moment of cations and their local environment³⁰. The GPR model has been widely employed to investigate structure-properties relation of materials^38,39. It is a Bayesian non-parametric regression model that uses a kernel function to define a prior over function. The prior is refined with the training data to facilitate probabilistic predictions about unknown test data. In GPR, the hyperparameters that define the properties of the kernel function are typically optimized by maximizing the marginal likelihood of the training data⁴⁰. Our four-fold cross-validation showed that the GPR model using a radial basis function kernel had the test performance metric with RMSE of 0.006 μ_B, R² of 0.987 and ML prediction uncertainty of 0.007 μ_B on the Co cation dataset and with RMSE of 0.006 μ_B, R² of 0.994 and ML prediction uncertainty of 0.006 μ_B on the Fe cation dataset. Figure 4a, b presents a comparison between the magnetic moments predicted by GPR and DFT, demonstrating minimal deviation of data points around the reference lines. The high fitting score of R² and slight scattering of data in the figures indicate the efficacy of GPR in accurately predicting the magnetic moments of cations.

Fig. 4: Magnetic moment predictions from GPR model.

DFT-calculated magnetic moments as compared to those predicted from GPR for a Co cations, b Fe cations in spinel CoFe₂O₄ crystal. Bonds with the top four highest variable importance from GPR model for prediction of the magnetic moment of c Co cations, d Fe cations.

Furthermore, we used the Permutation Importance method to assess the importance of each type of M₁-O-M₂ bond for its contribution to the local environment on influencing the value of magnetic moment of a cation in CoFe₂O₄^41,42. The permutation importance of a bond is measured as the decrease in the fitting score (R²) when the number of this bond is assigned a random value: thus, the larger the drop in the fitting score, the higher the importance of the select bond^43,44. As reported in Tables S3 and S4 in SI, the four most important bonds affecting the magnetic moment of a cation are identified to be bond Co-O-Co-125°^(b), Co-O-Fe-125°^(b), Fe-O-Co-125°^(b), and Co-O-Fe-90° for Co, whereas bond Fe-O-Fe-125°^(b), Fe-O-Fe-79°, and Fe-O-Fe-154° and Fe-O-Fe-125°^(a) for Fe. Note that bonds M₁-O-M₂-125°^(a) and M₁-O-M₂-125°^(b) have the same bond angle but differ in bond length: M₁-O-M₂-125°^(a) has bond lengths of 1.83 Å (M₁-O) and 2.11 Å (O-M₂), while M₁-O-M₂-125°^(b) has bond lengths of 2.11 Å (M₁-O) and 3.66 Å (O-M₂) in the modeled CoFe₂O₄ spinel crystal with a degree of inversion of 0.75.

Superexchange constants of spinel CoFe₂O₄

The system energies of magnetic spinel ferrites can be described by a classical Heisenberg model⁴⁵ in the form:

$${{H}}={{{J}}}_{0}-\sum _{{{i}}\ne {{j}}}{{{J}}}_{{{i}},{{j}}}{\vec{{\bf{S}}}}_{{\rm{i}}}{\vec{{\bf{S}}}}_{{\rm{j}}}$$

(1)

where J₀ is a constant term, ${{{J}}}_{{{i}},{{j}}}$ represents the superexchange constant between magnetic cations on sites i and j, and ${\vec{{\bf{S}}}}_{{\rm{i}}/{\rm{j}}}$ is the spin vector of the cation at lattice site i/j^46,47,48. As shown in Fig. 5a–c, bond M₁-O-M₂-79° connects two tetrahedral cations (A-A), bond M₁-O-M₂-125°^(a) with M₁ at A site, M₁-O-M₂-154°, and M₁-O-M₂-180° link a tetrahedral cation to an octahedral cation (A-B), whereas bond M₁-O-M₂-90° and M₁-O-M₂-125°^(b) with M₁ at B site connect two octahedral cations (B-B). The permutation of two distinct ions (Co and Fe) results in 23 distinct types of M₁-O-M₂ bonds, with each type of the bond corresponding to a specific type of superexchange interaction constant in spinel CoFe₂O₄ crystal, as summarized in Table S5 of SI.

Fig. 5: Superexchange interactions in CoFe₂O₄ crystal.

Illustration of a A-A, b A-B, c B-B types of superexchange interactions. d DFT-calculated energies of non-ground spin configurations as compared to linear regression predicted energies. e Average energy changes to reverse the spin direction of a cation from the ground state spin configuration of spinel CoFe₂O₄ with a degree of inversion of 0.75.

The values of the 23 superexchange constants of CoFe₂O₄ with a degree of inversion of 0.75 were predicted using the ordinary least squares linear regression fitting of all the data in Dataset C. Figure 5d shows the comparison between the energies predicted by DFT and by linear regression. The comparison yields a RMSE of 1.65 meV/atom and R² value of 0.99, demonstrating excellent agreement between DFT calculations and linear regression prediction. Figure 5e presents the average energy change associated with reversing the spin direction of a cation from the ground spin configuration of CoFe₂O₄. It is noticeable that our results indicate that it is most difficult to flip the spin of Fe ions at the tetrahedral sites. Moreover, regression analysis reveals that magnetic interactions Fe-O-Co-125° (A-B type) and Fe-O-Co-154° (A-B type) exhibit the strongest strength and both have a value of −3.66 meV. In comparison, Fe-O-Fe-180° (A-B type) only shows weak superexchange strength of −0.17 meV.

M vs. T relation of spinel CoFe₂O₄

Using the derived 23 superexchange constants (Table S5 of SI), we applied magnetic Monte Carlo (MC) simulations to predict the temperature dependent magnetization of CoFe₂O₄, specifically with a degree of inversion of 0.75. The simulation model was a 4$\times$4$\times$4 supercell of the conventional eight f.u. spinel cell, containing a total of 1536 cations with spins²⁴. We chose the ground state spin configuration as the start configuration. In each MC iteration, a 5° rotation was attempted to added onto a randomly selected spin moment vector⁴⁶, and the associated energy change was calculated using the Heisenberg model (Eq. (1)). The MC simulation was based on the Metropolis algorithm with a Boltzmann distribution-based probability (p) used to determine the acceptance or rejection of the attempted spin configuration change. The temperature of the MC simulation was set to vary from 100 K to 800 K, with an increment step of 50 K. All MC simulations ran for 1,500,000 iterations. The convergence of these magnetic MC simulations was confirmed by finding a negligible difference in the average system energy of the sampled magnetic configurations after 800,000 MC steps. The magnetic moments of Co and Fe cations were recorded every 100 iterations during the final 500,000 iterations. The equilibrium magnetization at the tetrahedral and octahedral sites was determined by averaging these sampled magnetic moments, and the total magnetization was calculated as the sum of magnetization at these sites.

As shown in Fig. 6a, during the initial stage of the MC simulation at 700 K, the energy of the system increasingly deviates from that of the ground state spin configuration. This energy increase stems from that sufficient thermal fluctuations permit the crystal to exhibit non-ground state spin configurations with high energy. Figure 6b shows that the values of magnetization at both tetrahedral and octahedral sites decrease with increasing temperature, and the MC predicted magnetizations closely align with experimental results from our neutron diffraction measurement, ranging from 4 K to 750 K³⁶. Regarding magnetic structure determination in our neutron diffraction measurements, basis vectors obtained from SARAH were used for refinement. These were {4,4,4} & {4,−2,−2} for octahedral and {8,0,0} for tetrahedral sites, respectively. The resultant structure belongs to the I41/am’d’ magnetic space group with a k = (0,0,0) propagation vector. Subsequently neutron diffraction data was fitted to obtain occupancies and basis vector coefficients. Resultant fit at 300 K (Rwp = 10.8 and χ² = 6.613) along with the assumed magnetic structure are shown in Fig. 7. All peaks in the diffraction pattern were indexed apart from the peak at q = 2.68 Å⁻¹ which is attributed to an impurity phase and does not contribute to the intensity of the spinel pattern. Refined basis vector coefficients along with the basis vectors coefficients were used to determine the net magnetic moment according to the following procedure (Eqs. (2)–(4)):

$${\vec{m}}_{o}\left({{\rm{B}}\,{\rm{site}}}\right)=\left({C}_{O1}\times < 4,4,4 > +{C}_{O2}\times < 4,-2,-2 > \right)$$

(2)

$${\vec{m}}_{t}\left({{\rm{A}}\,{\rm{site}}}\right)={C}_{T1}\times < 8,0,0 >$$

(3)

$${M}_{{{\rm{total}}}}\left({{\rm{Average}}\; {\rm{moment}}\; {\rm{per}}\; {\rm{formula}}\; {\rm{unit}}}\right)=2* \left|{m}_{o}\right|-\left|{m}_{t}\right|$$

(4)

where C_O1, C_O2 and C_T1 are the respective basis vector coefficients. M_total represents the average ferromagnetism per unit cell. Temperature variation of nuclear and magnetic structure parameters, profile are reported in Table S1 of SI.

Fig. 6: Magnetic Monte Carlo simulation.

a Evolution of energy and magnetization of CoFe₂O₄ during the MC simulation at 700 K. b Comparison of the MC predicted and neutron diffraction measured temperature-dependent magnetization of spinel CoFe₂O₄ with a degree of inversion of 0.75.

Fig. 7: Experimental validation.

a Neutron powder diffraction and Rietveld refinement of CoFe₂O₄ obtained at 300 K. Y_obs and Y_calc are the observed and calculated intensities, q is the scattering vector and Bragg positions refer to those positions of non-zero diffracted intensities are allowed by the symmetry of the crystal structure. b The best fit magnetic structure at 300 K in which the blue and yellow balls represent the tetrahedral and octahedral sites in a spinel crystal, respectively.

Up to 600 K, the discrepancy between experimentally measured total magnetization and the MC predicted values is found to be less than 4%. With temperature increases to 750 K, the deviation of our prediction from the experimental data increases to 9%. It is noticeable that our model predictions for the magnetization at the two sublattices differ appreciably with the experimentally measured values at temperature above 600 K. Additionally, we computed the Curie temperature of CoFe₂O₄ from both experimental data and model predictions. Using the neutron scattering data of CoFe₂O₄ spinel, the Curie temperature was determined to be 825 K with a standard error of 11 K, by assuming magnetization M depends on temperature following a relation of $M \sim {\left({T}_{C}-T\right)}^{1/2}$²⁴. In comparison, our computational approach predicted a Curie temperature of 914 K with an uncertainty of 4 K from the magnetic MC simulations on three different CoFe₂O₄ structures with a degree of inversion of 0.75. Hence, our computational prediction of Curie temperature of CoFe₂O₄ crystal is found to be 11% higher than the experimental value obtained from neutron diffraction.

Discussion

The machine learning enabled computational approach to predict the magnetic properties of CoFe₂O₄ has improved features as compared to previously reported computational methods, as summarized in Table 4. In previous models, Bercoff et al. and Das et al. used experimental data of temperature-dependent magnetization to derive superexchange constants^22,49, whereas Das et al. and Ansari et al. employed the first-principles DFT-calculated magnetic stabilization energies to extract superexchange constants^23,50. These models took different numbers of superexchange constants into account. Bercoff et al. assumed only one type of magnetic interaction between A-A, A-B and B-B sublattices, consistent to the scenario in a normal spinel crystal²². Considering composition complexity in a fully inverse spinel CoFe₂O₄ crystal, Das et al. and Ansari et al. included more types of superexchange constants, namely one AA (i.e., Fe-Fe), three BB (i.e., Co-Co, Co-Fe, and Fe-Fe), and two AB (i.e., Fe-Fe and Fe-Co), in their magnetic model^23,50. Furthermore, Ansari et al. extended their model to a CoFe₂O₄ crystal with a degree of inversion of 0.3125 by using three AA, three BB, and four AB superexchange constants. It should be pointed out that all these previous studies neglected the variation of superexchange constants with the length and angle of M₁-O-M₂ bonds. As presented in Table 4, our model considered all the possible factors (i.e., element type, bond length, and bond angle) affecting the superexchange strength and was applied to predict the magnetic property of CoFe₂O₄ crystal with an experimentally determined degree of inversion of 0.75^27,36. Moreover, using the Monte Carlo simulations with full atomic details, we predicted a Curie temperature of 914 K for the modeled CoFe₂O₄ crystal. Our model prediction is close to the experimentally measured Curie temperature of 825 K. Therefore, we present the first theoretical model to predict the magnetic properties of spinel ferrites explicitly including all the possible types of superexchange interactions and in an atomistic scale.

Table 4 Comparison of various theoretical models used for calculating magnetic superexchange constants (J) and Curie temperature (T_C) of spinel CoFe₂O₄ crystal with given degree of inversion (x)

Moreover, the machine learning enabled computational approach can provide insights into magnetic interactions between cations mediated by O ions in spinel ferrites. Surveying the predicted values of superexchange constants (as reported in Table S5 of SI), we find that the strength of magnetic interaction is related to the element type, length (i.e., the distance from cation to O ion), and angle of M₁-O-M₂ bonds. (A) Element type effect: Taking bond M₁-O-M₂-125°^(a) (here M₁ at A site and M₂ at B site) as an example, Fe-O-Co-125°^(a) and Co-O-Fe-125°^(a) have the same bond length and angle but Fe-O-Co-125°^(a) was predicted to have a more negative superexchange strength of −3.663 meV than Co-O-Fe-125°^(a) of −2.762 meV. (B) Bond length effect: There are two types of M₁-O-M₂-125° bonds in spinel crystal differing by the location of cation M₁. Consequently, Fe₁-O-Fe₂-125°^(a) (Fe₁ at A site and Fe₁ at B site) and Fe₁-O-Fe₂-125°^(b) (both Fe₁ and Fe₂ at B sites) would have the same element type and bond angle, but different bond length of Fe₁-O to be 1.83 Å and 3.66 Å, respectively. It was found that Fe-O-Fe-125°^(a) with a shorter bond length has much more negative superexchange strength of −3.654 meV as compared to a value of −0.233 meV for one with longer bond length. (C) Bond angle effect: bonds Fe-O-Fe-154° and Fe-O-Fe-79° have the same element type and very similar bond length but different bond angles. Our results show that Fe-O-Fe-154° has superexchange strength of −3.654 meV which is much stronger interaction than Fe-O-Fe-79° with predicted strength of −0.258 meV. In addition, our results confirmed the previous prediction that M₁-O-M₂-154° interaction have the strongest superexchange effect in ferrite systems based on Goodenough-Kanamori-Anderson rules of superexchange²¹.

Furthermore, the average superexchange constants ${\bar{{\rm{J}}}}_{{\rm{AB}}}$, ${\bar{{\rm{J}}}}_{{\rm{AA}}}$ and ${\bar{{\rm{J}}}}_{{\rm{BB}}}$ were calculated by summing of the J values weighted by the total number of those M₁-O-M₂ bonds within respective category (i.e., AA, AB, and BB) in a spinel crystal²⁹. It was predicted that the values of ${\bar{{\rm{J}}}}_{{\rm{AB}}}$, ${\bar{{\rm{J}}}}_{{\rm{AA}}}$ and ${\bar{{\rm{J}}}}_{{\rm{BB}}}$ were −4.87 meV, −0.24 meV and −0.06 meV, respectively, in a CoFe₂O₄ crystal with a degree of inversion of 0.75. Thus, the superexchange constants averaged over all types of bonds for AA, AB, and BB magnetic interaction are all negative, consistent with results from previous studies^23,50. Negative value of superexchange constant indicates that the spins of the two cations favor anti-parallel alignment. Our prediction of negative values of ${\bar{{\rm{J}}}}_{{\rm{AB}}}$, ${\bar{{\rm{J}}}}_{{\rm{AA}}}$ and ${\bar{{\rm{J}}}}_{{\rm{BB}}}$ is consistent with Goodenough’s theory, which predict that cations (here, Fe²⁺, Fe³⁺, Co²⁺, and Co³⁺) would favor antiferromagnetic interaction in spinel crystal since they have a half-filled e_g orbital²⁰. Notably, the superexchange constants of A-B interactions is predicted to have much larger magnitude than that of A-A and B-B interactions, explaining the observed ground state magnetic configuration of CoFe₂O₄ to be antiparallel alignment between spins at tetrahedral (A) and octahedral (B) sites^22,23,50. To further validate our computational approach, we applied the averaged superexchange constants (${\bar{{\rm{J}}}}_{{\rm{AB}}}$, ${\bar{{\rm{J}}}}_{{\rm{AA}}}$ and ${\bar{{\rm{J}}}}_{{\rm{BB}}}$) to the two-sublattice model²² and predicted a Curie temperature of 835 K for CoFe₂O₄ crystal, close to the value of 825 K from our neutron scattering experiments. Here, it should be noted that we must tune the value of total angular momentum quantum number in Brillouin function to be 3/2 at A sublattice and 1 at B sublattice in order to achieve the agreement between the two-sublattice model and experimental data. By contrast, our MC simulations (shown in Fig. 6) do not rely on any empirical inputs and hence can be used for discovering novel materials unexplored previously.

It is noticeable in Fig. 6 that the discrepancy between experimental data and computational predictions become pronounced at temperatures above 600 K. This deficiency of our computation method might stem from an underlying approximation that the superexchange constants (J_ij) of CoFe₂O₄ are independent of temperature and remain their values determined from the DFT calculations for fully relaxed crystal structures. It is conceivable that the length and angle of M₁-O-M₂ bonds could deviate appreciably from their equilibrium values due to thermal vibrations and hence have possibly reduced superexchange constants at high temperature. One possible way to derive temperature-dependent superexchange constants is to include the DFT data on the spinel CoFe₂O₄ crystal in high-temperature paramagnetic state after properly structural relaxation⁵¹. In recent years, some machine learning (ML) potentials have also been developed and implemented to predict the structure and properties of magnetic materials^{34,52,53,54,55,56}. These ML potentials were most often trained over the database containing the structures and energies of the magnetic crystal with various atomic and spin configurations produced by ab initio molecular dynamics simulations and shown to be capable of predicting the properties such as ground magnetic state, phonon spectra for different magnetic states and Curie temperature^52,53,55,56. As compared to these ML potential based approaches, the presented computational method requires only a small amount of data (as given in Table 2) for training and thus is facile to be extended for modeling and design of more complex multi-cation spinel systems, which is the primary objective of the current study.

In this study, we developed and applied a new computational approach to predict the equilibrium cation distribution and magnetic properties of spinel CoFe₂O₄ crystal by considering the full atomistic details. To this end, we first constructed a comprehensive database of DFT-predicted structures, energies, and magnetic moments of the spinel CoFe₂O₄ with various distinct cation distributions and spin configurations. A key feature of the database is that distinct spinel crystal structure is represented as a high-dimensional vector containing the numbers of different types of M₁-O-M₂ chemical bonds. Subsequently, advanced machine learning models were tested to detect patterns in our database. Specifically, support vector regression model was employed to derive the relation between the system energy and structure features of CoFe₂O₄, achieving a test RMSE of 0.0058 eV/atom; Gaussian process regression model was used to establish the relation between the magnetic moment of cations and their local environment, with a test RMSE of 0.006 μ_B per Co and Fe cation. Moreover, linear regression model was used to extract twenty-three superexchange constants in a CoFe₂O₄ crystal, achieving RMSE of 1.65 meV/atom and R² value of 0.99.

Furthermore, the trained support vector regression was applied in atomistic Monte Carlo simulations to predict the equilibrium degree of inversion of CoFe₂O₄ at temperature range from 873 K to 1473 K. Our simulation results indicated that the equilibrium degree of inversion of CoFe₂O₄ would be 0.755 at 1273 K, closely agreeing with our experimentally measured value of 0.7495 ± 0.00768. In addition, the superexchange constants derived from the linear regression model were used in magnetic Monte Carlo simulations to predict the variation of magnetization of CoFe₂O₄ at individual sites as well as total crystal with temperature varying from 100 K to 800 K. Our predicted curve for dependency of total magnetization on temperature was found to agree quite well with the results attained from neutron diffraction measurement. From the curves, the Curie temperature of a CoFe₂O₄ crystal with the experimentally measured degree of inversion of 0.75 was predicted to be 914 K, as compared to the experimental value of 825 K.

It is noteworthy to mention that the developed computational approach considers all possible types, including four AA, seven BB, and twelve AB, of superexchange interactions existing in a spinel CoFe₂O₄ crystal with a degree of inversion of 0.75, and thus does not employ any mean field approximations. The values of the superexchange constants derived from machine learning indicate that the strength of superexchange interaction is determined by the element type, length, and angle of various types of M₁-O-M₂ bonds. This study confirmed a previous prediction based on Goodenough’s theory that M₁-O-M₂-154° interaction across the A and B sublattices should have the strongest superexchange effect in ferrite systems. The averaged values of superexchange constant ${\bar{{\rm{J}}}}_{{\rm{AB}}}$, ${\bar{{\rm{J}}}}_{{\rm{AA}}}$ and ${\bar{{\rm{J}}}}_{{\rm{BB}}}$ were predicted to be −4.87 meV, −0.24 meV and −0.06 meV, respectively. Consequently, the superexchange effects of A-B interactions are found to be stronger than that of A-A and B-B interactions, explaining the observed ground state magnetic configuration of CoFe₂O₄ to be antiparallel alignment between spins at the tetrahedral and octahedral sites.

Herein, we demonstrated that the DFT data informed, machine learning enabled computational approach could be used to predict the equilibrium cation distribution and magnetization of spinel CoFe₂O₄ as a function of temperature. A notable feature is that the machine leaning models are used to establish a quantitative relationship between complex structural features and magnetic properties of spinel CoFe₂O₄ and subsequently applied in physics-based Monte Carlo simulations to predict key physical properties of the ferrite as a function of temperature. The developed computational approach has been well validated by the temperature-dependent degree of inversion and magnetization of spinel CoFe₂O₄ measured from neutron diffraction. Hence, the developed computational approach is expected to be a vital computational tool extendable for future studies that aim to predict the equilibrium structure and magnetic properties of complex ferrite systems containing more than two types of cations.

Methods

Density functional theory

The first-principles spin-polarized DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP)⁵⁷, which employs the plane wave basis associated with the projector-augmented wave approach⁵⁸. The exchange-correlation term was corrected with the generalized gradient approximation (GGA) in the form of Perdew-Birke-Ernzerhof (PBE) functional⁵⁹. The bulk crystal structure of spinel CoFe₂O₄ was modeled using a cubic cell consisting of eight formular units (i.e., in total of 56 ions) (Fig. 1). Such a cubic cell is sufficiently large to allow modeling different spinel structures with a change in degree of inversion by a step of 0.25. The special quasi-random structures (SQS) method implemented in Alloy Theoretic Automated Toolkit (ATAT) was used to construct the crystal structures that mimic the cation distribution in a random oxide⁶⁰. In this work, the structures were generated with SQS by optimizing both two-body (pair) and three-body (triplet) correlation functions up to a cutoff distance of 5.8 Å. In all the calculations, the plane-wave cut-off energy was set as 500 eV, and the total energy of system was converged within 10⁻⁶ eV. As in GGA + U approach, the effective on-site Coulomb interaction parameter U_eff was set to be 3.3 eV on Co ions and 4.0 eV on Fe ions⁶¹. The selection of these U values was validated by accurately predicting the formation of enthalpies of ternary oxides, including CoFe₂O₄, with a mean absolute error below 2%⁶¹. During structural optimization, a 4 × 4 × 4 Monkhorst-Pack k-point mesh was used and each structure was relaxed until the force on each atom was reduced to below 0.01 eV/Å⁶².

Neutron diffraction measurement

Traditional powder processing technique was used to synthesize CoFe₂O₄ crystal samples³⁶. Co₃O₄ and Fe₃O₄ powders were mixed in 1:2 ratio, milled in ZrO₂ media, and dried to obtain a homogenous mixture. Subsequently, the dried powder was treated inside a tube furnace at 1000 °C (i.e., 1273 K) in atmospheric conditions for 24 h and then air quenched to room temperature. Neutron powder diffraction measurements were carried at the HB-2A powder diffractometer located at Oak Ridge National Laboratory⁶³. Diffraction patterns were collected using the 1.54 Å incident wavelength with op-21’-12’ collimation settings for the pre-monochromator, pre-sample and pre-detector collimation respectively. The FULLPROF software suite was employed for all structural and magnetic refinements⁶⁴. The Thompson-Cox-Hasting formulation for a pseudo-Voight peak shape with axial divergence asymmetry was used to fit instrumental profile of HB-2A. Representational analysis, as implemented in Simulated Annealing and Representational Analysis (SARAh), was used to generate the magnetic basis vectors for magnetic structure determination⁶⁵. Lattice parameters, atomic displacement parameters, occupancies, magnetic basis vector coefficients and the oxygen atomic position of spinel CoFe₂O₄ were fully refined in the data analysis.