Introduction

In the intersecting realms of computational chemistry, materials science, and mechanics, machine learning has made substantial strides, particularly through the development of machine learning interatomic potentials (MLIPs). These innovative tools have transformed atomic-scale simulations by facilitating the accurate modeling of complex material behavior with quantum-level accuracy1,2,3,4,5,6. A diverse array of MLIPs leveraging unique descriptors has emerged. For instance, Neural Network Potentials (NNPs) employ the Atom-Centered Symmetry Functions (ACSF)7, while Gaussian Approximation Potentials (GAP) utilize the Smooth Overlap of Atomic Positions (SOAP)8, and Spectral Neighbor Analysis Potentials (SNAP) depend on bispectrum components9. Additionally, both Moment Tensor Potential (MTP)10 and Atomic Cluster Expansion (ACE)11 have found extensive applications across various materials, from metals and alloys to 2D materials and complex systems like carbon and silicon12,13,14. The computational accuracy-efficiency analysis reveals that while GAP achieves the highest accuracy, it lacks computational efficiency15. In contrast, MTP and ACE present a more balanced profile of accuracy and computational demand, with ACE being notably faster than MTP14,16,17.

An essential element in developing MLIPs is constructing a good training database that adequately covers the configuration space relevant to the intended simulations. Typically, this database is curated by domain knowledge, such as ground-state structures, structures deformed under various elastic strains, ab initio molecular dynamics (AIMD) configurations at different temperatures, and simple defects such as vacancy, interstitial, crack tip, and dislocation core18. Advancements in machine learning have driven the adoption of on-the-fly active learning (OTF-AL)19,20,21, a sophisticated approach that accelerates the development of MLIPs by efficiently selecting new configurations exclusively for necessary DFT calculations. The effectiveness of OTF-AL strategies hinges on the ability to calculate similarities among configurations by comparing their local atomic environments (LAEs). MTP with OTF-AL, utilizing the D-optimality criterion and the MaxVol algorithm, exemplifies one of the most widely employed MLIPs, which has been used in numerous studies22,23. Other active learning strategies, such as uncertainty-driven dynamics24 and hyperactive learning25, also significantly contribute to efficiently sampling the configuration space.

Two primary challenges persist in the construction of databases for the development of MLIPs. The first challenge is the comprehensive coverage of defect. For metals, it is relatively straightforward to train MLIPs that can reproduce lattice constants, elastic constants, vacancy formation energy, and energies of simple grain boundaries. However, it remains unclear whether existing MLIPs can effectively model extended defects and their interactions, even if some of them are deemed for general-purpose18,26,27,28,29. This uncertainty primarily stems from the lack of quantification for unknown defects. Although OTF-AL has emerged as a promising strategy to accelerate MLIP development, existing frameworks struggle to achieve comprehensive defect sampling across all loading conditions, notably in computationally demanding simulations involving large-scale atomic systems and extended time scaless. Qi et al. suggested that an ideal strategy would be to efficiently generate and sample configuration space before conducting any DFT calculations30. They used M3GNet31 as the engine for effective and efficient database generation for atomic hydrogen diffusion in titanium hydride system. This strategy however is unsuitable for modeling extended defects in metals due to the low accuracy and computational efficiency of universal MLIPs in large-scale simulations.

The second challenge involves the accurate modeling of extended defects. For instance, while current MLIPs can handle local defects such as vacancies, screw dislocations, and simple grain boundaries, they often exclude extended defects such as dislocation nucleation and multiplication, general grain boundaries (GBs), and interactions among them32. This exclusion is due to the inability of these extended defects to fit within the small periodic configurations typically used in DFT calculations. One workaround has been to extract a non-periodic atomic cluster with a spherical shape from large-scale simulations. To restore periodic boundary conditions required for plane-wave DFT calculations, a sufficiently large vacuum layer is added to prevent image interaction, as implemented in the MLIP-3 package23. This strategy has been applied in nanoindentation simulations33 and elastic constant calculations of polycrystals34 for diamond. Nevertheless, this approach can introduce irrelevant free surfaces or other boundaries35. To overcome these limitations, new strategies have been developed to maintain periodic boundary conditions without additional vacuum layers. For instance, Zhang et al. created a periodic crack-tip DFT cell through duplication and rotation operations36. Hodapp et al. utilized a screw dislocation in BCC W as an example to construct a periodic configuration37, while Mismetti et al. designed periodic configurations containing leading and trailing parts of edge dislocation in face-centered cubic aluminum (FCC Al)38. However, these methods fall short in handling aforementioned extended defects.

In this study, we introduce a generalized framework for developing MLIPs specifically designed to model extensive defects in metals. This framework integrates two key components: (1) Empirical Interatomic Potentials-Guided Sampling (EIP-GS), and (2) Periodic Configuration Construction via Grand Canonical Monte Carlo simulations (PCC-GCMC). These components are crucial for overcoming the challenges previously discussed. The EIP-GS method is designed to enhance defect sampling capabilities during large-scale simulations under a wide range of loading conditions. The PCC-GCMC technique, on the other hand, converts non-periodic atomic clusters of selected defects into periodic configurations without the need for vacuum layers. This conversion is essential to ensure that these configurations are compatible with standard plane-wave DFT calculations. Focusing on body-centered cubic tungsten (BCC W), our analysis underscores the critical role of the EIP-GS and PCC-GCMC techniques in enhancing the predictive accuracy and reliability of MLIPs for large-scale simulations. Ultimately, we have developed a set of MLIPs optimized for BCC W, capable of simulating a wide range of plastic deformations. We demonstrate the capabilities of our MLIPs through polycrystal tension and nanoindentation simulations. The exceptionally low uncertainty of new MLIPs underscores the robustness and adaptability of our approach across diverse simulation challenges.

Results

MLIP development framework for modeling extensive defects

In this study, we introduce a generalized framework designed to develop versatile MLIPs for accurately modeling extensive defects in metals, as depicted in Fig. 1. This framework is implemented through a sequential three-step process. Initially, a comprehensive pool of defect structures is generated using large-scale simulations based on well-established EIPs, notably the Embedded-Atom Method (EAM) potentials for metals. These potentials have been instrumental for over three decades, enabling the rapid simulation of complex defects across millions of atoms, albeit with lower accuracy compared to DFT. These capabilities are indispensable for simulating a broad spectrum of deformation scenarios, encompassing general GBs in polycrystals, as well as compression, tension, shear, and nanoindentation tests in both polycrystalline and single-crystal systems (Fig. 1a). For a particular metal (BCC W in this study), we employed EAM potentials to generate a diverse set of LAEs for various defects, addressing phenomena such as grain boundary relaxation and deformation, dislocation nucleation from material inside and exposed surfaces, dislocation multiplication, and complex dislocation-grain boundary interactions. The details of these MD simulations are presented in the “METHODS” section. Subsequently, the D-optimality criterion-based algorithm implemented in MLIP-323 is used to select representative LAEs according to the local atomic neighborhoods. This strategy meticulously evaluates the extensive pool of generated configurations against an established basic dataset (obtained through domain knowledge, as detailed in Supplementary Note 1), enabling the precise selection of the most representative LAEs. This process yields distinct atomic clusters with typical size of 100-200 atoms. For these clusters, vacuum layers of 8 Å thickness are added in all three dimensions of the simulation box to minimize image interaction. We develop an MLIP, named C-MLIP-0, combining the basic dataset with these cluster configurations. It should be noted that this C-MLIP-0 is very similar to the outcome of MLIP-323, with the only diffence is that OTF-AL is used in MLIP-3, while EIP-GS is used in our approach.

Fig. 1: The framework of versatile MLIP development for modeling extensive defects.
figure 1

a Empirical interatomic potential-guided sampling (EIP-GS). b Construction of periodic configurations from non-periodic atomic clusters through precise atom insertion using grand canonical Monte Carlo simulations (PCC-GCMC). c MLIP refinement by combining EIP-GS, on-the-fly (OTF-AL), and PCC-GCMC.

Full size image

In the second step, our PCC-GCMC strategy is employed to convert all clusters from the first step into periodic configurations, as shown in Fig. 1b. For each atomic cluster, we begin by initializing the simulation box size slightly larger than the atomic coordinates in all directions. Subsequently, new atoms (depicted in blue in Fig. 1b) are inserted into the box via GCMC simulations, continuing until no additional atoms can be accommodated. EAM potentials are used in GCMC simulations. During this insertion phase, the core atoms (shown in red) remain fixed to preserve the original LAE of the center atom. After the insertion is complete, both the coordinates of the newly inserted blue atoms and the box size are relaxed simultaneously. This step is crucial to prevent highly distorted LAEs among the newly inserted atoms. This procedure is iteratively repeated, with the box size gradually increasing to enable the insertion of atoms into lower energy states. By selecting only the lowest-energy configurations from PCC-GCMC, we ensure that all LAEs in these configurations are physically pertinent to the central LAE. The resulting new DFT dataset, combined with the basic dataset, is utilized to train a foundational model, termed P-MLIP-0, designed to be suitable for simulating common defects.

The final stage, Step 3, is the MLIP refinement phase, as illustrated in Fig. 1c. For specific applications not addressed in the initial EIP-GS of Step 1, such as crack propagation and radiation damage, further EIP-GS and PCC-GCMC operations are required, utilizing appropriate EIPs. A limitation of EIP-GS is its potential bias in generating necessary LAEs due to the inherent bias of EIPs. Consequently, MLIP-based large-scale simulations may generate unforeseen LAEs. To ensure the transferability of MLIPs across diverse applications, we implement the traditional OTF-AL process here for specific cases. All generated atomic clusters are converted into periodic configurations via PCC-GCMC and reincorporated into the training dataset. This process is repeated until no new LAEs are produced by OTF-AL. The final version of our MLIP, named P-MLIP-1, represents the culmination of our development efforts and is designed to robustly model a wide range of defect phenomena.

Inconsistent data in periodic configuration and cluster with vacuum layers

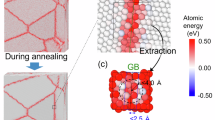
First, we investigate the potential issues arising from the use of clusters with vacuum layers in DFT calculations. In Fig. 2, we compare the DFT results for a periodic configuration and an isolated cluster with vacuum layers. The periodic configuration consists of a relaxed BCC supercell, where all atoms exhibit vanishing forces due to the equilibrium conditions (such as atom A in Fig. 2a). A spherical cluster with a radius of 9 Å is then extracted from the relaxed BCC supercell, as illustrated in Fig. 2b. Since the central atom of the cluster retains the same LAE as in the pristine BCC lattice, we expect its force to be zero. However, the results in Fig. 2c reveal a non-zero force magnitude of 18.7 meV/Å for the central atom B. Atom C, the first nearest neighbor of atom B, exhibits a force magnitude of 11.7 meV/Å, while the second nearest neighbor atom D shows a significantly larger force of 527.5 meV/Å. We further compare the LAEs of atoms A-D by plotting their SOAP (Smooth Overlap of Atomic Positions) vectors in Fig. 2d. We use the SOAP descriptor39 parameters set as rcut = 5Å, \({n}_{\max }\) = 12, and \({l}_{\max }\) = 1040. The SOAP analysis confirms that atoms A and B have identical environments, while atoms C and D exhibit environments very close to those of A and B. However, the force calculations performed on the cluster with vacuum layers in Fig. 2c yield inconsistent results. These findings highlight a critical discrepancy between DFT results obtained from periodic configurations and those from clusters with vacuum layers. Such inconsistencies can pose significant challenges for MLIP training, as a single atomic environment may correspond to distinct atomic forces.

Fig. 2: Inconsistent DFT results in a periodic configuration and an isolated cluster.
figure 2

a A relaxed BCC W supercell containing 256 atoms. b An isolated spherical cluster cut from a relaxed BCC W supercell. c Magnitude of atomic forces in the core region of the cluster. Only the center atom and its first two neighbors are color-coded by the force magnitude. Atom B is the center atom, while atoms C and D represent the first and second neighbors, respectively. d Comparison of SOAP vectors for the atomic environments of atoms A, B, C, and D.

Full size image

The atomic forces on the central atom in an ideal BCC W structure exhibit marked differences between periodic and truncated cluster-vacuum models due to contrasting boundary conditions and interaction truncation. In the periodic model, forces arise from long-range Hellmann-Feynman contributions of all periodic images, preserving lattice symmetry and yielding near-zero net forces at equilibrium positions. In contrast, the cluster model restricts interactions to finite atomic neighbors while introducing surface-induced symmetry breaking. This truncation eliminates long-range electronic screening and imposes asymmetric force distributions from edge atoms, resulting in non-vanishing residual forces on the central atom. These force discrepancies correlate directly with asymmetric charge density redistributions near the cluster surface and disrupted delocalization patterns, as visualized through comparative CHGCAR analysis of charge density gradients as shown in Fig. S2.

Significance of PCC-GCMC

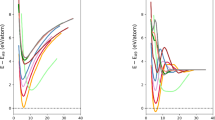
In this section, we discuss the significance of PCC-GCMC in modeling complex defects. To demonstrate the functionality of PCC-GCMC, we employ the example of a screw dislocation core in BCC W, as illustrated in Fig. 3a. The atomic cluster includes a screw dislocation core with three compact core atoms, labeled 1-3. This configuration maintains periodic boundary conditions along the z-direction, with free boundary conditions along the x and y directions. The PCC-GCMC process is repeated with varying box dimensions, Δx and Δy, from 1 to 10Å. Fig. 3b shows the average potential energies of each configuration constructed via PCC-GCMC. Notably, configurations with potential energies below -8.8 eV/atom, depicted in blue, approach the cohesive energy of -8.9 eV/atom which are nearly close to a perfect BCC W. Fig. 3c highlights two representative configurations. In the top panel, we observe a periodic configuration featuring a new non-compact core crossing the periodic boundary along the y-axis dislocation, with the rest of the atoms conforming to the perfect BCC lattice structure, excluding the original screw core. The bottom panel reveals a periodic configuration that includes a screw dislocation dipole, akin to typical screw dislocation dipole configurations with a tilted box. Both configurations depicted in Fig. 3c are generated entirely through automated processes. All newly inserted atoms either form a pure BCC lattice or constitute relevant LAEs, making them suitable for DFT calculation and MLIP training.

Fig. 3: Significance of PCC-GCMC in defect structure generation.
figure 3

a Atomic cluster containing a screw dislocation core. The lower panel shows atoms color-coded by common neighbor analysis (CNA): blue denotes pristine BCC lattice atoms, while white highlights disordered atoms at the defect core and surface. b PCC-GCMC-based grid search for energetically stable periodic configurations, with each data point colored by the system’s average energy (lower energy = darker blue). c Representative periodic configurations (A and B) reconstructed via PCC-GCMC, demonstrating its capability to generate DFT-compatible configurations from defect clusters. d Principal component analysis (PCA) of different datasets. e MTP training performance comparison between datasets B+C and B+P, evaluated across increasing model complexity levels (levels 12–20).

Full size image

It should be noted that we strictly enforce a 140-atom system size threshold in our PCC-GCMC methodology to ensure inserted atoms physically occupy vacancy regions through energy-minimized configuration selection. While larger atomic configurations would enable more physically representative models, particularly for achieving defect-free bulk regions surrounding isolated defects (e.g., the screw dislocation core shown in Fig. 2), DFT-based approaches remain computationally intractable for atomistic-scale defect modeling at these system sizes. This fundamental limitation necessitates our optimized balance between physical fidelity and computational feasibility.

All plastic deformations utilized in EIP-GS are illustrated in Fig. S1. Large-scale simulations are conducted using the EAM-Zhou potential41. Following the procedure outlined in Fig. 1a, we generate both cluster and periodic datasets. We systematically compare three datasets: (1) the cluster dataset (Fig. 1a), (2) the periodic dataset (Fig. 1b), and (3) the basic dataset curated through domain knowledge. These comparisons employ the Smooth Overlap of Atomic Positions (SOAP) descriptor39 with parameters rcut = 5 Å, \({n}_{\max }=12\), and \({l}_{\max }=10\)40. The results, visualized in Fig. 3d through principal component analysis (PCA), reveal distinct patterns. The basic dataset predominantly occupies PC1 < 0, with an extended arm representing surface atoms with PC1 > 0. The cluster dataset bifurcates into two groups: a minor cluster overlapping with the core of the basic dataset, and a major cluster positioned above its extended arm. This dominant group corresponds to surface atoms near free surfaces, while the smaller group reflects defect-related LAEs at cluster centers. The size disparity between groups indicates that only a minority of LAEs (central atoms) directly influence defect modeling, whereas most surface atoms do not contribute meaningfully to force/energy calculations of bulk atoms.

Unlike the cluster dataset, the periodic dataset forms a single cohesive group containing all target atoms from the cluster dataset. There is an overlapping region between the periodic and basic datasets, marked by a dashed line, suggesting shared common LAEs. This overlap signifies that the periodic configurations created via our PCC-GCMC method exhibit characteristics similar to those identified in ref. 42, with data points in this region likely corresponding to the perfect BCC lattice. Additionally, other data points in the periodic dataset represent inserted atoms from the GCMC process and atoms close to the surfaces in the original clusters. Although these LAEs are not explicitly defined in the initial EIP-GS (such as the non-compact screw core discovered in Fig. 3c), they may prove instrumental in exploring other types of unknown plastic deformations, which we will discuss further in the following section. Another interesting observation is that the LAEs of defects are not included in the basic dataset (3d), indicating that the existing MLIPs obtained through domain knowledge are unsuitable for modeling general defects.

Next, we proceed to train C-MLIP-0 and P-MLIP-0, using the cluster dataset (C) and the periodic dataset (P), respectively, with both datasets integrated into the basic dataset (B). Training is performed using the MTP framework. The performance of these models is evaluated by comparing the root mean square error (RMSE) of configuration energies, as shown in Fig. 3(e). Consistently, the B+P combination outperforms B+C across all MTP levels. The superior performance of B+P can be attributed to the simpler and more consistent nature of the periodic dataset, which avoids the inclusion of complex and irrelevant LAEs, such as surface atoms, that are present in the cluster dataset (illustrated in Fig. 3d). More importantly, DFT calculations of clusters with vacuum layers may introduce inconsistencies in the data compared to the basic dataset (B), which primarily consists of periodic configurations. These inconsistencies possibly arise from the truncation of long-range interactions and the introduction of surface effects in the cluster model, which are absent in the periodic case (Fig. 2). This finding highlights the first significant advantage of using the periodic dataset for MLIP training: by eliminating irrelevant LAEs and data inconsistencies, the training process becomes more robust, leading to more accurate and reliable MLIPs.

Uncertainty quantification across diverse plastic deformations

Our datasets, i.e., B+C and B+P, are designed to accommodate a wide range of defect simulations including dislocations, GBs, dislocation nucleation and multiplication, and dislocation-GB interactions. To verify the transferability of our datasets, we utilize per-atom uncertainty quantification available in MLIP-323 (the extrapolation grade γ) to evaluate various defects in BCC W. Values of γ ranging from 0 to 1 signify interpolation, while values greater than 1 imply extrapolation. Figure 4a–c display three common types of dislocation loops encountered in the plastic deformation of BCC metals: a 〈100〉 interstitial loop, a 〈111〉 glide loop, and a 〈111〉 climb loop. Given that the performance outcomes of the basic dataset combined with cluster one (B+C) and the basic dataset with periodic one (B+P) are comparable, we present only the results for B+C for clarity. Notably, using the basic dataset (B), all atoms within the 〈100〉 interstitial loop and those near the edge segments of the 〈111〉 glide loop, along with some atoms in the 〈111〉 climb loop, exhibit γ values significantly greater than 1, indicating a higher level of uncertainty (left panels of Fig. 4a–c). In contrast, all atoms within these dislocation loops, when analyzed using the B+C dataset, show γ values less than 1. This demonstrates our datasets’ enhanced effectiveness in capturing complex dislocations, with energies and forces of all LAEs obtainable through interpolation.

Fig. 4: Uncertainty quantification of various defects in BCC W based on different dataset.
figure 4

a–c Three types of dislocation loop, < 100 > interstitial loop, < 111 > glide loop, and < 111 > climb loop. Left panels are results from B, and right panels are results from B+C. Blue lines are edge dislocation segments, and red lines are screw segments. d Polycrystal model. e, f The probability density function (PDF) of extrapolation grade (γ) at 300 K and 2000 K. g, h Defect structures at the maximum indentation depth from B and B+C. i Evolution of the maximum extrapolation grade (\({\gamma }_{\max }\)) during the whole indentation process. All atoms in (a, b, c, d, g, h) are color-coded by γ. Red arrows in (b, c, g) indicate the atoms with high uncertainty. A value of γ between 0 and 1 indicates interpolation, while a γ greater than 1 suggests extrapolation.

Full size image

Additionally, we assess the transferability of our models regarding general GBs in polycrystals and their temperature-induced evolution. We calculate the extrapolation grade γ for all the atoms in a polycrystal relaxed by a MEAM potential43 at 300 K and 2000 K. It should be noted that our EIP-GS in the initial EIP-GS only uses the EAM-Zhou potential41, such that the GBs obtained by MEAM may have different LAEs. Fig. 4d illustrates the polycrystal at 300 K, with each atom color-coded according to the γ value obtained from B+C. Notably, all atoms in this representation exhibit γ values less than 1, indicating low uncertainty and high confidence in the predictions. Fig. 4e and f display histogram plots of the γ values for this polycrystal calculated using different datasets: B, B+C, and B+P at 300 K and 2000 K. The analysis reveals that the dataset B predicts γ values greater than 2 for atoms at both 300 K and 2000 K, indicating higher uncertainty. In contrast, γ values calculated by datasets B+C and B+P are consistently below 1 at 300 K. However, at 2000 K, there are a few exceptions with values of γ slightly higher than 2. This indicates that although B+C and B+P perform well at lower temperatures, at higher temperatures the uncertainty escalates but stays manageable. These results underscore the high transferability and effectiveness of generated defect genome in simulating the behavior of general GB and the thermodynamics of polycrystals.

We further evaluate the uncertainty quantification of our datasets during a continuous nanoindentation simulation, illustrated in Fig. 4g–i. Fig. 4g and h display the distribution of defect atoms color-coded by γ values at the maximum depth (4 nm), calculated using B and B+C, respectively. For the case of B, several regions exhibit γ values above 1, particularly in regions involving dislocation interactions and surface regions, as indicated by red arrows in Fig. 4g. In contrast, all defect atoms analyzed with B+C demonstrate γ values lower than 1 (Fig. 4h), indicating significantly lower uncertainty. Additionally, we calculate the maximum γ values (\({\gamma }_{\max }\)) among all defect atoms for each snapshot throughout the nanoindentation process. Comparisons of \({\gamma }_{\max }\) for B, B+C, and B+P reveal that B consistently shows \({\gamma }_{\max }\) values above 2, reflecting high uncertainty throughout the nanoindentation process. Conversely, both B+C and B+P maintain γ values around 1. These results indicate that our new datasets encompasses all the plastic LAEs during nanoindentation, including dislocation nucleation from open surfaces and complex multiplication beneath the indenter. It should be noted that datasets B+C and B+P exhibit comparable performance in uncertainty quantification analysis in Fig. 4. This is because the key LAEs for these defects are included in the core atoms of both datasets. However, this does not imply that dataset P, constructed using PCC-GCMC, is unnecessary. Firstly, DFT calculations of clusters introduce inconsistencies into the training data, as highlighted earlier in Fig. 2. Secondly, the periodic configurations in the dataset P enhance the extrapolation capability of the resulting MLIP. This advantage will be discussed in detail later.

MLIP refinement

It should be noted that all LAEs discussed above are generated using the EAM-Zhou potential41. The applicability of the MLIP-0 models developed based on these LAEs for modeling extended defects in large-scale simulations, particularly within MLIP simulations, remains uncertain. To address this issue, we employ the traditional on-the-fly AL (OTF-AL) implemented in MLIP-323. This process allows us to monitor the extrapolation grade γ during MLIP-based simulations and to identify unknown LAEs. These activities correspond to Step 3 in Fig. 1c.

We focus on the high-temperature relaxation of a polycrystal. Fig. 4e shows that our dataset, constructed via the initial EIP-GS, includes all LAEs in a polycrystal relaxed by the MEAM potential at 300 K. However, Fig. 4f reveals that these LAEs do not fully represent those at 2000 K, making EIP-GS ineffective for high temperatures. To address this, we use OTF-AL to model polycrystal relaxation at 300 K, 900 K, 1200 K, and 2000 K, starting with the dataset B+P. In the first AL loop, no new configurations are generated at 300 K and 900 K. However, the simulation at 1200 K is terminated due to atom loss, leading to the selection of 21 new configurations with γ > 2. These are converted into periodic configurations via PCC-GCMC and added to the training database to develop an updated MLIP. In the next loop, relaxation simulations proceed smoothly across all temperatures, with 25 additional configurations identified at 2000 K. This ensures a comprehensive defect genome for modeling general GBs in random polycrystals, all embedded in periodic configurations via PCC-GCMC. These configurations form the dataset OTF-AL-GB. To assess the uncertainty of our MLIP trained on B+P+OTF-AL-GB, we use ensemble learning (detailed in the METHODS section) to evaluate a polycrystal relaxed at 300 K and 2000 K (Fig. 5). The results show significantly reduced uncertainty, with most force standard deviations (σF) below 0.2 eV/Å, comparable to MLIP force prediction errors (Table S2). This confirms the high accuracy of the new MLIP in modeling general GBs.

Fig. 5: Uncertainty quantification based on ensemble learning for a polycrystal.
figure 5

a Results obtained using the basic dataset (B). b Probability density function (PDF) of the force uncertainty (σF) at temperatures of 300 K and 2000 K, considering only non-BCC atoms. c Results obtained using the combined dataset (B+P+OTF-GB). d Probability density function (PDF) of σF at 300 K and 2000 K, derived from the combined dataset, with only non-BCC atoms considered.

Full size image

Additionally, we refine our MLIP model by incorporating crack propagation, as detailed in Supplementary Note 1. Our approach successfully captures LAEs associated with diverse fracture mechanisms, as demonstrated in Fig. S2 using both EAM and MEAM potentials. Finally, we consolidate all datasets in Table S1 and train hierarchical MTPs alongside a high-dimensional ACE potential. Due to the excellent training accuracy of ACE, good performance for fundamental properties of BCC W, and computational efficiency (Supplementary Note 2 and Table S2), we select ACE as the final MLIP for large-scale MD simulations. The training performance of the ACE potential is summarized in Fig. S4. Further validation is provided by comparing the ACE-predicted phonon spectrum with the DFT results in Fig. S5, which shows excellent agreement. The DFT reference data are sourced from a recent study44, reinforcing the reliability of our ACE model.

Direct validation through comparison with DFT calculations

To demonstrate the superiority of our approach and the resulting MLIP, we validate MLIPs trained on datasets B, B+C, B+P (Fig. 3), and the final composite dataset against new DFT calculations, while benchmarking against two existing W datasets: the 2014 and 2019 datasets45,46. Six ACE potentials are trained and evaluated spanning five distinct validation scenarios: (1) GBs relaxed at 300 K, 900 K, and 2000 K (equilibrium structures from47), (2) severe compression-induced deformations and phase transitions (FCC/HCP lattices, amorphous phases; Fig. S10), (3) random 2D polycrystals, (4) 3D polycrystals generated via Voronoi tessellation, and (5) crack propagation configurations from36. Representative configurations and energy/force errors comparing MLIP predictions with DFT references are shown in Fig. 6. For GBs (task 1), nine symmetric configurations exhibit temperature-dependent structural evolution, while compression (task 2) reveals pressure-driven transformations detailed in Fig. S10. In tasks 3–4 (random 2D/3D polycrystals) and task 5 (crack systems), the MLIPs are rigorously evaluated across multifaceted defect environments, probing their robustness under extreme structural complexity.

Fig. 6: Direct validation of MLIPs for grain boundaries (GBs) and crack propagation through comparison with DFT-calculated energies and forces.
figure 6

a Structures including a simple GB under thermal perturbation and compressive loading, random 2D and 3D polycrystals, and crack propagation. Atoms in (a) are color-coded by common neighbor analysis (CNA), where blue represents perfect BCC lattices and white indicates defects or GBs. Performance of various MLIPs trained on different DFT datasets in terms of (b) energy and (c) force predictions.

Full size image

For validation tasks 1-4 in Fig. 6a, focusing on general grain boundaries (GBs), datasets B+C and B+P consistently outperform dataset B across all scenarios. A notable exception occurs in energy comparisons for thermally perturbed simple GBs, where B achieves marginally lower errors than B+C and B+P. However, B exhibits significantly higher force RMSE compared to B+C and B+P, underscoring the critical role of defect datasets in force prediction. These results confirm that incorporating cluster (C) or periodic (P) configurations enhances MLIP accuracy. Remarkably, B+P surpasses B+C in both energy and force accuracy, particularly for compressed simple GBs. This superiority stems from two factors: (1) PCC-GCMC introduces additional atoms as shown in Fig. 3d, enriching the representation of critical LAEs missing in B+C, and (2) periodic configurations mitigate data inconsistencies inherent to clusters with vacuum layers, as demonstrated in Fig. 2. These findings collectively validate the superiority of PCC-GCMC-derived periodic configurations over conventional cluster-based approaches.

Additionally, our final dataset demonstrates superior performance compared to the 2014 dataset45 and the 2019 dataset46. The latter dataset is widely adopted for large-scale applications such as radiation damage studies48. Notably, our approach achieves higher force prediction accuracy across all validation tasks. With only 39 crack-related configurations (Fig. S1 and Table S1), our dataset outperforms the 2019 dataset in crack propagation modeling, underscoring its exceptional data representativeness. This performance advantage persists even when tested on complex deformation mechanisms, highlighting the robustness of our curated atomic environments. The strength of our dataset stems from its systematic inclusion of diverse atomic configurations spanning multiple deformation modes (dislocation glide, phase transitions, fracture) in Fig. 1a, ensuring broad transferability to different material systems and extreme loading conditions. Combined with its compact size and reduced computational overhead, these features make our approach uniquely suited for both fundamental studies of material behavior and large-scale simulations of engineering-relevant scenarios.

MLIP applications in polycrystal tension

To demonstrate the high reliability of our final MLIP model in modeling general defects in BCC W, we have conducted MD simulations of polycrystal tension at room temperature (300 K). The results are presented in Fig. 7. The MD snapshot at the end of the simulation, shown in Fig. 7a, reveals a classical intergranular fracture pattern. Dislocation analysis in Fig. 7b indicates that very few dislocations are present within the grains, while dislocation networks primarily result from GB deformation. The stress-strain curve in Fig. 7c demonstrates that the W polycrystal exhibits very limited plasticity. The decreasing stress is attributed to crack initiation and propagation, with the sample fracturing completely at a strain of 0.32. These results align with previous experimental findings49,50,51, confirming that BCC W polycrystals are highly brittle at room temperature and that intergranular fracture is the dominant deformation mechanism.

Fig. 7: Tensile deformation of BCC W polycrystals.
figure 7

a Final fracture morphology after tensile loading. b Dislocation network analysis and crack initiation pathways. c Macroscopic stress-strain response under uniaxial tension. d Evolution of maximum extrapolation grade (\({\gamma }_{\max }\)) during tensile deformation. e Distribution of extrapolation grade (γ) across the fractured microstructure in (a). f Distribution of force standard deviation (σF) for the fractured configuration in (a).

Full size image

Importantly, we monitor the extrapolation grade (\({\gamma }_{\max }\)) throughout the tension simulation, as shown in Fig. 7d. It is evident that all atomic environments encountered during the simulation have counterparts in our final dataset, highlighting the comprehensiveness of the dataset. Furthermore, we provide a detailed uncertainty quantification analysis for the MD snapshot in Fig. 7a. The distribution of γ for each atom in Fig. 7e and the force standard deviation in Fig. 7f and Fig. S7 demonstrate that our MLIP is highly reliable, with minimal uncertainty in force predictions. These findings further validate the robustness and transferability of our MLIP for modeling complex deformation scenarios in BCC W.

Additionally, we have conducted comprehensive validation tasks to demonstrate the high reliability of our MLIP across different scenarios, including crack initiation (Fig. S8), nanoindentation into a single crystal (Fig. S9), nanoindentation into a bicrystal containing a twin boundary (Fig. S10), and structural transitions of GBs (Fig. S11). In all cases, the results exhibit very low extrapolation grade (γ) values and minimal force standard deviation, further confirming the robustness and accuracy of our MLIP in modeling diverse deformation mechanisms and defect behaviors.

Discussion

Over the past decade, MLIPs have emerged as a cornerstone in computational science, significantly impacting fields such as chemistry, materials science, and mechanics1,2,3,4,5,6. Various frameworks employing a range of atomic descriptors, including ASCF7, SNAP9, moment tensor10, and ACE11, have been developed. These frameworks have implemented diverse training strategies, from linear regression to neural networks, primarily focusing on enhancing the accuracy and computational efficiency of MLIPs. Such advancements are crucial, as they significantly improve the ability of MLIPs to model complex atomic interactions both accurately and efficiently, thereby paving the way for groundbreaking discoveries in multiple scientific domains. However, the construction of a robust training dataset is equally essential. The quality and comprehensiveness of the data used for training directly impact the effectiveness and reliability of MLIPs. Despite these developments, the scrutiny applied to most MLIPs remains insufficient. These potentials are often deployed in large-scale applications without undergoing rigorous validation across diverse conditions or against a wide spectrum of atomic configurations. Consequently, due to inadequately comprehensive training datasets, many existing MLIPs fail to accurately model general defects, thereby limiting their applicability in complex simulations.

Our approach demonstrates significant advancements over previous studies36,37,38. While these earlier methods are restricted to simple defects and often rely on manual operations, such as rotation and merging in ref. 36, they also require elastic solutions for simple defects to construct atomistic positions, as seen in refs. 37,38. In contrast, our methodology is uniquely capable of addressing complex defects, including mixed dislocations and general GBs, where prior approaches prove inadequate. An alternative strategy for developing a general-purpose MLIP involves systematic exploration of all possible space groups in random crystal structures, which generates the RANDSPG dataset52,53. Although MLIPs trained on the RANDSPG dataset achieve accurate modeling of simple GBs in Mg and general GBs in BCC Fe53, recent findings reveal substantial limitations. Specifically, high extrapolation grade (γ > 2) and significant force errors are observed in the polycrystal deformations of BCC Fe54, as reported by the same authors in the previous study53. In comparison, our MLIPs exhibit markedly lower uncertainty (γ < 2) in polycrystal tension even with significant fracture (Fig. 7e) and nanoindentation (Fig. S9 and S10). These results underscore the insufficiency of the RANDSPG dataset for modeling extensive defects and highlight the superior robustness of our approach.

While MLIP-3 enables OTF-AL with MTPs to address similar challenges23, our framework integrating EIP-GS and PCC-GCMC delivers key advancements. EIP-GS significantly reduces the computational expense of OTF-AL, which improves MLIP training efficiency. Conventional OTF-AL struggles with large-scale (million-atom) defect systems due to slow MLIP inference speeds15, especially for rare events such as diffusion and phase transitions. By leveraging EIP-GS with classical potentials (e.g., EAM, which is at least 100 times faster than MTPs), we bypass this bottleneck. Additionally, OTF-AL requires iterative retraining cycles30 — whether using linear regression or neural networks — which remain computationally costly. Although our method retains OTF-AL, it operates as a lightweight safety check. As evidenced in Table S1, only 72 of 348 configurations derive from OTF-AL, and only one retraining is required, underscoring its minimal role in our workflow.

Our PCC-GCMC method significantly advances MLIP development for modeling extended defects, serving as a critical enhancement to both EIP-GS and OTF-AL. Unlike conventional approaches in frameworks such as MLIP-323–which rely on vacuum layers to mitigate image interactions–PCC-GCMC eliminates both data inconsistencies and computational inefficiencies inherent to cluster-based methods. These limitations manifest in two critical ways: (1) Data inconsistencies from vacuum-containing clusters degrade model performance during both training (Fig. 3e) and inference (Fig. 6), and (2) surface-dominated LAEs in clusters underutilize critical defect-environment information (Fig. 3a). PCC-GCMC addresses these issues by generating periodic configurations directly compatible with DFT calculations, ensuring seamless integration into training datasets. This approach circumvents artificial surface effects while enabling systematic sampling of bulk-like defect environments. The inserted atoms either reconstruct pristine lattices/defects (Fig. 3c) or reveal previously uncharacterized defect configurations, significantly enhancing MLIP transferability (Fig. 6). By completely bypassing vacuum-layer approximations, PCC-GCMC provides a robust framework for capturing complex defect interactions essential to predictive large-scale simulations.

Finally, we demonstrate that our framework is generalizable to diverse crystalline materials for modeling extended defects, as illustrated in Fig. 8. The methodology applies universally across common crystal structures–including FCC, BCC, HCP, and diamond-cubic systems–and leverages the vast repository of EIPs from resources, such as the NIST Interatomic Potentials Repository (NIST-IPR) https://www.ctcms.nist.gov/potentials and OpenKIM55. These platforms collectively provide over 644 potentials (predominantly EIPs) spanning EAM, modified EAM (MEAM), bond-order (BOP), Stillinger-Weber (SW), Tersoff, and reactive force field (ReaxFF) formulations. While EIPs exhibit larger force/energy errors compared to DFT, their physics-driven consistency has fueled computational materials science for three decades56, which remains valuable despite the MLIP revolution. Our framework could harnesses these EIPs through three synergistic strategies: (1) lattice-constant-rescaled adaptation of isostructural material potentials, (2) mechanical-property-optimized parametrization57,58, and (3) average-atom potential generation for random alloys59. This enables the systematic creation of defect genome libraries for crystalline materials by sampling diverse LAEs across loading conditions. Critically, the approach transforms historical EIP investments into MLIP training assets, combining the interpretability of physical models with the accuracy of machine learning. The resulting LAE diversity–particularly for rare defect configurations–positions our methodology as both computationally efficient and physically insightful for next-generation materials simulation.

Fig. 8
figure 8

Implications of this study on MLIP development for modeling extensive defects in general crystalline materials.

Full size image

It is worth noting that extending PCC-GCMC to crystalline compounds requires careful adaptation of the GCMC algorithm to handle multiple atomic species. Nevertheless, PCC-GCMC remains applicable in certain scenarios. For high-entropy alloys, where elements are often interchangeable, PCC-GCMC can insert atoms of a single element during sampling and later substitute them with target elements. This approach prioritizes the generation of diverse structural environments while deferring the chemical complexity to post-processing steps. For non-exchangeable compounds like FeO, PCC-GCMC can insert atoms of a single element (e.g., Fe) around the oxide core, producing atomic environments relevant to interfaces (e.g., Fe/FeO boundaries). These environments are crucial for studying processes such as oxidation.

In summary, this work introduces an advanced framework for developing MLIPs by integrating EIP-GS, PCC-GCMC, and OTF-AL. This framework enables automated, ab initio-accurate, large-scale atomistic modeling of general defects in metals. The developed MLIPs are highly transferable and are based on comprehensive datasets that facilitate simulations of complex behaviors, including general GBs in polycrystals, dislocation nucleation and interactions, dislocation-GB interactions, and crack propagation in BCC W. Rigorous uncertainty quantification analyses, employing D-optimality criterion and ensemble learning techniques, confirm the accuracy of our models in these scenarios. This approach proves versatile enough to be generalized for modeling extensive defects in other BCC metals, FCC metals, and high-entropy alloys, demonstrating its broad applicability across various material systems.

Methods

First principles calculations

We utilize the Vienna Ab initio Simulation Package (VASP) to perform first-principles calculations of all new configurations necessary for MLIP development60. A gradient-corrected functional in the Perdew-Burke-Ernzerhof (PBE) form is used to describe the exchange and correlation interactions61. Electron-ion interactions are treated within the projector-augmented-wave (PAW) method, using the standard PAW pseudopotentials provided by VASP. The energy convergence criterion is set to 10−6 eV for electronic self-consistency calculations. The plane-wave cutoff energy is chosen to be 520 eV. The KPOINTS are generated by VASPKIT62, based on the Monkhorst-Pack scheme, with a consistent density of 2π × 0.03 Å across the entire dataset. For clusters with vacuum layers, only a single KPOINT is employed.

Empirical interatomic potentials

In our simulations, we utilize both the Embedded-Atom Model (EAM) and the Modified Embedded-Atom Model (MEAM) to perform large-scale molecular dynamics simulations of body-centered cubic tungsten (BCC W) under various loading conditions. Specifically, we employ the EAM-Zhou potential41 for simulating the relaxation, compression, and tension of W polycrystals, as well as single-crystal compression, tension, and nanoindentation processes. Additionally, the MEAM potential referenced in ref. 43 is applied to model crack propagation in single-crystal W.

Atomistic simulations and analysis

We employ the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package for all atomistic simulations63. For visualizing atomic configurations and post-processing results, such as extracting dislocation structures, we use OVITO64. Additionally, Atomsk is used to generate polycrystalline structures65. These packages provide a comprehensive suite of tools to support our study of the mechanical properties and plastic deformation mechanisms of BCC W. All MD simulation details are shown in Supplementary Note 3.

Machine learning potential development

We employ the MLIP-2 package22 and pacemarker16 to develop MTPs and ACE potential for BCC W. MLIP-2 utilizes moment tensor descriptors and applies linear regression to train the machine learning model, enabling it to predict the energy, force, and stress of atomistic systems. In our study, the weights of energy, force, and stress are set as 1, 0.01 and 0, respectively. For ACE, we utilize the highly nonlinear potential energy function with the complex form of \({E}_{i}=\varphi +\sqrt{\varphi }+{\sum }_{i}{\varphi }^{{f}_{i}}\), where \({E}_{i}=\varphi +\sqrt{\varphi }+{\sum }_{i}{\varphi }^{{f}_{i}},\quad {f}_{i}\in \left\{\frac{1}{8},\frac{1}{4},\frac{3}{8},\frac{3}{4},\frac{7}{8},2\right\}\), obtained from ref. 26. For the expansion of the atomic properties, we used 72 basis functions with 801 parameters. Bessel functions are used as the radial basis. The ratio between the force and the energy weights during the fitting, κ, is set as 0.01. For optimization, we use the BFGS algorithm for 4000 steps. The cutoff distance is set as 5 Å for both MTP and ACE.

More importantly, we utilize MLIP-323 to perform direct sampling based on the MaxVol algorithm from extensive simulations conducted with EAM or MEAM potentials. This method was originally developed for the OFT-AL of atomic environments, incorporating a cycle of MTP-based simulations, DFT calculations, and subsequent MTP retraining. In this study, to expedite the process, we exclusively utilize the EIP-GS to identify representative defects from a comprehensive pool of large-scale simulations. This approach and its implications are elaborated in Section 3.

We employ the regular on-the-fly active learning (OTF-AL) implemented in MLIP-323 to sample new local atomic environments (LAEs) during high temperature relaxation of polycrystals and crack propagation. This methodology utilizes an extrapolation grade γ, which quantifies the deviation of atomic configurations from those in the training set. The process begins by training an initial moment tensor potential (MTP) on a baseline dataset. This MTP is then deployed to simulate the target system under application-specific conditions such as mechanical loading. During simulations, configurations with γ > γbreak = 10 trigger immediate termination to avoid unreliable predictions, while those with γ > γselect = 2 are flagged for DFT validation and subsequent inclusion in the updated training set. The MTP is iteratively retrained until all configurations in production simulations are maintained γ < γbreak, ensuring robustness across target deformation regimes.

Uncertainty quantification

We adopt two methodologies for uncertainty quantification. The first utilizes atomic descriptors, specifically the extrapolation grade γ, as implemented in MLIP-323 and similarly applied in ACE35, based on the D-optimality criterion and the MaxVol algorithm. A value of γ between 0 and 1 indicates interpolation, while a γ between 1 and 2 indicates reliable extrapolation, and greater than 10 means risky extrapolation.

The second employs ensemble learning, where we train six independent MTPs on the same dataset to compute the standard deviation of atomic force:

$${\sigma }_{F}=\sqrt{\sum _{i\in \{x,y,z\}}\sigma {({F}_{\alpha ,i}^{(1..N)})}^{2}}.$$
(1)

Here, \({F}_{\alpha ,i}^{(1..N)}\) is the i-th component of the force acting on atom α as obtained by one of the 5 committee members (MTPs) for a particular configuration; σ denotes the standard deviation. It should be noted that while both approaches are valuable for uncertainty quantification, they fulfill different objectives. Each method can identify new local atomic environments (LAEs), but the extrapolation grade, γ, is specifically designed for this purpose and is particularly useful for OTF-AL. However, merely having a good sampling of LAE does not ensure the effectiveness of an MLIP. It is essential to implement a robust MLIP framework that can effectively train these datasets. Therefore, we integrate both methods in our work to leverage their distinct advantages.