Introduction

Two-dimensional (2D) materials, consisting of atomically thin sheets, have garnered significant attention since the discovery of graphene1,2, largely due to their remarkable properties. Notable examples include the Dirac cone in graphene, valley-selective light absorption in 2D transition metal dichalcogenides (TMDs), and the exceptional insulation offered by hexagonal boron nitride (h-BN) nanolayers3,4,5. The weak van der Waals (vdW) interactions between adjacent layers allow for tunable properties through techniques such as vertical stacking and horizontal twisting of multiple layers6. Since the pioneering proposal of magic-angle graphene in refs. 7,8, the deliberate rotation between adjacent layers has become a key strategy to manipulate moiré periodic potentials and interlayer electronic coupling7,8,9,10. This method not only modifies the intrinsic properties of the constituent layers, but also gives rise to a series of novel interface effect, such as unconventional superconductivity7,11,12, topological conducting channels13,14,15,16, and other correlated electronic phases. Its application has rapidly gained prominence in the study of 2D materials. As a result, twist-angle control has rapidly established itself as a transformative tool in the exploration of 2D materials and their emergent quantum properties.

Within this category, 2D topological materials—comprising insulators and semimetals—have emerged as a focal point due to their intriguing physics and experimental potential17,18,19,20,21. Notably, 2D topological insulators (TIs) exhibit a bulk energy gap and helical edge states, enabling dissipationless transport channels and the quantum spin Hall (QSH) effect22,23,24,25, provided time-reversal symmetry (TRS) remains intact. In particular, the superconductivity and magnetism can be induced through proximity effect, combined with the structural flexibility enabled by vdW interactions, which makes stacked 2D heterostructures a versatile platform for exploring topological phenomena26,27,28,29. Such as in the heterojunction consists of a graphene single layer sandwiched between two Bi2Se3 slabs, the 2D TI character of graphene and the strong SOC effect in Bi2Se3 layers lead to a strong band inversion with a large intrinsic bulk band gap30. Similarly, 1D topological superconductivity has been demonstrated in the proximity-induced MoS2 layer by NbS231,32. These examples highlight how the construction of tailored heterostructures offers an effective strategy for designing and realizing topological quantum materials.

Recently, a layered BaCu electride was synthesized33, exhibiting a monolayer structure with half-metal conductivity and distinctive band characteristics. Notably, its lower exfoliation energy (~0.84 J/m²) compared to the first 2D electride Ca₂N34 (~1.11 J/m², obtained via liquid exfoliation35) suggests the feasibility of isolating monolayers from the bulk material. As a novel layered electride, its monolayer structure exhibits multiple intriguing band crossings near Fermi level (EF)33, which may lead to 2D TI behavior while retaining its characteristic electride properties. In this study, we identify the BaCu monolayer as a nodal-line semimetal without SOC, with a nodal ring encircling the K and K′ points, as shown in Fig. 2b. When SOC is introduced, the nodal line is gapped, transforming the BaCu monolayer into a topological metal with 2D TI characteristic. Inspired by recent advancements in twisted bilayer physics7,8, we also investigate twisted heterostructures combining a BaCu monolayer and a hexagonal boron-nitride (h-BN) monolayer. Our findings reveal that the global minimum α-BaCu/BN configuration hosts six Weyl points, indicative of tunable topological properties. Additionally, the low energy barrier between α-BaCu/BN and local minimum β-BaCu/BN configuration suggests the potential for structural modulation. The β-BaCu/BN system, with Ba and Cu atoms aligned to the honeycomb voids of h-BN, is identified as a Dirac semimetal featuring a nearly flat band crossing the Γ−K line at the EF. Due to the lack of inversion symmetry, SOC-induced band splitting results in two Weyl points with opposite chirality. The small magnitude of this SOC splitting (~3.9 meV) underscores the robustness of Dirac fermions in the twisted system, highlighting their potential for further exploration in 2D topological materials.

Results and discussions

BaCu monolayer

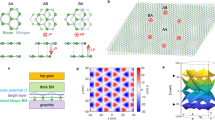
Figure 1a, b illustrates the crystal structure of the single-layer BaCu in side and top views. The monolayer has a lattice constant of a = b ≈ 4.33 Å and belongs to the P6/mmm space group (SG.191), corresponding to the p6/mmm layer group (LG.80). The BaCu monolayer consists of a Ba-Cu-Ba triple-layer configuration, with Cu atoms arranged in a hexagonal honeycomb pattern at 2 d Wyckoff positions (0.667, 0.333, 0.5). Ba atoms are located above and below the Cu-honeycomb layer at 2e Wyckoff positions (0, 0, 0.576). Detailed structural parameters, provided in Supplementary Information Table SI, confirm the optimized geometry. The phonon spectrum, free of imaginary frequencies (Fig. S1a), indicates the dynamical stability of the BaCu monolayer. Furthermore, the evolution of total potential energy and the preservation of ground-state geometry during ab initio molecular dynamics (AIMD) simulations over 6 ps at 0 GPa and both 300 K and 700 K (Fig. S1b, c) confirm its thermal stability at ambient and higher temperature conditions.

Fig. 1: Crystal structure and charge distribution analysis of BaCu monolayer.
figure 1

Single layer structure of BaCu with a side and b top view. c DCDD of BaCu monolayer in (110) plane. The ELF contours of BaCu monolayer on the d (110), e S1 and f S2 planes with the 0.1 linear divide.

Full size image

To elucidate the electronic properties of the BaCu monolayer, the deformation charge density difference (DCDD) and electron localization function (ELF) were analyzed. As shown in Fig. 1c, Ba atoms act as electron donors, while the regions surrounding Cu atoms and their corresponding surface positions serve as electron acceptors. The ELF further corroborates this, revealing an attractor near the (0.333,0.667,0.36) position with a charge density of above 0.4 (Fig. 1d). These attractors are indicative of interstitial anionic electrons (IAEs), suggesting the electride nature. A transverse section plane (S1) through the IAEs reveals a weak honeycomb-like electronic network (Fig. 1e), which closely resembles the electron distribution observed in the Cu transverse section plane (S2) (Fig. 1f). This similarity underscores the presence of metallic bonding characteristics. This electronic configuration likely contributes to the low work function (WF) of the BaCu monolayer (calculated value of 2.659 eV), which is lower than the WF of monolayered Ca2N (3.51 eV) and comparable to Ca2C (2.45 eV)36. Projected density of states (PDOS) analysis in Fig. 2a further confirms the metallic nature of the BaCu monolayer and highlights the strong hybridization between Ba and Cu atoms. Further analysis reveals the Ba-\({d}_{{xy}({x}^{2}-{y}^{2})}\) orbital contributes most among d-orbitals and shows stronger hybridization with Cu-\({d}_{{xy}({x}^{2}-{y}^{2})}\) and Cu-\({d}_{{xz}({yz})}\) orbitals. Moreover, the Cu-\({d}_{{z}^{2}}\) orbital shows a relatively localized peak near −0.18 eV in the PDOS, which indicates the Cu-\({d}_{{z}^{2}}\) orbital hosts a visible contribution to the band crossing along K-Γ.

Fig. 2: Topological band structure and 2D scanning of BaCu monolayer.
figure 2

a The orbital-projected band structure and PDOS (states/eV/f.u.) of BaCu monolayer with the calculated local area band structures without/with SOC. 2D scanning of the b nodal line in the BZ and c the gap between CBM and VBM for k points. d The BZ of BaCu monolayer and α/β-BaCu/BN systems, with the high-symmetry k-points indicated. The blue and green lines represent the projection of BZ along [100] and [120] miller index directions, respectively. e Edge states of BaCu monolayer in the (010) surface, which exhibits a 2D Dirac cone.

Full size image

The band structure without SOC, presented in Fig. 2a, reveals a band inversion between Ba-s and Cu-d orbitals near the K point, resulting in band crossings near the EF along K-M and K-Γ, respectively. The irreducible representations of the high-symmetry k-points, calculated and labeled in Fig. 2a, indicate that these band crossings are protected by Mz symmetry. Given that (kx, ky) in the 2D Brillouin zone (BZ) remain invariant under Mz, the Mz-protected band crossings (i.e., the two bands host different mirror eigenvalues \({g}_{z}=+1\) and − 1) correspond to a one-dimensional nodal line37, as determined through codimension analysis. The condition for such a nodal line can be described by the equation:

$${E}_{+}\left(\vec{k}\right)={E}_{-}\left(\vec{k}\right)$$
(1)

where \(\vec{k}\) has two independent components, \({E}_{+}\left(\vec{k}\right)\) and \({E}_{-}\left(\vec{k}\right)\) denote eigenvalues of the crossing bands with \({g}_{z}=+1\) and − 1, respectively. This implies that the solution space to the equation is generically one-dimensional, forming a nodal line. To validate this theoretical prediction, a two-dimensional band scan was performed with a 101\(\times\)101 k -mesh over 1/6 BZ. The resulting 2D density plots, shown in Fig. 2b, c, clearly exhibit nodal rings encircling both K and K′, confirming the presence of these one-dimensional nodal lines.

SOC is critical for engineering topological states, as demonstrated in phenomena like the QSH effect in graphene17,22 and Ta2M3Te5 (M=Pd, Ni) compounds38,39 and large-SOC-gap three dimensional topological insulators such as Bi2Se3 and NaCaBi families40,41. In the BaCu monolayer system, the refined projected band shows a gap opening after considering SOC (Fig. 2a). The inclusion of SOC ensures that P∗T-related degenerate states share the same Mz eigenvalue42, leading to the gapping of both nodal rings. This SOC-induced band gap around the K-point, as shown in Fig. 2c, is a clear manifestation of this effect. Symmetry eigenvalues, or irreducible representations (irreps), are essential for identifying TIs and topological crystalline insulators (TCIs) in solid systems43,44,45. Since SOC induces a direct band gap at each k point, the wavefunctions of the N lowest bands (where N corresponds to the number of valence electrons) can be defined throughout the entire 2D BZ, even though the system has a negative indirect band gap. Thus, using the method by Fu and Kane46, the Z2 index is calculated by multiplying all the parities for the occupied bands at all time-reversal-invariant momenta (TRIMs). The resultant parity of Γ and M is calculated to be “+” and “−”, respectively. Therefore, the calculated topological invariant Z2 = 1, which indicates that the BaCu monolayer exhibits the characteristics of a 2D TI. In the other hand, since the existence of the negative indirect band gap, i.e., there are electron and hole pockets crossing the EF, the monolayer is a metal. Thus, the BaCu monolayer is a topological metal with Z₂ = 1 for the N lowest bands. To identify the nontrivial topological metal phase, we perform the edge state calculations based on a tight-binding model constructed using maximally localized Wannier functions, combined with surface Green’s function methods47,48. As shown in the projected Brillouin zone (BZ) in Fig. 2d, the k-points corresponding to translation symmetries preserved along the (100) and (120) edges are marked by the blue and green lines, respectively. The calculated edge states with SOC, displayed in Fig. 2e, reveal a Dirac cone along the (100) direction. This observation confirms the presence of a topological metal phase in the BaCu monolayer.

Given its metallic nature, as indicated by N(EF) ~ 1.61 states/eV/f.u. from TDOS, the superconducting properties of the BaCu monolayer were investigated. However, the results reveal that it does not exhibit conventional superconductivity, with a negligible critical temperature (Tc) at ambient pressure. This can be attributed to the presence of heavy elements, which result in a very low logarithmic average phonon frequency (ωlog) about 64.9 cm−1 and a weak electron-phonon coupling constant (λ) of about 0.21(for MgB2, the N(EF) = 0.37 states/eV/f.u., the ωlog = 740.3 cm−1 and the λ = 0.6949). Although the BaCu monolayer does not exhibit intrinsic superconductivity, previous studies have reported that applying a 10% biaxial tensile strain can induce a superconducting phase with Tc of approximately 0.2 K50. This demonstrates that strain engineering could serve as an effective approach for modulating the electronic properties of the BaCu monolayer and realizing a superconducting phase transition. Furthermore, the effect of increasing the number of BaCu layers was examined. This multilayer configuration leads to a more complex charge distribution and band structure, as shown in Fig. S2. Importantly, these changes disrupt the topological property observed in the monolayer, highlighting the sensitivity of these features to the dimensionality and structural configuration of the material.

Twisted heterobilayer α-BaCu/BN

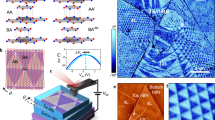
Given the intriguing properties of the BaCu monolayer, which is a 2D TI with a weak IAEs honeycomb network on its surface, it is worth exploring whether twisted heterostructures incorporating BaCu and other classical 2D materials might yield additional fascinating physics. To explore this possibility, we construct a twisted BaCu/h-BN heterostructure, selecting h-BN as the substrate due to its wide band gap (~4.9 eV51) and semiconducting nature. Given the strong metallic character of the BaCu monolayer discussed above, h-BN provides an ideal insulating counterpart for investigating interfacial effects in the heterostructure. Among various configurations, the heterostructure with a 30° twist angle exhibits the simplest crystal structure and the smallest atomic count. This system comprises a 1 × 1 BaCu monolayer and a \(\sqrt{3}\times \sqrt{3}\) supercell of h-BN, resulting in a stoichiometric composition of B1.5N1.5BaCu. The lattice mismatch between the two layers is less than 0.5%, ensuring structural compatibility. Despite the absence of a moiré superlattice due to the large twist angle, the BaCu/h-BN heterostructure demonstrates distinctive topological band properties, highlighting its potential for uncovering new quantum phenomena.

Determined through systematic scanning of the relative slip and interlayer distance between the BaCu and h-BN layers in heterobilayer (Fig. S3), the energetically favorable configuration is designated as α-BaCu/BN. Its configuration with a layer group of LG.70 and a corresponding space group of P31m (SG.157), as shown in Fig. 3a, b, the optimized lattice parameters are a = b ≈ 4.355 Å, with an interlayer spacing of 2.9 Å. The h-BN layer in this configuration displays a minor “wrinkle” with a displacement amplitude of less than 0.111 Å, as shown in Fig. 3a, which arises from interlayer interactions. In the α-BaCu/BN structure, boron atoms occupy the 1a (0,0,0.381) and 2b (0.667,0.333,0.384) Wyckoff positions, while nitrogen atoms are located at the 3c (0,0.331,0.383) Wyckoff positions. The thermodynamic stability of this twisted BaCu/h-BN heterostructure is confirmed by its calculated formation energy of about −85.2 meV/atom. The formation energy is defined as Uf (α-BaCu/BN) = [U (α-BaCu/BN) − U (BaCu monolayer) − 3 × U (h-BN monolayer)]/10, where the terms represent the total energies of the heterobilayer and two constituent monolayers, respectively. Additionally, the absence of imaginary frequencies in the phonon spectrum (Fig. S1d) at 0 GPa and the retention of structural integrity during AIMD simulations at 0 GPa and both 300 K and 1000 K (Fig. S1e, f) further confirm that α-BaCu/BN is both dynamically and thermally stable.

Fig. 3: Crystal structure, electronic and topological band analysis of α-BaCu/BN.
figure 3

The structure of α-BaCu/BN with a side and b top view. c CDD between its two layers of it in side view with the isosurface values of 10−3 e/Bohr3 and d the corresponding ab-plane-averaged charge density difference. The ELF contours of α-BaCu/BN on e (110) and f (-110) planes with the 0.1 linear divide. g The orbital-projected band structure and PDOS (states/eV/f.u.) of α-BaCu/BN with the calculated local area band structures without/with SOC.

Full size image

Charge density difference (CDD) between the two layers (Fig. 3c) reveals that electron depletion primarily occurs near the h-BN layer. As shown in Fig. 3d, the h-BN layer donates charge along the c-axis, influencing the interlayer interaction. Compared to the BaCu monolayer, the IAEs are altered due to interlayer effects, with partial charge transfer observed above the B atoms. WF decreases slightly from 2.66 eV for the BaCu monolayer to 2.48 eV for α-BaCu/BN, reflecting its subtle electronic modifications. Although these changes in charge density are relatively minor (10−3 e/Bohr3), they alter the local electronic distribution (Fig. 3e, f), leading to a reduction in the N(EF) from ∼1.61 states/eV/f.u. for the BaCu monolayer to ∼1.27 states/eV/f.u. for α-BaCu/BN. These variations are accompanied by slight shifts in the band structure (Fig. 3g), as anticipated.

As shown in Fig. 3g, the orbital-resolved band structures show a pronounced band inversion between the Ba-s and Cu-d dominated bands, resulting in a band crossing along the Γ-K direction, protected by M110 symmetry. Due to R3z symmetry, this crossing generates three 2D Dirac points, which are related by the same symmetry. TRS further introduces three additional Dirac points along Γ-K′. When SOC is included, these Dirac points split due to the absence of inversion symmetry. A detailed band scan (inset Fig. 3g) shows negligible SOC-induced splitting for the Cu-d band, while a visible splitting is observed for the Ba-s band due to the large SOC of Ba atoms. Consequently, each Dirac point evolves into a Weyl point, forming three pairs of Weyl points with opposite chirality along Γ-K and Γ-K′, respectively. The twist operation which heterojunction construction apparently affects the topology characteristics.

Adjusted heterobilayer β-BaCu/BN

Tuning the relative sliding52 and interlayer spacing53 between neighboring layers is effective method for engineering the band structures in vdW heterostructures. We considered a local minimum structure with Ba and Cu atoms aligned to honeycomb voids of h-BN (named as β-BaCu/BN). The energy of β-BaCu/BN is just larger ~0.9 meV/atom than α-BaCu/BN, exhibits unique type-III Dirac points. The optimized structure of β-BaCu/BN, shown in Fig. 4a, b, retains the same layer group (LG.70) and space group (SG.157) as α-BaCu/BN. However, it exhibits slightly adjusted lattice parameters (a = b ≈ 4.354 Å) and an increased interlayer spacing of ~3.076 Å. Within β-BaCu/BN, the boron and nitrogen atoms occupy the 3c Wyckoff positions at coordinates (0.665,0.665,0.361) and (0.331,0.331,0.362), respectively. Interestingly, the AIMD simulations at 0 GPa and 300 K reveal a spontaneous shift of the h-BN layer along the [110] direction to the configuration of α-BaCu/BN (Fig. 4c) within 0.6 ps (Fig. 4d-i). This spontaneous shift suggests a low energy barrier between α and β phases, indicating experimental feasibility of structural modulation.

Fig. 4: Crystal structure of β-BaCu/BN and its spontaneous transition in AIMD simulation.
figure 4

The structure of β-BaCu/BN in a side and b top view. c AIMD of β-BaCu/BN at 0 GPa 300 K with the initial and final structures, and d–i the spontaneous shifted process captured from 0.1 to 0.6 ps.

Full size image

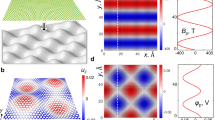
The CDD between BaCu and h-BN layers in β-BaCu/BN (Fig. 5a) shows some differences in charge transfer with the α-phase. Above B atoms, the obtained charge is tilted, which is contributed by the slip operation, B and Ba atoms are not strictly arranged along the c-axis now. But the global charge transfer can only see a subtle decrease (Fig. 5b), consistent with its larger interlayer spacing (3.067 Å). Overall, the structural differences lead to the variation in electron distribution (Fig. 5c, d). These give rise to the distinct type-III Dirac points in β-BaCu/BN, as shown in Fig. 5e.

Fig. 5: Crystal structure, electronic and topological scanning analysis of β-BaCu/BN.
figure 5

a The CDD between two layers of β-BaCu/BN in side view with the isosurface values of 10−3 e/Bohr3 and b the corresponding ab-plane-averaged charge density difference. The ELF contours of β-BaCu/BN on c (110) and d (-110) planes with the 0.1 linear divide. e The orbital-projected band structure and PDOS (states/eV/f.u.) of β-BaCu/BN with the calculated local area band structures without/with SOC. f Berry curvature density of β-BaCu/BN.

Full size image

Like the α-BaCu/BN, β-BaCu/BN also hold a band crossing along the Γ-K direction protected by M110 symmetry and generates three 2D Dirac points through R3z symmetry. Differently, the nearly dispersionless Ba-dominated bands along Γ-K contribute to these crossings, classifying them as type-III Dirac points—a critical state between type-I and type-II Dirac fermions, characterized by a Dirac cone touching the EF at its surface. The Dirac point is located at (\({k}_{c}\), \({k}_{c}\)) where \({k}_{c}=0.128\frac{2\pi }{a}\), with a representing the lattice constant. In addition, similar with the 2D Mn3Sn system, the flat band contributed to the type-III Dirac point near the EF remind us of the potential existence of the kondo lattice and kondo effect in the 2D (twisted) system54,55,56,57. When SOC is introduced, these Dirac points become gapped, as illustrated inset Fig. 5e. However, detailed band scanning with finer k-point spacing reveals that the SOC-induced gap is minimal (∼3.9 meV), underscoring the robustness of type-III Dirac fermions in this system. The Berry curvature density plot (Fig. 5f) further corroborates the existence of type-III Dirac points. Distinct k-points exhibiting maximum positive and minimum negative Berry curvature are observed near the Dirac points, providing additional verification of their presence and properties. Since the PBE functional tends to underestimate band gaps, we also calculate the local band structures with the Heyd–Scuseria–Ernzerhof hybrid exchange–correlation functional (HSE06)58, as shown in Fig. S4. The energy dispersions at the band crossing points from HSE06 are similar to those from PBE, confirming the robustness of the topological characteristics. In addition, we calculate the corresponding edge states for both the α- and β-twisted systems (Fig. S5), comparing the band structures obtained from the Wannier-based tight-binding model with those from first-principles DFT calculations. The close agreement between the two methods confirms the reliability of our data.

In summary, we have investigated the stability, electronic structures, and topological properties of the BaCu monolayer and the twisted α/β-BaCu/BN heterostructures. These twisted heterostructures consist of a BaCu monolayer stacking on a \(\sqrt{3}\times \sqrt{3}\) supercell of the h-BN monolayer, twisted by 30°. Although this large twist angle prevents the formation of moiré superlattice, the resulting heterostructures exhibit unique topological band characteristics. First-principles calculations reveal that the BaCu monolayer is a nodal line semimetal without SOC, transitioning to a topological metal with 2D TI features when SOC is included. Attributed to the heavy mass of Ba and Cu, the calculated Tc based on BCS theory is negligible. Furthermore, the 30° twisted bilayer α-BaCu/BN hosts six Weyl points, demonstrating that twisting can effectively tune topological properties. Considered the adjust of relative sliding and interlayer spacing between neighboring layers can effectively modulate the electronic property in vdW heterostructures, β-BaCu/BN with Ba and Cu atoms aligned to the honeycomb voids of h-BN is picked out. Its energy lager then α-BaCu/BN ~ 0.9 meV/atom, with lager larger interlayer spacing (~3.067 Å, α-BaCu/BN ~ 2.9 Å). Notably, AIMD simulations performed at 0 GPa and 300 K reveal a spontaneous transition from the metastable β-BaCu/BN to α-BaCu/BN, indicating a low potential barrier between these structures and the feasibility of modulating this twisted heterobilayer. The β-BaCu/BN configuration exhibits unique type-III Dirac points at the EF, highlighting the potential of twisted structures to modulate topological properties. This work establishes a robust theoretical and experimental platform for exploring twist-angle-induced topological electride states, offering broad opportunity for further research in tailored topological materials.

Methods

Density functional theory calculations

Calculations of the structural relaxations and electronic band structure are performed under the frame of the density functional theory integrated in the Vienna ab initio simulations package (VASP)59. The exchange–correlation functional is given by the generalized gradient approximation parameterized by Perdew, Burke, and Ernzerhof60. The van der Waals interactions were explicitly included in all VASP calculations by adopting the DFT-D461 functional. The plane-wave cutoff energy of 600 eV and Monkhorst–Pack k meshes with a grid spacing of 2π × 0.02 Å−1 were adopted. The dynamic stabilities were verified by calculations of the phonon spectra using the direct supercell method with PHONOPY code62. Ab initio molecular dynamics (AIMD) simulations were carried out using the Nosé–Hoover chain thermostat with the temperature of 300 K for 6 ps with a time step of 1 fs. The WF value was calculated through the formula of ΦWF = Evac − EF (Evac is vacuum level, EF is Fermi level). The IRVSP63 were used for the irreducible representations. The Berry curvature is calculated from wavefunctions derived via first-principles methods64,65.