Digitalizing metallic materials from image segmentation to multiscale solutions via physics informed operator learning

Abstract

Fast prediction of microstructural responses based on realistic material topology is vital for linking process, structure, and properties. This work presents a digital framework for metallic materials using microscale features. We explore deep learning for two primary goals: (1) segmenting experimental images to extract microstructural topology, translated into spatial property distributions; and (2) learning mappings from digital microstructures to mechanical fields using physics-informed operator learning. Loss functions are formulated using discretized weak or strong forms, and boundary conditions-Dirichlet and periodic-are embedded in the network. Input space is reduced to focus on key features of 2D and 3D materials, and generalization to varying loads and input topologies are demonstrated. Compared to FEM and FFT solvers, our models yield errors under 1–5% for averaged quantities and are over 1000× faster during 3D inference.

Introduction

Multiscale material modeling is essential for optimizing metallic materials and linking process parameters to product performance. Integrated computational materials engineering (ICME) combines approaches across scales, from atomic interactions and phase diagrams (CALPHAD) to phase field models and finite element simulations. While these methods excel in material design, their real-time application during production is limited by computational demands. This challenge is critical as the shift towards a circular steel economy introduces variability in compositions and process parameters¹.

Digital twins^2,3 and digital shadows (DS)⁴ have been explored as solutions for real-time feedback. However, these concepts are unsuitable for describing materials during production due to their multi-layered nature. To address this, the digital material twin (DMT) and digital material shadow (DMS) were introduced⁵. The DMT integrates the nano-, micro-, and macroscopic material structures, enabling comprehensive material description during processing. This framework accelerates material innovation and improves predictions for properties like strength and durability, bridging microstructural design to large-scale applications.

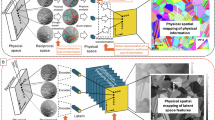
A digital material shadow framework⁶ is crucial for capturing data from machines and simulations, enabling cross-domain collaboration and defining real-world applications. This is especially relevant when microstructures evolve through distinct processes, as in drive shaft manufacturing⁷, involving forging, heat treatment, and machining. Using an ICME approach, the DMS tracks production data to predict microstructural changes at each stage, as shown in Fig. 1. The final microstructure analysis supports evaluations of local properties like surface integrity and component service life.

Fig. 1: Data pipeline of the drive shaft digital material shadow.

The production data and simulation results in each step of process chain is used in reduced models to predict the local microstructure and the material properties. The reduced models can be AI based or analytical, all linked by a data pipeline. By employing physics-informed operator learning, we aim to map the microstructure property to its mechanical deformation field. Consequently, this approach eliminates the necessity of data generation in forward problems.

The microstructure of the workpiece, material 42CrMo4 (1.7225), through the forging process undergoes static and dynamic recrystallization, resulting into an austenitic microstructure at the end. As this workpiece cools during heat treatment, the two-phase ferrite perlite microstructure is formed, which determines the properties of the material. The local properties are thus to be analyzed from the microstructure for the DMS of the shaft component.

The first challenge to address is the automatic detection of different microstructural features from experimental images, creating a digitalized version of the material for further analysis. The application of artificial intelligence (AI), particularly deep learning and convolutional neural networks (CNNs), has recently garnered significant attention for automating the identification, categorization, and analysis of material properties from two-dimensional experimental images^8,9. Agbozo and Jin¹⁰ utilized Mask R-CNN¹¹ to segment carbide particles, achieving an accuracy exceeding 90%. Similarly, Fu et al.¹² employed Faster R-CNN¹³ with transfer learning to detect dendrite cores in Ni-based superalloys, demonstrating high precision. Studies by Mulewicz et al.¹⁴ and Elbana et al.¹⁵ validated the utility of CNNs for classifying microstructural features in steels and ultrahigh carbon steel, while Banerjee and Sparks¹⁶ applied CNNs to categorize dendritic microstructures. Liotti et al.¹⁷ developed a supervised method that used real-time X-ray imaging to monitor crystal nucleation events during aluminum alloy solidification, achieving remarkable accuracy with automated image analysis algorithms. Further advancements by Breumier et al.¹⁸, Martinez-Ostormujof et al.¹⁹, and Germain et al.²⁰ demonstrated that U-Net-based deep learning models²¹ surpassed conventional thresholding techniques for tasks such as graphite shape characterization and phase discrimination in steels. The reviewed articles and advancements clearly demonstrate the potential of deep learning to automate the digitalization of experimental images, enabling the next level of progress in computational aspects.

In order to link macroscopic properties directly to the microscale without any ad-hoc assumptions, one needs to solve the microscale with appropriate numerical methods. Notable examples of simulation techniques include finite difference, finite volume, spectral methods²², boundary element methods^23,24,25, virtual element method^26,27,28 and finite element methods (FEM)²⁹. See also examples literature on FE² methods^30,31,32, a review of FE-FFT-based two-scale methods²² and hybrid DL-FE based ones for multiscaling^33,34.

Despite their predictive power, obtaining the solution from these methods can easily become time-consuming, which is problematic for many upcoming design applications. Secondly, as soon as any parameter changes (e.g., the morphology of the microstructure), one has to recompile the adapted model and redo the computation to obtain the new solution. In other words, the standard solvers are limited to one particular boundary value problem (BVP) and do not seem to be a sustainable and green choice, since they are designed to be used only once.

Deep learning (DL) methods provide solutions to the stated problem by leveraging their interpolation capabilities. For an overview of the potential of deep learning methods in the field of computational material mechanics see refs. ^35,36,37. The interpolation power of deep learning models is raised to a level that encourages researchers to train the neural network to learn the solution to a given boundary value problem in a parametric way. This idea is now pressed as operator learning, which involves the mapping of two infinite spaces or functions to each other. In the ideal case, the evaluation of a single forward pass of a neural network is similar to analytical solutions for partial differential equations, which provide the solution in a very fast way and under any given physical parameters. Some well-established methods for operator learning include but are not limited to, DeepOnet³⁸, Fourier Neural Operator³⁹, Graph Neural Operator⁴⁰ and Laplace Neural Operator^41,42.

In this category, the data for the training is obtained from the available resources or by performing offline computations and/or experimental measurements for a set of parameters of interest. The idea can also be combined with different architectures of convolutional neural networks (CNN), recurrent neural networks, etc., depending on the application. Winovich et al.⁴³ proposed and trained networks that are capable of predicting the solutions to linear and nonlinear elliptic problems with heterogeneous source terms. Yang et al.⁴⁴ employed a DL method to predict complex stress and strain fields in composites. Mohammadzadeh and Lejeune⁴⁵ provided a dataset for mechanical tests under various conditions and heterogeneities and predicted full-field solutions with MultiRes-WNet architecture. Koric et al.⁴⁶ applied the DeepONet formulation to solve the stress distribution in homogeneous elastoplastic solids with variable loads and material properties. Lu et al.⁴⁷ employed a deep neural operator to learn the transient response of interpenetrating phase composites under dynamic loading. He et al.⁴⁸ introduced a deep operator network with a residual U-Net to predict elastic-plastic stress response for complex geometries under variable loads. To further explore this topic, one can find comparative studies on available operator learning algorithms^49,50. Despite their benefits, deep learning methods face challenges: high training costs, limited performance beyond training data, and ensuring physical consistency in predictions.

Another mainstream goes in the direction of integrating the model equations into the loss function of the neural network^51,52. It is known as Physics-Informed Neural Networks (PINNs) as introduced by Raissi et al.⁵³. When the underlying physics of the problem is completely known, we can train the neural network without any initial data. Among many contributions, see its applications in fluid dynamics^54,55, solid mechanics^56,57,58,59, and constitutive material behavior^60,61. On the other hand, applying PINNs to forward problems without any training data remains an active area of research. To date, PINNs generally may match classical numerical methods (e.g., FEM) in terms of accuracy and computational efficiency for fixed boundary value problems⁵⁷.

An emerging area of research explores combining operator learning with PINNs. For example, Li et al.⁶² used Fourier neural operators to integrate training data and physical constraints. Wang et al.⁶³ introduced physics-informed DeepONets, enforcing physical laws through soft penalty constraints to improve prediction accuracy and reduce training data needs. Other approaches include combining CNNs with physical constraints^64,65,66, and Zhang and Gu⁶⁷ trained PINNs on digitalized materials without labeled data, using minimum energy criteria. Zhang and Garikipati⁶⁸ proposed encoder-decoder models to solve differential equations in weak form across varying conditions. In these methods, automatic differentiation is mainly used to build the loss function from physical knowledge.

Despite the current active progress reviewed above, key challenges remain. Accurately capturing high-frequency oscillations and sharp discontinuities is still difficult, and the generalizability of such models to out-of-distribution cases or different resolutions is not yet fully understood especially in the context of materials micromechanics. Moreover, eliminating the need for data generation by directly combining deep learning with classical numerical methods opens a promising research direction. Finally, an end-to-end pipeline-from image segmentation to solution prediction-remains largely unexplored (see also Fig. 1).

In this paper, we propose a novel method combining ideas from numerical methods (e.g., finite element and fast Fourier transform) for loss construction and neural operators to efficiently predict mechanical behavior in heterogeneous polycrystalline solids. By discretizing the loss function, we handle complex geometries and boundary conditions while improving training efficiency. The approach maps elasticity parameters to deformation states. Additionally, automated image segmentation is integrated to create digital microstructure representations, allowing direct use of light optical as well as scanning electron microscopy (LOM and SEM) for material property prediction (see e.g., ^69,70). This streamlines the workflow and extends applicability to complex microstructures, such as bainitic steels.

Results

Preparation of collocation fields

The neural network introduced in Section “Method” should be trained using initial input samples representing the Young’s modulus distribution. On the other hand, these samples should align with the realistic LOM images. It is important to note that the training process is entirely unsupervised (i.e., no FE solution is required) and random fields are sufficient to initiate the training by having the loss function based on discretized FEM residual vector.

In this work, we focus on the study of dual phase polycrystalline materials. Additionally, to ensure the completeness of the proposed methodology and the provided study strategies, we will also explore training the model for multiphase heterogeneous materials. These types of materials are commonly found in many alloys and composite materials^71,72. An overview of the LOM-based investigations, along with examples of randomly generated two-phase and multiphase polycrystalline structures, is shown in Fig. 2.

Fig. 2: Polycrystalline-based microstructures of 42CrMo4.

Left: LOM image of a ferritic-pearlitic steel grade. Right: Artificially generated random samples for unsupervised training of the finite operator learning framework.

The samples that were examined were from shafts made of 42CrMo4 (1.7225). In order to be able to examine the sample under the light microscope, small pieces were first removed from the shaft, which were then heat-embedded with ATM Duroplast black with graphite. The embedded sample was then grinded with silicon carbide paper up to 2500 grit and polished with a diamond paste. To make the microstructure visible, the surface was etched with three percent nitric acid. Microstructural images with a 100x or 500x magnification were then taken using a Leica DM 2500 reflected-light microscope and SIS software. The samples show a ferritic-pearlitic microstructure. The majority of the micorstructure is pearlitic, with some ferritic grains on the prior austenite grain boundaries.

On a typical production line, after forging one end of the shaft, the gripping end is forged after reheating. This produces two distinct microstructures in two different parts of the workpiece. Thus during experimentation, one shaft was forged without reheating, the other was cooled and reheated. The different process steps resulted in different grain sizes. The samples with reheating were coarser than the samples without reheating.

Our objective is to modify the morphology of these microstructures by controlling the number and distribution of grains. We have developed a straightforward yet effective algorithm to generate random input files, allowing control over the shape, quantity, and spatial distribution of grains. Although inspired by LOM images, the algorithm is adaptable and can be customized for different applications as needed. A detailed description of the algorithm is described in Supplementary Information.

For the LOM images, we converted them to grayscale and performed inference using the same trained network. The ferrite appears white in the original images, and the conversion to grayscale enhances its brightness. As a result, the Mask R-CNN model, trained on solidification results, effectively segments grains surrounded by ferrite and large ferrite grains. This provides a reasonable approximation of the grain distributions and sizes.

An example of the inference results is shown in Fig. 3. In Fig. 3a, the initial microstructure image, used as input for the Mask R-CNN model, is displayed. The segmentation results are presented in Fig. 3b, where the contours primarily align with the ferrite precipitates. From Fig. 3b, we selected a specific area, as shown in Fig. 3c. Based on the contours in Fig. 3c, we isolated each grain individually, with each grain represented in different colors in Fig. 3d. Finally, we propagated these grain contours isotropically to create a Voronoi structure, as shown in Fig. 3e.

Fig. 3: An example of the inference results.

a Initial image provided to the Mask R-CNN model (before conversion to grayscale); b Segmentation results using Mask R-CNN; c Specific area from the region outlined by the black square in (b); d Isolated grains based on the contours in (c); e Voronoi construction derived from (d).

This image will serve as input for the next model by assigning different material properties to each identified phase. Given a segmented microstructure image with distinct phases, the spatial distribution of a material property E(X), such as Young’s modulus, can be defined as:

$$E({\bf{X}})={E}_{i}\,\text{if}\,{\bf{X}}\in {\Omega }_{i},$$

(1)

where ${\bf{X}}\in {{\mathbb{R}}}^{d}$ is the spatial position (2D or 3D), Ω_i denotes the region occupied by phase i, E_i is the assigned material property for phase i. This expression assigns a constant material property E_i to each spatial point X based on the recognized phase from the segmented image.

We present a statistical analysis of the synthetic samples used to train the FOL and SPiFOL models, highlighting differences between training and test set topologies. For the 2D FOL model, 8000 dual-phase samples are analyzed based on phase fraction and dispersion, as shown in Fig. 4.

Fig. 4: The histogram of training and some of unseen test samples.

These samples are used for the unsupervised training of FOL in a 2D setting and are generated using Voronoi-based parameterization.

The unseen test cases derived from segmentation exhibit similar patterns to the artificially generated training samples. Their positions in the histograms, marked by red dashed lines, indicate that while some fall within the typical sample distribution, others lie further from the training data, suggesting a degree of generalization challenge.

The setup for the 2D and 3D SPiFOL frameworks presents a more challenging test for the deep learning models. Specifically, training was performed solely on Fourier-based samples at a resolution of 32³, while testing involved higher-resolution samples (up to 128³) with entirely different topologies inspired by polycrystalline microstructures.

Unlike the 2D case-where test samples were obtained via image segmentation-the 3D microstructures were synthetically generated to represent the target material (See Figure. 5). In future work, one could explore generative models to reconstruct 3D structures directly from 2D images. For more details on sample generation, see^73,74 and “Method” section. To quantitatively demonstrate that the test samples are out of distribution, we compute the Wasserstein distance between the training and test images, which shows a clear deviation. Additional details are provided in the Supplementary Information.

Fig. 5: Unsupervised training of SPiFOL in a 3D setting.

Training samples are based on Fourier parametrization. For testing, we use extreme out-of-distribution samples derived from polycrystalline microstructures.

Network parameters

The algorithms developed in this study are implemented using JAX⁷⁵ software and the methodology can be adapted to other programming platforms as well. A comprehensive summary of the network’s hyperparameters and configurations for all the models is provided in Table 1.

Table 1 Summary of the network parameters

The hyperparameters listed in Table 1 were selected based on extensive experimentation and represent configurations with some of the best performance. We explored the effects of various activation functions, network architectures, batch sizes, and even multi-stage training strategies to improve network initialization. Model selection was guided by the average error over 1000 reserved test samples in the final stage. For the FOL framework, we found that Swish and LeakyReLU activation functions performed best. Other activation functions, such as tanh, often led to trivial solutions dominated primarily by the boundary conditions.

Increasing the number of layers and neurons generally improved accuracy, but at the cost of higher training time. The final architecture balances performance and efficiency, based on systematic trial and error rather than global optimization (see Supplementary Information). Regarding batch size, we recommend using ~10% of the training dataset. Smaller batches lead to slower training but can yield better accuracy, while larger batches accelerate training but may be limited by GPU memory. Showing the network moderate-sized batches may also help avoid convergence to trivial solutions dominated by boundary conditions. For the SPiFOL model, increasing the number of Fourier layers and modes tends to improve performance, as illustrated in Supplementary Information.

The loss function for training all models follows a standard decay over epochs, as shown in Supplementary Information. We stopped the training when there is no significant improvement by increasing epochs.

Quadro RTX 6000s with 24 GB of RAM is utilized for the training of all models. An important aspect of parametric training for the proposed network is the proper initialization of its free parameters. From a mathematical perspective, we are dealing with a multi-objective optimization problem with a highly complex loss function. This loss function aims to map microstructural features to the physical solution space while strictly satisfying boundary conditions. Consequently, it is highly challenging to avoid local minima and trivial solutions that fail to capture the complex deformation patterns in heterogeneous material systems. This challenge is commonly associated with capturing high frequencies and sharp jumps in the solution response, as well as ensuring the network remains unbiased toward these features. To address this issue, we drew inspiration from transfer learning. Specifically, we gradually train the system using an increasing number of samples, rather than training the network all at once with the entire set of randomly generated samples. This stepwise approach enables the network to progressively refine its performance, benefiting from improved initialization at each stage.

For the material parameters, we primarily focus on varying the Young’s modulus. The normalized values range from 0.05 to 1.0, depending on each example. We intentionally examine a wide range of phase contrasts to demonstrate the applicability of the proposed approach to higher phase contrast values, which are common in various material engineering applications. In other words, for the training we go beyond the typical properties of 42CrMo4 (1.7225). In the “Result” section, we specify the corresponding values for each test case. Furthermore, for the multiphase material system, random values are assigned to each grain. These values are normalized so that the normalized Young’s modulus values remain between 0 and 1.

Finally, we address the applied boundary conditions. In the first set of studies with the 2D setup, we focus on an arbitrary set of boundary conditions (BCs), which consist of a mix of Dirichlet and Neumann conditions. The applied displacement on the right edge is (U_R, V_R) = (0.05, 0.05) mm, while the upper and lower edges remain traction-free.

For the SPiFOL setup, where periodic boundary conditions (PBCs) are enforced, the macroscopic strain tensor, denoted by $\bar{{\boldsymbol{\varepsilon }}}$, is fixed for all reported results, as

$${\bar{{\boldsymbol{\varepsilon }}}}_{2D}\,=\,\left[\begin{array}{cc}0.05&0.0\\ 0.0&0.0\end{array}\right],\quad \,{\text{and}}\,\quad {\bar{{\boldsymbol{\varepsilon }}}}_{3D}\,=\,\left[\begin{array}{ccc}0.05&0.0&0.0\\ 0.0&0.0&0.0\\ 0.0&0.0&0.0.\end{array}\right].$$

(2)

For the 3D setup within the FOL framework, we aim to learn the solution for randomly applied boundary conditions, while the microstructure topology remains fixed. In this setup, the back surface is fixed, arbitrary boundary conditions are applied to the front surface, and all other surfaces are traction-free.

FOL prediction for 2D test cases: learning on different topologies

We train the network using the parameters listed in Table 1 and the artificially generated samples discussed in Fig. 4 and Supplementary Information. Once training is complete, we evaluate the performance of the deep learning model on unseen test cases derived from segmented LOM images, as described in Section “Method” and illustrated in Fig. 3. The evaluation results for the 2D cases are presented in the following sections.

The results presented in the following are selected examples from the test set, consisting of either segmented images or synthetically generated samples with similar characteristics such as grain size and phase fraction. More comprehensive statistical analysis and systematic error evaluations of the trained models are provided later. Note that most results show the absolute pointwise error between the DL model and classical FEM or FFT solvers. While this is common in the operator learning literature, relative errors are less meaningful here due to potential division by zero. Instead, we later report relative errors of homogenized (averaged) quantities, which offer more useful insights for future multiscale applications. For convenience, all the reported values are presented in normalized notation. Further error analysis and comparisons of computational costs are provided later on.

In Figs. 6 and 7, the solutions obtained from FOL and FEM for the deformation component U are compared, showing an excellent match between the two methods. Similar results are observed for the deformation component V, although these are not shown for brevity.

Fig. 6: Results of the FOL model.

Prediction of the displacement field for an unseen test case (Case 1).

Fig. 7: Results of the FOL model.

Prediction of the displacement field for an unseen test case (Case 2).

In Fig. 8, we repeat the same study for a multiphase polycrystalline material, where similar observations confirm the effectiveness of the proposed approach for approximating solutions solely based on governing equations. Next, we use the predicted deformation components from the trained network, apply spatial gradients based on standard FEM routines, and calculate the stress components.

Fig. 8: Results of the FOL model.

Prediction of the displacement field for an unseen test case (Case 3).

In Fig. 9, the comparison is presented for the stress components σ_xx and σ_yy. While the overall behavior matches very well, small fluctuations in the predicted solution lead to slightly more oscillatory behavior in the DL model. Nevertheless, the peak values and averages are captured with less than 5%. Here, FOL is trained to predict displacement, not stress directly. Although displacement errors are low, stress errors can be amplified due to sensitivity to derivatives, which explains the higher errors. A potential solution is to train the model to predict stress directly, as demonstrated in the next section. An alternative not explored here would be to enhance FOL using a mixed formulation to directly learn stress fields, as suggested in ref. ⁵⁷.

Fig. 9: Results of the FOL model.

Prediction of the stress field for an unseen multi-phase test case (Case 3).

SPiFOL prediction for 2D test cases: learning on different topologies

The SPiFOL model is now evaluated and tested on unseen periodic samples, and the results of the predicted stress components are shown in Fig. 10 for one unseen test case. Similar to the previous section, the results shown here are a few representative cases for demonstration purposes. A more comprehensive statistical error analysis over larger test sets and varying training sample sizes will be presented later.

Fig. 10: Results of the SPiFOL model.

Prediction of the stress field for an unseen test case (Case 4).

The stress profile errors are lower in the SPiFOL model compared to the FOL model. This improvement arises because the SPiFOL model’s loss function directly targets the strain components, which can be used to evaluate the stress. In contrast, the FOL framework, while accurately capturing the deformation field, shows increased errors in predicting spatial derivatives due to their higher sensitivity to deviations. It is important to note that SPiFOL, based on the FNO architecture and FFT algorithm, is restricted to regular grids with periodic topologies.

It is important to note that the test sample topologies shown above satisfy geometric periodicity and may not exactly replicate experimental microstructures. Nevertheless, they preserve key statistical features such as grain count, phase fraction, and phase contrast. Additionally, these test cases represent challenging scenarios, as the SPiFOL model was trained exclusively on Fourier-based samples without prior exposure to any Voronoi-based structures.

Extension to 3D: learning on different boundary conditions

Here, the model learns with respect to the applied Dirichlet boundary conditions on the front surface. The morphology of the microstructure is kept constant, representing a chosen volume element, while we investigate how deformation and stress components develop under various boundary conditions.

The details of the boundary value problem are illustrated in Fig. 11, where two different cases with two-phase and multiphase polycrystalline materials are analyzed. For the meshing process, the approach is highly adaptable, allowing the use of either structured or unstructured meshes with any element type, seamlessly integrated into the proposed FOL framework.

Fig. 11: 3D microstructure and its corresponding mesh.

This test is used to learn the system response under arbitrary loading directions.

For more details on the type and distribution of the training samples as well as the NN hyperparameters, see Supplementary Information. According to Fig. 12 where distribution plots of the Dirichlet boundary condition components are shown, the selected test cases are intentionally chosen outside the typical range to evaluate the interpolation capability of the trained network.

Fig. 12: Distribution of the applied displacement components.

The colored markers represent selected test cases and the histograms depict the distribution of 1000 training samples. The test cases are intentionally chosen outside the typical range.

Deformation magnitude ($\sqrt{{U}^{2}+{V}^{2}+{W}^{2}}$), as well as the σ_x stress component are reported. For the two-phase 3D volume element, we present two entirely different test cases for the applied deformation: one predominantly in tensile mode and the other primarily involving shear and compression, as illustrated in Fig. 13. The corresponding predicted values for the stress component σ_x are shown in Fig. 14. Due to the strong heterogeneity, we observe sharp jumps in the deformation and stress fields, which are both captured very accurately.

Fig. 13: Results of the FOL model.

Prediction of the displacement for two different unseen loading directions.

Fig. 14: Results of the FOL model.

Prediction of the stress field for two different unseen loading directions.

Extension to 3D: learning on different topologies using SPiFOL

Finally, we examine the performance of the trained 3D SPiFOL model. The test cases are selected to feature topologies similar to experimental images and yet very different from those in the training set, and the evaluation is carried out at various resolutions to assess the model’s zero-shot super-resolution capability. Figures 15 and 16 compare the SPiFOL predictions with those of the FFT solver for two selected stress components and two representative morphologies: one dual-phase and one multi-phase polycrystalline microstructure.

Fig. 15: Results of SPiFOL model.

A 3D dual-phase polycrystalline is used as an extreme unseen test case.

Fig. 16: Results of SPiFOL model.

A 3D multi-phase polycrystalline used as an extreme unseen test case.

In Fig. 17, we evaluate the same dual-phase polycrystalline test topology at different resolutions. Importantly, no re-training is performed; the model trained on a 32³ grid is directly evaluated on finer grids of 64³ and 128³. As expected, the maximum pointwise error increases with resolution, primarily due to fine-scale features in the microstructure that may be missed when training on lower-resolution data. This highlights the challenge of applying models across significantly different resolutions. Therefore, we recommend conducting a proper mesh or grid convergence study, similar to the one in Supplementary Information, before selecting the training resolution.

Fig. 17: Results of SPiFOL model.

Upscaling the results of SPiFOL (from 32³ to 128³ grid points) using zero shot super resolution.

A potential remedy is to integrate the model with microstructure-embedded autoencoders, as proposed in ref. ⁷⁶, to retain critical details lost during downsampling. Nevertheless, when considering the error in homogenized (averaged) stress values, the results remain low and within acceptable limits. This suggests that SPiFOL effectively reduces the dimensionality of the problem, enabling training at low resolution while still capturing meaningful averaged quantities when evaluated at higher resolutions.

Computational costs and error analysis

Here, we evaluate the current methodology by comparing its performance in training and evaluation against classical numerical solvers. The results of such comparisons are summarized in Table 2. For brevity, FEM and FOL are used for comparison, with similar trends also observed when comparing SPiFOL to the FFT solver.

Table 2 Comparison of the computational costs

The test cases presented above demonstrate the potential of the trained model to generalize to unseen scenarios, even those outside the training patterns. In this section, we critically evaluate the performance of the trained models using a larger set of test cases. Three main aspects are explored: first, we analyze the distribution of errors across a broader range of test samples, examining variations in topology; second, we investigate the impact of the number of training samples on model performance; and third, we compare the purely physics-informed training (i.e., label-free) with a data-driven approach, where we first solve for all training samples using classical numerical solvers and then train the network using these labeled data. The results of these investigations are summarized in the following figures. Note that, due to the presence of two models and numerous possible variations, we alternate between them for the sake of brevity in these studies. However, similar results and trends are expected, unless stated otherwise.

In order to report the relative errors in percentage, we introduce the following measure, which applies to an arbitrary quantity.

$${\rm{Relative}}\,{\rm{Error}}( \% )=\frac{\left\vert \hat{\bullet }-{\hat{\bullet }}_{{\rm{numerical}}}\right\vert }{\left\vert {\hat{\bullet }}_{{\rm{numerical}}}\right\vert }\times 100,\quad \hat{\bullet }=\frac{1}{V}{\int}_{V}\bullet \,dV$$

Here, $\hat{\bullet }$ represents the volume-averaged value predicted by the model, ${\hat{\bullet }}_{{\rm{numerical}}}$ represents the volume-averaged value obtained from the numerical method (e.g., classical FEM, FFT solver, etc.). Moreover, the volume-averaged value is defined as $\hat{\bullet }$ is the volume-averaged quantity, V is the volume over which the averaging is performed, • is the quantity of interest (e.g., stress, deformation, etc.).

In the left panel of Fig. 18, the relative averaged error in displacement components (primary field) over 500 unseen samples is shown. The trained FOL model demonstrates excellent performance, with overall average errors consistently below 4%. Dual-phase topologies exhibit slightly higher and more widely distributed errors, reflecting the increased difficulty due to sharp field variations. A similar level of accuracy is observed for stress components, as discussed earlier, since local fluctuations have minimal influence on averaged quantities. The overall relative error in homogenized stress remains below 3%. Same pattern for the results also holds for the 3D FOL model. In the 3D case, the reported errors are even lower, as the training was based solely on varied boundary conditions while maintaining a constant topology. This observation suggests that the solution’s sensitivity to topology is significantly higher than to the applied boundary conditions, which aligns with intuitive expectations.

Fig. 18: Error analysis of the FOL model.

About 500 test samples for dual- and multi-phase polycrystalline microstructures are evaluated using the trained 2D FOL models. Higher errors are observed for the dual-phase case which is likely due to the increased complexity and presence of high-frequency solution modes caused by abrupt phase transitions.

We now turn to the SPiFOL model. In Fig. 19, two key analyses are presented. First, we observe how the error decreases as the number of training samples increases. Second, we compare the error distributions between two models: one trained with physics-informed constraints in Fourier space, and another trained purely on data from an FFT solver. Notably, the physics-informed model consistently outperforms the data-driven counterpart, showing both lower average errors and reduced standard deviation. Similar trends are also observed for the FOL model. In some cases, the data-driven model captures only trivial solutions, missing critical gradients arising from material heterogeneity, whereas the physics-informed model better resolves such complexities. Same pattern of results also repeat itself for the 3D SPiFOL model.

Fig. 19: Error analysis of the trained 2D SPiFOL model.

About 100 unseen test cases are evaluated where we also compare its performance against a purely data-driven method and examining how the error decreases as more training samples are provided⁷⁴.

Discussion

This work discusses and aims to further motivate the application of advanced deep learning algorithms for the chain of metallic material engineering. We address two main challenges: one is translating experimental images into digitized images for numerical analysis, and the second is solving the system of equations via again DL techniques in a complex heterogeneous domain.

To address the first challenge, we utilize Mask R-CNN deep learning models to segment the LOM images of the metallic microstructure. The backbone of the proposed model builds on established literature, particularly⁷⁷ and references therein. To address the second challenge, we utilize the Finite Operator Learning method. This approach is data-free, physics-informed, and notably supports parametric learning of partial differential equations. The key novelty lies in formulating the loss function using either the parametric discretized weak form or the strong form in Fourier space. Furthermore, the proposed framework inherently satisfies Dirichlet and PBCs through its architectural design. See also refs. ^73,74,78.

We demonstrate the performance of DL models in 2D and 3D setting with multi- and dual-phase distributions of properties, where we feed different topologies of the microstructure (elasticity distribution) as input. The results of the analysis show acceptable agreement compared to the classical numerical method, making it an attractive surrogate model to replace costly calculations for this particular set of materials.

While the proposed framework shows promising generalization-especially with embedded physical constraints-it shares common limitations of deep learning methods. Performance may decline when inputs deviate significantly from the training distribution or when low-resolution models are applied to much finer grids, leading to local errors. However, integral quantities remain accurate, underscoring the potential of neural operators for zero-shot super-resolution in computational material mechanics (see also ref. ⁷⁹).

The current work can be extended in several important directions. Future efforts should incorporate anisotropic behavior and nonlinear material responses such as plasticity and damage. Promising contributions in this direction have been reported in refs. ^60,80, where information on yield surfaces and evolution laws is embedded into the physical loss terms.

The concept of FOL can be extended to other numerical methods such as the Boundary Element Method²⁴ and the Virtual Element Method²⁷, both of which are well-suited for simulating material micromechanics. VEM provides enhanced meshing flexibility, broadening the applicability of traditional FEM approaches, while BEM offers significant mesh reduction advantages for specific classes of problems.

The presented framework demonstrates strong potential for advancing computational materials engineering. In particular, the development of multiscale models and homogenized datasets lays a foundation for improved machinability predictions and optimization of manufacturing processes. These data-driven insights, when integrated with Industry 4.0 technologies, offer a path toward real-time monitoring and adaptive control. Furthermore, the generated data can support Digital Twin systems for predictive simulation and optimization. This approach is broadly applicable to machining, and processes such as metal forming and additive manufacturing, and future work will explore these directions in more detail.

Methods

In this work, we primarily focus on two-phase and multi-phase material systems, addressing a broad range of potential applications through two distinct models. The first model integrates ideas from FEM and is designed to handle arbitrary combinations of Neumann and Dirichlet boundary conditions, accommodating complex shapes and geometries. The second model is tailored for PBCs and microstructures, leveraging spectral methods for efficient analysis. Both models are constructed based on physical domain knowledge and do not require any labeled data for training. Moreover, they are designed to learn the governing equations in a parametric manner, enabling them to generalize and solve a class of problems once the training stage is complete. In what follows, we refer to the 2D formulation for simplicity; however, extension to 3D is straightforward, and the results of the 3D calculations are reported later.

Continuum model and elastic theory

Here we shall summarize the mechanical problem in a 2D heterogeneous solid where the position of material points is denoted by X^T = [x, y]. We denote the displacement components by U and V in the x and y directions, respectively. The kinematic relation defines the strain tensor ε in terms of the deformation vector U^T = [U, V] and reads:

$${\boldsymbol{\varepsilon }}\,=\,\,\text{sym}(\text{grad}\,({\boldsymbol{U}}))={\nabla }^{s}{\boldsymbol{U}}=\frac{1}{2}\left(\nabla {\boldsymbol{U}}+\nabla {{\boldsymbol{U}}}^{T}\right).$$

(3)

In the context of linear elasticity, we define the elastic energy of the solid as ${\psi }_{lin}=\frac{1}{2}\,{\boldsymbol{\varepsilon }}:{\mathbb{C}}({\boldsymbol{X}}):{\boldsymbol{\varepsilon }}$, where ${\mathbb{C}}$ is the fourth-order elasticity tensor. Through the constitutive relation, one relates the stress tensor to the strain tensor via ${\boldsymbol{\sigma }}={\mathbb{C}}({\boldsymbol{X}})\,{\boldsymbol{\varepsilon }},$ where we have ${\mathbb{C}}({\boldsymbol{X}})=\Lambda ({\boldsymbol{X}})\,{\bf{I}}\otimes {\bf{I}}+2\mu ({\boldsymbol{X}})\,{{\mathbb{I}}}^{s}$. Defining I as the second-order identity tensor and ${{\mathbb{I}}}^{s}$ as the symmetric fourth-order identity tensor, the above relation can also be written in the following form

$${\boldsymbol{\sigma }}=\Lambda ({\boldsymbol{X}})\,\,\text{tr}\,({\boldsymbol{\varepsilon }})\,{\bf{I}}+2\mu ({\boldsymbol{X}})\,{\boldsymbol{\varepsilon }}.$$

(4)

Here, we have position-dependent Lamé constants which can be written in terms of Young’s modulus E and Poisson’s ratio ν as Λ = Eν/[(1 − 2ν)(1 + ν)] and μ = E/[2(1 + ν)]. Here, the elastic properties are phase-dependent and vary throughout the microstructure. Finally, the mechanical equilibrium in the absence of body force, as well as the Dirichlet and Neumann boundary conditions, are written as:

$$\,\text{div}\,({\boldsymbol{\sigma }})=\,\text{div}\,({\mathbb{C}}({\boldsymbol{X}}){\nabla }^{s}{\boldsymbol{U}})\,={\boldsymbol{0}}\quad \,\text{in}\,\quad \Omega$$

(5)

$${\boldsymbol{U}}=\bar{{\boldsymbol{U}}}\quad \,\text{on}\,\,\,{\Gamma }_{D}$$

(6)

$${\boldsymbol{\sigma }}\cdot {\boldsymbol{n}}={\boldsymbol{t}}=\bar{{\boldsymbol{t}}}\quad \,\text{on}\,\,\,{\Gamma }_{N}$$

(7)

In the above relations, Ω and Γ denote the material points in the body and on the boundary area, respectively. Moreover, the Dirichlet and Neumann boundary conditions are introduced in Eq. (6) and Eq. (7), respectively. Rewriting in the Voigt notation, we have $\hat{{\boldsymbol{\sigma }}}={\boldsymbol{C}}({\boldsymbol{X}})\hat{{\boldsymbol{\varepsilon }}}$. Considering the plane stress assumption in 2D, we write:

$${\boldsymbol{C}}({\boldsymbol{X}})\,=\,\frac{E({\boldsymbol{X}})}{1-{\nu }^{2}({\boldsymbol{X}})}\,\left[\begin{array}{ccc}1&\nu ({\boldsymbol{X}})&0\\ \nu ({\boldsymbol{X}})&1&0\\ 0&0&\frac{1-\nu ({\boldsymbol{X}})}{2}\end{array}\right].$$

(8)

Finite element method

By introducing δU^T = [δU, δV] as standard test functions and performing integration by parts, the weak form of the mechanical equilibrium problem reads:

$${\int}_{\Omega }\delta {{\hat{\boldsymbol{\varepsilon }}}}^{T}\,{\boldsymbol{C}}({\boldsymbol{X}})\,\hat{{\boldsymbol{\varepsilon }}}\,\,dV\,-\,{\int}_{{\Gamma }_{N}}\delta {{\boldsymbol{U}}}^{T}\,\bar{{\boldsymbol{t}}}\,dA=0.$$

(9)

The corresponding linear shape functions N and the deformation matrix B used to discretize the mechanical weak form. To compute these derivatives, we utilize the Jacobian matrix J = ∂X/∂ξ.

Utilizing the standard finite element method, for each element the deformation field, stress tensor $\hat{{\boldsymbol{\sigma }}}$ as well as elasticity field E, ν are approximated as

$$U={\boldsymbol{N}}{{\boldsymbol{U}}}_{e},\,V={\boldsymbol{N}}{{\boldsymbol{V}}}_{e},\,E={\boldsymbol{N}}{{\boldsymbol{E}}}_{e},\,\nu ={\boldsymbol{N}}{{\boldsymbol{\nu }}}_{e},\,\hat{{\boldsymbol{\sigma }}}={\boldsymbol{C}}{\boldsymbol{B}}{{\boldsymbol{U}}}_{e}.$$

(10)

Here, ${{\boldsymbol{U}}}_{e}^{T}$, V_e, ν_e and ${{\boldsymbol{E}}}_{e}^{T}$ are the nodal values of the deformation field and elastic properties of element e. One can write the so-called discretized residual vector for one element as

$${{\boldsymbol{r}}}_{e}=-{\int}_{{\Omega }_{e}}{[{\boldsymbol{B}}]}^{T}{\boldsymbol{C}}\,[{\boldsymbol{B}}]{{\boldsymbol{U}}}_{e}\,dV+{\int}_{{\Omega }_{t}}{[{\boldsymbol{N}}]}^{T}\mathop{\underbrace{{\boldsymbol{C}}{[{\boldsymbol{B}}{{\boldsymbol{u}}}_{e}]}^{T}{\boldsymbol{n}}}}\limits_{\begin{array}{c}\bar{{\boldsymbol{t}}}\end{array}}\,dS.$$

(11)

FFT-based homogenization

Building upon the approach proposed by⁸¹, the FFT-based homogenization method begins with an additive decomposition of the strain field ε into the macroscopic averaged strain field $\bar{{\boldsymbol{\varepsilon }}}$ and a fluctuation contribution $\widetilde{{\boldsymbol{\varepsilon }}}$ as ${\boldsymbol{\varepsilon }}\,=\,\bar{{\boldsymbol{\varepsilon }}}+\widetilde{{\boldsymbol{\varepsilon }}}.$

The constitutive relationship, we consider a homogeneous medium with stiffness ${{\mathbb{C}}}^{0}$, leading to the expression for the stress field as ${\boldsymbol{\sigma }}\,=\,{{\mathbb{C}}}^{0}:(\bar{{\boldsymbol{\varepsilon }}}\,+\,\widetilde{{\boldsymbol{\varepsilon }}})+{\boldsymbol{\tau }}$. Here, τ is the polarization stress, defined as ${\boldsymbol{\tau }}=\left({\mathbb{C}}-{{\mathbb{C}}}^{0}\right):\left(\bar{{\boldsymbol{\varepsilon }}}+\widetilde{{\boldsymbol{\varepsilon }}}\right).$ The balance of linear momentum will then take the form

$$\mathrm{div}\,\left({{\mathbb{C}}}^{0}:\widetilde{{\boldsymbol{\varepsilon }}}\right)+\mathrm{div}\,{\boldsymbol{\tau }}={\boldsymbol{0}}.$$

(12)

By employing the Green’s function approach, Eq. (12) is converted to the integral equation

(13)

which is known as the Lippmann-Schwinger equation. In Eq. (13), is the Lippmann-Schwinger or Green’s operator, which is expressed by the following closed form in the Fourier space:

$${\hat{\Gamma }}_{ijkl}^{0}({\boldsymbol{\xi }})=\frac{1}{4{\mu }^{0}| {\boldsymbol{\xi }}{| }^{2}}\left({\delta }_{ki}{\xi }_{l}{\xi }_{j}+{\delta }_{li}{\xi }_{k}{\xi }_{j}+{\delta }_{kj}{\xi }_{l}{\xi }_{i}+{\delta }_{lj}{\xi }_{k}{\xi }_{i}\right)-\frac{\left({\lambda }^{0}+{\mu }^{0}\right)}{{\mu }^{0}\left({\lambda }^{0}+2{\mu }^{0}\right)}\frac{{\xi }_{i}{\xi }_{j}{\xi }_{k}{\xi }_{l}}{| {\boldsymbol{\xi }}{| }^{4}}.$$

(14)

Here, ξ is the frequency vector, δ denotes the Kronecker delta function, and λ⁰ and μ⁰ are the Lamé constants of the homogeneous reference medium. Moreover, $\hat{(\cdot )}$ is used to represent a quantity in the Fourier space. Finally, the total strain field in the real space is obtained via

(15)

Physics-informed finite operator learning

This model relies solely on standard feed-forward neural networks. The computation of each component of the vector z^l is expressed as follows:

$${z}_{m}^{l}=a\left(\mathop{\sum }\limits_{n=1}^{{N}_{l}}{w}_{mn}^{l}{z}_{n}^{l-1}+{b}_{m}^{l}\right),\quad l=1,\ldots ,L.$$

(16)

The component w_mn shows the weight between the n-th neuron of the layer l − 1 and the m-th neuron of the layer l. Every neuron in the l-th hidden layer owns a bias variable ${b}_{m}^{l}$. The number N_l corresponds to the number of neurons in the l-th hidden layer. The total number of hidden layers is L. The letter a stands for the activation function.

In the context of the current work which we coined as Finite Operator Learning (FOL)⁷⁸, we utilize the so-called collocation fields, which constitute randomly generated and admissible parametric spaces used to train the neural network. For the current work, collocation fields represent possible choices for the elastic properties. More details on how to generate samples are provided in Supplementry Information. Therefore, the input layer consists of information on Young’s modulus {E_i} = {E₁, ⋯ , E_N} and Poisson’s ratios {ν_i} = {ν₁, ⋯ , ν_N} at all the nodes, and the output layer consists of the components of the mechanical deformation at each discretization node i, i.e., {U_i} = {U₁, ⋯ , U_N} and {V_i} = {V₁, ⋯ , V_N}. The model is summarized in the following steps which are also depicted on the right-hand side of Fig. 20.

$${\boldsymbol{X}}=[\{{E}_{i}\},\,\{{\nu }_{i}\}],\quad {\boldsymbol{Y}}=[\{{U}_{i}\},\,\{{V}_{i}\}],\quad i=1\cdots N,$$

(17)

$${\boldsymbol{Y}}={\mathcal{N}}({\boldsymbol{X}};{\boldsymbol{\theta }}),\quad {\boldsymbol{\theta }}=\{{\boldsymbol{W}},{\boldsymbol{b}}\}.$$

(18)

Here, the trainable parameters are represented as W and b, and are collectively denoted by θ. The domain of interest is inspired by micromechanical examples and is thus represented as a square shape. However, this formulation is inherently flexible and can be readily adapted to accommodate irregular geometries and unstructured meshes^78,82.

Fig. 20: Network architecture for finite operator learning (FOL).

Information about the Young’s modulus distribution goes in and the unknown displacement components are evaluated utilizing deep neural networks.

Given the polycrystalline nature of the samples, modeled using the concept of Voronoi tessellation, the input layer can be significantly simplified. The input now consists of the spatial coordinates of the seed points and the material properties associated with each seed point, effectively representing individual grains within the structure. We denote this as the so-called Voronoi parametrization, P_i = {X_i, Y_i, E_i}. Accordingly, we rewrite the expressions in Eq. (17) as follows:

$${\boldsymbol{P}}=\{{X}_{j},\,{Y}_{j},\,{E}_{j}\},\quad {\boldsymbol{Y}}=[{U}_{i},\,{V}_{i}],\quad i=1\cdots N,\quad j=1\cdots M,\quad M\ll N,$$

(19)

$${\boldsymbol{Y}}={\mathcal{N}}({\boldsymbol{P}};{\boldsymbol{\theta }}),\quad {\boldsymbol{\theta }}=\{{\boldsymbol{W}},{\boldsymbol{b}}\}.$$

(20)

In Fig. 20 and throughout this work, we assume a constant Poisson’s ratio within the domain, focusing solely on variations in Young’s modulus. This assumption does not limit the generality of the methodology. Moreover, the output of the model consists of the deformation components, while the stress components can be subsequently derived using standard FEM procedures.

Next, we introduce the loss function. The loss term simply combines the elemental energy form of the governing equation. Note that, thanks to the weak formulation, the Neumann boundary conditions are automatically included and the Dirichlet boundary terms are satisfied in a hard way exactly following the FEM routines (see also Rezaei et al.⁷³). The total loss function involves the integration of element residual vectors using Gaussian integration, resulting in

$${{\mathcal{L}}}_{FOL}=\mathop{\sum }\limits_{e=1}^{{n}_{el}}{{\boldsymbol{U}}}_{e}^{T}({\boldsymbol{\theta }})\left[{{\boldsymbol{K}}}_{e}\,{{\boldsymbol{U}}}_{e}({\boldsymbol{\theta }})\right],$$

(21)

$${{\boldsymbol{K}}}_{e}=\mathop{\sum }\limits_{n=1}^{{n}_{int}}\frac{{w}_{n}}{2}\,\,\text{det}\,({\boldsymbol{J}})\,{[{\boldsymbol{B}}({{\boldsymbol{\xi }}}_{n})]}^{T}{{\boldsymbol{C}}}_{e}({{\boldsymbol{\xi }}}_{n}){\boldsymbol{B}}({{\boldsymbol{\xi }}}_{n}),$$

(22)

In the above set of equations, n_int = 4 represents the number of Gaussian integration points and ξ_n and w_n denote the coordinates and weight of the n-th integration point. The determinant of the Jacobian matrix is denoted by det(J). The final loss function reads as

$${{\mathcal{L}}}_{FOL}={a}_{e}\mathop{\sum }\limits_{e=1}^{{n}_{el}}{{\boldsymbol{U}}}_{e}^{T}\left[\mathop{{{\sum }}}\limits_{n = 1}^{{n}_{int}}\,{{\boldsymbol{B}}}^{T}{{\boldsymbol{C}}}_{e}{\boldsymbol{B}}\right]{\boldsymbol{.}}$$

(23)

Note that we assume here that the determinant of the Jacobian matrix remains constant which holds only for quadrilateral elements. Additionally, in the four integration points we have w_n = 1. Based on the energy formulation, we obtain ${a}_{e}=\frac{1}{2}\,\text{det}\,({\boldsymbol{J}})$.

Spectral-based physics-informed finite operator learning

For many applications in the multiscale modeling of materials, PBCs and periodic microstructure topologies are often preferred. The approach involves solving microscale problems and homogenizing the results to derive macroscopic properties. However, this process can become computationally expensive, particularly for repetitive calculations in FE² methods. To address this challenge, we designed a novel deep learning model that operates on similar principles to the one introduced earlier, but with adaptations tailored to periodic systems and their unique demands. In this section, we employ Fourier Neural Operator (FNO) architectures⁸³ to map various microstructures to their corresponding strain fields (ε_xx, ε_yy, ε_xy). The physical loss functions in this framework are formulated based on the strong form of mechanical equilibrium expressed in Fourier space. This approach is coined as spectral-based physics-informed finite operator learning (SPiFOL) according to the developments presented by Harandi et al.⁷⁴.

In the SPiFOL framework, the FNO architecture begins with a dense layer that projects the input function into a higher-dimensional latent space, enabling sufficient channels for Fourier layers. Each Fourier layer transforms the input into the frequency domain using the Fourier transform (${\mathcal{F}}$), truncates higher frequencies via a weight tensor R, applies convolution in the truncated space, and then returns to the spatial domain using the inverse transform (${{\mathcal{F}}}^{-1}$). A non-linear activation (e.g., GeLU) is applied, and a final dense layer maps the output to the target strain fields. The computation of the output at the l + 1-th Fourier layer is expressed as:

$${{\boldsymbol{z}}}^{l+1}\,=GeLu\left({{\mathcal{F}}}^{-1}(R\cdot {\mathcal{F}}({{\boldsymbol{z}}}^{l}))\,+\,{{\boldsymbol{W}}}_{l}\cdot {{\boldsymbol{z}}}^{l}+{{\boldsymbol{b}}}_{l}\right).$$

(24)

In Eq. (24), b_l is the bias, W_l is the weight matrix, and z^l refers to the output of the previous Fourier layer. The loss function is formulated using the output and the computed Lippmann-Schwinger operator, following the fixed-point scheme for FFT-based mechanical methods. It is expressed as the mean square error (MSE) of Eq. (15). Due to the varying scales of strain field components, influenced by the applied macroscopic strain $\bar{{\boldsymbol{\varepsilon }}}$, a weighting scheme is applied to normalize these components, ensuring comparable magnitudes in the loss function. This normalization enhances model accuracy. The final loss is constructed as the sum of weighted losses over all spatial points, defined as:

(25)

where N_n is the total number of points and X_i stands for the coordinates at that point. The MSE can be calculated for each strain component to ensure that the network learns the solution for each component and that their corresponding loss functions are in the same order.

$${\mathcal{L}}\,=\,{w}_{1}\,\underbrace{\text{MAE}\left({\boldsymbol{L}}(1,1)\right)}_{\begin{array}{c}{\text{corresponds}}\,{\text{to}}\,{\varepsilon }_{xx}\end{array}}\,+\,{w}_{2}\,\underbrace{\text{MAE}\left({\boldsymbol{L}}(1,2)+{\boldsymbol{L}}(2,1)\right)}_{\begin{array}{c}{\text{corresponds}}\,{\text{to}}\,{\varepsilon }_{xy}+{\varepsilon }_{yx}\end{array}}\,+\,{w}_{3}\,\underbrace{\text{MAE}\left({\boldsymbol{L}}(2,2)\right)}_{\begin{array}{c}\text{MAE}{\varepsilon }_{yy}\end{array}}.$$

(26)

In Eq.,(26), MAE denotes the mean absolute error and w₁, w₂, and w₃ show the weighting factor for strain field components. These weighting factors can be adjusted by neural tangent kernels^74,84. See also Figure 21. By considering Eq. (25), the final loss in Eq. (26) can be interpreted as MSE. When the weighting factors are equal, one can simply write the total loss as

(27)

Fig. 21: Network architecture for spectral-based physics-informed finite operator learning (SPiFOL).

Information about the Young’s modulus distribution goes in and the unknown strain components are evaluated. Here, the Lippmann-Schwinger operator is built based on the fixed finite output space and FFT based physical loss is defined.

Digitalization of LOM images through deep learning-based image segmentation

To test the trained networks from the previous sections, it is essential to automatically delimit grains in LOM images. This enables either direct input of the images into the trained neural operators or the design of additional test cases that mimic similar topologies.

A useful methodology is presented and discussed in ref. ⁷⁷ where a deep learning model called Mask R-CNN^11,77 is utilized to automatically detect and segment closely spaced dendrites in CT tomography sections of polycrystalline Al-Cu alloys. UNet performs semantic segmentation by grouping all grains of the same class together, while Mask R-CNN achieves instance segmentation, identifying and isolating each grain individually, even if they belong to the same class. This model was chosen due to the difficulty of separating dendrites that are closely packed or interconnected. Mask R-CNN is a deep learning model that performs three tasks simultaneously: object detection, bounding box prediction, and mask generation for each object in the image. The model starts by using a convolutional neural network to extract features from the input image. Then, a Region Proposal Network (RPN) identifies regions of interest. For each region, the model predicts the object class, refines the bounding box, and generates a pixel-wise mask, allowing for precise segmentation of even overlapping objects. This makes Mask R-CNN highly effective for tasks where detailed, instance-level segmentation is required, such as detecting and segmenting dendrites or grains in microstructures.

Here is a short desscription of the steps of the Mask R-CNN algorithm for alloy microstructure segmentation illustrated on Fig. 22. The input image, typically obtained through a microscope, displays the alloy’s microstructure, revealing various phases and grains within the sample. This image is processed through a feature extraction network, commonly ResNet50, which identifies hierarchical features such as edges, textures, and patterns relevant to the microstructure. A RPN then generates region proposals that may contain distinct microstructural features like grains or precipitates. These proposed regions are standardized using RoI Pooling, allowing consistent processing across the network. The extracted features are further refined using a Feature Pyramid Network, which creates feature maps at multiple scales to detect both small and large structures effectively. RoI Align follows, ensuring proposed regions are uniformly resized while maintaining spatial accuracy. Fully connected layers handle classification and bounding box regression based on these standardized features. Additionally, a convolutional network generates spatial masks for each region, enabling instance segmentation to precisely identify object shapes. The final output includes an image annotated with masks and bounding boxes that delineate and highlight the various microstructural components of the alloy.

Fig. 22: Mask R-CNN Diagram with input and output images.

For more information, readers are referred to the supplementary information and ref. ⁷⁷.

Details on the data generation and training of the Mask R-CNN model are provided and summarized in Supplementary Information.

The results from applying Mask R-CNN achieving a detection rate of more than 90% as illustrated in Fig. 22, where the input image for inference and mask results of grain segmentation are shown. The model successfully segmented most dendrites, even in areas where they were densely packed or strongly interconnected. It segments dendrites based on the white boundaries delimiting the grains, where high segregation is present. However, some grains at the edges were not well detected, as they were cropped from a larger original experimental image and therefore do not share the same characteristics as the traditional dendrites in the training/test dataset.

Fourier-based parametrization

The Fourier-based approach combines specific frequencies with random amplitudes to generate diverse microstructures. To enhance variability, the sigmoid function is applied as a transformation, enabling the creation of smoother and more intricate patterns.

$${\boldsymbol{\phi }}=\frac{sigmoid({t}_{1}({{\boldsymbol{\phi }}}^{\star }-{t}_{2}))+0.05}{1+0.05},$$

(28)

where ϕ^⋆, the summation value of frequencies and random amplitudes, is defined as

$${{\boldsymbol{\phi }}}^{\star }=\mathop{\sum }\limits_{i=1}^{{N}_{x}}\mathop{\sum }\limits_{j=1}^{{N}_{y}}{a}_{i}{a}_{j}\,\cos (2\pi \,f{x}_{i}\,{\boldsymbol{x}})\,\cos (2\pi f{y}_{j}\,{\boldsymbol{y}}).$$

(29)

In Eq. (28), ϕ devotes to the final distribution of phases. t₁ and t₂ are the tuning parameters of the sigmoid function. Moreover, a_i and a_j denote the normalized random amplitudes, while fx_i and fy_i represent the Fourier frequencies in x and y directions and are integers. x and y show the coordinates of mesh points.