Introduction

X-ray Diffraction (XRD) is a powerful technique for determining lattice parameters and cell angles, which are crucial for understanding crystal growth mechanisms and lattice defects1,2,3. This technique can also reveal structural changes under various conditions and assess critical material properties such as strength and stability. Traditionally, XRD analysis involves comparing their peak characteristics like position and intensity against the established databases. Accurately identifying phases from XRD spectra necessitates a deep understanding of crystallography and experience in pattern recognition. However, the manual process of analysis is often labor-intensive and time-consuming, which significantly hinders swift decision-making due to its relatively low efficiency4,5.

The fourth-generation synchrotron radiation sources have significantly improved the resolution and sensitivity of XRD analysis, enabling more accurate characterization of complex materials6. At the same time, advances in laboratory technology are driving the move towards greater automation and self-manipulation, which has created a need to modernize traditional analytical methods. The integration of artificial intelligence (AI) with XRD analysis is opening up new possibilities for material characterization and crystallography. Deep learning models, such as variational autoencoders (VAE) and convolutional neural networks (CNN) have proved instrumental in analyzing data and identifying novel phases7,8,9. The combination of machine learning (ML) and open-access datasets has streamlined the classification of complex material data, minimizing the data volume necessary for descriptor extraction10. Deep learning is also used to simulate XRD patterns, addressing challenges in phase identification and quantification in multi-phase compounds11,12. Zhao et al. introduced a robotic platform featuring a data mining–synthesis–inverse design framework, revolutionizing the synthesis of colloidal nanocrystals13. Moreover, a review by Lookman et al. explores the integration of information science methods, such as active learning strategies, into the materials discovery process. These methods use uncertainties to prioritize promising candidates for experiments and computations, thereby accelerating the innovation process in materials science14. These approaches also support continuous learning and integration with other datasets, resulting in more comprehensive and cost-effective research outcomes. Innovative machine-learning approaches predict crystal dimensions and space groups from limited XRD data, while tools like FCN, T-encoders, and VAEs recognize crystal symmetry and predict properties from powder XRD spectra15,16,17,18,19. Deep neural networks are now being used to automate phase identification and crystal symmetry classification, offering powerful tools for material characterization and crystallography research20,21,22,23.

Despite recent advancements, the field of XRD analysis using deep learning faces certain challenges24,25,26,27: i) Data Acquisition and Diversity: Obtaining comprehensive XRD datasets remains a challenging and costly endeavor, exacerbating data scarcity—a critical obstacle for training robust and accurate predictive models. The costs associated with maintaining and operating XRD facilities can deter smaller research groups or institutions with limited budgets from conducting extensive data collection, leading to a lack of diversity in available datasets. ii) Autonomous Material Characterization: The ultimate ambition of autonomous XRD analysis is to identify constituent phases without human intervention, advancing beyond the mere deduction of structural attributes to fully automated material characterization. While existing research has made significant strides in inferring structural properties such as lattice parameters and space groups, the field aims to transcend these capabilities and achieve a paradigm shift towards a fully autonomous process28,29,30. iii) Uncertainty Quantification: Deep Neural Networks often struggle to quantify and communicate the uncertainty in their predictions, which can lead to misleading or overconfident results, undermining the reliability of the analysis31,32,33. Providing only point predictions, without a corresponding measure of uncertainty, is insufficient for researchers who need to assess the confidence and robustness of the model’s classifications, especially when identifying crystal structures where the model’s degree of certainty can guide informed decision-making34,35. iv) Interpretability: The “black box” nature of ML models obscures their decision-making processes, complicating model validation and raising concerns about their adherence to fundamental physical principles. This lack of transparency challenges their acceptance in the scientific community, as it is difficult to ensure that the models’ predictions align with established physical principles and material science theories36,37,38.

This work presented an integrated approach to addressing the challenges inherent in deep learning-based XRD analysis. First, to enrich training data and probe how models learn the spectrum-structure mapping, we developed a Template Element Replacement (TER) strategy combined with data synthesis. We demonstrate TER on a perovskite dataset—leveraging the ABX₃ framework’s well-defined lattice archetype and chemically diverse substitution space—to generate a richly varied virtual library. Moreover, perovskites are widely studied in functional materials research, such as photovoltaics and ferroelectrics, and perovskites exhibit rich structural diversity. It is important to emphasize, however, that the TER strategy itself is not inherently restricted to perovskites. The methodology is theoretically applicable to other material systems with parameterizable structural archetypes, and future studies will extend its application accordingly. This method effectively enriched the dataset, enhancing diversity and addressing the high costs and limitations associated with data acquisition. Secondly, to achieve autonomous characterization, the model was trained on virtual structure spectral data for crystal structure and space group classification, tested on real structure spectral data, and finally validated using experimental XRD spectra. This process goes beyond merely inferring structural attributes and moves towards a fully automated workflow that can directly identify constituent phases without human intervention. Thirdly, to address the quantification of prediction uncertainty, the model incorporated Bayesian methods, which were explored through variational inference, Laplace approximation, and Monte Carlo dropout. This feature was pivotal for researchers who need to assess the confidence in the model’s classifications, especially in identifying crystal structures.

Through the seamless integration of the B-VGGNet model for uncertainty quantification, the TER method and data synthesis for addressing data scarcity, and SHAP (SHapley Additive exPlanations) for interpretability, our study establishes a robust and extensible framework for deep‐learning-based XRD analysis. This comprehensive framework addresses key limitations of conventional XRD analysis and delivers practical improvements in data diversity, confidence assessment, and interpretability, thereby enhancing the reliability of phase identification in materials research.

Results

Dataset construction

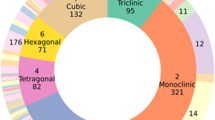
The framework for classifying, predicting, and analyzing XRD spectra based on crystal symmetry and structure is illustrated in Fig. 1. Crystal structure information had been extracted from Inorganic Crystal Structure Database (ICSD). Subsequently, the CIF files of 93 space group classes from the Materials Project (MP) database were used to learn the template through TER. Three types of XRD spectral data were defined in this work: virtual structure spectral data (VSS), real structure spectral data (RSS), and synthetic spectra data (SYN). Figure 2a, b shows the space‐group distributions of the RSS and VSS datasets, respectively; Fig. 2c illustrates an example of TER, and a comparison between the VSS and RSS is provided in Fig. 2d. Based on these, the 30 most popular structure types were selected to construct the structure classification model. The VSS dataset was constructed by introducing common variables in real scenarios to better replicate experimental conditions, supporting that the model was trained on data that closely resembled the complexities and nuances of real XRD experiments. After data augmentation, the VSS dataset comprised a total of 24,645 XRD spectra. The RSS dataset comprised 1894 XRD spectra. When models were trained solely on the VSS and validated on the RSS, the results were unsatisfactory. To address this, SYN were generated by combining VSS and RSS. The differences between SYN and RSS were significantly reduced compared to those between VSS and RSS, and the classification accuracy was also substantially improved.

Fig. 1: B-VGGNet based XRD analysis framework.
figure 1

The framework illustrates the integrated approach of classification, interpretability analysis and uncertainty quantification for XRD data using B-VGGNet.

Full size image
Fig. 2: Distribution and characteristics of spectral data in real and virtual structural contexts.
figure 2

a Distribution of real structure spectral data (RSS) by space group, color‐coded by crystal system. b Distribution of virtual structure spectral data (VSS) by space group, the red sector represents the space group distribution of the experimental data. c Example of template element replacement (TER): the BaTiO₃ template can be transformed into CaTiO₃ or PbTiO₃ by substituting elements. d Comparison of VSS, RSS, and SYN based on their intensity differences.

Full size image

The classification of space group

To ensure a fair evaluation, a portion of the RSS was set aside prior to any synthetic data generation. After preprocessing, this reserved RSS was evenly split into two parts: one used as the final test set, and the other used for pre-training the model. For training, we constructed several dataset combinations using VSS, SYN, and part of the RSS. The remaining RSS samples that were not used in training served as the test set. We evaluated multiple classical machine learning models, including Naive Bayes (NB), Random Forest (RF), Logistic Regression (LR), Support Vector Machine (SVM), k-Nearest Neighbors (KNN), Decision Tree, and a fully connected neural network (Multilayer Perceptron, MLP). Hyperparameter configurations are detailed in Supplementary Table 1, and classification accuracies are shown in Fig. 3a. It can be seen that all classical ML models exhibit <70% accuracy in space cluster classification tasks. In contrast, B-VGGNet’s accuracy is improved by at least 10% for all different datasets.

Fig. 3: Performance evaluation of machine learning (ML) models for spectral data classification.
figure 3

a The classification accuracy across various ML models verified in real structure spectral data (RSS), with color intensity representing accuracy levels. The vertical coordinate is the training set and the horizontal coordinate is the model. b The variation in accuracy when applying different proportions of RSS to synthetic data. c The classification accuracy before and after the application of the template element replacement (TER).

Full size image

The methodical integration of RSS into synthetic datasets represents a targeted calibration effort, which significantly affects model performance, as evidenced by Fig. 3b. The observed variations in classification accuracy across different proportions of RSS incorporated into SYN suggest a complex relationship between synthesized and real structure spectrum. Incorporating the optimal proportion (70%) of RSS improved accuracy, suggesting that effective model training necessitates a strategic selection of real data that reflects genuine sample variability, without burdening the model with excess noise.

In addition, this study compares the effects of the datasets constructed before and after using TER. Both datasets were used for model training and then validated with RSS. The results show a slight improvement in accuracy, as shown in Fig. 3c. This strategy effectively circumvents the common accuracy degradation problem during dataset expansion and supports a steady improvement in model performance.

The classification of structure type

This study has constructed a fundamental “Yes or No” classification model to identify whether a given sample structure belongs to the pre-screened 30 structural categories. Systematic training and validation were performed using a dataset of 3600 VSS samples, which included 2100 samples from the target structure types and 1500 samples from other categories. The model achieved a high accuracy rate of 97.3% on the validation set, demonstrating its effectiveness in practical applications, as illustrated in Fig. 4a, b. Moreover, the area under the ROC curve (AUC) reached 0.98, approaching the performance of an ideal classifier, indicating that the model possesses a very strong discriminative ability across various threshold settings. The precision-recall curve analysis further corroborates this, with the model’s Average Precision (AP) at 0.97, signifying that the model maintains a balance between high precision and high recall rates at different thresholds.

Fig. 4: Evaluation metrics and performance comparison of the classification models.
figure 4

a, b Confusion matrix, receiver operating characteristic (ROC), and precision-recall (PR) curve of the “Yes or No” model. c Structure classification accuracy across machine learning (ML) models verified on real structure spectral data (RSS), with color intensity representing accuracy levels. The vertical axis represents the training set, and the horizontal axis represents the model used.

Full size image

Following the completion of the binary classification task, classic ML models were employed to classify 30 structural categories. The RSS served as the test set, with different training sets constructed from VSS, SYN, and portions of RSS for comparative evaluation. The results are presented in Fig. 4c. The findings reveal that purely virtual structure data cannot be directly applied to practical problems due to significant differences from real structure data, resulting in extremely low accuracy. The effectiveness of the data synthesis method is evident: when using SYN for training and RSS for validation, accuracy rates consistently exceeded 80%, with RF and KNN algorithms even surpassing 90%. The data synthesis method proposed in this study successfully integrated the features of both virtual and real structure spectral datasets, creating training data that more closely resembles real-world scenarios. Additionally, the study employed a portion of the RSS for pre-training, which enhanced the utilization efficiency of the training set. This pre-training strategy proved particularly effective when applied to VSS, improving accuracy by up to 70% in the best cases, as can be seen from the comparison between the first and third rows of Fig. 4c.

Uncertainty analysis

This study employed three distinct methods for uncertainty assessment: LA, VI, and MCD, to analyze the model’s predictive uncertainty across various space groups from multiple perspectives. Figure 5a illustrated the mean predictive probabilities of the LA, MCD and VI methods across different space groups. Based on the entropy distribution in Fig. 5b, the entropy values of the LA method were predominantly concentrated in the lower region (0–0.5), indicating that the B-VGGNet can provide quite “confident” predictions. In contrast, the VI method exhibits slightly lower mean predictive probabilities, While the two showed similar overall performance, the VI method predicts slightly lower probabilities for complex space groups, such as “P4/mbm” and “Pm-3m”. This reflects its advantage in capturing model uncertainty, which is crucial for the identification of crystals with complex geometric structures. This capability is attributed to its more flexible distribution assumptions, allowing it to adapt to more complex or multimodal posterior distributions39. Conversely, LA predicts higher probabilities for these space groups, suggesting that it is more confident when dealing with simpler posterior distributions but may have limitations when handling complex structures. Figure 5c, d presented the predictive means and error bars for the MCD and LA methods, respectively. The results indicate that the MCD method exhibits the widest error ranges and the lowest mean predictive probabilities, especially for space groups “Cmcm” and “C2/c”. This fully demonstrates the characteristic of MCD to simulate model structural uncertainty by randomly dropping neurons multiple times. MCD obtains uncertainty from different neural network substructures through multiple samplings, but due to its reliance on the stochastic dropout strategy, it may introduce additional uncertainty when dealing with complex structures. In comparison, the LA method captures model uncertainty through Gaussian approximation, with relatively shorter error bars, indicating that it can provide more stable predictive results when dealing with complex space groups.

Fig. 5: Analysis of uncertainty measures and prediction performance across different space groups.
figure 5

a The mean prediction probability of Monte Carlo Dropout. (MCD), Variational Inference (VI) and Laplace Approximation (LA) for different space groups. b The entropy distribution diagram of LA. c–e The mean prediction probability and error bar of LA, MCD and VI for different space groups, respectively.

Full size image

In summary, these three uncertainty assessment methods each have their strengths and limitations. The LA method is more confident when dealing with simpler posterior distributions but may underestimate uncertainty in complex scenarios; the VI method, with its flexible distribution assumptions, is better suited for handling multimodal posterior distributions; and the MCD method can capture more model structural uncertainty, but its randomness may lead to excessive uncertainty. In practical applications, one should choose or combine these methods based on the complexity of the specific problem, computational resource constraints, and the requirements for predictive accuracy to obtain a more comprehensive and accurate assessment of uncertainty40.

To gain deeper insights into the classification decision-making process of the B-VGGNet model, this study introduces the SHAP value analysis to provide a more intuitive interpretation of model behavior. SHAP values were computed for each input feature across all classified samples, and the results were aggregated by averaging the values within each space group. Figure 6a takes the space group Pna2₁ as an example, where two RSS patterns are randomly selected and plotted as solid lines. The dashed lines indicate the 2θ positions with high SHAP values—that is, features making significant contributions to the model’s prediction. This visualization enables a direct comparison between the model’s classification-relevant features and the actual peak positions in the RSS patterns, thereby verifying the physical validity of the model’s decision-making process. The strong peak observed around 2θ ≈ 33–34° likely corresponds to the (110) and (002) crystal planes41. In orthorhombic structures, such as Pna2₁, these peaks appear as separate reflections, whereas they are often overlapping in cubic systems. This comprehensive perspective not only deepens the interpretability of the model but also ensures that its decisions are grounded in actual diffraction peak positions. This transforms the traditional search paradigm by enabling high-throughput screening of large databases. Additionally, by averaging SHAP values across samples sharing the same crystal system, the study uncovers commonalities in how the model interprets structurally similar patterns during classification. Detailed peak-to-angle correspondences are provided in the Supplementary Table 2.

Fig. 6: Feature importance analysis using SHAP values in spectral data interpretation.
figure 6

a Real structure spectral data (RSS) pattern and SHAP-based feature importance for space group Pna2₁. The solid line represents the averaged RSS of all samples labeled as Pna2₁, while the dashed vertical lines indicate 2θ angles with high SHAP values. b Mean absolute SHAP values at selected 2θ angles for four representative space groups: Imma (dark blue), P4mm (light blue), I4/mcm (yellow), and Pm-3m (red). Each bar represents the average SHAP value computed over all samples within that group at the corresponding diffraction angle.

Full size image

The study then selected the four space groups with the largest sample sizes to analyze the feature importance distributions across diffraction angles, as shown in Fig. 6b. For each group, SHAP values were averaged over all corresponding samples. The Imma space group exhibits prominent SHAP values in the 29–32° range, with the highest contribution observed at 31.7°. This region is consistent with characteristic reflections from orthorhombic perovskite structures, such as (110), (020), or (112), which are strongly influenced by octahedral tilting. Imma is defined by the Glazer tilt system a⁻b⁺a⁻ 42, involving out-of-phase rotations along the [100] and [001] directions and in-phase rotation along [010]. These distortions result in anisotropic lattice parameters and lead to the splitting or shifting of diffraction peaks that are otherwise degenerate in cubic structures. For example, in distorted perovskites like CaTiO₃, (110)-type reflections typically appear in the 2θ ≈ 29–32° region due to lattice deformation induced by tilt modes3. The SHAP-based importance at 31.7° suggests that the model effectively captures these structural signatures when distinguishing Imma from other space groups. Additionally, Fig. 6b shows that P4mm exhibits a significantly high SHAP value at 39.0°, while Pm-3m shows a much lower value at the same angle. This is consistent with their group–subgroup relationship: P4mm is a tetragonal distortion of the cubic Pm-3m structure, often observed in perovskites like BaTiO₃. The diffraction peak near 39.0° likely corresponds to the (200) plane, which is sensitive to lattice elongation along the c-axis during the cubic-to-tetragonal phase transition. These results confirm that the model’s classification decisions are aligned with crystallographic principles, providing physically interpretable insights via the SHAP framework.

Model evaluation on experimental XRD data

To further evaluate the practical applicability and robustness of the proposed model on real experimental data, we retrieved “perovskite” labeled XRD patterns from the RRUFF database under the ABX₃ configuration (Supplementary Table 3). These spectra were never seen during training or validation, providing a test of generalization. On this external dataset, our classifier achieved 0.75 accuracy, underscoring its practical applicability.

We then investigated the sole misclassification—sample R050456—which exhibited pronounced structural and spectral anomalies. Specifically, although R050456 shares the same chemical formula and space group as standard CaTiO₃, its structure was determined at high temperature (T = 1373 K). As Liebermann’s high-temperature studies43 show, CaTiO₃’s orthorhombic distortion relaxes with heat: Ti-O-Ti bond angles approach 180° and atomic coordinates shift toward those of an ideal cubic phase, driving a continuous transition to a pseudo-tetragonal or cubic polymorph. These systematic high-temperature structural changes are reflected not only in crystallographic parameters at the atomic scale, but also directly influence multiple features of the XRD pattern. We computed both Euclidean and cosine distance matrices (Supplementary Tables 4 and 5). In terms of XRD characteristics, the pattern of R050456 is distinctly separated from other samples in the feature space. Both Euclidean distance and cosine distance matrix analyses show that the distance between R050456 and the other samples is much greater than that among the other samples. Its diffraction pattern exhibits pronounced anomalies in relative intensity distribution, peak morphology, and key reflection positions. For instance, the intensity ratios of characteristic peaks—such as (112) versus (200)—are inverted or abnormally amplified, and the splitting of principal reflections is significantly weakened or even absent, reflecting reduced octahedral distortion and enhanced high-temperature dynamics. Although crystal structures and their XRD signatures are fundamentally correlated, our TER-generated dataset—restricted to ambient-condition compositional substitutions—never encounters the altered structure-to-spectrum relationships produced by high-temperature phase transitions. As a result, the model fails to learn how these thermal polymorphisms reshape diffraction intensities.

Discussion

This study presents a framework for systematically probing the gaps between virtual and real‐structure spectra and assessing whether TER-generated, physically unstable templates can enhance spectrum-structure learning. By employing the TER method and data synthesis techniques, the dataset was expanded, enhancing the model’s generalization capabilities. Subsequently, the study leveraged deep learning to extract more intricate and detailed information from XRD spectra than conventional methods. Beyond the traditional identification of crystal properties such as space group classification, the study also achieved the classification of crystal structures. This advancement not only accelerated the process of automated crystal analysis but also facilitated the discovery of new materials by unveiling a richer understanding of their structural nuances44,45,46. Finally, external validation on perovskite XRD patterns from the RRUFF database demonstrated the framework’s practicality and robustness: our model achieved 75% accuracy on previously unseen experimental XRD data.

Furthermore, Bayesian theory was introduced to quantify the confidence of model predictions and the B-VGGNet was constructed. By assessing the confidence level in prediction results, the model provided timely feedback to avoid incorrect decisions in low-confidence scenarios, enabling a wide range of applications. Finally, the study employed SHAP values to measure the contribution of different features and activation function analysis, thereby elucidating the decision-making process of deep learning models. This aspect of interpretability was vital for the broader acceptance and application of deep learning in material science.

Perovskites served as an effective illustrative example in this study owing to their rich substitution chemistry and clearly defined structural prototypes. Nevertheless, the core methodologies underpinning our framework rest on broadly applicable principles. Our systematic data synthesis strategy leverages structural templates and chemically sensible substitution rules to augment datasets in a controlled manner. This method is, in principle, applicable to all material systems possessing clearly defined structural templates or characteristic motifs. Probabilistic modeling provides quantitative assessments of model prediction uncertainties. This probabilistic approach is independent of specific material systems and can be universally applied across diverse data types and structural analysis tasks to enhance decision-making reliability. Additionally, the SHAP-based interpretability tools enhance transparency in the model’s prediction process by attributing each output to its most influential input features. The architecture of B-VGGNet emphasizes small-kernel convolutions, multi-layer convolutional structures, and hierarchical feature extraction. These general design principles enable efficient capture of complex patterns from spectral or diffraction data in diverse material systems, demonstrating generalization capability across different classes of materials.

Nonetheless, several limitations should be acknowledged. First, template-based augmentation, as implemented in TER, relies on the existence of dominant structural motifs and chemically reasonable substitution rules. For material classes lacking clear prototypes, or exhibiting substantial disorder, partial occupancy, or stacking faults, this approach may become less systematic or even inapplicable. Second, the availability of high-quality, experimentally labeled XRD spectra remains limited for many non-perovskite materials. Third, applying our uncertainty and interpretability tools to datasets from systems without fixed structural templates require additional calibration or domain expertise to yield meaningful results. Finally, the misclassification of the high-temperature CaTiO₃ sample highlights that TER—being limited to ambient-condition compositional substitutions—cannot capture the altered structure-spectrum correspondence induced by thermal polymorphism.

Future work will extend this framework to other structural families to further validate its robustness and adaptability across diverse crystallographic domains. They offered not only a faster and more efficient way to analyze and classify material structures but also a transformative approach that enhanced the depth and breadth of material investigation. By simulating and aligning data with real data, the study reduced dependency on costly and time-consuming experimental procedures, facilitating low-cost simulations and research. Incorporating uncertainty and interpretability analyses enhanced confidence in and understanding of model predictions, which was crucial for deep learning’s broader acceptance and application in material science. This intelligent framework stands poised to become a powerful tool for researchers and practitioners in verifying and understanding complex materials.

Methods

Framework for XRD prediction and its analysis

VSS are simulated within structural templates, covering a wide range of hypothetical and potentially physically unstable structures. This broad diversity supports the learning of general structure-spectrum relationships, but may also introduce significant discrepancies from real experimental spectra. In contrast, RSS are derived from experimentally confirmed, physically stable structures in the ICSD database. In this study, we consider that their spectra more closely resemble real experimental conditions compared to VSS, and thus serve as the ground truth for model evaluation. To effectively bridge the physical discrepancies between real and virtual structure spectral data, data synthesis was performed on both datasets according to their classification labels. By structuring the data in this way, we can directly test whether the mappings learned on VSS enhance the model’s predictive performance on real structure XRD spectra, thereby improving phase identification accuracy on experimental spectra.

The architecture of the B-VGGNet, as presented in the paper, was adapted from the VGGnet used in computer vision. This adaptation was employed to classify and predict crystal spatial clusters and structures. A Bayesian layer was added to the penultimate layer of the network to evaluate model uncertainty. The Bayesian layer utilized three methods: MCD, VI, and LA. Ultimately, the degree of contribution of each feature to the classification was calculated, aligning with its physical significance. The model’s classification results were then analyzed to enhance interpretability. This approach integrated the power of deep learning with Bayesian statistical methods, providing a comprehensive tool for the analysis and interpretation of XRD spectra.

Dataset construction

The goal of this module is to conduct a detailed exploration of the structural diversity of perovskite compounds, with the aim of feeding subsequent ML models to map XRD data to materials information. By leveraging extensive crystallographic data repositories, this research seeks to uncover the broad range of structural flexibility and variability inherent to the perovskite family. Perovskites, characterized by the ABX3 stoichiometry, exhibit remarkable structural versatility. Central to their structure is the B site, encapsulated within BX6 octahedra, which can adopt various arrangements and undergo multiple distortions and displacements. The inherent flexibility of the perovskite lattice allows for a wide array of cations and anions to be incorporated, theoretically enabling any combination of atoms to form a potential perovskite structure47.

The initial step is to mine all 93 space groups with ABX3 chemical structure frameworks from the MP database48. These groups extend beyond the typical perovskite space groups conventionally recognized. At the same time, 53 perovskite chemical formulas were found in the ICSD based on real structure.49. This method systematically generates hypothetical perovskite compounds by substituting chemically compatible elements into known perovskite structure templates. A total of 53 representative perovskite compositions extracted from the ICSD database were selected as structural templates. In principle, any composition corresponding to one of the 93 space groups in MP dataset can be mapped to any of these templates for element substitution. The key criterion for element replacement is charge neutrality, following the general formula ABX₃. Since the anion X can be either chalcogen (e.g., O2−, S2−) or halogen (e.g., Cl−, Br−, I−), charge neutrality requires

$${\rm{valence}}({\rm{A}})+{\rm{valence}}({\rm{B}})+3\times {\rm{valence}}({\rm{X}})=0$$
(1)

To implement this, we developed automated scripts that read CIF files of template structures, identify A- and B-site elements, and replace them according to a predefined list of elements grouped by oxidation state. These substitutions ensure that every resulting structure satisfies Eq. (1). All modified structures were saved as new CIF files, resulting in a virtual dataset of 4929 chemically valid perovskite candidates. The detailed template element replacement List can be found in Table 1.

Table 1 Templet element replacement list
Full size table

Data simulation and alignment

This module utilized pymatgen50 to simulate XRD spectra. In the simulation process, element-specific Debye–Waller factors were assigned to account for thermal vibrations and improve spectral accuracy. Wherever possible, these factors were obtained from experimental or computational literature; for elements without reliable references, we substituted values from chemically similar species with the same oxidation state. This strategy ensured internal consistency while mitigating the impact of missing parameters. A complete list of Debye–Waller factors is provided in Table 2. The VSS are essential for expanding the structural hypothesis space and enabling the model to learn robust spectrum-structure mappings. However, a gap exists between real structure spectral data and virtual structure spectral data, which can negatively impact the performance of deep learning models. Therefore, this study aims to help bridge this gap, allowing VSS to more effectively support the analysis of RSS. This strategy was crucial for enhancing the realism of virtual structure spectral datasets, making them more representative of actual conditions.

Table 2 Pymatgen simulation parameters
Full size table

A fundamental component of this approach was the simulation of unintended phases or contaminants, which are often encountered in experimental samples. By introducing random impurity peaks into the VSS, this study created datasets that were more realistic and challenging, aligning closely with real-world scenarios. This targeted augmentation was vital for robust model training and substantially enhances predictive accuracy on experimental spectra.

In addition to simulating impurity peaks, this study varied the intensities of diffraction peaks to mimic the effect of preferred crystallographic orientation, or ‘texture’. This was done by randomly adjusting peak intensities up to ±50%, to represent the varied orientations of crystallites typically found in real samples. The impact of crystal size on peak broadening, a prevalent phenomenon in XRD analysis, was accounted for by simulating a range of grain sizes employing the Scherrer equation. The simulation spanned from very fine grains resulting in broad peaks to coarser grains producing narrower peaks.

Furthermore, lattice strain-induced peak shifts were introduced by modifying the lattice parameters of each phase, with shifts of up to ±3%. This effectively mimicked the stress and strain effects commonly seen in real samples, which can significantly alter peak positions. Lastly, uniform shifts were applied to all peaks in a spectrum to represent consistent changes in lattice parameters due to factors like temperature variations or chemical composition changes. Crucially, these five methods are not sequential but parallel approaches in this data simulation strategy36.

The resultant VSS, having undergone these augmentation processes, was then combined with RSS to generate synthetic spectra data for model training. To facilitate model evaluation, the RSS were grouped by class labels and stratified sampling was performed to construct multiple subsets with varying proportions. A portion of these subsets was used for data synthesis, while the remaining data were held out in advance for downstream model training and final testing. In this data synthesis algorithm, RSS and VSS are first normalized, respectively5. By randomly selecting one positive sample \({e}_{i}\) from RSS and one negative sample \({t}_{i}\) from VSS, the synthetic sample is created as Eq. (2).

$${X}_{{ac}}={e}_{i}+\varepsilon \cdot {t}_{i}$$
(2)

Where ε is a random number and ε ∈ (0,1).

B-VGG model construction

The model-building process began with the strategic conversion of the VGGNet into a form specifically optimized for processing XRD data. This was achieved by employing a series of 1D convolutional layers with ReLU activation functions, designed to capture the subtle details within the spectra. The model was meticulously optimized to prevent overfitting, with the number of neurons in each convolutional layer being carefully adjusted. This adjustment balanced the extraction of detailed features with the model’s capacity to generalize.

Subsequent max-pooling layers were implemented to reduce dimensionality and distill the most relevant features for classification tasks, further enhancing the model’s efficiency. A key innovation of this model was its structural optimization, as it innovatively integrated Bayesian neural networks (BNNs) to quantify the uncertainty inherent in the predictions. This integration allowed the B-VGGNet to provide not only classifications but also an estimate of prediction uncertainty, which was critical for decision-making in the presence of variability and noise commonly found in XRD data.

The BNN approach introduced a probabilistic framework that assigned weight distributions to the model parameters, capturing both epistemic and aleatory uncertainties. It allowed the posterior distribution of these weights to be estimated using methods such as variational inference, Markov chain monte carlo, or laplace approximation. This feature made the B-VGGNet a robust tool for handling the complexities and uncertainties intrinsic to XRD data analysis.

Uncertainty analysis

Monte carlo dropout (MCD) is recognized as a straightforward yet powerful approach for estimating uncertainty within deep neural networks. The technique hinges on training a model with dropout regularization and maintaining the dropout layers active during the inference phase. By conducting a series of forward passes through the network with varying dropout masks, a collection of predictions is generated, which collectively provide an approximation to the samples from the posterior distribution of the model’s outputs. In this study, VGGNet models were trained with dropout layers strategically placed after each convolutional and fully-connected block. During the inference phase, a multitude of forward passes were executed, each with a unique dropout mask, yielding an ensemble of predictions for each input instance. The aggregation of these predictions, through their mean and variance, provided an estimate of the model’s predictive uncertainty31.

The laplace approximation (LA) is a technique employed for approximating the posterior distribution in Bayesian neural networks, which involves fitting a Gaussian distribution centered on the maximum a posteriori (MAP) estimates of the weights. Initially, the VGGNet models were trained using standard optimization techniques to determine the MAP estimates of the weights. Subsequently, the Hessian matrix of the negative log-posterior concerning the weights was calculated at the MAP estimate. The inverse of this Hessian matrix was utilized as the covariance matrix for the Gaussian approximation to the posterior distribution. This process was repeated with various random initializations and architectures to generate an ensemble of models, culminating in a collection of VGGNet models, each with a LA to its respective posterior distribution51.

Variational inference (VI) is another method used to approximate the posterior distributions that are otherwise intractable in Bayesian neural networks. In this study, VI was applied to approximate the posterior distribution over the weights of the VGGNet models. The goal of VI is to minimize the kullback-leibler (KL) divergence between a computationally feasible variational distribution and the actual posterior distribution. A factorized Gaussian distribution was selected as the variational distribution, characterized by individual means and variances for each weight. These parameters were refined using stochastic gradient descent, to minimize the negative evidence lower bound (ELBO). The ELBO consists of the expected log-likelihood and the KL divergence between the variational and prior distributions. By initiating multiple training sessions with distinct random seeds, an ensemble of VGGNet models was produced, each with an approximated posterior distribution over its weights52.

SHAP value computation for model interpretability

To quantify the contribution of individual diffraction angles to the classification predictions made by the B-VGGNet model, we employed SHAP as a post hoc feature attribution method. SHAP is grounded in cooperative game theory and provides a unified approach to interpret the output of any machine learning model by computing the Shapley value for each input feature.

The Shapley value ϕi for a feature i is defined as the average marginal contribution of that feature across all possible subsets of features. In the context of this study, each input sample is a one-dimensional vector representing the XRD pattern, where each element corresponds to the intensity at a specific 2θ angle. The model output is a probability distribution over the set of space groups, obtained via the softmax function in the final layer of B-VGGNet.

We used the SHAP Python library’s DeepExplainer, designed for deep learning models, to compute these values. The explainer takes the trained B-VGGNet model and a background dataset of reference XRD patterns (typically a subset of training data) as input. For a given sample, SHAP values are computed for each 2θ feature with respect to the predicted class. These values indicate how much the presence of each feature shifts the model output from the expected value (baseline) to the actual prediction.

More formally, for an input sample x ∈ \({{\mathbb{R}}}^{n}\), the SHAP value \({\phi }_{i}\) for the \({\rm{i}}\) feature is computed as Eq. (3).

$${\phi }_{i}=\sum _{S\subseteq F,\{i\}}\frac{|S|!(|F|-|S|-1)!}{|F|!}\left[\,f(S\cup \{i\})-f(S)\right]$$
(3)

Where \(F\) is the set of all features, \(S\) is a subset of features excluding \({\rm{i}}\), and \(f(S)\) denotes the model prediction when only features in subset \(S\) are present.

After computing SHAP values for each sample, we obtained a matrix of shape \(N\times M\), where \(N\) is the number of input samples and\(M\) is the number of 2θ points. These values were used for further statistical aggregation and visualization of feature importance across different space groups.