Introduction

Global annual electricity consumption is approximately 2.7 × 1013 kW·h. It is estimated that the generation and consumption of up to 80% of electric power are based on the utilization of power electronics (PEs). Power semiconductor materials are indispensable for converting and controlling electrical energy, enabling efficient and reliable power transmission and distribution. The improvement on the efficiency of power conversion and control not only reduces overall energy consumption but also mitigates greenhouse gas emissions and pollutant generation, thereby contributing to environmental sustainability1,2. Power electronics play an important role in diverse industrial sectors, including consumer devices, renewable energy systems (e.g., wind and solar), electric vehicles (EVs), and telecommunications infrastructure. These systems have critical functions in energy conversion and control, including rectification for mobile charging, inversion/conversion for solar/wind power integration, and variable-frequency motor regulation in EVs and industrial machinery1,2. The global market for PEs is projected to surpass $50 billion by 2025 (www.marketsandmarkets.com/Market-Reports/powerelectronics-market-204729766.html). Despite its extensive applications, a limited number of materials, such as silicon (Si), silicon carbide (SiC), and gallium nitride (GaN), dominate the PE market.

Silicon is widely used due to its low cost and compatibility with existing fabrication technologies, exhibiting limited efficiency, particularly in high-power applications3,4. Si-based PE devices face a fundamental trade-off, i.e., they achieve either a low breakdown field at low on-state resistance or a high breakdown field at high on-state resistance, restricting their efficiency and application scenarios5. Despite these limitations, Si accounts for approximately 95% of PE devices3. The second generation of power semiconductor materials, including GaAs and InP, offers higher electron mobility than Si and Ge6. However, their thermal conductivities (below 100 W/mK) are inadequate to meet the demands for heat dissipation7. The third-generation power semiconductors, exemplified by silicon carbide (SiC) and gallium nitride (GaN), are characterized by their wide bandgaps (>3 eV), exceptional electron mobility (>900 cm²/Vs), elevated breakdown field strengths (>3 MV/cm), and robust thermal stability at high operating temperatures (>300 °C). Nevertheless, their widespread application is hindered by high defect densities and synthesis costs4,8,9. Gallium oxide (Ga2O3) has gained attention as a cost-effective alternative for power electronics; however, its limited thermal conductivity and stability pose a substantial challenge10. Additional candidates, including diamond11, cubic boron nitride (c-BN)12,13,14, aluminum nitride (AlN)15, and zinc oxide (ZnO)15, have also been explored for their potential in high-performance applications. However, PE devices based on these materials are still underdeveloped or have not yet reached their full potential. The Materials Project database currently reports 153,235 inorganic crystal structures, encompassing potential power semiconductor materials such as oxides, sulfides, nitrides, carbides, silicides, and borides16. Notably, only a small fraction of these known materials is currently used in PE devices, underscoring the need to explore next-generation power semiconductors.

A comprehensive computational search offers a promising pathway for discovering novel materials for PEs. Computational approaches have proven to be effective in accelerating materials discovery, offering a substantial efficiency advantage over traditional trial-and-error methodologies. Advances in first-principles methodologies, computational tools, and infrastructure have enabled high-throughput (HT) screening of large material datasets to pinpoint high-performance candidates17. These workflows employ structure–property descriptors and application-specific figures of merit, which are derived through efficient ab initio simulations and reduced-order modeling17,18. Approximations, such as assumptions about material dopability, are often employed to expedite searches without significantly compromising accuracy. HT computations have successfully identified novel materials for diverse applications, including solid-state batteries19,20, thermoelectrics18,21, field-effect transistors22, and photovoltaics19,23. They have also driven the development of open-access materials databases, facilitating data sharing and accelerating materials discovery across various fields16,24,25,26. Despite their potential, previous studies have only investigated 10,600 stoichiometric and ordered structures from the Inorganic Crystal Structure Database (ICSD) in searching for new PE materials9. In particular, comprehensive efforts to explore next-generation power semiconductors within the entire Materials Project database remain limited.

Results

Database screening and high-throughput calculations

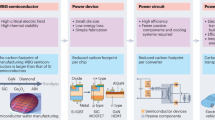
Figure 1a illustrates the development trends of power semiconductors and highlights the role of a new generation of power semiconductor materials in reducing energy loss. High bandgap, superior carrier mobility, and excellent thermal conductivity are essential properties for semiconductor materials used in power devices. We develop the screening process depicted in Fig. 1b to identify new power semiconductor materials using HT methods (details of the screening process are referred to “Methods” section). Figure 1b outlines the workflow for screening next-generation power semiconductors and HT computations. Starting from all 153,235 materials in the Materials Project database, we focus on studying potential semiconductor materials with a bandgap greater than 0. Due to the complexity of calculations and corresponding literature reports, we exclude ternary compounds and those with more than 3 constituent elements. Materials composed of elements with an atomic number greater than 54 are also excluded. There are 1009 materials that are preliminarily screened, whose stability is then evaluated. In addition, we also screen materials with high hull energy and cohesive energy. As a result, there are 500 materials remaining after the preliminary screening, and their bandgap, electron mobility, and thermal conductivity are calculated in sequence using the HT methods (Supplementary Tables 9–11), eventually determining 44 promising new generation power semiconductor materials (Supplementary Table 12). The filtering methodology for steps 1–5 (orange background) utilizes Materials Project data, while in steps 6–8 (blue background), the high-throughput calculation results are incorporated.

Fig. 1: Schematic diagrams illustrating the discovery of wide-bandgap (WBG) semiconductors, and a flowchart of the proposed ab initio screening methodology.
figure 1

a Compared to the 1st and 2nd generation semiconductors (e.g., Si with Eg = 1.1 eV, GaAs with Eg = 1.4 eV), the 3rd generation wide-bandgap (WBG) semiconductors (e.g., 4H-SiC with Eg = 3.2 eV, wurtzite-GaN with Eg = 3.4 eV) can reduce the energy loss of PE devices by over 50%. b Using ab initio HT simulation, all (a total number of 153,235) materials in the Materials Project are massively screened to search for the best next-generation ultra-wide-bandgap (UWBG) candidates. Here, ns is atom species; na is atom number; a.n. is maximum atomic number; Eg is bandgap; Eh is hull energy; Ec is cohesive energy; μ is electron mobility; к is thermal conductivity. c Retrieve intrinsic properties of materials from the Materials Project (MP) website. d The Baliga figure of merit (FOM), FB, and the Johnson FOM, FJ, are obtained by combining DFT, DFPT, and BTE. Here, C is elastic constant, D is deformation constant, Eg is bandgap, Eb is breakdown field, m* is electron effective mass of; En(k) is electronic dispersion; ωpo is maximum polar optical phonon frequency at Г-point in the Brillouin zone; εs is static dielectric constant; ε∞ is high-frequency dielectric constant; vs is electron saturation velocity; sadp, spop, and simp are differential scattering rates of acoustic deformation potential scattering, polar optical phonon scattering and impurity scattering; μ is electron mobility. e Through the screening process, promising next-generation power semiconductor materials can be identified.

Full size image

Simultaneously, to reduce computational complexity and optimize the screening process, we derive the intrinsic properties of existing materials from the Materials Project database, as shown in Fig. 1c. These properties include the types of elements in the materials (ns), the number of atoms per cell (na), the atomic numbers of each element (a.n.), bandgap (Eg), hull energy (Eh), and cohesive energy (Ec). The data correspond to the first five steps of the screening process, significantly accelerating the screening speed and efficiency. In Fig. 1d, HT methods combined with first-principles based density functional theory (DFT), density functional perturbation theory (DFPT) and Boltzmann transport equation (BTE) based calculation methods are employed to compute the bandgap of totally 500 materials (Supplementary Table 9), electron mobility of totally 212 materials (Supplementary Table 10), and thermal conductivity of totally 67 materials (Supplementary Table 11). Eventually, 44 high-performance power semiconductor materials are identified (Supplementary Table 12). As shown in Fig. 1e, we select the most promising next-generation power semiconductor materials from the remaining 44 candidates. We focus on the performance of pristine materials, which relies on intrinsic properties such as ns, na, Eg, Eh, Ec, μ, and к. Extrinsic factors such as doping need to be appropriately adjusted for the 44 promising candidates identified. To compute the parameters that determine the Baliga figure of merit (FOM), Johnson FOM, and lattice thermal conductivity for the identified materials, we use ab initio methods combined with semi-empirical models of transport properties and a phenomenological model of critical breakdown field. Our computational search reveals several promising candidates with an optimal combination of high figure of merit and lattice thermal conductivity. These resultant candidates include two types of BeO, one type of BN, and one type of B2O3, exhibiting superior n-type Baliga and Johnson figures of merit. Furthermore, the lattice thermal conductivity of the materials surpasses that of Ga2O3. Further experimental and computational investigations on these identified materials are suggested.

Accuracy verification

To validate our high-throughput (HT) computations, the calculated properties of bandgap (Eg), static dielectric constant (εs), high-frequency dielectric constant (ε∞), electron effective mass (m*), carrier saturation velocity (vs), elastic constants (cij), electron mobility (μ), and thermal conductivity (κ) are compared with experimental data. The comparisons are presented in Fig. 2a–h and Supplementary Tables 1–8, estimating the HT computational accuracy. All experimental values were manually obtained through searching relevant references at Google Scholar.

Fig. 2: Comparison between the calculated and experimental results.
figure 2

a bandgap, Eg, b static dielectric constant, εs, c high-frequency dielectric constant, ε∞, d electron effective mass, me, e carrier saturation velocity, vs, f elastic constants, cij, g electron mobility, μ, and h thermal conductivity, κ.

Full size image

In Fig. 2, the shadowed areas represent the maximum computational error of 90% of the sampling points. The bandgaps (Eg) calculated by the HSE06 functional are typically within 25% of experimental values27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63; the static dielectric constants (εs)64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90 are within 18%; the high-frequency dielectric constants (ε∞)65,66,68,72,74,75,76,77,79,80,81,82,87,90 are within 17%; the electron effective masses (me)36,75,91,92,93,94,95,96,97,98,99,100,101 are within 14%; the carrier saturation velocities (vs)10,11,75,102,103,104,105,106,107,108,109 are within 23%; the elastic constants (cij)110,111,112,113,114,115,116 are within 15%; the electron mobilities (μ)72,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131 are within 60%, and the thermal conductivities (κ)132,133,134,135,136,137,138,139,140,141 are within 37%. It is worth noting that due to the strong influences of breakdown field strength on the values of Baliga figure of merit (BFOM) and Johnson figure of merit (JFOM), the HSE06 exchange-correlation functional is used to calculate Eg, resulting in reliable FOM values as obtained. Additionally, the errors of the calculated electron mobility are mostly within 50%, which exhibits significantly higher accuracy than that reported in ref. 9 (where the discrepancy between the calculated electron mobility and experimental values is within half an order of magnitude). The errors in our calculated thermal conductivity are mostly below 37%, which is higher than those reported in ref. 9 (where the error in calculating thermal conductivity is within 150%).

Candidates for next-generation wide-bandgap (WBG) semiconductors

Figure 3a illustrates the distribution of hull energy relative to bandgap (calculated using HSE) for 500 materials, which are screened using specific criteria (ns = 2, na ≤ 10, a.n. ≤ 54, Eg > 0 eV, Ec ≤ −2.9 eV/atom) based on the database at the Materials Project website. The figure reveals that halides and oxides exhibit higher bandgaps, while other compounds (such as silicides, borides, arsenides, and phosphides) exhibit lower bandgaps. For power semiconductors, high breakdown field strength, which correlates positively with bandgap, is essential. Hence, we focus on materials with a bandgap exceeding 2.8 eV (represented by a horizontal dashed line in Fig. 3a).

Fig. 3: The distributions of band gap, hull energy, thermal conductivity, electron mobility and figures of merit.
figure 3

a hull energy and bandgap, b bandgap and electron mobility, c electron mobility and thermal conductivity, and d thermal conductivity and Baliga Figure of Merit (BFOM) are plotted for 44 materials with a bandgap greater than 2.8 eV, an electron mobility higher than 100 cm2/Vs, and a thermal conductivity above 10 W/mK. Different colors in the images represent oxides, sulfides, nitrides, carbides, selenides, tellurides, halides, and other compounds (such as silicides, borides, arsenides, and phosphides). Horizontal dashed lines indicate bandgap values of 2.8 eV in (a), while horizontal and vertical gray dashed lines mark an electron mobility of 100 cm2/Vs and a bandgap of 2.8 eV in (b). In (c), the horizontal and vertical gray dashed lines denote a thermal conductivity of 10 W/mK and an electron mobility of 100 cm2/Vs. In (d), the horizontal and vertical gray dashed lines correspond to a BFOM of 53,077 and a thermal conductivity of 10 W/mK, and cubic boron nitride (c-BN) shows the highest calculated BFOM value among the existing power semiconductor materials.

Full size image

Figure 3b illustrates the distribution of bandgap relative to electron mobility for the remaining 212 materials after the sixth screening step (Eg > 2.8 eV). The graph reveals that the majority of halide compounds exhibit low electron mobility (μ < 100 cm2/Vs), leading to their exclusion. Similarly, some oxides, as well as a few nitrides, tellurides, selenides, sulfides, and carbides, are excluded due to their low electron mobility. On the contrary, nitrides and sulfides are more prevalent among materials with high electron mobility.

Figure 3c presents the relationship between electron mobility and thermal conductivity for the remaining 67 materials after the seventh screening (μ > 100 cm2/Vs). The graph indicates that all remaining halide compounds exhibit low thermal conductivity (κ < 10 W/mK), resulting in their exclusion. Similarly, most oxides, some sulfides, and a few carbides are excluded due to their low thermal conductivity. The figure also reveals that materials possessing both high thermal conductivity and high electron mobility (in the upper right corner of Fig. 3c) are predominantly nitrides and carbides. Mainstream semiconductor materials, including SiC, GaN, diamond, Ga2O3, BN, and AlN, all meet our screening criteria (Fig. 3a–c), validating the effectiveness of our screening method. Different polytypes within the same space group exhibit distinct electronic properties, resulting in different electron mobilities, such as in BN and SiC.

To compare the performance of the screened materials, we calculate BFOM and JFOM for 44 materials (as shown in the upper right corner of Fig. 3c), as listed in Table 12. Most of the screened materials consist of the main group elements in the periodic table. The 44 materials are categorized into three types: oxides and their derivatives (sulfides, selenides, and tellurides), including Ga2O3, MgO, SnO2, GeO2, B2O3, BeO, BeS, ZnS, BeTe, and MgTe; nitrides that include GaN, AlN, BN, Be3N2, and P3N5, and carbides that include SiC. Interestingly, the highest bandgap is found to be 10.90 eV in B2O3 (material ID: mp-717), suggesting that it is a good candidate for high breakdown field applications. The highest thermal conductivity, 1122 W/mK, is observed in cubic BN (material ID: mp-1639), indicating that it is a promising heat dissipation material. The highest electron mobility, 1293 cm2/Vs, is observed in wurtzite BN (material ID: mp-2653), indicating that it is a promising material for high electron mobility transistors.

To identify the most promising power semiconductor materials, we use the value of BFOM for c-BN as the screening criterion (BFOM > 36,882), which is the highest among those of currently discovered power semiconductors, as illustrated in Fig. 3d. This process results in the identification of four highly promising power semiconductor materials (as listed in Table 1): i.e., B2O3 (material ID: mp-717), z-BeO (material ID: mp-1778), w-BeO (material ID: mp-2542), and w-BN (material ID: mp-2653). These materials exhibit ultra-wide bandgaps (>6.55 eV), excellent electron mobility (>110 cm2/Vs), and high thermal conductivity (>90 W/mK). Additionally, they possess outstanding BFOM performance indicators (BFOM > 88,900). Consequently, these four power semiconductor materials deserve further exploration through theoretical calculations and experiments.

Table 1 Screened materials and their properties
Full size table

Since the intermediate parameters have computational errors transferred to the final values of FOM, classical power semiconductor materials are used to further verify the calculated errors. We have demonstrated that the experimental and computed values of BFOM and JFOM are within one order of magnitude. Furthermore, the relative values of calculated BFOM and JFOM for various wide-bandgap semiconductor materials align with experimental results. It is noteworthy that we also calculate the relationship between εs and bandgap for 500 materials selected after the fifth round of screening. The εs of those materials, including the four potential power semiconductor materials as screened (B2O3, z-BeO, w-BeO, and w-BN), exhibit an inverse relationship with bandgap values (Supplementary Fig. 1). Over 90% of the materials are within an error margin of 30%, which aligns with previous analysis for 3D materials142,143. The analysis is reasonable, which is based on the calculation formula of the dielectric matrix22, suggesting that the four screened materials conform to the conventional intrinsic properties of materials.

Next, we explore the band structures of diamond, c-BN, the as-screened four candidate WBG materials, and a commonly used material, 4H-SiC, as illustrated in Fig. 4a. Figure 4c illustrates the structural diagrams of these materials. The band structures of c-BN, diamond, silicon, and the as-screened four candidate materials are calculated using the HSE06 functional. The gray and red bars indicate the maximum value of VBM and the minimum value of CBM, respectively. The gray and red dashed lines denote the VBM and CBM of 4H-SiC, respectively. The light purple region represents the energy range with an extension of 1 eV above and below the CBM of 4H-SiC, respectively. Diamond, c-BN, and the as-screened four candidate WBG materials can serve as channel materials for power devices, and the p-type and n-type field-effect transistors (FETs) can be formed through doping. Additionally, these materials can be directly used as FET materials when 4H-SiC is the channel material. When 4H-SiC is used as a channel material, z-BeO dielectrics are ideal for p-type field-effect transistors (FETs) because of their high tunnel barrier for hole carriers. In contrast, diamond, c-BN, and w-BN dielectrics are suitable for n-type FETs due to their high tunnel barrier for electron carriers. Additionally, B2O3 and w-BeO are also appropriate for p-type FETs. We also compare the band structures of the widely used w-GaN with those of six other materials, as shown in Supplementary Fig. 4. Our results show that when w-GaN is used as a channel material, diamond, c-BN, and w-BN dielectrics are ideal for n-type FETs because of their high tunnel barriers for electron carriers. Furthermore, B2O3, z-BeO, and w-BeO are suitable for both n-type and p-type FETs.

Fig. 4: Comparison of band edge and atomic structure between next-generation WBG semiconductor candidate materials and the two best-performing WBG semiconductor materials currently known (diamond and c-BN).
figure 4

a The band structures of c-BN, diamond, silicon, and four candidate materials are calculated using the HSE06 functional. The gray and red bars represent the maximum value of the valence band (VBM) and the minimum value of the conduction band (CBM), respectively. The gray and red dashed lines indicate the VBM and CBM of 4H-SiC, respectively. The light purple region shows the energy range with an extension of 1 eV above and below the CBM of 4H-SiC, respectively. b Comparisons between the properties (Ec, μ, κ, BFOM, and JFOM) of the as-screened power semiconductor materials (B2O3, z-BeO, w-BeO, and w-BN) and the best-performing WBG semiconductor materials currently known (Diamond and c-BN) using radar charts. c Top views of the lattice of diamond, c-BN, and the as-screened candidates for WBG materials, revealing distinct crystal compositions. The side views of the lattice of these materials are shown in Supplementary Fig. 2. The dashed lines in the figure represent individual unit cells of the materials.

Full size image

Finally, as shown in the comparison chart of the properties between the four as-screened materials and the two best-performing power semiconductor materials (Fig. 4b), it is evident that B2O3 has the best breakdown field strength and JFOM value, making it suitable for further exploration in high breakdown field strength and switching devices. The BFOM, thermal conductivity, and electron mobility of z-BeO and w-BeO demonstrate that they have excellent performance and deserve further exploration in the field of power devices. Moreover, w-BN exhibits the highest BFOM, outstanding thermal conductivity, and electron mobility, making it a promising candidate for power devices and heat dissipation applications.

Statistical analysis of element preference for the 5th–8th screening rounds

To screen potential wide-bandgap (WBG) materials, we systematically evaluated structural parameters and elemental composition across 500 candidate compounds. They are classified into four distinct groups defined by their computed hull energy, bandgap, electron mobility, and thermal conductivity values. As shown in Fig. 5a–d, group 1 materials exhibit hull energies below 0.1 eV, which are retained through five iterative screening stages (Fig. 5a); those in group 2 have a bandgap higher than 2.8 eV and a hull energy value lower than 0.1 eV after six screening rounds (Fig. 5b). Group 3 contains materials demonstrating electron mobilities exceeding 100 cm2/V·s, bandgaps greater than 2.8 eV, and hull energies below 0.1 eV, which survive seven iterative screening stages (Fig. 5c). Group 4 contains materials exhibiting a thermal conductivity exceeding 10 W/mK, an electron mobility value larger than 100 cm2/Vs, a bandgap higher than 2.8 eV, and a hull energy value lower than 0.1 eV after eight screening rounds (Fig. 5d). As shown in Fig. 4e, there are 500, 212, 67, and 44 materials in groups 1–4, respectively.

Fig. 5: Statistical analysis of 500 calculated materials.
figure 5

a–d Guided by the first-principles calculation-derived bandgap, electron mobility, and thermal conductivity, the remaining 500 materials after the fifth screening round will undergo subsequent screening processes. e The materials can be divided into four categories to study the element preferences. f Histograms quantifying the five most abundant anions and cations across groups, with gray and orange bars denoting material proportions of specific anions and cations, respectively. Periodic table heatmaps visualize g anion and h cation prevalence within each group, where elemental blocks are partitioned into quadrants (one per group), with color intensity scaled to elemental frequency in the corresponding group.

Full size image

To investigate anion/cation distributions across groups, Supplementary Fig. 3 provides a quantitative analysis of their prevalence via histograms for each classification, while Fig. 5g, h maps these trends onto periodic table heatmaps. Figure 5f identifies the five most abundant ionic species per group, omitting the hydrogen cation due to its propensity for hydroxyl anion formation via oxygen bonding. Comparative analysis of the five most abundant anions (gray bars, Fig. 5f) across groups reveals that after five screening rounds, 500 materials with hull energy lower than 0.1 eV (Group 1 materials) primarily employ oxygen (O), sulfur (S), fluorine (F), selenium (Se), and chlorine (Cl) as anionic species, and most of these elements demonstrate high electronegativity, resulting in the materials’ enhanced structural stability and elevated melting points. Group 2 materials (with a bandgap >2.8 eV) predominantly employ oxygen (O), sulfur (S), nitrogen (N), chlorine (Cl), fluorine (F), and bromine (Br) as anionic constituents, and most of these elements exhibit high electronegativity. In contrast, compounds with narrower bandgaps (<2.8 eV) preferentially incorporate selenium (Se), phosphorus (P), arsenic (As), and tellurium (Te) as anions, and most of these elements demonstrate comparatively low electronegativity. Group 3 materials (bandgap >2.8 eV, electron mobility >100 cm2/V·s) predominantly employ oxygen (O), sulfur (S), and nitrogen (N) as anions, and most halides are excluded due to their strong chemical bonds formed between halogen elements and other elements, which limit the movement of electrons in the materials. Group 4 materials (bandgap >2.8 eV, electron mobility >100 cm2/V·s, thermal conductivity >10 W/(m·K)) primarily incorporate sulfur (S), nitrogen (N), and carbon (C) as anionic constituents. The strength of chemical bonds formed between nitrogen, sulfur, and carbon, and other elements is relatively high, especially the carbon–carbon bond in carbides. These strong bonds effectively conduct heat, reduce phonon scattering, and thus improve thermal conductivity.

Our investigation systematically quantifies cation distributions across all groups, with corresponding prevalence data displayed in salmon-colored bars (Fig. 5f). After five screening rounds, 500 materials with hull energy lower than 0.1 eV (Group 1 materials) predominantly contain tin, aluminum, gallium, silicon, and magnesium. These elements often behave as either metals or non-metals, forming covalent bonds that result in stable structures and high melting points. Group 2 materials (bandgap >2.8 eV) predominantly feature magnesium (Mg), aluminum (Al), calcium (Ca), silicon (Si), and lithium (Li) cations, which exhibit relatively low average electronegativity characteristic for the formation of wide-bandgap compounds. Group 3 (bandgap >2.8 eV, electron mobility >100 cm2/Vs) and Group 4 (additional thermal conductivity >10 W/mK) materials share common cationic constituents of boron (B), magnesium (Mg), zinc (Zn), and beryllium (Be), benefiting from their low atomic mass and directional covalent bonding that could collectively enhance electronic properties. The lightweight cations (e.g., ions of B, Mg, Be) exhibit low atomic masses, which reduce electron effective mass and minimize lattice scattering effects—a critical factor that enhances electron mobility (>100 cm2/Vs) in high-performance semiconductors. Additionally, the relatively simple atomic structure of these elements can effectively conduct heat, improving thermal conductivity (>10 W/mK).

Our systematic investigation reveals that wide-bandgap materials prioritize two distinct compositional strategies, i.e., strongly electronegative anions (O, F, S, N, Cl) and low-electronegativity cations (e.g., Li, Mg). In contrast, narrow-bandgap systems predominantly employ metalloid anions (As, Se, Te, P). Notably, compounds with optimized transport properties (μ > 100 cm2/Vs, κ > 10 W/mK) favor lightweight, low-valence cations (B, Be, Mg, Ga, Zn) due to their reduced orbital complexity and suppressed electron-phonon scattering.

The electronic bandgap is fundamentally governed by the relative positions of band edges. Specifically, the VBM and CBM are primarily regulated by anionic and cationic valence electron energy levels, respectively, according to the molecular orbital theory144,145. Strategic substitution of oxide matrices with less electronegative non-oxide anions (e.g., S, Se) serves as a proven bandgap-narrowing strategy for visible-light photocatalysis146,147. Over decades, extensive studies have established semi-empirical relationships between bandgap and electronegativity differences (Δχ), and notably, the quadratic dependence Eg∝(Δχ)2 is observed in oxides, where Δχ represents the Pauling electronegativity contrast between cations and anions148,149. Lighter cations such as boron, beryllium, magnesium, gallium, and zinc have lower atomic masses, reducing phonon scattering in the material. Lower phonon scattering allows electrons to move more freely, thereby increasing electron mobility. Low-atomic-mass cations (e.g., Be, B) are preferentially incorporated into high-κ semiconductors such as silicon carbide (SiC) and gallium nitride (GaN), where their reduced ionic mass suppresses phonon scattering and enhances thermal transport efficiency. These materials have a compact lattice structure and strong chemical bonds, which can effectively conduct heat, reduce phonon scattering, and improve thermal conductivity. Materials formed by lighter cations typically have a simple and ordered lattice structure, facilitating heat transfer and thus improving thermal conductivity. To identify high-performance dielectrics with large bandgaps (>2.8 eV), high electron mobility (>100 cm2/Vs), and elevated thermal conductivity (>10 W/mK), materials incorporating strong electronegative anions (O, F, S, N, Cl) paired with low-atomic-mass cations (B, Be, Si, Mg) can be prioritized. Ultimately, beyond atomic mass considerations, structural parameters including crystal symmetry, bonding configuration, and defect density critically modulate thermal and electronic transport properties in ionic material systems.

In addition, we conducted additional analyses using Matminer150 to characterize the crystal structures and formation energies of selected materials. Supplementary Fig. 4 presents the correlation between formation energy and energy above hull across different crystal systems. Notably, all of our 500 preliminarily screened materials exhibit negative formation energies, confirming their thermodynamic stability. Significantly, the cubic, trigonal, and hexagonal configurations predominantly occupy the lower-left quadrant of the plot (Supplementary Fig. 4), indicating low formation energies and hull energy values consistent with high structural stability. Further analysis of crystal system distributions across material groups reveals that for Group 1 (Supplementary Fig. 5a), the cubic, trigonal, and hexagonal systems dominate (with a bandgap-PEB > 0 eV, an energy above hull <0.1 eV), suggesting these symmetries favor electronic stability. For Group 2 (Supplementary Fig. 5b), post-bandgap screening (with a bandgap-HSE > 2.8 eV) still suggests the prevalence of cubic/trigonal/hexagonal systems. The reduced monoclinic and orthorhombic representations correlate with smaller bandgaps, while the increased tetragonal prevalence indicates larger bandgaps. For Group 3 (Supplementary Fig. 5c), the cubic/trigonal/hexagonal fractions increase remarkably as other systems diminish, demonstrating superior electron mobility in these configurations. For Group 4 (Supplementary Fig. 5d), the cubic systems disappear, indicating poor thermal conductivity, while the hexagonal configurations surge to 59% prevalence, highlighting exceptional thermal transport properties.

Discussion

In this work, we focus on materials cataloged in the Materials Project database, which have been extensively studied and characterized, providing a well-established understanding of their properties. However, it is worth noting that some unexplored materials, which may exhibit superior properties for power semiconductor applications, remain absent from the database. Future research should prioritize the exploration of those novel materials, employing advanced screening and evaluation techniques. Machine learning algorithms and HT computational methods could play a pivotal role in rapidly screening large material datasets and identifying promising candidates for further dedicated investigation. Additionally, the development of comprehensive and standardized testing protocols for evaluating power semiconductor properties is essential.

While this computational analysis elucidates structure–property relationships in wide-bandgap semiconductors, we emphasize that ultimate device performance remains intricately linked to fabrication parameters such as doping uniformity, interface engineering, and thermal budget control, which lie beyond the scope of this work. The operational performance of power semiconductor devices is critically determined by both inherent material characteristics and extrinsic engineering parameters such as metallization interface quality and doping profile optimization, which collectively govern charge carrier dynamics and junction behavior. Variations in fabrication processes, even minor ones, can lead to significant differences in device performance. Thus, precise control over fabrication is crucial to achieving desired device properties. Moreover, the doping profile, which determines the carrier concentration and mobility within the semiconductor, significantly impacts key attributes such as electrical conductivity and overall device performance.

In previous work9, some reports have highlighted certain power semiconductor materials not included in our screened dataset, such as ZnO. Our computational validation indicates that the performance of these materials, as exemplified by ZnO’s relatively low BFOM compared to that of 4H-SiC, is substantially inferior to the oxide materials identified in our study, such as BN, BeO, and B2O3. The omission of certain materials thus does not materially impact the central findings of this work.

Our study emphasizes oxide materials that demonstrate superior performance for the intended applications, while recognizing the ongoing discovery and development of new materials in this field. Continued monitoring and evaluation of advancements in power semiconductor materials will ensure the relevance and accuracy of our conclusions. While this study establishes foundational structure–property correlations in the established wide-bandgap semiconductors, systematic investigation remains imperative to achieve performance optimization through defect engineering and interfacial design, expanding into uncharted chemical spaces (e.g., rare-earth chalcogenides, complex perovskites) that may exhibit superior electronic-thermal characteristics for next-generation power electronics.

Methods

Details for database screening

High-performance power semiconductors necessitate simultaneous optimization of Baliga’s (BFOM = εsμEb3) and Johnson’s (JFOM = Ebvs/2π) figures of merit (FOMs). To address their neglect of thermal dissipation, we explicitly incorporated lattice thermal conductivity (κ) as a critical screening parameter. Ideal candidates require a large breakdown field (Eb), governed by intrinsic factors (bandgap Eg > 3 eV, dielectric constant εs > 10, and strong Fröhlich electron-phonon coupling151,152) and extrinsic defect engineering5. Concurrently, high current density (J = σE = μne E) demands both intrinsic electron mobility (μ) and extrinsically tunable electron concentration (n). Finally, effective Joule heat dissipation necessitates high κ (>100 W/mK), as quantified by Callaway’s phonon transport model153.

Our systematic evaluation of 153,902 inorganic compounds from the Materials Project database employed a multi-stage selection protocol (Fig. 1b) to identify high-performance power semiconductor candidates. Based on this, we established the following criteria to search for the best next-generation wide-bandgap (WBG) candidates.

  1. (1)

    Previous studies9 have shown that materials with more than two elements tend to have low thermal conductivity; therefore, we focused on binary compounds, resulting in 20,627 candidates (ns = 2).

  2. (2)

    Recent computational analyses have demonstrated an inverse proportionality between lattice thermal conductivity (κ) and the cube root of atomic density per unit cell154, with increased unit cell complexity leading to suppressed κ values, which are attributed to dominant low-group-velocity optical phonon modes155,156. Thus, we screened for compounds with fewer than 10 atoms per primitive cell (na ≤ 10) and the maximum atomic number is less than 54 in unit cells (a.n. ≤ 54), resulting in 5690 candidates.

  3. (3)

    Next, the system must not be metallic, so the bandgap (Eg) of power semiconductor materials should be above 0 eV. Querying the bandgap of all materials calculated by the PBE functional from the Materials Project database, we identified 1009 materials with Eg > 0 eV.

  4. (4)

    Materials with high melting points (Tm) can withstand higher operating temperatures, and cohesive energy (Ec) measures the strength of interatomic bonds, correlating positively with the melting point of crystalline materials157. Thus, Ec is a suitable descriptor here. We identified 706 materials with Ec ≤ −2.9 eV/atom, corresponding to Tm above 800 K.

  5. (5)

    Additionally, high thermodynamic phase stability and melting points contribute to improved device performance, increasing the lifetime and operating temperature of PEs. Employing the energy above hull (Eh) metric from the Materials Project157, we assessed thermodynamic stability at 0 K and ambient pressure, where Eh quantifies the energy penalty for a compound to decompose into its ground-state phases. As a result, 500 phase-stable candidates with Eh ≤ 0.1 eV/atom are screened, which is a threshold balancing synthesizability and computational accuracy.

  6. (6)

    Furthermore, a high breakdown field is required, as the bandgap and breakdown field are positively correlated4,13,158, Considering the fact that the PBE functional underestimates the bandgap by ~40% compared to experiments157, we used the HSE06 functional159 to calculate the bandgap, resulting in 212 materials with Eg > 2.8 eV.

  7. (7)

    High transport velocity is essential in power semiconductor devices, necessitating large electron mobility, and there are 67 materials that satisfy this criterion (μ > 100 cm2/Vs).

  8. (8)

    Finally, power semiconductor materials need to effectively manage heat loss, necessitating high thermal conductivity, and there are 44 materials that meet this requirement (к > 10 W/mK).

The settings for screening steps 7–8 are based on properties of the current power semiconductorβ-Ga2O3 (μ = 150 cm2/V·s, κ = 14 W/mK), which exhibits low electron mobility and thermal conductivity despite its excellent BFOM values. Therefore, we intentionally relax the electron mobility and thermal conductivity criteria (μ ≥ 100 cm2/Vs and κ ≥ 10 W/mK) to ensure that potential next-generation power semiconductors are not inadvertently excluded. In addition, the filtering methodology for steps 1–5 utilizes Materials Project data, while in steps 6–8, the high-throughput calculation results are incorporated.

Models for evaluating FOM parameters

Domain-specific FOM, including that for thermoelectric21, topological invariant indices160, photovoltaic efficiency metrics23, and power electronics benchmarks9,161 could serve as critical descriptors for high-throughput (HT) materials discovery when paired with rapid computational parameterization. Building on this framework, the performance-critical properties for PE materials, FOMs derived from these attributes, and first-principles models enabling efficient computation of requisite parameters (band structure, electron mobility, thermal transport) are examined.

In power electronics, intrinsic material performance is quantified through established figures of merit (FOMs), including Johnson’s JFOM162,163, Baliga’s BFOM161,164, and metrics by Kim165 and Huang166, primarily for unipolar switching devices. FOMs distinguish between low-frequency (BFOM = εsμEb3, where εs is the dielectric constant, μ is the electron mobility, Eb is the breakdown field)161 and high-frequency (JFOM = Ebvs/2π, where vs is the saturated carrier velocity, Eb is the breakdown field)164 operation. BFOMassumes that on-state conduction losses are dominant, making it apt for low-frequency applications. For high-frequency regimes, JFOM supersedes BFOM due to its incorporation of carrier velocity dynamics. Crucially, neither FOM accounts for thermal conductivity (κ), despite its necessity in mitigating Joule heating and preventing interfacial/mechanical failure. We therefore explicitly evaluate κ alongside BFOM and JFOM as screening criteria. Under non-degenerate carrier concentrations (n ≪ 1019 cm−3), electronic-thermal conductivity contributions are negligible, justifying our focus on lattice-derived κ.

Computational evaluation of Baliga’s (BFOM = εsμEb3) and Johnson’s (JFOM = Ebvs/2π) figures of merit requires determination of four critical parameters: static dielectric constant (εs) calculated via density functional perturbation theory (DFPT) to account for ionic and electronic contributions (“Methods” section), charge carrier mobility (μ) and saturated velocity (vs) derived from ab initio carrier transport models, and breakdown field (Eb) estimated using bandgap-dependent empirical scaling relations. Figure 1d illustrates the integrated computational workflow, combining DFPT, Boltzmann transport theory, and empirical correlations within a unified ab initio framework.

A first-principles computational framework for carrier mobility prediction in solid-state systems was developed by Alex et al.117 extending conventional scattering models (polar/non-polar electron-phonon coupling, ionized impurity, and acoustic deformation potential) to address anisotropic band structures. This method achieves parity with full iterative Boltzmann transport equation (BTE) solutions in accuracy while enabling a 500-fold computational cost reduction, making it uniquely suitable for high-throughput screening of carrier transport properties in complex materials. Three scattering mechanisms are considered as below167:

The ionized impurity differential scattering rate

$${s}_{\mathrm{imp}}({\boldsymbol{k}},{\boldsymbol{k}}{\text{'}})=\frac{{e}^{4}{N}_{\mathrm{imp}}}{4{\pi }^{2}\hslash {{\rm{\varepsilon }}}_{s}^{2}}\times \frac{G({\boldsymbol{k}},{\boldsymbol{k}}{\text{'}})}{{({|{\boldsymbol{k}}-{\boldsymbol{k}}{\text{'}}|}^{2}+{\beta }^{2})}^{2}}\times \delta (E-{E}^{{\text{'}}}),$$
(1)

where \(\hslash\) is the reduced Planck constant, E is the electron energy, e is the electron charge, \(\delta\) is the Dirac delta function, \({N}_{\text{imp}}\) is the concentration of ionized impurities, β is the inverse screening length, εs is the static dielectric tensor, G is the coupling matrix element.

The polar optical phonon differential scattering rate

$${s}_{\mathrm{pop}}({\boldsymbol{k}},{\boldsymbol{k}}{\boldsymbol{\text{'}}})=\frac{{e}^{2}{\omega }_{p{\rm{o}}}}{8{\pi }^{2}}\left(\frac{1}{{{\rm{\varepsilon }}}_{\infty }}-\frac{1}{{{\rm{\varepsilon }}}_{s}}\right)\frac{G({\boldsymbol{k}},{\boldsymbol{k}}{\boldsymbol{\text{'}}})}{{|{\boldsymbol{k}}-{\boldsymbol{k}}{\boldsymbol{\text{'}}}|}^{2}}\times \left\{\begin{array}{l}\delta \left(E-E{\text{'}}+\hslash {\omega }_{p{\rm{o}}}\right)\left({N}_{po}+1\right),\,\mathrm{emission}\\ \delta \left(E-E{\text{'}}+\hslash {\omega }_{p{\rm{o}}}\right){N}_{po\,},\mathrm{absorption}\end{array}\right.$$
(2)

where ωpo is the frequency of dispersion less longitudinal optical phonon mode, ε∞ is the high-frequency dielectric tensor.

The acoustic deformation potential differential scattering rate

$${s}_{\mathrm{adp}}({\boldsymbol{k}},{\boldsymbol{k}}{\boldsymbol{\text{'}}})=\frac{{e}^{2}{k}_{B}T{E}_{1}^{2}}{4{\pi }^{2}\hslash {c}_{{\rm{l}}}}\times G({\boldsymbol{k}},{\boldsymbol{k}}{\boldsymbol{\text{'}}})\times {\rm{\delta }}(E-E{\text{'}})$$
(3)

where T is temperature, c is the elastic constant, the subscript l indicates properties belonging to the longitudinal modes, kB is the Boltzmann constant. The electron mobility is calculated using the AMSET software117 through employing the linearized BTE while considering three scattering mechanisms.

Accurate determination of the critical breakdown field (Eb) is fundamental for evaluating BFOM and JFOM. While Eb can theoretically be derived from first-principles calculations, practical limitations arise due to the computational expense of electron-phonon coupling matrix evaluations, rendering such approaches intractable for large-scale screening5. Empirical models bypass this bottleneck by correlating Eb with bandgap (Eg), leveraging the established positive Eg relationship10. For narrow-bandgap materials, Eb follows a quadratic dependence on Eg(Eb∝Eg2)4,158, whereas a linear scaling (Eb∝Eg) dominates in wide-bandgap systems158,168. The fitted expression is:

$${E}_{b}=\left\{\begin{array}{l}0.25\times {E}_{g}^{2},\,{E}_{g}\le 4.30\,{\text{eV}}\\ 5.43\times {E}_{g}-18.67,{E}_{g} > 4.30\,{\text{eV}}\end{array}\right.$$
(4)

where Eg is the bandgap in eV and Eb is the breakdown field in MV/cm.

As shown in Supplementary Fig. 6, we fitted the expression of Eb as a function of bandgap using experimental data from classical semiconductor materials4,13,158 (e.g., Ge, Si, GaAs, GaP, SiC, GaN, Ga2O3, diamond, AlN, BN, and SiO2). The abscissa corresponds to the experimentally determined bandgap (Eg), while the ordinate denotes the measured breakdown field (Eb). The black curve shows the Eb value calculated by fitting the formula. The graph indicates that the errors between the calculated values and experimental values are within 10%. When Eg is greater than 4.3 eV, most errors fall within 5%, demonstrating the accuracy of the fitting formula. Therefore, we will use this model to calculate Eb based on Eg obtained from DFT calculations. A critical limitation of existing empirical and phenomenological Eb models lies in their exclusion of impurity doping effects, which are known to degrade breakdown field strength9. Our analysis focuses on intrinsic material performance, adhering to established high-throughput screening protocols. Extrinsic factors, including influences of doping, warrant case-specific evaluation through subsequent computational refinement and experimental validation.

Thermal conductivity consists of two components: phonon (кp) and electron (кe) contributions, i.e., к = кp + кe. Due to the high bandgap (>3.0 eV) of power semiconductor materials, thermal conductivity is mainly attributed to phonons. Therefore, we only calculate lattice thermal conductivity using the Phono3py package169. Within the single-mode relaxation time (SMRT) approximation framework for solving the linearized phonon Boltzmann transport equation (BTE), the lattice thermal conductivity tensor (κ) admits an analytical closed-form expression169:

$$\kappa =\frac{1}{N{V}_{0}}\sum _{\lambda }{C}_{\lambda }{V}_{\lambda }\otimes {V}_{\lambda }{\tau }_{\lambda }^{{\rm{SMRT}}}$$
(5)

where N is the total number of unit cells in the crystal, V0 is the unit cell volume, Cλ is the Mode-dependent heat capacity of phonon mode λ, Vλ is the group velocity vector of mode λ, and \({{\boldsymbol{\tau }}}_{{\boldsymbol{\lambda }}}^{{\bf{SMRT}}}\) is the SMRT relaxation time for mode λ.

The electron saturation velocity can be written:

$${v}_{s}=\sqrt{2\hslash {\omega }_{po}/{m}^{\ast }}$$
(6)

where ωpo is the polar optical phonon frequency, m* is the electron effective mass.

Finally, as shown in Fig. 1d, the FOMs are calculated using parameters extracted from DFT, DFPT, and BTE. The Baliga FOM can be expressed as:

$${F}_{B}=\frac{1}{4}{\varepsilon }_{s}\mu {E}_{b}^{3}$$
(7)

where εs denotes the static dielectric constant, μ represents the electron mobility and Eb is the breakdown field. In this study, we primarily calculate electron mobility, assuming a carrier concentration of 1 × 1016 cm−3 throughout the calculation process.

The Johnson FOM can be written as:

$${F}_{J}=\frac{1}{2{\rm{\pi }}}{v}_{s}{E}_{b}$$
(8)

where vs is the electron saturation velocity.

Calculation details

Figure 1d illustrates the fully ab initio computational workflow employed in this study. First-principles calculations were performed using density functional theory (DFT) within the Vienna ab initio Simulation Package (VASP)170, with the following parameters: Pseudopotentials, Projector augmented wave (PAW) method171; Exchange-correlation, Perdew-Burke-Ernzerhof (PBE) functional172; Plane-wave cutoff, 600 eV; Geometry optimization, Force convergence criterion of 0.01 eV/Å; Electronic convergence: Gaussian smearing (width = 0.01 eV). Key electronic and lattice properties—including elastic constants, deformation potentials, carrier effective masses, band dispersion, polar optical phonon frequencies, static/high-frequency dielectric constants, and saturation velocities—were derived from DFT and DFPT outputs. For bandgap accuracy, the hybrid HSE06 functional173 was selectively applied to address PBE’s known underestimation of semiconductor bandgaps.