A versatile multimodal learning framework bridging multiscale knowledge for material design

Abstract

Artificial intelligence has achieved remarkable success in materials science, accelerating novel material design. However, real-world material systems exhibit multiscale complexity—spanning composition, processing, structure, and properties—posing significant challenges for modeling. While some approaches fuse multiscale features to improve prediction, important modalities such as microstructure are often missing due to high acquisition costs. Existing methods struggle with incomplete data and lack a framework to bridge multiscale material knowledge. To address this, we propose MatMCL, a structure-guided multimodal learning framework that jointly analyzes multiscale material information and enables robust property prediction with incomplete modalities. Using a self-constructed multimodal dataset of electrospun nanofibers, we demonstrate that MatMCL improves mechanical property prediction without structural information, generates microstructures from processing parameters, and enables cross-modal retrieval. We further extend it via multi-stage learning and apply it to nanofiber-reinforced composite design. MatMCL uncovers processing-structure-property relationships, suggesting its promise as a generalizable approach for AI-driven material design.

Introduction

Artificial intelligence (AI) has had a transformative impact on the material development process due to its ability to model complex and diverse material systems^1,2,3. Recently, major breakthroughs in materials science driven by AI have been achieved, including crystal structure discovery^4,5,6, alloy development^7,8,9, nanomaterial formulation optimization^10,11,12, polymer material design^{13,14,15,16,17,18}, which greatly accelerated the design of new materials.

Despite these advancements, AI still faces significant obstacles when tackling complex problems in materials science¹⁹. One key difficulty stems from the inherent complexity and hierarchical nature of materials, which are characterized by multiple scales of information and heterogeneous data types—including chemical composition, microstructure, macroscopic morphology, spectral characteristics—that are often correlated or complementary. Consequently, capturing and integrating these multiscale features is crucial for accurately representing material systems and enhancing model generalization, yet remains a considerable challenge for AI in material modeling. Moreover, due to the high cost and complexity of material synthesis and characterization, the amount of available data in materials science remains severely limited, creating substantial barriers to model training and reducing predictive reliability²⁰.

To address these challenges, we propose the adoption of multimodal learning (MML) in the field of materials science. MML aims to integrate and process multiple types of data, referred to as modalities, including text, images, audio, and video, and has achieved significant success in domains such as natural language processing and computer vision²¹. In recent years, several studies have extended MML to material research by integrating diverse material data obtained through multiple characterization techniques^{22,23,24,25,26,27}. These approaches enhance the model’s understanding of complex material systems and mitigate data scarcity, ultimately improving predictive performance. However, these MML approaches remain limited in two key aspects: (1) Material datasets are frequently incomplete due to experimental constraints and the high cost of acquiring certain measurements. For instance, synthesis parameters are often readily available, whereas microstructural data, such as those obtained from SEM or XRD, are more expensive and difficult to obtain, resulting in missing modalities. Conventional MML models rely on complete modality availability, and their performance deteriorates significantly when modalities are missing, thereby limiting their practical applicability²⁸. (2) Furthermore, existing methods lack efficient cross-modal alignment and typically do not provide a systematic framework for modality transformation or mapping mechanisms. These limitations pose obstacles to the broader application of AI in materials science, particularly for complex material systems where multimodal data and incomplete characterizations are prevalent.

Recent advances in MML, such as CLIP²⁹, ImageBind³⁰, and DALLE-2³¹ have demonstrated impressive cross-modal understanding capabilities. Inspired by these developments, we propose MatMCL, a versatile MML framework tailored to materials science that flexibly handles missing modalities and facilitates effective interaction and transformation across diverse and multiscale material features. As a case study to validate the effectiveness of the proposed framework, we construct a multimodal dataset of electrospun nanofibers through laboratory preparation and characterization. A geometric multimodal contrastive learning strategy, named structure-guided pre-training (SGPT), is employed to align modality-specific and fused representations. By guiding the model to capture structural features, this approach enhances representation learning and mitigates the impact of missing modalities, ultimately boosting material property prediction performance. To further enhance cross-modal understanding, MatMCL incorporates a retrieval module for knowledge extraction across modalities and a conditional generation module that enables the generation of structures according to given conditions. Additionally, we introduce a multi-stage learning strategy (MSL) to extend the applicability of the framework, as demonstrated by guiding the design of nanofiber-reinforced composites. In summary, MatMCL provides an effective framework for modeling the relationships among processing conditions, microstructure, and properties in electrospun nanofiber materials, even under limited or incomplete data. Its flexibility and robustness highlight its promise for broader applications in multiscale, multimodal materials modeling.

Results

In this work, we propose a versatile multimodal learning framework for material design, referred to as MatMCL. We evaluate MatMCL using a multimodal dataset of electrospun nanofibers. The framework includes four modules: (1) A structure-guided pre-training module that guides the model to learn structural knowledge through self-supervised learning; and three downstream modules for (2) property prediction under missing structure, (3) cross-modal retrieval, and (4) conditional structure generation.

Multimodal dataset construction

To verify the feasibility of MatMCL, we first construct a multimodal benchmark dataset through laboratory preparation and characterization. Nanofibers have received extensive attention due to their high surface area, high porosity, and considerable mechanical strength³². Electrospinning is one of the most widely used methods for fabricating nanofibers. The morphology and arrangement of fibers can be flexibly regulated by adjusting the processing conditions, thus exhibiting multimodal features³³. Therefore, we use electrospun nanofibers to create a benchmark dataset as a case study.

During the preparation process, we controlled the morphology and arrangement of the nanofibers by adjusting various combinations of flow rate, concentration, voltage, rotation speed, and ambient temperature, humidity (Fig. 1a). The microstructure was characterized using scanning electron microscopy (SEM). Subsequently, we tested the mechanical properties of the electrospun films in both the longitudinal and transverse directions using tensile tests, including fracture strength, yield strength, elastic modulus, tangent modulus, and fracture elongation. To facilitate the representation, a binary indicator was added to the processing conditions to specify the tensile direction. For more details on dataset construction, refer to the Methods section.

Fig. 1: Overview of multimodal dataset construction, model pre-training, and downstream tasks.

a Multimodal dataset preparation. Nanofibers were fabricated via electrospinning with tunable fiber structures by adjusting environmental, solution, and electrospinning variables. The structure of each material was characterized using SEM. Tensile tests were conducted to evaluate the mechanical properties in both transverse and longitudinal directions. Each data includes processing conditions, microstructures and mechanical properties. b Structure-guided pre-training. The processing conditions, nanofiber structures, and fused inputs are encoded by the table encoder, vision encoder, and multimodal fusion encoder, respectively, and projected into a shared latent space. These modules are trained jointly using a contrastive loss that aligns representations from the same material as positive pairs and treats those from different materials as negatives. c Downstream applications. After pre-training, the pre-trained weights are loaded to support three downstream tasks. For property prediction, a prediction head is added to predict mechanical properties. For cross-modal retrieval, the pre-trained encoders are used to embed both queries (processing conditions or microstructures) and gallery samples into a shared latent space for similarity-based retrieval. For conditional structure generation, a prior model maps condition embeddings to structure embeddings, which are then decoded into microstructures using a diffusion-based decoder. d Symbols and color codes used in the figure.

Structure-guided pre-training

In this study, we propose the use of multimodal learning to capture the complex, multi-level features of materials and alleviate the issue of data scarcity. However, as mentioned above, existing approaches may suffer from significant limitations in cross-modal understanding and are not designed to handle missing data, which is a common challenge in materials science.

Inspired by contrastive learning and multimodal learning in natural language processing^29,34 and computer vision³⁵, we propose a structure-guided pre-training (SGPT) strategy to align processing and structural modalities via a fused material representation (Fig. 1b). A table encoder models the nonlinear effects of processing parameters known to influence fiber formation in electrospinning. A vision encoder learns rich microstructural features of materials directly from raw SEM images in an end-to-end manner, capturing complex morphologies such as fiber alignment, diameter distribution, and porosity. A multimodal encoder integrates processing and structural information to construct a fused embedding representing the material system. For each sample, this fused representation serves as the anchor in contrastive learning, which is aligned with its corresponding unimodal embeddings (processing conditions and structures) as positive pairs, while embeddings from other samples serve as negatives. All embeddings are projected into a joint latent space via a projector head. This approach provides an efficient mechanism for improving the model’s robustness during inference, especially in scenarios where certain modalities (e.g., microstructural images) are missing. More importantly, SGPT enables the model to uncover potential correlations between the multiscale information of materials, thereby facilitating various downstream tasks (Fig. 1c).

Specifically, given a batch containing N samples, the processing conditions ${\{{{\bf{x}}}_{i}^{{\rm{t}}}\}}_{i=1}^{N}$, microstructure ${\{{{\bf{x}}}_{i}^{{\rm{v}}}\}}_{i=1}^{N}$, and fused inputs ${\{{{\bf{x}}}_{i}^{{\rm{t}}},{{\bf{x}}}_{i}^{{\rm{v}}}\}}_{i=1}^{N}$ are processed by a table encoder ${f}_{{\rm{t}}}(\cdot )$, a vision encoder ${f}_{{\rm{v}}}(\cdot )$, and a multimodal encoder ${f}_{{\rm{m}}}(\cdot )$, respectively, resulting in ${\{{{\bf{h}}}_{i}^{{\rm{t}}}\}}_{i=1}^{N},{\{{{\bf{h}}}_{i}^{{\rm{v}}}\}}_{i=1}^{N},{\{{{\bf{h}}}_{i}^{{\rm{m}}}\}}_{i=1}^{N}$, which correspond to the learned representations from the table, vision, and multimodal encoders. Next, a shared projector $g(\cdot )$ is employed to map the encoded representations into a joint space for multimodal contrastive learning, resulting in three sets of representations ${\{{{\bf{z}}}_{i}^{{\rm{t}}}\}}_{i=1}^{N},{\{{{\bf{z}}}_{i}^{{\rm{v}}}\}}_{i=1}^{N},{\{{{\bf{z}}}_{i}^{{\rm{m}}}\}}_{i=1}^{N}$, corresponding to the table, vision, and multimodal modalities, respectively. The fused representations ${\{{{\bf{z}}}_{i}^{{\rm{m}}}\}}_{i=1}^{N}$ are used as anchors to align information from other modalities. To construct contrastive pairs, embeddings derived from the same material, such as ${{\bf{z}}}_{i}^{{\rm{t}}}$ and ${{\bf{z}}}_{i}^{{\rm{m}}}$, are treated as positive pairs, while the remaining embeddings are considered negative pairs. A contrastive loss is applied to these latent vectors to jointly train the encoders and projector by maximizing the agreement between positive pairs while minimizing it for negative pairs. More details on SGPT can be found in the Methods section.

To illustrate the generality of MatMCL, we implemented two network architectures in this work. The first architecture utilizes a Multilayer Perceptron (MLP) to extract features of processing conditions and a Convolutional Neural Network (CNN) to extract microstructural features (Supplementary Fig. S1). The features from each modality are then concatenated to obtain a fused multimodal representation. Additionally, we also implemented a Transformer-based MatMCL model, where an FT-Transformer³⁶ serves as the table encoder and a Vision Transformer (ViT)³⁷ act as the vision encoder (Supplementary Fig. S2–S4). We incorporated a multimodal Transformer with cross-attention³⁸ to effectively capture interactions between processing conditions and structures to further improve multimodal representation learning. A consistent decrease in multimodal contrastive loss is observed during training (Supplementary Fig. S5), indicating that the model is progressively learning the underlying correlations between processing conditions and microstructures of nanofibers.

Mechanical property prediction

After SGPT, we first utilized the joint latent space for property prediction. In this stage, the pre-trained encoder and projector were loaded and kept frozen, while a trainable multi-task predictor was added to predict mechanical properties (Fig. 2a). Notably, while multimodal interactions enable models to capture multiscale information of materials during training, certain modalities such as spectroscopic and structural characterization data are often missing at inference time due to experimental constraints and acquisition costs. In the case of nanofiber materials, processing conditions are readily accessible and can even be arbitrarily selected within a certain range without the need to fabricate the corresponding materials. However, the acquisition of microstructures is a laborious process, requiring the preparation of materials and subsequent characterization using expensive imaging techniques. Therefore, model performance with missing structures is more important for virtual screening.

Fig. 2: Predicting mechanical properties using the pre-trained material representations.

a Model training process. The table encoder and projector are loaded from the structure-guided pre-training stage and remain frozen during this phase. A new multi-task predictor head is added to simultaneously predict five mechanical properties. Modules marked with a snowflake symbol are frozen, while those marked with a flame symbol are trainable. b, c Test performance of MatMCL on five mechanical properties tasks using MLP (CNN) and FT-Transformer (ViT). Higher R² and lower RMSE value indicates better model performance. d Similarity matrix of learned embeddings. Diagonal line represents embeddings derived from the same material, others from different materials. e Alignment evaluation of learned embeddings. Higher IPR value indicates a better alignment. f The distribution of the material representation. Material representations were visualized using t-SNE and each point was colored according to structural feature. The Pearson’s correlation between the generated representations and structural features was shown in each subplot. g Test performance of the generated representations using KNN regression.

We evaluated the test performance of MatMCL, implemented with both architectures, without prior exposure to the structural information of the test samples. MatMCL (fusion) consistently achieves the highest performance across all mechanical properties, as expected (Fig. 2b, c). This result reinforces the idea that the processing conditions and microstructure of nanofiber materials contain complementary information, thereby enhancing feature representations. Moreover, compared to conventional models without SGPT, MatMCL (conditions) achieves a significant improvement in R² and root-mean-square error (RMSE) for most mechanical properties on the test set. This finding suggests that the proposed pre-training strategy enables the model to learn higher-quality representations with stronger generalization capabilities. Additionally, as anticipated, MatMCL (conditions) has close or even equivalent performance to MatMCL (fusion) for most mechanical properties, further validating the effectiveness of the learned representations. We also conducted an ablation study (Supplementary Fig. S6), which confirms the importance of the multimodal encoder in improving prediction performance.

To validate the alignment between the processing conditions of nanofibers and the fused information, we computed the cosine similarity between the condition embeddings and the fused embeddings for all samples. The similarity matrix of MatMCL exhibits a distinct diagonal pattern, whereas the similarity matrices of models without alignment do not (Fig. 2d). This indicates that embeddings from the same material exhibit significantly higher similarity than those from different materials. We further quantified the alignment of the model using Improved Precision and Recall (IPR)³⁹, a metric designed to assess the geometric and topological properties of an evaluation set of representations in comparison to a reference set. A higher IPR value indicates greater similarity in both global and local structures between the two sets, i.e., better alignment. As shown in Fig. 2e, MatMCL exhibits strong alignment in both conditions and structures with multimodal representations, which is consistent with the training objective. Notably, although no explicit constraint is imposed between conditions and structures during training, an indirect correlation emerges through the fused representations as a medium. In addition, an interpretability analysis using SHapley Additive exPlanations (SHAP) and Grad-CAM was also performed (Supplementary Fig. S7–S12).

We further analyzed the latent space to investigate why MatMCL achieves superior performance in predicting mechanical properties. We visualized the material representations generated by different models using t-SNE (Fig. 2f). Each sample point was colored based on three manually defined structural features, including degree of orientation, nanofiber diameter, and pore size, extracted from the microstructure (Supplementary Table S1). Pearson correlation coefficients between representations and structural features were calculated. The results indicate that the original processing conditions exhibit the weakest correlation with structural features. In contrast, MatMCL (fusion) achieves the highest correlation due to the integration of microstructural information. Interestingly, MatMCL (conditions) shows a correlation comparable to that of MatMCL (fusion). Moreover, we also employ the K-nearest neighbors (KNN) algorithm to quantify this correlation, following the approach of previous studies⁴⁰. Specifically, 80% of the dataset is used to train a KNN regression model to predict the structural features of materials using representations generated by different models. In comparison, the remaining 20% is used to evaluate the model’s performance. The predictive capability of KNN relies on local similarity in the feature space, where higher performance indicates that similar representations correspond to similar microstructures. As shown in Fig. 2g, the representations of MatMCL (fusion) achieve the highest performance, followed by MatMCL (conditions), while the original processing conditions exhibit the worst performance. The results show that MatMCL (conditions) can better capture the information related to the structural features of nanofibers than the original processing conditions. Therefore, we conclude that the proposed methods can guide the model to learn structure-related information, thereby enhancing its ability to predict mechanical properties.

Cross-modal retrieval

After achieving property prediction, establishing an efficient retrieval mechanism can also help researchers optimize processing conditions and analyze structural characteristics. Furthermore, with advancements in experimental and computational methods, the variety and amount of material data are rapidly increasing. As a result, cross-modal retrieval is essential for the construction and application of large-scale multimodal materials databases⁴¹. Traditional retrieval methods primarily rely on numerical indexing or similarity matching, which limits the understanding and generalization of complex material systems. In the case of nanofibers presented in this study, our goal is to retrieve the corresponding microstructure given specific conditions, or to reverse-identify the conditions associated with a given microstructure.

Figure 2e demonstrates that through the binding of a specific modality with the anchor, conditions and structures of MatMCL are well aligned. Therefore, similar to the implementation of CLIP, we utilized the trained table encoder ${f}_{{\rm{t}}}(\cdot )$ and the vision encoder ${f}_{{\rm{v}}}(\cdot )$ to encode the query and gallery data into a joint space. The cosine similarity between the query and each sample in the gallery is calculated and ranked, with the top-ranked samples serving as the retrieval results, which is consistent with the objective of pre-training (Fig. 3a, b).

Fig. 3: Cross-modal retrieval based on the pre-trained material representations.

a, b Retrieval process. Query and gallery were encoded by the frozen encoder and similarities are compared in the joint space. c, d Retrieval accuracy on test data. e, f The top-6 ranked retrieved results are shown here, with actual matched results highlighted in blue box.

To better evaluate retrieval performance, we employed random retrieval and a similarity-based method as baselines. For the similarity-based method, given a condition ${\bf{q}}$, we identify the closest condition ${{\bf{q}}}^{{\boldsymbol{{\prime} }}}$ in the training data based on Euclidean distance⁴². The corresponding structure ${{\bf{p}}}^{{\boldsymbol{{\prime} }}}$ of ${{\bf{q}}}^{{\boldsymbol{{\prime} }}}$ is then used to retrieve the most similar structure ${\bf{p}}$ from the gallery, which serves as the final retrieval result. The dataset used for retrieval was not used for the training. MatMCL achieves significantly higher retrieval accuracy compared to the baselines, while the specific model architecture has little impact on the results (Fig. 3c, d). Therefore, MLP (CNN) is adopted in subsequent experiments of this study for computational efficiency. It is important to note that there is not a strict one-to-one correspondence between the processing conditions and structures of nanofibers; that is, very similar structures may be obtained from markedly different conditions. We present six retrieval examples, in which most cases successfully identify the true matching samples within the top-ranked retrieved results (highlighted in blue line) (Fig. 3e, f). In the first and third cases of structure retrieval, although the top-1 result is not the exact ground truth match, its structural features exhibit high visual similarity to the actual matching structure. These findings suggest that the model can effectively capture key structural patterns of nanofibers and retrieve samples with high similarity to the target structure. In conclusion, MatMCL demonstrates a strong capability to uncover complex correlations within multimodal materials data, highlighting its potential in advancing materials understanding and design.

Conditional structure generation

Although cross-modal retrieval enables researchers to quickly locate material samples that meet specific criteria within existing datasets, it is inherently limited by the coverage of the database. When relevant experimental data is absent, retrieval fails to yield meaningful results. Thus, cross-modal generation holds promise for overcoming this limitation. In this study, we aim to generate possible microstructures directly based on the given processing conditions.

Inspired by the architecture of DALLE-2, a novel text-to-image generation model, we developed a cross-modal generation module for materials science based on a prior model and a decoder. In this pipeline, we first loaded the pre-trained encoder from SGPT to encode processing conditions and structures into the joint latent space (Fig. 4a). Next, a prior model was trained to map these condition embeddings ${{\bf{z}}}_{i}^{{\rm{t}}}$ to structure embeddings ${{\bf{z}}}_{i}^{{\rm{v}}}$, bridging the distribution gap between the two modalities. Separately, a diffusion-based decoder was trained to generate microstructures from structure embeddings ${{\bf{z}}}_{i}^{{\rm{v}}}$^43,44. During inference, the generation process began with random noise and progressively denoised it under the guidance of structure embeddings predicted from the given processing conditions, ultimately producing the target microstructure. Notably, the prior model and decoder were trained independently.

Fig. 4: Conditional structure generation and inverse design.

a Training process of the generation module. A prior model was trained to map condition embeddings to structure embeddings. A diffusion decoder was trained to generate structures by denoising random noise, guided by the predicted structure embeddings. Additionally, a proxy model with a trainable prediction head is introduced to estimate structural features from processing conditions for inverse design. The prior, decoder, and proxy model are trained independently, without a strict sequential order. b Distributional differences between real and generated structures. Diagonal elements represent the FID between real and generated structures of the same material, while other elements correspond to different materials. Lower FID value indicates a more similar distribution. c The real structural features versus generated plots. d Analysis of instances. The displayed real structures are randomly selected regions from SEM images. Processing conditions and structural features are normalized using Min-Max scaling. e Material reverse design process. The processing conditions are optimized using the gradient descent algorithm to generate the set structural features. The initial state of the condition is randomly generated. f Time-varying sequences of processing conditions, structural features, and generated structures. The red dashed lines are the set structural features.

To evaluate the quality of the generated structures and their alignment with the given conditions, we employed the Frechet Inception Distance (FID), a commonly used metric for measuring the distributional difference between generated and real images⁴⁵. A lower FID value indicates a higher similarity between distributions. For each condition in the dataset, ten structures were generated, and their features were extracted using the trained vision encoder ${f}_{{\rm{v}}}(\cdot )$. The FID between the real and generated structures was then computed (Fig. 4b). For conditions seen by the model, the FID values along the diagonal of the heatmap are significantly lower than those in the surrounding areas. This result indicates that the given prompts effectively guide the model in generating the corresponding structures, and the generated results are highly consistent with real structures. For unseen conditions, the FID values remain low despite the increased challenge, suggesting that the model exhibits strong generalization capabilities even for previously unencountered conditions. We then computed the structural features (orientation degree, fiber diameter, and pore size) to more intuitively assess the reliability of the generated structures (Fig. 4c). The generated structures exhibit a strong correlation with the real structures in all three features, regardless of whether the conditions were seen or unseen. We also present eight sets of unseen instances (Fig. 4d). In each set, we displayed the input conditions, the corresponding real structure, and the generated structure along with its features. It can be observed that the generated structures exhibit similar features to the real ones, making them nearly indistinguishable to the naked eye. Some generated structures exhibit slightly curved or thick fibers, which are also observed in the training data due to experimental effects such as jet splitting⁴⁶, hygroscopicity⁴⁷, and local concentration variations^48,49. These deviations may also be partly influenced by the absence of explicit physics priors in the generative model. These results indicate that MatMCL not only accurately learns the distribution of seen data but also infers and generates structures that conform to physical and statistical principles under specified unseen conditions.

To generate structures with specified features and enable inverse material design, we further developed a gradient-based material structure optimization process. To improve optimization efficiency, we first trained a proxy to rapidly predict the three structural features corresponding to given processing conditions. Researchers can specify desired structural features (in this example, an orientation degree of 0.75, a fiber diameter of 0.15 μm, and a pore size of 0.48 μm) and then employ the gradient descent algorithm to optimize processing conditions based on the proxy (Fig. 4e). Finally, the optimized conditions and the generated structure are returned. As the conditions are optimized, the material structure progressively approaches the target features (Fig. 4f). The generated structure changes from being randomly oriented to exhibiting a distinct orientation. To further demonstrate the flexibility of the inverse design pipeline, we performed a mechanical property-driven variant under fixed environmental constraints (temperature and humidity), optimizing conditions and generating corresponding structures that satisfy the target mechanical properties (Supplementary Fig. S7). These results demonstrate a strong capability for cross-modal understanding and structure generation, supporting intelligent material design beyond database limitations.

Nanofiber-reinforced composite material design

Nanofiber-reinforced composites exhibit excellent mechanical properties, good environmental resistance, and tunable functionality, making them highly promising for applications in biomedical engineering, flexible electronics, and other fields⁵⁰. However, the fabrication of composite materials involves numerous process parameters, complex manufacturing routes, and high experimental costs with long verification cycles, significantly limiting the rapid development and practical application of novel composites. Moreover, the scarcity of high-quality experimental data further increases the difficulty of data-driven material design. After successfully developing the functional modules of MatMCL, we applied it to the design of nanofiber-reinforced composites to further validate its powerful capabilities and broad applicability.

As depicted in Fig. 5a, electrospun nanofibers were immersed in a silicone-based polyurethane solution and subsequently dried to obtain nanofiber-reinforced composite films. Due to the laborious preparation process, we only collected 40 samples, posing a considerable obstacle for AI modeling. To address the issue of extreme data scarcity in composite materials, we employ a multi-stage learning (MSL) strategy⁵¹. As demonstrated in Fig. 2f, g, the table encoder ${f}_{{\rm{t}}}(\cdot )$ of MatMCL acquires structural knowledge of nanofibers through SGPT, which is essential for understanding material properties. The pre-trained encoder is then fine-tuned to learn the mechanical properties of nanofibers. Notably, during composite fabrication, the morphology of the nanofibers remains largely unchanged; ideally, only the air among fibers is replaced by the polymer matrix. Therefore, we hypothesize that the learned structural and mechanical properties of nanofibers can also contribute to predicting the mechanical properties of composites. Finally, the model was fine-tuned using composite material data to adapt it to the new task (Fig. 5b). The performance of MSL was evaluated on the test set (Fig. 5c, d). Models trained from random initialization fail to converge due to the extreme scarcity of data, making them impractical for real-world applications. In contrast, MSL achieves a much lower prediction error compared to other baselines, demonstrating its ability to generalize well despite the limited dataset. MSL simulates the hierarchical evolution of composite materials from fabrication to structure and ultimately to properties, by progressively learning the structural features of nanofibers, their mechanical properties, and the mechanical properties of the resulting composites, thereby enhancing its predictive performance on composite materials. Moreover, the ablation study in Fig. 5c, d further confirms the importance of each pre-training stage, as removing any stage leads to a noticeable drop in performance.

Fig. 5: Nanofiber-reinforced composite material design.

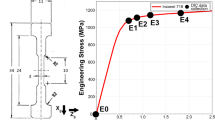
a The fabrication process of nanofiber-reinforced composite materials. b Multi-stage learning for composite material prediction. The model originally trained for predicting the mechanical properties of nanofibers was further fine-tuned using a layer-wise learning rate decay strategy to predict the mechanical properties of nanofiber-reinforced composites. c Test performance of different training strategy. Lower RMSE indicates better performance. d The measured tensile strength versus predicted plots. The dashed line represents y = x. The gray zone represents the predictions with absolute errors in the range of [-5, 5]. Color blocks represent training stages. CP, FP, and S denote training with composite material data, nanofiber data, and microstructure data, respectively. e, f Macroscopic and microscopic morphology of nanofibers and composites. g Longitudinal and transverse stress-strain curves of nanofibers and composites. Each experiment was independently repeated three times. h, i Measured and predicted fracture strength of nanofibers and composites.

Finally, we employed the trained model to screen composite materials. To evaluate its reliability, we selected two sets of randomly generated conditions for validation. Additionally, we identified three sets of conditions predicted to possess the high mechanical anisotropy, which hold potential applications in tissue engineering⁵². We further fabricated and characterized these five samples, with one representative high-anisotropy instance exhibited here (Fig. 5e). The gaps among the nanofibers were completely filled with the polymer matrix, resulting in a smooth surface with no exposed fibers (Fig. 5f). The fracture strength in the longitudinal and transverse directions displayed pronounced anisotropy (Fig. 5g). Notably, the predicted fracture strengths for both the nanofibers and the composite materials closely match the measured values (Fig. 5h). Furthermore, the prediction errors for all samples remained within a narrow range, confirming the model’s high accuracy and robustness (Fig. 5i). These findings indicate that the proposed method can effectively guide the design of nanofibers and nanofiber-reinforced composites. In summary, MatMCL has strong scalability and can be extended to more complex material systems.

Discussion

In this study, we focused on electrospun nanofiber materials as a representative system to address a critical challenge in AI-driven materials design: the integration of multiscale and multimodal information under data scarcity and missing modalities. To this end, we proposed MatMCL, a versatile framework that leverages multimodal contrastive learning to bridge diverse material knowledge sources. Rather than relying on complete inputs, MatMCL demonstrates strong robustness to missing modalities, while enabling accurate property prediction, flexible cross-modal retrieval, and structure generation. Notably, MatMCL is capable of aligning an arbitrary number of modalities, not limited to just two, indicating strong scalability and adaptability.

Our current evaluation is limited to electrospun nanofibers, which were selected for their relatively facile fabrication process, tunable morphology, and inherent multimodal characteristics. Nevertheless, MatMCL is designed to be material-agnostic and future efforts will focus on extending and validating the framework across a broader range of material systems. Notably, multimodal data are pervasive in the field of materials science, encompassing chemical composition, processing conditions, structures, and spectroscopic features. This makes MatMCL a promising foundation for AI-driven material discovery pipelines, particularly suited to handling missing modalities and modeling the multi-level correlations inherent in complex material systems.

Methods

Materials

Nylon-6 (PA 6) was purchased from Macklin Inc. The silicone-based polyurethane (Si content: 20 wt%, Shore A hardness: 80) was sourced from Dongguan Fulin Plastic Materials Co., Ltd. (China). N,N-Dimethylformamide (DMF), formic acid (FA, ≥98 wt%) and acetic acid (AcOH, ≥98 wt%), were acquired by Sigma-Aldrich. All the reagents were of analytical grade and were directly used as received without further purification.

Preparation of electrospun nanofibers

First, PA 6 was added to a closed vessel containing a mixture of FA/AcOH (mass fraction ratio 2:3). The mixture was stirred at 300 rpm for 12 h at 35 °C to obtain PA 6 spinning solution (named spinning solution I) at a concentration of x₁. Subsequently, spinning solution I was added to a 5 mL syringe. Finally, electrostatic spinning was carried out on a horizontal electrostatic spinning device (Changsha Nayi Instrument Technology Co., Ltd., China, JDF-05). The rotating voltage was adjusted to x₂ kV, the rotating distance was 15–20 cm, the drum rotational speed was x₃ rpm, the nozzle moved horizontally at 20 cm, and the rotating liquid flow rate was x₄ mL/h, and the temperature x₅ and humidity x₆ were recorded. After 3 h, the electrospun PA 6 nanofiber membranes were taken out of the drum sequentially and dried in a vacuum oven for 12 h to remove the residual solvent for subsequent experiments. We selected a total of 235 sets of processing conditions ${\{{{\bf{x}}}_{i}^{{\rm{t}}}=({x}_{i,1},{x}_{i,2},\mathrm{..}.,{x}_{i,6})\}}_{i=1}^{N}$.

Preparation of nanofibers-reinforced composites

The composite membrane was fabricated by initially filling a 6 cm × 6 cm square quartz cell with 2.5 mL of silicone-based polyurethane solution (50 mg/mL). A 6 cm × 6 cm electrospun membrane was subsequently carefully placed onto the liquid surface to ensure uniform coverage, followed by the gradual addition of another 2.5 mL of polyurethane solution (50 mg/mL) to fully encapsulate the electrospun layer. The entire assembly was then transferred to a convection oven at 70 °C, where it underwent hot-air drying for 12 h to achieve complete solidification and structural integration.

Dataset construction

Processing conditions

Continuous processing conditions were standardized using a Standard Scaler, while binary features (direction indicator) were left unchanged.

Structure characterization

The structure of the electrospun nanofibers was examined using scanning electron microscopy (SEM, SU5000, Hitachi). For each sample, two arbitrary locations were selected, from which square pieces measuring 5 mm × 5 mm were carefully cut. SEM imaging was conducted at a magnification of 1000×, and images were captured at a resolution of 2560 × 1920 pixels. At least four images were acquired per sample to ensure representative structural features. Each SEM image was further divided into 15 non-overlapping patches of 512 × 512 pixels for subsequent analysis. To reduce bias caused by differences in brightness and contrast during SEM imaging, all cropped image patches were normalized via histogram matching algorithm.

Data annotation

The mechanical properties of the electrospun nanofibers were measured using a universal testing machine (UTM2102, Shenzhen Suns Technology Stock, Shenzhen, China). Samples were cut into rectangular strips with dimensions of 3 cm in length and 1 cm in width. Each sample was tested with a stretch rate of 20 mm/min. From the stress-strain curves, five mechanical properties were extracted. The fracture strength was defined as the maximum stress recorded during the tensile test. Elongation at break was calculated as the strain corresponding to this maximum stress. The elastic modulus was determined from the initial linear portion of the curve by calculating the slope at 10% strain. The yield strength was identified as the stress at the intersection between the stress-strain curve and a line offset by 1% strain from the initial elastic modulus. The tangent modulus was defined by performing a linear fit to the stress-strain curve in the region after yielding. For each film, tensile tests were conducted in both the longitudinal and transverse directions, with three replicates performed in each direction. The average of the three measurements was reported as the representative mechanical properties for each direction. The structure of the dataset is shown in Supplementary Table S2.

Structure-guided pre-training (SGPT)

SGPT based on multimodal contrastive learning was implemented to align modality-specific and fused representations. Given a mini batch of N samples, each sample includes processing parameters x_t, microstructures image x_v. These inputs are encoded as:

$${{\boldsymbol{h}}}_{{\rm{t}}}={f}_{{\rm{t}}}({{\boldsymbol{x}}}_{{\rm{t}}}),{{\boldsymbol{h}}}_{{\rm{v}}}={f}_{{\rm{v}}}({{\boldsymbol{x}}}_{{\rm{v}}}),{{\boldsymbol{h}}}_{{\rm{m}}}={f}_{{\rm{m}}}({{\boldsymbol{x}}}_{{\rm{t}}},{{\boldsymbol{x}}}_{{\rm{v}}})$$

where ${f}_{{\rm{t}}}(\cdot ),{f}_{{\rm{v}}}(\cdot ),{f}_{{\rm{m}}}(\cdot )$ denote table encoder, vision encoder, multimodal encoder, respectively. All encoded vectors are projected to a joint latent space via a shared projection head $g(\cdot )$:

$${{\boldsymbol{z}}}_{{\rm{t}}}=g({{\boldsymbol{h}}}_{{\rm{t}}}),{{\boldsymbol{z}}}_{{\rm{v}}}=g({{\boldsymbol{h}}}_{{\rm{v}}}),{{\boldsymbol{z}}}_{{\rm{m}}}=g({{\boldsymbol{h}}}_{{\rm{m}}})$$

The fused representation h_m serves as the anchor for contrastive learning. For each modality, positive pairs are formed with the anchor of the same sample, while embeddings from other samples in the batch are treated as negatives. The contrastive loss for a single positive pair $({{\boldsymbol{h}}}_{{\rm{s}}}^{i},{{\boldsymbol{h}}}_{{\rm{m}}}^{i})$, where ${\rm{s}}\in \{{\rm{t}},{\rm{v}}\}$, is defined as³⁴:

$$\begin{array}{c}{{\mathcal{L}}}_{{\rm{s}},{\rm{m}}}^{i}=-\,\log \frac{\exp ({{\boldsymbol{h}}}_{{\rm{s}}}^{i}{{\boldsymbol{h}}}_{{\rm{m}}}^{i}/\tau )}{{\sum }_{i\ne j}\exp ({{\boldsymbol{h}}}_{{\rm{s}}}^{i}{{\boldsymbol{h}}}_{{\rm{s}}}^{j}/\tau )+{\sum }_{j}\exp ({{\boldsymbol{h}}}_{{\rm{s}}}^{i}{{\boldsymbol{h}}}_{{\rm{m}}}^{j}/\tau )}\\ {{\mathcal{L}}}_{{\rm{s}}}^{i}={{\mathcal{L}}}_{{\rm{s}},{\rm{m}}}^{i}+{{\mathcal{L}}}_{{\rm{m}},{\rm{s}}}^{i}\end{array}$$

where τ is the temperature hyperparameter. The total loss is computed by summing over all samples and modalities:

$${{\mathcal{L}}}_{\mathrm{total}}=\mathop{\sum }\limits_{i=1}^{N}({{\mathcal{L}}}_{{\rm{t}}}^{i}+{{\mathcal{L}}}_{{\rm{v}}}^{i})$$

Two architectures were implemented for encoding and fusion:

Convolutional style

A 5-layer multilayer perceptron (MLP) with ReLU activation was used to encode tabular processing conditions, and a ResNet-50 model was used to extract microstructure features⁵³. The multimodal fusion encoder is constructed by extracting features from both MLP and ResNet-50.

Transformer style

The tabular encoder is implemented using an FT-Transformer, and the image encoder is a Vision Transformer (ViT). The two modality-specific embeddings are fused via a multimodal Transformer with cross-attention layers.

All encoder modules output 128-dimensional feature vectors and apply a dropout rate of 0.1. The model was pre-trained using the Adam optimizer with a learning rate of 1 × 10⁻⁴ for 200 epochs. The implementation was based on PyTorch and all experiments were conducted on NVIDIA RTX 4090 GPU.

Mechanical properties prediction

Following structure-guided pre-training, the tabular encoder was frozen, and a randomly initialized multi-task predictor was added for mechanical properties prediction. Both the Convolutional style and Transformer style architectures were evaluated. The dataset was randomly divided into training, validation, and test sets using a 7:1.5:1.5 split. Model training was performed using the Adam optimizer with a learning rate of 5 × 10^-4, weight decay of 1 × 10^-4, and a batch size of 32. Early stopping with a patience of 20 epochs was applied. All hyperparameters were selected via grid search. The loss function was defined as the mean squared error (MSE) summed across all predicted properties.

Cross-modal retrieval

Cross-modal retrieval was performed using the pre-trained table and vision encoders. Given a query from one modality (either processing conditions or microstructure image), both the query and all gallery samples were encoded into the joint latent space using the respective encoders. Cosine similarity was computed between the query embedding and all gallery embeddings. Samples in the gallery were then ranked based on similarity scores, and the top-k ranked results were returned as retrieval outputs. Retrieval was performed in both directions: from conditions to microstructure, and from microstructure to conditions.

Conditional structure generation

To generate microstructure images from processing conditions, we implemented a two-stage cross-modal generative pipeline based on latent diffusion modeling. The system consists of a diffusion prior module that maps condition embeddings to structure embeddings, followed by a decoder that translates the predicted latent embedding into a full-resolution microstructure image.

Diffusion prior

Given the condition inputs x_t, the latent embedding ${{\bf{z}}}_{{\rm{t}}}=g({f}_{{\rm{t}}}({{\bf{x}}}_{{\rm{t}}}))$ was extracted using the pre-trained encoder. The ground truth structure embedding ${{\bf{z}}}_{{\rm{v}}}=g({f}_{{\rm{v}}}({{\bf{x}}}_{{\rm{v}}}))$ was obtained via the vision encoder. During training, the prior model was trained to reconstruct ${{\bf{z}}}_{{\rm{v}}}$ from its noisy version ${{\bf{z}}}_{{\rm{v}}}^{(t)}$, using the following loss function:

$${{\mathcal{L}}}_{\mathrm{prior}}={{\mathbb{E}}}_{{{\bf{z}}}_{{\rm{v}}},{{\bf{z}}}_{{\rm{t}}},\epsilon ,t}[{\Vert {{\bf{z}}}_{{\rm{v}}}-{\epsilon }_{\theta }({{\bf{z}}}_{{\rm{v}}}^{(t)},t|{{\bf{z}}}_{{\rm{t}}})\Vert }_{2}^{2}]$$

where ${\epsilon }_{\theta }$ was a causal Transformer, ${{\bf{z}}}_{{\rm{v}}}^{(t)}=\sqrt{{\bar{\alpha }}_{t}}{{\bf{z}}}_{{\rm{v}}}+\sqrt{1-{\bar{\alpha }}_{t}}\epsilon$, with $\epsilon \sim {\mathscr{N}}(0,I)$, and ${\bar{\alpha }}_{t}$ defined by a cosine noise schedule. Classifier-free guidance (CFG) was enabled by randomly dropping the condition embedding during training. At inference, sampling was applied using:

$${\hat{\epsilon }}_{\theta }=(1+w)\cdot {\epsilon }_{\theta }(\cdot |{{\bf{z}}}_{{\rm{t}}})-w\cdot {\epsilon }_{\theta }(\cdot |\varnothing )$$

where w is the guidance scale hyperparameter (w = 1). Sampling was conducted using DDPM with cosine noise schedule, and all modules were trained using the Adam optimizer with a learning rate of 1 × 10^-4, weight decay of 1 × 10^-2, and gradient clipping (max norm 0.5). The resulting latent vector ${\hat{{\bf{z}}}}_{{\rm{v}}}$ was then used to guide the subsequent image-level structure generation via a separate diffusion decoder.

Diffusion decoder

The second stage was a conditional diffusion decoder that generated microstructure x_v from structure embeddings z_v. The decoder was also trained using the DDPM framework. For a given real structure x_v, the noisy input is:

$${{\bf{x}}}_{{\rm{v}}}^{(t)}=\sqrt{{\bar{\alpha }}_{t}}{{\bf{x}}}_{{\rm{v}}}+\sqrt{1-{\bar{\alpha }}_{t}}\epsilon ,\epsilon \sim {\mathscr{N}}(0,I)$$

and the network is trained to minimize the conditional denoising loss:

$${{\mathcal{L}}}_{\mathrm{decoder}}={{\mathbb{E}}}_{{{\bf{x}}}_{{\rm{v}}},\epsilon ,t}[{\Vert \epsilon -{\epsilon }_{\phi }({{\bf{x}}}_{{\rm{v}}}^{(t)},t|{{\bf{z}}}_{{\rm{v}}})\Vert }_{2}^{2}]$$

Inference is performed using the same CFG mechanism:

$${\hat{\epsilon }}_{\phi }=(1+w)\cdot {\epsilon }_{\phi }(\cdot |{{\bf{z}}}_{{\rm{v}}})-w\cdot {\epsilon }_{\phi }(\cdot |\varnothing ),w=1$$

The decoder was trained for 50 epochs using the Adam optimizer with a learning rate of 1 × 10^-4, weight decay of 1 × 10^-2, and gradient clipping (max norm 0.5).

Finally, the full generation process can be formally expressed as a two-stage, autoregressive sampling procedure:

$${{\bf{x}}}_{{\rm{v}}} \sim \mathop{\prod }\limits_{t=1}^{T}{p}_{\phi }({{\bf{x}}}^{(t-1)}|{{\bf{x}}}^{(t)},t,{{\bf{z}}}_{{\rm{v}}}),\,{\text{where}}\,{{\bf{z}}}_{{\rm{v}}} \sim \mathop{\prod }\limits_{t=1}^{T}{p}_{\theta }({{\bf{z}}}^{(t-1)}|{{\bf{z}}}^{(t)},t,{{\bf{z}}}_{{\rm{t}}})$$

Inverse design

To enable inverse design, a proxy model ${\mathcal{P}}({{\bf{x}}}_{{\rm{t}}})$ was trained to predict structural features from processing conditions x_t, enabling fast and differentiable approximation of the condition-structure relationship. Given a target feature vector ${{\boldsymbol{y}}}_{\mathrm{target}}\in {{\mathbb{R}}}^{3}$, the condition x_t was iteratively optimized to minimize the prediction error. At each step t, the gradient

$${\nabla }_{{{\bf{x}}}_{{\rm{t}}}}{\Vert {\mathcal{P}}({{\bf{x}}}_{{\rm{t}}})-{{\bf{y}}}_{\mathrm{target}}\Vert }_{2}^{2}$$

was computed via backpropagation, and the condition vector was updated for 120 steps, using the Adam optimizer with a learning rate of 0.1.