Free surface bubbly flow in an open capillary channel

Abstract

This study investigates bubbly flow in a rectangular open channel under microgravity. A homogeneous flow model is used to compute frictional pressure loss and then establish a correlation between the drag coefficient and mass quality, leading to a one-dimensional model of free surface bubbly flow. Furthermore, the homogeneous flow model is integrated into computational fluid dynamics simulations, which align closely with experimental observations. The theoretical model and simulations show a strong concordance, with a critical flow rate determined through calculations exhibiting an average relative error of 4.93%. The findings reveal a positive correlation between mass quality and critical flow rate; increasing mass quality enhances the critical flow rate and stabilizes the free surface but reduces the liquid phase’s flow efficiency. This research contributes to the theoretical understanding of microgravity free surface flow.

Introduction

Capillary transportation of liquids is commonly present in purification filtration systems, heat pipes, and fuel transport from tanks in weightlessness¹. Open capillary channels, as a specific type, are commonly utilized for the management of liquid in space, featuring one or more free surfaces that experience capillary forces. Investigating the dynamics of liquid flow within open capillary channels can enhance space liquid management proficiency which holds substantial theoretical and practical significance.

When the internal pressure of the liquid in the flow channel is lower than the external pressure, the free surface exhibits concave inward behavior. By simplifying the problem and disregarding complex geometric boundary conditions, the issue can be reduced to a free surface flow with differential pressure as the driving force². Jaekle³ introduced a theoretical model for T-type open channel flow and subsequently solved the governing equations numerically after simplification to one dimension. Subsequently, Srinivasan⁴ proposed a semi-analytical method for the governing equations of three-dimensional flow in an open parallel-plate channel. In 2004, Rosendahl et al.^5,6,7 conducted microgravity experiments on pressure-differential driven flow between parallel plates, encompassing drop towers and probe rocket flights. They considered curvature along the flow direction in a one-dimensional theoretical model and provided a more comprehensive analysis and experimental observation of the choking phenomenon, which refers to a maximum flow rate is achieved when volumetric flow rate exceeds a certain limit causing the free surface to collapse and bubbles to enter the channel. Subsequently, the one-dimensional theoretical model was extended to open rectangular channels and wedge-shaped flow channels^8,9. Wu et al.¹⁰ investigated the impact of channel curvature on pressure-differential driven flow, taking into account the effect of centrifugal force from bending motion on pressure loss.

In the study referenced above, it is noted that the liquid within the flow channel and the external gas maintain distinct separation. Nevertheless, in a microgravity environment, gas bubbles have a propensity to become entrained within the liquid, thereby giving rise to a gas-liquid two-phase mixed flow. This phenomenon is exemplified in the presence of free surface bubbly flow within surface tension plate storage tanks¹¹. When juxtaposed with alternative two-phase mixed flow configurations, such as slug flow and annular flow, bubbly flow exhibits a smaller gas phase proportion, resulting in a more uniform distribution of gas within the continuous liquid phase in the form of diminutive, discontinuous bubbles.

But due to the difficulty of bubble management in microgravity, and to the limited access to high quality microgravity environments¹², relevant experimental studies and data are relatively scarce. Salim et al.^13,14 analyzed laminar bubbly flow propelled by pressure differential in a rectangular flow channel using a rocket, revealing that the average bubble velocity is directly proportional to the mixing velocity. Jenson et al.¹⁵ and Weislogel et al.¹⁶ conducted experiments on free-surface bubbly flow in a wedge-shaped channel aboard the International Space Station, observing bubble migration towards the free surface.

In the realm of free-surface bubbly flow modeling, the assessment of pressure loss within the channel holds significant importance. Extensive research has been conducted on the pressure loss of two-phase flow in closed pipes. The early split-phase flow model was introduced by Lockhart-Martinelli¹⁷, derived from the study of gas-liquid two-phase flow in a horizontal pipe. Later, Chisholm¹⁸ completed this part of the research by proposing the classical fractional liquid phase conversion factor, and then subsequent modifications to the Chisholm relation’s parameter have been made based on this formula^19,20,21,22. Taitel and Dukler²³ proposed the homogeneous phase flow model, considering factors like consistent fluid velocities between phases, uniform gas-liquid mixing, and absence of phase sliding, leading to a relatively straightforward calculation process. Chen et al.²⁴ highlighted the applicability of the homogeneous flow model in smaller channels (with an equivalent diameter of less than 10 mm) due to effective gas-liquid phase mixing. Zhang et al.²⁵ explored Alternative correlations of two-phase friction pressure drop and void fraction. Dhahri et al.²⁶ established a correlation between two-phase frictional pressure drop and mixture viscosity within the homogeneous flow model. These studies offer theoretical underpinnings for calculating pressure loss in theoretical models of free-surface bubbly flow.

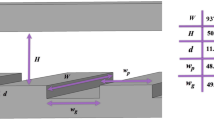
In order to describe the free surface of the bubbly flow, a physical model as shown in Fig. 1 is set up: the bubbly flow with a volume flow rate of Q and a mass fraction of gas (mass quality χ) passes through a closed straight rectangular channel with a length of L₁ and then enters into a one-sided open channel with a length of L₂. The open channel described here is a rectangular channel closed at the bottom and sides, open at the top. At the top of this channel, the flow is in direct contact with an external pressurized gas, forming a clear gas-liquid surface. Next, the bubbly flow continues to flow into a closed channel of length L₃. In this paper, the model is investigated using one-dimensional theoretical model and CFD simulations respectively.

Fig. 1

Bubbly flows through a rectangular open capillary channel with a flow rate Q.

Results and discussion

Theoretical results

By analyzing the flow channel in Fig. 1, the shape of the free surface for a certain void fraction can be obtained after one-dimensional calculations. Figure 2 shows the free surface for the same total flow rate (Q_m) but different void fraction, indicating that the height of the free surface gets higher as the void fraction increases. In fact, the density of the mixture decreases as the void fraction increases, while the mixing viscosity and pressure loss change. This result is a consequence of several parameters mentioned above.

Fig. 2

Free surface for different flow rate conditions.

In the calculations, the free surface will not be solvable if the value of the total flow rate reaches a certain limit, which is called the critical flow rate, and this is verified during the simulation.

CFD simulation results

A symmetric cross-sectional representation of the channel has been specifically chosen to exhibit the simulation outcomes pertaining to the configuration of the free surface, as visually depicted in Fig. 3. With a progressive escalation in the flow rate, a discernible trend emerges where in the liquid surface gradually assumes a concave shape (see Fig. 3a), accompanied by an amplification in the curvature magnitude. Upon surpassing a critical threshold of flow rate, a noteworthy phenomenon unfolds: the rear segment of the liquid surface undergoes concavity and destabilization, leading to the formation of downstream-propagating bubbles (see Fig. 3c). Subsequently, the liquid-phase flow rate at the outlet reaches a saturation point, signifying a cessation in the rate increment. This pivotal juncture of flow at the inlet, characterized by the critical state, is commonly referred to as the critical flow condition.

Fig. 3: Three representative free surface profiles.

a Subcritical flow, b critical flow and c supercritical flow.

Given the utilization of a transient simulation technique with consistent boundary conditions, the free surface undergoes continuous minor oscillations over time. To achieve a stabilized surface representation, the contour line data of the free surface extracted from the simulation at distinct temporal intervals are meticulously analyzed. This process involves averaging the surface height corresponding to each x-coordinate, culminating in the derivation of definitive simulation outcomes, as illustrated in Fig. 4.

Fig. 4

Post-processing of the surface at different moments obtained by simulation.

When the outlet flow rate increases linearly with time, the inlet flow rate eventually reaches its maximum value at a certain moment, at which the outlet flow rate at that moment is defined as the critical flow rate. Through simulation, the critical flow rate under varying mass quality conditions is determined, as depicted in the Fig. 5. The data illustrates a positive correlation between the critical flow rate and mass quality. A comparison with results from one-dimensional calculations reveals a slightly lower critical flow rate from simulations. The max relative error and average relative error between the two methods are respectively calculated at 5.92% and 4.93%, and the root mean square error is 0.3398 ml/s.

Fig. 5

Critical flow rate Q_c versus mass quality χ.

Comparison and analysis

The results of the calculation and CFD simulation are compared with the experimental data to verify the correctness of the model. The geometric data and gas-liquid parameters used in the calculations are shown in Table 1. The parameters in Table 1 and the flow rates in Table 2 are substituted into the theoretical model of homogeneous phase flow to obtain the calculation results.

Table 1 Parameters in the experiment

Table 2 Liquid and gas flow rates in the experiment

The fluid undergoes a constriction process as it transits into the channel, resulting in pressure loss attributed to the inlet effect. The lack of data regarding the geometry and dimensions of the experimental section’s inlet precluded an accurate analysis of the inlet pressure loss. Consequently, a value of 0 was assigned to ${w}_{Sf1}$ in the calculations, theoretically yielding a marginally elevated outcome compared to the true surface height. And the simulation calculation results are obtained according to the phase fraction 0.3 in the CFD simulation.

Comparison of calculation results, simulation results and experimental data are shown in Figs. 6 and 7. The absence of simulated surfaces in Figs. 6b and 7c is attributed to the destabilization of the free surfaces at the corresponding flow rates, resulting in bubble formation during the simulation. The calculated critical flow values stand at 6.34 ml/s and 6.55 ml/s for the respective cases, while the simulated critical flow rates are 5.91 ml/s and 6.2 ml/s, respectively. The discrepancy where the simulated critical flow rates are lower than the calculated values indicates that the simulation has already reached a critical state during the simulation, precluding the attainment of stabilized free surfaces.

Fig. 6: Free surfaces for single-phase flow in two flow scenarios.

a Free surface at a flow rate of 5.2 ml/s, b free surface at a flow rate of 6.3 ml/s.

Fig. 7: Free surfaces for two-phase flow in three flow scenarios.

a Free surface at a mixing flow rate of 5.2 ml/s and a gas flow rate of 0.51 ml/s, b free surface at a mixing flow rate of 5.2 ml/s and a gas flow rate of 0.62 ml/s, c free surface at a mixing flow rate of 6.3 ml/s and a gas flow rate of 0.62 ml/s.

As illustrated in Figs. 6 and 7, the contour lines derived from the calculated results exhibit a closer alignment with the experimental values. It is worth noting that the absence of the wall shear stress factor associated with the entrance effect in the calculation process results in a lower h₀ at the entrance during the calculation, thereby leading to a slightly higher calculated surface height. Conversely, the simulated surface tends to be lower than both the experimental and calculated values. This discrepancy can be attributed to inherent errors in the simulation methodology as well as the presence of the inlet effect in the simulation. The combined impact of these errors contributes to a marginally larger deviation in the simulation results. Introducing the inlet effect into the calculation process would likely yield more congruent results with the simulation outcomes, as depicted in the Fig. 8, which underscores the compatibility of the one-dimensional theoretical model with the outcomes of the three-dimensional simulation.

Fig. 8: Comparison of calculation and simulation after introduction of entrance effect.

a Free surfaces for single-phase flow at a flow rate of 5.2 ml/s, b free surface for two-phase flow at a mixing flow rate of 5.2 ml/s and a gas flow rate of 0.51 ml/s.

Effect of mass quality on critical flow rate

The critical flow rate serves as a key indicator of the flow performance within the capillary channel. The mass quality in a bubbly flow plays a significant role in determining the critical flow rate, necessitating a thorough analysis of the underlying mechanisms through which mass quality impacts the flow. The mass quality is intricately linked to the density and viscosity coefficients of the flow. Figure 9a depicts the variation curve of the critical flow rate as influenced by the mass quality.

Fig. 9: Flow rate versus mass quality curves for different categories of flow rates.

a Critical mass flux G_c and volume flow rate Q_c versus mass quality curves χ, b Gas mass flux Gc_g, liquid mass flux Gc_l versus mass quality χ.

In addition to ensuring the stability of the flow channel, it is imperative to consider the circulation efficiency of the propellant within the channel. Figure 9b illustrates the variation curve of the critical mass flux (G_c) in relation to the mass quality. With an increase in mass quality, the critical total mass flux decreases, despite an increase in the fluid critical volume flow rate (Q_c). The increase in the mass flux of the gas phase and the decrease in the mass flux of the liquid phase imply a gradual decrease in the flow efficiency of the liquid phase.

The critical flow rate exhibits an approximately linear increase with rising mass quality. Given the substantial disparity between liquid and gas densities, the flow density of the two-phase system decreases as the mass quality increases. Furthermore, the kinematic viscosity (v) of the two-phase flow diminishes with an increase in mass quality. These combined effects influence the momentum equation, contributing to the escalation of the critical flow rate. In summary, the augmentation of mass quality serves to stabilize the free surface and enhance the critical flow rate within the flow channel to a certain degree.

For the same flow rate, the change in mass quality did not lead to a significant change in the shape of the free surface, while there were lower flow velocities and higher liquid surface heights for higher mass quality. In addition, the mean curvature difference is lower at higher mass quality, indicating that the viscous pressure loss is higher at higher mass quality.

Figure 10 presents the graphical representations of critical flow rate Q_c as a function of channel length (l), aspect ratio (Ʌ), liquid phase viscosity (μ_l), and contact angle (θ) under varying mass quality conditions. The results demonstrate a clear trend where higher mass quality corresponds to higher critical flow rates across all parameters. Specifically, the impact of mass quality on the critical flow rate is particularly significant for higher aspect ratios, as illustrated in Fig. 10b. Additionally, Fig. 10d highlights that a smaller contact angle correlates with a greater impact of mass quality on critical flow rates.

Fig. 10: Parametric investigation of critical flow rate under different mass quality conditions.

a Variation curves of critical flow rate with channel length under different mass quality conditions, b variation curves of critical flow rate with aspect ratio under different mass quality conditions, c variation curves of critical flow rate with liquid phase viscosity under different mass quality conditions, d variation curves of critical flow rate with contact angle under different mass quality conditions.

Summary of the discussion

In summary, the free-surface bubbly flow in a rectangular capillary channel under microgravity conditions is investigated by theory and simulation, and a homogeneous flow model is introduced on the basis of the free surface flow theory for the first time, which realizes the discounting of the flow pressure loss of the bubbly flow, and more accurately calculates the free surface of the bubbly flow as well as the critical flow rate under the conditions of different mass quality. The model developed in this paper establishes a relationship between mass quality and the drag coefficient, enabling rapid calculations of the free interface across various mass quality scenarios, which is more extensive.

Furthermore, the impact of mass quality on the critical flow rate of bubbly flow is examined. The critical flow rate of bubbly flow escalates with the augmentation of mass quality. In contrast to single-phase flow, bubbly flow exerts a stabilizing influence on the free surface within the flow channel, resulting in an elevation of the critical volume flow rate. However, concurrently, this phenomenon diminishes the critical mass flux of the liquid phase.

Methods

Analysis methods

The flow density ${\rho }_{m}$ of a two-phase medium in a bubbly flow is the ratio of the mass and volume of the two-phase medium flowing through a certain cross-section of the flow channel per unit time:

$${\rho }_{m}=\frac{M}{Q}=\frac{{V}_{g}\cdot {\rho }_{g}+{V}_{l}\cdot {\rho }_{l}}{Q}=\beta \cdot {\rho }_{g}+(1-\beta ){\rho }_{l},$$

(1)

where M is the total mass flow rate of the two-phase flow in kg/s. Q is the total volumetric flow rate of the two-phase flow in m³/s. β is the volumetric gas fraction, which is the ratio of the gas-phase volume passing through the cross-section of the flow channel to the total volume in a unit time. It is related to mass quality χ

$$\beta =\frac{\chi /{\rho }_{g}}{\chi /{\rho }_{g}+(1-\chi )/{\rho }_{l}},$$

(2)

where ${\rho }_{g}$ and ${\rho }_{l}$ are the densities of the gas and liquid phases, respectively.

The mass flux G is the mass flow rate through a unit cross-section of the flow channel in kg/(m²·s)

$$G=\frac{M}{A}={\rho }_{m}\cdot j={\rho }_{m}\cdot \frac{Q}{A},$$

(3)

where A is the area of the flow cross section. j is the converted velocity, defined as the volumetric flow rate of the two-phase flow per unit of channel cross-section in m/s, which also represents the average velocity of the two-phase flow.

The viscosity coefficient μ of two-phase flow is generally calculated by using the average viscosity, the most widely used is the Mecadam formula²⁷

$$\frac{1}{\mu }=\frac{\chi }{{\mu }_{g}}+\frac{1-\chi }{{\mu }_{l}}.$$

(4)

Under microgravity conditions, the gas-liquid surface in the open flow channel is depressed inward by surface tension. A Cartesian coordinate system is established with the flow direction as the x-axis. The description of the free surface is a three-dimensional problem, and in order to reduce the problem to a one-dimensional one, the free surface in the cross section of the channel needs to be analyzed first.

For the gas-liquid free surface flow in a rectangular channel flowing along the x-direction, the shape of the y-z cross-section is given schematically in Fig. 11a. The pressure difference between the two sides of the gas-liquid surface satisfies the Gauss–Laplace equation, and Wu²⁸ analyzes the shape of the cross-section and analyzes the expression of the surface as

$$Z=\frac{1}{\cos \,\theta }-\sqrt{\frac{1}{{\cos }^{2}\theta }-{Y}^{2}},$$

(5)

where $r=a/2$, $Z=z/r$, $Y=y/r$. For rectangular channels, θ is the contact angle. In a microgravity environment that satisfies $g\le {10}^{-4}{g}_{0}$, the free surface can be considered as a circular arc.

Fig. 11: Cross-section of the open capillary channel.

a A Cartesian coordinate is built at the lowest point of the free surface. b The critical height above which the contact angle is forced to change.

Consider a gas-liquid bubbly flow in which both phases are incompressible and the flow process remains isothermal. In the microgravity environment, the flow is more stable because the motion of the bubbles is greatly weakened and flows along with the liquid phase. When both the flow rate and mass quality in the channel are low, the flow behaves as a laminar flow. The velocity component along the direction of the flow channel is significantly higher than the other directions, so the two-dimensional and three-dimensional effects in the flow can be ignored and it can be regarded as a one-dimensional flow. Since the flow is mainly along the direction of the contact line, the contact angle is considered to be constant and dynamic contact angle effects are not considered. In addition, the flow is steady, so the time term can be eliminated from the momentum conservation equation.

After the above simplification, the momentum conservation equation contains a convection term, a capillary pressure term, and a pressure loss term

$${\rho }_{m}\cdot j\frac{{\rm{d}}j}{{\rm{d}}x}=-\frac{{\rm{d}}P}{{\rm{d}}x}-\frac{{\rm{d}}w}{{\rm{d}}x},$$

(6)

where P is the fluid pressure, w is the pressure loss, and j is the flow velocity.

The volume flow rate Q satisfies the continuity equation

$$\frac{{\rm{d}}Q}{{\rm{d}}x}=\frac{{\rm{d}}(j\cdot A)}{{\rm{d}}x}=j\frac{{\rm{d}}A}{{\rm{d}}x}+A\frac{{\rm{d}}j}{{\rm{d}}x}=0$$

(7)

According to the continuity equation, the convective term in the momentum equation can be expressed as

$${\rho }_{m}\cdot j\frac{{\rm{d}}j}{{\rm{d}}x}=-{\rho }_{m}\frac{{Q}^{2}}{{A}^{3}}\frac{{\rm{d}}A}{{\rm{d}}x}.$$

(8)

The cross-sectional area A is obtained from the geometric relationship shown in Fig. 11a

$$A=a\frac{\Gamma -a}{2}+{R}_{1}^{2}\,\sin \,\theta \,\cos \,\theta -\left(\frac{\pi }{2}-\theta \right){R}_{1}^{2},$$

(9)

where the radius of curvature R₁ of the free surface of the cross section is

$$\begin{array}{l}\begin{array}{l}\begin{array}{l}{R}_{1}=\left\{\begin{array}{l}\begin{array}{ll}\frac{b-k}{2}+\frac{{a}^{2}}{8(b-k)} & ,k > {k}_{l}\end{array}\\ \begin{array}{ll}\frac{a}{2\,\cos \,\theta } & ,k\le {k}_{l}\end{array}\end{array}\right.,\end{array}\end{array}\end{array}$$

(10)

Γ is the wetted perimeter

$$\varGamma =\left\{\begin{array}{l}\begin{array}{cc}a+2b & ,k\ge {k}_{c}\end{array}\\ \begin{array}{cc}a+2[k+R(1-\,\sin \,\theta )] & ,k\le {k}_{c}\end{array}\end{array}\right.,$$

(11)

The parameter k_c, known as the critical height of the free surface (As shown in Fig. 11b), represents the height of the liquid surface when the contact line of the liquid surface makes contact with the top edge of the channel while maintaining a contact angle of θ. This critical height can be determined through geometric relationships

$${k}_{c}=b-\frac{a(1-\,\sin \,\theta )}{2\,\cos \,\theta }.$$

(12)

For wetting perimeter and cross-section radius of curvature, both need to be discussed in a categorized way. When the liquid surface is higher than k_c, the cross-section radius of curvature and contact angle are larger than the critical value; when the liquid surface height is lower than k_c, the cross-section radius of curvature and contact angle are fixed.

The pressure term on the right-hand side of the momentum in Eq. (6) represents the pressure gradient in the direction of flow. Under conditions where the contact angle is less than 90 degrees and the gravitational acceleration is 0, the ambient pressure will be higher than the internal pressure of the liquid. The gas-liquid free surface is depressed to the liquid side by surface tension, and the pressure difference between the gas and liquid is balanced by additional pressure in the form of an additional pressure, allowing the liquid level to maintain a steady state.

A capillary pressure difference, caused by surface tension and variations of curvature, exists across the surface at each point on it²⁹. The relationship between surface tension and pressure can be derived from the Young-Laplace equation

$${P}_{a}-P=\sigma \left(\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}\right)$$

(13)

where σ is the surface tension coefficient in N/m. R₁ and R₂ are the two principal radii of curvature at any point K on the free surface, and the curvature in the x and y directions is adopted in the flow channel. R is the radius of curvature of the cross-section, which is given by Eq. (10), and R₂ is the radius of curvature of the profile line of the free surface, which is obtained from the curvature equation that

$${R}_{2}=\frac{{[1+{({{\rm{d}}}_{x}k)}^{2}]}^{3/2}}{{{\rm{d}}}_{xx}k},$$

(14)

where, ${{\rm{d}}}_{x}k={\rm{d}}k/{\rm{d}}x$ and ${{\rm{d}}}_{xx}k={{\rm{d}}}^{2}k/{\rm{d}}{x}^{2}$.

Define the mean curvature h as

$$h=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}.$$

(15)

Then, according to Eq. (13), the pressure term is expressed as

$$\frac{{\rm{d}}P}{{\rm{d}}x}=-\sigma \frac{{\rm{d}}h}{{\rm{d}}x}.$$

(16)

The pressure loss term w on the right side of the momentum equation in Eq. (6) consists of four components

$$w={w}_{Pf}+{w}_{Sf}+{w}_{g}+{w}_{a},$$

(17)

where ${w}_{Pf}$ is the viscous pressure loss; ${w}_{Sf}$ is the additional pressure loss due to the change in flow pattern; ${w}_{g}$ is the gravitational pressure drop, which is zero in the microgravity environment; and ${w}_{a}$ is the accelerated pressure drop, which is ignored in this case.

In fact, the fundamental model of the free surface for bubbly flow is presented in the referenced work¹³. However, when calculating flow resistance, the paper provides varying values of the drag coefficient for different examples. This study aims to establish a correlation between the drag coefficient and mass quality, allowing for the determination of the free surface under varying mass quality conditions without the need to adjust parameter values.

Before the fluid enters the open channel, it first passes through a closed channel where the pressure loss consists of two items

$${w}_{f1}={w}_{Pf1}+{w}_{Sf1}.$$

(18)

Similarly, the pressure loss in the open channel is

$${w}_{f2}={w}_{Pf2}+{w}_{Sf2},$$

(19)

where ${w}_{Sf1}$ is the additional pressure loss due to the inlet effect of a straight rectangular pipe. Its value is determined by the shape of the channel inlet. ${w}_{Sf2}$ is the additional pressure loss in the linear rectangular open channel, and the fitting equation is

$${w}_{Sf2}=\frac{\rho {j}^{2}}{2}\cdot ({c}_{1}{e}^{{c}_{2}{x\text{'}}_{2}}+{c}_{3}{e}^{{c}_{4}{x\text{'}}_{2}}),$$

(20)

where the coefficients ${c}_{1}=0.5957$, ${c}_{2}=3.236$, ${c}_{3}=-0.5957$, ${c}_{4}=-353$¹⁰. ${x\text{'}}_{2}$ is the normalized flow distance

$${x\text{'}}_{2}=\frac{{x}_{2}}{R{e}_{2}\cdot {D}_{2}},$$

(21)

x₂ refers to the flow distance in the open channel section. ${D}_{2}=4ab/(a+2b)$ is the hydraulic diameter of the rectangular open channel, $R{e}_{2}=G{D}_{2}/\mu$ is the Reynolds number in the rectangular open channel.

Viscous pressure loss calculations for two-phase flow have been studied extensively. But due to the many factors affecting the viscous pressure loss of two-phase flow, there is no relation that can include all the influencing factors, the current common calculation method is to calculate the defined conversion factor, and then multiply the conversion factor by the corresponding single-phase friction pressure drop gradient to obtain the viscous pressure drop gradient of two-phase flow. For bubbly flow, the applicable pressure loss model is the homogeneous flow model.

In the homogeneous flow model, the two-phase medium is regarded as a homogeneously mixed medium and its physical parameters are set to the average values of the corresponding two-phase flow parameters. In applying the model, the following conditions need to be satisfied: First, the flow rates of the gas and liquid phases are equal, which means that there is no slip velocity between the bubbles and the liquid phase; Then, the gas and liquid phases are in thermal equilibrium; Last, use of more accurate single-phase friction drag coefficients.

In the homogeneous phase flow model, the viscous pressure gradient relation is given by

$$\frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}=\frac{\lambda }{D}\frac{{\rho }_{m}{j}^{2}}{2},$$

(22)

where λ is the coefficient of friction, D is the hydraulic diameter of the rectangular duct.

The pressure gradient for a liquid mass passing through the channel with the same total mass flow rate as the two-phase flow is

$${\left(\frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}\right)}_{lo}=\frac{{\lambda }_{lo}}{D}\frac{{\rho }_{l}{W}_{0}^{2}}{2}=\frac{{\lambda }_{lo}}{D}\frac{{G}^{2}}{2{\rho }_{l}},$$

(23)

where λ_lo is the molecular resistance coefficient of the single–liquid phase and W₀ is the circulation speed.

Define the full liquid-phase conversion factor (${\phi }_{lo}^{2}$) for two-phase flow friction

$${\phi }_{lo}^{2}=\frac{\displaystyle \frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}}{{\left(\frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}\right)}_{lo}}.$$

(24)

Then according to Eq. (1), (2), (22) and (23):

$${\phi }_{lo}^{2}=\frac{\lambda }{{\lambda }_{lo}}\left[1+\chi \left(\frac{{\rho }_{l}}{{\rho }_{g}}-1\right)\right].$$

(25)

The key to calculating the viscous pressure drop gradient is the calculation of the friction factor λ, which is given by

$$\lambda =\frac{{K}_{Pf}}{{R}_{e}},$$

(26)

$${\lambda }_{lo}=\frac{{K}_{Pf}}{R{e}_{lo}}.$$

(27)

${K}_{Pf}$ is the drag coefficient for fully developed flow and its value is obtained by fitting the function³⁰

$${K}_{Pf}=\left\{\begin{array}{l}{c}_{5}{e}^{{c}_{6}\varLambda }+{c}_{7}{e}^{{c}_{8}\varLambda },\varLambda \le 1\\ {c}_{5}{e}^{\frac{{c}_{6}}{\varLambda }}+{c}_{7}{e}^{\frac{{c}_{8}}{\varLambda }},\varLambda > 1\end{array}\right.,$$

(28)

where, $\varLambda =b/a$ is the aspect ratio. ${c}_{5}=51.72$, ${c}_{6}=-2.668$, ${c}_{7}=44.26$, ${c}_{8}=0.1863$. $Re=GD/\mu$ is the Reynolds number for two-phase flow, and $R{e}_{lo}=GD/{\mu }_{l}$ is the Reynolds number of single–liquid phase, where μ is the dynamic viscous coefficient of two-phase flow and μ_l is the dynamic viscous coefficient of the liquid phase. It can be seen that the physical parameter related to the drag coefficient is mainly the viscous coefficient.

In summary, the viscous pressure loss gradient is calculated as

$$\frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}={\phi }_{lo}^{2}\cdot {\left(\frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}\right)}_{lo}$$

(29)

Substituting the convection term, capillary pressure term, and pressure loss term into the momentum equation, the governing equation for the gas-liquid surface in the linear rectangular channel is obtained:

$$-\sigma \frac{{\rm{d}}h}{{\rm{d}}x}-{\rho }_{m}\frac{{Q}^{2}}{{A}^{3}}\cdot \frac{{\rm{d}}A}{{\rm{d}}x}+\frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}+\frac{{\rho }_{m}{(\frac{Q}{A})}^{2}}{2R{e}_{2}{D}_{2}}\cdot ({c}_{1}{c}_{2}{e}^{{c}_{2}{x\text{'}}_{2}}+{c}_{3}{c}_{4}{e}^{{c}_{4}{x\text{'}}_{2}})=0.$$

(30)

The positional and pressure boundary conditions for the control equations are as follows:

$$\left\{\begin{array}{l}\begin{array}{l}k(x=0)=b\\ k(x={l}_{2})=b\end{array}\\ P(x=0)={P}_{0}-\frac{{\rm{d}}{w}_{Pf}}{{\rm{d}}x}{l}_{1}-{w}_{Sf1}\end{array},\right.$$

(31)

where P₀ is the inlet pressure of the straight rectangular pipe. And x is the origin from the end of the inlet pipe, which is also the beginning of the open channel. ${D}_{1}=2ab/(a+b)$ is the hydraulic diameter of the closed channel in the entrance section. ${w}_{Sf1}$ is the pressure loss due to the inlet effect at the front end of the channel, determined by the shape of the channel inlet.

The control equation is a nonlinear partial differential equation, which in combination with the expressions for A and h, allows the calculation of the free surface height k. Since an analytical solution cannot be obtained for this control equation, it is solved numerically.

The differentials of k, A, and h are discretized using a differential discretization

$$\left\{\begin{array}{l}\begin{array}{l}{k}_{x}^{i}=\frac{({k}^{i+1}-{k}^{i-1})}{2\Delta x}\\ {k}_{xx}^{i}=\frac{({k}^{i+1}-2{k}^{i}+{k}^{i-1})}{{(\Delta x)}^{2}}\end{array}\\ \begin{array}{l}{A}^{i}=\frac{({A}^{i}-{A}^{i-1})}{\Delta x}\\ {h}^{i}=\frac{({h}^{i}-{h}^{i-1})}{\Delta x}\end{array}\end{array}.\right.$$

(32)

Once the equations are discretized, given the values of Q, Ʌ, θ, l₂, A₀, and χ, k(x) can be found by the Newton damping method

$$k(x)=f(Q,\varLambda ,\theta ,{l}_{2},{A}_{0},\chi ),$$

(33)

when the values of Ʌ, θ, l₂, A₀, and χ are fixed, there exists a critical flow rate of Q₂. In fact, damped Newton’s method of solving the process of differential matrix singularity leads to a diverged solution when $Q > {Q}_{c}$.

Simulation methods

The one-dimensional model is a simplified model of the real flow, which is based on one-dimensional assumptions and ignores the velocity component perpendicular to the flow direction. In the one-dimensional model, the calculation of the viscous pressure loss term is based on the commutation formula of the molecular resistance coefficient, which has a certain error. Meanwhile, the one-dimensional theoretical model can only calculate the stable surface in the subcritical state, and cannot describe the state after the surface is destabilized. Therefore, three-dimensional CFD numerical simulation is used to assist the study of this problem.

CFD numerical simulation is usually applied to the calculation of two-phase flow, and in this paper, the open source CFD simulation software OpenFOAM is used to simulate the homogeneous flow model of free surface bubbly flow. Calculation of the free surface of two-phase flow can use the InterFoam solver based on the Volume of Fluid (VOF) method.

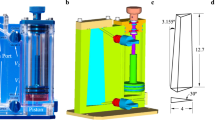
The simulation setup is based on the experiments conducted by Salim et al.¹³ on bubbly flow using a sounding rocket. In his experiment, the capillary channel consists of two transparent parallel quartz plates with width b = 25 mm and spacing a = 10 mm, and the length of the unilateral open channel is l = 80 mm.

At the inlet of the capillary channel, bubbles are injected horizontally through a nozzle to form a bubbly flow. The distance between the outlet of the bubble tube and the inlet of the open capillary channel is l₁ = 35 mm, which is taken as the length of the inlet closed channel. The gas used in the experiment was nitrogen, and the liquid was FC-72 produced by 3 M Company with the parameters of $\sigma =0.01$N/m and kinematic viscosity $\mu =6.38\times {10}^{-4}$Pa·s. The ambient temperature was 21 °C. Specific parameters are shown in Table 1. And the inlet pressure of the straight rectangular pipe ${P}_{0}=2/{R}_{CT}$, where R_CT is the compensation tube radius which equals 3 cm.

Five sets of data were obtained from the experiment, two of which were for single–liquid-phase flow and the other three were for bubbly flow with different gas-liquid flow rates, and the flow rates for each set are shown in Table 2.

Simulation of the flow used for the experiment based on the above data. The mesh used in the simulation is a structured hexahedral mesh as shown in Fig. 12 with a mesh number of 236000. An additional region is added above the opening of the capillary channel to provide constant ambient pressure. The inlet of the capillary channel is a constant total pressure boundary condition, and the outlet is a volumetric flow boundary condition. The channel wall contact angle θ = 0 was set.

Fig. 12

A typical hexahedral structural mesh used for CFD simulation.

Given the complexity introduced by simulating bubbly flow due to the presence of bubbles, the focus of the simulation in this study is specifically on elucidating the correlation between the free surface shape and fluid dynamics, rather than on the intricate distribution and movement of bubbles. Consequently, the simulation of bubbly flow adopted in this research is treated as a homogeneous single-phase fluid system, aligning with the principle of homogeneous flow. The determination of flow density and average viscosity coefficient in the experimental setup is achieved through the utilization of Eqs. (1) and (4) as essential physical parameters characterizing the liquid phase within the simulation, as detailed in Table 3. Notably, nitrogen is designated as the gas phase in the simulation framework.

Table 3 Parameterization of the simulation