Cryogenic helium subsurface pressurization in terrestrial and low-gravity: experiments and flow visualization

Abstract

Pressurization of cryogenic propellant storage tanks is required for propellant thermodynamic conditioning and for enabling propellant transfer from a supply tank to another tank or an engine. In microgravity, the pressurization gas may be injected directly into the liquid propellant if the nozzle is submerged in liquid. Known as helium subsurface pressurization (HSP), the incoming warm helium gas causes immediate evaporation of the propellant into the helium bubbles which subcools the liquid. For HSP of cryogenic liquids in reduced gravity environments, there are many unknowns such as the rate of evaporation, change in temperature of helium after injection, bubble growth rate, and boil-off and pressurization rates. The purpose of this paper is to present new experimental data and flow visualization of subsurface gaseous helium injection into liquid nitrogen in terrestrial gravity and low-gravity. Varied parameters include injector size (0.25, 1.0 mm), injection flow rate (10⁻⁹–10⁻⁵ kg/s), and temperature (170–260 K). The new data clearly shows the role of gravity, buoyancy, and inertial forces on multiple cryogenic subsurface parameters of interest.

Introduction

In-space cryogenic propellant transfer systems will play a vital role in NASA and the aerospace community’s future missions and vehicles, which include nuclear thermal propulsion systems¹, nuclear electric propulsion systems², ascent stages, descent stages³, and propellant depots⁴. To initiate propellant transfer from a cryogenic storage tank to either an engine or receiver tank (depot), the storage tank must be first pressurized. There are multiple parameters that affect pressurization system performance, which include the pressurization method (normal where liquid and vapor phases are separated and gas is injected into the vapor versus subsurface where gas is injected into the liquid), gravitational level (settled versus unsettled), type of pressurant gas (vapor versus using a non-condensable like helium), temperature of the pressurant gas relative to the liquid, and method of control (on-off versus regulation). The focus of the current work is HSP of an unsettled liquid in a reduced gravity environment. In microgravity, the liquid and vapor phases in the tank are in an unknown location, and there is a high probability that the pressurant gas injector may become submerged in liquid; this is especially true at high liquid fill levels.

The fluid physics and heat and mass transfer between gaseous pressurant and liquid propellant is notably different for normal versus subsurface pressurization. Generally, pressure control is more predictable for cryogenic propellant tanks for normal pressurization. Furthermore, there is a large body of publicly available data for a variety of cryogenic fluids for this configuration, see example⁵. For subsurface pressurization in 1-g, there are fewer studies. For subsurface pressurization in a cryogenic liquid in microgravity, there is no publicly available data. For subsurface pressurization in 1-g, buoyancy forces move pressurant gas bubbles through the liquid and spread the extent of evaporation to a larger volume of liquid as compared to limited smaller liquid volume in reduced gravity due to smaller range of bubble dispersion. “The combined effects of bubble injection are (1) the pressurant bubbles locally cool the liquid due to evaporation, and (2) the bubbles create a stirring motion which mixes the liquid, allowing for the bulk to be cooled”.

In microgravity where surface tension forces dominate over gravitational forces, the pressurant gas may be directly injected into the propellant; minimal motion of the bubbles is expected so the evaporation would be concentrated near the pressurization inlet. Relative to 1-g, heat transfer at the liquid/bubble interface is also expected to be different in low-g due to a lack of natural convective forces. In low-g, there are many unknowns such as the rate of evaporation, change in temperature of helium after injection, bubble growth rate, and boil-off, all of which are needed to understand and predict higher system-level phenomena such as pressurization rates, required pressurant gas mass, boil off rates, etc.

From a system-level perspective, submerged injection systems for cryogenic tank pressurization can result in subcooled propellant being delivered to the engine and with the potential to decrease the mass of the pressurant system necessary for pressurization. Reducing the temperature difference between the liquid propellant and pressurant injection temperatures may also reduce the time necessary to achieve thermal equilibrium.

The motivation for this paper is as follows: First, there is no public data available on low-g cryogenic subsurface pressurization. Second, there are fundamental gaps in understanding of the subsurface pressurization bubble dynamics, heat, and mass transfer in low-g. Third, there are no accurate low-g cryogenic subsurface pressurization models. This is the first in a series of two papers to address these concerns. The purpose of this paper is to present new experimental data and flow visualization of subsurface gaseous helium injection into liquid nitrogen in a reduced gravity environment across a range of injector types (0.25, 1.0 mm), injection flow rates (2.73 × 10⁻⁹, 2.73 × 10⁻⁸, 2.73 × 10⁻⁷, 2.73 × 10⁻⁶, 8.18 × 10⁻⁶kg/s) and injection temperatures (170–260 K), while the purpose of the second paper will be focused on numerical modeling aspects.

The outline of this paper is as follows: first, in the Introduction a literature review is given on prior works regarding regime maps and bubble and jet flows, bubble formation, and heat and mass transfer effects associated with subsurface gas injection. Bubble dynamics in reduced gravity are also discussed. Next, experimental hardware, instrumentation, visualization system, and experimental methodology are presented. Experimental results and discussion are then presented for reduced gravity tests and compared to 1-g ground tests. Finally, a summary of trends is presented in the Discussion section.

Before examining heat and mass transfer effects or submerged bubble dynamics in reduced gravity, it is first instructive to briefly describe an overall picture of flow regimes for submerged bubbles and jets in 1-g. Muller and Prince⁶ visualized six distinct regimes based on liquid depth and gas velocity for an air/water system.

• 1. Meniscus: surface tension forces restrain the liquid to the orifice and lead to a steady void above the orifice at extremely low depth.

• 2. Steady jet: as gas velocity increases at low depth, a stable gas channel appears which also produces droplets from the interface; the diameter of jet is nearly same as the diameter of orifice.

• 3. Pulsating jet: as liquid depth increases at constant gas flow rate, pulsating jets result; the diameter of the jet ranges from the orifice diameter to several times its size.

• 4. Perfect bubbling: at high liquid depth and low gas flow rate, perfect single bubbles of near-spherical shape are observed.

• 5. Imperfect bubbling: bubbles will start breaking up at low liquid depth and low gas flow rate because the liquid seal is not established at that moment.

• 6. Deformed bubbling: When the gas flow rate and the liquid depth both increase the bubbles tend to deform.

Miyahara et al.⁷ investigated the bubbling-to-jet transition experimentally using multiple different orifice sizes and three different liquids (water, ethanol, and millet jelly) and observed similar flow regimes as ref. ⁶. However, as the orifice diameter increased, jet flow was not observed.

The effect of liquid depth has been investigated in several studies. Spells and Bakowski⁸ examined air bubble formation at vertical slots submerged under water; a perfect single bubble regime was observed at high liquid depth at low gas injection velocity. Next, Quigley et al.⁹ conducted submerged gas experiments in water and found that there was not significant difference in results for depths from 7.6 cm to 30.5 cm. Soon after, Davidson and Amick¹⁰ and Hayes et al.¹¹ claimed that liquid depth was not a crucial factor in regimes of bubbling and jetting for depth >2.5 cm at low gas injection velocity, but the lack of visualization at high gas injection velocity leads to an incomplete conclusion.

Several researchers have attempted to describe these flow regimes using dimensionless numbers, particularly for transitions between regimes. The physical mechanisms to consider are that (1) inertia stabilizes the jet, (2) gravity causes the collapse of the jet, and (3) surface tension destabilizes the jet. Based on these considerations, Payne et al.¹² proposed the modified Froude number (${{Fr}}^{* }$) considering gas inertia and buoyancy, and the Bond number (Bo), which balances surface tension and gravity as follows:

$${Fr}^{\ast}=[{\rho}_{g}{v}_{g}^{2}/\{({\rho}_{l}-{\rho}_{g})g{D}\}]^{\frac{1}{2}}$$

(1)

$${Bo}=({\rho }_{l}-{\rho }_{g})g{D}^{2}/\sigma$$

(2)

The transition from steady to pulsating jets and from pulsating to transient jets were correlated with these dimensionless numbers. For the transition from steady to pulsating jets, the following empirical equation was developed:

$$\frac{H}{D}=0.12{{{Fr}}^{* }}^{0.8}\,4 < {{Fr}}^{* } < 30,\,0.55 < {Bo} < 10$$

(3)

For transition from pulsating to transient jets, the following was proposed:

$$\frac{H}{D}=0.12{{{Fr}}^{* }}^{1.23}{{Bo}}^{0.8}\,4 < {{Fr}}^{* } < 30,\,0.55 < {Bo} < 4$$

(4)

$$\frac{H}{D}={{{Fr}}^{* }}^{0.65}\,1 < {{Fr}}^{* } < 10,\,4 < {Bo} < 50$$

(5)

The difference between Eqs. (4) and (5) is attributed to the fact that the gas inertia force becomes a dominating factor when Bo > 4. In the work by Miyahara et al.⁷, transient jetting was marked in addition to the six regimes proposed by ref. ⁶. Although⁷ has postulated empirical equations for bubbling to jetting transition by means of the Froude number and Bond number, the lack of analysis of the physical mechanism of flow regimes raises concerns about the validity of the result.

In 1999, Sundar et al.¹³ suggested a new model to predict the transition between different flow regimes based on momentum exchange between gas and liquid. This momentum exchange acts principally in the vicinity of the gas core and the liquid film adjacent to the gas core that is subjected to positive acceleration given by the liquid momentum. Meanwhile, the liquid is also subjected to negative acceleration due to gravity. Thus, because of these two inverse forces, the liquid film tends to collapse, which tends to shut off the gas channel. Thus¹³, reported that the transition from bubbling to jetting appeared when the upward acceleration of the liquid film is zero at the top of the liquid level. Work by Taitel et al.¹⁴ was analogical to this report as well. After comparison with their mathematical model and experimental data, the final empirical equation¹³ for transition was obtained:

$$\frac{H}{D}=0.794\,{F}_{r}^{* }{{Bo}}^{0.25}+2.124$$

(6)

where¹³ presumed this expression covered all fluids, however this correlation has yet to be validated against cryogenic liquids.

During the last fifty years, factors such as gas velocity, pressure, surface tension, surface wetting characteristics, viscosity, etc. have been taken into consideration. However, the dynamics of bubble formation, mainly the regimes of bubble formation, were not studied in detail. Badam et al.¹⁵ investigated regimes of bubble formation on submerged orifices under constant flow rate conditions experimentally. They proposed how the previously formed bubbles influenced the growth of the next bubble forming at the orifice, leading to different bubbling regimes. From their visual observations, the bubbling regimes transitioned from (1) single bubbling to (2) bubble coalescence (at the orifice before detachment) or bubble pairing (coalescence far above the injector), to (3) triple coalescence, to (4) quadruple coalescence, and finally (5) chaotic bubbling. Further, from Badam et al.¹⁵, the bubble formation process was found by governing forces. The lifting forces are buoyancy force, pressure force, and gas momentum force while the restraining forces are surface tension force, drag force and inertial force. At the time of bubble detachment, the lifting forces are larger than the restraining forces; under this consideration, several previous empirical and analytical bubble volume prediction models have been proposed by using Fr and Bo number. Badam et al.¹⁵ noted that these empirical predictions did not consider effects of previous bubbles acting on the next bubble. Zhang and Shoji¹⁶ suggested a new nonlinear bubble model to account for the nonlinear interactions of the bubble forming at the orifice with the previously formed bubble. However, the applicability of this model has not been validated for a large range of operating parameters.

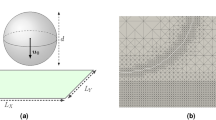
To improve upon previous models, Badam et al.¹⁵ carried out experiments using a square cross-section glass column for an air/water mixture. As proposed by Delnoij et al.¹⁷, the liquid height to column width ratio was ensured to be less than 1, significantly eliminating re-circulatory flow. Different bubble regimes are shown in Fig. 1. The perfect single bubble regime can be observed at low Fr and Bo. At a large range of Fr, the regime transition from single bubbling to bubble pairing and coalescence appears with increase in Bo, obtained by enlarging the diameter of the orifice or lowering the surface tension of the liquid. Then, the transition to chaotic bubbling occurs as Fr is increased, achieved by an increase in gas injection velocity or decrease in diameter of the orifice at a particular Bo. It is worth noting that the bubble volume or the bubble formation time increased with increase in diameter of the orifice. The critical flow rate at the regime transition decreased as diameter of the orifice was increased. The observed range of bubble pairing or coalescence regime decreased with a decrease in the diameter of the orifice. Similar results were reported by Tufaile et al.¹⁸; for tiny diameter orifices, the transition happened directly from the single bubble to the chaotic bubbling regime without the presence of any other bubbling regimes.

Fig. 1: Bubble dynamics.

Bubble formation regime map for a stainless-steel orifice (liquid: water). With increased gas velocity, the flow maps change from single bubble flow to chaotic flow.

Increasing the overall surface area of bubbles for subsurface pressurization has been shown to be beneficial for cooling purposes⁹. However, when the population of bubbles increases, collisions occur, causing the bubbles to merge, reducing the surface area abruptly. To prevent this interaction, it is preferable to restrict the bubble population. Wallis¹⁹ observed that for a volume fraction of gas less than 10%, the rate of collision and agglomeration of bubbles is usually slow, and for that gas volume fraction range the bubbles can be treated independently from other bubbles. In this case, single bubble characteristics can be extended to account for the whole bubbling system without significant error for that range of gas volume.

The dynamic regime is characteristic of systems using an intermediate range of gas flow rate, that is, the flow rates which are most often used in industrial applications. The main feature of the dynamic regime is that the bubbles may be considered independently from one another. For the dynamic regime, Davidson and Schuller²⁰ have made calculations for viscous liquids and obtained the following correlation:

$${V}_{b}={(4\pi /3)}^{\frac{1}{4}}{\left\{\frac{15{\rm{\mu }}Q}{2({\rho }_{l}-{\rho }_{g})g}\right\}}^{\frac{3}{4}}$$

(7)

After detachment from the orifice, a bubble rapidly accelerates to its terminal velocity ${v}_{b}$, determined by the balance between the buoyant force and the drag force. The rise in velocity of a single bubble inherently depends on its size²¹. For bubbles with diameters greater than 5 mm²², proposed the drag coefficient and the bubble terminal velocity as in Eq. (8):

$${v}_{b}=1.05{\left[\frac{{gD}\left({\rho }_{l}-{\rho }_{g}\right)}{{\rho }_{l}}* \left(\frac{{c}_{d}}{2}\right)\right]}^{\frac{1}{2}}$$

(8)

Helium subsurface injection is considered one of the most effective methods of subcooling the propellant. This method relies on diffusion mass transfer as illustrated in Fig. 2, adopted from refs. ^23,24. Here, the injected pure helium going into liquid oxygen causes a difference in the partial pressure of propellant vapor in the helium bubble and the vapor pressure of the liquid propellant, leading to the diffusion of propellant vapor into the helium gas. This process results in cooling due to the removal of vaporization heat from the surrounding liquid oxygen. Previous researchers have assumed instantaneous phase equilibrium in the injected helium and oxygen vapor to achieve maximum subcooling, but this assumption is limited by the finite rate of heat and mass transfer. To design efficient cooling systems, it is necessary to understand the limitations of these heat and mass transfer rates.

Fig. 2: Helium injection physics.

Schematics of principle on helium injection cooling, adopted from²³ with permission.

Three main assumptions have been asserted in the literature to model heat and mass transfer in subsurface pressurization systems. The first case²⁵ is instantaneous heat and mass transfer which applies for systems where the rising bubbles can achieve thermal equilibrium with the liquid and the mass transfer rate is high enough to achieve thermodynamic equilibrium prior to the bubbles exiting the liquid and entering the ullage. Here, helium enters the liquid near the bottom of the tank at a specified temperature, typically warmer than the temperature of the liquid propellant. The bubble generally cools to the temperature of the surrounding propellant, providing the propellant with energy equivalent to the change in helium bubble enthalpy. Injecting helium gas into the propellant creates a vapor concentration gradient across the helium bubble interface. Some of the liquid propellant evaporates and diffuses into the helium bubbles until the concentration equilibrium state is reached. The equilibrium state is achieved when the partial pressure of vapor in the bubble is balanced by the vapor saturation pressure at the liquid propellant temperature. The instantaneous diffusion assumption thus assumes that this condition is reached immediately, where the total pressure of the rising bubble is equal to the ullage pressure upon merging with the ullage. This case is useful for initial design studies and for estimating the maximum achievable subcooling.

The second case²³ is for finite heat transfer and instantaneous mass transfer. It is useful when the heat transfer rate is not high enough to achieve thermal equilibrium, but the mass transfer rate is still very high. In this case, the oxygen partial pressure at the ‘s’ surface in Fig. 2 is assumed to be equal to the bulk gas partial pressure of oxygen.

The third case²⁶ is for finite heat and mass transfer. It is the most realistic but involves more complex calculations and requires more information about the transport properties of the system. It is typically used for detailed analyses and for predicting the actual subcooling that can be achieved in a specific system.

The second case of finite heat transfer and instantaneous diffusion mass transfer was chosen by Cho et al.²³, since the bubbles injected into the LOX tank are unlikely to reach thermal equilibrium in small tanks or in the upper stage pipes. The Biot number condition was used to determine the applicability of the instantaneous diffusion assumption, and it was found that if Bi < 0.1, a lumped heat capacity model could be used. In their experiments, the measured temperature of the ullage increased during helium injection, indicating a thermal non-equilibrium situation between the LOX and the bubbles. Therefore, the assumption of instantaneous diffusion was applied for this study.

The model by Cho et al.²³ is illustrated in Fig. 2. Surfaces ‘u’ and ‘s’ are introduced on both sides of the real interface (i), each is infinitely close to the real interface, for the liquid oxygen (LOX) evaporating into the helium gas stream. The oxygen mole fraction at the ‘u’ surface is 1. Unless under extreme conditions, the mixture of oxygen vapor and helium gas at the ‘s’ surface must be in thermodynamic equilibrium with the LOX at the ‘u’ surface. The oxygen mole fraction at the “s” surface is, therefore, determined by assuming that the partial pressure is equal to the saturation vapor pressure of oxygen at the liquid temperature.

The second case was also found to agree best with the experiments from Frederking and Clark²⁷. However, the heat transfer at the liquid-vapor interface was modeled using a film boiling correlation on the liquid side and natural convection on the gas side; for subsurface pressurization, the interface temperature is typically only a few degrees lower than the liquid temperature, whereas for film boiling, the surface can be 10s–100s degrees hotter than the liquid.

Saha and Sandilya^26,28 developed a mathematical model to analyze the injection cooling system using a lumped parameter model that considered the liquid evaporation into both the helium bubbles and the ullage. They found that much higher gas flow rates than those used in the experiments were necessary to cause the observed liquid cooling and theorized that the liquid evaporation into the ullage dictated the liquid cooling.

The most recent subsurface helium pressurization modeling with heat and mass transfer effects was performed by Baldwin et al.²⁵ using the Generalized Fluid System Simulation Program (GFSSP) and Case 1 instantaneous heat and mass transfer assumption, on Cho’s experiments²³ and Centaur tank vehicle data. The goal of the model was to estimate the amount of oxygen vapor absorbed by the rising helium bubbles and the amount of subcooling of liquid oxygen due to evaporative heat and mass transfer. The model comprised an ullage node, liquid propellant node, pressurant gas supply node, and a draining branch leading to the engine boundary node. A pseudo-boundary node served to separate the ullage and liquid propellant nodes, thereby preventing two-phase mixing that might otherwise occur in a homogeneous code. The model was able to predict the propellant subcooling and helium consumption within 30% of the data.

As mentioned, there is no publicly available reduced gravity cryogenic subsurface pressurization data, which limits the ability to model such systems. However, there are some reduced gravity studies involving bubbling with non-cryogenic fluids from which general observations can be withdrawn. Pamperin and Rath²⁹ observed that at very low gravity, the air bubble in water did not leave the orifice mouth but instead elongates axially. Additionally, they proposed that the size of the bubble at departure is directly proportional to the orifice mouth radius in the absence of gravitational force due to surface tension, as demonstrated through experiments. Tsuge et al.³⁰ experimentally supported the observations made by ref. ²⁰ and developed a non-spherical model for bubble formation under low gravity and demonstrating that bubbles become attached to the orifice mouth under lower gravitational pull. Next, Di Marco et al.³¹ studied the formation of nitrogen bubbles in a pool of FC-72 under at ~10⁻⁴*g. At low flow rates (8–9mm³/s), bubbles never departed from the orifice mouth, but they did depart at high flow rates ( >43mm³/s). Carrera et al.³² observed the detachment of bubbles from an orifice for an air/water system. The range of the Weber number was 0.28–31.12. In their observations, bubbles coalesced with the preceding bubble at low flow rates before dispersing due to gas momentum.

For numerical modeling of reduced gravity subsurface injection one study was found. Chakraborty et al.³³ conducted a numerical study of air bubble detachment from a submerged orifice in water under constant inflow conditions at normal and reduced gravity levels (0.1 g and 0.01 g) using a combined volume of fluid level set method. They found that the increasing trend of bubble size at detachment, with increasing air flow rate under normal gravity is reversed in the case of reduced gravity g_t/g = 10⁻².

General observations from these studies are as follows: at lower flow rates, the detachment and reattachment of bubbles to the embryo at the orifice mouth occurs repeatedly for a longer period. At higher flow rates, the number of periodic attachments and detachments is smaller. This behavior depends on the gravity level and the difference in gas bubble and liquid densities.

If the mass of the bubble is enough to overcome the surface tension force, it moves upward. However, if the bubble mass is not sufficient, it falls back over the succeeding embryo after detachment and cannot continue its upward movement.

This work builds upon previous studies in terrestrial gravity by providing new experimental data and flow visualization of subsurface gaseous helium injection into LN₂ in 1-g and in low-gravity across a range of injector types, injection flow rate and temperature, and tank pressure to fill some gaps in the current understanding of subsurface pressurization bubble dynamics, heat, and mass transfer in reduced gravity.

Results

Table 1 is the parabolic flight test matrix of experimental conditions under which HSP data was taken. In total 19 cases were successfully completed onboard the flights. After collecting all the experimental results, the obtained reduced gravity data and flow visualization videos were quantitatively and qualitatively analyzed and compared against ground testing over similar helium mass injection flow rate and temperature.

Table 1 Flight test matrix

The first parameter analyzed is the bubble diameter at the instance of detachment from the helium gas injector, deemed the bubble departure diameter (BDD). Table 2 provides a summary of the cases analyzed. It is noted that the orifice diameter was 1 mm for all cases. Figure 3 plots the BDDs as a function of injection mass flow rate and gravity level. The orange dashed line in Fig. 3 separates the low gravity zone from the 1-g zone. As clearly shown, BDD is significantly larger in reduced gravity than that in terrestrial gravity for low injection flow rates. This is because the buoyancy force is significantly reduced in low gravity, and the surface tension force becomes the dominant resistance force in controlling the bubble departure mechanism. It is noted that the surface tension force decreases with increasing bubble diameter. As a result, since the lifting force that is responsible for the bubble departure comes mainly from the thrust of the injection mass flows, the bubble finally departs when the bubble grows to a size that results in a condition that the thrust force from the injected helium finally overcomes the surface tension force. This hypothesis is further reinforced by the low gravity data that shows the bubble departure diameter is smaller for the 2.73 × 10⁻⁸kg/s helium mass flow rate than that for the 2.73 × 10⁻⁹ kg/s flow rate. In other words, the larger the gas mass flow rate, the smaller the diameter of the bubble when it departs from the nozzle in low gravity.

Fig. 3: Bubble departure characteristics.

Bubble departure diameter as a function of injection mass flow rate and gravity.

Table 2 Summary of bubble departure diameters (orifice diameter:1 mm)

The data in Fig. 3 shows that the spread of bubble departure diameters at 2.73 × 10⁻⁹ kg/s injection flow rate under low gravity is relatively large. There are two major factors responsible: first the injection temperature is obviously different between points, and second, there were instantaneous gravity fluctuations (g-jitters) that ranged between 0.064g_e (minimum) and 0.027g_e (maximum). As shown in Table 2, the helium inlet temperature affected the bubble density, and the g-jitter resulted in the force fluctuations to the bubble; both factors affect the bubble departure mechanisms in reduced gravity. However, under 1-g condition, the BBDs are all smaller than those in low-g mainly due to the additional lifting force by buoyancy. The BBD increases with an increasing mass flow rate that is due to the fact that buoyancy force is playing a significant role in 1-g. Case 3-7 has the smallest BDD due to its largest buoyancy force at the highest injection temperature of 260 K. This 1-g trend is consistent with the 1-g data of Badam et al.¹⁵ who used air/water system.

The following trends can be summarized from the BDD data:

• 1. Effect of gravity: Between Cases 3-3 and 3-4 with similar gas temperatures, Case 3-4 has a smaller departure diameter due to a larger gravity level.

• 2. Effect of gas temperature: Among Cases 3-1, 3-2, 3-3, and 3-4 at the same mass flow rate of 2.73 × 10⁻⁹kg/s, the higher the gas temperature, the larger the departure diameter. This is due to the fact that helium density is lower for higher temperature that results in lower thrust.

• 3. Repeatability: Between Cases 3-5 and 3-6, for 2.73 × 10⁻⁹kg/s helium mass flow rate, both cases have relatively the same helium inlet temperatures and g levels, the departure diameters are also very close to each other.

The second parameter analyzed is the bubble formation time (BFT) defined as the time between the instance when a bubble begins to form on the injector to the instance when it detaches from the injector. Figure 4 plots the BFT as a function of injection mass flow rate and gravity level. As shown, with similar injection mass flow rates, the bubbles take longer to form before detaching from the injector in low gravity. The rationale is similar to BDD, in that the reduction in buoyancy force in low-g causes, the bubble to remain attached to the injector longer relative to 1-g. The bubble formation time is also shorter for higher mass flow rates that provides higher thrust in low gravity.

Fig. 4: Bubble formation characteristics.

Bubble formation time versus injection mass flow rate.

The third parameter analyzed is the bubble size history in the pool after departure, defined as the time-dependent diameter of the bubble translating in the pool from the moment of detachment onward. This is an important parameter for future modeling of the heat and mass transfer between injected helium gas and LN₂. First, the bubble total area was measured by the software ImageJ. Then the bubble radius, ${R}_{bubble}$, was determined based on the formula, $Bubble\,Area\,=\,\pi {R}_{Bubble}^{2}$. So, the bubble diameter is essentially an equivalent diameter. Figure 5 plots this transient bubble size after departure as a function of time and injection temperature for 2.73 × 10⁻⁹kg/s injection flow rate and in low-gravity.

Fig. 5: Bubble departure characteristics.

Bubble size history after departure.

In general, bubble sizes showed fluctuations for all eight cases reported. The largest amplitude of size fluctuation belongs to the bubble that was the largest ( ~9 mm) when leaving the nozzle. The main reason for the large amplitude fluctuation is that in reduced gravity, the bubble size and shape are controlled by the surface tension, which is inversely proportional to the bubble size. As a result, the larger size bubbles would tend to exhibit larger size fluctuations. Also, the bubbles with the lowest helium temperature (208 K) were found to have smaller fluctuation amplitudes.

Videos and images were analyzed to compare trends between 1-g and reduced gravity HSP. Figures 6 and 7 plot observed flow patterns in reduced and terrestrial gravity, respectively, over a range of injection flow rates. Figure 8 plot observed flow patterns for the same injection flow rate and orifice but for different gravity levels. In general, in reduced gravity, the patterns of the injected helium flow can be divided into three categories: 1) individual bubbly flow, 2) slug flow, and 3) jet stream flow.

Fig. 6: Flow visualization in reduced gravity.

(Left) Individual bubbly flow, 2.73 × 10⁻⁹kg/s, 1 mm orifice; (middle) bubble chunks and slugs, 2.73 × 10⁻⁷ kg/s, 1 mm orifice; (right) Jet stream flow, 8.18 × 10⁻⁶kg/s, 0.25 mm orifice.

Fig. 7: Flow visualization in terrestrial gravity.

(Left) individual Bubbly flow, 2.73 × 10⁻⁹kg/s, 1 mm orifice; (right) slug flow, 2.73 × 10⁻⁶kg/s, 1 mm orifice.

Fig. 8: Flow visualization comparison.

(Left) individual bubbly flow in terrestrial gravity; (right) slug or intermittent jet flow in reduced gravity. Both are 2.73 × 10⁻⁷kg/s helium mass flow rate and 1 mm orifice.

As shown in Fig. 6, in reduced gravity, the helium flow pattern is directly correlated with the mass flow rate. As the mass flow rate increased from 2.73 × 10⁻⁹kg/s to 2.73 × 10⁻⁷kg/s, the gas flow pattern transitioned from bubbly flow to slug flow; when the mass flow was further increased to 8.18×10⁻⁶kg/s, the flow became jet stream flow. Comparatively, in 1-g, as indicated in Fig. 7, the flow transitioned from individual bubbly flow to slug flow when the helium mass flow rate was increased from 2.73 × 10⁻⁹kg/s to 2.73 × 10⁻⁶kg/s.

Meanwhile, in Fig. 8, at the same 2.73 × 10⁻⁷kg/s helium mass flow rate and 1 mm orifice, the helium flow is the individual bubbly flow in 1-g, but the helium flow was found in the slug flow regime in reduced gravity. Echoing trends in Figs. 4 and 20, comparing the left photograph in Fig. 6 for reduced gravity with the left photo in Fig. 7 for 1-g (both cases are at 2.73 × 10⁻⁹kg/s helium mass flow rate with 1 mm orifice), the bubbles in reduced gravity are 50% larger than those under earth gravity.

Table 3 summarizes flow visualization observations based on gravity level, injection orifice size, and helium mass flow rate. For 0.25 mm orifice, the gravity level did not appear to affect helium gas flow pattern versus the injection helium mass flow rate. However, for the 1 mm orifice, the transition from individual bubbly flow to slug flow took place between 2.73 × 10-8 kg/s and 2.73 × 10-7kg/s injection mass flow rates in reduced gravity. However, in 1-g, the same transition took place between 2.73 × 10-7kg/s and 2.73 × 10-6kg/s helium mass flow rates.

Table 3 Injected helium flow pattern vs. mass flow rate and gravity condition. Units are 1 × 10⁻⁹kg/s

Helium two-phase flow regime maps have been developed for both 1-g and reduced gravity conditions. Figure 9 depicts the 1-g helium flow regime map using the Bond number (Bo) and the Froude number (Fr). As can be seen in Fig. 9, the three flow regimes are clearly separated by the orange dash lines. The flow regime is primarily a strong function of the Fr since buoyancy and helium flow momentum dominate in terrestrial gravity. In our flight experiment, we also recorded one Martian and one lunar flow patterns. The flow regime map for these two reduced gravity cases is shown in Fig.10 where the regime map is consistent with that of the 1-g cases plotted in Fig. 9. The helium flow regime map for the low-gravity condition is given in Fig. 11. As suggested by Balasubramaniam et al.³⁴, for the reduced gravity regime map, the Suratman number (Su) and the Reynolds number (Re) must be used as gravity is no longer an influencing factor. Figure 10 clearly reveals that the flow regime is basically dependent on Re. As the Re increases, the two-phase flow regime switches from bubbly flow, then to slug flow, finally to jet flow.

Fig. 9: Two-phase flow regime map.

1-g helium injection two-phase flow regime map.

Fig. 10: Two-phase flow regime map.

Martian and Lunar gravity helium injection two-phase flow regime map.

Fig. 11: Two-phase flow regime map.

Low-g helium injection two-phase flow regime map.

For an overall comparison among all gravity levels, Fig. 12 shows the two-phase flow regime map that includes low-g, Martial gravity, Lunar gravity, and 1-g data points. Among all gravity levels, a general trend is established that the Fr number sets the boundary between the jet flow and slug flow and that between the slug flow and the bubbly flow.

Fig. 12: Two-phase flow regime map.

All gravity levels two-phase flow regime map.

To evaluate the extent of helium injection facilitated LN₂ cooling, the transient LN₂ pool temperature distributions were mapped using the thermocouples placed on a rack shown in Fig. 18. Figure 13 plots the transient temperatures recorded by TCs 2, 3 and 4, the three closest temperatures from the injector, during the third parabola set. It is reminded that helium bubbles were injected only during the reduced gravity periods. As shown in Fig. 13, the pool temperatures continued to drop due to the fact that the cooling capacity of injected bubbles had not been exhausted when the reduced gravity periods ended. The temperature spikes prior to low-g period were caused by the residual heating from the outside environment after the cooling capacity of the injected bubbles had been exhausted.

Fig. 13: Pool cooling by helium injection.

Transient Temperatures Recorded by TC 2, 3, and 4.

Table 4 provides the calculated results for the helium injection cooling. The liquid pool cooling rate, in general, increases with the gas injection mass flow rate, but the cooling rate is not a linear function of the gas mass flow rate. The 8.18 × 10⁻⁶kg/s mass flow case has the highest cooling rate. The cooling rate is strongly affected by the gas flow rate, gas flow pattern in the pool, and bubble departure diameter. Another evaluation parameter is the gas cooling effectiveness that is defined as the cooling rate per mass flow rate. In essence, cooling effectiveness represents the cooling capacity per unit mass of injection gas. Table 3 clearly indicates that the cooling effectiveness is inversely proportional to the gas mass flow rate. The main reason for the opposite trends between the cooling rate and the cooling effectiveness is explained next. According to the low-gravity gas flow regime map, Fig. 11, the different flow patterns are mainly determined by the Re(G), gas flow Reynolds number. As the gas flow rate increases, the Re(G) also increases and the flow pattern transitions from bubbly flow to slug flow to jet flow. It is a known fact that rates of heat and mass transfer are highest for bubbly flow³⁵. The next is slug flow and the lowest is jet flow as the bubbly flow has the largest liquid-gas interfacial area per unit gas volume for heat transfer.

Table 4 Helium Gas Injection Cooling Rates

Discussion

The first important finding is that for the same injection mass flow rate, the BDD is significantly larger in low gravity than that in terrestrial gravity, especially for low injection flow rates. This is because the buoyancy force is significantly reduced in low gravity, and the surface tension force becomes the dominant resistance force in controlling the bubble departure mechanism as well as the surface tension force decreases with increasing bubble diameter. Additionally, the larger the gas mass flow rate, the smaller the diameter of the bubble when it departs from the nozzle in low gravity.

On the bubble formation time, with similar injection mass flow rates, the bubbles take longer to form before detaching from the injector in low gravity. The rationale is similar to BDD, in that the reduction in buoyancy force in low-g causes the bubble to remain attached to the injector longer relative to 1-g. The bubble formation time is also shorter for higher mass flow rates that provides higher thrust to facilitate the bubble departure in reduced gravity.

In general, bubble dispersion size history showed fluctuations for all eight cases reported. The largest amplitude of size fluctuation belongs to the bubble that was the largest ( ~9 mm) when leaving the nozzle. The main reason for the large amplitude fluctuation is that in reduced gravity, the bubble size and shape are controlled by the surface tension, which is inversely proportional to the bubble size. Also, the bubbles with the lowest helium temperature (208 K) at the injection were found to have smaller fluctuation amplitudes.

In reduced gravity, the patterns of the injected helium flow can be divided into three categories: 1) individual bubbly flow, 2) slug flow, and 3) jet stream flow. In low-g, the helium flow pattern in the LN2 pool is directly correlated with the mass flow rate. In low-g, as the mass flow rate increased from 2.73 × 10⁻⁹kg/s to 2.73 × 10⁻⁷kg/s, the gas flow pattern transitioned from bubbly flow to slug flow; when the mass flow was further increased to 8.18 × 10⁻⁶kg/s, the flow became jet stream flow. Comparatively, in 1-g, the flow transitioned from individual bubbly flow to slug flow when the helium mass flow rate was increased from 2.73 × 10⁻⁹kg/s to 2.73 × 10⁻⁶kg/s. For the same pattern transition, the mass flow rate required in 1-g is two orders of magnitude higher than that in low-g.

The liquid pool cooling rate by helium gas injection, in general, increases with the gas injection mass flow rate, but the cooling rate is not a linear function of the gas mass flow rate. However, the cooling effectiveness is inversely proportional to the mass flow rate of gas.

Since our main objective is to investigate the feasibility and characteristics of HSP in low gravity, it is believed that we have successfully accomplished this objective based on the results presented in this paper.

Methods

The HSP experiment was designed and built based on concepts from prior parabolic flight experiments on pipe and tank chill down^36,37. The HSP system was designed and built for testing in both 1-g and parabolic flights. The HSP system is shown in Fig. 14, which flew alongside a secondary flight cryogenic pool boiling experiment.

Fig. 14: Experimental system.

Flight Cryogenic Helium Subsurface Pressurization and Pool Boiling Rig.

The system, flow network, piping, and instrumentation diagram of the HSP experiment are shown in Fig. 15. Computer-aided drawings of the HSP cylindrical tank are shown in Fig. 16. A 20.3 cm diameter, 30.5 cm tall, 8.34 L LN₂ storage tank was used to submerge the pressurant gas injector. Submerged orifices (either 0.25 mm or 1.0 mm) were located near the bottom of the tank. An 8 cm tall, 6 cm wide view port was located on the side wall aligned with the injector to visualize the bubble formation, departure, and ensuing two-phase flow from the injector. The tank lid had multiple feedthroughs for liquid supply, drain, vent, relief, light for visualization, a temperature rake, and pressure transducer, while helium gas was injected via a bottom port.

Fig. 15: Experimental system.

Schematic of Tank, Flow Network, and Instrumentation.

Fig. 16: Major components.

Computer-Aided drawings of the helium subsurface pressurization tank and feedthroughs. A The HSP tank, B the front view of tank, C the lid, and D the view port.

The HSP tank was filled through a manual valve (MV1) using a supply line from a 180 L double-walled Airgas dewar, with a relief valve set at 963 kPa (125 psig). During parabolic flights, the HSP tank could be topped-off using a 10 L auxiliary supply tank. A gaseous nitrogen (GN₂) cylinder initially pressurized at 17.3 MPa was used to pressurize the HSP tank to a pre-set value for each test. However, the HSP tank was designed to hold a maximum pressure up to 200 kPa. Tank pressure was managed by the pressure regulator (PR2), which controlled the tank pressure to within 35 kPa of the set value during each test. Depressurization was carried out by opening the ball valve (BV3) to vent ullage gas to the atmosphere. The two relief valves (RV2 and RV3) were installed for emergency tank overpressure relief.

To control helium gas injection flow rate, there were two supply lines as shown in Fig. 15, each equipped with a flow meter. The first flow controller (FC1) supplied flow rates from 2.73 × 10⁻⁹−2.73 × 10⁻⁷kg/s (1-100 standard cubic centimeters per minute), while the second flow controller (FC2) supplied flow rates up to 8.18 × 10⁻⁶kg/s (3000sccm). The flow rates were adjusted by needle valves (NV1 and NV2).

To control helium gas injection temperature, a shell and tube heat exchanger shown in Fig. 17 was designed and built. The helium entered the tube side while the shell side was filled with LN₂. Based on allowable parabolic system volume and other constraints, calculations showed that a 1.27 cm diameter, 25 cm tube length would be adequate to supply helium gas injection temperatures between 170 and 260 K over the range of injection flow rates. Figure 17 also include the nozzle design geometry.

Fig. 17: System components.

a CAD drawing of heat exchanger and b Nozzle geometry.

To measure the temperature of the LN₂ under the influence of subsurface injection and bubbling, a thermocouple rack shown in Fig. 18 was mounted inside the HSP tank. Ten Omega type-T thermocouples were mounted at various locations within the tank to measure spatial changes in the liquid temperature as the testing evolved. The rack was designed such that the minimum horizontal separation length between the nozzle and the rack is 5.1 cm. The rack effect on the results should be negligible. The above two sentences have been added to the revised version. Meanwhile, tank pressure was measured with an Omega absolute 0–345 kPa (0–50 psia) pressure transducer.

Fig. 18: Thermal couple rack.

Location of thermocouples on the rack inside helium subsurface pressurization tank.

To record and display all sensor data, a LabVIEW virtual instrument (VI) software system was used in conjunction with a National Instruments (NI) CompactDAQ hardware. LabVIEW VI controlled the opening and closing of two mass flow controllers. An NI-9214 module reads all thermocouples, while an NI-9205 module reads all pressure transducers. The sampling rate of all measurements was 10 Hz.

For flow visualization, a MIC Hotshot 1700cc high-speed video camera shown in Fig. 19 (200,000 maximum frames per second and 16GB internal storage) was used to record videos. The camera was mounted in-line with the viewport on the side of the HSP tank. For most experiments, 1080 × 960 resolution and 1000 frames per second frame rate were found sufficient to visualize the flow. Camera images were imported into the image processing software ImageJ™ and processed.

Fig. 19

Flow visualization system.

Figure 20 shows the acceleration level as a function of time during a parabolic flight experiment. As shown, a typical flight consists of six sets of five parabolas. Each parabola lasts approximately 60–70 seconds, with 17–20 seconds at 0 ± 0.01 g and the balance of time at 1.8 g as the plane moves from the peak to the valley of a parabolic trajectory.

Fig. 20: Gravity map.

Gravity as a function of time during typical parabolic flight experiment.

The experimental methodology to conduct an HSP experiment onboard the parabolic aircraft is described in four main steps referring to Fig. 14: initial system start-up, setting the helium mass flow rate and temperature, initializing the video recording unit, and shutdown. For system start-up, the HSP tank and plumbing upstream was chilled down and the HSP tank filled to the desired fill level, typically 90% by volume. This was done while the rig was loaded on the plane, several hours before take-off. In between fill and the first parabola at elevation, the tank was set to vent at 101.3 kPa. Once at altitude, a pre-programmed LabVIEW script was initialized to engage the mass flow controllers and to record all temperature, pressure, and mass flow rate data. NV1 and BV2 were closed. The HSP tank pressure was then set to the desired value using the gaseous nitrogen bottle, typically 101.3 kPa.

For step 2, the helium injection flow rate and temperature were set, typically minutes before the first parabola in the series. Flow rate would typically stabilize within tens of seconds. For each set of five parabolas, the injection temperature was fixed by adjusting both NV1 and NV2 for a total of six temperature set points per flight. Meanwhile, within each set of five parabolas, for each individual parabola, flow rate was varied from 2.73 × 10⁻⁹ to 8.18 × 10⁻⁶kg/s corresponding to individual values of approximately 2.73 × 10⁻⁹, 2.73 × 10⁻⁸, 2.73 × 10⁻⁷, 2.73 × 10⁻⁶, and 8.18×10⁻⁶kg/s. To achieve such a broad range of flow rates, typically FC1 was used to control the first two flow rates while FC2 was used to control the last three flow rates. Thus, adjustments in injection mass flow rates were done in between successive parabolas, while adjustments to injection temperature were done in between sets of five parabolas. At the beginning of each reduced gravity period, the video recording was turned on and then turned off at the end of each reduced gravity period. The pressurant flow rate was also stopped at the end of each reduced gravity period. The system shutdown was performed at the end of the last reduced gravity period. The methodology for 1-g is very similar to that for reduced gravity except that the duration of each test was not limited by the reduced gravity period.

The uncertainty associated with the HSP experiment was estimated using the root-sum-square method shown in Eq. 9:

$${{{\rm{\sigma }}}_{{\rm{y}}}}^{2}=\mathop{\sum }\limits_{i=1}^{n}{\left(\frac{\partial y}{\partial {x}_{i}}\right)}^{2}{{{\rm{\sigma }}}_{{x}_{i}}}^{2}$$

(9)

where y is the variable, whose uncertainty is to be determined for, and ${x}_{i}$ is the parameter used to determine y. The values of the LN₂ and helium properties were determined using REFPROP³⁸. The uncertainty associated with these parameters was calculated by finding the values of these parameters at the upper and lower ends of the test pressure uncertainty (+/− 0.276 kPa).

The uncertainty in tank pressure and helium pressure is 0.08% of the full-scale reading (345 kPa for the PT) and are therefore 0.276 kPa. The uncertainty in all temperature measurements is ±1 K or ±0.75% full scale, whichever was greater. The uncertainty in injection gas mass flow rate is ±0.32% of flow controller reading or ±0.02% of full scale, whichever was greater.

The uncertainty in the amount of time that has passed since the formation of the bubble was taken to be half of the minimum unit presented by the video processing software ImageJ™. ImageJ™ presented the time in each frame within an accuracy of 0.002 s. The uncertainty in the time measurement is therefore half of that or 0.001 s. In the image analysis, the calibration unit is the length of a pixel. The length of a pixel was determined based on a known length scale that is the outer diameter of the orifice. That was the method we used to determine the length of a pixel of 0.052 mm as the calibration length scale. The uncertainty associated with the bubble diameter was taken as 2 pixels or 0.104 mm. As the tube fitting was used as the criterion for actual length scale, the uncertainty of its diameter ${D}_{{tube}}$ was gained from the manufacturer, quoted at 0.016 mm. Thus, the uncertainty of bubble diameter increased to 0.12 mm. The specific values of some variables are shown in Table 5.

Table 5 Uncertainty values associated with key parameters