Introduction

Unmanned aerial vehicles (UAVs) are typically exposed to complex aerodynamic conditions, including low Reynolds number flight, complex building density, and atmospheric turbulence1,2. Precise assessment of flight parameters contributes to enhancing the stable control capability of UAVs under complex aerodynamic conditions3,4. The critical flight parameters include angle of attack (AOA), angle of sideslip (AOS), and airspeed, which can be decoded from aerodynamic information around UAVs. Conventional air data sensing systems include probe-type systems based on airspeed tubes and wind vane sensors5, and embedded systems based on fuselage pressure measurement holes and pneumatic piping6,7. However, the impact on the structure and aerodynamic configuration renders these systems unsuitable for meeting the miniaturization demands of UAVs.

Benefiting from superior flexibility8,9,10, the UAV-integrated flexible electronic skins with aerodynamic sensing capabilities offer an effective strategy for flight parameter decoding. Unlike traditional single-modal sensing, the fusion of flow velocity and pressure modalities facilitates precise sensing and analysis of complex flow fields. For instance, the flexible integrated skin developed by Pang et al.11 employed a dual-layer hot-film flow velocity sensor array and commercial pressure sensor device, enabling the sensing of pressure distribution on the wing surface. However, rigid pressure sensors pose challenges in attaching the skin to the highly curved surfaces of the wing’s leading edge. Fully flexible electronic skins provided an effective solution to increase the integration capability of flexible electronic skins onto UAVs. For instance, we previously reported an ultrathin flexible skin with an all-polyimide pressure and airflow sensor array12, enabling the resolution of AOA and airspeed. However, due to the limitations of the classical triple-sensor algorithm, the sensors arranged on the leading edge of the airfoil are insensitive to the AOS. Therefore, there is an urgent need for a highly sensitive and intelligent flexible skin, together with advanced algorithms, to enable the accurate resolution of flight parameters such as AOA, AOS, and airspeed.

The flexible intelligent skin only measures and collects the aerodynamic information around the vehicle, while the efficient and accurate resolution of flight parameters additionally requires algorithm integration. The classical analytical approach for flight parameter estimation is the triplets algorithm13,14,15. It relies on multiple pressure measurement points (typically five or nine) and uses algebraic algorithms to calculate parameters such as AOA, AOS, and airspeed. However, this algorithm involves high computational complexity and cannot determine AOS or airspeed when the measurement points are near the leading edge of the wing. Recently, non-analytical methods, such as neural network algorithms, have been introduced12. While promising, these methods are computationally intensive and require large training datasets6,16,17,18. Therefore, the development of flight parameter analytical methods with high accuracy and low computational cost has become a critical focus of research.

To address these issues, we propose an ultrathin flexible sensing patch that integrates differential pressure and vector flow velocity sensors. The flexible capacitive differential pressure sensor array reaches a high resolution of 0.14 Pa and an acute sensitivity of 2.0 × 10² fF/Pa within the range of ±1.0 kPa. Furthermore, an analytical pressure-velocity fusion (PVF) algorithm is developed for flight parameter detection with high accuracy and low computational cost.

Results

Design and development of flexible sensing patch

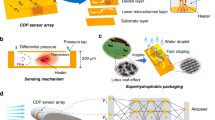
To precisely decode flight parameters, we designed and developed a wing-integrated flexible electronic sensing patch with bimodal pressure and velocity aerodynamic sensing capabilities, as illustrated in Fig. 1a. The flexible sensing patch consists of a vector flow velocity sensor (attached to the upper surface), a capacitive differential pressure sensor array (composed of flexible printed circuits FPC1 and FPC2, with a PI sensitive layer in between), a microfluidic layer, and a PI substrate. The total thickness of the multilayered flexible sensing patch is 0.21 mm, and a multilayer polyimide bonding process was used to form it (Fig. S1).

Fig. 1: Schemes of flexible sensing patch and analytical PVF algorithm.
figure 1

a Exploded view of the flexible sensing patch. b Working principle of the capacitive differential pressure sensor. c Optical image of the differential pressure sensor array (i) and flow velocity sensor (ii). d Illustration of the flexible sensing patch attached on a wing surface and multiple flight parameter sensing principles with the analytical PVF algorithm.

Full size image

We designed a dual-layer capacitive differential pressure sensor array to evaluate aerodynamic pressure. Capacitive pressure sensors are one of the mainstream options for surface pressure acquisition on UAVs surfaces19,20,21. However, existing flexible thin-film capacitive sensors exhibit poor sensitivity and linearity when subjected to alternating positive and negative pressure variations22,23,24,25,26,27. Compared to traditional single-layer capacitive pressure sensors, the designed dual-layer differential pressure sensor offers higher sensitivity, better linearity across the full measurement range, and more accurate positioning of angle locations. The structure of the capacitive differential pressure sensor is shown in Fig. 1b. It consists of upper and lower pressure chambers, a microchannel layer, and a reference pressure hole. When airflow enters the reference pressure hole and passes through the microchannel, the pressure in the lower chamber equals the reference pressure P0 at the reference pressure hole. The pressure in the upper chamber equals the pressure P1,2 at the sensor surface. With a small diameter of 1.1 mm, the pressure chambers provide precise localization of measurement points while maintaining high sensitivity. Three electrode layers are integrated into the sensor design, positioned at the top, middle, and bottom. The middle electrode, embedded within polyimide (PI) films, prevents electrical short circuits with the top and bottom electrodes. When P1 exceeds P0, the strain film bends downward, leading to a decrease in CP and an increase in CM. In contrast, when P1 falls below P0, CP increases and CM decreases. By subtracting CM from CP, the differential capacitance (ΔC) is obtained, which is then used to calculate the pressure difference (ΔP) between the reference pressure hole and the sensor surface. By incorporating two pressure sensors (Sp1 and Sp2 in Fig. 1c(i)), the capacitive differential pressure sensor array measures P1–P0 and P2–P0, respectively. The design of combining two pressure sensors with a reference pressure hole enables the determination of pressure differences among the three points.

Meanwhile, aerodynamic velocity was assessed by the integrated vector flow sensor based on a suspended array of highly sensitive vanadium oxide thermistors28. The vector flow sensor operates based on the calorimetric principle, utilizing a central micro-heater to establish a stable temperature gradient, while an array of thermistors positioned around the heater measures the resulting temperature distribution. The temperature differentials captured by the thermistor array enable precise characterization of flow velocity and direction. Figure 1c(ii) shows this vector flow velocity sensor developed in our previous work, which mainly consists of four thermistors and a heating unit positioned in the center. The thermistors are made of vanadium oxide, a material with a high temperature coefficient of resistance, to increase the sensitivity of the sensor. Thermistors 1 and 3 are employed in this study to measure the spanwise velocity. A Wheatstone bridge circuit is implemented for differential amplification of the signals, resulting in highly sensitive measurement of the spanwise flow velocity.

In addition to highly sensitive and flexible electronic skins, a novel analytical PVF algorithm based on a triple algorithm was developed for precise evaluation of flight parameters, including AOA (α), AOS (β), and airspeed (V∞). By decoupling the AOA and AOS, the algorithm directly utilizes pressure data (ΔP1, ΔP2) to solve for AOA and spanwise flow velocity (Vz) to determine AOS. This approach also streamlines the calculation of calibration coefficients, significantly reducing computational complexity. The flexible sensing patch is mounted on the wing surface to collect ΔP1, ΔP2, and Vz (Fig. 1d), and the PVF algorithm calculates the AOA, AOS, and airspeed (V∞).

Aerodynamic sensing performance evaluation of flexible sensing patch

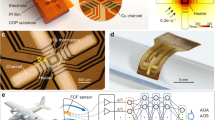
The flexible sensing patch was mounted on the leading edge of a wing model (NACA0024) for characterization and wind tunnel tests, as illustrated in Fig. 2a. The position angles of the reference pressure hole and the two pressure sensors, Sp1 and Sp2, were set at −50°, 25°, and 50°, respectively. Additionally, the flow velocity sensor (Sv) was installed at the frontmost part of the wing to measure the spanwise velocity.

Fig. 2: Aerodynamic sensing performance evaluation of a fabricated flexible sensing patch.
figure 2

a The flexible sensing patch mounted on the wing model; b Differential capacitance variation with applied pressure difference; c Fitting curve between sensor outputs and pressure difference (±1000 Pa); d Fitting curve between sensor outputs and pressure difference (0–1 Pa); e Fitting curve between voltage outputs and Vz.

Full size image

Firstly, the aerodynamic pressure sensing performance of the capacitive differential pressure sensor array was evaluated. To calibrate the capacitive differential pressure sensor array, the reference pressure was modified using a differential pressure calibrator, ranging from −1.0 kPa to 1.0 kPa in 0.20 kPa increments. Each calibration was repeated three times, during which an LCR meter recorded the capacitance output of the sensor array. The output data consisted of the capacitance changes in the upper and lower pressure chambers of each sensor, which were then processed differentially to obtain ΔC (Fig. 2b). The data was further processed by averaging each segment of the sensor output, as illustrated in Fig. 2c (with the output of Sp2 in Fig. S2). It was calculated that within a pressure range of ±1000 Pa, the differential pressure sensor Sp1 achieved a resolution of 0.14 Pa. Subsequently, the output curves of the sensors were fitted to obtain the fitting equations S1 and S2. The capacitance difference outputs of the sensors were substituted into the fitting equations to back-calculate the pressure difference. Then the calculated results were compared with the actual pressure difference, revealing maximum errors of 13 Pa and 10 Pa for the two sensors, respectively (Fig. S3). The fitting accuracy meets the requirements for subsequent flight parameter calculations. In addition to calibration, we also used a differential pressure calibrator to test the pressure sensor’s ultimate resolution performance in the range of 0.0–1.0 Pa (Fig. 2d). With a noise level of 2.4 fF, the pressure sensor array demonstrates a sensitivity of 2.0 × 10² fF/Pa and an ultimate resolution of 12 mPa within the range of 0.0–1.0 Pa. Supplementary Table S1 provides a comprehensive comparison of the reported pressure sensors in terms of flexibility, sensing principles, resolution, and detection range. Notably, our capacitive differential pressure sensor demonstrates unprecedented performance when considering resolution and detection range.

Following this, the flow velocity sensor was calibrated to ensure accurate performance across a range of operating conditions. The standard airfoil attached with flow velocity sensors was placed in the wind tunnel, and the actual flow velocities were set to 10, 15, 20, 25, 30, and 35 m s−1, while the AOS were adjusted to 0°, 2°, 4°, and 6°. The outputs were recorded, and the fitting curve between the sensor outputs and Vz was developed (Fig. 2e). The fitting equation S3 can be obtained based on the fitted curve.

Principle of analytical PVF algorithm

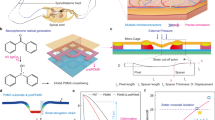
The developed high-sensitivity flexible sensing patch enables precise measurements of aerodynamic information, including flow velocity and pressure. However, utilizing this aerodynamic data to further derive flight parameters requires the integration of atmospheric parameter analysis algorithms. In this context, we proposed a computationally efficient analytical PVF algorithm to solve flight parameters such as AOA, AOS, and airspeed. Building upon the classical triples algorithm, the PVF algorithm introduces spanwise velocity (Vz) to achieve the decoupling of AOA and AOS, enabling the calculation of the AOS and airspeed at the leading edge of the wing. As shown in Fig. 3a, the actual airspeed V∞ is decomposed into the normal speed component Vxy and the spanwise speed component Vz. Taking any point on the leading edge of the wing as the origin, the X axis is defined as the perpendicular line passing through the leading edge in the central section of the wing model, and the Z axis is oriented along the spanwise direction of the wing. A three-axis coordinate system is established, where the X axis and Y axis form the airfoil plane of the wing. Vxy is the projection of the actual airspeed on the airfoil plane of the wing, while Vz is the projection of the actual airspeed on the leading edge of the wing. The sideslip angle β is calculated as

$$tan\beta =\frac{{V}_{z}}{{V}_{xy}}$$
(1)
Fig. 3: Analytical PVF algorithm for flight parameters decoding.
figure 3

a Schematic illustration of the airspeed decomposition diagram and the distribution of pressure measuring points. b Airflow velocity contour and velocity vector plots at different AOA and AOS. The far-right column shows the top view of the wing. c Comparison of the calculated value and the actual value of the AOA in simulation. d Comparison of the calculated value and the actual value of the AOS in simulation. e Comparison of the calculated value and the actual value of the airspeed in the simulation.

Full size image

The main steps to solve flight parameters include: (1) solve the AOA and Vxy according to the triples algorithm using pressure data; (2) directly read out Vz through the flow velocity sensor; (3) solve the AOS and airspeed.

First, according to the triples algorithm and the pressure distribution equation of the wing21,22,23, the pressure distribution equation at a certain point is:

$$P={q}_{c}(co{s}^{2}\theta +{\rm{\varepsilon }}si{n}^{2}\theta )+{P}_{\infty }$$
(2)

P∞ is free stream static pressure, θ is the local flow incidence angle, ε is the position error calibration parameter, qc is impact pressure expressed as:

$${q}_{c}=\frac{1}{2}\rho {{V}_{\infty }}^{2}$$
(3)

ρ is the air density, V∞ is the airspeed.

If the pressure value at the first point i is Pi, the pressure value at the second point j is Pj, and the pressure value at the third point k is Pk, then

$${\varGamma }_{ij}={P}_{i}-{P}_{j},{\varGamma }_{jk}={P}_{j}-{P}_{k},{\varGamma }_{ki}={P}_{k}-{P}_{i}$$
(4)

The predicted AOA αe is expressed as:

$${{\rm{\alpha }}}_{{\rm{e}}}=\frac{1}{2}\arctan \left(\frac{{\rm{A}}}{{\rm{B}}}\right)$$
(5)

while \(\,\left\{\begin{array}{l}{A\,=\,\varGamma }_{ij}{b}_{\,k}^{2}{\,+\,\varGamma }_{jk}{b}_{i}^{2}{\,+\,\varGamma }_{ki}{b}_{j}^{2}\\ {B\,=\,\varGamma }_{ij}{a}_{k}{b}_{k}{\varGamma }_{jk}{a}_{i}{b}_{i}{\,+\,\varGamma }_{ki}{a}_{j}{b}_{j}\end{array}\right.\), \(\left\{\begin{array}{l}{a}_{i\,}{=\,cos\,\lambda }_{i}\\ {b}_{i}{\,=\,sin\,\lambda }_{i}\,cos\,{\phi }_{i}\end{array}\right.\), \(\left\{\begin{array}{l}{a}_{j}{\,=\,cos\,\lambda }_{j}\\ {b}_{j}{\,=\,sin\,\lambda }_{j}\,cos\,{\phi }_{j}\end{array}\right.\), \(\left\{\begin{array}{l}{a}_{{k}}{\,{=}\,{c}{o}{s}\,{\lambda }}_{{k}}\\ {b}_{{k}}{\,{=}\,{s}{i}{n}\,{\lambda }}_{{k}}\,cos\,{\phi }_{{k}}\end{array}\right.\), both ai, bi, aj, bj, ak, and bk are intermediate parameters, λ is the cone angle of the point, and ϕ is the local flow incidence angle. According to different airspeeds and AOS conditions, the test data under multiple working conditions is obtained. The αe needs to be corrected by introducing the AOA flow correction angle, δα:

$$\alpha \,=\,{\alpha }_{e}+\delta \alpha$$
(6)

where α is the actual AOA, and δα needs to be calibrated through tests.

The position error calibration parameter \(\varepsilon\) can be calculated using Eq. (7)

$$\varepsilon \,=\,\frac{\frac{{\Gamma }_{ij}}{{{\rm{q}}}_{c}\,}{\,+\,\cos }^{2}{\theta }_{j}{\,-\,\cos }^{2}{\theta }_{i}}{{\cos }^{2}{\theta }_{j}{\,-\,\cos }^{2}{\theta }_{i}}$$
(7)

where θi, and θj represent the airflow incidence angle at pressure points i and j, respectively. By substituting αe and \(\varepsilon\) into Eq. (2), the normal flow velocity component can be calculated using Eq. (8)

$${V}_{{x}{y}}=\sqrt{\frac{{2\Gamma }_{ij}}{{\rho (\varepsilon -1)(\cos }^{2}{\theta }_{{j}}-{\cos }^{2}{\theta }_{{i}})\,}}$$
(8)

Finally, we obtained the AOS using Eq. (1), and the actual airspeed using Eq. (9)

$${V}_{\infty }=\sqrt{{V}_{xy\,}^{{2}}{+V}_{z}^{{2}}}$$
(9)

To validate the reliability of the proposed analytical PVF algorithm, we conducted a simulation analysis of the leading edge airflow under varying AOA, AOS, and airspeeds. Instead of employing a simplified semicircular leading edge wing model, we utilized the standard NACA0024 airfoil with a chord length of 0.30 m (Fig. 3a). To provide the necessary inputs for the triples algorithm, three pressure points were designated with position angles of 50°, 30°, and −50°. The airflow velocity contour and velocity vector plots near the wing are shown in Fig. 3b. The third column presents a top view of the airflow velocity distribution over the wing model to more intuitively demonstrate the effect of AOS variation. It can be observed that as the AOA changes from −20° to 0°, the stagnation point moves from the upper surface of the leading edge to its center. To further validate the analytical PVF algorithm, we selected 20 different conditions for testing and prediction (Fig. S4). The CFD simulations provided pressure data at different measurement points and Vz under different operating conditions (Fig. S5), which were then applied to solve for the flight parameters based on the analytical PVF algorithm.

When comparing the calculated AOA with the actual values (Fig. 3c), the corrected AOA exhibits a high degree of linearity, with the curves for different conditions nearly overlapping. This indicates that the solution for AOA is independent of AOS and airspeed. The error in the calculated AOA is within ±0.20°, demonstrating a high level of accuracy. Similarly, as shown in Fig. 3d, the solutions for AOS of 3°, 6°, and 8° at airspeeds of 20 m s−1 and 60 m s−1 show an error within ±0.50°. Figure 3e presents the calculated airspeeds under conditions of 20, 40, and 60 m s−1 with AOS of 3° and 8°, exhibiting an error within ±0.90 m s−1. These results confirmed the reliability of the proposed analytical PVF algorithm.

High-resolution decoding of flight parameters

Incorporating validated analytical PVF algorithms, the developed highly sensitive and wing-integrated flexible sensing patch can precisely decode flight parameters solely based on collected aerodynamic information. To further validate the performance of the flexible sensing patch, the wing model was tested in a wind tunnel under controlled conditions (Fig. S6). The AOA was adjustable within a range of ±10°, while the AOS was set to 0°, 2°, 4°, and 6°, respectively. The airspeed was controlled by the wind tunnel and set to 10, 15, 20, 25, 30, and 35 m s−1. The real-time outputs variation of the pressure sensor for incident flow velocities of 10 m s−1 and 35 m s−1 are shown in Fig. 4a, b, respectively, and data for other operating conditions can be found in Fig. S7. The data were divided into testing and prediction groups based on operating conditions (Fig. 4c). The testing group included twenty datasets for calibration of the predicted AOA (αe) and the position error calibration parameter (ε), while the prediction group comprised four datasets that were used to evaluate solution accuracy.

Fig. 4: Flight parameter calculation in the wind tunnel.
figure 4

a Real-time variation signals of ΔC at 10 m s−1 velocity; b real-time variation signals of ΔC at 35 m s−1 velocity; c Predicting group and testing group setting; d fitted curves of the αe; e fitted curves of the ε.

Full size image

According to Equation (S1, S2), the capacitance outputs of the sensors were converted into pressure differences. As described earlier, the pressures at Sp1 and Sp2 are denoted as P1 and P2, respectively, while the reference pressure is denoted as P0. Therefore, the pressure differences for the two sensors are: P01 = P0–P1 and P02 = P2–P0. Here, P01 can be directly measured by Sp1, the other two pressure differences can be calculated as P12 = P02–P01 and P20 = P2–P0. After performing these calculations, all three differential pressures were obtained. By averaging the signal output of each segment, the test results were obtained, showing the variation of three differential pressure values (P01, P12, and P20) with AOA under different V∞ and AOS (Fig. S8). Simultaneously, the average signal from the flow velocity sensor during testing was substituted into the flow velocity calibration equation (S3) to calculate the Vz at different V∞ and AOS (Fig. S9).

The fitting and calibration of the predicted AOA (αe) and position error calibration parameter (ε) were performed using the differential pressure values (P01, P12, and P20) from the testing group datasets. The datasets were first substituted into the triples algorithm to solve for αe. Considering the influence of δα, the αe is fitted to the actual AOA for computational convenience (Fig. 4d). In subsequent calculations, the αe is substituted into the fitting equation to determine the actual AOA. Next, the actual AOA, AOS (0°), and the normal component of the airspeed (Vxy) were substituted into the pressure distribution equation to solve for the ε (Fig. 4e). The fitted curves of the αe and the ε were found to depend primarily on the AOA, with minimal influence from AOS and airspeed, which was consistent with the simulation results.

The prediction group datasets were then substituted into the analytical PVF algorithm, and the calculated values of AOA, AOS, and V∞ were obtained using the fitting equation (S4, S5) of the αe and the ε (Fig. 5a–c). To verify the effect of the flexible sensing patch and the accuracy of the algorithm, the calculated results are compared with the actual input values (Fig. 5d). The average AOA solution error was 0.22°, and the maximum AOA solution error was less than 0.60°. The average AOS and airspeed solution errors were 0.35° and 0.73 m s−1, respectively. The maximum solution error for V∞ was relatively noticeable, occurring at an AOA of 10°. This was attributed to fluctuations in the sensor output signal at this angle, which reduces the accuracy. Such fluctuations are believed to be caused by sensor chattering at an AOA of 10°. Table S2 summarizes relevant studies on sensor arrays for UAVs, highlighting more predictive parameters and leading predictive accuracy demonstrated in this study.

Fig. 5: Evaluation results of flight parameters.
figure 5

a AOA solution results; b AOS solution results; c Airspeed solution results; d Solution errors. SC1, SC2, SC3, and SC4 represent four distinct input conditions, corresponding to 20 m s−1 AOS 6°, 25 m s−1 AOS 0°, 30 m s−1 AOS 4°, and 35 m s−1 AOS 0°, respectively.

Full size image

Discussion

We developed an ultrathin, flexible sensing patch featuring a dual-layer flexible capacitive differential pressure sensor and designed an analytical PVF algorithm for enhanced flight parameter estimation. Within a pressure range of ±1.0 kPa, the proposed flexible sensing patch exhibits high sensitivity (2.0 × 10² fF/Pa), high resolution (0.14 Pa), and high precision, with average errors of 0.22° for the AOA, 0.35° for the AOS, and 0.73 m s−1 for airspeed. The proposed analytical PVF algorithm enables fast and direct decoupling of the AOA and AOS using an analytical approach. These outstanding features highlight the potential for practical application of the flexible sensing patch and the analytical PVF algorithm in UAVs flight parameter estimation.

The dual-layer flexible differential structure of the pressure sensor underpins its high performance. By exploiting the opposing capacitance changes in the upper and lower pressure chambers, the sensor’s sensitivity is significantly enhanced through differential processing, while maintaining linear output across both positive and negative pressure differences. The pressure values provided by the sensor correspond to the pressure differential between the two measurement holes, and the small diameter of these holes allows for precise localization of the sensor’s pressure measurement points without compromising sensitivity. In addition, the encapsulation design of the measurement holes ensures high sensitivity while minimizing system errors during atmospheric parameter calculations using analytical methods. The analytical PVF algorithm offers a novel framework for high-precision UAV flight parameter estimation using the flexible sensing patch. By introducing the concept of spanwise velocity and integrating data from two pressure differential sensors and one vector flow velocity sensor, the algorithm successfully decouples AOA and AOS with minimal computational requirements, as validated through both CFD simulations and wind tunnel experiments.

In conclusion, this study presents an ultrathin, fully flexible sensing patch that integrates differential pressure and vector flow velocity sensors. By utilizing the analytical PVF algorithm, the flexible sensing patch enables high-accuracy estimation of flight parameters. This work provides a promising strategy for the design and analytical methodology of flexible multi-parameter integrated sensors, expanding the application of MEMS-based flexible skins in distributed atmospheric parameter sensing systems. In future work, we will develop a dedicated data acquisition system with a suitable capacitance-to-voltage converter and real-time microcontroller interface for flight tests. What’s more, to further reduce the effects of vibration, optimized vibration isolation structures and improved sensor layout will be adopted.

Methods

Fabrication of the flexible sensing patch

The fabrication process of the sensor array can be divided into four main steps (the process flow is illustrated in Fig. S1): preparation of the central sensing thin-film, bonding of the lower pressure chambers and microchannels, bonding of the top pressure chambers, and integration of the flow velocity sensors.

The central sensor thin film was fabricated first. The PI precursor solution was spin-coated at 8000 rpm for 60 s on the COP layer and then prebaked at 150 °C on a hot plate for 10 min to remove the organic solvent, after which the PI film was fully cured at 280 °C on a hot plate under ambient conditions for 30 min to form to form a 1.50 μm thick PI film. A lift-off process was employed to form electrodes and resistive heater metal layers (Cr/Au; 30 nm/60 nm). A layer of PI with the same thickness was then spin-coated onto the electrodes.

AD hot melt adhesive with a melting point of 180 °C was used as the bonding layer, and a 25-μm-thick PI film was selected as the substrate. The microchannel layer was made from PI film with AD adhesive on both sides (PI/AD adhesive; 60 μm/20 μm), and a hollow structure for the microchannels was formed via laser etching. FPC2 had AD adhesive (10 μm) on the top surface, while FPC1 had AD adhesive (10 μm) on the bottom surface, with the pressure chamber structure machined by mechanical milling. The PI substrate, microchannel layer, FPC2, and PI film were aligned and vacuum heat-pressed together at 5.0 Pa pressure, 0.10 MPa bonding pressure, 200 °C for 30 minutes, and then naturally cooled to room temperature, followed by device detachment from the silicon wafer. The device was then bonded to FPC1 using the same method, and the flow rate sensor was attached to the device, connected to FPC2 via a flexible flat cable.

CFD simulation analysis

Simulation analysis of the model was conducted utilizing the finite element method. To simulate the variation of the AOA while simplifying the workload, a user-defined function (UDF) was employed. With both the wing model and computational domain remaining stationary, the UDF controlled the inlet flow direction to change with time, thereby simulating the variation in the AOA. The fluid computational domain combined a hemisphere and a cylinder, which facilitated changes in the inflow angle. Both the spherical and cylindrical surfaces of the computational domain were set as velocity inlets, with inlet velocity and direction defined through the UDF, and the bottom surface set as a pressure outlet. The Apalart-Allmaras turbulence model was used for the solution. Under each operating condition, the AOA varied from −20° to 20°, with a 0.10° change at each step, totaling 400 steps. The pressure and velocity distribution at three pressure measurement points along the wing’s leading edge were collected during the simulation. Due to the presence of the boundary layer, the spanwise flow velocity was extracted at a location 1 mm from the surface.

Sensor characterization and wind tunnel tests

Sensor calibration was performed using a differential pressure calibrator (ConST811A, ConST, CN), connecting its output to the pressure ports of the flexible sensing patch via tubing, with the pressure controller’s output serving as the internal reference. Atmospheric pressure was applied to the external sensors, and calibration was achieved by adjusting the reference pressure. A wing model with a NACA0024 airfoil was 3D printed, and an internal two-axis rotating platform, connected to a micro-motion stage, adjusted the AOA and AOS. Due to wind tunnel size constraints, the trailing edge was omitted, causing slight changes in the airfoil shape, which affected the pressure coefficient and AOA correction but did not influence the atmospheric parameter calculations. The performance of the flexible sensing patch was characterized using a desktop wind tunnel (WT4401-D, OMEGA, USA). The flexible sensing patch was attached to the leading edge of a wing for AOA, AOS, and flow velocity estimation. The capacitance changes of the pressure sensor were measured using an LCR meter (IM3536, HIOKI, JP). The output signal of the flow velocity sensor was input into a DAQ card (USB-6366, NI) through a differential amplifier circuit, acquired by the host computer, and then subjected to 5.0 Hz low-pass digital filtering.