Mechanically stable, and reversible integration of microchips on textile: liquid metal-based anisotropic conductive adhesive

Abstract

Integrating surface-mounted devices (SMDs) onto textiles remains a key challenge in wearable electronics due to textile surface irregularities and heat sensitivity. Conventional methods like soldering or anisotropic conductive films (ACFs) often fail in such environments. We introduce a low-stress anisotropic conductive adhesive (LS-ACA) composed of eutectic gallium–indium (EGaIn) liquid metal particles (LMPs) embedded in a pressure-sensitive SIS matrix. LS-ACA offers excellent electrical conductivity, mechanical flexibility, and durability under bending, stretching, and crumpling. Finite element analysis shows it reduces interfacial stress concentrations compared to soldering, maintaining uniform stress even under 10% strain. It achieves ultra-low contact resistance (1.5 mΩ at >64 wt% LMPs) and enables low-temperature bonding on diverse substrates. Moreover, LS-ACA supports over 10 reuse cycles without surface damage or performance loss. This scalable, reusable material offers a promising path for integrating electronics into fabrics, advancing sustainable and flexible wearable technologies.

Introduction

The advancement of electronic textiles incorporated with stretchable electrodes and embedded sensors is revolutionizing the field of wearable healthcare¹. This technology combines electronic functionality with the flexibility of textiles by directly integrating electronic circuits into fabric², overcoming current limitations in flexible and wearable electronics. For instance, Zhuang et al. proposed a circuit integration method using multilayered liquid metal interconnects on a textured electronic skin³. However, integrating rigid and bulky surface-mounted devices (SMDs), currently available devices such as sensors and microchips, onto a fabric remains a significant technical challenge. This integration presents unique challenges due to the inherent characteristics of textiles. Unlike rigid printed circuit boards, textiles are highly sensitive to heat, making conventional methods such as soldering—which requires processing temperatures above 200 °C—or anisotropic conductive films (ACFs), which require temperatures of 150–200 °C and several MPa of pressure, are ineffective. Fabrics made of cotton or synthetic fibers tend to deform, melt, or shrink under high temperatures, leading to structural damage. In addition, ACFs often require precise alignment between the device and substrate, which can be particularly challenging on uneven textile surfaces, leading to poor contact or electrical failure^4,5,6,7. Textiles also have irregular surfaces, making them especially vulnerable to mechanical stimuli such as bending and stretching. Therefore, innovative approaches are required to ensure reliable bonding of SMDs to textiles.

One approach developed to overcome these issues is the use of anisotropic conductive adhesives (ACAs)⁸. ACAs are polymeric adhesives embedded with conductive fillers that provide vertical interconnection while maintaining lateral insulation. In our previous work, we developed a nanoscale dewetting-based ACA formulation using a UV-curable adhesive containing indium (In) particles, which enabled the room-temperature electrical connection of over 10,000 micro-pitch LEDs without short circuits⁹. However, these metallic particles possess a high elastic modulus, which presents challenges when applied to flexible or uneven surfaces such as textiles. Rigid particles can lead to contact failures due to mechanical stress on flexible substrates, and these problems become more pronounced on soft textile surfaces. A promising alternative ACA formulation involves the use of liquid metal particles (LMPs). In particular, eutectic gallium-indium (EGaIn) exhibits a low elastic modulus and adapts well to mechanical deformation, making it ideal for soft and flexible surfaces like fabrics. Recent studies have shown that the interaction between LMPs and adhesives harnesses the fluidic nature of the LM droplets, enhancing the material’s mechanical compliance and stability, enabling controllable electrical conductivity and repeatable adhesive characteristics^10,11. Furthermore, LMPs can form metallic alloys with other metals even at low temperatures, enabling low-temperature electrical bonding. This is crucial for preventing thermal damage in heat-sensitive textiles. Despite the low processing temperature, LMPs provide robust electrical connections, ensuring high reliability in flexible electronic devices.

Here, we introduce an all-soft, low-stress anisotropic conductive adhesive (LS-ACA) representing a significant advancement over traditional soldering processes and conventional ACF, effectively addressing challenges in flexible and textile-based electronics. As the LS-ACA, composed of LMPs and pressure-sensitive adhesive (PSA) polymer, specifically polystyrene-block-polyisoprene-block-polystyrene (SIS), is easily deformed and placed on uneven surfaces, it enables low-pressure/temperature processes for vertical interconnect on arbitrary substrates. Owing to the intrinsic nature of LM, integrating LMPs into the polymer significantly reduces the elastic modulus of the LS-ACA, and allows it to maintain stable and reliable electrical connections even under large deformations. This property contributes directly to improved stress management at the interface. Finite element analysis (FEA) simulation confirms that LS-ACA effectively mitigates stress concentration at the interface between electronic devices and fabric substrates, compared to conventional soldering, enabling more uniform stress distribution under mechanical strain. This capability is particularly critical for applications exposed to mechanical stresses, such as bending, stretching, and crumpling, ensuring consistent performance under dynamic conditions. In addition to its mechanical adaptability, the LS-ACA leverages the unique electrical properties of LM to form metallic alloys with electrodes like copper at low temperatures, including ambient conditions. This enables ultra-low contact resistance, with values reaching 1.5 mΩ at LMP concentrations exceeding 64 wt%, as measured using 4-point Kelvin circuits. Furthermore, LS-ACA offers exceptional functionality of a PSA, which enables reliable adhesion and easy detachment. Also, it is reattached without causing surface damage or leaving residues. This unique feature ensures LS-ACA maintains stable resistance even after more than 10 times reuse cycles on PCBs integrated with mobile integrated circuit (IC) and SMD chips, demonstrating its reliability and durability. Such reusability simplifies assembly processes, reduces waste, and supports cost-effective manufacturing, positioning LS-ACA as a sustainable solution for modern electronics. With superior mechanical and electrical stability for vertical interconnection via LM on textile, it can offer a robust and versatile approach to meeting the demands of flexible and wearable electronics.

Results

Low elastic modulus property of LS-ACA for stable electrical connections

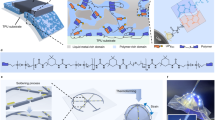
Figure 1a illustrates an assembly procedure in a microchip printing on a textile using the LS-ACA. The LS-ACA has a polymeric adhesive (sky blue) and LMP (black dots, average diameter: 1.7 μm) was coated on a piece of fabric with pre-defined electrodes. A modified mask-aligner transferred a microchip onto the LS-ACA with gentle pressure (less than 1 bar). Under the pressure load, the LMPs randomly dispersed in the LS-ACA are subjected to pressure from the upper and lower electrodes. As shown in the scanning electron microscope (SEM, bottom) image in Fig. 1b, the LMPs, due to their low elastic modulus, were easily deformed between the electrodes, forming vertical electrical pathways. The LS-ACA provides stable electrical connections even on uneven surfaces like fabric. As shown in Fig. 1c, LS-ACA successfully attaches LEDs to fabric surfaces without losing its anisotropic conductive property. The LEDs attached on the fabric using LS-ACA exhibit the same level of I/V (current/voltage) characteristic (green) compared to silver paste-based (gray) interconnection (Fig. 1d). As demonstrated by the I–V curve, LS-ACA exhibits a stable contact resistance, showing a resistance level comparable to that of commercially available silver paste, which is known for its typically low contact resistance.

Fig. 1: Overview and analysis of low-stress anisotropic conductive adhesive (LS-ACA) using SIS block copolymer and liquid metal particles (LMPs) for flexible and uneven substrates.

a Schematic illustrations explain how LS-ACA to be used on fabric substrates. b Schematics and SEM images of LMPs between the upper and bottom electrodes. c Red-green-blue (RGB) LEDs with different sizes connected by LS-ACA on a cotton fabric. d The I/V curve data of the LEDs on fabric in (c). When electrically connected using either reference (silver paste) or LS-ACA, there is no notable difference in electrical resistance. Since silver paste has a low contact resistance of less than 1 mΩ, LS-ACA also exhibits a similar level of performance. e Schematic illustration of a micro-LED electrically bonded to fabric using either solder or LS-ACA, along with finite element analysis (FEA) results under 5% and 10% tensile strain conditions using a cohesive zone model (CZM). The simulation results show that no interfacial failure occurred under 10% stretching, and the bonds are maintained. A comparison of the normalized stress distributions reveals that the soldered configuration exhibits localized stress concentrations in both the fabric and the LED pad, whereas the LS-ACA structure demonstrates a more uniform stress distribution. This difference is attributed to the fact that the interfacial bonding area between LS-ACA and the fabric is ~33% larger than that of the soldered configuration, making the LS-ACA structure more effective in stress dispersion. f, g Normalized stress profile graphs along the a–a′ cross-section shown in (e). The soldered joint clearly exhibits higher stress levels in the fabric and the LED pad compared to the LS-ACA case. This indicates that, in contrast, the LS-ACA connection can alleviate stress in adjacent elements through its relative deformability. For quantitative comparison, the average deviation of normalized stress values from a reference median (0.3) is calculated across the a–a′ cross-section. Under 5% strain, the average deviation is 47.7% for the LS-ACA structure and 66.2% for the soldered joint. At 10% strain, these values are 33.4% and 63.7%, respectively. These metrics show the stress distribution uniformity achieved with the LS-ACA connection compared to the soldering. h Bending, stretching, and clumping test of LEDs on fabric.

Figure 1e shows a schematic illustration and simulation result of a LED electrically bonded to fabric using either solder (upper) or LS-ACA (bottom), along with FEA results under 5% (middle) and 10% (right) tensile strain conditions using a cohesive zone model (CZM)¹². In this CZM-based FEA, the results are highly dependent on the cohesive parameters, making it essential to determine parameters that accurately reflect the experimental data¹³. In this study, the cohesive parameters are inversely estimated using a peel test of LS-ACA, and the obtained parameters are applied to FEA simulations. Figure 1e shows a comparison of the normalized stress distributions, indicating the soldered configuration (upper) results in localized stress concentrations within both the fabric and the LED pad. In contrast, the LS-ACA bonded structure (bottom) exhibits a more uniform stress distribution across the interface. This improvement is primarily attributed to the ~33% larger bonding area between the LS-ACA and the fabric compared to that of the solder joint. Also, this is closely related to the elastic modulus property of LS-ACA. The elastic modulus and conductivity of each component are presented in Supplementary Fig. S1. The area indicated by the blue arrow represents the elastic modulus range of LS-ACA. Even after full curing, the pristine PSA (Supplementary Fig. S1, brown dot), which exhibits a semi-solid characteristic between solid and liquid states, and the EGaIn (Supplementary Fig. S1, red dot) both maintain a low elastic modulus below 10⁻³ GPa. This allows LS-ACA to achieve a low elastic modulus compared to conventional electrical interconnection technologies. This suggests that the LS-ACA structure is more effective in stress dispersion. Figure 1f, g shows the normalized stress distribution of the soldered structure and LS-ACA measured along the a–a′ cross-section indicated in Fig. 1e. In the solder configuration (Fig. 1f), larger stress level is observed in both the fabric and the LED pad, whereas the LS-ACA bonded structure (Fig. 1g) exhibits a much lower stress distribution across the same region. For quantitative comparison, the average deviation of the normalized stress values from the reference median value (0.3) is calculated along the a–a′ line. At 5% strain, the LS-ACA structure shows an average deviation of 47.7%, while the soldered structure shows 66.2%. At 10% strain, the deviations are 33.4% for LS-ACA and 63.7% for the solder joint. These results confirm that LS-ACA enables a more balanced stress distribution across the fabric and the LED pad, providing a more stable and reliable electrical interconnection under stretching conditions than conventional soldering. Supplementary Fig. S2 demonstrates that under a bending condition with a curvature of 2 mm, LS-ACA exhibits a more uniform stress distribution across both the fabric and the LED pad compared to the soldering. Figure 1h demonstrates bending, stretching, and crumping tests. Owing to the low elastic modulus characteristic of LS-ACA, it effectively maintains stable electrical connections between LEDs and uneven surfaces such as fabric. As shown in Supplementary Fig. S3, we perform cyclic bending and stretching tests after bonding an LED onto the fabric using LS-ACA. The bending test is conducted with a 5 mm bending radius for 2500 cycles, and the electrical resistance is measured every 500 cycles by recording current and voltage. No change in resistance is observed throughout the 2500 bending cycles, confirming the electrical stability of LS-ACA. A 10% strain stretching test is also conducted for 2500 cycles, and similar to the bending test, no significant change in resistance is observed, indicating that LS-ACA maintained stable adhesion under repeated deformation.

Metallic alloy of LS-ACA with Cu electrodes

Conventional soldering techniques involve heating the solder to its melting point, causing the metal on the electrode surface to react with the solder and form an intermetallic layer. This layer is crucial for bonding the solder to the electrode, decreasing contact resistance in electrical connections by enhancing chemical and mechanical stabilities. However, this process typically requires temperatures exceeding 200 °C (i.e. SAC305’s melting point ~220 °C), which can cause thermal deformation and damage to the fabric substrates. In contrast, LM reacts with metals at room temperature without additional heat treatment to form an alloy. Figure 2a, b illustrates a schematic of the metallic alloy formation process between LS-ACA and the Cu electrode. First, LS-ACA is coated onto a Cu electrode pretreated with NaOH to remove the surface oxide layer, and compressed using an upper Cu electrode (Fig. 2a). During this process, the oxide layer (Ga₂O₃) surrounding the LMP breaks, allowing the EGaIn to contact the Cu electrode. At room temperature, EGaIn, which exhibits high reactivity with solid metals^14,15, reacts with the Cu electrode to form a Cu_xGa_y alloy, while some In components from EGaIn were extracted (Fig. 2b). The extraction of In during the formation of Cu_xGa_y alloy can be explained by mixing enthalpy. The mixing enthalpy represents the energy change that occurs when two different elements combine, reflecting the attraction and repulsion forces between atoms. A lower mixing enthalpy indicates that the elements can bond more easily, whereas a higher value implies difficulty in bonding or a dominance of repulsive forces. In the reaction between Cu and EGaIn, the mixing enthalpy of Cu and Ga is as low as 1 kJ mol⁻¹, resulting in a strong attraction between the two elements that facilitates the formation of the Cu_xGa_y alloy¹⁶. In contrast, the mixing enthalpy of Cu and In is 10 kJ mol⁻¹, making their bonding significantly less favorable, leading to the precipitation and separation of In. Additionally, the mixing enthalpy of Ga and In is 3 kJ mol⁻¹, which does not hinder the formation of the Cu_xGa_y alloy but instead contributes to its stability¹⁶. Therefore, the difference in mixing enthalpy values explains the preferential formation of the Cu_xGa_y alloy and the subsequent precipitation of In. This mixing enthalpy-based energy analysis systematically elucidates the reaction mechanism and alloy formation process between Cu and EGaIn¹⁶. After removing the upper electrode and selectively washing away the adhesive with acetone, we elucidated the surface as shown in Fig. 2c. Figure 2d provides a magnified SEM image of the dashed region from the Fig. 2c. By energy dispersive X-ray spectroscopy (EDS), the dashed region a Cu_xGa_y alloy composed of Cu (purple) and Ga (yellow), with both elements appearing in the same phase. In contrast, extracted In (orange) remains in a separate phase. Supplementary Fig. S4 compares EDS images of LMPs subjected to pressure from the Cu electrode (Supplementary Fig. S3a) and left unpressed (Supplementary Fig. S3b), showing that unalloyed LMPs contain Ga and In in the same phase while Cu remains in a separated phase. This confirms that LMPs compressed by the electrode undergo metallic alloy formation with Cu. Figure 2e presents X-ray diffraction (XRD) data, showing the formation of CuGa₂ (purple dot) and Cu₉Ga₄ (green triangle) on the Cu surface (blue pentagon). Cu₉Ga₄, formed during the alloying process or under copper-rich conditions, serves as an intermediate phase that eventually transforms into CuGa₂ when sufficient Ga is supplied¹⁷. The intensity of the Cu₉Ga₄ peak is lower than one of CuGa₂, indicating its intermediate nature. Figure 2f provides X-ray photoelectron spectroscopy (XPS) results, further confirming the reaction between LMPs and the Cu electrode. This metallic alloy formation enhances both the electrical and mechanical performance of LS-ACA when used as an electrical interconnection material.

Fig. 2: Metallic alloy of the LS-ACA and Cu electrode.

a, b Schematic illustration of the procedure for alloy formation between LMPs and Cu electrodes. When LS-ACA is placed between Cu electrodes and subjected to compression, the Ga₂O₃ layer breaks under pressure, enabling internal EGaIn to react with Cu and form an alloy. Upon completion of the alloy formation, Cu and Ga react to produce Cu_xGa_y (gray), while the unalloyed In (orange) is separated. c Tilted SEM image showing the formation of a Cu_xGa_y alloys on the Cu electrodes after washing out adhesive and non-alloyed LM particles. The upper-right inset shows a schematic illustration of alloyed LMPs remaining on the Cu electrode highlighting the alloyed Cu_xGa_y (gray) and the separated In (orange). d Magnified SEM image of the region highlighted in the green dash in (c). Energy dispersive X-ray spectroscopy analysis indicating that Ga and Cu are part of the same phase, while unalloyed In remains in a separate phase. e X-ray diffraction data confirming the formation of the CuGa₂ (purple dot) and Cu₉Ga₄ (green triangle) alloy. f X-ray photoelectron spectroscopy data further supporting alloy formation.

Uniformity and distribution of LM Particles

Figure 3a and Supplementary Fig. S5 show top and cross-sectional SEM images of LS-ACA with increasing LM concentrations. At low LM (LLM, 64.3 wt%) concentrations, the LMPs size remains small and uniformly dispersed. However, as LM concentration increases at high LM (HLM, 90.0 wt%) concentrations, aggregation of LMPs occurs within the adhesive, forming diverse sizes of LMPs. The LMP formation process in LS-ACA is as follows: when high-frequency ultrasonics are applied, LM droplets are formed within the adhesive and solvent, and the interfacial force between the adhesive and the LM generates shear at the boundary, inducing the formation of smaller droplets from the surface of the LM droplets¹⁸. After the sonication is done, the individually suspended LMPs can collide and merge together, and eventually determine their size. Figure 3b illustrates the distribution of particle size depending on LM concentrations. Due to the high density of EGaIn (6.28 g ml⁻¹) compared to the SIS (0.92 g ml⁻¹), the weight fraction of LM is significantly higher than its volume fraction. At a lower concentration of LM (64.3 wt%), the distribution of the LMP’s sizes is very narrow. On the other hand, high concentration has diverse sizes of particles. We believe that a high concentration of LM allows to have particle-particle coalescence and merges into bigger particles as shown in Supplementary Fig. S6. Such a big particle and the uncontrollable particle size of LM usually cause electrical failure. Thus, it determines the minimum feature size of electrodes and theoretically prevents lateral conduction between fine-pitched terminals. To evaluate lateral conduction, Fig. 3c illustrates the insulating properties of LS-ACA with varying LM concentrations between two microelectrode gaps. LLM, containing LMPs smaller than 5 μm that are uniformly distributed, maintains electrical insulation even at a gap of 6.6 μm. In contrast, the HLM condition leads to lateral conduction due to the formation of larger, aggregated LMPs. When the LM concentration is below 64.3 wt% (20.9 vol%), all LMPs remain below 5 μm. However, at concentrations above 75 wt% (30.6 vol%), LMPs exceeding 5 μm are observed. Such large LMPs are capable of bridging gaps smaller than 6.6 μm, thereby compromising lateral insulation. The LMP dispersion characteristics of LS-ACA over a large area are presented in Fig. 3d, when spin-cast. As shown in Supplementary Fig. S7, the number of particles is quantified using ImageJ software based on SEM images of an 80 × 60 μm area for both LLM and HLM conditions. In this area, 56 ea LMPs with an average size of 1.7 μm are observed for LLM, while 156 LMPs with an average size of 3.8 μm are observed for HLM. These results indicate that HLM exhibits approximately three times the particle density of LLM within the same area. Figure 3e, f shows the analysis of center-to-center distances between LMPs (green bars) and their diameter distributions (graphs) in both LLM and HLM conditions, conducted using ImageJ. Based on the diameter distribution and center-to-center distance data, the LLM condition suggests a lower probability of particle merging or aggregation. In LLM, the minimum measured center-to-center distance is 6.3 μm, and the largest particle diameter is 4.0 μm. From these values, the minimum edge-to-edge distance is calculated to be ~2.3 μm, indicating sufficient spacing between particles that reduces the likelihood of merging or aggregation. Additionally, 90% of LMPs are smaller than 3.3 μm in diameter, further supporting the presence of a well-dispersed and stable particle distribution. In contrast, under the HLM condition, the minimum center-to-center distance is 1.7 μm, while the largest particle diameter reaches 7.1 μm, and 90% of particles are smaller than 6.1 μm. In this case, the edge-to-edge distance can fall below 0 μm, meaning that particles may physically overlap or be in contact. This significantly increases the likelihood of particle merging and aggregation, potentially forming larger LMPs and raising the risk of lateral conduction under narrow electrode gap conditions.

Fig. 3: Particle size distribution and sedimentation dynamics in LS-ACA.

a SEM image of LS-ACA with low (LLM, 64.3 wt%) and high (HLM, 90.0 wt%) concentrations of LMPs. b Size distribution curves of LMPs according to LM concentration. c Measured lateral resistances between two microelectrodes with various gap widths (ranging from 6.6 to 26.4 μm) using low (LLM) and high (HLM)-concentration LMPs in LS-ACA. The inset images show that for LLM, LMPs with an average size of 1.7 μm are too small to bridge a 6.6 μm electrode gap, thus maintaining lateral insulation. In contrast, in the HLM condition, LMPs exceeding 6.6 μm form conductive bridges across the gap, resulting in lateral conduction. d SEM images of large-area high-concentration (HLM) and low-concentration (LLM) LS-ACA. To measure the number of particles, the images are processed using ImageJ software. The images are modified so that only particles with a size of 1 μm or larger are counted. e, f The red numbers in (d) (right), indicating particle counts analyzed via ImageJ, are assumed to represent the centers of the particles. All possible combinations of the detected center coordinates are used to calculate center-to-center distances. The measured distances are then visualized in the form of a histogram. g–i Comparison of theoretical and experimental particle size distributions of low concentration (37.5 wt%), LLM (64.3 wt%) and HLM (90.0 wt%). LMP sizes in LS-ACA are measured at different time points: immediately after fabrication (0 days), after 7 days and 14 days. The number of particles used for plotting the dispersion graph is as follows: 0 days (low concentration: n = 30, LLM: n = 30 and HLM: n = 30), 7 days (low concentration: n = 30, LLM: n = 25 and HLM: n = 9), and 14 days (low concentration: n = 27, LLM: n = 16 and HLM: n = 4), indicating a gradual decrease in the number of LMPs over time due to sedimentation.

To maintain the electrical stability of LS-ACA over time, the size and distribution of LMPs must remain consistent during storage, before curing. Since the LS-ACA cures as the solvent evaporates, LMPs movement and sedimentation no longer occur once it has solidified. Therefore, sedimentation behavior should be analyzed in the pre-cured state. If the LMPs settle slowly during this stage, it indicates good dispersion stability, which in turn enables reliable electrical connections. In short, a slower sedimentation rate means that the LMPs remain well-dispersed during storage, making it a key indicator for evaluating the overall reliability of LS-ACA. First, as shown in Supplementary Fig. S8, the forces acting on the LMPs can be divided into three components. By applying Newton’s second law, we obtain the following equation:

$$m\frac{{dv}}{{dt}}={F}_{g}-{F}_{b}-{F}_{d}$$

(1)

where $m$ is the mass of the LMP, $v$ is the sedimentation velocity of the particle, ${F}_{g}$ is the gravitational force acting on the LMP, ${F}_{b}$ is the buoyant force, and ${F}_{d}$ is the drag force due to viscosity. Supplementary Table S1 summarizes the density and viscosity data for the adhesive, which is prepared by diluting SIS with toluene. The adhesive used for LS-ACA fabrication, with a SIS/toluene mass ratio of 1:2, has a density of approximately 0.88 g ml⁻¹ and a viscosity of 19.6 Pa·s at room temperature. Based on these properties, Reynolds number calculations for different particle sizes in Supplementary Table S2 show that for LMPs smaller than 10 μm, all values are significantly less than 1, confirming that the drag force (${F}_{d}$) acting on LMPs satisfies the conditions for Stokes’ law^19,20. Rearranging Eq. (1) under this assumption, we obtain

$$\frac{4}{3}\pi {r}^{3}{\rho }_{e}\frac{{dv}}{{dt}}=\frac{4}{3}\pi {r}^{3}({\rho }_{e}-{\rho }_{a})g-6\pi \eta {rv}$$

(2)

where $g$ is gravity (9.8 m s⁻²), $r$ is the radius of the LMP, ${\rho }_{e}$ is the density of EGaIn, ${\rho }_{a}$ is the density of the adhesive, and $\eta$ is the viscosity of the adhesive. Following the derivation process detailed in Supplementary Description S1, the final equation for the sedimentation velocity of LMPs in LS-ACA is given by

$$v=\frac{g{D}^{2}({\rho }_{e}-{\rho }_{a})}{18\eta }$$

(3)

LMP size ($D$, diameter) plays a crucial role in determining sedimentation velocity, as settling speed is proportional to the square of the particle size. Applying Eq. (3) to the average LLM particle size of 1.7 μm, the sedimentation velocity is calculated to be 0.4 nm s⁻¹, corresponding to a settling distance of ~260 μm over 7 days, indicating high dispersion stability within LS-ACA. This means that smaller particles have low settling velocity, and remain stably dispersed in LS-ACA for a longer period. To experimentally verify sedimentation velocity, SEM analysis is conducted at a depth of 0.5 mm from the surface at different time points: immediately after fabrication (0 days), after 7 days, and after 14 days (Supplementary Figs. S9 and S10). The analysis is performed for three different concentrations, and the initial average particle sizes for each condition are as follows: low concentration (37.5 wt%, average particle size = 1.2 μm), LLM (64.3 wt%, average particle size = 1.7 μm), and HLM (90.0 wt%, average particle size = 3.8 μm). The experimental method compares the theoretical and experimental particle size distributions at different time points: 0 days, after 7 days, and after 14 days. Initially, thirty individual LMPs are analyzed using SEM, and their respective sedimentation velocities are calculated. LMPs that are theoretically predicted to settle beyond 0.5 mm are excluded from the distribution at each time point, and the remaining LMPs are depicted by the green dashed line (7 days) and the blue dashed line (14 days). The experimentally analyzed LMPs are represented by the green solid line (7 days) and the blue solid line (14 days). To ensure a reliable analysis, particle size measurements are conducted by analyzing 10 separate SEM images, with each image contributing to an individual size distribution graph. As shown in Fig. 3g, in the case of low concentration of EGaIn, most of the LMPs with an average size of 1.2 μm do not theoretically settle beyond 0.5 mm even after 7 and 14 days, resulting in no change in the number of LMPs for both theoretical and experimental values. However, in the case of LLM (Fig. 3h), the number of LMPs theoretically decreases from 30 to 25 after 7 days and further decreases to 16 after 14 days due to sedimentation. The experimentally obtained particle size distributions are represented by the green solid line (7 days) and the blue solid line (14 days), which closely match the theoretical predictions, confirming the validity of the calculated sedimentation velocity equation. Finally, in the case of HLM (Fig. 3i), most of the LMPs are larger; out of the initial 30 particles, 16 particles remain after 7 days, and only 4 particles remain after 14 days, indicating that most of the particles have settled at the bottom of the vial (Supplementary Fig. S8). These results demonstrate that the theoretical model accurately predicts the sedimentation behavior of LMPs in LS-ACA.

Electrical properties of LS-ACA

Figure 4a presents a graph of the dielectric constant of LS-ACA across GHz frequency ranges and LM concentrations. The dielectric constant in the GHz range plays a crucial role in semiconductor packaging connections and wireless device applications. For LLM, where small LMPs below 5 μm are uniformly dispersed, the dielectric constant remains similar to that of pure adhesive, indicating minimal impact of LMPs on dielectric properties. In contrast, HLM exhibits a significant increase in dielectric constant, exceeding 10. This phenomenon suggests that in HLM, LMPs aggregation generates particles exceeding 5 μm, which then form conductive networks, potentially reducing the maximum voltage strength the material can withstand under an external electric field. However, the high dielectric constant of HLM decreases under compressive force. As explained in Fig. 4b, this phenomenon can be described using the parallel-plate capacitor model²¹. The opposing field (E_p), created by the vertical dipole polarization of micro-scale LMPs, weakens as the LMPs are compressed from spherical to ellipsoidal shapes. This reduction in E_p leads to an increase in E_net and ultimately reduces the effective dielectric constant (ε_eff). As shown in the graph in Fig. 4c, when LS-ACA is subjected to a compressive force of 8 kPa, the dielectric constant decreases. Pure adhesive exhibits an increase in dielectric constant under pressure, whereas both LLM and HLM exhibit decreases. Notably, HLM shows a significant reduction in dielectric constant compared to its pristine state. These results confirm that the parallel-plate capacitor model effectively describes the behavior of LS-ACA.

Fig. 4: Electrical properties of the LS-ACA.

a Dielectric constant as a function of frequency. The GHz range is suitable for frequency bands of semiconductor packaging or wireless devices. b Schematic illustration of the pressure effect on the dielectric constant in LS-ACA. Pressure causes geometrical deformation of LMPs, which alters the net electric field, leading to a reduction in dielectric constant. c Graph of dielectric constant in the presence of pressure as a LMP concentration. d Schematic illustration of the 4-point Kelvin circuit used to measure the contact resistance and lateral resistance of the LS-ACA. e Contact resistance and lateral resistance as a function of LM concentration. f I/V curves with micro-LED (200 × 100 μm) connections using LLM (green) and HLM (cyan) concentrations of LMPs and traditional soldering (gray).

Contact resistance is a critical factor in the field of electrical interconnection as it directly impacts the efficiency and reliability of electrical connections. The contact resistance of LS-ACA is measured using a 4-point Kelvin structure. Figure 4d provides a schematic illustrating the process of measuring LS-ACA’s contact resistance. First, LS-ACA is coated onto the circuit, and lateral resistance between two electrodes with a 120 μm gap is measured. Next, the upper circuit is pressed, and the contact resistance is measured using the 4-point method. When current is applied, the voltage is recorded at the point where the potential difference and measurement overlap, as indicated by the red arrow. Using the measured current and voltage, the resistance at the single contact area marked by the red arrow is accurately determined. The detailed circuit for the 4-point Kelvin structure is shown in Supplementary Fig. S11. Figure 4e illustrates the relationship between LM concentration, contact resistance, and lateral resistance. The measured contact area is 14,400 μm². When the LM concentration is below 64 wt%, contact resistance is significantly higher, likely due to insufficient LMPs establishing contact with the electrodes. When the concentration exceeds 64 wt%, the contact resistance reaches 1.5 mΩ, with no further reduction observed at higher concentrations. For lateral resistance, LS-ACA remains fully insulated laterally at a 120 μm microelectrode gap, regardless of LM concentration, maintaining high lateral resistance. To verify LS-ACA’s low contact resistance, Fig. 4f compares the I/V curves of micro-LEDs (200 × 100 μm) bonded to fPCB electrodes using LS-ACA and traditional soldering. Supplementary Fig. S12 shows SEM images of micro-LEDs bonded to fPCB using LS-ACA. The I/V characteristics indicate no significant difference in resistance between LS-ACA (LLM-green, HLM-cyan) and soldering (gray), demonstrating that LS-ACA achieves a contact resistance level comparable to eutectic solder (~1 mΩ). The optimal concentration of LS-ACA, as shown in the graph in Supplementary Fig. S13, is determined by balancing dispersion stability and electrical performance. At lower LM concentrations, particle sedimentation is reduced, and dispersion stability is high; however, contact resistance increases significantly. In contrast, higher LM concentrations lead to LM aggregation and the formation of LMPs larger than 8 In addition, the increased microns, resulting in poor dispersion stability and accelerated sedimentation. Therefore, LLM at 64.3 wt%, which provides both stable dispersion of LMPs and low contact resistance, is selected as the optimal condition from an application standpoint.

Mechanical properties of LS-ACA

LS-ACA provides strong adhesion, ensuring excellent mechanical stability under mechanical stresses such as bending and stretching, effectively preventing electrical disconnections or short circuits. To evaluate its adhesive performance, a 90° peel test is conducted as shown in Fig. 5a. A 25-mm-wide sample is pulled at a speed of 300 mm min⁻¹, and the adhesion energy on various substrates is presented in Fig. 5b. Adhesion energy, representing the resistance to detachment, is calculated by averaging data points from the plateau peel force regime in Supplementary Fig. S14. On smooth PET surfaces, HLM exhibits the highest adhesion energy, measured at 41.5 J m⁻². For Cu film, the adhesion energy increased significantly compared to PET, reaching an improved value of 464.6 J m⁻². For fabric, which is the primary focus of this study, the adhesion energy is the highest at 843.3 J m⁻². This result is attributed to the uneven surface of the fabric, allowing the low elastic modulus LS-ACA to conform better to the substrate, thereby increasing the effective contact area. For PET, Cu film, and fabric, LLM shows adhesion strength similar to pristine adhesive, but adhesion strength improved as the LM concentration increased. To analyze this improvement, storage (G’) and loss (G”) modulus measurement of adhesive, LLM, and HLM are performed over the temperature range of −50–150 °C, as shown in Fig. 5c. Pristine adhesive and LLM exhibit similar storage modulus values across the entire temperature range, indicating that LLM behaves mechanically similar to the adhesive due to its relatively low concentration of LMPs. This is because individual LMPs inherently possess a lower elastic modulus than the adhesiv matrix. However, when the concentration of LMPs increases significantly—as in HLM—these particles begin to form an internal mechanical network structure within the adhesive matrix²². This network leads to a notable increase in the storage modulus, particularly in the 25–45 °C range. In addition, the increased number of particles leads to a greater amount of oxide shells surrounding the LMPs, which further contributes to the increase in both the storage and loss moduli of LS-ACA. As shown in Supplementary Fig. S15, both the storage modulus (G′) and loss modulus (G″) of the fully cured samples increased with higher LM content. HLM exhibited the highest values across all frequencies, indicating a stiffer and more dissipative network than LLM or the pristine adhesive. This trend correlates with adhesion strength measurements: a slight increase from Adhesive to LLM, and a significant improvement in HLM. These results suggest that the enhanced elasticity and energy dissipation of the cured HLM contribute to improved interfacial adhesion and mechanical reliability.

Fig. 5: Mechanical characteristics of LS-ACA.

a Schematic illustration for peel test. The pulling speed is set to 300 mm min⁻¹, and the sample has a width of 25 mm. b Adhesion energy with various substrates and LS-ACAs (pristine adhesive, LLM, and HLM). c Storage (G’) and loss (G”) moduli of the LS-ACA as a function of temperature. The storage modulus is similar to that of the adhesive and LLM but increases with concentration increase. Photograph of turn-off (d) and turn-on (e) LEDs on a fabric. f Fabric surface of the electrode after mechanical removal of LEDs. g Photograph of a 3 × 3 micro-LED (200 × 100 μm) array adhered to a flexible PCB (fPCB) using LS-ACA. h Variations of operating voltage and light intensity of the micro-LED array at 5 mA current bias under varying curvature conditions. The insets show an enlarged view of data. i Mechanically durability test by applying 2500 repeated bending cycles with 5 mA current. The insets show an enlarged view of data.

Consequently, the HLM formulation cures into a stiffer structure compared to LLM, which enhances its resistance to interfacial deformation. This increased rigidity at the interface directly contributes to improved adhesion performance.

Additionally, LS-ACA demonstrates reversible adhesive properties. Composed of PSA, LS-ACA exhibits a semi-solid characteristic between solid and liquid states, allowing it to be cleanly removed without damaging the adhered surface. Furthermore, due to the strong adhesion between the adhesive and LMPs, the LMPs can also be removed along with the adhesive when detaching LS-ACA from the surface. To verify this reusability, functional mini-LEDs on fabric are used, as shown in Fig. 5d, e. The circuit on the fabric is fabricated by depositing Au, which has also been reported to effectively form an alloy with EGaIn at room temperature, resulting in the formation of AuIn₂^23,24. Therefore, similar to the case with Cu, we expect that alloy formation at the interface can lead to reduced contact resistance and enhanced interfacial performance. The process of detaching and reattaching the LEDs and LS-ACA for reuse is presented in Supplementary Movie S1. After removal, as shown in Fig. 5f, the electrodes remain clean and undamaged, confirming that the circuit can be reused. The reliability of LS-ACA is experimentally validated through bending and stretching cycle tests. As shown in Fig. 5g, nine micro-LEDs bonded to a PET-based fPCB remain stable and functional even when wrapped around a cylindrical rod with a radius of 1 mm. Furthermore, when the fPCB bends from a radius of 14 mm to 1 mm while applying a constant bias current of 5 mA, there are no changes in voltage or LED irradiance, confirming consistent resistance. Finally, during a 2500-cycle test involving curvature changes between 1.3 mm and 2.6 mm while applying a constant bias current of 5 mA, no variations in voltage or irradiance are observed, demonstrating highly stable adhesion. The experimental setup for the cycle test is detailed in Supplementary Fig. S16 and Supplementary Movie S2. This exceptional reliability is attributed to the low-modulus platform of LS-ACA, which is based on LMPs. The low elastic modulus effectively absorbs deformation energy generated during mechanical stress, maintaining both electrical and mechanical stability. The thermal stability of LS-ACA is further demonstrated in Supplementary Fig. S17. A fPCB connected to nine micro-LEDs is placed on a hot plate, and the temperature change of both the LS-ACA and the LEDs is monitored using an IR camera. As a result, it is confirmed that LS-ACA maintained a constant voltage under a bias current of 5 mA, even as the temperature increased from 30 °C to 150 °C, indicating no change in resistance.

Device integration on a fabric with LS-ACA

A simple strobe light-emitting circuit is fabricated using a commercial NE555 timer chip. The NE555 timer operates in free-running mode, continuously outputting rectangular waveforms with a specific frequency. As shown in Fig. 6a, the NE555 chip is adhered to an fPCB along with various surface-mounted devices (SMDs) using a stencil method. Figure 6b shows top-view image of the device. As depicted in Fig. 6c, the circuit is composed of a 10 μF capacitor, a 100 kΩ resistor (R1), and a second resistor (R2), operating at a frequency of 0.48 Hz. The signal frequency and duty cycle of this circuit are determined by the values of R1, R2, and C, and can be calculated using the formula: f = 1.44/(R1 + 2R2)·C. During the reusability process, circuit damage alters circuit resistance, resulting in a frequency shift. As shown in the last image of Fig. 6c, LS-ACA and SMD components are mechanically removed from the circuit without any damage, leaving the circuit cleanly restored. Supplementary Fig. S18 shows the SEM and EDS images of the area where the LS-ACA has been removed. The LS-ACA has been cleanly removed from the fPCB without leaving any residue. Furthermore, as demonstrated in Fig. 6d, even after 10 reuse cycles, the circuit maintains a consistent frequency of 0.48 Hz, confirming the absence of any resistance changes.

Fig. 6: Circuits demonstration with conventional microchips using the LS-ACA.

a Schematic illustration of 555 timer, various surface SMDs with the fPCB. b Photograph of the fabricated system. c Photograph of 555 timer system. The frequency is set to 0.48 Hz based on the circuit’s resistance and capacitance values, causing the LED to blink at this frequency. The last image shows the LS-ACA and SMD chips being removed cleanly from the circuit, leaving no damage or residue on electrode and substrate. d Graph showing no change in frequency after ten reuse tests of the fPCB. e Photograph of cloth-attached bluetooth low energy (BLE) device system integrating microdevices onto a fabric using LS-ACA. f Magnified image of the BLE device system. g Schematic illustration of BLE system attached to the human chest for real-time wireless skin temperature monitoring. h Photograph of a person measuring skin temperature with a BLE system attached. i Graph showing surface temperature measurements recorded wirelessly at minute intervals using a BLE device and infrared thermometer.

Figure 6e presents a cloth-based Bluetooth low energy (BLE) system integrating microdevices onto fabric using LS-ACA. As shown in Fig. 6f and Supplementary Fig. S19, the BLE system consists of a commercial BLE chip and SMD components bonded onto fabric using LS-ACA. When a power source is applied to both ends of the electrodes, the BLE chip on the fabric detects the skin temperature beneath the fabric and wirelessly transmits the data to a mobile device. Figure 6g, h shows a schematic illustration and photograph of a BLE system attached to the human chest. The person runs for 3 min, rests for 2 min, and measures the skin temperature at 1-minute intervals. Figure 6i presents a comparison between the skin temperature measurement system integrated with LS-ACA and a commercial infrared thermometer. The BLE device demonstrates equivalent temperature measurements to the infrared thermometer, confirming that the wireless system fabricated with LS-ACA functions successfully on fabric-based substrates.

Discussion

In this study, we introduce a LM-based microchip integration method for textile-based electronics. LS-ACA demonstrates seamless adaptation even on uneven surfaces like textiles while maintaining stable electrical connections under mechanical stresses. LS-ACA represents a significant advancement in flexible electronics, addressing existing challenges in integrating microchips components into textiles. With exceptional mechanical adaptability with low moduli, and low-temperature/pressure processing, the LS-ACA offers a promising platform for the next generation of wearable and textile-based electronic devices.

Methods

Materials and fabrication of low stress-ACA

The polymer adhesive consists of polystyrene-block-polyisoprene-block-polystyrene (SIS; styrene 14%, Sigma-Aldrich, USA) and toluene (anhydrous, 99.8%, Sigma-Aldrich, USA). SIS and toluene are mixed at a weight ratio of 1:2 and stirred for 24 h. The adhesive is mixed with eutectic gallium-indium (EGaIn; 75 wt% Ga and 25 wt% In) and processed using tip sonication at 75 W for 30 min. The LS-ACA is prepared by adjusting the ratio of EGaIn and SIS in weight percent.

Preparation of a fabric substrate and assembly of light-emitting diodes (LEDs), and mechanical cyclic testing

A 50-nm-thick Au is deposited onto the cotton fabric using vacuum sputtering (Q300TD, Quorum Technologies Inc.) with a patterned stencil mask. Afterward, the LEDs are manually attached to the LS-ACA-coated metal-patterned fabric or substrate. Bending and stretching cyclic tests are conducted using a universal testing machine (UTM).

Simulation for finite element analysis (FEA)

Commercial finite element analysis software, Abaqus is used for the analysis. The fabric surfaces are assumed to be a 2D plane with a sinusoidal pattern with a wavelength of 0.5 mm and an approximate amplitude of 0.03 mm with an elastic modulus of 3.7 GPa. For stress distribution analysis, specific material modulus values are applied: LED (E = 77.2 GPa, pad thickness = 0.07 mm, LED thickness = 0.35 mm), eutectic solder (E = 32.5 GPa, thickness = 0.1 mm), EGaIn particle (E = 0.01 MPa), indium particle (E = 10.8 GPa), conductive ball (E = 1.7 GPa), and SIS adhesive (E = 0.3 MPa). The size of all particles is assumed to be 5 μm. The total ACA thickness is set to 0.1 mm, with an assumed thickness of 0.01 mm between the fabric and the pad. The fabric substrate is subjected to ~10% and 5% strain.

Characteristics of the alloyed micro-particle

The two copper films are treated with 5 wt% NaOH to remove native oxides and then bonded using LS-ACA. Afterward, the bonded copper films are soaked in acetone and sonicated for 1 h to remove the adhesive. The alloyed micro-particles formed after adhesive removal are characterized by field-emission scanning microscopy (S-5000, Hitachi, Japan), energy dispersive X-ray spectroscopy (Ultim Max 65, Oxford Instrument, UK), X-ray photoelectron spectroscopy (NEXSA G2, UVP Inc., Germany), and X-ray diffraction (Smartlab, Rigaku, Japan).

Sedimentation dynamics in LS-ACA

To verify the sedimentation dynamics, LS-ACA samples are spin-coated onto a glass substrate at 2000 rpm for 30 s and subsequently cured at three different time points: immediately after fabrication, after 7 days, and after 14 days. In each case, the LS-ACA is collected from ~0.5 mm below the surface. SEM measurement is then performed to measure the size of the LMPs.

Fabrication of microelectrodes for short circuit test and mechanical test

Two microelectrodes are fabricated on a glass substrate using photolithography. First, 5-nm-thick Cr and 50-nm-thick Au are deposited onto a cleaned glass substrate using vacuum sputtering (Q300TD, Quorum Technologies Inc., USA). A positive photoresist (AZ5214, MicroChem. GmbH, Germany) is spin-coated at 4000 rpm for 30 s. The substrate is then exposed for 30 s using UV exposure with a mask aligner (TKCESD100, Taekwang, Korea). The UV-exposed substrate is developed using a developer (AZ300 MIF, Merck KGaA, Germany). Cr and Au are etched using an etchant. Finally, the photoresist is removed using acetone, completing the fabrication of the micro-gap electrode. The micro-gap electrode is characterized by field-emission scanning microscopy (S-5000, Hitachi, Japan). For the bending test, a microresistor (Red, 300 μm × 600 μm) is used. A poly(dimethyl siloxane) (PDMS) protruding stamp is employed for the alignment of the mini resistor. The aligned resistor on the PDMS is then lowered onto the LS-ACA coated substrate using a UTM at a speed of 1 mm/min. The minimum force required for current to flow is measured using the UTM, and the current is measured with a precision source/measure unit (B2900, Keysight Technologies Inc., USA). Nine pieces of micro-LEDs (Blue, 464 nm wavelength, 100 μm × 200 μm) are used. The mini-LEDs are attached to the fabricated fPCB. Repeated bending tests are performed using a UTM. The voltage across the micro-LEDs and the irradiance emitted by the micro-LEDs are measured using a precision source/measure unit (B2900, Keysight Technologies Inc., USA) and an optical power meter (PM100D, Thorlabs Inc., USA). A cyclic bending test is conducted with a bending radius from 1.3 mm to 2.6 mm at a rate of 600 mm min⁻¹.

Electrical and dielectric characterization of LS-ACA

LS-ACA’s relative permittivity is measured using a dielectric probe kit (Agilent 85070E) connected to a network analyzer (Agilent 8719ES). Measurements are taken across a 1–5 GHz frequency range from three samples. The GHz range is suitable for frequency bands of semiconductor chips or wireless devices. The relative permittivity of the samples is measured under pressures of 0 kPa and 8 kPa. To measure the resistance between micro-gap electrodes, LS-ACA is drop-cast onto the fabricated micro-gap electrode. The resistance at both ends of the electrode is then measured using a precision source/measure unit (B2900, Keysight Technologies Inc., USA). For contact resistance, 4-point Kelvin structured fPCBs are fabricated by PCBWay Technology Co. and contact resistance and lateral resistance are measured using a precision source/measure unit.

Characteristics of adhesion property

The 90° peel force between the strip (25 mm width) and the substrate is measured using an ultimate testing machine (UTM; 3342 Machine, Instron Co., USA) at a displacement rate of 300 mm min⁻¹. The copper strip and substrate are pre-treated with 5 wt% NaOH. Temperature-related rheology data are measured using a rheometer (ARES-G2, TA, USA). Fully cured storage and loss moduli of LS-ACA are measured using dynamic mechanical analysis (DMA7100, Hitachi, Japan).

Demonstration of LS-ACA on a fabric for a 555 timer and BLE device

The fPCB is fabricated by JLCPCB technology. The components of the circuit include a 555 timer (NE555DR, Texas Instruments, USA), a resistor (100 kΩ, TA-I, Taiwan), and a capacitor (10 μF, SAMSUNG, Korea). These components are interconnected on the fPCB with the patterned circuit using LS-ACA. A 50-nm-thick Au is deposited onto the cotton fabric using vacuum sputtering (Q300TD, Quorum Technologies Inc.) with a patterned stencil mask. The components of the circuit include a BLE device (BMD-350-A-R, U-Blox, Swiss), oscillator (ABS05-32.768KHZ-7-T, Abracon LLC, USA), regulator (TLV70033DCKR, Texas Instruments, USA), resistor (100 kΩ, TA-I, Taiwan), thermistor (100 kΩ, Panasonic, Japan), and capacitor (5.6 pF, KYOCERA AVX, Japan). These components are interconnected on the fabric with the patterned circuit using LS-ACA. The surface temperature is confirmed using an infrared thermometer.

The study of human subjects

The individual depicted in the image is the first author of this manuscript and has full awareness and understanding of both the experimental procedures and the image intended for publication.