Introduction

The rising demand for ultradense information storage and highly sensitive microscale magnetic sensors1 has sparked significant interest in magnetic nano- and micro-structures, particularly those capable of sustaining flux-closure magnetic domains with minimal crosstalk between elements2,3,4. Tubular ferromagnetic membranes5 have emerged as a highly promising solution for such devices, as their distinct geometry enables the stabilization of flux-closure domains6. Furthermore, these tubular architectures eliminate the magnetic singularities associated with vortex states and vortex domain walls in cylindrical nanowires7, as well as the edge effects typically present in planar thin films and stripes8,9,10. The elimination of those two effects not only ensures the stability of the flux-closure domains but also promotes ultrafast chiral domain wall dynamics in soft ferromagnetic nanotubes11, positioning tubular architectures as exceptional candidates for next-generation 3-dimensional memory12,13,14,15 and sensor technologies16,17,18,19,20.

Using strain engineering21,22, rolled-up nanotechnology23,24 entails the fabrication of planar thin-film membranes via conventional deposition methods and lithography techniques and converting them into high-quality tubular architectures with rolling diameters ranging from a few to tens of micrometers. Unlike closed cylindrical tubes, these tubes have a tunable number of windings and open edges. The magnetic properties of these tubular structures are influenced by the shape of the initial flat membrane, possible strain-induced magnetoelastic anisotropies, magnetostatic interactions between the open edges, and curvature-related Dzyaloshinskii-Moriya-like exchange interactions1,6,25,26. The latter, however, becomes insignificant if the tube’s diameter exceeds the characteristic exchange length (at most some tens of nanometers) of the magnetic material27,28,29.

Spin-wave dynamics in rolled-up Permalloy tubes have revealed the formation of quantized azimuthal modes, whose characteristics can be tuned by adjusting the tube’s radius and the number of windings, highlighting the role of geometry in governing dynamic magnetic excitations30.

In contrast, static studies on closed magnetic tubes31,32,33,34,35,36 and rolled-up membranes1,25,26 have focused mainly on thin membranes with non-zero magnetostrictive properties; thus, magnetoelastic contributions were, to a large part, responsible for the observed magnetic domain structures.

In our own earlier work37, we analyzed the impact of strain on domain patterns by employing permalloy-related material (Ni78Fe22) with nonzero magnetostriction to enhance the magnetoelastic effect. We also designed the shape of the initial flat magnetic membrane to minimize the impact of magnetostatic interaction. Nevertheless, materials with zero magnetostriction have advantages in magnetic sensor applications and data storage due to their ability to reduce domain wall pinning and facilitate high mobility of domain walls10,38.

Therefore, from the perspective of both fundamental interest and applications, a thorough understanding of geometry-induced changes in the magnetostatic interaction between the side edges of zero magnetostrictive membranes is highly desirable. One can expect a continuous change in magnetostatic interactions when, due to rolling, opposite membrane edges approach. Ideally, this can lead to a transition from a single domain state with magnetization along the long side of the membrane (Fig. 1a) to a flux closure configuration when the membrane adopts a cylindrical shape (Fig. 1c). We experimentally explore this hypothesis by designing planar membranes with varying width W, which, after rolling into tubular structures of comparable radius R, corresponds to a varying arc length S = W (Fig. 1b–d) or closing angle,

$$\varphi =\frac{18{0}^{\circ }}{\pi }\cdot \frac{W}{R}.$$

Rolling-induced magnetic anisotropy as a function of closing angles is probed using anisotropic magnetoresistance (AMR) measurements. It allows us to distinguish clearly between a pure axial remanent magnetization state, such as Fig. 1b, and a configuration with azimuthal components (Fig. 1c). To ensure that the induced changes are exclusively attributed to magnetostatic interactions rather than rolling-induced stress (minor unforeseen magnetoelastic effects have to be ruled out), we deliberately applied stress in a compressive and tensile manner by rolling membranes in the upward and downward direction, respectively. A similar change in AMR measurements observed when rolling the membranes in both directions confirms that the rolling-induced anisotropy arises from a magnetostatic origin, with no contribution from stress.

Fig. 1: Schematics illustrating the influence of magnetostatic interaction between the boundaries of a magnetostriction-free in-plane magnetized membrane on domain configuration.
figure 1

a Before rolling, a rectangular membrane will prefer magnetization along the long axis (axial). After rolling, the domain configuration will change as a function of membrane width or closing angle φ from (b) axial to (c, d) azimuthal. In addition to the 3D view, a 2D sketch (black lines) illustrates the cross-sectional view of planar and curved membranes.

Full size image

Theoretical calculations supplement the experimental results by first calculating the demagnetization factors for curved membranes with varied closing angles, which are then used to compute the shape anisotropy constant. These calculations lead to an anisotropy phase diagram covering a large parameter range concerning membrane thickness, size, tube diameter, and fractional winding number.

Thus, this study offers great promise for advancements in various applications by exploring the interplay between geometric features and magnetic domains.

Results

Sample design and self-assembly of tubular structures

The fabrication of planar NiFe structures on a shapeable polymeric platform enables their self-assembly into three-dimensional tubular architectures. This platform consists of photo-patternable, thermally stable, and chemically resistant imide- and acrylic-based polymers, which maintain stability up to 270 °C and exhibit chemical inertness in common organic nonpolar, polar, protic, and aprotic solvents, as well as moderate acids and bases, ensuring compatibility with photolithography processing. The polymeric platform comprises a 400 nm thick sacrificial (SL) layer and a bilayer consisting of a 400 nm thick hydrogel (HG) and a 1000 nm thick polyimide (PI), as illustrated in Fig. 2a, d. These polymer layers are deposited via spin-coating and are patterned using direct UV lithography onto a 50 × 50 mm2 glass substrate, forming arrays of polymer rectangles with typical dimensions of 3.5 × 3.2 mm2, enabling the simultaneous processing of up to 126 functional polymer layer stacks. After polymer patterning, Ni80Fe20 films are deposited by magnetron sputtering at room temperature using a power of 40 W and a pressure of 7.5 × 10−7 Torr. These films are subsequently patterned using a lift-off process into membranes of fixed length and varying widths within the platform’s central 1 mm × 1 mm region. On top of magnetic structures, 100 nm thick gold contact pads are sputter-deposited and patterned using a lift-off process for four-point anisotropic magnetoresistance measurements, creating planar devices (Fig. 2b). Exposure to a slightly alkaline (pH 7.0–8.0) ethylenediaminetetraacetic acid (EDTA) solution etches the sacrificial layer and causes the hydrogel to swell, counteracting the retaining force of the polyimide (PI) layer, which acts as a stiff constraint. This results in the self-assembly of the layer stack into a rolled three-dimensional tubular architecture (Fig. 2a). The rolling occurs either upwards when the PI layer is positioned above the hydrogel (Fig. 2a) or downwards when PI is below the hydrogel (Fig. 2d), with a yield of 90−95%. After etching and rolling, the samples are dried under ambient conditions. The resulting tube diameters range from 55 μm to 100 μm, with the permalloy structures on top of the tubes conforming to the same curvature as the tubes.

Fig. 2: Self-assembly rolling of magnetic membranes.
figure 2

a Schematic representation of the fabrication process for rolled-up magnetic membranes. Optical images of the layer stack are shown before (b) and after (c) the rolling process, which involves rolling the polymeric platform along with the magnetic membrane. In (b), planar permalloy membranes of increasing widths (labeled structures, 1–8) with their contact lines are visible. After rolling, these transform into tubular membranes with various winding numbers. A schematic representation above the rolled membranes depicts a simplified cross-sectional view of the rolled structures in (c). d Schematic illustration of the fabrication process for rolled-down magnetic membranes.

Full size image

This method offers precise control over strain within the functional magnetic layer. The magnitude of the strain can be adjusted by modifying the rolling radius, while the sign of the strain—compressive (negative) or tensile (positive)—depends on the rolling direction. Specifically, when the magnetic layers are fabricated on top of the polymeric platform, rolling upwards induces compressive stress along the azimuthal direction, whereas rolling downwards results in tensile stress.

Using this method, the impact of strain was examined for NiFe membranes with both positive and negative magnetostriction in our previous research. For positive magnetostrictive Ni78Fe2237, rolling-up induced a magnetoelastic anisotropy perpendicular to the stress axis, i.e., in the axial direction, while rolling-down resulted in an azimuthal anisotropy. In contrast, for negative magnetostrictive Ni81Fe1939, rolling-down leads to an axial anisotropy. It was concluded that the induced anisotropy followed the well-known equation40, \({K}_{u}=\frac{3}{2}\sigma \lambda\), observing the sign of both the magnetostriction constant λ and the stress σ.

In this work, a stoichiometric permalloy (Ni80Fe20) with vanishing magnetostriction was used to minimize the magnetoelastic anisotropy. A reference film was deposited on a thin glass substrate and mounted on a recently introduced strain stage in a Kerr microscopy setup to verify the negligible magnetoelastic anisotropy41. Longitudinal Kerr effect magnetization loops were measured at various in-plane field directions to construct polar plots of remanent magnetization and coercivity. Negligible modifications in the anisotropy direction of the strained and unstrained film indicate that the deposited permalloy has significantly low magnetostriction. Measurements and setup details are included in the Supporting Information, Section 1.

The rolling-induced magnetostatic interactions were investigated in 100 nm thick layers of vanishing magnetostriction Ni80Fe20, patterned as rectangular membranes of constant length L = 480 μm and varying width W, with 150 μm < W < 270 μm < L, on top of the polymeric platform (Fig. 2b). In the planar membrane, this leads to a shape-induced easy magnetization direction along the long rectangular side.

After rolling, these patterned planar membranes transform into 3D curved membranes with various closing angles φ (Fig. 2c), determined by the known magnetic membrane width W and the rolling radius R. In the first estimate, the latter is extracted from on-view optical micrographs of the tubes after rolling (Fig. 3). However, additional 3D X-ray computed tomography (XCT) measurements of two exemplary tubes revealed that the actual membrane shape deviates from a cylinder by being elliptically distorted. The orientation of the short and long elliptical axes even depends on the position along the tube length (see Supporting Information, Section 2).

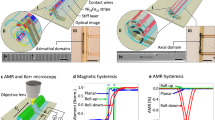
Fig. 3: Magnetoresistance measurements before and after rolling the membranes.
figure 3

a-i, b-i Self-assembled rolled-up and (c-i) rolled-down membranes. Inset in (a-i, b-i) shows magnetooptical Kerr images of magnetic domains in the membrane after rolling, and in (c-i), a cross-section image of the rolled-down membrane imaged using x-ray computed tomography. Schematic images of (a-ii, b-ii) rolled-up and (c-ii) rolled-down membranes, demonstrating the number of windings and possible magnetic domain orientations in tubular architectures. AMR hysteresis loops before and after rolling the membranes (a-iii, b-iii) upwards and (c-iii) downwards. Blue and yellow colors in the AMR loops indicate azimuthal and axial anisotropies, respectively, in the rolled membranes.

Full size image

The XCT measurements are experimentally cost-prohibitive when applied to our large sample set. Still, they suggest a modified procedure for estimating the effective diameter of the tubes by combining measurements in the lateral dimension (optical diameters) with profilometer measurements in the vertical direction. These two quantities are interpreted as the two half-axes of an elliptical cross-section, from which the equivalent circular diameter is calculated. This leads to errors in R only when the actual elliptical axes are rotated with respect to the two orthogonal measurement axes. The estimated diameter for the elliptical cross-section was then used to determine the magnetic membranes’ approximate closing angle, φ.

Magnetostatic anisotropies in curved magnetic membranes

The results for membranes with two distinct widths, 180 μm and 230 μm in rolled-up geometry, and a membrane of width 230 μm in rolled-down geometry, are shown in Fig. 3. The AMR measurements displayed in the right column provide an easy and versatile approach for characterizing the global magnetization states, particularly in scenarios involving 3D curved structures where conventional methods such as magneto-optical imaging become less straightforward. The magnetic field is applied parallel to the membrane’s long axis (z-axis), which aligns with the direction of the current flow. All three membranes display a consistently high magnetoresistance when exposed to a sweeping magnetic field before being rolled. This results from the shape anisotropy of the planar membrane, which causes the magnetization to align along the long axis, coinciding with the direction of current flow.

For the rolled-up membrane with a width of 180 μm corresponding to a closing angle of 260° (Fig. 3a-i), the AMR signal remains unchanged (Fig. 3a-iii). The magnetization continues to point along the tube axis (Fig. 3a-ii) despite the rolling of the membrane. Contrarily, for the membrane with 230 μm width (Fig. 3b-i), the AMR signal shows notable changes, particularly near zero magnetic fields (Fig. 3b-iii), where the anisotropy direction solely governs the magnetic moment direction. A minimum in the AMR signal corresponds to a moment alignment perpendicular to the current flow. It indicates a change toward an azimuthal anisotropy (Fig. 3b-ii) induced by the large closing angle of 360°. A microscopic confirmation is seen in the Kerr images obtained at zero field on the dome of the curved membranes (insets of Fig. 3a-i, b-i), with axial magnetization for φ = 260° and an apparent tilting toward the azimuthal orientation for φ = 360°.

This effect is predominantly due to magnetostatic interactions in these rolled structures rather than due to magnetoelastic interactions, and azimuthal anisotropy must also occur in rolled-down membranes, where possible magnetoelastic contributions reverse sign.

Figure 3c-i displays a membrane of comparable width (230 μm) now transformed into a rolled-down tubular structure. Based on the measured optical diameter and the cross section extracted from an XCT measurement (see inset in Fig. 3c-i), this membrane has approximately 1.25 windings, corresponding to a closing angle of 450°. According to the AMR signal (Fig. 3c-iii), this rolled-down tubular structure shows an apparent change in its magnetization alignment from axial to azimuthal (Fig. 3c-ii). The smaller change in the absolute AMR value (0.8%) compared to the rolled-up membrane with a closing angle of roughly 360° (1.2%) can be attributed to a lower azimuthal magnetization component and is understood from the larger distance of the straight membrane edges in this case. These experiments thus clearly demonstrate that geometry-driven flux closure can induce an azimuthal magnetostatic anisotropy in rolled membranes. To estimate the magnitude of this induced anisotropy, the field is applied along the axis of the tube, which is a hard axis in this case37. The uniaxial magnetic anisotropy (UMA) constant Ku can thus be determined from the saturation field Hsat observed in the AMR measurements using the relation40:

$${K}_{u}=\frac{1}{2}{\mu }_{0}{M}_{s}{H}_{sat},$$

where Ms = 690 kA/m is the saturation magnetization of permalloy. The AMR curves and saturation fields for all rolled membranes are provided in Supporting Information, Section 3. The saturation fields of all the examined rolled membranes range from 0.16 mT to 0.37 mT, which leads to a Ku of magnitude between 0.055 kJ/m3 and 0.13 kJ/m3. These experimental anisotropy magnitudes align well with the analytically calculated azimuthal anisotropies (see Ku < 0, region of Fig. 4b-iii).

Fig. 4: Shape anisotropy of curved membranes (length = 480 μm, thickness = 100 nm) and their planar counterparts.
figure 4

The illustrations show (a-i) a planar membrane and (b-i) a curved membrane, along with the coordinate system used for calculating demagnetizing factors. The anisotropy constants Ku are plotted against the closing angle for (a-ii) planar and (b-ii) curved membranes for varying radii of curvature (25 μm to 75 μm). For planar films, the closing angle is, \(\varphi =\frac{18{0}^{\circ }}{\pi }\cdot \frac{W}{R}\). Yellow arrows indicate the direction of increasing radii. a-iii, b-iii display magnified views (the shaded regions) of figures (a-ii and b-ii), focusing on the data near a 360° closing angle (equivalent to one full winding).

Full size image

These flux-closure-induced anisotropies are thus 4–5 times smaller than the previously reported magnetoelastic anisotropies for Ni78Fe22 membranes of equal length and thickness37.

Analytical calculation of magnetostatic anisotropies

To provide a theoretical estimate of magnetostatic energies in curved membranes, we consider rectangular membranes of varying dimensions rolled to various degrees of curvature. We adopt a monodomain macrospin approach analogous to the Stoner-Wohlfarth model (which strictly applies to elliptical single domain particles) and calculate the (purely magnetostatic) uniaxial anisotropy constant Ku with respect to the long membrane axis for an arbitrary in-plane magnetization direction M within the membrane given by the angle θ.

The magnetostatic energy Ed for a given magnetization configuration M and the corresponding demagnetizing field Hd is most generally expressed as42,

$${E}_{d}=-\frac{1}{2}{\mu }_{0}\int{\bf{M}}\cdot {{\bf{H}}}_{{\bf{d}}}\,{d}^{3}r$$
(1)

Here, μ0 = 4π × 10−7 [H/m] is the vacuum permeability, and Hd = − ∇ Φ, which can be obtained as the negative gradient of the magnetostatic potential Φ, defined as42,

$$\Phi (r)=\frac{1}{4\pi }{\int}_{\!\!V}\frac{\rho (r^{\prime} )}{| r-r^{\prime} | }\,{d}^{3}r^{\prime} +\frac{1}{4\pi }{\int}_{\!\!S}\frac{\sigma (r^{\prime} )}{| r-r^{\prime} | }\,dS^{\prime} ,$$
(2)

where \(\rho (r^{\prime} )\) and \(\sigma (r^{\prime} )\) represent the volume and surface magnetic charge densities, respectively, and are linked to the magnetization via \(\rho (r^{\prime} )=-\nabla \cdot {\bf{M}}\) and \(\sigma (r{^\prime} )=\hat{n}\cdot {\bf{M}}\).

In the case of a monodomain, the field Hd can also be related to the magnetization M by means of demagnetizing factors Nij, such that the magnetostatic energy takes the alternative expression42:

$${E}_{d}=\frac{1}{2}{\mu }_{0}V{M}_{s}^{2}\sum _{i,j}{N}_{ij}{m}_{i}{m}_{j}={K}_{u}V,$$
(3)

where Ms is the saturation magnetization, mi, mj are the vector components of the magnetization linked to the angle θ, and Ku is the anisotropy constant describing the uniaxial shape anisotropy with respect to a sample axis. The planar membranes are described by a rectangular prism in Cartesian coordinates, whereas the curved membranes are described in cylindrical coordinates with parameters as seen in Fig. 4a-i and b-i. To simplify the notation, the unit vector \(\hat{\beta }\) is introduced to represent the \(\hat{y}\)-direction in the planar membrane and the \(\hat{\varphi }\)-direction in the curved membrane. Therefore, if magnetization forms an angle θ with respect to the z-axis, we can separate it into its components,

$${\bf{M}}={M}_{s}\sin (\theta )\hat{\beta }+{M}_{s}\cos (\theta )\hat{z}.$$

By equating Eq. (1), where Hd is determined through the magnetostatic potential, and Eq. (3), the relevant demagnetizing factors Nzz and Nββ for curved membranes can be calculated. The anisotropy constant can be expressed as:

$${K}_{u}=\frac{1}{2}{\mu }_{0}{M}_{s}^{2}({N}_{\beta \beta }-{N}_{zz})$$
(4)

Details on the above equations and the calculation of Nzz and Nββ are provided in the Supporting Information, Section 4 (A-G). The Cartesian demagnetizing factors for rectangular prisms are taken from ref. 43.

The Nii and Ku were calculated for membranes of several dimensions ranging from the nanoscale to the microscale. Here, the anisotropy data are presented for membranes of thickness 100 nm, length 480 μm, bending radii 25–75 μm, and varying membrane widths W, according to the experimentally studied case. Figures 4a and b display Ku for planar and curved membranes as a function of the closing angle φ, which relates to the membrane width via φ. In the case of the rectangular prism, R serves only as a scaling factor; in the case of the curved membrane, W equals the arc length \(S=\frac{\pi }{18{0}^{\circ }}R\cdot \varphi\) and R is calculated using a mean radius approximation \(R=\frac{{r}_{0}+{r}_{i}}{2}\), with r0 and ri being the outer and inner radii, respectively, and t = r0 − ri being the thickness of the curved membrane.

As a general behavior of demagnetizing factors, an increase in a geometrical dimension reduces the corresponding demagnetizing factor while increasing the orthogonal one. In the case of the studied membranes, an increase in φ thus corresponds to a decrease in Nφφ, and an increase in the orthogonal Nzz. Thus (Nββ − Nzz) and therefore Ku, must decrease. This behavior agrees with the results obtained for the membranes shown in Fig. 4a (ii, iii) and b (ii, iii). We note that the shape anisotropy for the planar and curved membranes displays quite similar behavior until reaching a point of large closing angle. Since the length of the membranes is always larger than the width, Ku always remains positive for the planar membranes, which corresponds to an anisotropy along the length of the structure. However, a drastic drop in Ku is observed for the curved membranes as the closing angle approaches 360°. When, for a given bending radius R, the closing angle φ exceeds a threshold value φ0, Ku becomes negative, and a magnetization direction parallel to the bending axis \(\hat{\varphi }\) is preferred. This critical angle φ0 approaches 360° for the smallest bending radii. Analogous to the closing angle φ, the behavior can be expressed with the membrane width \(W=\frac{\pi }{18{0}^{\circ }}R\cdot \varphi\). Azimuthal anisotropy is always preferred when the membrane width surpasses the full circumferential length 2πR, allowing for full flux closure irrespective of the radius. With increasing radius R, and thus, increasing membrane width W (to maintain the same closing angle), azimuthal anisotropy can occur even at closing angles ϕ < 360°, indicating partial flux closure.

These calculations are extended to smaller and thinner membranes down to a length and thickness of 480 nm and 10 nm, respectively. Figure 5 displays phase boundaries Ku(φ0, R) = 0 in the (φ, R)-phase space, which separates azimuthal (φ > φ0) and axial (φ < φ0) anisotropy. Phase boundaries are given for curved membranes of four different lengths and two thicknesses: t = 10 nm (stars) and t = 100 nm (disks). We restrict to thin membranes with t < W < L. In the case of flat membranes (full squares), the phase boundary is independent of the membrane thickness. The phase transition z-anisotropy → φ-anisotropy simply occurs when the membrane width (described by φ) surpasses the membrane length L, i.e., for \(\varphi =\frac{18{0}^{\circ }}{\pi }\cdot\frac{L}{R}\). In all curved membranes, the transition occurs at membrane widths smaller than or equal to the membrane length (W ≤ L). For two limiting cases, this is easily understood: (i) a full curving of the membrane, i.e., a closing angle of 360°, guarantees azimuthal anisotropy even for a membrane width W = 2πR much smaller than the membrane length, that would otherwise favor z-anisotropy. This behavior is seen in the limit of small R and large L. It is important to note that the phase boundaries shown in Figs. 4 and 5 do not account for the effects of exchange interaction. (ii) For membrane widths approaching the length L, azimuthal anisotropy is possible irrespective of the closing angle, simply from the membrane’s aspect ratio approaching 1. This behavior is visible for the smaller L-values at large R. The interesting region occurs for intermediate aspect ratios 0.7 < W/L < 1. Despite the rectangular membrane shape, azimuthal anisotropy is obtained for closing angles clearly below 360°, i.e., for partial flux closure. This bending-induced phenomenon has its origin in the demagnetizing energy connected to the demagnetizing field produced by the edges of the curved membrane, which differs completely from the demagnetizing field at the edges of the flat membrane. Bending the membrane reduces the energy (or the corresponding Nφφ) for a magnetization orientation in the azimuthal direction and allows for azimuthal anisotropy also in a non-fully closed membrane. Furthermore, when the membrane thickness is reduced from 100 nm to 10 nm, the azimuthal flux closure occurs at smaller closing angles for longer membranes and larger closing angles for shorter membranes (Supporting Information, Section 4-H). Analyzing all calculated phase boundaries, we observe that the behavior is scale invariant. The critical closing angles calculated, e.g., for a 10 nm thin membrane of length L = 4.8 μm is identical to that of a 100 nm thick membrane of length 48 μm at 10 times larger width W (shown in Supporting Information, Section 4-I).

Fig. 5: Analytical phase diagram.
figure 5

Analytically calculated phase diagrams (threshold angles φ0 vs R) of curved membranes and their planar counterparts for various membrane sizes. The phase boundaries Ku(φ0, R) = 0 separate azimuthal (φ > φ0) and axial (φ < φ0) anisotropy.

Full size image

Phase diagram/comparison with experiment

Figure 6 summarizes the analytically calculated threshold angles φ0 (taken for 480 μm long and 100 nm thick curved membrane from Fig. 5) and corresponding circumferential lengths \({S}_{0}=\frac{\pi }{18{0}^{\circ }}R\cdot {\varphi }_{0}\) vs. curvature radius. In the φ0-R phase diagram (Fig. 6a), the phase boundary Ku(φ0, R) = 0 is seen as a slightly downward-bent line at φ ≈ 360°. In the S-R phase diagram (Fig. 6b), the phase boundary is seen as a diagonal line initially following the relation S = 2πR, signifying that for small radii, the membrane width needs to reach the full circumferential length of the tube to enter the azimuthal anisotropy state.

Fig. 6: Comparison between experimental and analytical results.
figure 6

Analytically calculated phase boundary (circles in magenta) separating axial (light yellow) and azimuthal (light blue) anisotropy regions presented in a as threshold (a) closing angles φ0 vs R and (b) circumferential length S0 vs R for the curved membrane of length = 480 μm, thickness = 100 nm. Experimental data for rolled-up (RU) and rolled-down (RD) membranes are included, with data points color-coded based on the observed anisotropy: blue indicates azimuthal anisotropy, and yellow represents axial anisotropy.

Full size image

The experimental results, i.e., the occurrence of either axial or azimuthal anisotropy for structured membranes of systematically varying width W and somewhat dispersed diameters 2R, are added as colored symbols to the phase diagrams. The blue triangles represent the curved membranes with azimuthal anisotropy, while the yellow triangles represent the curved membranes with axial anisotropy. Except for a few data points where the azimuthal anisotropy was observed at a smaller closure angle than the theoretically expected value, the experimental data are consistent with the theoretical prediction.

Discussion

We have calculated and verified the shape anisotropy of curved magnetic membranes through theoretical and experimental means, comparing the results with their planar counterparts. Analytical expressions for demagnetizing factors and anisotropy constants were derived for the curved membranes. The results reveal how the shape anisotropy of curved membranes can be tuned by varying their width and radius of curvature. For the curved membranes, the shape anisotropy is axial below a critical closing angle and becomes azimuthal above it. Importantly, this transition can occur at closing angles well below 360°, allowing for geometry-induced azimuthal anisotropy in fully tubular structures and partially closed membranes or multi-winding tubes, which necessarily possess open membrane edges. The transition in anisotropy is attributed to the magnetostatic interaction of the side edges of the membrane as they get closer to each other at larger closing angles. The experimental data on rolled membranes agree well with the theoretical predictions, confirming the model’s validity. By using soft magnetic membranes with vanishing magnetostriction, the strength of the shape anisotropy is larger than possible stress-induced anisotropies, and the magnetization configuration adopts the geometry-induced shape anisotropy expected from the analytical model. The ability to control the magnetic anisotropy by simply varying the geometry of the magnetic structures and understanding the influence of solely magnetostatic interaction-induced anisotropy can open new possibilities for designing efficient magnetic components in various microelectronic applications.

Methods

Kerr microscopy

A digitally enhanced wide-field Kerr microscope set-up, making use of the magneto-optical Kerr effect (MOKE) and equipped with an electromagnet, was applied to measure magnetic hysteresis loops (MOKE magnetometry) for investigating the magnetoelastic anisotropy (detailed in Supporting Information, Section 1) and to image the magnetic domains shown in the inset of Fig. 3a-i and b-i. Before observing the domain configuration, the ground state of the ferromagnetic element was set by an ac-field demagnetizing procedure (frequency = 35 Hz, maximal amplitude = 20 mT, decay time to zero field = 5 s) with the field pointing along the tube axis.

AMR measurements

AMR measurements provide an easy and versatile approach for characterizing the global magnetization states, particularly in 3D curved structures where conventional methods such as magneto-optical imaging become less straightforward. Changes in the magnetic states and anisotropy before and after rolling are thus obtained through four-probe magnetoresistance measurements under sweeping magnetic fields. In these experiments, the field was applied along the membranes’ long axis, corresponding to the tube axis after rolling. The application of a magnetic field alters the magnetic domain state. Thus, it affects the local orientation of magnetic moments with respect to the current direction. This results in configuration-dependent resistance, as the magnetoresistance, \(R\propto \cos (\theta )\), depends on the relative angle θ between the current and the local magnetization m(H).

X-ray computed tomography (XCT)

To determine the winding number and overall morphology of the film and carrier film, the samples were investigated with a Zeiss Versa 520 X-ray microscope, which allows for a combination of geometric magnification using cone-beam X-rays onto a thin scintillator and a subsequent visible light-optical magnification of the scintillator onto a CCD camera with a pixel size of 13.5 μm. The tubular samples were mounted in their rolled form on top of a syringe needle parallel to the needle axis and successively rotated by 360° while acquiring 801 projection images. The source-object distance was set to 17.02 mm while the object-detector distance varied between 4.31 mm and 4.67 mm, resulting in geometric magnifications between 1.25 and 1.27. The W transmission X-ray source was run at an acceleration voltage of 40 kV, a power of 3 W, with a beam hardening filter (LE3) and visible light magnification of 40, resulting in a voxel size of 0.26 μm. For 3D representation, the sample was rendered using the Avizo software.

Profilometer

Profilometer measurements have been performed with a Bruker Dektak XT profilometer to evaluate the rolled membranes’ height (or vertical diameter). Measurements were applied using a stylus with a 2 μm radius and a low stylus force of 1 mg. They were conducted in three parallel scan lines with a lateral spacing of about 200 μm running transversely across the rolled membrane. The profile maximum of the three measurements typically agreed to within 1 μm.

Statistical analysis

AMR hysteresis presented are results of single scan measurements. The error bars in the x- and y-axis in Fig. 6 are errors calculated from the estimation of the radius of curvature and closing angle.