Molecular dynamics study of grain boundaries as defect sinks under irradiation in LiAlO₂ and LiAl₅O₈

Abstract

Lithium aluminate ceramics, LiAlO₂ and LiAl₅O₈, show promise in nuclear environments due to their excellent radiation tolerance. Molecular dynamics simulations investigate grain boundaries (GB) and their role in defect evolution. Results reveal that GBs act as efficient defect sinks, with Li and Al atoms exhibiting distinct behaviors during displacement cascades. Tritium migration in LiAlO₂ is also studied, showing rapid diffusion and stable configurations with oxygen, corroborated by ab initio simulations from the literature. The calculated tritium diffusion coefficient of 1.33 × 10⁻¹⁴ m²/s aligns with the literature, validating the model. LiAl₅O₈ demonstrates superior defect healing compared to LiAlO₂, attributed to enhanced atomic transfer between grains and GBs. These findings reveal key insights into defect dynamics, providing essential insights for their application in tritium-producing burnable absorber rods (TPBARs).

Introduction

Tritium, an essential isotope for both strategic stockpiles^1,2 and fusion reactors^3,4, can be efficiently generated using gamma-phase lithium aluminate (γ-LiAlO₂) as a breeder material^1,2,3,5,6. The tritium production occurs via the thermal neutron reaction ${{\scriptstyle}{6}\atop{3}}{}^{Li}+n\to {{\scriptstyle}{3}\atop{1}}H+{{\scriptstyle}{4}\atop{2}}{He}+2.75{MeV}$⁶$.$ The resulting high-energy particles interact with the γ-LiAlO₂ lattice, causing point defects through atomic collisions. The subsequent accumulation and interaction of these defects and fission products result in the formation of extended defects like vacancies^7,8,9, interstitials^10,11, and dislocation loops^12,13. Radiation-induced defects in materials can be absorbed by effective sinks like interfaces and grain boundaries (GBs). The capture of mobile defects migrating towards these GBs can lower the energy of the system, thereby facilitating defect trapping or annihilation processes^14,15,16.

Molecular dynamics (MD) simulations of cascades with primary knock-on atom (PKA) energies between 1 and 5 keV near a Σ5 twist grain boundary in Ag have shown that grain boundaries preferentially absorb interstitials¹⁷. The associated strain field directed interstitial clusters towards the boundary via 〈110〉 crowdion motion with minimal barriers, and this biased absorption led to a vacancy-rich interior. Comprehensive simulations of radiation damage within nanocrystalline nickel (Ni)^18,19,20,21 for PKA energies ranging from 5 to 30 keV have demonstrated that grain boundaries preferentially absorbed interstitials, resulting in a vacancy-dense configuration in the grains. Demkowicz et al.²² examined defect production near a Σ3 twin grain boundary in Cu. Their findings showed that the GB had minimal impact on damage creation, especially for low-energy cascades. This study attributed the finding to the minimal thermodynamic interaction between defects and the boundary, meaning the defect formation energy at the boundary is nearly the same as in bulk Cu. Interestingly, at higher energies, fewer defects were created near the Σ3 twin boundary compared to the case of single-crystal cascades. This reduction is due to the longer recombination distance of Frenkel pairs near the boundary and the disruption of the cascade’s spatial extent due to the orientation change at the boundary, hindering channeling.

The evolution of defects in ceramics under irradiation exhibits unique characteristics. For example, in Gd₂Zr₂O under irradiation, distinct defect structures such as small Kr bubbles, large Kr bubbles, microcracks formation, and grain growth happens depending on the grain size and irradiation conditions²³. Irradiation-induced grain growth has also been reported in materials such as CeO₂²⁴, YSZ²⁵, and ZrO₂²⁶. This phenomenon is attributed to the reduction in total grain boundary energy and curvature, driven by the migration of grain boundaries under increased temperatures and defect accumulation²³. During ion irradiation, cascade collisions generate numerous point defects, which accumulate and destabilize the lattice thermodynamically. In nanograined ceramics, the proximity of defects to grain boundaries, often within the mean free path of the defects, results in defect diffusion toward the boundaries, which serve as defect sinks²⁵. This coordinated defect movement induces grain boundary migration and facilitates grain growth.

Metallic bonding allows for bond dissociation and reformation during deformation, which can be effectively represented through computational potentials designed to simulate metallic interactions. Conversely, ionic compounds pose a greater challenge for simulations due to the necessity of accounting for electron transfer during bond breakage and reformation, which introduces additional complexity in accurately modeling these phenomena. In cascade damage studies, focusing on single crystals simplifies the modeling task, as the ordered atomic structure facilitates more predictable defect formation and evolution. However, the introduction of grain boundaries complicates this scenario significantly. Grain boundaries elevate the interfacial energy and create localized high-energy sites that are difficult to accurately replicate for ionic materials using existing interatomic potentials. This increased complexity in modeling interfacial phenomena and the associated energy states at grain boundaries results in fewer cascade simulations being conducted on ionic compounds with grain boundaries. The accurate representation of these high-energy interfaces remains a significant challenge in MD, particularly for ionic systems resulting in relatively fewer studies in this area limited to UO₂^27,28,29 and TiO₂³⁰.

Previous studies have investigated LiAlO₂ using MD to analyze radiation damage via cascade simulations; however, these studies have been confined to single crystals^3,31,32. Similarly, the secondary-phase LiAl₅O₈, that is formed in LiAlO₂ as a result of Li consumption, has only recently been examined through MD, but has been limited to a single-crystal system^3,6. For practical applications, there is a need to understand tritium diffusion both in the bulk material and at the grain boundaries. Understanding the behavior of tritium within these different regions could provide valuable insights into optimizing the material for tritium production, enhancing efficiency, and ensuring structural integrity under irradiation conditions. In tritium-producing burnable absorber rods (TPBARs), LiAlO₂ pellets are polycrystalline and experience the evolution of gas (tritium) during irradiation. GBs, which function as interfacial defects, are known to significantly impact the mechanical properties of the material and speed up the diffusion of tritium. For example, GBs can act as sinks for radiation-induced defects, thereby enhancing the tolerance to irradiation. Despite the importance of GBs, there have been limited numerical studies on their effects, with most research focusing on metallic systems^{14,19,20,21,33,34,35,36}. The impact of GBs on the formation and annihilation of point defects, as well as their influence on transport properties in LiAlO₂, remains inadequately understood and warrants further investigation.

In general, GBs are complex structures involving a multitude of orientations and sizes. In this article, we will first analyze the suitability of the available interatomic potentials for simulating a high angle GB. Then we will present the results of displacement cascades initiated close to GBs. The performance of both LiAlO₂ and LiAl₅O₈ will be compared under irradiation, and the role of GBs will be quantitatively elaborated. The lower damage observed in LiAl₅O₈ will be reasoned by higher transfer of interstitials between the bulk of the grain and GB. Lastly, we will analyze the suitability of this potential for tritium and compare tritium diffusion with existing modeling and experimental results.

Results

The usage of Buckingham potential for both ceramics was elaborated in our previous works^3,6. However, the potential was found to not be well suited for simulating GBs due to excessively high energies encountered at the interface which will be shown in the following sections. Alternatively, the ReaxFF potential³⁷ has previously been validated for $\gamma$-LiAlO₂ and shown to produce good results for formation energy and lattice constants. Since the transferability to LiAl₅O₈ was not tested, its validity on the LiAl₅O₈ system was checked in this work.

The radial distribution functions (RDF) of γ-LiAlO₂ and LiAl₅O₈ are illustrated in Fig. 1a, b, respectively. The computed densities were 2.52 gm/cc for LiAlO₂ and 3.52 gm/cc for LiAl₅O₈ which agree well with the experimental values of 2.53 gm/cc³⁸ and 3.52 gm/cc³⁸, respectively, thus providing robust preliminary validation of the ReaxFF potentials. The bond distances derived from these potentials are detailed in Table 1 for LiAlO₂ and Table 2 for LiAl₅O₈. For LiAlO₂, the results show strong agreement with those obtained through DFT³⁹ and experimental data⁴⁰. Similarly, the results for LiAl₅O₈ are consistent with the DFT data from materials project (MP)³⁸, further validating the suitability of the potentials for both γ-LiAlO₂ and LiAl₅O₈. The positions of the first three peaks in the radial distribution functions at 0 K for both systems depicted in Fig. 1a, b, respectively, correspond to the bond distances listed in Tables 1,2. Specifically, the Al-O bond lengths (1.76 and 1.78 Å) are seen as the first two peaks in Fig. 1a, while Li-O appears as the second peak at 1.98 Å. A similar pattern is observed for the LiAl₅O₈ system in Fig. 1b where the first two peaks at 1.78 and 1.86 Å correspond to the Al-O bond lengths (see Table 2). The presence of distinct peaks at defined bond distances, indicates that crystallinity is maintained in the optimized structures.

Fig. 1: Structural integrity and validation of LiAlO₂ and LiAl₅O₈ crystals through RDF and XRD analysis.

RDF for a LiAlO₂ and b LiAl₅O₈ highlighting the bond lengths with sharp peaks indicating that the structural integrity of the crystals are preserved after structure optimization. c Experimental XRD pattern of LiAlO₂, adapted from Jiang et al.⁴¹ (reprinted from ref. ⁴⁸ with permission from Elsevier) showing diffraction peaks obtained between 10° and 65°. Key peaks are highlighted for comparison with simulation results. d Virtual XRD pattern of LiAlO₂ generated using MD simulations. The alignment of prominent peaks with experimental data (black circles) demonstrates the ReaxFF potential’s capability to replicate the crystal structure accurately.

Table 1 Calculated bond distances from optimized systems of γ-LiAlO₂ using ReaxFF compared with experimental results⁴⁰

Table 2 Calculated bond distances from optimized systems of LiAl₅O₈ using ReaxFF compared with DFT results³⁸

Figure 1c, d demonstrate the validation of the ReaxFF potential in reproducing the crystal structures of LiAlO₂ and LiAl₅O₈ by comparing experimental XRD patterns taken from Jiang et al.⁴¹ with virtual XRD patterns obtained from MD simulations in this work. The diffraction patterns, covering the range of 10° to 65°, show strong correspondence between experimental and simulated peaks, as indicated by the black circles. This alignment suggests that the ReaxFF potential accurately captures the crystal structures, preserving both lattice parameters and atomic arrangements. The agreement between the experimental and simulated data supports the reliability of the ReaxFF potential in modeling these materials. The post-relaxation state of the simulation cell for LiAlO₂ is illustrated in Fig. 2a, where the interface between the two grains delineates a perturbed region, referred to as the GB width²⁷. Figure 2b exhibits the average potential energy profile of Li atoms as a function of their z-distance from the GB central plane, comparing the results obtained using Buckingham and ReaxFF potentials. The Buckingham potential yields substantially higher energy values than ReaxFF, reflecting the differences in the parameterization of interatomic interactions for each potential.

Fig. 2: Grain boundary structure and energy profile analysis of LiAlO₂.

a Perspective view of the grain boundary between the top and bottom grains of LiAlO₂, where the top grain is rotated by 95°, 36°, and −106° and the bottom grain by 90°, −30°, and 145° about the x, y, and z axes, respectively. The region between the dashed lines represents the grain boundary core. b Average potential energy of Li atoms along the Z-axis, perpendicular to the interfaces, as a function of the distance from the central interface calculated from the Buckingham potential (red solid line) and the ReaxFF potential (black solid line).

Due to the implementation of periodic boundary conditions, the simulation inherently generates two interfaces, situated at z = 0 and z = L_z. At these interfaces, the crystalline lattice undergoes distortion, causing atoms to be positioned closer than in an ideal lattice arrangement. This misalignment results in elevated potential energies for atoms close to the GB, whereas atoms residing within the bulk grains exhibit reduced energy levels, as depicted in Fig. 2b.

The higher GB energy values derived from the Buckingham potential can be attributed to its limited adaptability of its parameterization, which may not fully capture the complex atomic interactions and charge transfer at the GB. Buckingham potential, being primarily parameterized for simple pairwise interactions, often results in higher repulsive forces at short interatomic distances³ typical of GB regions, thus leading to elevated energy values. Conversely, the ReaxFF potential, which is designed to accommodate more complex and flexible interactions, including bond formation and breaking, provides a more accurate representation of the atomic environment at the GB. Consequently, the ReaxFF potential yields energy values of −18 eV or lower compared to the Buckingham potential for atoms near the GB or within the grains, signifying a more stable GB configuration. This emphasizes the superior ability of the ReaxFF potential to accurately model the energetics of grain boundaries.

The GB energy per surface area, $\gamma$, quantifies the energy required to create a GB and is expressed as:

$$\gamma =\frac{\left\langle {E}_{{GB}}\right\rangle -\left\langle {E}_{{bulk}}\right\rangle }{A}$$

(1)

Where E_GB is the average potential energy of the atoms located in GB core and E_bulk is the average potential energy of atoms located in the bulk with A being the GB surface area. Using this formulation, the GB energy is calculated to be 2.60 J/m². This calculated GB energy of 2.60 J/m² provides insight into the thermodynamic stability and structural integrity of the grain boundary. A higher GB energy indicates a less stable GB, as more energy is required to maintain the boundary as shown by Olmsted et al.⁴² for Ni, where GB energy increased with disorientation angle, peaked to a maximum and then showed a decrease. This instability can arise from increased atomic misalignment and disrupted bonding at the GB^42,43,44. Conversely, a lower GB energy suggests a more stable boundary with better atomic alignment and bonding continuity. The GB energy obtained in our work is comparable with the values reported for most metals like W, Cr, Mo, and Fe, falling in the range of 1.5–3 J/m^{2 45}.

Displacement cascade simulations were conducted to elucidate the influence of GBs on damage evolution using both Buckingham and ReaxFF potentials. Figure 3a illustrates the initial configuration of the simulation cell prior to cascade initiation. Notably, the core-shell model for oxygen atoms was implemented solely with the Buckingham potential, whereas the ReaxFF potential did not incorporate such a model for oxygen.

Fig. 3: Displacement cascade evolution and defect formation in LiAlO₂ under different potentials.

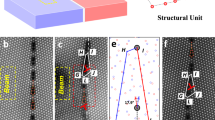
a The initial configuration of the simulation cell, illustrating the top and bottom grains. b The simulation cell after the initiation of displacement cascades using the Buckingham potential, where the formation of void regions is attributed to artifacts inherent to this potential. c The simulation cell post-initiation of displacement cascades using the ReaxFF potential, demonstrating greater stability. d The initial position of the 40 keV lithium PKA, highlighted and enlarged in blue, within the bottom grain prior to displacement. e The final position of the lithium PKA after it came to rest following the cascade evolution along the solid black trajectory. f Visualization of the cascade at the peak damage state, where vacancies are depicted in white and interstitial atoms are color-coded according to their respective elements.

The simulation cell’s state post-cascade evolution is depicted in Fig. 3b for the Buckingham potential and in Fig. 3c for the ReaxFF potential. As previously noted, the Buckingham potential produces significantly elevated energy values for atoms near GBs (positive energies), which likely contributes to the formation of pronounced voids within the simulation cell, as observed in Fig. 3b. Such a void formation is noticed in both LiAlO₂ and LiAl₅O₈ ceramics. This artifact results in an excessive number of defects, reflecting a limitation of the Buckingham potential. In contrast, the ReaxFF potential demonstrates superior performance by preserving the crystallinity of the simulation cell and generating a cascade size that is consistent with that observed in single-crystal simulations reported in our earlier work³.

Figure 3d, e show the trajectory of the primary knock-on atom (PKA), with the PKA’s initial position marked before launch and its final position after coming to rest, respectively. The black solid line indicates the PKA’s trajectory. Figure 3f presents the cascade size at the peak damage state, which is just slightly larger than the damage size observed for a 15 keV PKA in single-crystal LiAlO₂ as documented in our previous study³.

Since the ReaxFF potential has superior performance, the defect analysis was carried out using the results from ReaxFF potentials. Displacement cascade simulations were performed in both LiAlO₂ and LiAl₅O₈ ceramics. Figures 4, 5 illustrate the evolution of vacancies and interstitials in the top and bottom grains for LiAlO₂ and LiAl₅O₈ during cascades. Figure 4 highlights defects in LiAlO₂, where Li vacancies consistently exceed interstitials in both bottom (Fig. 4a) and top grains (Fig. 4b), indicating interstitial migration to the GB. In contrast, Al interstitials dominate over vacancies in the bottom grain (Fig. 4c), likely due to Li atoms occupying Al vacancies, supported by the low antisite defect energy (1.76 eV) reported in our prior work⁶. The Al defects in the top grain are nearly balanced (Fig. 4d), reflecting minimal net exchange.

Fig. 4: Defect evolution in LiAlO₂.

The evolution of defects is quantified in terms of cation vacancies and interstitials for both lithium and aluminum in LiAlO₂. Specifically, for lithium, the defects are analyzed in a for the bottom grain and b for the top grain, while for aluminum in c for the bottom grain and d for the top grain. The observed discrepancy between the numbers of vacancies and interstitials indicates that the grain boundary is effectively acting as a sink for interstitials.

Fig. 5: Defect evolution in LiAl₅O₈.

The evolution of defects is quantified in terms of cation vacancies and interstitials for both lithium and aluminum in LiAl₅O₈. Lithium defects are analyzed in a for the bottom grain and b for the top grain, while aluminum defects are shown in c for the bottom grain and d for the top grain.

Figure 5 shows similar trends for Li in LiAl₅O₈, with vacancies outnumbering interstitials in both grains (Fig. 5a, b). For Al, the bottom grain exhibits a slight interstitial surplus (Fig. 5c) (the difference is considerably smaller than in Fig. 4c), attributed to the higher antisite defect energy (3.22 eV)⁶ as compared to that in LiAlO₂, while the top grain shows comparable counts of vacancies and interstitials (Fig. 5d). These findings show the distinct defect behavior in the two ceramics and the interplay between grain and boundary dynamics.

This discrepancy in interstitials and vacancies can also be attributed to the different atomic sizes and mobility of Li and Al atoms. Li atoms, being smaller and more mobile, are more likely to migrate to grain boundaries, where they can be easily accommodated, thus resulting in a higher number of vacancies within the grains. Conversely, Al atoms, being larger and less mobile, are less likely to migrate to grain boundaries and tend to remain within the grains as interstitials. The bonding environment and energy landscape for Al atoms may favor the retention of interstitials within the grains rather than diffusing to the boundaries. This difference highlights the complex interplay of atomic size, mobility, and local bonding environments in determining defect migration and accommodation within grain boundaries.

Discussion

The role of GB in cascade simulations has been investigated widely but most of the modeling studies have focused on metals, specifically tungsten, as it is the most promising candidate for fusion materials^46,47. Liu et al.³³ investigated the segregation of transmutation induced Re in W using MD, and found that Re preferentially accumulates as substitutional sites near the GB. It impacts the tensile strength by significantly reducing the fracture strength. Their follow-up work¹⁴ found that Re not only segregates at the grain boundary but also forms the $\sigma$-phase WRe complex. The aggregation of rhenium atoms in the σ-phase and GB regions suggests potential for σ-phase growth over long-term evolution.

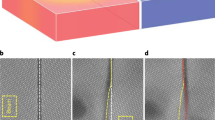
In the present work, STEM analysis of the microstructure and EELS for the composition mapping were performed at a triple junction grain boundary with a pre-existing secondary-phase LiAl₅O₈ particle in the irradiated and annealed γ-LiAlO₂ pellet shown in Fig. 6a. It is important to note that the LiAl₅O₈ particle located at the grain boundary was not formed as a result of ion irradiation; rather, it pre-existed in the as-fabricated pellet. In neutron or ion-irradiated samples, LiAl₅O₈ precipitates are generally observed away from grain boundaries⁴⁸. The Li map, shown in Fig. 6b, clearly indicates Li enrichment at the grain boundary, where fluorine is also enriched and oxygen is depleted, as shown in Fig. 6c, d, respectively. This suggests that the grain boundary likely comprises lithium fluoride, which is immobile, stable to high temperatures, and resistant to ion irradiation. The results provide direct evidence that grain boundaries serve as a preferred pathway for Li diffusion. As discussed elsewhere¹, fluorine was incidentally introduced into the pellet, possibly due to residual F gas in the target chamber during the ion irradiation. When present, fluorine can diffuse into the bulk through grain boundaries, where migrating Li can chemically bond with F to form immobile lithium fluoride.

Fig. 6: Irradiation effects and elemental distribution at triple junction grain boundary in γ-LiAlO₂.

a STEM micrograph and EELS maps showing the distribution of b Li, c F, and d O at a triple junction grain boundary in a γ-LiAlO₂ pellet sequentially irradiated with 90 keV He⁺ and 80 keV H₂⁺ ions to an equal fluence of 2 × 10¹⁷ (He⁺ + H⁺)/cm² at 573 K, followed by vacuum annealing at 873 K for 30 min.

In our MD simulations, we observe a significantly higher number of Li vacancies within the grains compared to interstitials, indicating that Li interstitials are effectively migrating to and being absorbed by the GBs. This migration and absorption by GBs underscore the GB’s role as a sink for Li interstitials, preventing the formation of Li precipitates near the GB and leading to the formation of a denuded zone. For Al atoms, the simulations reveal a reversed trend: a higher concentration of Al interstitials compared to Al vacancies within the grains. This suggests that Al interstitials do not migrate to the GB as readily as Li interstitials. The lower mobility of Al interstitials can be attributed to the larger atomic size and stronger bonding of Al atoms, which hinder their diffusion. Consequently, the accumulation of Al interstitials within the grains provides a high concentration of Al, promoting the nucleation and growth of LiAl₅O₈ precipitates in the grain centers. These findings validate our MD simulations by demonstrating that the GB acts as a sink for Li atoms, leading to the observed denuded zones in LiAlO₂. Simultaneously, the retention of Al interstitials within the grains aligns with the experimental observation of LiAl₅O₈ precipitate formation in the grain centers. This understanding of defect dynamics and precipitate formation under irradiation conditions highlights the crucial role of atomic size, bonding characteristics, and GB interactions in determining the stability and behavior of irradiated ceramics.

Similar observations have been reported by refs. ^35,36 who explored grain boundaries such as tilt and twist boundaries in BCC Fe, while varying the PKA parameters (distance and direction) relative to the GB plane. Their findings revealed that these GBs behave similarly to those in FCC metals, where interstitials are preferentially absorbed during collision cascades. Also, they found that the GBs acted as barriers to the cascade, preventing focused collisions from crossing the GB plane. Furthermore, they found that boundary structure significantly influenced defect absorption, with the twist boundary producing four times more defects than the tilt boundary during collision cascades.

The specific roles of GBs in LiAlO₂ and LiAl₅O₈ are elucidated through the analysis of Li and Al atom concentrations in a small region enclosing the PKA, as depicted by the region illustrated in Fig. 3d, e respectively. Figure 7a, b present the temporal concentration profiles of Li atoms within the small region of nanocrystalline grain and at the GB of LiAlO₂ as shown in Fig. 3d, e. The analyses presented henceforth are for a single simulation for the PKA direction $\hat{i}=0.17,\,\hat{j}=0.62$ ${and}$ $\hat{k}=0.77$ only. Since these are localized dynamic analyses, only one simulation was chosen for detailed analysis to reveal and understand the atomic exchanges taking place between the GB and the grain. Over the 200 ps simulation period, the cumulative exchange of Li atoms between the grain and the GB in LiAlO₂ amounts to 28 atoms, with 9 atoms in the grain and 19 atoms in the GB. In contrast, Fig. 7c, d illustrate the temporal concentration profiles of Li atoms in the grain and at the GB of LiAl₅O₈. The total transfer of Li atoms between the grain and the GB in LiAl₅O₈ during the same simulation duration is 13 atoms. When adjusted for stoichiometry, considering the approximate atomic concentrations of 7% in LiAl₅O₈ and 25% in LiAlO₂, the Li atom transfer in LiAl₅O₈ should be multiplied by a factor of 3.5. This adjustment yields an effective total transfer of approximately 46 Li atoms for LiAl₅O₈. This comparison reveals a notable difference in the dynamics of Li atom exchange between the two materials. For every 28 Li atoms exchanged between the grain and the GB in LiAlO₂, an equivalent exchange of approximately 46 Li atoms occurs in LiAl₅O₈. This discrepancy suggests a potentially superior defect healing capability in LiAl₅O₈, attributed to its higher efficiency in Li atom exchange between the grain and the GB. In our prior study⁶, we quantified the migration barriers for Li interstitials in LiAlO₂ and LiAl₅O₈, highlighting a substantial enhancement in mobility for the latter. In LiAlO₂, interstitial migration occurs predominantly along a quadrangular channel aligned with the 〈001〉 crystallographic direction, with a calculated energy barrier of 1.41 eV, which correlates closely with the 1.28 eV reported by ref. ⁴⁹. Conversely, in LiAl₅O₈, interstitials navigate a more complex zigzag trajectory between tetrahedral and octahedral voids. The highest energy barrier along this migration path is 0.42 eV reported in our prior work⁶, in close agreement with the 0.33 eV reported by ref. ⁵⁰. The substantially lower migration barrier in LiAl₅O₈, less than one-third of that in LiAlO₂, directly correlates to a marked increase in Li interstitial mobility. This difference in mobility explains the observed higher exchange rates and reflects the fundamental disparities in atomic migration mechanisms between these two ceramic systems. The enhanced mobility and higher exchange rate of Li atoms in LiAl₅O₈ facilitate more effective annealing of vacancies generated during damage evolution, thereby contributing to the material’s overall defect mitigation and structural stability.

Fig. 7: Temporal evolution of Li atom concentration in grains and grain boundaries of LiAlO₂ and LiAl₅O₈.

Concentration profiles of Li atoms during the cascade evolution for (a) Li in LiAlO₂ grain, (b) Li in LiAlO₂ grain boundary, (c) Li in LiAl₅O₈ grain and (d) Li in LiAl₅O₈ grain boundary.

A similar analysis for Al atoms has been conducted and is presented in Fig. 8. Figure 8a, b depict the temporal concentration profiles of Al atoms in the grain and at the GB of LiAlO₂, respectively. Figure 8c, d show the corresponding profiles for Al atoms in LiAl₅O₈. In LiAlO₂, there is a transfer of 27 Al atoms between the grain and the GB over the course of the 200 ps simulation. For LiAl₅O₈, the total transfer of Al atoms between the grain and the GB is 45 atoms. When adjusting for stoichiometry, the results yield an effective transfer of approximately 31 Al atoms in LiAl₅O₈ for every 27 Al atoms transferred in LiAlO₂. This analysis further supports the notion of enhanced atomic mobility in LiAl₅O₈. The faster exchange of Al atoms between the grain and the GB in LiAl₅O₈ suggests a more efficient mechanism for damage annealing in this material. The increased transfer rate of both Li and Al atoms in LiAl₅O₈ facilitates the rapid healing of vacancies and interstitials created during displacement cascades, contributing to superior defect mitigation. This enhanced atomic mobility emphasizes the potential of LiAl₅O₈ for applications where radiation damage and defect accumulation are critical concerns, offering insights into the material’s intrinsic capability for maintaining structural stability under irradiation conditions.

Fig. 8: Temporal evolution of Al atom concentration in grains and grain boundaries of LiAlO₂ and LiAl₅O₈.

Concentration profiles of Al atoms during the cascade evolution for (a) Al in LiAlO₂ grain, (b) Al in LiAlO₂ grain boundary, (c) Al in LiAl₅O₈ grain and (d) Al in LiAl₅O₈ grain boundary.

Our analysis based on this temporal concentration of cations in the grain and GB have been previously explained in an experimental work by Dey et al.²⁵. In nanocrystalline materials, the proximity of GB significantly increases the likelihood of defects being located close to these boundaries, where close signifies a distance substantially shorter than the mean diffusion path of a defect²⁵. The grain boundaries serve as effective sinks for these radiation-induced defects, leading to their preferential migration towards the boundaries. This phenomenon resembles recrystallization, wherein atoms from smaller, defect-rich grains migrate across boundaries and integrate into larger, more pristine grains²⁴. Consequently, this process leads to a reduction in net defect concentration, as defects from the smaller grains are not transferred to the larger ones. Thus, the material undergoes a transition to defect-free grains, enhancing the material’s resilience against radiation damage.

Figure 7a, b present the temporal evolution of Li atom concentrations within a localized region of the nanocrystalline grain and at the adjacent GB, as illustrated in Fig. 3d, e. However, since this analysis pertains to a subsection of the entire GB system, it does not account for atom flux across the boundaries of the analyzed regions. Consequently, the total number of Li and Al atoms in these plots is not strictly conserved, leading to the apparent inconsistencies noted in the earlier discussion. Figure 9 provide insights into the behavior of Li and Al atoms when the analysis encompasses the entire GB for LiAlO₂. For Li atoms (Fig. 9a), the GB exhibits a net increase in concentration following the initiation of the cascade, rising from 2088 atoms initially to 2099 atoms at 200 ps. Concurrently, the bottom grain loses 5 Li atoms, and the top grain loses 4, resulting in a total loss of 9 atoms from the grains. This net increase in GB concentration and corresponding depletion in the grains indicate a clear migration of Li atoms from the grains to the GB. The small discrepancy between the GB gain (11 atoms) and the grain loss (9 atoms) is attributed to double counting at the boundary, likely arising from atom deletion expressions in OVITO during trajectory analysis. Interestingly, the profiles of Li atom concentrations in the top and bottom grains, as shown in Fig. 9b, reveal a mirror-like relationship. As Li atoms leave the bottom grain, a nearly equivalent number is gained by the top grain, showing a dynamic intergranular exchange mediated by the GB. This continuous flux highlights the critical role of defect mobility in redistributing Li atoms and promoting defect recombination at the GB interface. In contrast to Li, the behavior of Al atoms is markedly different. As illustrated in Fig. 9c, the GB experiences a net reduction of 6 Al atoms over the simulation period. Simultaneously, Fig. 9d shows that the top grain gains 7 Al atoms, while the bottom grain retains its initial number. This suggests a preferential redistribution of Al atoms from the GB into the grains. The contrasting trends for Li and Al atom dynamics point to a phase evolution mechanism in which the GB becomes enriched in Li while the grains preferentially retain or gain Al. This behavior aligns with the formation of Li-depleted LiAl₅O₈ phases, driven by the migration of Al atoms to the grain interiors. These findings provide crucial insights into the atomistic processes occurring during irradiation in nanocrystalline LiAlO₂. The preferential migration of Li atoms to the GB and the complementary movement of Al atoms into the grains signify a defect-mediated phase evolution pathway. Such dynamics emphasize the interplay between vacancy and interstitial behaviors, defect mobilities, and interfacial sinks in determining the structural and compositional evolution of irradiated materials.

Fig. 9: Temporal evolution of atom counts for Li and Al in the grain boundary and top and bottom grains of LiAlO₂.

a Shows the changes in Li atom counts in the grain boundary and b shows the same for top and bottom grain, revealing a net migration of Li atoms from the grains to the grain boundary after the initiation of the cascade. The mirror-like profiles between the top and bottom grains in (b) indicate a continuous intergranular exchange of Li atoms across the grain boundary. c, d Display the corresponding changes in Al atom counts, showing a net loss of Al atoms from the grain boundary (c) and a preferential accumulation of Al in the top grain (d). These dynamics highlight the contrasting behaviors of Li and Al during irradiation, with Li atoms enriching the grain boundary while Al atoms migrate into the grains.

An analogous analysis of LiAl₅O₈ in Fig. 10 reveals striking differences in atomic migration behaviors when compared to LiAlO₂. The lithium content within the grain boundary region rises from an initial 519 to 525 atoms by the conclusion of the cascade, as shown in Fig. 10 a, signifying a net gain of 6 atoms. This is accompanied by a loss of 4 Li atoms from the top grain and a marginal gain of 1 Li atom in the bottom grain (Fig. 10b). When adjusted for the stoichiometric factor of 3.5 in LiAl₅O₈, the observed gain in the GB equates to a transfer of approximately 21 Li atoms in a comparable LiAlO₂ framework. This finding shows a higher flux of lithium from the grains to the grain boundary in LiAl₅O₈, indicative of enhanced lithium mobility or a stronger thermodynamic affinity for accumulation in the GB of this compound under cascade conditions. In contrast, aluminum atoms in LiAl₅O₈ display a behavior distinctly contrary to that in LiAlO₂. The grain boundary in LiAl₅O₈ exhibits an increase in aluminum concentration by the cascade’s end (Fig. 10c), signifying the preferential retention of Al interstitials, while both the top and bottom grains experience a net depletion of Al atoms (Fig. 10d). This inversion of behavior suggests that the structural and chemical environment of LiAl₅O₈ promotes a stronger driving force for aluminum migration toward the GB. The findings reveal a phase-dependent divergence in atomic redistribution mechanisms, with LiAl₅O₈ exhibiting pronounced lithium flux to the GB and aluminum interstitial retention. These unique dynamics may play a critical role in the formation of defect phases and the stability of the material under irradiation.

Fig. 10: Temporal evolution of Li and Al atom counts in the grain boundary and top and bottom grains of LiAl₅O₈ after a cascade event.

a Lithium shows a net increase of 6 atoms in the grain boundary, with b the top grain losing 4 atoms and the bottom grain gaining 1 atom. c Aluminum exhibits an increase in the grain boundary, while d both grains lose atoms, indicating preferential accumulation of Al interstitials at the grain boundary.

Simulating fission gas behavior using MD poses significant computational challenges, primarily due to the limited availability of interatomic potentials that accurately define the interactions between fission gases and fuel or structural components. Existing literature predominantly addresses well-studied materials, such as helium (He) and xenon (Xe) evolution in uranium dioxide (UO₂)^51,52,53. Given the pivotal role of LiAlO₂ pellets in tritium production within TPBARs, MD simulations investigating tritium behavior in LiAlO₂ are crucial for understanding its performance. Key areas of interest include tritium diffusion within the grain and at GBs, tritium defect cluster formation, migration to surfaces, and diffusion as a function of displacements per atom (DPA). Motivated by these considerations, we have conducted preliminary simulations to evaluate tritium behavior in single-crystal LiAlO₂, focusing on its interactions at predefined Li and Al vacancies to assess the adequacy of the ReaxFF potential employed.

The simulations depicted in Fig. 11 illustrate the behavior of tritium atoms in a LiAlO₂ single crystal, starting from its random distribution in the lattice (Fig. 11a, b). As the simulation progresses, tritium atoms exhibit significant mobility, migrating rapidly within the crystal structure (Fig. 11c, d). This migration leads to the formation of stable configurations with oxygen atoms, specifically T₃O and T₄O complexes at aluminum vacancies, and T-O complexes at lithium vacancies (Fig. 11e) following the trajectory shown in Fig. 11f. These findings are consistent with previous studies, which have reported low formation energies for T₃O (−4.27 eV) and T₄O (−2.28 eV) at Al vacancies, and T-O (−0.31 eV) at Li vacancies⁵⁴.

Fig. 11: Tritium migration, interaction, and diffusion dynamics in LiAlO₂.

a Initial configuration of LiAlO₂ featuring tritium atoms randomly distributed at lithium (Li) and aluminum (Al) vacancies. b–d Temporal evolution of the tritium atoms, showing their positions at the initial, intermediary, and final stages of the simulation, respectively. e Configurations of T-O atoms resulting from tritiation. f Trajectory of tritium atoms throughout the simulation at 300 K, illustrating their migration patterns. g Mean squared displacement (MSD) curves for tritium, used to determine the diffusion coefficients.

The diffusion coefficient for tritium, calculated from the MSD curves (averaged over all tritium atoms in the system) at 300 K (Fig. 11g), was found to be 1.33 × 10⁻¹⁴ m²/s. This value is slightly higher than reported in our earlier work, which reported a diffusion coefficient of 2.65 × 10⁻¹⁵ m²/s at 500 K using free energy cluster dynamics (FECD)⁵⁵. This discrepancy highlights a fundamental limitation inherent in MD simulations, which rely on the slope of MSD curves to calculate diffusion coefficients. These curves are often corrugated and irregular, making it challenging to determine slopes with a precision greater than 3–4 decimal places⁵⁶. Achieving such precision would require a near-horizontal MSD curve with an almost zero slope, indicative of negligible diffusion. For instance, when the MSD is expressed in Ų/ps, a slope of 10⁻⁴ corresponds to a diffusion coefficient of approximately 10⁻¹² m²/s, which is generally the lower boundary achievable through MD simulations. In contrast, experimental diffusion coefficients often reach orders as low as 10^-20m²/s, a range virtually unattainable with MD due to these methodological constraints. The inherent differences between MD and alternative approaches, such as cluster dynamics, exacerbate these discrepancies. While MD directly models atomic trajectories, cluster dynamics solves rate equations defined by defect types and cluster interactions, leading to fundamentally distinct outcomes. Given these differences, achieving matching coefficients across MD and cluster dynamics, or other experimental techniques, is inherently challenging, and discrepancies of this nature are expected.

These preliminary simulations provide valuable insights into the defect dynamics and diffusion mechanisms of tritium in LiAlO₂. They reveal that tritium atoms preferentially form stable configurations with oxygen atoms, which likely contributes to their mobility and interaction with the crystal lattice. The rapid migration and stable defect formation suggest that LiAlO₂ can efficiently accommodate tritium, potentially mitigating the adverse effects of radiation damage through defect recombination and migration, however this hypothesis needs to be investigated with further simulations.

Overall, these results lay the groundwork for more comprehensive studies on tritium behavior in LiAlO₂, particularly under irradiation. Future work will extend these simulations to explore tritium dynamics in the presence of GB, which are expected to act as sinks for defects, thereby enhancing the radiation tolerance of the material. This research direction is essential for optimizing the performance and longevity of LiAlO₂ in TPBARs and other nuclear applications where tritium management is critical.

In summary, this study provides an analysis of radiation-induced defect dynamics in lithium aluminate ceramics, specifically LiAlO₂ and LiAl₅O₈, using MD simulations. Our findings demonstrate the critical role of GBs in mitigating radiation damage by acting as efficient sinks for defects. The GBs facilitate defect recombination and significantly reduce the net concentration of radiation-induced defects within the grains. For Li atoms, our simulations show a higher number of vacancies compared to interstitials, indicating that interstitials migrate to the GBs. Conversely, for Al atoms, a higher number of interstitials than vacancies were observed within the grains of LiAlO₂, suggesting the formation of LiAl₅O₈ precipitates, consistent with experimental observations. The GBs in LiAl₅O₈ exhibited superior defect healing properties, attributed to more efficient atomic exchange between the grain and GB compared to LiAlO₂. Furthermore, our study on tritium behavior in LiAlO₂ revealed rapid migration and stable configuration formation with oxygen atoms, with a diffusion coefficient of 1.33 × 10⁻¹⁴ m²/s aligning closely with experimental data.

Overall, our findings establish a foundational understanding of defect dynamics in LiAlO₂ and LiAl₅O₈ ceramics, emphasizing the importance of GBs in radiation damage mitigation. These insights are essential for the development and optimization of materials for use in radiation-intensive environments, such as in TPBARs in nuclear reactors. Future work will focus on further elucidating tritium dynamics under irradiation and exploring the long-term stability of these materials under prolonged radiation exposure.

Computer simulation methods

Potential selection

Previous works have employed several potentials for LiAlO₂ like the 1996 Jacob’s potential⁵⁷, the Tsuchihira-Oda-Tanaka (TOT) potential developed in 2009⁵⁸, and the more recent Buckingham potentials⁵⁹. Jacob’s potential is limited by its inability to stabilize the crystal structure effectively³² while the TOT potential is specifically parameterized for LiAlO₂, rendering it incompatible with LiAl₅O₈ due to its unique set of charges.^3,6. Therefore, Roy et al.^3,6 adopted the Buckingham potential combined with the Ziegler–Biersack–Littmark (ZBL)⁶⁰ potential to simulate cascade damage in LiAlO₂ and LiAl₅O₈. In this work, we adopt the Buckingham potential once again to evaluate its suitability for simulating grain boundary (GB) behavior under cascade damage conditions. The details of the potential have been provided in our prior publications^3,6.

During our simulations, we encountered limitations of the Buckingham potential in accurately representing cascade events in systems containing GBs. To address these limitations, we identified and implemented an alternative, the reactive force field (ReaxFF)⁶¹ potential developed by Narayanan et al.³⁷.

The total energy of a system simulated by ReaxFF is expressed as⁶¹:

$$\begin{array}{ll}E=\mathop{\sum}\nolimits_{\begin{array}{c}i,j\\ i < j\end{array}}{E}_{{bond},{ij}}+\mathop{\sum}\nolimits_{i}{E}_{{over},i}\\\quad+\mathop{\sum}\limits_{i}{E}_{{under},i}+\mathop{\sum} \limits_{i}{E}_{{lp},i}\mathop{\sum}\nolimits_{\begin{array}{c}i,j,k\\ i < j < k\end{array}}{E}_{{val},{ijk}}\\\quad+\mathop{\sum}\nolimits_{\begin{array}{c}i,j\\ i < j\end{array}}{E}_{{van},{ij}}+\mathop{\sum} \nolimits_{\begin{array}{c}i,j\\ i < j\end{array}}{E}_{{Col},{ij}}\end{array}$$

(2)

Where ${E}_{{bond},{ij}}$ is the bond energy between ith and jth atoms, ${E}_{{over},i}$ and ${E}_{{under},i}$ denote the energy penalties for over and under coordination around ith atom. ${E}_{{lp},i}$ is the energy of the lone pair electrons around the ith atom, ${E}_{{val},{ijk}}$ describes the energy related to the deviation of the valence angle formed at the jth atom by the ith and kth atoms from their equilibrium positions. ${E}_{{van},{ij}}$ and ${E}_{{Col},{ij}}$ are contributions from van der Waals and Coulomb interactions, respectively.

Both Buckingham and ReaxFF are smoothly combined with ZBL potential to yield an effective short-range interaction for atoms coming closer than 0.5 Å. The ReaxFF potential is particularly advantageous as it includes a comprehensive definition of hydrogen interactions with the Li-Al-O system, which can be adapted for tritium by modifying the hydrogen mass in the potential file. We conducted a comparative analysis of the Buckingham and ReaxFF potentials, assessing their effectiveness in simulating GB behavior and cascade damage. The ReaxFF potential demonstrating superior performance in accurately capturing the necessary physical phenomena was selected for further detailed analysis.

GB creation and energy analysis

The grain boundary was generated by constructing two grains converging at an interface, using the Voronoi tessellation method implemented in the ATOMSK toolkit⁶². The unit cell data were supplied to ATOMSK, along with the coordinates of two nodes, one for each grain. This resulted in a supercell containing two grains, with the first grain rotated by 95°, 36°, and −106° and the second by 90°, −30°, and 145° about the x, y, and z axes, respectively. This approach was applied to both LiAlO₂ and LiAl₅O₈. The edge lengths of the resulting supercells are 18 × 18 × 18 nm, comprising approximately 500,000 atoms. After generating the GB, the system is relaxed for 20 ps in the NVE ensemble. A Berendsen thermostat is used to rescale the velocity of the atoms at every successive timestep to maintain a constant temperature.

Cascade simulations

We employed the LAMMPS⁶³ code to simulate displacement cascades, with periodic boundaries on all sides. Displacement cascades were simulated in an isolated system with a fixed number of particles and constant volume (NVE ensemble). Additionally, a 5 Å thick Langevin bath maintained at 300 K was used to dissipate the heat generated by the high-energy primary knock-on atom (PKA). This thermostat effectively limited the maximum temperature rise during PKA initiation while having a negligible effect on defect production due to the small volume of atoms involved. The velocities of atoms within the thermostat region were rescaled to correspond to 300 K at each timestep, simulating the dissipation of heat energy from the cascade region into the bulk material. A lithium (Li) atom located 5 Å below the GB and at the center of the plane was selected as the PKA and initiated in 8 randomly chosen directions towards the positive z-axis, ensuring it traveled from one grain into the other through the GB. The PKA energy was set to 40 keV. This energy level is sufficient to capture the essential physical mechanisms occurring during displacement cascades.

Experimental details

To corroborate the simulation results with empirical evidence, targeted irradiation experiments were performed on LiAlO₂ pellets to investigate the migration behavior of Li atoms. A γ-LiAlO₂ pellet was sequentially irradiated at 60° off the surface normal with 90 keV He⁺ and 80 keV H₂⁺ ions to an equal fluence of 2 × 10¹⁷ (He⁺+H⁺)/cm² at 573 K. The ion flux was approximately 2 × 10¹³ ions/cm²/s. After irradiation, the sample was annealed in vacuum at 873 K for 30 min, with ramping-up and ramping-down rates of 1 K/s. A cross-sectional scanning transmission electron microscopy (STEM) specimen was prepared using a FEI Helios NanoLab dual-beam focused ion beam (FIB) microscope. A standard lift-out procedure was used, involving Ga⁺ ions at 30 keV for cutting/thinning, and 5 keV for polishing the specimen. STEM was performed using an aberration-corrected JEOL JEM-ARM 200CF microscope operating at an accelerating voltage of 200 kV. Elemental mapping was conducted using electron energy loss spectroscopy (EELS) with a 1 eV ch⁻¹ dispersion.