Introduction

Corrosion is a pervasive degradation mechanism of materials, posing serious challenges to many high-stake industries1,2. The corrosion behaviors of materials have been extensively studied as a means to devise effective corrosion prevention and control strategies. Corrosion rate is one of the most critical parameters of a corrosion system, directly determining the service life of the substrate involved3. In situ electrochemical techniques, including the Tafel extrapolation method4, the linear polarization resistance (LPR) method2,5, and electrochemical impedance spectroscopy (EIS)6, constitute the mostly commonly used approach for measuring corrosion rates in real time. Nevertheless, these techniques suffer from two major limitations that could compromise their measurement accuracy. Firstly, they all depend upon empirical quantities, i.e., Tafel coefficients, for converting raw data, i.e., polarization resistances or charge transfer resistances, into corrosion rates7,8, rendering the measurement process tedious and prone to uncertainty. Secondly, the derivation process of the Tafel coefficients of a corrosion system, which essentially relies on the polarization of the substrate over a wide range of electric potentials, could permanently alter the surface condition of the substrate, thus changing its corrosion behavior.

The ability to measure real-time corrosion rates in a more straightforward and non-destructive manner would be significant to understanding the kinetics of corrosion systems. Recently, in situ ultrasonic testing, which employs low-energy, harmless mechanical waves as diagnostic signals, has been utilized to directly monitor corrosion-induced wall thickness losses (WTLs)9,10,11. While the corrosion rate at a given time instant can be evaluated by taking the gradient of a certain number of preceding wall thickness (WT) data points12,13,14, the performance of such measurement protocol is highly dependent on the number of data points considered. More specifically, on one hand, if the number of data points considered is too little, the measurement accuracy could be jeopardized due to the noise associated with the data, but on the other hand, if the number of data points considered is too large, the measurement time would be prolonged, causing transient changes in corrosion rate to be missed out on. Therefore, it would be desirable to introduce a measurement protocol that could first detect changes in corrosion rate based on WT data acquired in real time and then make an evaluation of the new corrosion rate once a change has been detected.

In this work, we integrate the Generalized Likelihood Ratio (GLR) algorithm into an ultra-high-precision ultrasonic WTL monitoring system, which was introduced by us in previous work10,11, with a view to realize rational determination of real-time corrosion rates. During a corrosion process, the GLR algorithm will calculate the probability of occurrence of a change in corrosion rate whenever a new WT data point has been acquired; if it is deemed that a change in corrosion rate has occurred, i.e., if the probability of occurrence calculated has exceeded the preset threshold, the new corrosion rate will be evaluated by taking the gradient of the WT data points within the time period bounded by the current time instant and the time of occurrence of the preceding change in corrosion rate. To prepare the proposed ultrasonic technique for real-world applications, the influence of a key user-defined parameter of the GLR algorithm on the two main performance indicators, i.e., detection speed and measurement accuracy, was thoroughly investigated by both numerical modeling and physical experimentation. Further, the measurement accuracy of the proposed technique was assessed through potentiostatic corrosion experiments, where the real-time corrosion rates provided by the proposed technique matched very well with those calculated from the corrosion currents. Finally, when the proposed technique was applied to monitoring natural acidic corrosion processes, it successfully resolved the evolutions in corrosion rate during the destruction and re-establishment of protective layers, demonstrating promising application prospect.

Results and discussion

Ultrasonic corrosion monitoring system

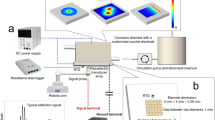
The experimental setup shown in Fig. 1(a) is used as the hardware system for ultrasonic monitoring of corrosion-induced WTLs. For each corrosion substrate (see the “Preparation of corrosion substrates” section), a 4 × 4 × 0.25 mm piezoelectric transducer (PZT-5H, Kaiqing Optoelectronic Materials, China) is adhered to the center of the non-working surface, and a resistance temperature detector (RTD) is installed near the piezoelectric transducer. The edges of the working surface of the substrate are covered by PET tape, leaving a circular opening with a diameter of 32 mm in the center as the corrosion area. A 3D printed, 40 × 40 × 60 mm corrosion chamber is glued onto the PET tape. A three-electrode system that comprises the substrate, a copper mesh counter electrode and an Ag/AgCl reference electrode, is set up using an electrochemical workstation (Autolab PGSTAT302N, Metrohm, Switzerland).

Fig. 1: The ultrasonic system for monitoring corrosion-induced WTLs.
figure 1

a The hardware configuration of the ultrasonic system. b An example of the ultrasonic signals output by the ultrasonic system.

Full size image

During a corrosion experiment, electrolyte solution is circulated through the corrosion chamber by a pump. The three-electrode system is used either to apply anodic polarization to the substrate or to carry out electrochemical testing. An arbitrary waveform generator & oscilloscope unit (Handyscope HS5, TiePie Engineering, Netherlands) commands the piezoelectric transducer to continuously excite ultrasonic shear waves that propagate along the thickness direction of the substrate, in the form of Hann-windowed 5-cycle sinusoidal tonebursts with a center frequency of 2 MHz, and to acquire the reflections off the working surface of the substrate. According to Huygens’ principle15,16,17, a 5 × 5 mm area of working surface of the substrate is insonified by the ultrasonic waves. A resistance temperature data logger (PT104, Pico Technology, UK) instructs the RTD to record the temperature variation of the substrate. The WTLs of the substrate are determined in real time based on the ultrasonic signals acquired and the temperature variation recorded (see the “Ultrasonic wall thickness measurement” section).

Ultrasonic wall thickness measurement

Figure 1(b) plots a typical ultrasonic signal acquired by the aforementioned ultrasonic system. The WT that the signal would correspond to can be calculated by

$${WT}=\frac{\left({{ToA}}_{2}-{{ToA}}_{1}\right)V\left(T\right)}{2}$$
(1)

where \({{ToA}}_{1}\) and \({{ToA}}_{2}\) are the time-of-arrival’s of the first and the second reflected wavepacket, and V(T) is the current temperature-dependent shear wave velocity. From Eq. (1), it can be seen that the measurement accuracy of WTs depends on how accurate ToAs and shear wave velocities are determined. The procedures for determining ToAs and shear wave velocities are provided in the “Determination of time-of-arrival’s” and “Determination of shear wave velocities” sections.

Determination of corrosion rates using GLR algorithm

During a corrosion experiment, whenever a new WT data point is acquired, the accumulated logarithmic likelihood that a certain change in corrosion rate (η) has taken place is calculated by refs. 18,19,20

$$Z\left(k\right)=\mathop{\sum }\limits_{i=j}^{k}\frac{2\eta \left({t}_{i}-{t}_{j}\right)\left({y}_{i}-{c}_{0}+{w}_{0}{t}_{i}\right)-{\eta }^{2}{\left({t}_{i}-{t}_{j}\right)}^{2}}{2{{\sigma }_{d}}^{2}}$$
(2)

where k is sequence number of the newly acquired WT data point, j is the sequence number of the WT data point after the acquisition of which the preceding change in corrosion rate was detected, t stands for time, yi is the thickness of the substrate at the ith WT data point, c0 is the thickness of the substrate at the jth WT data point, w0 is the last known corrosion rate (i.e., the corrosion rate evaluated after the acquisition of the jth WT data point and the detection of the preceding change in corrosion rate), σd is the expected standard deviation of the noise of the WT data, and η is expressed as

$$\eta =\frac{{\sum }_{i=j}^{k}({t}_{i}-{t}_{j})({y}_{i}-{c}_{0}+{w}_{0}t)}{{\sum }_{i=j}^{k}{\left({t}_{i}-{t}_{j}\right)}^{2}}$$
(3)

Before a corrosion rate has been identified, w0 is set to zero and c0 is set to the initial thickness of the substrate. Note that the true standard deviation of the noise of the WT data is given by σs.

A change in corrosion rate is deemed to have been detected at the kth time instant if

$$Z\left(k\right) > {\mathrm{ln}}\left(\frac{1-\beta }{\alpha }\right)$$
(4)

where α is the probability of false-calling (i.e., opposite to confidence level) and β is the probability of non-detection (i.e., opposite to probability of detection). In this work, both α and β are set to 0.01 with a view to enforce a 99% probability of detection and a 99% confidence level20. Following the detection of the change in corrosion rate, the corrosion rate is updated by applying linear regression to the WT data points within the time period bounded by j and k.

Numerical analysis of GLR algorithm-enabled ultrasonic corrosion rate monitoring

The calculation of Z in Eq. (2) relies on the assumed noise level of the WT data acquired (i.e., σd). If σd is set to a small value, the increase in the value of Z with respect to the number of WT data points (i.e., k) would be rapid, resulting in fast detection of changes in corrosion rate. However, the corrosion rates determined in these cases could suffer from low accuracy due to insufficient mitigation of the influence of noise. Therefore, in this section, the impact of the user-defined parameter σd on both the detection speed and the measurement accuracy of the proposed GLR algorithm-enabled ultrasonic corrosion rate monitoring technique is investigated using simulated WT data.

As shown in Fig. 2(a), WT data that correspond to corrosion rate changes of 10 nm/s, 20 nm/s and 50 nm/s were generated and were further added with normally distributed noise with a standard deviation (σs) of 100 nm. For each change in corrosion rate, 1000 sets of noise-contaminated WT data were produced and processed by the GLR algorithm under different σd values. Expectedly, the use of a larger \({\sigma }_{d}\) value will lead to a lower detection speed but a higher measurement accuracy, as confirmed by Fig. 2b, c. Note that the measurement errors were each calculated by (Rg − Rs)/Rs, where Rs is the corrosion rate simulated, and \({R}_{g}\) is the corrosion rate evaluated by the GLR algorithm. Since the improvement in measurement accuracy with respect to σd/σs is significant when σd/σs < 1, the use of \({\sigma }_{d}\) values that obey σd/σs > 1 is recommended. Moreover, Fig. 2(c) also shows that the higher the change in corrosion rate, the higher the detection speed will be. Mathematically, this is due to the fact that the value of Z is directly proportional to the value of \({y}_{i}-{c}_{0}+{w}_{0}{t}_{i}\), which stands for the difference between the true current WT and the current WT predicted based on the last known corrosion rate.

Fig. 2: Numerical performance analysis of the GLR algorithm-enabled ultrasonic corrosion rate monitoring technique.
figure 2

a Examples of simulated wall thickness data containing noise. b Detection times of changes in corrosion rate. c Measurement errors of corrosion rates. In (b) and (c), the shaded areas each stand for the standard deviation of the results obtained based on the 1000 sets of wall thickness data simulated.

Full size image

Shear wave velocity vs. temperature relationship

Figure 3(a) shows the shear wave velocity vs. temperature relationship of one of the substrates used in this work. As anticipated, a linearly decreasing trend is observed. For this specific substrate, its shear wave velocity vs. temperature relationship was found to be \(v=-0.5177\cdot T+3284.8\).

Fig. 3: Compensation for the effect of temperature.
figure 3

a The shear wave velocity vs. temperature relationship of an example substrate. b Ultrasonic thickness measurements of the substrate.

Full size image

For the aforementioned substrate, the ultrasonic thickness measurements that were made with and without compensation for the effect of temperature on shear wave velocity, in the absence of corrosion, are compared in Fig. 3b. When a constant shear wave velocity was considered, the thickness measurements obtained fluctuated significantly with the temperature variation. On the other hand, when shear wave velocities that were calculated based on instantaneous temperatures were used, the thickness measurements obtained fluctuated only mildly around the true thickness of the substrate, agreeing with the fact that the substrate was not subjected to corrosion. The standard deviation of the temperature-compensated thickness measurements is approximately 100 nm. For all the subsequent corrosion experiments, σs, i.e., the true standard deviation of the WT data, is set to 100 nm.

Corrosion rate monitoring under anodic polarization

Galvanostatic and potentiostatic corrosion experiments were conducted to assess the performance of the proposed ultrasonic corrosion rate monitoring technique. During each experiment, the electric current or electric potential applied caused the substrate, i.e., the anode, to dissolve according to \({Fe}\to {{Fe}}^{2+}+2{e}^{-}\), and the theoretical corrosion rate was calculated by

$$R=\frac{M\cdot i}{F\cdot \rho \cdot n}$$
(5)

where F is the Faraday constant, M and ρ are the molar mass and the density of N80 steel, respectively, n is the number of electrons released when one iron atom is oxidized, and i is the corrosion current. For steels, n is equal to 2.1921,22,23. The corrosion current is either the applied electric current in the case of a galvanostatic experiment or the resultant electric current in the case of a potentiostatic experiment.

Corrosion rate monitoring under galvanostatic corrosion

From the numerical analysis presented above, it was found that the user-defined parameter σd, i.e., the expected noise level of the WT data, directly affects the detection speed and the measurement accuracy of the proposed ultrasonic corrosion rate monitoring technique. Also, it was suggested that in order to ensure that sufficient measurement accuracy is achieved, σd values that obey σd/σs > 1 should be adopted. In this section, the aforementioned findings, which were attained via numerical modeling, are further examined through physical experimentation.

Table 1 provides the details of the experiments conducted and the theoretical corrosion rates. The ultrasonic thickness measurements of the substrates, which are plotted in Fig. 4a, were processed by the GLR algorithm under different σd values. From Fig. 4b, c, it is observed that the trends exhibited by the experimental results concur with that demonstrated by the numerical ones (i.e., Fig. 2b, c). More specifically, the detection speed of the proposed technique decreases with σd but increases with corrosion rate, while its measurement accuracy increases with σd. In addition, the criterion for choosing σd values should be toughened from \({\sigma }_{d}/{\sigma }_{s} > 1\) to \({\sigma }_{d}/{\sigma }_{s} > 1.5\) to account for the higher level of uncertainty associated with physical experiments, limiting measurement errors to less than 20%.

Fig. 4: Results of galvanostatic corrosion experiments.
figure 4

a WT data obtained during the experiments. b Detection times of changes in corrosion rate. c Measurement errors of corrosion rates. The corrosion rates at \({\sigma }_{d}/{\sigma }_{s}=1.5\) are 24.69 mm/y, 61.72 mm/y, 125.27 mm/y, and 235.47 mm/y. For (b) and (c), σs is set to 100 nm.

Full size image
Table 1 Details of galvanostatic corrosion experiments
Full size table

Corrosion rate monitoring under potentiostatic corrosion

In a real-world corrosion system, the corrosion rate could vary with time. Table 2 provides the details of the potentiostatic corrosion experiments conducted, where the corrosion rates were not controlled. From the ultrasonic thickness measurements presented in Fig. 5a, it can be seen that all substrates exhibited a varying corrosion rate, thanks to corrosion initiation and/or the manually enforced changes in electric potential. After each experiment, the corrosion products on the working surface of the substrate were removed using deionized water, and the thickness loss of the substrate was characterized by a white light interferometer (see the “Characterization of WTL by white light interferometry” section). As shown in Fig. 5a, the ultrasonic measurements of the final thickness losses of the substrates match very well with the optical measurements.

Fig. 5: Results of potentiostatic corrosion experiments.
figure 5

a WT data obtained during the experiments. For the optical measurements, the error bars each stand for the standard deviation of the results of the different points of the optically scanned area of the substrate. b Real-time corrosion rates. For the proposed ultrasonic technique, σs and σd/σs are set to 100 nm and 1.5, respectively.

Full size image
Table 2 Details of potentiostatic corrosion experiments
Full size table

Figure 5b compares the real-time corrosion rates determined by the proposed ultrasonic technique and those calculated from the electric currents recorded. The exceptionally high level of agreement between the two sets of results, which were obtained via two different completely different sets of physics, confirms the measurement accuracy of the proposed technique. What’s more, the proposed technique precisely resolved the changes in corrosion rate during the different stages of the corrosion processes, including the corrosion initiation stages and the transition stages of the applied electric potential. The minor mismatch between the two sets of results could be attributed to the fact that the ultrasonic thickness measurements reflect only the state of a local area of each substrate, whereas the electric currents reflect the overall state of each substrate.

Corrosion rate monitoring under natural acidic corrosion

The proposed ultrasonic technique was further applied to monitoring natural acidic corrosion processes, where the corrosion rates could be altered by the corrosion product layers formed. More specifically, HCl solutions with pH levels of 1.5, 2.0 and 2.6 were used as the electrolytes, and the experiments were each conducted for 72 h. During each experiment, LPR measurements were carried out concurrently by polarizing the substrate repeatedly from −10 mV to +10 mV vs. OCP at 0.1 mV/s. Since the conversion of polarization resistances to corrosion rates necessitates knowledge of Tafel coefficients, the precise values of which are difficult to attain and could actually vary with time during a corrosion process24,25,26,27,28,29, in this work the polarization resistance obtained were not converted to corrosion rates but were directly used to as the benchmark for the corrosion rates determined by the proposed technique. Such benchmarking approach is considered valid in this context since only uniform corrosion rate was anticipated30. After each experiment, the corrosion product layer was analyzed by XRD (SmartLab, Rigaku, Japan) and the scan was performed over a 2θ range of 10°–90° at 0.02° per second.

Figure 6a illustrates the real-time corrosion rates determined by the proposed technique, together with the real-time polarization resistances. The observation that the two sets of results are inversely proportional with one another, which agrees with expectation, highlights the robustness of the proposed technique in rather complex corrosion systems. From Fig. 6a, it can be seen that in each experiment, the corrosion rate was always higher at the beginning and then gradually decreased. Also, the higher the acidity of the electrolyte solution, the higher the overall corrosion rate was, and the later in time the corrosion rate started to decrease at (i.e., pH 2.6: 1st hour, pH 2.0: 13th hour, pH 1.5: 55th hour). These trends are consistent with the existing understanding of the corrosion behavior of mild steel in HCl solution31, where H+ and Cl− ions, the concentrations of which are directly proportional to the acidity of the solution, would tend to destroy any protective layer that would form on the substrate, but as these ions are depleted with time, the formation of a stable and compact corrosion product layer would become possible, impeding the diffusion of these ions from the electrolyte solution to the corrosion site and hence causing the corrosion process to slow down. As shown in Fig. 6b, typical iron corrosion products, i.e., FeOOH, Fe2O3 and Fe3O4, were detected on all the substrates.

Fig. 6: Results of natural acidic corrosion experiments.
figure 6

a Real-time corrosion rates and real-time polarization resistances obtained during the experiments. The corrosion rates were determined by the proposed ultrasonic technique. b XRD spectra of the corrosion product layers on the substrates.

Full size image

In this work, the GLR algorithm is introduced to realize rational determination of real-time corrosion rates based on wall thickness measurements acquired by in situ ultrasonic testing. Through numerical modeling and galvanostatic corrosion experiments, it was found that the detection speed and the measurement accuracy of the proposed ultrasonic technique are inversely proportional to one another, and the balance between the two performance indicators can be tuned by adjusting the user-defined parameter of the GLR algorithm, i.e., σd or the expected noise level of WT data. Galvanostatic corrosion experiments were conducted to assess the measurement accuracy of the proposed technique, showing that the real-time corrosion rates determined by the proposed technique matched very well with those calculated from the corrosion currents. When using the proposed technique in natural acidic corrosion experiments, the real-time corrosion rates determined not only showed the expected correlation with the polarization resistances obtained, but also accurately reproduced the expected changes in corrosion rate due to the destruction and re-establishment of protective layers. All in all, the proposed technique has demonstrated much potential to become an important tool for measuring real-time corrosion rates in both laboratory research and field applications.

Methods

Preparation of corrosion substrates

N80 steel substrates that measure 45 × 45 × 10 mm were prepared. The chemical composition of N80 steel is shown in Table 3. For each substrate, its working surface was polished using sandpapers with increasing fineness (grit size: 60–600) and was then thoroughly cleaned using ethanol and acetone.

Table 3 The chemical composition of N80 steel (unit: wt.%)
Full size table

Determination of time-of-arrival’s

To maximize the measurement accuracy of ToAs, the following signal processing approach is implemented.

  1. (i)

    For each WT data point, 300 ultrasonic signals are acquired consecutively and averaged over.

  2. (ii)

    The average signal is filtered using a 5th-order Butterworth band-pass filter with cutoff frequencies at 1.2 MHz and 2.8 MHz.

  3. (iii)

    The filtered signal is upsampled from 200 to 800 MHz.

  4. (iv)

    The upsampled signal is auto-correlated. The first two peaks in the auto-correlation correspond to the ToAs of first two reflected wavepackets in the upsampled signal.

  5. (v)

    The true location of each of the first two peaks in the auto-correlation, at where the gradient ought to be zero, is pinpointed by interpolating between the gradients at the two highest sampling points in the vicinity of the peak11.

Determination of shear wave velocities

For each substrate that is to be used for corrosion experiments, its shear wave velocity vs. temperature relationship needs to be pre-determined in order to minimize the influence of temperature variation on the measurement accuracy of WTs. This is done so via a calibration experiment, where the substrate is exposed to the ambient environment and is free from corrosion, while both ultrasonic signal generation & acquisition and temperature measurement are carried out simultaneously. The ultrasonic signals acquired are converted into shear wave velocities via a modified version of Eq. (1), i.e., \(V\left(T\right)=2 \,\cdot \, {WT}/\left({{ToA}}_{2}-{{ToA}}_{1}\right)\), where WT is a constant, and \({{ToA}}_{1}\) and \({{ToA}}_{2}\) are obtained following the process mentioned in the “Determination of time-of-arrival’s” section). The shear wave velocities obtained are each plotted against the corresponding temperature, and the shear wave velocity vs. temperature relationship of the substrate is then attained by linear regression.

During a corrosion experiment, the shear wave velocity at any moment in time is determined based on the shear wave velocity vs. temperature relationship of the substrate and the instantaneous temperature of the substrate.

Characterization of WTL by white light interferometry

For each substrate, the morphology of the working surface was scanned twice using a white light interferometer (TMS-150 TopMap Metro.Lab, Polytec, Germany), once before the corrosion experiment and another time after the experiment and the removal of any corrosion product. Figure 7 displays the optical scan of the end-state working surface morphology of one of the substrates used in this work. The actual corrosion-induced morphology change of the substrate was obtained by subtracting the end-state morphology from the initial one. The mean thickness loss of a 10 × 10 mm area in the center of the corrosion area was taken as the optical measurement of the final thickness loss of the substrate, against which the corresponding ultrasonic measurement was benchmarked. It is worth mentioning that the substrate area to which a given ultrasonic thickness measurement corresponds depends on numerous factors, including the size of the piezoelectric transducer used, the frequency of the ultrasonic wave excited, and the thickness and the shear wave velocity of the substrate16,17. The assumption that the ultrasonic thickness measurements obtained in this work all correspond to a 10 × 10 mm area at the center of the corrosion area concerned was made with due consideration to the theoretical monitoring area of the ultrasonic system presented in this work and the practical uncertainty associated with the positioning of piezoelectric transducers during installation.

Fig. 7
figure 7

Optical scan of the end-state morphology of the working surface of an example substrate.

Full size image