Introduction

Quantum key distribution (QKD) has the potential to generate the information-theoretical-secure keys between distant users (Alice and Bob)1,2,3. Since the first BB84 protocol proposed4, QKD has stepped into realistic applications from the laboratory5,6,7,8,9,10,11. The communication distance of QKD over different communication scenarios is significantly improved, such as 509, 511, 830 km with fiber link12,13,14, 4600 km space-to-ground communication network15, 1120 km space-to-ground entanglement distribution16, 1 km optical-relayed entanglement distribution over drones17.

In general, the realistic QKD systems have a common need of establishing a shared reference frame between distant users by characterizing and calibrating the polarization or phase of photons. Nevertheless, an actively or inappropriately implemented calibration scheme may increase the complexity of the systems and may open an unpredictable security loophole18,19.

Reference-frame-independent (RFI) QKD protocol, proposed in 2010, is robust for slowly varying reference frames and suitable to the satellite-to-ground and drone-based systems20,21. The secure key rate of RFI QKD systems varies a lot with given misalignment (θ0) of reference frames22. Furthermore, Wang et al. show that the valid condition of RFI-QKD is the misalignment variation Δθ ≤ π23. With the assumption of Δθ ≈ 0, the fiber link distance of RFI QKD reaches 300 km implemented with measurement-device-independent scheme11,24,25,26,27,28, and the free space RFI QKD experiment was demonstrated with a total loss of 38.0 dB9. However, the misalignment of reference frames in realistic RFI QKD scenarios varies randomly, the key accumulation time is limited by the upper bound of the variation, and the communication distance will be reduced heavily. W. Liang et al. performed a proof-of-principle experiment of RFI QKD with random θ0 in a slowly varying phase environment, nevertheless, the communication distance was limited to 65 km when considering the statistical fluctuations29,30.

In this article, we proposed a free-running RFI QKD scheme that can be adapted to the long-distance QKD systems with randomly and rapidly varying misalignment of reference frames. In our free-running RFI QKD scheme, the misalignment variation rate tolerance of the reference frame is highly enhanced, and the physical communication procedure is free-running without the limitation of Δθ ≤ π. We implemented a free-running RFI QKD experiment over 100 km fiber link with a total loss of 31.5 dB and system repetition rate of 80 MHz. The experiment is implemented with phase encoding, while our free-running RFI QKD scheme is not limited to the phase encoding. In the experiment, time-bin encoded photons in Z basis are used for generating secure keys and the phase-encoded photons in the X (Y) basis are used for quantifying the characteristics of the quantum link. The experiment ran for 50.7 h and the misalignment of reference frame between Alice and Bob varied for more than 29 periods. The secure key rate of our implementation reaches about 742.98 bps, which achieves the state-of-art performance of the long-distance RFI QKD systems.

Results

Model of free-running RFI QKD

The schematic diagram of our free-running RFI QKD scheme is shown in Fig. 1. The scheme mainly contains four phases: physical communication, data classification, secure key length estimation, and post-processing. In the physical communication phase, the communication parties (Alice and Bob) prepare and measure the quantum state as same as the original RFI scheme, and generate the raw data. Especially, the physical communication is free-running without considering the misalignment variation (Δθ < π in the original RFI schemes) of the reference frames. Then, the sifted data s0, s1, … , sn−1 of n intervals are generated after the basis/key sifting and quantum bit error rate (QBER) calculation procedures. Afterwards, each interval sifted data is split into m datasets according to the estimated classification parameter in the data classification phase. In the secure key length estimation phase, the leakage information and the single photon number of each dataset are calculated according to the decoy-state RFI analysis, and the secure key length L is estimated. Finally, the secure key K is generated in the post-processing phase.

Fig. 1: The schematic diagram of the proposed free-running RFI QKD scheme.
figure 1

The scheme mainly contains four phases: physical communication, data classification, secure key length estimation and post-processing. Alice (Bob) prepares (measures) the quantum state, and generates raw data. Then, n interval sifted data s0, s1, … , sn−1 are generated in the basis/sifting and quantum bit error rate (QBER) calculation procedure. Afterwards, s0, s1, … , sn−1 are classified into m datasets \(({{{{\mathscr{D}}}}}_{0},{{{{\mathscr{D}}}}}_{1},\ldots \,,{{{{\mathscr{D}}}}}_{m-1})\) according to the estimated classification parameter. The final secure key length is estimated based on the classified datasets \(({{{{\mathscr{D}}}}}_{0},{{{{\mathscr{D}}}}}_{1},\ldots \,,{{{{\mathscr{D}}}}}_{m-1})\). (ρ0, ρ1, … , ρn−1) represent the classification parameter of n interval sifted data. m and \({\rho }^{\prime}\) are used to split [0, 2π) as m slices: P0, P1, … , Pm−1.

Full size image

In the free-running RFI QKD scheme, three encoding bases (X, Y, Z) are used and the reference frames of the bases are defined as

$$\begin{array}{l}{Z}_{B}={Z}_{A},\\ {X}_{B}={X}_{A}\cos \theta +{Y}_{A}\sin \theta ,\\ {Y}_{B}={Y}_{A}\cos \theta -{X}_{A}\sin \theta ,\end{array}$$
(1)

where θ is the misalignment angle of reference frames between Alice and Bob.

Alice randomly prepares the pulses with the bit s, the basis α and the intensity of k, where s ∈ {0, 1}, α ∈ {X, Y, Z} and k ∈ {μ, ν, 0} is the mean photon number of signal, decoy, and vacuum states. Bob randomly measures the received photons in the X, Y, and Z basis.

After repeating the preparation and measurement for Nt times, Alice and Bob acquire the raw data which contains n interval raw data of the interval time T.

Assume \({E}_{k}^{\alpha \beta }\) and \({N}_{k}^{\alpha \beta }\) represent the QBER and measured event number respectively, where k ∈ {μ, ν, 0}, α is the preparation basis, β is the measurement basis.

The key/basis sifting are conducted on the measured events of each interval with the basis of αβ and the measured event numbers \({N}_{k}^{\alpha \beta }\) of each interval are also calculated, where αβ ∈ {ZZ, XX, XY, YY, YX}. Meanwhile, the QBERs \({E}_{k}^{\alpha \beta },{E}_{l}^{ZZ}\) are calculated by exposing the corresponding quantum bits, k ∈ {μ, ν, 0}, l ∈ {ν, 0}, α, β ∈ {X, Y}. Meanwhile, the sifted keys Ks are generated from the quantum bits of the signal state on Z basis.

Here, the interval sifted data s0, s1, … , sn−1 are generated, each sifted data si contains the QBERs \({E}_{k}^{\alpha \beta },{E}_{l}^{ZZ}\), the measured event number \({N}_{k}^{\alpha \beta },{N}_{k}^{ZZ}\) and the sifted key of interval i, i = 0, 1, … , n − 1. Afterwards, s0, s1, … , sn−1 are classified into m datasets \({{{{\mathscr{D}}}}}_{0},{{{{\mathscr{D}}}}}_{1},\ldots \,,{{{{\mathscr{D}}}}}_{m-1}\) according to the estimated classification parameter, which is described in subsection “Data classification” in detail.

The sifted keys in the dataset \({{{{\mathscr{D}}}}}_{i}\) are merged to \({K}_{s}^{i}\), i = 0, 1, … , m − 1. The error estimation and error correction are conducted on \({K}_{s}^{0},{K}_{s}^{1},\ldots \,,{K}_{s}^{m-1}\) to gain the corrected keys \({K}_{{{{\rm{EC}}}}}^{0},{K}_{{{{\rm{EC}}}}}^{1},\ldots \,,{K}_{{{{\rm{EC}}}}}^{m-1}\), respectively. By comparing the corrected keys with the sifted keys, the QBERs of sifted keys are calculated, which is the QBER \({E}_{\mu ,i}^{ZZ}\) of the signal state on Z basis.

Afterwards, the bits in the corrected keys \({K}_{{{{\rm{EC}}}}}^{0},{K}_{{{{\rm{EC}}}}}^{1},\ldots \,,{K}_{{{{\rm{EC}}}}}^{m-1}\) are rearranged according the measurement order and merged as KEC. Finally, the privacy amplification is conducted on the corrected key KEC to generate the secure key K with the length L, which is described in subsection “Secure key length estimation and noise tolerance analysis”.

Data classification

After the key/basis sifting and the QBER calculation procedures, the interval sifted data is generated, which contains QBERs \({E}_{\mu }^{\alpha \beta }\) and \({E}_{\nu }^{\alpha \beta }\), α, β ∈ {X, Y}. According to the decoy-state practical RFI QKD protocol with weak coherent sources24, the QBER of X and Y bases varies approximately in a cosine curve when the misalignment θ changes. The QBER can be used to classify the generated interval sifted data into the datasets with the similar misalignment angles, but the classification interval is nonlinear and difficult to understand. Thus, we defined a classification parameter ρ ∈ [0, 2π) which is calculated according to the mapping from misalignment θ to QBER. The classification parameter is only used to classify the interval sifted data and cannot accurately characterize the misalignment of reference frames. The detailed description of the classification parameter is in Supplementary Note 1.

Then, the classification parameter ρ of the sifted data in each interval is calculated from the measured QBER as

$$\rho =\left\{\begin{array}{ll}\arccos \left(\frac{2}{\eta \mu }\ln \frac{H({\widehat{E}}_{\mu }^{XX})}{2{\widehat{E}}_{\mu }^{XX}}-1\right)\quad &{E}_{\mu }^{XY} <\, 0.5\\ 2\pi -\arccos \left(\frac{2}{\eta \mu }\ln \frac{H({\widehat{E}}_{\mu }^{XX})}{2{\widehat{E}}_{\mu }^{XX}}-1\right)\quad &{E}_{\mu }^{XY}\ge 0.5\end{array}\right.,$$
(2)

where \(H({\widehat{E}}_{\mu }^{XX})\) and \({\widehat{E}}_{\mu }^{XX}\) are calculated as

$$H({\widehat{E}}_{\mu }^{XX})=\left(1-{d}_{c}\right)\left(2{\widehat{E}}_{\mu }^{XX}-1\right)+\sqrt{4{e}^{\eta \mu }{\widehat{E}}_{\mu }^{XX}\left(1-{\widehat{E}}_{\mu }^{XX}\right)+{\left(1-{d}_{c}\right)}^{2}{\left(1-2{\widehat{E}}_{\mu }^{XX}\right)}^{2}},$$
(3)
$${\widehat{E}}_{\mu }^{XX}=\frac{{E}_{\mu }^{XX}-{e}_{s}}{1-{e}_{s}}.$$
(4)

dc is the dark count of detectors and es is the optical system error.

Especially, when \(\eta \mu (1-\cos \rho )/2\ll 1\), \(\eta \mu (1+\cos \rho )/2\ll 1\) and dc ≪ ημ, the ρ can also be calculated as

$$\rho =\left\{\begin{array}{ll}\arccos (1-2{\widehat{E}}_{\mu }^{XX})\quad &{E}_{\mu }^{XY} <\, 0.5\\ 2\pi -\arccos (1-2{\widehat{E}}_{\mu }^{XX})\quad &{E}_{\mu }^{XY}\ge 0.5\end{array}\right.,$$
(5)

The detailed calculation is shown in Supplementary Note 1.

Meanwhile, we split the classification parameter \(\rho \in \left[0,2\pi \right)\) into m slices as

$${P}_{i}=\left\{\begin{array}{ll}\{\rho | \frac{2(m-1)}{m}\pi +{\rho }^{\prime}\le \rho \,<\, 2\pi \,or\,0\le \rho \,<\, {\rho }^{\prime}\},\quad &i=0\\ \{\rho | \frac{2i-2}{m}\pi +{\rho }^{\prime}\le \rho \,<\, \frac{2i}{m}\pi +{\rho }^{\prime}\},\quad &i \,>\, 0\end{array}\right.$$
(6)

where i = 0, 1, …, m − 1, \({\rho }^{\prime}\) is constant and could be optimized to achieve the highest secure key rate.

The classification parameter ρ0, ρ1, … , ρn−1 of s0, s1, … , sn−1 are calculated, respectively. Afterwards, the measured data could be classified into m datasets \(\{{{{{\mathscr{D}}}}}_{0},{{{{\mathscr{D}}}}}_{1},\ldots \,,{{{{\mathscr{D}}}}}_{m-1}\}\) when the interval sifted data corresponding to the Pi are classified to the dataset \({{{{\mathscr{D}}}}}_{i}\).

Secure key length estimation and noise tolerance analysis

Assume the eαβ is the QBER of single-photons with preparation basis α and measurement basis β, \({N}_{1}^{Z}\) is the single photon number of Z basis.

After classifying the measured data into m datasets, each with similar classification angle, QBER \({E}_{k,i}^{\alpha \beta }\) and \({E}_{l,i}^{ZZ}\) of \({{{{\mathscr{D}}}}}_{i}\) are calculated from the measured event number and the QBERs of the composed interval sifted data, k ∈ {μ, ν, 0}, l ∈ {ν, 0}, α, β ∈ {X, Y}, i = 0, 1, … , m − 1. Meanwhile, the measured event number \({N}_{k,i}^{\alpha \beta }\) and \({N}_{l,i}^{ZZ}\) of \({{{{\mathscr{D}}}}}_{i}\) are also determined. The QBER \({E}_{\mu ,i}^{ZZ}\) and measured photons \({N}_{\mu ,i}^{ZZ}\) of dataset \({{{{\mathscr{D}}}}}_{i}\) are determined in the error estimation and error correction procedure. The \({e}_{\alpha \beta }^{i}\) and \({N}_{1,i}^{Z}\) of each dataset can be calculated according to the decoy-state protocol and statistical fluctuations analysis5.

Based on the RFI protocol20,31, we estimate the leakage information \({I}_{E}^{i}\) of each dataset as

$${I}_{E}\le (1-{e}_{ZZ}){h}_{2}\left(\frac{1+{v}_{\max }}{2}\right)+{e}_{ZZ}{h}_{2}\left(\frac{1+g\left({v}_{\max }\right)}{2}\right)$$
(7)

where \({v}_{\max }\) and \(g({v}_{\max })\) are calculated as

$$\begin{array}{l}{v}_{\max }=\min \left(\frac{1}{1-{e}_{ZZ}}\sqrt{\frac{C}{2}},1\right),\\ g({v}_{\max })=\frac{\sqrt{C/2-{\left(1-{e}_{ZZ}\right)}^{2}{v}_{\max }^{2}}}{{e}_{ZZ}}.\end{array}$$
(8)

The quantum channel quality C is estimated from the X, Y basis as

$$\begin{array}{l}C={\left\langle {X}_{A}{X}_{B}\right\rangle }^{2}+{\left\langle {Y}_{A}{Y}_{B}\right\rangle }^{2}+{\left\langle {X}_{A}{Y}_{B}\right\rangle }^{2}+{\left\langle {Y}_{A}{X}_{B}\right\rangle }^{2}\\ \quad=\,{\left(1-2{e}_{XX}\right)}^{2}+{\left(1-2{e}_{YY}\right)}^{2}\\ \quad=\,+{\left(1-2{e}_{XY}\right)}^{2}+{\left(1-2{e}_{YX}\right)}^{2}.\end{array}$$
(9)

Then, the upper (lower) bounds of \({e}_{\alpha \beta }^{i}\), \({N}_{1,i}^{Z}\), and \({I}_{E}^{i}\) are estimated by considering the statistical fluctuation5,32. The superscript ‘+’ (‘−’) are used to represent the upper (lower) bound of the variable.

Finally, the secure key length L is calculated as

$$L\ge \mathop{\sum }\limits_{i=0}^{m-1}{L}_{i},$$
(10)

Li is the secure key length of dataset \({{{{\mathscr{D}}}}}_{i}\) and is estimated as

$${L}_{i}\ge \max \left[{N}_{1,i}^{Z,-}(1-{I}_{E}^{i,+})-{\lambda }_{i}^{{{{\rm{IR}}}}},0\right].$$
(11)

\({\lambda }_{{{{\rm{IR}}}}}^{i}\) is the leakage information bits of dataset \({{{{\mathscr{D}}}}}_{i}\) in the information reconciliation procedure and equals to

$${\lambda }_{i}^{{{{\rm{IR}}}}}={N}_{\mu ,i}^{ZZ}f\left({E}_{\mu ,i}^{ZZ}\right){h}_{2}\left({E}_{\mu ,i}^{ZZ}\right),$$
(12)

where f(x) is the reconciliation efficiency corresponding to QBER x.

Additionally, the secure key rate is calculated as

$$R=\frac{L}{\mathop{\sum }\nolimits_{i = 0}^{m-1}{t}_{i}},$$
(13)

where ti is the enduring time of dataset \({{{{\mathscr{D}}}}}_{i}\).

Assume εPA is the failure probability of privacy amplification, εEC is the failure probability of information reconciliation and \(\overline{\varepsilon }\) measures the accuracy of estimating the smooth min-entropy.

Considering the finite-key analysis30, the secure key length LFK of our free-running RFI scheme is recalculated as

$$\begin{array}{l}{L}_{{{{\rm{FK}}}}}\ge L-\mathop{\sum }\limits_{i=0}^{m-1}{\sigma }_{i}{\log }_{2}\frac{2}{{\varepsilon }_{{{{\rm{EC}}}}}}-{\log }_{2}\frac{2}{{\varepsilon }_{{{{\rm{PA}}}}}}\\ \qquad-\,7\mathop{\sum }\limits_{i=0}^{m-1}\sqrt{{N}_{i}^{ZZ}{\log }_{2}\frac{2}{\overline{\varepsilon }}}\\ \qquad-\,30\mathop{\sum }\limits_{i=0}^{m-1}{\log }_{2}({N}_{i}+1)\end{array},$$
(14)

where σi = 0 (1) represents dataset \({{{{\mathscr{D}}}}}_{i}\) is (not) empty, \({N}_{i}^{ZZ}\) represents the measurement events number of Z basis in dataset \({{{{\mathscr{D}}}}}_{i}\), and Ni is the total measurement events number in dataset \({{{{\mathscr{D}}}}}_{i}\).

Furthermore, the secure key rate RFK with the finite-key analysis is calculated as

$${R}_{{{{\rm{FK}}}}}=\frac{{L}_{{{{\rm{FK}}}}}}{\mathop{\sum }\nolimits_{i = 0}^{m-1}{t}_{i}}.$$
(15)

In our free-running RFI scheme, the misalignment variation Δθ of each dataset has the upper bound as

$$\Delta \theta \le \frac{2\pi }{m}+2\omega T,$$
(16)

where ω is the experimental noise (variation rate of reference frames). Meanwhile, the variation Δθ and the interval T have the constraint conditions23 as

$$\begin{array}{l}\Delta \theta \le \pi,\, T\ge \frac{{N}_{\min }}{{N}_{\mu }^{XX}+{N}_{\mu }^{YY}}.\end{array}$$
(17)

We set the standard deviation of the error rate estimation as 0.01 with the confidence level higher than 95.45%. Thus, the \({N}_{\min }\) should be larger than 2.5 × 103. The calculation procedure is described in Supplementary Note 2.

Thus, our free-running RFI scheme is valid as long as the experimental noise ω satisfies

$$\omega \le \frac{m-2}{2mT}\pi .$$
(18)

In the experiment, photons encoded in Z basis are sent with the probability of 50%, photons encoded in X and Y basis are sent with the probability of 25%. The signal, decoy, and vacuum states are sent with the probability of 50, 40, and 10%, respectively. The mean photon number of the signal and decoy states are 0.722 and 0.104. The experiment has run free-running for about 50.7 h. The interval time T is set to 5 s. The information reconciliation efficiency is set to 1.1633.

Experimental QBERs, count rates, and secure key rates

Figure 2 shows the QBER of signal and decoy states for each basis and the count rate of Z basis. The QBER of the X, Y basis varied periodically with the time due to the environmental noise which affects the phase of the two interferometers, while the QBER of the Z basis maintained stable with small fluctuations. The intrinsic error of the optical system es is estimated as about 0.4% according to the upper (lower) bound of error rate on X, Y basis. The average QBER of the signal state on the Z basis is about 0.6%. The fluctuations in Z basis are caused by the active compensation, in which the intensity of signal quantum is monitored and the control signal of the intensity modulator IM2 (shown in section “Methods”) is adjusted when the misalignment of Z basis is out of the preset interval. The upper bound of the misalignment error on Z basis is set as 0.7%. Meanwhile, the jitters of the statistics might activate the feedback program even when \({E}_{\mu }^{ZZ}\) is smaller than 0.7%. And the small jitters of \({E}_{\mu }^{ZZ}\) causes the huge variation of error rate on decoy state, so that \({E}_{\nu }^{ZZ}\) jumps fast sometimes. The average count rate of the signal and decoy states of Z basis is about 2.6 and 0.4 kbps. During the whole experiment, the reference frame varied for more than 29 periods and the noise ω reaches an upper bound of 6.9 × 10−3 rad/s.

Fig. 2: The measured QBER in each basis, and the count rate in Z basis.
figure 2

Each point is measured within 5 s. a, b shows the QBER of signal (decoy) state on X, Y basis for the total 50.7 h, c shows the QBER of signal state and decoy state on Z basis: \({E}_{\mu }^{ZZ}\) and \({E}_{\nu }^{ZZ}\), and d shows the count rate of signal and decoy state on Z basis: \({N}_{\mu }^{ZZ}\) and \({N}_{\nu }^{ZZ}\).

Full size image

In the experiment, we first calculated the average secure key rate of the 50.7 h experiment with m = 3, 4, … , 40 and the optimal \({\rho }^{\prime}\). The result is shown in Fig. 3. The secure key rate reaches the maximum when m = 12 and \({\rho }^{\prime}=\frac{\pi }{12}\). The high secure key rate is achieved when m ∈ {4i∣i ∈ N+}, for the four datasets with the upper bound are acquired shown as Fig. 4. When m ≤ 14, the secure key rate is improved with the increase of m, which decreases misalignment variation in each dataset. When m ≥ 15, the secure key rate is reduced by the increase of m, which causes the higher statistical fluctuations.

Fig. 3: The average secure key rate with different m.
figure 3

m ranges from 3 to 40 and ρ′ is optimized.

Full size image
Fig. 4: The C value, secure key rate of the merged datasets and the simulated result with Nt = 1.46 × 1013 and m = 12.
figure 4

a and b show the C value and secure key rate respectively. The C value and secure key rate varies corresponding to varying misalignment of reference frame leaks different amounts of secure key information22.

Full size image

Figure 5 shows the average QBER of each dataset when m = 12. The QBERs of X, Y basis vary against the rotation ρ while the QBERs of signal and decoy state on Z basis are stabilized at around 0.6 and 2.3%.

Fig. 5: The QBER of the merged datasets with the experimental measured data, here m = 12.
figure 5

The index of dataset i corresponds to Pi. a shows the QBER of signal state on X,Y basis, b shows the QBER of decoy state on X,Y basis, c shows the QBER on Z basis. Each point represents the merged result of each dataset.

Full size image

The original RFI analysis is conducted on each dataset and the corresponding C value and secure key rate of each dataset are shown in Fig. 4 with red circles. The blue dash lines in Fig. 4 illustrate the simulated results with Nt = 1.46 × 1013 5,10,22,32. In principle, the C value and the secure key rate reach the maximum values with ρ ∈ {0, π/2, π, 3π/2}, which correspond to the dataset of {\({{{{\mathscr{D}}}}}_{0}\), \({{{{\mathscr{D}}}}}_{3}\), \({{{{\mathscr{D}}}}}_{6}\), \({{{{\mathscr{D}}}}}_{9}\)}, respectively. The experimental C value and secure key rate are slightly less than the simulated results due to the imperfect preparation and measurement of photons. Then, the measured average secure key rate in our experiment is calculated as 742.98 bps bps with our free-running RFI analysis when the finite length is 1.46 × 1013 and the acquisition time is 50.7 h.

The secure key rate of our experiment is also calculated with the different finite length of 1010, 1011, 1012, and 1013 when m and \({\rho }^{\prime}\) are both optimized. The average secure key rate is shown in Table 1 and the secure key rate in each run is shown in Supplementary Note 3.

Table 1 Secure key rate calculated with different finite length when m and \({\rho }^{\prime}\) are both optimized.
Full size table

The average secure key rate of our free-running RFI scheme is same to the original RFI scheme when the finite length Nt = 1010. Afterwards, our free-running RFI scheme achieves higher average secure key rate than the original RFI scheme with Nt = 1011 for the lower misalignment variation. Furthermore, the secure key rate is further improved as the finite length is increased to 1012 and 1013, while the original RFI scheme couldn’t generate secure key.

In addition, the average secure key rate RFK with the finite-key analysis of our free-running RFI scheme is also calculated with the finite-key analysis and different finite length. εPA, εEC and \(\overline{\varepsilon }\) are all set to 10−10. The secure key rate of 724.87 bps has been achieved with Nt = 1.46 × 1013.

Secure key rate with different misalignment variation rates

Furthermore, we simulated the average secure key rate of the free-running RFI QKD versus the total loss with Nt = 108, 109, 1010, 1011, 1012, 1013 and our experimental settings. In the simulation, the dataset size m is optimized for each point. The misalignment variation rate is set as 0 and 6.9 × 10−3 rad/s, respectively. Meanwhile, the secure key rate of the original RFI scheme is also simulated with the same settings. The simulation result is shown in Fig. 6.

Fig. 6: The simulated secure key rate of our free-running RFI (FR) scheme and the original RFI scheme (OR) with different finite lengths (Nt) and misalignment variation rate (ω).
figure 6

Solid lines show the result of our scheme, while the dash lines with dots show the result of the original scheme. a–c show the simulated secure key rate when ω equals to 0, 6.9 × 10−3 rad/s and 3.3 × 10−2 rad/s, respectively. In b and c, the original RFI scheme couldn't generate secure key when Nt ≥ 1011. In the simulation, the dataset size m and \({\rho }^{\prime}\) are optimized.

Full size image

When ω = 0, our free-running RFI scheme has the same performance with the original RFI scheme. The total loss tolerance is improved from about 16.65 dB to about 44.39 dB by increasing the finite length Nt from 108 to 1013.

When ω = 6.9 × 10−3 rad/s, the performance of the both RFI schemes are reduced by the reference frame misalignment variation in the key accumulation procedure as shown in Fig. 6b. In the original RFI QKD protocol, the increase of Nt would reduce the statistical fluctuations, and increase the secure key rate, however, the larger variation Δθ would decrease secure key rate. The performance of the original RFI scheme is improved when the finite length increases from 108 to 1010, however, no secure key could be generated with Nt ≥ 1011. Thus, the total loss tolerance of the original RFI QKD protocol is limited to 32.6 dB even with the optimized finite length. And the existing RFI QKD experiment reaches the distance of 65 km29. For Nt = 108, 109, 1010, our free-running RFI scheme achieves a slightly higher secure key rate than the original RFI scheme because the measured data are classified into optimal m slices instead of the random slice in the acquisition time. Nevertheless, for Nt = 1011, 1012, and 1013, our scheme can still generate secure key rate with better performance and achieves the total loss tolerance of 43.8 dB with Nt = 1013.

In the experiment, two asymmetric Mach–Zehnder interferometers (AMZI) are in the same room and the experimental noise is lower than the practical cases. We tested the experimental noise ω when the AMZIs are in different rooms, and the reference frame variation result is shown in Supplementary Note 4. The ω reaches upper bound of 3.3 × 10−2 rad/s. Figure 6c shows the simulated secure key rate of the free-running RFI scheme and the original RFI scheme with our experimental settings. We achieved a slightly higher secure key rate than the original RFI scheme when Nt = 108, 109. Then, the secure key rate of our scheme is further improved as the finite length increases and the total loss tolerance of 43.8 dB is achieved with the finite length of 1013. While the total loss of the original RFI scheme is reduced to about 2 dB as the finite length increases to 1010. And no secure key could be generated with Nt ≥ 1011.

Moreover, the proposed free-running RFI scheme can tolerate a faster drifting of reference frames than the original RFI scheme. Instead of the \(\omega \le \frac{\pi }{\sum {t}_{i}}\) in the original RFI scheme, the variation rate ω in our scheme is limited by the Eq. (18). With our experimental settings, the misalignment variation rate tolerance is up to 0.262 rad/s, which means the reference frame varies a period within 24 s.

Discussion

In this article, we proposed a free-running RFI quantum key distribution (QKD) scheme, and performed a 50.7-hours experiment test over 100 km fiber, which reaches the secure key rate of 742.98 bps. Our free-running RFI scheme increases the loss tolerance to 43.3 dB while the original RFI scheme reaches to 32.6 dB when the experimental noise ω is 6.9 × 10−3 rad/s. The reason why our free-running RFI scheme overcomes the original RFI QKD scheme is that the measured data could be accumulated for a long time and would not result in a higher misalignment variation Δθ in our scheme.

Besides, a 150 km free-running RFI QKD experiment running for about 0.5 h has been conducted with the optimized intensities of quantum states and the experiment is explained in Supplementary Note 5.

Moreover, the interval time T in our experiment can be reduced to 1 s, and the misalignment variation rate tolerance could be increased to 1.309 rad/s (4.8 s per period). Therefore, our free-running RFI scheme can be efficiently adapted into complex scenarios with rapid and random drifting reference frames, such as satellite-to-ground systems (≤0.12 rad/s)34 and drone-based systems.

Methods

Experimental setup

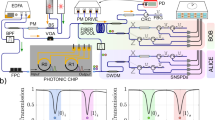
The setup of our free-running RFI QKD experiment is shown in Fig. 7. At Alice’s side, photons are generated by a homemade laser with a repetition rate of 80 MHz and a pulse width of 1.0 ns. The laser is driven by electronic pulses and vacuum state is modulated when no driving electronics pulse is sent to laser. An intensity modulator (IM1) and an attenuator (ATT) is used to modulate quantum (signal and decoy) states to the corresponding intensity. An asymmetric Mach–Zehnder interferometer (AMZI1) divides each pulse into two adjacent pulses (s and l) with a separation time of 4.6 ns. The intensity modulator IM2 prepares the bit 0 or 1 of Z basis by suppressing s or l randomly. When both s and l pulses pass through IM2, a phase of {0, π/2, π, 3π/2} will be randomly added to s pulse with two phase modulators (PM1 and PM2), where 0 and π indicate bit 0 and 1 in X basis, π/2 and 3π/2 indicate bit 0 and 1 in Y basis. Then, pulses are sent to Bob through a 100 km optical fiber with a loss of 0.235 dB/km. Meanwhile, an active feedback mechanism is performed to stabilize the intensity of the quantum states, which mainly consisted of a beam splitter (BS) and an avalanche photon detector (APD).

Fig. 7: Illustration of the 100 km free-running RFI QKD experiment.
figure 7

Two NI 6556 boards control the lasers and modulators. The computers are used for data acquisition, post-processing, and classical communication. An APD is used to measure the intensity of the signal and decoy states and the bits of Z basis, so that NI 6556 adjusts the control signal of IM1 and IM2. IM intensity modulator, BS beam splitter, PM phase modulator, PC polarization controller, AMZI asymmetric Mach–Zehnder interferometer, SNSPD superconducting nanowire single photon detector, TDC Time-to-Digital converter, APD avalanche photon detector, NI 6556 National Instruments 6556.

Full size image

At Bob’s side, the detection basis (X and Y) is randomly chosen by the phase modulator (PM3), where a phase of 0 (π/2) is added to the s pulse. Then another asymmetric Mach-Zehnder interferometer (AMZI2) which has the same path difference with the AMZI1 divides each pulse into two pulses, resulting four pulses, {s + s, s + l, l + s, l + l}. s + l and l + s pulses will merge into one pulse due to the same arriving time and interfere at AMZI2. The interference determines the exiting port of the s + l (l + s) pulse at the AMZI2, indicating the bit 0 or 1 of X(Y) basis, respectively. s + s and l + l pulses represent bit 0 and 1 of Z basis. Then, photons are coupled to two channels of the superconducting nanowire single photon detector (SNSPD), and the arriving time is recorded with a time-to-digital converter (TDC). The optimal detection efficiency, about 80%, is ensured by the polarization controllers (PC2 and PC3). The dark count rate of the SNSPD is about 200 per second. Two programmable modules (National Instruments 6556) are used to control the laser and modulators. The total loss of Bob’s receiving module is around 8 dB. Furthermore, a programmable polarization controller (PC1) is used to compensate the polarization drift of the transmitted photons.