Introduction

We are currently in the era where the first devices which exhibit a quantum advantage have become available, i.e., devices which outperform a classical supercomputer at some well-defined computational task1,2,3,4. Ultimately, quantum computing promises orders of magnitude speedup in solving problems of practical interest. Although some of these problems are connected to classical tasks5,6,7, many problems are concerned with solving the quantum dynamics of complex systems8. In the early 1980’s, both Manin and Feynman independently conjectured that quantum dynamics cannot run efficiently on classical computers, but could be efficiently simulated on quantum systems9,10,11. If the desired quantum dynamics are such that they can be simulated on a particular quantum system, implementation of a full-scale quantum computer may not be necessary. While universal, fault-tolerant quantum computers are possibly decades away, the timeline towards large-scale quantum simulators is potentially much shorter, making this an approach of interest for near-term applications of quantum computing.

Integrated quantum photonics is one of the most promising platforms for quantum information processing protocols. Its small footprint and high stability make it a promising route for building large-scale quantum systems12. Various quantum protocols have been suggested and demonstrated on photonic chips13. In quantum communication, a few types of quantum key distribution have been realized on photonic chips14,15,16. In quantum computing, cluster states have been generated17, also with error-protected logic qubits18, for one-way quantum computing19. And in quantum simulation, photonic chips have been used for boson sampling6,20,21,22, Gaussian boson sampling4,7, and quantum chemistry23,24. Additionally, quantum simulations have been proposed for fundamental science25, suitable for a photonic chip architecture26.

Let us briefly introduce Loop Quantum Gravity (LQG) and its connection to quantum simulations (a more detailed and quantitative description is in Supplementary Note 1. The main goal of quantum gravity is to formulate a generalized theory, unifying general relativity and quantum mechanics. LQG is a background-independent and non-perturbative approach, which attempts to present the quantum spacetime geometry lacking in other quantum field theories27,28,29. As one of the key objects in LQG, the spinfoam vertex is a building block in the 4-dimensional quantum spacetime, and it is the transition of LQG within a 4-simplex, which is the elementary (undivided) cell in the discrete 4-dimensional spacetime30,31,32. Any discrete spacetime is composed of a cluster of 4-simplices as illustrated in Fig. 1a and b. The 4-simplex’s boundary is made by five tetrahedra as shown in Fig. 1c. Since the spinfoam describes the spacetime evolution of the tetrahedra boundary states, same as the evolution of quantum gates on quantum states, we can connect between the two theories and simulate the transition of a spinfoam with our optical simulator. In the simulation the gate represents the spinfoam and defines the transition of the photonic state, representing the tetrahedra boundary states. When the vertex amplitudes are understood as quantum gates, the full spinfoam amplitude is constructed by the scalar products of quantum tetrahedron states after experiencing the operation of the quantum gate26. Now, we simulate the spinfoam transition by preparing the evolution of the simulator as the evolution of the spinfoam. Then, we can measure the transition amplitudes and by that find the most probable geometry of the boundary, which is one of the important tasks in LQG.

Fig. 1: Concept of loop quantum gravity.
figure 1

a A sphere is triangulated with a finite number of triangles, demonstrating triangulation of a simple geometry. In LQG the idea is to tile spacetime with cells, called 4-simplices. b Illustration of discretization of continuous spacetime into a complex, made of 4-simplices. A line between two 4-simplices indicates a shared tetrahedron, which is the 3D-hypersurface shared between two 4-simplices. c A single 4-simplex has 5 boundary tetrahedron states. In this work, a 4-simplex is simulated with a linear photonic chip.

Full size image

Drawing the connection between quantum gravity, or quantum field theories in general, and the evolution of quantum states is the key for enabling the simulations. While many approaches were proposed to use quantum simulators33,34 and computers35,36,37 for this task, experimental demonstrations are limited in scale38,39,40 and quantum resources41. Here we adapt one approach which is potentially scalable to large-scale simulations since it only requires a single photon and a single linear-optical chip per vertex26. This approach is particularly suitable for, but not limited to, simulating LQG. The key idea in this design is to map LQG quantum tetrahedron states (see Fig. 1b) to optical modes, and to encode the spinfoam vertex amplitude in an optical quantum circuit as a chain of linear-optical unitary operations followed by post-selection.

In this work, we experimentally simulate a spinfoam vertex amplitude on a quantum photonic processor based on silicon nitride waveguides. The spinfoam vertex amplitudes are simulated on chip by encoding them in the unitary matrix U that relates the input to output modes. The simulation not only encodes the vertex amplitude in a linear-optical system, but also displays the semiclassical relation between the vertex amplitude and the geometry of a 4-simplex. Our experiment permits the simulation of spinfoam amplitudes with many vertices, due to the inherent scalability of linear-optical quantum photonic processors and the generated path entanglement.

Results

Chip unitary transformation

We implement a non-unitary 8 × 4 quantum gate of two input qubits to three output qubits, and this gate is unitarized to a 12 × 12 transformation42 and programmed on our processor (see Methods)43,44. The gate simulates the LQG quantum evolution in a 4-simplex26. The general LQG evolution on quantum spacetime defines the spinfoam amplitude as the analog of the Feynman amplitude, while the 4-simplex is the analog of a vertex in the Feynman diagram, so the amplitude of a 4-simplex is called the vertex amplitude in LQG. The boundary of a 4-simplex is made by five quantum tetrahedra (see Fig. 1c), which are simulated by the input and output qubits. To understand the non-unitarity, the vertex amplitude in quantum electrodynamics is not unitary, although the full transition amplitude is. This quantum gate converts input and output states into amplitudes (complex numbers). This is analogous to process amplitudes in quantum mechanics, which is equal to the scalar product of the input states and the output states separated by the process operator. In concrete, we formulate the amplitude following the formalism of Engle-Pereira-Rovelli-Livine (EPRL)45. The numerical data for the comparison to the experiment is obtained by the algorithm in ref. 46.

To ascertain the quality with which we have done so, we must measure the experimentally produced transition amplitude matrix, so that we can compare it with the target matrix. To measure the produced matrix, we use the fact that a linear-optical transformation can be characterized with only one and two-photon measurements47,48. We measure 12 single-photon transmission measurements and 21 Hong-Ou-Mandel (HOM) dip measurements were carried out to infer amplitudes and phases of the unitary transformation respectively. We run the experiment for 60 seconds per one-photon measurement, and 25 minutes per HOM dip measurement.

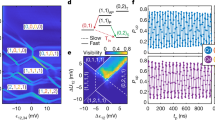
Figure 2 shows the results of the matrix characterization of the experimentally measured matrix \({U}_{\exp }\) against the target (theory) matrix Uth. In Fig. 2a and b the normalized amplitudes of the matrix elements ∣Ui,j∣ are plotted using a color scheme, for the experiment and theory matrices, respectively. Each one of the colored blocks represents a matrix element of the unitary transformation that relates specific inputs and outputs of the photonic processor. In Fig. 2c and d the phases of the matrix elements Ui,j are plotted using a color scheme, for the experiment and target matrices, respectively. We note parenthetically that there is more disagreement between experiment and theory in the phases than in the amplitudes. We speculate that this is due to the fact that phase reconstruction is dependent on the two-photon interference part of the characterization process, which occurs at lower rates than the single-photon interference. We leave the topic of error propagation in matrix reconstruction for further study.

Fig. 2: Reconstructed matrix.
figure 2

The top row shows the matrix amplitudes for the experimentally observed matrix (a) and for the target matrix (b). The second row shows the matrix element’s phases for the experiment (c) and target (d), respectively. The reduced 8 × 4 matrix, connected to the 4-simplex transformation, is marked by a red box.

Full size image

To make the comparison between theory and experiment more quantitative, we use the matrix fidelity, a standard measure in the field44,49 used to quantify the degree of similarity between two matrices. Depending on whether the role of phase is of interest, one considers either the amplitude-only fidelity \({F}_{a}=\frac{1}{N}{{{\rm{Tr}}}}(| {U}_{{{{\rm{target}}}}}^{{\dagger} }| | {U}_{\exp }| )\), or the full fidelity \(F=\frac{1}{N}{{{\rm{Tr}}}}(| {U}_{{{{\rm{target}}}}}^{{\dagger} }{U}_{\exp }| )\). Noting that linear-optical circuits are defined up to an equivalence class defined by multiplications with phases at the input and output of the circuit, we compute the fidelity of our resulting matrix to that class by optimizing over those phases. For our full N = 12-mode matrix, we find Fa = 0.975, and F = 0.941, respectively. For the submatrix of interest corresponding to the 4-simplex, (indicated with a box in all subfigures of Fig. 2), we find Fa = 0.982 and F = 0.947. We note that for this case the normalization is \(\scriptstyle {\sqrt{{{{\rm{Tr}}}}(| {U}_{{{{\rm{target}}}}}^{{\dagger} }| | {U}_{{{{\rm{target}}}}}| ){{{\rm{Tr}}}}(| {U}_{\exp }^{{\dagger} }| | {U}_{\exp }| )}}\) and not N. In a preliminary analysis, we found that the quantities of interest in LQG are more dependent on fluctuations in amplitude than in phase, which motivates us to state both quantities. In all further data processing we use the full reconstructed matrix, including phase information.

LQG experimental transition amplitudes

To assess the quality of our implemented 4-symplex simulation from an LQG perspective, we choose a class of specific boundary states where all the face spins are 1/2. These boundary states are tensor products of five single-qubit states39. Now, to estimate the degree of similarity between theory and experiment we compare the spinfoam amplitudes, computed with the chosen boundary states and the experimental and theoretical quantum gates. The 4-simplex is projected onto a theoretical amplitude function, Ath(θ1, ϕ1 ⋯ θ5, ϕ5), by taking the scalar product with five qubit as defined in Eq. 6 of Supplementary Note 1. The function is parameterized by five pairs of inclination angle θi and azimuth angle ϕi on the Bloch spheres of the single-qubit states. Similarly, the experimental 8 × 4 reduced matrix defines an amplitude function, \({A}_{\exp }({\theta }_{1},{\phi }_{1}\cdots {\theta }_{5},{\phi }_{5})\). We use these functions to compute spinfoam amplitudes for three types of boundary setups. In the first setup, we let all the inclination angles and azimuth angles equal to θ and ϕ. The contour plots of the experimental and theoretical amplitude functions are presented in Fig. 3a and b. The shared features of the two contour plots indicate the agreement between theory and experiment, e.g., there is a “Y”-shape valley in the upper part of both plots, the positions of the peak in both plots are nearly the same. The second setup sets four out of five quantum tetrahedra as regular quantum tetrahedra, i.e., their angle pairs are either (π/2, π/2) or (π/2, 3π/2) depending on the orientation of the 4-simplex. In this setup, Ath and \({A}_{\exp }\) are functions depending on the θ and ϕ of the fifth tetrahedron. Figure 3h–l and c–g is the contour plots of ∣Ath∣ and \(| {A}_{\exp }|\) given by varying a different quantum tetrahedron. In the third setup, the five boundary quantum tetrahedra are random states given by circular unitary distribution. The expectation value of Ath is 0.0196 + i0.000146, and the expectation value of \({A}_{\exp }\) is 0.0204 + i0.0000521, which results in a percentage difference around 4.10%.

Fig. 3: Contour plots.
figure 3

The contour plots of the absolute values of the vertex amplitude given by different boundary states. θ and ϕ parameterize the boundary quantum tetrahedra states. a is calculated based on the experimental matrix and b by the theoretical matrix. The shapes of the contours in (a) and (b) share some common features, e.g., the Y-shape valley in the top half and the trough in the bottom-left corner. The maximum values in both plots are marked by red dots. The positions where these maximum values appear are nearly the same in both plots. Panels c–l show the contour plot where 4 tetrahedra are regular (i.e., (θ, ϕ) = (π/2, π/2) or (θ, ϕ) = (π/2, 3π/2)) and we change (θ, ϕ) of the fifth tetrahedron. Panels c–g are calculated based on the experimental matrix and h–l by the theoretical matrix.

Full size image

Furthermore, by LQG theory and given our boundary state class, Ath(θ1, ϕ1 ⋯ θ5, ϕ5) is invariant under the transformation of swapping between label 1 and label 2, and the permutations of labels 3, 4, and 5. Figure 3h–l shows this symmetry clearly. This can also be observed in the experimental results (Fig. 3c–g), except of Fig. 3d, which contains large deviations.

Discussion

Both the fidelity F and the comparison between the amplitude functions, Ath and \({A}_{\exp }\), show agreement between experiment and theory expectations with tolerable errors. When we set the boundary states as random states, the small 4% difference between the theoretical and experimental expectation values supports this overall agreement from a different point of view than the fidelity. The agreement indicates that the experimental operation of the chip encodes the LQG dynamics in a 4-simplex. In addition, the contour plots of Fig. 3 show that our experimental result captures the semiclassical geometry emergent from the vertex amplitude. Indeed, in LQG, the saddle points where the amplitude reaches its extreme values relates to the semiclassical geometry, which links the quantum theory to its semiclassical approximation. In both Fig. 3b and c, the maximum value of the \(| {A}_{\exp }|\) appears around (θ, ϕ) = (π/2, π/2). Although with some error, Fig. 3d–g also shows a tendency that the maximum value would appears around (θ, ϕ) = (π/2, π/2) or (θ, ϕ) = (π/2, 3π/2). In LQG39, the expectation values of the geometric operators on a qubit state with (θ, ϕ) = (π/2, π/2) or with (θ, ϕ) = (π/2, 3π/2) indicate the quantum tetrahedron can be interpreted as a regular tetrahedron. This means that our experimental results show a trend that the amplitude picks up the boundary state given by the one that all boundary tetrahedra are regular in semiclassical approximation. In classical simplicial geometry, five regular tetrahedra make the boundary of a classical regular 4-simplex. By this means, the quantum gate in our chip carries the proper physical information which makes the mostly weighted boundary state as the one matches the classical simplicial geometry.

Aside from the aforementioned achievements, there are aspects yet to be improved. When setting all boundary tetrahedra to be regular, the resultant amplitude is \({A}_{\exp }=-0.363-{{{\rm{i}}}}0.183\). Compared to Ath = − 0.287 − i0.497, the percentage error of the absolute value of these quantities is around 29%. The peaks in Fig. 3d–g deviate from the one giving regular tetrahedra. All deviations come from the errors in some elements of the matrix \({U}_{\exp }\). The subplots of Fig. 3 represent different projections of the matrix \({U}_{\exp }\). A projection (or a subplot) deviates more from the theoretical expectation, if this projection involves more noisy matrix elements. Decreasing these element-wise errors can be done by circuit optimization algorithms50,51 possibly by embedding the 12-mode chip in a larger chip, but this improvement is left for future research.

Scaling the experimental demonstration to a larger number of vertices with more chips requires implementation of the vertices’ connection. In general, this connection corresponds to a scalar product of two tetrahedra, applied by a projection of two quantum states. We highlight the question of implementing connections in an arbitrary encoding as a problem of interest. Since we implement the quantum states with spatial modes of single photons, the required projection involves photon-photon interaction. HOM can be used as a projection of one photon onto another, even if the photons are in superposition of many modes52. Thus, we speculate that the connection between chips can be implemented by HOM interference. Even if this is not possible, only a single two-photon gate is necessary. Although it is not a linear-optical simulator anymore, it is still a much simpler setup than a universal quantum computer. Further numerical investigation reveals that the tolerable error is scaled linearly with the number of vertices. This means that simulations of multi vertices will require reducing the error by one over the number of vertices (see Supplementary Note 2 for more details). This is in agreement with intuition, since the number of elements grows linearly and thus the error increases linearly.

For quantum simulation to demonstrate quantum advantage, the entire process of receiving the desired information has to be computationally efficient only if quantum devices are used. This includes both the performance of the quantum simulation and the data post-processing to decipher the desired information. We have solid reasons to believe that the first is efficient since the number of resources (photons and chips) increase linearly with the number of vertices and the number of tetrahedra which is needed for quantum advantage. This is not correct if classical devices are used since the resources (e.g., memory) increase exponentially with the number of vertices (see also Supplementary Note 1). Notably, the preparation of the quantum gate is efficient also for large transitions, since all chips are prepared to emulate a single vertex which can be done easily with classical computers due to the small size of it. Also, the post-processing is efficient since it involves only matrix multiplications.

Another interesting topic is to analysis the computing complexity when we have a fixed triangulation with N 4-simplices. The recent interesting models in LQG include, e.g., a model of a black hole with N = 1453 and a few models with N = 3, 5, 6 on the semiclassical analysis54,55,56. Denoting C as the complexity of a gate representing one 4-simplex with spin-1/2, the total complexity of the spinfoam in this case is CN. The vertex amplitudes become more complicated, when spin is greater than 1/2. In this case, two types of factors are introduced into the total complexity. One is caused by the fact that each quantum tetrahedron Δ becomes a qudit whose complexity is bounded by MΔ = \({{d}}\choose{2}\), where d is the dimension of the quantum tetrahedron Hilbert space26. The other factor Jf describes the effect caused by the summing over the spin of the internal triangle f. Thus, in this case, the total complexity is bounded by CN∏ΔMΔ∏fJf where the ∏Δ products over all the tetrahedra and ∏f is done over all the bulk triangles26.

The spinfoam model is a special case of tensor-network models57. The tensor-network models are generally made of quantum gates of qubits58, similar to the spinfoam amplitude that we study here. Thus, our experimental method should have wide applications to other tensor-network models.

In conclusion, we have demonstrated that we can simulate a single 4-simplex using a linear-optical quantum system. We have shown that both by metrics current in the field of linear optics and by metrics oriented specifically towards the application of these systems in loop quantum gravity, we have faithfully implemented the properties of this 4-simplex in linear optics.

This demonstration—simulating a simple LQG transition with linear optics—is the first step towards full-scale simulations of loop quantum gravity, which is currently intractable with classical computers. The rapid growth in integrated photonic technology44 is moving towards demonstration of quantum advantage. Using our method, this quantum advantage, which is not available in today’s classical computing toolbox, can be used as a tool for investigating LQG,

Methods

Experimental setup

Our experimental setup (see Fig. 4) is based on linear quantum optics, a non-universal platform for quantum simulations. In this model, bosonic interference between indistinguishable photons is used to process information encoded in the spatial degree of freedom of the photons. More specifically, we use a quantum photonic processor to implement the quantum simulation, and a single-photon source and single-photon detectors to test the quality of our implemented simulation.

Fig. 4: Setup.
figure 4

A pulsed laser is used to generate pairs of photons in a ppKTP crystal. The generated photons have orthogonal polarizations and are separated by a polarizing beam splitter (PBS) and subsequently coupled into a polarization-maintaining fibers which are connected to the optical network. After the optical network, the photons go through a single-mode fiber to the single-photon detectors via a fiber polarization controller (not shown). The experiment requires proper indistinguishable photons. Hence, a 12 nm bandpass filter (BPF) is placed to remove spectral correlations between the photons. Furthermore, one of the fiber couplers is placed on a linear stage to guarantee temporal overlap of the photons. A beam sampler is used to monitor the power using a calibrated photo diode and the pump beam is filtered out after the ppKTP crystal (both not shown).

Full size image

The optical path of this experiment is as follows: heralded single-photon states (Fock states) are produced in a spontaneous parametric down-conversion (SPDC)59 source on periodically poled potassium titanyl phosphate (ppKTP). These single photons are then fed into our large-scale integrated quantum photonic processor, in which linear-optical quantum interference occurs. Finally, the photons are measured at the output of the interferometer by superconducting nanowire single-photon detectors (SNSPDs).

The single-photon source consists of a Ti:Sapphire pulsed laser (Tsunami), producing pulses duration of Δτ ≈ 100 fs centered at λ = 775 nm and with a width of Δλ = 5.6 nm (full witdth at half maximum) at a repetition rate of 80 MHz. The laser is used to pump a 2 mm ppKTP non-linear crystal. Inside this crystal, a pump photon is spontaneously down-converted into a pair of single photons with degenerate spectra, centered at λ = 1550 nm. A spectral bandpass filter of Δλ = 12 nm (full width at half maximum) is used to remove any residual spectral correlations between the photons, and thus guaranteeing maximum indistinguishability. The photons are collected into polarization-maintaining single-mode optical fiber by fiber couplers, and fed into the chip at the desired input modes. The temporal overlap of the photons can be continuously tuned by a fibercoupler placed onto a motorized linear displacement stage. The HOM effect is used as a benchmarking tool to measure the degree of two-photon wave function overlap \(x=\langle {\psi }_{\scriptstyle{{{{\rm{photon}}}}}_{1}}| {\psi }_{{{{{\rm{photon}}}}}_{2}}\rangle\) according to x2 ≥ V, where V is the visibility of the HOM dip60. In our experiment we measure x = 0.9899 ± 0.0015, which showcases the high quality of our source.

The photonic processor is a 12-channel integrated linear interferometer based on silicon nitride (Si3N4) waveguides, with an overall optical loss of 2.2–2.7 dB, corresponding to a transmission of 54–60%, depending on the optical channel44 (Note that the optical losses of the interferometer have been improved since this publication). The linear network consists of an array of unit cells arranged in a square mesh architecture, whose geometry guarantees universality on the space of linear-optical transformations43. Each unit cell of the interferometer corresponds to a Mach-Zehnder interferometer (MZI) between adjacent modes, and is tunable by the thermo-optic effect. For a full 12-mode transformation, the average amplitude fidelity is F = 0.98. On the photonic processor, we encoded a vertex gate of two input spins-1/2 to three output spins-1/2. The 8 × 4 non-unitary gate is embedded in a 12 × 12 unitary gate. For a general spin j, (2j + 2)(2j+1)2 chip modes are needed. For high spins multiplexing methods are required, for example by using orbital momentum modes61.

Detection of the photons after the interferometer is achieved using standard single-photon threshold (click) detectors. The output channels of the chip are connected via single-mode polarization-maintaining optical fiber to a bank of 12 superconducting nanowire single-photon detectors (SNSPDs), which are read out using conventional correlation electronics.

When performing measurements, the pump laser is operated at relatively low power (≈5 mW), to avoid introducing cross-correlations between different experimental runs, since the dead time of the detectors is longer than the repetition rate of the source. At these power levels, with a photon-generation probability of ~0.1% per pulse, we achieve single-photon rates of 19.6 ± 0.16 kHz and two-photon coincidence rates of 2.56 ± 0.11 kHz, where the errors correspond to Poissonian noise.