Introduction

Computationally accurate prediction of physical properties can accelerate the development of functional materials such as batteries1,2, catalysis3, and photochemical materials4,5. The physical properties are mainly governed by the electrons in the materials, and the computational cost of calculating electronic structures increases exponentially with system size in general, which often prevents classical computers from achieving the required accuracy to predict the properties.

Quantum computers are expected to solve such classically intractable problems in quantum chemistry and materials science6. Current quantum computers, called noisy intermediate scale-quantum (NISQ) devices7, have limitations on the numbers of qubits and quantum gates due to physical noise, and various approaches for the NISQ devices have been proposed8,9. One of the most popular algorithms is the variational quantum eigensolver (VQE)10, which is used to obtain the ground state energy by minimizing energy cost function using a variational quantum circuit, where its parameters are updated by a classical computer. Contrary to the traditional quantum algorithms such as the quantum phase estimation11, VQE requires reduced hardware resources. However, VQE suffers from many issues such as insufficient accuracy12 and vanishing parameter gradients, so-called barren plateau13.

In addition to studies to avoid those issues14,15,16,17, there are multiple variants of quantum Monte Carlo (QMC), which were proposed for further relaxing the hardware requirements18,19,20,21,22,23,24. QMC is a computational method using stochastic sampling techniques to solve large quantum many-body problems such as molecular systems containing hundreds of electrons25,26. To date, various types of QMC approaches have been proposed, including variational Monte Carlo27,28, auxiliary field quantum Monte Carlo29,30, and full configuration interaction quantum Monte Carlo (FCIQMC)31. In this study, we adopt FCIQMC, which is useful for quantum chemistry, a stochastic imaginary-time evolution is executed in the space of all the orthonormal basis states (such as the Slater determinants) that can be constructed from a given spatial orbital basis. As in refs. 18,21,22, a type of QMC called quantum computing QMC (QC-QMC) was introduced. Combined with a quantum algorithm such as VQE, QC-QMC can improve the energy evaluation accuracy in ground-state calculations. Specifically, the wave function distribution, i.e., the walker distribution, is generated on a classical21 (or quantum18,22) device, and energy is evaluated by using a trial wave function prepared by VQE. Contrary to VQE where the accuracy depends on parameter optimization, QC-QMC has no such optimization and the accuracy relies on the quality of the trial wave functions, the algorithms, and calculation settings in the energy evaluation. Avoiding strict VQE optimizations lowers the hardware requirements; for example, there was a demonstration on a diamond model constructed in 16 qubits, the largest hardware experiment run nearly within the chemical accuracy (chemical precision)18.

While QC-QMC can provide highly accurate ground-state calculations, applying this method to large-scale systems is challenging. Although the electronic correlations outside the active space can be obtained by classical post-processing18, the available active space size32,33 is limited by the size of the trial wave function i.e., the number of qubits. The proposals for constructing wave functions larger than the quantum device size include the divide-and-conquer algorithm34,35, embedding theory36,37,38, circuit cutting39,40, perturbation41, and tensor network42,43. Hybrid tensor network (HTN)43 is a general tensor network framework that can be implemented on a reduced number of qubits and gates by decomposing the wave function in the original system into smaller-sized tensors. These tensors are processed by quantum or classical computation, i.e., quantum/classical hybrid computation. Such a decomposition can reduce the effective width and depth of the circuit, making it more robust to noise than the original circuit. There are several quantum algorithms or ansatze depending on the tensor network structure, including the matrix product states44, projected entangled pair states45, and tree tensor networks (TN)42,46. In the two-layer TN adopted in this study, the quantum states of the subsystem in the first layer are integrated with the second layer by using a quantum or classical method, referred to as the quantum-quantum TN (QQTN) and quantum-classical TN, respectively. The deep VQE35 and entanglement forging47,48 can be broadly classified into the quantum-quantum and quantum-classical ones, respectively. If gaining the quantum advantage (rather than noise robustness) is a priority, QQTN is preferred.

In this study, we propose an algorithm of QC-QMC in combination with HTN of a two-layered QQTN. In particular, we consider the following QQTN:

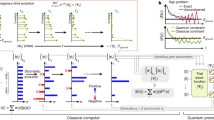
$$\begin{array}{l}\Big| {\psi }_{{{{\rm{HTN}}}}}({\vec{\theta }}_{{{{\rm{HTN}}}}})\Big\rangle \\ =\displaystyle\sum_{\vec{i}}{\psi }_{\vec{i}}({\vec{\theta }}_{U})\left(\mathop{\prod }\limits_{m=1}^{k}\sum_{{\vec{j}}_{m}}{\varphi }_{{\vec{j}}_{m}}^{{i}_{m}}({\vec{\theta }}_{Lm})\right)\left(\mathop{\bigotimes}\limits_{m = 1}^{k}\Big| {\vec{j}}_{m}\Big\rangle \right)\\ =\displaystyle\sum\limits_{\vec{i}}{\psi }_{\vec{i}}({\vec{\theta }}_{U})\mathop{\bigotimes}\limits_{m = 1}^{k}\Big| {\varphi }^{{i}_{m}}({\vec{\theta }}_{Lm})\Big\rangle .\end{array}$$
(1)

The tensor network representation of this state is depicted in Fig. 1a. The tensors \({\psi }_{\vec{i}}({\vec{\theta }}_{U})\) (\({\varphi }_{{\vec{j}}_{m}}^{{i}_{m}}({\vec{\theta }}_{Lm})\)) are defined using wave functions \(\left\vert * \right\rangle \psi ({\vec{\theta }}_{U})\) (\(\left\vert * \right\rangle {\varphi }^{{i}_{m}}({\vec{\theta }}_{Lm})\)) as \({\psi }_{\vec{i}}({\vec{\theta }}_{U})=\langle * | \vec{i}\rangle \psi ({\vec{\theta }}_{U})\) (\({\varphi }_{{\vec{j}}_{m}}^{{i}_{m}}({\vec{\theta }}_{Lm})=\langle * | {\vec{j}}_{m}\rangle {\varphi }^{{i}_{m}}({\vec{\theta }}_{Lm})\)), where \(\vec{i}={i}_{1}{i}_{2}\ldots {i}_{k}\) (\({\vec{j}}_{m}={j}_{m1}{j}_{m2}\ldots {j}_{mn}\)) represent a k (n)-qubit binary string, and the subscript \({\vec{j}}_{m}\) of \({\varphi }_{{\vec{j}}_{m}}^{{i}_{m}}({\vec{\theta }}_{Lm})\) is omitted in Fig. 1. \({\psi }_{\vec{i}}({\vec{\theta }}_{U})\) and \({\varphi }_{{\vec{j}}_{m}}^{{i}_{m}}({\vec{\theta }}_{Lm})\) are assumed to be constructed by quantum circuits, where \({\vec{\theta }}_{U}\) and \({\vec{\theta }}_{Lm}\) are variational parameters of the upper tensor (blue) and the m-th lower tensor (orange), respectively. The subscripts U and L designate the upper and lower tensors, respectively. k and nk represent the number of subsystems and system qubits, respectively. The algorithm details are given in Section IV (and Supplementary Informations 1, 2, and 3), where calculating the transition amplitude between a pair of the wave functions \(T({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(1)},{\vec{\theta }}_{{{{\rm{HTN}}}}}^{(2)})\) is a major part:

$$T({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(1)},{\vec{\theta }}_{{{{\rm{HTN}}}}}^{(2)})=\left\langle {\psi }_{{{{\rm{HTN}}}}}^{(1)}({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(1)})\right\vert O\left\vert {\psi }_{{{{\rm{HTN}}}}}^{(2)}({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(2)})\right\rangle ,$$
(2)

where the observable O is defined using tensor products O = ⨂m,rOmr and Omr is an observable attached on the r-th qubit of the m-th subsystem (r = 1, 2, …, n). As shown in Fig. 1b, the transition amplitude \(T({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(1)},{\vec{\theta }}_{{{{\rm{HTN}}}}}^{(2)})\) is calculated by performing a quantum computation on the lower tensor, classically processing the obtained results to generate the contracted operators Nm, and then contracting with a quantum computation on the upper tensor. Substituting \(\vert {\psi }_{{{{\rm{HTN}}}}}^{(1)}({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(1)})\rangle =\vert {\psi }_{{{{\rm{HTN}}}}}^{(2)}({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(2)})\rangle =\vert {\psi }_{{{{\rm{HTN}}}}}({\vec{\theta }}_{{{{\rm{HTN}}}}})\rangle\) in Eq. (2) yields the estimation of the observable

$$\left\langle {\psi }_{{{{\rm{HTN}}}}}({\vec{\theta }}_{{{{\rm{HTN}}}}})\right\vert O\left\vert {\psi }_{{{{\rm{HTN}}}}}({\vec{\theta }}_{{{{\rm{HTN}}}}})\right\rangle ,$$
(3)

and by substituting \(\vert {\psi }_{{{{\rm{HTN}}}}}^{(1)}({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(1)})\rangle =\vert {\psi }_{{{{\rm{HTN}}}}}({\vec{\theta }}_{{{{\rm{HTN}}}}})\rangle\), \(\vert {\psi }_{{{{\rm{HTN}}}}}^{(2)}({\vec{\theta }}_{{{{\rm{HTN}}}}}^{(2)})\rangle =\vert {\phi }_{h}\rangle\), and O = I⊗nk in Eq. (2), we obtain the overlap with the h-th orthonormal basis state \(\left\vert {\phi }_{h}\right\rangle\) (e.g., the Slater determinant)

$$\langle {\psi }_{{{{\rm{HTN}}}}}({\vec{\theta }}_{{{{\rm{HTN}}}}})| {\phi }_{h}\rangle .$$
(4)
Fig. 1: Representation and calculation of hybrid tensor network in the two-layer QQTN.
figure 1

a Hybrid tensor network representation of the two-layered QQTN state. b Calculation of T in Eq. (2), where we omit the parameters. See Section IV C for details.

Full size image

The HTN+QMC algorithm consists of two steps: first, we optimize \({\vec{\theta }}_{{{{\rm{HTN}}}}}=({\vec{\theta }}_{U},{\vec{\theta }}_{Lm})\) to prepare the trial wave function, by calculating Eq. (3). Second, we execute QMC by using the trial wave function \(\left\vert {\psi }_{{{{\rm{HTN}}}}}({\vec{\theta }}_{{{{\rm{HTN}}}}})\right\rangle\), which was optimized in the first step, and using Eq. (4). We will denote HTN+VQE when referring to the first step only and omit the parameter in \(\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\) hereafter. In this formalism, by using the contraction technique shown in Fig. 1b, we can construct a nk qubit tree-type trial wave function in QMC by using a n qubit device with a linear measurement overhead. Note that the dimension of the subsystem represented by each lower tensor is determined by the number of the legs connected to the upper tensor. Under such restrictions, therefore, how to decompose the target system into the subsystems is a crucial factor in achieving a high fidelity of the tensor product state.

We benchmarked the performance of our algorithm for the Heisenberg chain model, hydrogen (H4) plane model, graphite-based Hubbard model, and MonoArylBiImidazole (MABI), which are classified into four material categories: physical or chemical (solid or molecule) and basic or applied as in Fig. 2. The first two models are commonly used as the benchmark model18,49. Graphite is a two-dimensional layered material and is used as an anode in lithium-ion batteries50. MABI is a model system of the photochromic radical dimer PentaArylBiImidazole (PABI)51. We also execute on a real device ibmq_kolkata by developing a technique to calculate the overlap between the trial wave function and orthonormal basis state required in HTN+QMC. We call this technique a pseudo-Hadamard test because the Hadamard test type circuit is used in the technique. We mention that the proposed algorithm can be applied to other HTN structures and QMC types. For example, by changing the overlap calculation in the original QC-AFQMC18 to the calculation introduced in this paper, it could be extended to the HTN version.

Fig. 2: Models for benchmarking HTN+QMC.
figure 2

The structure of graphite is drawn by VESTA72. The qubit indices are labeled in (a, b) (see Section II A for details). a Heisenberg chain model. b Graphite-based Hubbard model. c Hydrogen plane model. d MonoArylBilmidazole (MABI).

Full size image

Finally, while our main objective is to large-scale QC-QMC by using HTN, we should comment on the treatment of the sign problem in this study. In previous research on QC-QMC18,21,22, there are two steps where quantum computation is utilized: one related to walker control, and the other (projected) energy evaluation. Both steps employ quantum computation for overlap or transition amplitude calculations. In this study, we adopted a method that applies quantum computation only to the energy calculation21. While this method reduces the variance of energy evaluation, it does not essentially address the sign problem of FCIQMC, where the required number of walkers exponentially increases with system size. To tackle the problem, we should address the method related to a walker control, for example, the construction of an orthonormal basis using a unitary transformation by VQE22, in which the QMC wave function is represented more sparsely than in the Slater determinant basis. In Supplementary Information 4, we provide an overview of the HTN+FCIQMC algorithm including the sparse basis construction. However, this algorithm was not tested in this study due to its high computational cost for verifications and the fact that it is far from the main purpose of this study, which is to extend QC-QMC to HTN.

Results

We first explain the benchmarking models. Next, we demonstrate the performance in HTN+QMC for the Heisenberg chain model, followed by the analysis of all the benchmarking models. Then, we describe the operational principle of the pseudo-Hadamard test technique and present the corresponding results of the real device experiments for the hydrogen plane model and MABI.

Benchmarking models

The performance of HTN+QMC is benchmarked with the Heisenberg chain model, graphite-based Hubbard model, hydrogen plane model, and MABI. The Heisenberg chain model, as shown in Fig. 2a, is defined as a chain of k clusters consisting of four sites

$$H=\mathop{\sum}\limits_{p=1}^{k}{H}_{p}+{J}_{{{{\rm{inter}}}}}\mathop{\sum}\limits_{{p}^{{\prime} }=1}^{k-1}{H}_{{p}^{{\prime} }},$$
(5)

where

$$\begin{array}{ll}{H}_{p}\,=\,\mathop{\sum}\limits_{f=1}^{3}{X}_{4(p-1)+f}{X}_{4(p-1)+f+1}\\\qquad+\,{Y}_{4(p-1)+f}{Y}_{4(p-1)+f+1}\\\qquad+\,{Z}_{4(p-1)+f}{Z}_{4(p-1)+f+1},\end{array}$$
(6)
$${H}_{{p}^{{\prime} }}={X}_{4{p}^{{\prime} }}{X}_{4{p}^{{\prime} }+1}+{Y}_{4{p}^{{\prime} }}{Y}_{4{p}^{{\prime} }+1}+{Z}_{4{p}^{{\prime} }}{Z}_{4{p}^{{\prime} }+1}.$$
(7)

The intra- and inter-cluster interactions are 1 and Jinter, respectively. In the benchmark, we consider k = 2 and 3, i.e., 8- and 12-qubit models and Jinter = 0.2, 0.4, …, 2.0. We assume that the Jinter is described by atomic unit (i.e., Hartree), but except when necessary, the unit is omitted according to convention.

Figure 2b shows our graphite-based Hubbard model (the graphite model hereafter), where two layers of graphene sheets are modeled with periodically aligned unit cells, in which two carbon atoms reside in each layer. Using two qubits to represent the up and down spin orbitals (pz orbitals) in each carbon atom, we define the Hamiltonian with 8 qubits as

$$\begin{array}{ll}H\,=\,3{t}_{1}{\sum}_{q=1,2,5,6}({a}_{q+2}^{{\dagger} }{a}_{q}+{a}_{q}^{{\dagger} }{a}_{q+2})\\ \qquad+\,2{t}_{2}{\sum}_{q=1,2}({a}_{q+4}^{{\dagger} }{a}_{q}+{a}_{q}^{{\dagger} }{a}_{q+4})\\\qquad+\,U{\sum}_{q=1,3,5,7}{n}_{q+1}{n}_{q},\end{array}$$
(8)

where q is the spin-orbital index for the pz orbital in carbon, and q = 1, 2, 3, and 4 (5, 6, 7, and 8) corresponds to the first (second) layer. \({a}_{q}^{{\dagger} }\) (aq) is the creation (annihilation) operators on the q-th site and nq is the number operator \({n}_{q}={a}_{q}^{{\dagger} }{a}_{q}\). t1 and t2 are the hopping energy between the first and second nearest neighbor sites corresponding to the intra- and inter-layer interaction energy, respectively, and U is the on-site Coulomb energy. The prefactors for t1 and t2 arise from periodic boundary conditions, e.g., the prefactor for t2 is 2 because two inter-layer interactions exist per carbon (one inside and the other outside the unit cell). The reason for t2 being only on two indices, q = 1 and 2, is because graphite is AB stacking. We determine the value of t1, t2, and U using the electronic structure calculation. See Supplementary Information 5 for details.

The Hamiltonians for the hydrogen plane model (8-qubit model) in Fig. 2c and MABI (12-qubit model) in Fig. 2d were constructed using their restricted Hartree-Fock orbitals of their ground states as molecular orbital bases. In the hydrogen plane model, the two hydrogen molecules are arranged vertically as in the index (ID) 0 of Fig. 2c. Then, the intermolecular and intramolecular distances are shortened and lengthened, respectively, until the hydrogen plane becomes a square as in ID 3. The two structures are interpolated between ID 0 and 3, benchmarking four structures.

Next, we present the specific conditions for constructing the benchmarking models. The decomposition settings used for individual models are as follows: for the Heisenberg chain model, the cluster and even-odd settings refer to decomposing the model into subsystems by the cluster and even-odd indices, respectively, as illustrated in Fig. 3a; for the graphite model, the horizontal and vertical settings refer to decomposing the model horizontally and vertically with respect to the sheet (in the ab-axis plane in Fig. 2b), respectively, as in Fig. 3b; for the chemical models (hydrogen plane model and MABI), the HOMO-LUMO, alpha-beta, and occ-unocc settings refer to decomposing the model using the pair of HOMO − x and LUMO + x as units (x = 0 and 1 in the hydrogen plane model and x = 0, 1, and 2 in MABI), based on alpha and beta spin-orbitals, as well as occupied and unoccupied orbitals, respectively, as in Fig. 3c, where the orbitals of the chemical models are shown in Supplementary Information 5; the no-decomposition setting refers to the calculation without decomposing the original system, i.e., not using HTN. The cluster setting for the Heisenberg model, the horizontal setting for the graphite model, and the HOMO-LUMO setting for chemical models are adopted as a default.

Fig. 3: Decomposition settings. n = 4 and k = 2 are assumed for all the models in this figure.
figure 3

a Heisenberg chain model. b Graphite-based Hubbard model. c Chemical models in the case of the eight-qubit model.

Full size image

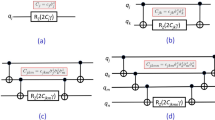
Figure 4 shows the quantum circuit called real amplitude ansatz, a popular hardware efficient ansatz employed for devices with linear connectivity layout, where dH, dN, and \({\tilde{d}}_{H}\) denote the depth in HTN, the no-decomposition setting, and HTN used for real device, i.e., the block surrounded by the dotted line is repeated dH or dN, and \({\tilde{d}}_{H}\) times, respectively. Figure 4a shows the original circuit, which is used for the statevector simulation, whereas, in order to run on real devices, a variant with ancilla qubit was considered, as in Fig. 4b; details on the operation are given in Section II C. In both ansatze, the rotation angle of the RY gate (i.e., the parameter) is updated at VQE and HTN+VQE iterations, while in the second step of QC-QMC and HTN+QMC, it is fixed. Because HTN+VQE demands quite a high computational cost due to its iterative process, the real device (ibmq_kolkata) was used only for the overlap calculation in the second step, i.e., not for HTN+VQE computations.

Fig. 4: Circuits of real amplitude ansatz in this study.
figure 4

a Circuit in statevector procedure. All the lines represent system qubits. b Circuit in real device procedure. The topmost line represents an ancilla qubit and the other lines represent system qubits.

Full size image

The depth represents a value for the real amplitude ansatze, which are k-qubit and n-qubit circuits for upper and lower tensors, respectively, in HTN, whereas nk-qubit circuits in the no-decomposition setting (in which ancilla qubit is not counted). Thus, the numbers of parameters in the HTN and no-decomposition settings are different even with dH = dN, whereas the numbers in the statevector and real device procedure of HTN are the same when \({d}_{H}={\tilde{d}}_{H}\). The numbers of parameters in the HTN settings with dH and the no-decomposition setting with dN are nk(dH + 1) + k(dH + 1) and nk(dN + 1), respectively. We set dH = 4 as a default by referring to the benchmark results in Supplementary Information 6. The initial parameters for HTN+VQE are chosen randomly from [0, 1) and [0, 2π) in the statevector and the real device procedure, respectively, and those for VQE are [ − 2π, 2π]. Note that only the results specifically relevant to the discussion are described in the main text, while the rest are presented in the supplementals.

In all the QMC methods (QMC, QC-QMC, and HTN+QMC), we evaluate the mean and standard deviation of the (projected) energy over 5,000 to 10000 iterations excluding the Heisenberg chain model, whereas 50,000 to 100,000 iterations in the Heisenberg chain model. Hereafter absolute deviation from the exact ground state is referred to by energy difference. In QMC, a leading single orthonormal basis state in the exact ground state (single reference state hereafter) is chosen as a trial wave function. See Supplementary Information 7 for the details of the VQE and QMC conditions.

Statevector simulation

Figure 5a shows the result of executing HTN+VQE for the Heisenberg chain model in the cluster setting with dH = 4, k = 2, and Jinter = 1.0. As in the inset, the energy difference from the exact ground state energy is 4.4 × 10−1 at the end of the optimization. Figure 5b shows the result for HTN+QMC, and the energy difference with standard deviation from the exact value is 1.1 × 10−4 ± 1.4 × 10−2, which is more accurate than QMC. Specifically, that for QMC is 2.5 × 10−2 ± 2.1 × 10−1. We discuss the details of this improvement in Sec. III, and we note the measurement cost scale in the QMC step of HTN+QMC in Sec. IV D.

Fig. 5: Results of the energy in the Heisenberg chain models of the cluster setting with n = 4, k = 2, Jinter = 1.0, and dH = 4. The black dashed line represents the energy of the exact ground state.
figure 5

a Result for HTN+VQE (blue line). The inset shows the enlarged view along the y-axis. b Results for QMC (blue line) and HTN+QMC (orange line).

Full size image

Here, we briefly comment on the other models; the computational results are described in detail in Supplementary Information 6. Table 1 shows the results summarized on HTN of the Heisenberg chain models with k = 2 and 3, the graphite model, the hydrogen plane model with ID 3, and MABI. In all the models, the variance for HTN+QMC is smaller than that for HTN+VQE or QMC. Except for the hydrogen plane model, the variance decreases as the fidelity increases. Here, the fidelity is defined as the square of the overlap between the target and exact ground states. See Supplementary Information 2 for the statistical analysis for the fidelity and the variance in simple cases. For the hydrogen plane model, the variance for HTN+QMC is smaller than that for QMC, even though the fidelity for HTN+VQE (0.44) is almost the same as that for the single reference state (0.45). The fidelity is not the only factor that determines the quality of the trial wave function52. In the hydrogen plane model, the trial state generated by the HTN+VQE shares multiple determinants with the exact ground state, and it can make energy estimation robust to fluctuations in the QMC wave function. Thus, the performance of QMC may be improved even if the trial wave function does not have high fidelity, and it is important to evaluate the trial wave function quality through QMC computation.

Table 1 Energy differences with a standard deviation in VQE, QMC, and HTN+QMC, and fidelity for HTN+VQE and the single reference state for the Heisenberg chain models of the cluster setting with k = 2 and 3 and Jinter = 1.0, the graphite model of the horizontal setting with k = 2, the hydrogen plane model of HOMO-LUMO setting with k = 2 and ID 3, and MABI of HOMO-LUMO setting with k = 3; n = 4 and dH = 4 for all the models
Full size table

Real device experiments

We consider performing the proposed HTN+QMC algorithm on a real device. For this purpose, we need to reduce the overlap computational cost between the trial wave function and the orthonormal basis state (as in Eq. (4)). Conventionally, the overlap 〈ψ∣ϕh〉 between a wave function \(\left\vert \psi \right\rangle ={U}_{\psi }{\left\vert 0\right\rangle }^{\otimes \nu }\) and the orthonormal basis state \(\left\vert {\phi }_{h}\right\rangle ={U}_{{\phi }_{h}}{\left\vert 0\right\rangle }^{\otimes \nu }\), can be calculated using the Hadamard test, as in Fig. 6a, where Uψ typically consists of a collection of one- and two-qubit gates depending on the ansatz and ν is the number of system qubits. The controlled-Uψ contains a much larger number of multi-qubit gates compared to Uψ because all one- and two-qubit gates in Uψ are modified to the controlled gates. Several techniques to calculate the overlaps in fermionic systems have been proposed that can avoid deep circuits, for example, by using the particle preserving ansatz21,53. However, the techniques are inadequate for HTN+QMC due to no electron number preservation in the subsystems, and we explain the details in Supplementary Information 8.1. Note that \({U}_{{\phi }_{h}}\) requires at most ν two-qubit gates because it applies the CNOT gates from the ancilla to target qubits, the latter of which is set to \(\left\vert 1\right\rangle\) in \(\left\vert {\phi }_{h}\right\rangle\).

Fig. 6: Quantum circuits for calculating the overlap.
figure 6

The topmost line represents the ancilla qubit, and the other lines the system qubits. a Hadamard test. b Pseudo-Hadamard test. c VQE circuit with constraint to determine \({\tilde{U}}_{\psi }\) used for the pseudo-Hadamard test. The ancilla qubit is set to \(\left\vert 0\right\rangle\) when calculating the constraints.

Full size image

We develop a gate-efficient technique to calculate the overlap executable on an arbitrary ansatz called the pseudo-Hadamard test. See Supplementary Information 8 for extending the technique to HTN. Figure 6b shows the circuit of the pseudo-Hadamard test, in which Uψ is replaced with \({\tilde{U}}_{\psi }\) involving the ancilla qubit. This circuit calculates the overlap \(\langle \tilde{\psi }| {\phi }_{h}\rangle\) if \({\tilde{U}}_{\psi }\) satisfies the following conditions:

$$\begin{array}{rcl}&&{\tilde{U}}_{\psi }\left\vert 1\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }=\left\vert 1\right\rangle \vert \tilde{\psi } \rangle ,\\ &&{\tilde{U}}_{\psi }\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }=\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }.\end{array}$$
(9)

The gate \({\tilde{U}}_{\psi }\) can be determined through the VQE under constraints that the ancilla qubit is measured to be one in the first condition and all the qubits are measured to be zero in the second condition in Eq. (9), which is formulated as

$$\begin{array}{ll}\,{\min }_{{\tilde{U}}_{\psi }}\quad \left\langle 1\right\vert {\left\langle 0\right\vert }^{\otimes \nu }{\tilde{U}}_{\psi }^{{\dagger} }(I\otimes H){\tilde{U}}_{\psi }\left\vert 1\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }\\\qquad\quad{{{\rm{s.}}}}{{{\rm{t.}}}}\quad \left\langle 1\right\vert {\left\langle 0\right\vert }^{\otimes \nu }{\tilde{U}}_{\psi }^{{\dagger} }({n}_{0}\otimes {I}^{\otimes \nu }){\tilde{U}}_{\psi }\left\vert 1\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }=1,\\\qquad\quad\left\langle 0\right\vert {\left\langle 0\right\vert }^{\otimes \nu }{\tilde{U}}_{\psi }^{{\dagger} }\left({\sum }_{\kappa =0}^{\nu }{I}^{\otimes \kappa }\otimes {n}_{\kappa }\right.\\\qquad\quad\left.\otimes {I}^{\otimes \nu -\kappa }\right){\tilde{U}}_{\psi }\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }=0,\end{array}$$
(10)

where the index of the ancilla qubit is set to 0. nκ is the number operator of κ-th qubit in Eq. (8). Figure 6c shows the quantum circuit used to run such VQE, where Oι (ι = 0, 1, …, ν) is an observable of the ι-th qubit. The constraints can be relaxed through the appropriate selection of ansatz, such as the real amplitude ansatz without rotation gates on the ancilla qubit, as shown in Fig. 4b. In this case, VQE can be simplified as

$$\begin{array}{lll} \mathop{\min}\limits_{{\tilde{U}}_{\psi}} & \left\langle 1\right\vert {\left\langle 0\right\vert }^{\otimes \nu }{\tilde{U}}_{\psi }^{{\dagger} }(I\otimes H){\tilde{U}}_{\psi }\left\vert 1\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }\\ {{{\rm{s.t.}}}}& \left\langle 0\right\vert {\left\langle 0\right\vert }^{\otimes \nu }{\tilde{U}}_{\psi }^{{\dagger} }\bigg(\sum\limits _{\kappa =1}^{\nu }{I}^{\otimes \kappa }\otimes {n}_{\kappa }\\ & \quad \otimes {I}^{\otimes \nu -\kappa }\bigg){\tilde{U}}_{\psi }\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }=0.\end{array}$$
(11)

We adopt this simplified formalism hereafter. Note that \({\tilde{U}}_{\psi }\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }\) takes either \(\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }\) or \(-\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }\) in the constraint, but the signs cancel out in a numerator and denominator of the projected energy in QC-QMC and HTN+QMC (see Eq. (14)), allowing one to ignore the sign. In cases where the technique is applied outside of QMC, the sign could be determined based on the overlap between a trial wave function and a specific orthonormal basis state, e.g., the Hartree-Fock state21. We also mention the extensions of the technique; a transition amplitude of \(\langle \tilde{\psi }|\tilde{O }| {\phi }_{h}\rangle \,\)\((\tilde{O}={I\bigotimes }_{\iota = 1}^{\nu }{O}_{\iota })\) can be calculated by measuring each system qubit in the basis corresponding to Oι for the pseudo-Hadamard test circuit; that of \(\langle \tilde{\psi }|\tilde{O }| {\tilde{\psi }}^{{\prime} }\rangle\) can be also calculated by using the additional constraint \(\left\langle 1\right\vert {\left\langle 0\right\vert }^{\otimes \nu }{\tilde{U}}_{\psi }^{{\dagger} }{\tilde{U}}_{{\psi }^{{\prime} }}^{{\dagger} }{\tilde{U}}_{\psi }(\sum\nolimits_{\kappa = 1}^{\nu }{I}^{\otimes \kappa }\otimes {n}_{\kappa }\otimes {I}^{\otimes \nu -\kappa }){\tilde{U}}_{\psi }^{{\dagger} }{\tilde{U}}_{{\psi }^{{\prime} }}{\tilde{U}}_{\psi }\left\vert 1\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }=0\), where \(\vert {\tilde{\psi }}^{{\prime} }\rangle\) is a trial wave function defined by \({\tilde{U}}_{{\psi }^{{\prime} }}\) with a property of \({\tilde{U}}_{{\psi }^{{\prime} }}\left\vert 0\right\rangle {\left\vert 0\right\rangle }^{\otimes \nu }=\left\vert 0\right\rangle \left\vert * \right\rangle {\tilde{\psi }}^{{\prime} }\), e.g., the ansatz changing the control qubit condition of CNOT gates in Fig. 4b from one to zero ; a transition probability \(| \langle \tilde{\psi }|\tilde{O }| {\tilde{\psi }}^{{\prime} }\rangle {| }^{2}\) 54,55 can be trivially obtained by the square of the transition amplitude.

We applied the pseudo-Hadamard test technique to the HTN+QMC calculations on a real device ibmq_kolkata for the hydrogen plane model with ID 3 and MABI. The best trial wave function was selected from 100 seeds of HTN+VQE runs under the constraint (\({\tilde{d}}_{H}=4\) and statevector execution), where at most five qubits including an ancilla qubit, are used in the overlap calculation. The energy accuracy decreased due to newly introduced constraints in the HTN+VQE, and thus we obtained the trial wave function of comparable accuracy by running 100 times, whereas the results without constraints in Table 1 were obtained with only one run. See Supplementary Information 8.2 for details on the extension to HTN and the calculation conditions. Figure 7a shows the result for the hydrogen plane model. A smaller fluctuation around the exact ground state energy was found in HTN+QMC than in QMC. The energy differences with a standard deviation obtained by the QMC, HTN+QMC (statevector) and HTN+QMC (ibmq_kolkata) are 9.1 × 10−4 ± 6.7 × 10−3, 2.3 × 10−5 ± 1.5 × 10−3, and 1.8 × 10−5 ± 1.8 × 10−3 Hartree, respectively. Importantly, there is only a slight difference in the fluctuation between the real device and statevector, indicating that there would be some robustness of HTN+QMC to noises. A previous study18 showed that QC-QMC is robust to the depolarization noise. We also show the analytical and numerical result of the noise robustness in Supplementary Information 8.3, and the results show that such robustness also holds in the current settings of HTN+QMC, even though it might be significant in HTN+VQE. The MABI results in Fig. 7b also showed small variance in the real device experiment, where the results are 6.6 × 10−5 ± 2.6 × 10−3, 2.3 × 10−5 ± 1.6 × 10−3, and 4.2 × 10−5 ± 1.8 × 10−3 Hartree in QMC, HTN+QMC (statevector) and HTN+QMC (ibmq_kolkata), respectively. These numerical and theoretical results suggest that HTN+QMC can be a promising candidate for calculating large systems beyond the scale of quantum devices while maintaining accuracy. Note that although we utilized the readout error mitigation and the dynamic decoupling in the overlap calculation, we confirmed that a comparable level of accuracy was achieved even without those options in HTN+QMC for the hydrogen plane model, where the energy difference with a standard deviation excluding the options is 2.6 × 10−5 ± 1.4 × 10−3 Hartree.

Fig. 7: Results of the energy on the real device execution for the hydrogen plane model and MABI.
figure 7

HOMO-LUMO setting and \({\tilde{d}}_{H}=4\) are adopted for the models. The blue line represents the QMC result, whereas the light green and red lines show the HTN+QMC results of the statevector and real device procedures, respectively. The exact ground state energy is depicted by the black dashed line. The inset in each figure presents an enlarged view along the y-axis. a Result of the hydrogen plane model with n = 4 and k = 2. b Result of MABI with n = 4 and k = 3.

Full size image

Discussion

We discuss dependencies of accuracy on the system decompositions in HTN. We consider the Heisenberg chain model with k = 2, n = 4, and Jinter = 1.0, computed in the cluster, even-odd, and no-decomposition settings. Figure 8a–c show the decomposition dependencies of the fidelity, energy difference, and standard deviation for the Heisenberg chain model. In cases of the decomposition settings, the fidelity Fig. 8a in the cluster setting (0.92) is four times higher than that in the even-odd setting (0.22). We also calculated the bipartite entanglement entropy of the exact ground state when decomposing the cluster and even-odd settings to be 0.66 and 3.46, respectively. Thus, an appropriate choice of the decomposition setting is crucial in the performance of the trial wave function. The fidelity of the cluster setting is equal to or slightly higher than that for the no-decomposition setting with dN = 10, whereas that for the even-odd setting is lower than that for the no-decomposition setting with dN = 2. Here, the numbers of the parameters for the cluster setting with dH = 4 and the no-decomposition setting with dN = 10 are nk(dH + 1) + k(dH + 1) = 50 and nk(dN + 1) = 88, respectively. That is, the cluster setting with fewer parameters shows comparable performance to the no-decomposition setting. The increase in fidelity is related to the decrease in the standard deviation of HTN+QMC as in Fig. 8c (and the decrease in the energy difference in HTN+VQE and HTN+QMC as in Fig. 8b. A similar tendency in fidelity, energy difference, and standard deviation can be found in the graphite model, the hydrogen plane model, and MABI (see Supplementary Information 9 for details). These results suggest that if the system is appropriately decomposed, i.e., if the interaction between the subsystems is small, HTN can prepare a trial wave function that performs as well as or better than the wave function generated by the quantum circuit of the original system size. For quantitative evaluations of the decomposition, we proposed measures in Supplementary Information 9, specifically, interaction strength between subsystems and mutual information. Note that one of the ways to increase the fidelity in VQE or HTN+VQE is to improve the initial wave function. As shown in Supplementary Information 9, the fidelity could increase in some cases by using the initial state which is close to the Hartree-Fock state. In addition, while the parameters of all the tensors are sequentially optimized in this study, separate optimization of one tensor by another could be an alternative56.

Fig. 8: Results of the analysis for the Heisenberg chain model with Jinter = 1.0.
figure 8

a–c show the decomposition dependencies. The average and error bar is obtained over 10 different random seeds used for the initial parameters in VQE or HTN+VQE. The fidelity of the single reference state is plotted by the black bar in (a), and the energy difference and standard deviation by the black cross markers in (b, c), respectively. The green (blue) circle and cross markers denote the results for the decomposition (no-decomposition) setting in HTN+VQE and HTN+QMC (VQE and QC-QMC), respectively, with dH = 4 (dN = 2, 4, …, 10). In HTN+VQE and HTN+QMC, n = 4 and k = 2 for all the settings. d, e show the wave function distributions for the Heisenberg chain model with Jinter = 1.0. The basis index is the value when the orthonormal basis state is expressed in the decimal number, e.g., \(\left\vert 10000010\right\rangle\) corresponds to 130. The black, red, green, and blue bars represent the coefficients for the exact ground state, HTN+VQE results with cluster setting, HTN+VQE results with even-odd setting, and VQE results with the no-decomposition setting, respectively. a Fidelity. b Energy difference. c Standard deviation. d Comparison of the exact ground state, cluster setting, and even-odd setting. e Comparison of the exact ground state, cluster setting, and no-decomposition setting (dN = 6).

Full size image

The high performance in the cluster setting seems to arise when the wave function represented by QQTN in Fig. 1a has a problem-inspired structure, whereas the ansatz used for each tensor is hardware efficient. To analyze the wave function in detail, we first compare the distribution of the absolute coefficient of the orthonormal basis state, calculated using one of the 10 random seeds in Fig. 8a–c. Figure. 8d shows the wave function distribution, where note that the value on the horizontal axis is the absolute value of the coefficient (not the square of the absolute value as in fidelity). The basis index is the value when the orthonormal basis state is expressed in the decimal number, e.g., \(\left\vert 10000010\right\rangle\) corresponds to 130. The cluster setting exhibits a distribution very close to that of the exact ground state compared to the even-odd setting. Note that for the even-odd setting, the distribution was calculated with the basis state encoding, where the qubit index was reordered from 8, 7, 6, 5/4, 3, 2, 1 to 8, 6, 4, 2/7, 5, 3, 1 as shown in Even-Odd of Fig. 3a. This qubit index was then changed back to that of Cluster in the plotting, allowing for direct comparison with the even-odd setting.

We next examine the wave function, represented as a linear combination of tensor products of the subsystems. In the cluster setting for the Heisenberg chain model, we approximately describe the exact ground state \(\vert {\psi }_{g-C}\rangle\) using the four dominant terms with respective coefficients of c1 = − 0.37, c2 = 0.24, c3 = − 0.23, and c4 = 0.18, as

$$\begin{array}{ll}\left\vert {\psi }_{g-C}\right\rangle \,\simeq \,{c}_{1}(\left\vert {{{\bf{0101}}}}\right\rangle \otimes \left\vert {{{\bf{0101}}}}\right\rangle +\left\vert 1010\right\rangle \otimes \left\vert 1010\right\rangle )\\\qquad\qquad+{c}_{2}\left(\left\vert {{{\bf{0101}}}}\right\rangle \otimes \left\vert {{{\bf{0110}}}}\right\rangle +\left\vert 1001\right\rangle \otimes \left\vert 0101\right\rangle \right.\\\qquad\qquad\left.+\left\vert 1010\right\rangle \otimes \left\vert 1001\right\rangle +\left\vert 0110\right\rangle \otimes \left\vert 1010\right\rangle \right)\\\qquad\qquad+{c}_{3}(\left\vert {{{\bf{1010}}}}\right\rangle \otimes \left\vert {{{\bf{0101}}}}\right\rangle +\left\vert 0101\right\rangle \otimes \left\vert 1010\right\rangle )\\\qquad\qquad+{c}_{4}\left(\left\vert 0101\right\rangle \otimes \left\vert 1001\right\rangle +\left\vert 0110\right\rangle \otimes \left\vert 0101\right\rangle \right.\\\qquad\qquad\left.+\left\vert 1001\right\rangle \otimes \left\vert 1010\right\rangle +\left\vert {{{\bf{1010}}}}\right\rangle \otimes \left\vert {{{\bf{0110}}}}\right\rangle \right).\end{array}$$
(12)

The state is energetically favored because of the (sub)antiferromagnetic spin configurations, with at most one spin pair having the same parity (e.g., 00 and 11), considering that all terms in the Hamiltonian of Eqs. (5), (6), and (7) are positive. Each term consists of a primitive basis state (in bold) and the spin and spatial inverted states, where the ground state redefined in this primitive basis \(\{\left\vert {{{\bf{0101}}}}\right\rangle ,\left\vert {{{\bf{1010}}}}\right\rangle \}\otimes \{\left\vert {{{\bf{0101}}}}\right\rangle ,\left\vert {{{\bf{0110}}}}\right\rangle \}\) is regarded as a separable state (with the same number of up/down spins in each subsystem), accurately prepared by the lower tensors with one leg connecting to the upper tensor. In case of the even-odd setting, where the qubit index is reordered and the number of up (or down) spins in the subsystem takes 0 to 4, the state in such a primitive basis, e.g., \(\{\left\vert {{{\bf{0000}}}}\right\rangle \otimes \left\vert {{{\bf{1111}}}}\right\rangle ,\left\vert {{{\bf{0001}}}}\right\rangle \otimes \left\vert {{{\bf{1110}}}}\right\rangle ,\left\vert {{{\bf{1100}}}}\right\rangle \otimes \left\vert {{{\bf{0011}}}}\right\rangle ,\left\vert {{{\bf{1101}}}}\right\rangle \otimes \left\vert {{{\bf{0010}}}}\right\rangle \}\), is no longer separable, resulting in a lower fidelity than in the cluster setting. Through the above mechanism, the decomposition setting affects the fidelity, where matching between the tensor network and target states is a crucial factor, being in analogy with the discussion in the area law with tensor networks. Note that the number of legs limits the dimension of the basis for state preparation.

HTN+VQE results with the cluster setting in Fig. 8d show that the coefficients for the above 12 basis states are of the same magnitude as c1, c2, …, c4. In contrast, the even-odd setting gives a much less accurate wave function; half of the basis states in Eq. (12) was negligibly small in magnitude, and the large coefficient of \(\left\vert 0101\right\rangle \otimes \left\vert 0101\right\rangle\) is 0.78, leading to a different distribution from the exact.

Next, Fig. 8e shows the distribution of the no-decomposition setting, where the distributions of the ground state and cluster settings are reproduced from Fig. 8a for comparison. The depth is set to dN = 6 such that the number of parameters in the no-decomposition and cluster settings becomes comparable, that is, 50 and 48, respectively. The distribution for the no-decomposition setting deviates from that for the exact wave function, and half of the basis states in Eq. (12) were negligibly small in magnitude. The no-decomposition setting would achieve higher performance than HTN. However, when the number of ansatz parameters is restricted, HTN may perform better if we find an ansatz and decomposition suited to the structure of the system. In fact, the coefficient of the basis state \(\left\vert 00101101\right\rangle\), which has the 10-th largest magnitude in the no-decomposition setting, is 0.14; in contrast, the corresponding values are −0.057 in the ground state and −0.00018 in the cluster setting. Thus, the cluster setting can efficiently prepare a trial wave function that incorporates system correlations with fewer parameters by eliminating the basis states with a small contribution to the ground state of the system. Note that these observations are verified by calculating over 10 random seeds.

As summary, we proposed an algorithm HTN+QMC that combines QC-QMC with HTN for calculating quantum chemistry problems beyond the size of a quantum device. As demonstrated on the benchmark models, our algorithm exhibits energy with smaller variance than QMC. We developed the gate-efficient pseudo-Hadamard test technique involving an ancilla qubit for conducting HTN+QMC experiments on real devices; the at most five qubits experiment showed an accuracy comparable to the statevector simulation for the hydrogen plane models (8 qubit model) and MABI (12 qubit model).

While this study assumed the target system size to be larger than that of the quantum device, there may be cases in which the proposed algorithm should be used even if the target system size equals that of the quantum device. For example, a quantum computer with thousands of qubits has appeared57. However, an accurate solution may not be obtained when calculating a chemical model of that size owing to noise in the quantum device. In such a case, decomposing the system into subsystems of about hundreds of qubits would lead to a more accurate result than that obtained by directly executing on a thousand qubits. In addition, the tree tensor that we have assumed has the advantage that the computation of the lower tensor can be performed in parallel.

The research on QC-QMC has not yet been extensive, and applying techniques developed for NISQ devices to QC-QMC is a possible future research item, as in HTN in this study. HTN is also an intriguing research area, where there are several classical decomposition approaches, which may inspire ideas for efficient quantum algorithms to deal with the correlations between subsystems58,59,60,61. Another interesting direction is applying QC-QMC to fields outside the electronic structure calculations such as machine learning for designing advanced materials.

Methods

Variational quantum eigensolver

Variational quantum eigensolver (VQE) takes a variational approach to obtain the ground state of a given Hamiltonian. Here, a trial wave function \(\left\vert \psi (\vec{\theta })\right\rangle\) is generated by a quantum circuit with variational parameters \(\vec{\theta }\), which is repeatedly updated using the classical computer until a termination condition is satisfied, e.g., the expectation value of the Hamiltonian \(\left\langle \psi (\vec{\theta })\right\vert H\left\vert \psi (\vec{\theta })\right\rangle\) takes a minimum. The expressibility of \(\left\vert \psi (\vec{\theta })\right\rangle\) depends on the quantum circuit, called ansatz. There are several problem-inspired ansatze, such as the unitary coupled cluster ansatz62 and Hamiltonian variational ansatz63. However, despite the high performance, the ansatze requires deeper quantum gates. In real device experiments, compromised strategy with hardware-efficient ansatze64 is often considered.

The Hamiltonian H in the electronic structure problems can be represented as

$$H=\mathop{\sum}_{a}{c{}_{a}\bigotimes }_{b}{P}_{ab},$$
(13)

where ca is the a-th coefficient of H and Pab ∈ {X, Y, Z, I} is the a-th Pauli or identity operator on the b-th site. In this study, we assume \({c}_{a}\in {\mathbb{R}}\) in all models (although \({c}_{a}\in {\mathbb{C}}\) in general). The number of terms is estimated to be \({{{\mathcal{O}}}}\left({N}_{so}^{4}\right)\) with Nso being the number of spin-orbitals65. We choose the Jordan-Wigner mapping66 for the fermion-qubit translation.

Quantum computing quantum Monte Carlo

In QC-QMC18, a stochastic algorithm such as the imaginary-time evolution is used to iteratively update the discretized coefficients of the wave function, i.e., walkers. As we explained in Sec. I, This study will validate a version of QC-QMC that uses quantum computation only for energy evaluation21. The following projected energy Eproj is used as a common energy estimator:

$${E}_{{{{\rm{proj}}}}}=\frac{\left\langle \xi \right\vert H\left\vert {\psi }_{{{{\rm{QMC}}}}}\right\rangle }{\langle \xi | {\psi }_{{{{\rm{QMC}}}}}\rangle },$$
(14)

where \(\left\vert \xi \right\rangle\) is a trial wave function. \(\vert {\psi }_{{{{\rm{QMC}}}}}\rangle\) denotes a wave function generated by QMC, defined as

$$\left\vert {\psi }_{{{{\rm{QMC}}}}}\right\rangle ={\sum}_{h}{w}_{h}\left\vert {\phi }_{h}\right\rangle ,$$
(15)

where wh is the h-th coefficient and is expressed using discretized units (walkers). \(\left\vert {\phi }_{h}\right\rangle\) is the h-th orthonormal basis state as in a Slater determinant and can be represented by a binary string, i.e., a computational basis. The procedure of generating the wave function \(\vert {\psi }_{{{{\rm{QMC}}}}}\rangle\) depends on the QMC method. In this work, we choose FCIQMC. See Supplementary Information 1 for process details. Eproj is not equivalent to the expectation value of the Hamiltonian 〈ψQMC∣H∣ψQMC〉/〈ψQMC∣ψQMC〉 (that is, not the pure estimator); however, we can obtain the exact ground state energy Eg when \(\vert {\psi }_{{{{\rm{QMC}}}}}\rangle\) approaches the ground state \(\vert {\psi }_{g}\rangle\), i.e., \(\vert {\psi }_{{{{\rm{QMC}}}}}\rangle \sim \vert {\psi }_{g}\rangle\) as

$${E}_{{{{\rm{proj}}}}} \sim \frac{\left\langle \xi \right\vert H\left\vert {\psi }_{g}\right\rangle }{\langle \xi | {\psi }_{g}\rangle }={E}_{g},$$
(16)

where \(H\left\vert {\psi }_{g}\right\rangle ={E}_{g}\left\vert {\psi }_{g}\right\rangle\) is used.

The trial function \(\left\vert \xi \right\rangle\) is fixed throughout the QMC, and a more sophisticated \(\left\vert \xi \right\rangle\) can be used to lower the statistical error. A trivial case is that, if the trial wave function coincides with the ground state, i.e., \(\vert \xi \rangle =\vert {\psi }_{g}\rangle\), then we can obtain Eg for any \(\vert {\psi }_{{{{\rm{QMC}}}}}\rangle\) with zero variance67. See Supplementary Information 2 for derivation details. For example, the Hartree-Fock state, the linear combination of mean-field states, and the Jastrow-type states25 are used as the trial wave functions conveniently available in classical computations. Therefore, we can considerably minimize energy estimation errors by preparing a suboptimal trial wave function in the exponentially large Hilbert space.

In QC-QMC, trial wave function \(\left\vert \xi \right\rangle\) is prepared by a quantum algorithm. Specifically, by decomposing \(\vert {\psi }_{{{{\rm{QMC}}}}}\rangle\), Eq. (14) is rewritten as

$${E}_{{{{\rm{proj}}}}}=\frac{{\sum }_{hl}{w}_{h}\langle \xi | {\phi }_{l}\rangle \left\langle {\phi }_{l}\right\vert H\left\vert {\phi }_{h}\right\rangle }{{\sum }_{h}{w}_{h}\langle \xi | {\phi }_{h}\rangle }.$$
(17)

The matrix elements \(\left\langle {\phi }_{l}\right\vert H\left\vert {\phi }_{h}\right\rangle\) can be obtained by trivial classical calculations. In contrast, quantum computation is required to calculate the overlap (〈ξ∣ϕl〉 and 〈ξ∣ϕh〉) for which the Hadamard test or classical shadow can be applied68,69, henceforth, 〈ξ∣ϕl〉 and 〈ξ∣ϕh〉 will both be described as 〈ξ∣ϕh〉. We discuss in Supplementary Information 2 that the variance of projected energy will decrease with the fidelity of the trial wave function in a simplified case. In this study, fidelity is defined as the square of the overlap between the target and ground states, assuming zero noise.

Hybrid tensor network

In the two-layer QQTN, the original nk-qubit system is decomposed into k subsystems of n qubit states \(\left\vert {\varphi }^{{i}_{m}}\right\rangle\), which are integrated with the k-qubit state \(\left\vert \psi \right\rangle\). These states can be associated with tensors, defined as the lower tensor \({\varphi }_{{\vec{j}}_{m}}^{{i}_{m}}=\langle {\vec{j}}_{m}| {\varphi }^{{i}_{m}}\rangle\) and upper tensor \({\psi }_{\vec{i}}=\langle \vec{i}| \psi \rangle\) with the vector indices \({\vec{j}}_{m}={j}_{m1}{j}_{m2}\ldots {j}_{mn}\) and \(\vec{i}={i}_{1}{i}_{2}\ldots {i}_{k}\) in n-qubit and k-qubit binary strings, respectively. The wave function \(\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\) is then decomposed into tensor products of \(\left\vert {\varphi }^{{i}_{m}}\right\rangle\)

$$\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle ={\sum}_{\vec{i}}{\psi }_{\vec{i}}{\bigotimes }_{m = 1}^{k}\left\vert {\varphi }^{{i}_{m}}\right\rangle ,$$
(18)

which is the same as Eq. (1) although omitting the parameters, where the number of vector coefficients \(\{{\psi }_{\vec{i}}\}\) is 2Lk with L denoting the number of bits (legs) used to construct each im. L = 1 is adopted in this study. If L = n, \(\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\) becomes the general nk-qubits wave function. When L ≪ n, \(\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\) lives in a subspace much smaller than the entire 2nk dimensional Hilbert space; however, it can be larger than the subspace consisting only of the classical tensor due to the exponentially large ranks of \({\psi }_{\vec{i}}\) and \({\varphi }_{{\vec{j}}_{m}}^{{i}_{m}}\). Moreover, the performance of QQTN depends on the decomposition setting of the system, which determines the entanglement between the subsystems.

Tensor-network quantum circuits can be implemented in various ways. For example, we can define a lower tensor as \(\left\vert {\varphi }^{{i}_{m}}\right\rangle ={U}_{Lm}\left\vert {i}_{m}\right\rangle {\left\vert 0\right\rangle }^{\otimes n-1}\), \({U}_{Lm}{\left\vert {i}_{m}\right\rangle }^{\otimes n}\), \({U}_{Lm}^{{i}_{m}}{\left\vert 0\right\rangle }^{\otimes n}\), etc., where the first two formulations give the index in initial states and the third a unitary matrix using unitary matrices ULm and \({U}_{Lm}^{{i}_{m}}\). In the present study, we choose \(\left\vert {\varphi }^{{i}_{m}}\right\rangle ={U}_{Lm}\left\vert {i}_{m}\right\rangle {\left\vert 0\right\rangle }^{\otimes n-1}\) and \(\left\vert \psi \right\rangle ={U}_{U}{\left\vert 0\right\rangle }^{\otimes k}\) for lower and upper tensors, respectively.

In our QQTN formulation, an observable is defined as the tensor product O = ⨂m,rOmr, where Omr is observable on the r-th qubit of the m-th subsystem (lower tensor). Transition amplitude is then defined as

$$T=\left\langle {\psi }_{{{{\rm{HTN}}}}}^{(1)}\right\vert O\left\vert {\psi }_{{{{\rm{HTN}}}}}^{(2)}\right\rangle ,$$
(19)

which is the same as Eq. (2) although omitting the parameters, where \(\vert {\psi }_{{{{\rm{HTN}}}}}^{(l)}\rangle ={\sum }_{\vec{i}}{\psi }_{\vec{i}}^{(l)}{\otimes }_{m}\vert {\varphi }^{{i}_{m}(l)}\rangle (l=1,2)\) are the two different of states for \(\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\). As explained in the next section, T is used in VQE and QMC to evaluate an observable and overlap, respectively.

We first calculate \({N}^{{i}_{m}^{{\prime} }(1){i}_{m}(2)}=\langle {\varphi }^{{i}_{m}^{{\prime} }(1)}{| \bigotimes }_{r}{O}_{mr}| {\varphi }^{{i}_{m}(2)}\rangle\) for the lower tensors by quantum computations, construct \({N}_{m}=\left(\begin{array}{cc}{N}^{00}&{N}^{01}\\ {N}^{10}&{N}^{11}\end{array}\right)\), which is a trivial classical process, and then integrate the results as T = 〈ψ(1)∣⨂mNm∣ψ(2)〉 on the upper tensor by quantum computations. Supplementary Information 3 shows the details of this procedure, which is based on the Hadamard test circuit as in Ref. 70. Our algorithm requires only \(\max (n,k)\) qubits except for ancilla qubits. In this study, only 8k + 2 terms are measured to calculate T; i.e., the overhead for calculating the expectation value is a linear scale for the system size nk. Note that the number of measurements is 2 × 4Lk + 2 in general.

Proposed algorithm: HTN+QMC

The procedure of HTN+QMC consists of two steps.

  1. 1.

    Perform VQE by minimizing \(\left\langle {\psi }_{{{{\rm{HTN}}}}}\right\vert H\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\) to obtain trial wave function \(\left\vert \xi \right\rangle =\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\).

  2. 2.

    Perform QC-QMC by using the obtained trial wave function \(\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\); the quantum computer is used to compute Eproj to accurately estimate the ground state energy.

Here, we will denote HTN+VQE when only the first step is mentioned. HTN+QMC can be performed for nk-qubit system by using only \({{{\mathcal{O}}}}(\max (n,k))\) qubits except for ancilla qubits. The Hamiltonian and projected energy can be evaluated in both steps by calculating T in Eq. (19).

In the first step, by splitting index b in Eq. (13) into indices m and r, we can rewrite H and its expectation value as

$$H={\sum}_{a}{c{}_{a}\bigotimes }_{m,r}{P}_{amr},$$
(20)

and

$$\left\langle {\psi }_{{{{\rm{HTN}}}}}\right\vert H\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle ={\sum}_{a}{c}_{a}{\left\langle {\psi }_{{{{\rm{HTN}}}}}\right\vert \bigotimes }_{m,r}{P}_{amr}\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle ,$$
(21)

respectively. The expectation value is evaluated through Eq. (19) by setting \(\vert {\psi }_{{{{\rm{HTN}}}}}^{(1)}\rangle =\vert {\psi }_{{{{\rm{HTN}}}}}^{(2)}\rangle =\vert {\psi }_{{{{\rm{HTN}}}}}\rangle\) and replacing Omr with Pamr; coefficient index a is implicitly included in the expression for Omr. The wave function \(\left\vert {\psi }_{{{{\rm{HTN}}}}}\right\rangle\) is prepared by parameterized quantum circuits equivalent to the unitary matrices ULm and UU.

In the second step, the overlap 〈ξ∣ϕh〉 = 〈ψHTN∣ϕh〉 in Eq. (17) is calculated by substituting \(\vert {\psi }_{{{{\rm{HTN}}}}}^{(1)}\rangle =\vert {\psi }_{{{{\rm{HTN}}}}}\rangle\), \(\vert {\psi }_{{{{\rm{HTN}}}}}^{(2)}\rangle =\vert {\phi }_{h}\rangle\), and O = I⊗nk in T in Eq. (19), where the circuit parameters are fixed to the values obtained in the first step. Specifically, we can prepare an arbitrary basis state \(\left\vert {\phi }_{h}\right\rangle ={\otimes }_{m,r}\left\vert {j}_{mr}(h)\right\rangle =({\otimes }_{m,r}{X}^{{j}_{mr}(h)}){\left\vert 0\right\rangle }^{\otimes nk}\) by setting \({U}_{U}^{(2)}={I}^{\otimes k}\) and \({U}_{Lm}^{(2)}={\otimes }_{m}{X}^{{j}_{mr}(h)}\), where jmr(h) is a function of h and takes a value on {0, 1}, and X is the Pauli X operator. Using the overlaps 〈ψHTN∣ϕh〉 of all \(\left\vert {\phi }_{h}\right\rangle\), corresponding to the orthnormal basis states appearing through the QMC wave function and matrix elements \(\left\langle {\phi }_{l}\right\vert H\left\vert {\phi }_{h}\right\rangle\) during the QMC execution at hand, we can perform QMC through iterative evaluations of the projected energy (Eqs. (14) and (17)) in principle. The scale of the measurement cost in the QMC step is \({{{\mathcal{O}}}}({N}_{so}^{4}{N}_{W}^{* }({\tau }_{{{{\rm{fin}}}}}/{{\Delta }}\tau ){2}^{2L}k/{\varepsilon }^{2})\), where Nso comes from \(\left\langle {\phi }_{h}\right\vert H\left\vert {\phi }_{{h}^{{\prime} }}\right\rangle\), \({N}_{W}^{* }\) is the maximum number of walkers that can be taken in a QMC iteration, τfin is a total time in QMC, Δτ is a time step in QMC, 22Lk comes from the overhead of HTN contraction, ε is an additive error43,71. We mention that in our actual run, for simplicity, the overlaps of all orthonormal basis states were computed before QMC in the statevector simulation. For real device execution, the overlaps of the states for all target electron numbers were computed.