Introduction

Si/SiGe heterostructures are one of the most promising host materials for spin qubits1, as they offer low potential fluctuations, charge noise, long coherence times2, high-fidelity control3,4,5,6 and are industry-compatible platforms that allow for fabrication in established silicon production lines7. However, some devices exhibit low-lying valley states that limit high-temperature operation of spin-initialization, -manipulation, and Pauli-spin blockade readout, and hinder spin-shuttling8,9,10,11. Local minima in the energy splitting between the low-lying valley states, EVS, pose the main obstacle to the scalability of this platform. Innovations in growth and fabrication strategies12,13,14, but also efficient methods to benchmark the local valley splitting are needed to overcome it.

A large range of local EVS, from 6 μeV to >200 μeV, was observed in gate-defined quantum dots (QDs) formed in Si/SiGe heterostructures8,15,16,17,18,19,20,21,22,23,24,25,26. The EVS is theorized to be a randomly distributed local material parameter, subject to atomic-scale crystal variations12,27,28,29,30,31 of the Si/SiGe heterostructure. Thus a few measurements of EVS at different spots do not suffice to confidently benchmark the quality of a heterostructure31. Many different methods to determine the EVS of a Si/SiGe QD were reported, such as thermal excitation8, pulsed-gate spectroscopy in a single21,24 or double23 QD, spin funnel measurement in two exchange-coupled QDs32,33 and the identification of the spin-valley relaxation hot-spot20,21. Other methods measure the singlet-triplet energy splitting EST, being a lower bound of the EVS, by Pauli-spin blockade19 or magnetospectroscopy15,16,17,22,26,31. High-energy resolution has been achieved by dispersive coupling, to a resonator18,34, and some attempts towards laterally mapping EVS21,24,25 have been published, but these are involved, time-consuming, and cover a small area. Determining EVS by Shubnikov-de-Haas oscillations35 grants information on the out-of-plane electric field dependence of EVS36, but lacks lateral resolution and tends to overestimate EVS due to localization by the out-of-plane magnetic field37. To this end, we need a time-efficient method with good energy resolution that can map the valley-splitting landscape of a realistic Si/SiGe quantum chip.

In this work, we present an efficient method for mapping the local valley splitting in silicon across a large area with a resolution that can capture the local variations of EVS. We employ singlet-triplet oscillations of a spatially separated pair of spin-entangled electrons, with one of them shuttled to a distant position as a probe to locally detect magnetic field-induced anticrossings between spin-valley states, from which we then obtain a magnitude for EVS38. Leveraging coherent conveyor-mode shuttling11,39,40,41, we extend this analysis to create a dense one-dimensional map of the valley splitting for a Spin-Qubit-Shuttle (SQS)11,41,42. Our method yields a nanometer resolution along the shuttle direction, which suffices to resolve local features in the valley-splitting landscape depending on the QD size. By applying voltage offsets to two long gates parallel to the shuttle direction, the shuttle trajectory can be displaced (here up to 18 nm), which results in a two-dimensional map of EVS. We thus present four valley splitting traces, each with an approximate length of 210 nm, with 150 EVS measurements per trace and a sub- μeV energy uncertainty. The position of the electron in the one-dimensional electron channel (1DEC) is derived from the ideal shuttling potential without taking disturbance of electrostatic disorder into account. Specifically, short-range tunneling of the electron across disorder-induced barriers cannot be fully excluded. We report measured values of the valley splitting that range from 4.6 μeV to 59.9 μeV, and that exhibit a continuous behavior punctuated by sudden jumps. We attribute these rapid changes to unintentional tunneling events during conveyor-mode shuttling, which we can mitigate by displacing the channel vertically. Our method enables efficient valley-splitting mapping, which provides sufficient statistics to infer an accurate mean and shape of the distribution by single-electron spin shuttling. In this study, the main limitation is the charge shuttle distance at high velocity. Disorder and limited confinement strength due to attenuation on the high-frequency lines hinders shuttling past 210 nm.

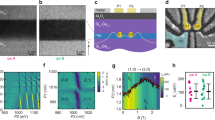
The device used for the experiments is the same as that described in ref. 41. It comprises three Ti/Pt gate layers, separated by 7.7 nm thick Al2O3, and is fabricated on an undoped Si/Si0.7Ge0.3 quantum well (see method section for layer stack). The 1DEC is formed by an ~1.2 μm-long split-gate with 200 nm spacing (shown in purple in Fig. 1a). By applying DC voltages VST, VSB to the split-gate, the 1DEC is confined in y direction. Seventeen clavier gates are fabricated on top of the device, with a combined gate pitch of 70 nm. Of these, eight are on the second metal-layer and labeled G2, G16, 3 × S1, and 3 × S3, while nine are on the third metal-layer and labeled G1, G3, G15, G17, 3 × S2, and 2 × S4. In conveyor mode11, two to three clavier gates are electrically connected to four so-called shuttle gates S1, S2, S3, and S440,41,43. The shuttle gates are named differently, as each shuttle gate comprises more than one clavier gate as indicated in Fig. 1a. As a result, every fourth clavier gate shares the same potential, which leads to a periodic electrostatic potential with a period of λ = 280 nm. Generating a traveling wave potential (see methods section for details on electron shuttling in conveyor mode), we coherently shuttle the electron spin for a nominal distance of up to 336 nm in a global in-plane magnetic field B. We shuttle at a frequency of 10 MHz, which corresponds to an electron velocity of 2.8 ms−1. The SQS has a single-electron transistor (SET) at each end, serving as electron reservoir and proximity charge sensors.

Fig. 1: Spin-Qubit shuttle (SQS) device and experimental method.
figure 1

a False-colored scanning electron micrograph (SEM) of the device used in the experiment, showing a top-view on the three metallic layers (1st purple, 2nd blue, 3rd green) of the SQS, and their electrical connection scheme. At both ends, single-electron transistors (SETs) are formed in the quantum well by gates LB1, LB2, and LP (RB1, RB2, and RP, respectively) on the second gate layer, with the current path induced by the yellow gates on the third layer. Scale bar corresponds to 280 nm. b Charge stability diagram of the outermost left DQD recorded by the left SET current ISET. DQD fillings are indicated by (n, m), with n and m denoting the number of electrons in the left and right QDs, respectively. The red dashed lines indicate the boundaries of the PSB region. Labeled circles indicate voltages on G2 and G3 and correspond to pulse stages used in subsequent experiments. Arrows indicate pulse order. Pulse stages T as well as F reach down to VG3 = 0.7 V.

Full size image

Results

DQD valley-splitting measurement

As a basis for the EVS mapping technique discussed later, we first consider a method to determine EVS in a static double quantum dot (DQD). Therefore, next to the left SET, we form a DQD under gate G2 and the leftmost clavier gate from S1. Gates G1, G3, and the leftmost clavier gate of S2 act as barrier gates. Figure 1b displays a charge stability diagram for the DQD. We measure the valley splittings El (Er) of the left (right) QD of the DQD using singlet-triplet oscillations, which probe the magnetic anticrossings induced by spin-valley couplings in each QD.

To this end, we apply the following pulse sequence: We load four electrons into the leftmost QD for 1 ms to initialize into a spin-singlet (S) state in the (4,0) charge state41 (Fig. 1b, stage I). Next, we split the spin-singlet by rapidly pulsing to the (3,1) charge state (stages I→S) within a rise-time of ≈1.2 ns (limited by 300 MHz bandwidth of our waveform generator). As a function of wait-time τDQD, singlet-triplet oscillations occur with a frequency ν proportional to B, and the difference of the electron g-factors Δg of the DQD. For detection of the S-state, we pulse into the Pauli-Spin-blockade (PSB) (area between red dashed lines in Fig. 1b) and wait for 500 ns. The PSB charge state is read out by the SET current ISET, after freezing this charge state by reducing the DQD tunnel-coupling (stages P→F; VG3(F) ≈ 0.7 V)44. There, we read the charge state via measuring ISET for 1 ms. We repeat this pulse sequence (Fig. 2a) while varying τDQD from 0 to 1.5 μs, in 100 equidistant time steps. Repeating this loop 1000 times, we calculate the spin-singlet return probability PS(τDQD) at a set B (Fig. 2b), while every 10 loop iterations the correct electron filling of the DQD is reinitialized as a precaution. In order to counter slow noise-related drifts on the PSB and the SET, both the PSB-stage voltage as well as the SET voltages are retuned after 1000 loop-iterations (details in the methods section).

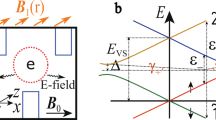
Fig. 2: Spin-valley anticrossing in a DQD.
figure 2

a Experiment flowchart explaining the microscopic pulse stages, parameter loops as well as stabilizing measures. Waiting times at pulse stages are indicated by times below. b Normalized singlet return probability as a function of the magnetic field B and DQD separation time τDQD. The singlet return probability PS is normalized such that each horizontal line averages to zero. c Fit to the data from b using Eq. (1). d Frequencies extracted from the fit in c. The orange curve is a least-square fit to the data. Uncertainties of frequencies are on the order of 100 kHz and smaller than the size of the black dots. e Energy spectrum of the Hamiltonian from Eq. (2). The color mixture represents the spin-state composed from colors of labeled spin base state, while the black symbols label the valley state. For clarity, the energy axis is upscaled around the \(\vert \uparrow \downarrow +-\rangle\) and \(\vert \downarrow \uparrow +-\rangle\) states with spin projection along the z axis ms = 0. For these states, their magnetic field dependence, proportional to ΔgμB, is four orders of magnitude smaller than that of the states \(\vert \downarrow \downarrow --\rangle\) and \(\vert \downarrow \downarrow ++\rangle\), with ms = −1. The parameters used in e are extracted from the fit in d.

Full size image

The singlet-triplet oscillation frequency ν contains the important information and is extracted as follows. We fit the measured PS(τDQD, B) line by line to

$${P}_{{{{\rm{S}}}}}({\tau }_{{{{\rm{DQD}}}}})=a\exp \left(-\frac{{\tau }_{{{{\rm{DQD}}}}}^{2}}{{{T}_{2}^{* }}^{2}}\right)\cos \left(2\pi \nu {\tau }_{{{{\rm{DQD}}}}}+\varphi \right)+c,$$
(1)

where a, ν, φ are the visibility, frequency, and phase of the spin-singlet-triplet oscillations, respectively, and \({T}_{2}^{* }\) is the ensemble spin-dephasing time of the entangled spin-state. The offset c is partly absorbed by subtraction of the linewise mean \(\langle {P}_{{{{\rm{S}}}}}({\tau }_{{{{\rm{DQD}}}}}) \rangle\). The fit with a Gaussian decay (Fig. 2c) captures all the relevant features of the measured data (cf. Fig. 2b). Here, we are interested in ν(B) (black dots in (Fig. 2d)), which reveals two distinct anticrossings on top of a constant slope p. The slope is expected to be proportional to \(\Delta g=\frac{ph}{{\mu }_{{{{\rm{B}}}}}}\) (with h and μB Planck’s constant and Bohr-magneton, respectively) provided the effective magnetic field gradient due to Δg exceeds the Overhauser field gradient (~0.01 mT) of the randomly fluctuating 29Si and 73Ge nuclear spin-baths. As this condition is easily fulfilled, we can fit Δg (Table 1).

Table 1 Fit results of the spin-valley anticrossing in a DQD
Full size table

Next, we argue that the two anticrossings stem from the spin-valley coupling in each of the QDs, and can be employed as a precise probe for the valley splittings El and Er. As we will show in the following sections, this anticrossing is crucial for mapping the valley splitting by coherent spin shuttling. We consider spin-conserving tunneling only, and assume that intervalley tunneling couples higher energy valley, \(\left\vert +\right\rangle\), in the left QD to the lower energy valley, \(\left\vert -\right\rangle\) in the right QD, so that charge separation (4, 0)→(3, 1) creates a state in which two electrons form a spin-singlet in the \(\left\vert -\right\rangle\) valley in the left QD33,45, while the remaining two electrons form a spin-singlet \(\vert {S}^{+-}\rangle =(\vert \uparrow \downarrow +-\rangle -\vert \downarrow \uparrow +-\rangle )/\sqrt{2}\), where the first (second) arrow and sign indicate the spin and valley state of the electrons in the singly-occupied valleys of the left (right) QD. This \(\vert {S}^{+-}\rangle\) is coupled to the unpolarized triplet \(\vert {T}_{0}^{+-}\rangle =(\vert \uparrow \downarrow +-\rangle +\vert \downarrow \uparrow +-\rangle )/\sqrt{2}\) by the difference between the Zeeman energies of the two electrons with opposite spin in different valley states, ΔEZ = μBB(gr,− − gl,+), which results from the g-factor difference between an electron in the right QD and \(\vert -\rangle\) valley (with g-factor gr,−) and an electron in the left QD and \(\vert +\rangle\) valley (with g-factor gl,+). Spin-valley interaction in the right QD couples \(\vert {S}^{+-}\rangle\) and \(\vert {T}_{0}^{+-}\rangle\) to states in which the electron in this QD occupies the \(\vert +\rangle\) valley, and the spins of the two electrons in singly-occupied valley states are aligned, i.e. \(\vert \downarrow \downarrow ++\rangle\) and \(\vert \uparrow \uparrow ++\rangle\). Spin-valley interaction in the left QD couples \(\vert {S}^{+-}\rangle\) and \(\vert {T}_{0}^{+-}\rangle\) to states in which the \(\vert -\rangle\) valley in the left QD is occupied by a single electron having its spin aligned with the electron in the right QD, i.e. \(\vert \downarrow \downarrow --\rangle\) and \(\vert \uparrow \uparrow --\rangle\).

Deep in the (3, 1) regime the dynamics in the relevant space of four lowest-energy states is modeled with a Hamiltonian38

$$H=\left(\begin{array}{cccc}-\Delta {E}_{{{{\rm{Z}}}}}/2&0&0&{v}_{{{{\rm{l}}}}}\\ 0&\Delta {E}_{{{{\rm{Z}}}}}/2&{v}_{{{{\rm{r}}}}}&0\\ 0&{v}_{{{{\rm{r}}}}}&{E}_{{{{\rm{r}}}}}-{\bar{E}}_{{{{\rm{Z}}}},+}&0\\ {v}_{{{{\rm{l}}}}}&0&0&{E}_{{{{\rm{l}}}}}-{\bar{E}}_{{{{\rm{Z}}}},-}\end{array}\right)$$
(2)

written in the basis of \(\{\vert \uparrow \downarrow +-\rangle ,\vert \downarrow \uparrow +-\rangle ,\vert \downarrow \downarrow ++\rangle ,\vert \downarrow \downarrow --\rangle \}\), where \({\bar{E}}_{{{{\rm{Z}}}},+}\) (\({\bar{E}}_{{{{\rm{Z}}}},-}\)) is the Zeeman energy for two electrons with parallel spins in the \(\vert ++\rangle\) (\(\vert --\rangle\)) states, and vl (vr) is the spin-valley coupling in the left (right) QD. Note that spin-valley mixing with \(\vert \uparrow \uparrow \rangle\) states can be safely neglected as \({v}_{{{{\rm{l(r)}}}}}\ll\, {E}_{{{{\rm{l(r)}}}}}+{\bar{E}}_{{{{\rm{Z}}}},\pm }\). Fits of data with a model involving also (4, 0) state, and tunnel coupling, tc, in the DQD, confirmed that tc has negligible effect on spin dynamics in (3, 1) regime. As explained above, the Overhauser field is disregarded.

We diagonalize the Hamiltonian and fit ν(B) in Fig. 2d (orange line) with parameters shown in Table 1 corresponding to the energy spectrum shown in Fig. 2e. Note that the assignment of the anticrossings to the left and right QDs is arbitrary at this stage of the analysis; the indices l and r in Table 1 can be swapped. Our model fits ν(B) very well. Hence, the occurrence of spin-valley anticrossings does not require any tunnel-coupling in the DQD except from initialization and detection of the S-state. This notion is decisive for valley mapping by shuttling, which involves separation of the two electrons. Assignment for the valley splitting is straightforward: the magnetic field BVS in the center of the anticrossing can be converted to a EVS by BVS = EVSμB/g, where g = 2 and the width of the anticrossing is proportional to the coupling strength v. Here, we omit the g-factor variation as Δg is less than 0.1 % of g and thus gives an error of less than 0.1 % on the detected EVS. A similar analysis of a DQD formed at different screening gate voltages can be found in Supplementary Fig. 1. Furthermore, note that the valley splitting measured for the left QD is the three-electron valley splitting.

Valley-splitting mapping

Next, we discuss the use of spin-valley anticrossing in a QD for mapping the valley splitting along the 1DEC. Therefore, in addition to the pulse scheme explained above (Fig. 2a), we shuttle the electron spin in the right QD fast by a distance d(τS) (for shuttle time τS, see Eq. (6) in the method section), let the entangled singlet-triplet-state evolve for a fixed waiting period (τw = 300 ns) and then shuttle it back by the same distance for PSB detection. Thus, the pulse scheme for mapping (Fig. 3a) is complemented by the 10 ns long stage T (voltages in Fig. 1b), a shuttle pulse for time τS, a fixed waiting period at stage d, the time-reversed shuttle pulse to enter stage T (DQD with large barrier) followed by stage S, the detuned tunnel-coupled DQD in charge state (3,1). Note that compared to the pulse scheme (Fig. 2a), we measure PS(d, B) instead of PS(τDQD, B), which turns out to be sufficient for mapping the valley splitting. Another parameter that can be varied is τw in stage d. Measurements of the three-dimensional parameter space PS(d, τw, B) are shown in Supplementary Fig. 2. A scan PS(d, τw, B = 800 mT) is employed to probe ν(d) fitted by Eq. (1) with τw replacing τDQD (Fig. 3b). Notably, the fitted frequency of the singlet-triplet oscillations ν(d) varies smoothly, with exception at d ≈ 120 nm, and drops close to zero at some di (black arrows). Presumably, ν(d) is governed mainly by variations of the electron g-factor in the propagating QD due to variations in confinement. These are expected partly due to the deterministic breathing of the confinement potential of the moving QD, partly due to electrostatic disorder in the quantum well11. Note that we cannot distinguish by measurement of ν(d), which of the QDs has the larger electron g-factor.

Fig. 3: Mapping of the local valley splitting using the ST0 oscillations.
figure 3

a Flowchart of the microscopic pulse stages, parameter loops as well as stabilizing measures. Waiting times at pulse stages are indicated below. Compared to Fig. 2a, the electron is shuttled by a distance d, waits there for τW = 300 ns and is shuttled back, prior to PSB. b Extracted frequencies ν(d) measured at a magnetic field of 0.8 T. The 1σ-intervals are smaller than the symbols. c Raw data of the singlet return probability PS as a function of shuttle-distance d and magnetic field B. To enhance contrast, we subtract the averaged return probability 〈PS〉 for each B. d same as c with additional markers (see text). The spin-valley anticrossing of the shuttled QD is indicated by blue points connected by a green spline curve.

Full size image

The local variations of the g-factor difference help us to understand features in PS(d, B) (Fig. 3c), our main result. Curved (spaghetti-like) features are clearly visible on top of the background that appears when changes of PS(d, B) along a certain direction in the (d, B) plane are much larger than changes along the corresponding perpendicular direction. For example, at distances di (highlighted by arrows in Fig. 3b), at which ν(d) approaches zero, the PS signal weakly depends on B, while it depends strongly on d (due to strong variation of ν(d), see Fig. 3b), resulting in the appearance of vertical features. Besides some horizontal features (marked by black dashed lines in Fig. 3d), which we explain below, there is a continuous widely varying feature marked by the green solid line in Fig. 3d (details in Supplementary Note V). This line follows the spin-valley anticrossing of the shuttled electron spin. It is generated by waiting at d for τw = 300 ns and accumulating phase due to a relatively large modification of the singlet-triplet oscillation frequency at the anticrossing. It is thus a measure of EVS(d) along the 1DEC. We support this notion by the PS(d, τw, B) data shown in Supplementary Note IV.

Notably, at d = 0 nm and B ≈ 0.4 T, this line overlaps with a horizontal feature (marked by the lower dashed line in Fig. 3d), and the B-field matches with one of the EVS of the DQD. This d-independent feature originates from the accumulation of a phase during the stages S and T, at which the DQD in charge state (3,1) is formed. There, the total waiting period is 40 ns (Fig. 3a), which is sufficient to identify the anticrossing by the singlet-triplet oscillations (cf. Fig. 2b). Presumably, this horizontal line is broadened in B as the QD position is slightly displaced in stage T compared to stage S, altering the B at which the anticrossing occurs. Now, it is justified to attribute this anticrossing to the right QD. The index of Er in Table 1 is, therefore, correct.

The counterpart of the lower horizontal line is the upper horizontal line at B = 0.54 T, which matches El in Table 1. At its origin (d = 0 nm), a wavy feature (black dotted line in Fig. 3d) around the upper dashed line is barely visible. We assign this line to the spin-valley anticrossing of the left (static) QD, due to which a phase is accumulated during τw = 300 ns. This is expected, since the sinusoidal voltages applied to the shuttle gates capacitively cross-couple to the left QD. Hence, the left QD is slightly displaced by the same period as the period of the shuttle voltages, and thus its valley splitting gets a tiny d-dependence with this period. This matches exactly the observation in Fig. 3c, d.

Hence, we could explain the features in Fig. 3c, and found striking evidence that the green solid line in Fig. 3d maps the EVS(d) along the 1DEC. The position along B of this line can be resolved with a precision of less than 1 μeV (see Supplementary Fig. 4). Care must be taken to interpret the plotted distance d in terms of a precise location. d(τS) is extracted from the phase of the sinusoidal driving signal (Eq. (6) in the method section). The traveling wave potential exhibits higher harmonics which leads to slight breathing and wobbling of the propagating QD, thus the QD velocity is not exactly constant. Slight variations in the velocity due to potential disorder from charged defects at the oxide interface are of the same order of magnitude11 imposing an uncertainty on QD position d. We note that we can shuttle the electron forth and back by a maximal one-way distance of d = 336 nm, equivalent to 1.2 λ. By reducing the shuttle velocity by a factor of five, we can shuttle the charge forth and back at least 2.0 λ (d = 480 nm). This points to a potential disorder peak at d ≈ 340 nm, which the electron cannot pass at the higher velocity. Here, we limit our mapping range to d = 210 nm (extended range shown in Supplementary Note V) to stay far away from this potential disorder peak, but also note that the abrupt change of ν and EVS at d ≈ 120 nm in Fig. 3b, d indicates some tunneling occurring during the conveyor-mode shuttle process.

2D valley splitting map

For simplicity, we approximate d as the location of the QD now. In order to extend the mapping to the perpendicular direction, we change the screening gate voltages—from VST = VSB = 100 mV while keeping the sum constant—in order to displace the 1DEC in the y direction. Figure 4a displays the extracted splines corresponding to four different screening gate configurations where the nominal displacement in y direction is indicated by colored labels. These distances are calculated by linearly converting the voltage difference VST − VSB into y displacement with a factor of 6 nm/100 mV (see Supplementary Fig. 7e). The splines are sampled at the measurement resolution of one point per nominal 1.4 nm. For some d marked by dotted lines in Fig. 4a (red trace: ~180–190 nm, violet trace: ~170–185 nm, blue trace: ~110–125 nm), we were unable to identify the EVS, probably because it was below the B-scan range.

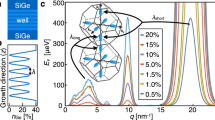
Fig. 4: Comparison of valley splitting mapping techniques.
figure 4

a Four EVS scan-lines of valley splitting along different y displacements measured by the same method as the data shown in Fig. 3 with the curve at y = 0 nm being taken from its panel d. Note that each EVS scan-line has its own color-coded energy axis. Dashed parts on the valley splitting traces indicate areas in which an anticrossing was not observable or out-of B range. b False-color 2D map of EVS exclusively based on the data shown in a. c Correlation coefficient (dots) of the set of measured EVS pairs separated by a geometric distance \(D=\sqrt{\Delta {y}^{2}+\Delta {d}^{2}}\), as a function of D, exclusively based on the data shown in a. A Gaussian least-square fit to the correlation for D < 28 nm is included as a red solid line. d 2D map of EST values obtained on the same wafer, but different device employing magnetospectroscopy. EST values are shown on the vertical axis as well as by the color of each bar. Green-blue stripes are the colored scanning electron micrograph of the clavier gates of the used device (cf. Fig. 1a). e Histogram of the measured EVS obtained by equidistant sampling of spline fits to the data of a (measured by coherent shuttling). f Histogram of the measured EST using all data from d (measured by magnetospectroscopy). Both datasets are plotted with a maximum-likelihood fitted Rician distribution (solid line) and folded Gaussian distribution (black, dashed line).

Full size image

Using all this data, we obtain a two-dimensional map of EVS by linear interpolation (Fig. 4b). The overall EVS values are in the lower range of values found in the literature. The important point is, however, that our shuttling-based mapping method gives us an insight into the lateral EVS distribution in our SQS device. There are regions of nearly zero EVS (e.g., d ≈ 180 nm and y = −12 nm), but strikingly they can be avoided by displacing the QD along the y direction (e.g., y = 6 nm). This is important for shaping a static QD containing a spin-qubit at a position, at which EVS is sufficiently large and qubit control is feasible. For conveyor-mode shuttling of spin qubits, it allows finding a trajectory of the moving QD, which avoids low EVS spots causing qubit decoherence. Similarly, tunneling of the moving QD across electrostatic disorder barriers (e.g., at d ≈ 125 nm and y = 6 nm) can be avoided by changing the y-displacement (e.g., y = −12 nm). The reason for the tuneability of EVS is its short correlation length.

We calculate the correlation coefficient of the set of EVS pairs (without regions of undefined EVS) separated by a geometric distance D as a function of D in Fig. 4c. Additionally, we fit a Gaussian curve as derived from ref. 12.

$${{{\rm{Corr}}}}(D)=\exp \left(-\frac{1}{4-\pi }\frac{{D}^{2}}{{a}_{{{{\rm{dot}}}}}^{2}}\right),$$
(3)

which takes atomistic alloy disorder in the SiGe barrier into account. Here, the fitting parameter \({a}_{{{{\rm{dot}}}}}=\hslash /\sqrt{{m}_{t}{E}_{{{{\rm{orb}}}}}}\) is the characteristic QD size, mt is the transversal effective electron mass in silicon, and Eorb is the orbital energy of the electron, assuming a harmonic confinement potential. The fit results in a QD size of adot ~16 nm, corresponding to Eorb ~1.6 meV being on the expected order of magnitude according to electrostatic simulations. Note that the correlation crosses zero and only vaguely follows a Gaussian decay, which is an effect of the limited scan area of the EVS map (correlations of subsets of the data are discussed in Supplementary Note IV). In addition, due to electrostatic disorder Eorb is not constant, though assumed to be such in derivation of Eq. (3).

Comparison to magnetospectroscopy

In order to benchmark our method for mapping the local EVS by shuttling, we measure another map using the well-established method of magnetospectroscopy. We employ a device with the same heterostructure, gate geometry, and fabrication process, but the 1DEC is half in length and nine (instead of 17) individually tuneable (i.e., not interconnected) clavier gates are fabricated on top of the 1DEC (SEM is shown in the Supplementary Fig. 6a). We form a single QD at a time in the 1DEC by biasing some clavier gates and by the voltages VST, VSB applied to the long split-gate. To conduct the magnetospectroscopy, we tunnel-couple the QD to an accumulated electron reservoir reaching out to one SET, while the closer SET detects the charge state of the QD (see Supplementary Note VII for all details). We repeat the magnetospectroscopy each time, forming a single QD at a different position in the 1DEC. The locations of these QDs (Fig. 4d) are determined by triangulation with the QD’s capacitive coupling to its four surrounding gates, and by a finite-element Poisson solver of the full device (see Supplementary Note VII). The orbital splitting Eorb of each QD is measured by pulsed-gate spectroscopy yielding values in the range Eorb ~1.4−3.6 meV. By magnetospectroscopy, the two-electron singlet-triplet energy splitting EST of the shaped QD can be directly measured. We nevertheless assume EVS ~EST to be a reasonable estimate, as the ratio between the two has been measured to be EST/EV S ≲ 124, if Eorb ≫ EVS with EVS then being weakly dependent on Eorb46.

This assumption allows comparing the histograms of both 2D maps (conveyor-mode shuttling in Fig. 4e and magnetospectroscopy in Fig. 4f). Assuming that EVS and EST are both governed by alloy disorder, their distributions are expected to be Rician12,31,47

$$f(x\,| \,\gamma ,\sigma )=\frac{x}{{\sigma }^{2}}\exp \left(-\frac{{x}^{2}+{\gamma }^{2}}{2{\sigma }^{2}}\right){I}_{0}\left(\frac{x\gamma }{{\sigma }^{2}}\right).$$
(4)

I0(x) is the modified Bessel function of the first kind and order zero. γ is the non-centrality parameter and σ the scaling parameter. The fitted parameters γ and σ for both distributions (Table 2) are very similar. The σ parameter expressing the randomness of the parameters is equal within the error range. The γ parameter for EST is a bit lower than the one of EVS as expected. This all strongly supports the validity of our shuttle-based method for mapping the valley splittings.

Table 2 Parameters fitting the distributions
Full size table

Intriguingly, we observe that γ > σ. Consequently, both histograms can be well-fitted by modified Gaussians (dashed lines in Fig. 4e, f):

$$\begin{array}{l}f(x\,| \,\mu ,\widetilde{\sigma })\,=\,\displaystyle\frac{1}{\sqrt{2\pi {\tilde{\sigma }}^{2}}}\\\qquad\qquad\;\; \times \,\left(\exp \left\{\left(-\displaystyle\frac{{(x-\mu )}^{2}}{2{\tilde{\sigma }}^{2}}\right)\right\}+\exp \left\{\left(-\displaystyle\frac{{(x+\mu )}^{2}}{2{\tilde{\sigma }}^{2}}\right)\right\}\right),\end{array}$$
(5)

with fitted parameters summarized in Table 2. This indicates that for both EVS and EST the randomness due to SiGe alloy disorder does not dominate over the deterministic contribution given by γ12,31,47. However, care must be taken for the analysis of the histograms presented here, since a larger number of uncorrelated EVS samples are required to reduce the error of the Gaussian tails. The samples for both histograms contain multiple points that are spatially closer than the fitted correlation length in Fig. 4c. In addition, both histograms are slightly biased by omitting potentially a few small values due to the non-valid EVS(d) in Fig. 4a. Especially, obtaining EST smaller than the electron temperature by magnetospectroscopy is challenging and might explain that all EST > 12 μeV. In comparison, detecting EVS lower than the electron temperature is possible by conveyor-mode shuttling.

Discussion

We introduced a method for 2D mapping of the valley splitting EVS in a Si/SiGe SQS with sub-μeV energy accuracy and nanometer lateral resolution. The method is based on the separation and rejoining of spin-entangled electron pairs by conveyor-mode shuttling. Spin-singlet-triplet oscillations serve as a probe to identify spin-valley anticrossings and to extract the EVS of both a static and a shuttled electron. The nanometer-fine tunability of the position of the shuttled QD allows for dense measurements, which allows us to identify local variations of the valley-splitting landscape. By DC biasing the screening gates confining the 1DEC, we record a two-dimensional map of a large area. The method requires devices very similar to the ones used for quantum computation. Thus, the method is easily applicable and captures typical influences on the valley splitting e.g., effects from device fabrication. In principle, shuttling a single electron spin set in a spin superposition is sufficient for our method.

We benchmarked our results with magnetospectroscopy measurements—a well-established measurement method—on the same heterostructure and found the distributions of the measured map of singlet-triplet splittings to agree very well with the developed method. Note that mapping by magnetospectroscopy is limited in range due to the need for a proximate charge detector, and that the pure recording time required to obtain the presented 2D EST map took us ~100 times longer than the more detailed EVS map obtained by conveyor-mode shuttling. While the extent of the latter map is spatially limited due to electrostatic disorder, we expect that higher confinement (large signal voltages) of the propagating QD will allow us to extend the mapped region until we reach fundamental limitations due to spin-dephasing, which is enhanced by shuttling across the EVS-hotspots11. This method offers a more comprehensive approach to heterostructure characterization and exploration, potentially aiding advancements in heterostructure growth and valley-splitting engineering. Our results highlight the immediate benefits of conveyor-mode spin-coherent shuttling, not only for scaling up quantum computing systems but also for efficient material parameter analysis. Finally, the valley splitting map of a specific shuttle device allows for optimization of its spin-shuttling strategy48.

Methods

Shuttle pulses

In this section, we explain conveyor-mode electron shuttling in the 1DEC39,40,41,43. During the pulse stages T, d, and again T of the experiment, we apply sinusoidal pulses VS,i on the shuttle gates Si (S1–S4):

$${V}_{{{{\rm{S}}}},i}({\tau }_{{{{\rm{S}}}}})={U}_{i}\cdot \sin (2\pi f{\tau }_{{{{\rm{S}}}}}+{\varphi }_{i})+{C}_{i}.$$
(6)

The amplitudes (U1, U3) applied to the gate sets S1 and S3 on the second layer (blue in Fig. 1a) is Ulower = 150 mV, whereas the amplitudes (U1, U3) applied to the gate sets S2 and S4 on the 3rd metal layer is slightly higher (Uupper = 1.28 ⋅ Ulower = 192 mV) to compensate for the difference of capacitive coupling of these layers to the quantum well41. This compensation extends to the DC-part of the shuttle gate voltages. The offsets C1 = C3 = 0.7 V are chosen to form a smooth DQD, whilst C2 = C4 = 0.896 V are chosen to form a smooth DC potential. The phases are chosen in order to build a traveling wave potential across the one-dimensional electron channel (φ1 = −π/2, φ2 = 0, φ3 = π/2, φ4 = π) with wavelength λ = 280 nm. The frequency f is set to 10 MHz resulting in a nominal shuttle velocity of 2.8 ms−1. The nominal shuttling distance d relates to the assumption that the electron travels at a constant velocity λ⋅f41. Deviations from this nominal shuttling distance by potential disorder or strain are possible49.

Retuning SET and PSB

In order to compensate for slow charge-noise drifts on the PSB and the SET, both the PSB-stage voltage as well as the SET voltages are retuned after 1000 repetitions. For this, we track the spin fractions as well as the readout threshold between the charge configurations for singlet (4,0) and triplet (3,1). If we detect a significant change (~10%) in spin fractions, this means the PSB region drifted, and a correction via the G2 DC voltage is done. Similarly, a significant change in the readout threshold indicates a drift of the Coulomb peak on the SET, resulting in the need to adjust its plunger voltage accordingly.

Layer stack of the used heterostructure

The used Si/SiGe heterostructure is grown by chemical vapor deposition and has the following layer stack according to specification (top-to-bottom): Si-cap (2 nm), Si0.7Ge0.3 spacer (30 nm), strained Si quantum well (10 nm), Si0.7Ge0.3 barrier on virtual SiGe substrate.