Calibration-independent bound on the unitarity of a quantum channel with application to a frequency converter

Abstract

We report on a method to certify a unitary operation with the help of source and measurement apparatuses whose calibration throughout the certification process needs not be trusted. As in the device-independent paradigm our certification method relies on a Bell test and requires no assumption on the underlying Hilbert space dimension, but it removes the need for high detection efficiencies by including the single additional assumption that non-detected events are independent of the measurement settings. The relevance of the proposed method is demonstrated experimentally by bounding the unitarity of a quantum frequency converter. The experiment starts with the heralded creation of a maximally entangled two-qubit state between a single ⁴⁰Ca⁺ ion and a 854 nm photon. Entanglement preserving frequency conversion to the telecom band is then realized with a non-linear waveguide embedded in a Sagnac interferometer. The resulting ion-telecom photon entangled state is assessed by means of a Bell-CHSH test from which the quality of the frequency conversion is quantified. We demonstrate frequency conversion with an average certified fidelity of ≥84% and an efficiency ≥3.1 × 10⁻⁶ at a confidence level of 99%. This ensures the suitability of the converter for integration in quantum networks from a trustful characterization procedure.

Introduction

The enabling technologies for the realization of networks capable of linking quantum systems together have been identified^1,2,3. This includes quantum frequency converters – nonlinear processes in which a photon of one frequency is converted to another frequency whilst preserving all other quantum properties. A converter acts as a quantum photonic adapter allowing one for example to interface high-energy photonic transitions of quantum matters with lower-energy photons better suited for long-distance travel. Together with quantum storage and processing devices, quantum frequency converters enable a range of technologies using quantum networks, from distributed quantum computing⁴, quantum-safe cryptography⁵, enhanced sensing^6,7 and time keeping⁸.

A natural question arising in view of this integration potential is how to certify the functioning of a quantum frequency converter independently of contingent details, i.e. without the need to know an exhaustive physical model of its inner functioning or to assume that the certification equipment (source and measurements) is well calibrated and remains perfectly calibrated for the whole duration of the certification procedure. Recent works have demonstrated that the quantum nature of a number of channels can be witnessed without any trust in the measurement apparatus^{9,10,11,12,13} — the entanglement shared between distinct devices was also quantified in this way^14,15,16. However, these methods do not fully quantify the channel quality because they concentrate on particular characteristics of the tested devices, such as the degree of non-classicality or entanglement preservation, and they continue to rely on assumptions about the proper calibration of the sources used. The direct estimation of the channel’s quality is important because a certification method should guarantee the converter’s suitability for all foreseeable uses. Gate-set tomography¹⁷ aims at certifying sets of channels with high precision without relying on the description of either the measurements or the sources employed in the characterization. Unfortunately, this method is not suitable to the certification of a set that only contain one channel. It also calls for channels to be applied numerous times in succession without memory effect, and relies on the knowledge of the Hilbert space dimension. The data-driven approach^18,19 also removes most reliance on state preparation but has the advantage of only needing single uses of the tested channel. However, this approach also relies on knowledge of the dimensionality of the quantum systems, which is generally unknown.

A radical solution free of these limitations is offered by the method of device-independent (DI) characterization, also known as self-testing²⁰, where the physical implementation of a device is analyzed through the correlations observed in a Bell-type experiment²¹. In this setting, the deviation of the device from an ideal implementation is bounded, typically in terms of fidelity. Such a conclusion is less precise than a full tomography or other approaches aiming at the reconstruction of the channel, which rely on more assumptions about the setup than self-testing. The device-independent approach relies on the separation and independence between the apparatuses at hand, but makes no assumption on their internal modeling. As far as we know, only two self-tests have been fully implemented experimentally to date, both related to state certification^22,23. The main reason for this scarcity is that device-independent certification is very demanding regarding the efficiency of measurement apparatuses²⁴. This requirement has been circumvented in a number of experimental state certifications based on post-selected Bell inequality violation – by considering only the statistics observed from detected events^25,26,27. The question of what remains device-independent in certifications using post-selections has not been discussed in these experimental realizations.

In this article, we provide an accessible method to certify trustworthily the unitarity of an operation. Inspired by the device-independent certification techniques presented in refs. ^28,29, our method bounds the quality of a unitary operation from a single Bell test but without requiring high detection efficiencies to be implemented. Precisely, we assume that the physical process responsible for the occurrence of no-detection events is independent of the choice of the measurement setting, but impose no further restriction on it³⁰. Therefore, no-detection events may still depend on the state being measured or on devices’ calibrations in an arbitrary way. This natural assumption allows us to substantially reduce the complexity of unitary certification by removing the need for high overall detection efficiencies without requiring to trust the calibration of the certification devices. We use this tool to set the first calibration-independent bound on the unitarity of a channel—a state-of-the-art polarization-preserving quantum frequency converter (QFC)^31,32,33,34. We employ a trapped-ion platform as source of light-matter entanglement between an atomic Zeeman qubit and the polarization state of a spontaneously emitted photon³⁵. A frequency conversion based on a highly-efficient difference frequency generation process in a nonlinear waveguide embedded in a polarization Sagnac interferometer connects the system wavelength at 854 nm to the telecom C-band at 1550 nm³². A Bell-CHSH test³⁶ is finally performed after the frequency conversion, using the ion-telecom photon entangled state. We demonstrate frequency conversion with an average certified fidelity of ≥ 84% and a probability to get a telecom photon detection conditioned on a successful ion state readout of 3.1 × 10⁻⁶ at a confidence level of 99%.

Results

Source, QFC and measurement apparatus modeling

We start by providing an “a priori” quantum model of several devices involved in the setup. The desired models rely on minimal assumptions on the internal functioning of the devices, which nevertheless have enough physical insight to describe the process of frequency conversion.

A QFC can be represented by a channel between two physical systems identified as its input and output. A priori, this channel is unknown so for instance it may not be unitary. In our case, the input and output systems are the photonic modes entering the QFC device from the source and exiting it towards the detectors. These modes are filtered to ensure that their frequencies lie in the desired bandwidth ω_i and ω_f, respectively. We can associate to these photonic modes two Hilbert spaces ${{{{\mathcal{H}}}}}_{A}^{(i)}$ and ${{{{\mathcal{H}}}}}_{A}^{(f)}$, that encompass all the degrees of freedom necessary to describe the emission of the source in addition to the frequencies. To describe the quality of the QFC to be characterized, we are only interested in how the device map the photonic states received from the source to the state it sends to the detector:

$${{{\rm{QFC}}}}:B({{{{\mathcal{H}}}}}_{A}^{(i)})\to B({{{{\mathcal{H}}}}}_{A}^{(f)}).$$

(1)

Here $B({{{{\mathcal{H}}}}}_{A}^{(i)})$ stands for the set of bounded operators on the Hilbert space ${{{{\mathcal{H}}}}}_{A}^{(i)}$ (similarly for $B({{{{\mathcal{H}}}}}_{A}^{(f)})$). All auxiliary outputs can be safely ignored, while auxiliary input systems are to be seen as part of the device. Note for example that the QFC is powered by a laser stimulating the difference frequency generation process, which in turn requires energy supply. These are required for the proper functioning of the device, and have to be seen as parts of the QFC. The completely positive and trace-preserving (CPTP) map QFC in Eq. (1) is unknown and our goal is to provide a recipe to demonstrate that it is not far from the ideal unitary.

In addition to the QFC itself, our setup involves an entanglement source preparing a state shared between two parties called Alice (A) and Bob (B). Alice’s system is carried by the electromagnetic field used to characterize the QFC, which is associated to Hilbert space ${{{{\mathcal{H}}}}}_{A}^{(i)}$ introduced above. The physics of Bob’s system is irrelevant for the purpose of the QFC characterization because the QFC resides entirely on Alice’s side. Its state spans a Hilbert space ${{{{\mathcal{H}}}}}_{B}$. We denote the state produced by the source by

$${\rho }^{(i)}\in B({{{{\mathcal{H}}}}}_{A}^{(i)}\otimes {{{{\mathcal{H}}}}}_{B}).$$

(2)

The state obtained after applying the converter on Alice’s side reads

$${\rho }^{(f)}=\left({{{\rm{QFC}}}}\otimes {{{\rm{id}}}}\right)[{\rho }^{(i)}]\in B({{{{\mathcal{H}}}}}_{A}^{(f)}\otimes {{{{\mathcal{H}}}}}_{B}).$$

(3)

Finally, the form of the quantum model for the measurement apparatus is needed in order to describe the occurrences of the measurement results. We introduce two possible measurements ${{{{\mathcal{M}}}}}_{A}^{(f)}$ and ${{{{\mathcal{M}}}}}_{B}$ which act on the system of Alice after the converter and the system of Bob, respectively. Ideally, the measurements should have binary inputs x, y = 0, 1 and binary outputs a, b = 0, 1. In practice however, a third outcome $a,b={{\emptyset}}$ is possible corresponding to a no-click event. Each of the measurements is given by two POVMs with three elements each, such as

$${{{{\mathcal{M}}}}}_{A}^{(f)}\simeq \{{M}_{a| x}^{(f)}\},\quad {{{{\mathcal{M}}}}}_{B}\simeq \{{M}_{b| y}\}$$

(4)

with the operators ${M}_{a| x}^{(f)}$ and M_b∣y acting on ${{{{\mathcal{H}}}}}_{A}^{(f)}$ and ${{{{\mathcal{H}}}}}_{B}$, respectively.

Weak fair-sampling assumptions

Following the results presented in Ref. ³⁰, we now introduce an assumption on the measurement structure which allows us to relax the requirement on the detection efficiency inherent to device-independent certification. Consider for example the measurement ${{{{\mathcal{M}}}}}_{B}$ specified by the POVM elements M_b∣y with settings y and outcomes b including a no-click outcome $b={{\emptyset}}$. The measurement ${{{{\mathcal{M}}}}}_{B}$ satisfies the weak fair-sampling assumption if

$${M}_{{{\emptyset}}| y}={M}_{{{\emptyset}}| {y}^{{\prime} }},$$

(5)

i.e. the occurrence of the no-click outcome is not influenced by the choice of the measurement setting. Note that the weak fair-sampling assumption is much less restrictive than the usual (strong) fair-sampling assumption and hence much easier to enforce in practice. Indeed, in addition to the weak fair-sampling condition, the strong fair-sampling assumption further requires that all POVM elements associated to no-click events should be a multiple of the identity operators. This imposes a strong structure on the underlying measurement, implying in particular that its behavior must be independent of the measured state, which is not the case for the weak fair-sampling assumption. Under this assumption, ${{{{\mathcal{M}}}}}_{B}$ can be decomposed as a filter R_B acting on the quantum input (a quantum instrument composed of a completely positive (CP) map and a failure branch that outputs $y={{\emptyset}}$) followed by a measurement $\overline{{{{{\mathcal{M}}}}}_{B}}$ with unit efficiency (without $b={{\emptyset}}$ output)³⁰, that is

$${{{{\mathcal{M}}}}}_{B}=\overline{{{{{\mathcal{M}}}}}_{B}}\,{\circ}\, {R}_{B}.$$

(6)

Assuming that Bob’s measurement fulfills the weak fair-sampling assumption, we can focus on the data post-selected on Bob’s successful detection only. This data can be associated to an experiment where a probabilistic source prepares a state

$${\varrho }^{(i)}=\frac{({{{\rm{id}}}}\otimes {R}_{B})[{\rho }^{(i)}]}{{{{\rm{tr}}}}\,({{{\rm{id}}}}\otimes {R}_{B})[{\rho }^{(i)}]},$$

(7)

conditional on the successful outcome of Bob’s filter R_B. We can therefore only consider the experimental runs where the state ϱ⁽ⁱ⁾ is prepared and Bob’s detector clicks.

Assuming that Alice’s measurement also fulfills the weak fair-sampling assumption, that is

$${{{{\mathcal{M}}}}}_{A}^{(f)}={\overline{{{{\mathcal{M}}}}}}_{A}^{(f)}\,{\circ}\, {R}_{A},$$

(8)

we perform a similar decomposition for the final state

$${\varrho }^{(f)}=\frac{\left(({R}_{A}\,{\circ}\, {{{\rm{QFC}}}})\otimes {{{\rm{id}}}}\right)[{\varrho }^{(i)}]}{{{{\rm{tr}}}}\,\left(({R}_{A}\,{\circ}\, {{{\rm{QFC}}}})\otimes {{{\rm{id}}}}\right)[{\varrho }^{(i)}]},$$

(9)

corresponding to post-selected events for both sides. The success rate ${{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({R}_{A})={{{\rm{tr}}}}\,(({R}_{A}\,{\circ}\, {{{\rm{QFC}}}})\otimes {{{\rm{id}}}})[{\varrho }^{(i)}]$ of the filtering R_A is given by the probability to observe a click event on Alice’s detector, conditional on the click event seen by Bob (defining ϱ⁽ⁱ⁾)

$${{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({R}_{A})={{{\rm{P}}}}(\,{{\mbox{click at Alice}}}| {{\mbox{click at Bob}}}).$$

(10)

Goal

To set our goal, we first specify what a frequency converter is expected to do. First, it must change the carrier frequency of the photons from ω_i to ω_f. Second, an ideal QFC should preserve the quantum information in the remaining degrees of freedom. Here we focus on the minimal nontrivial example, which is arguably the most relevant one from the quantum communication perspective. We require that the QFC preserves the qubit degree of freedom encoded in the polarization of a photon. Thus, an ideal QFC should act as the identity

$${{{{\rm{id}}}}}_{2}:B({{\mathbb{C}}}^{2})\to B({{\mathbb{C}}}^{2})$$

(11)

on the polarization of a single photon. Hence, we need to show that, while changing the frequency of the photons, the map (1) is capable of preserving a two-dimensional subspace.

Following Ref. ²⁹, this can be formalized by requiring the existence of two maps $V:B({{\mathbb{C}}}^{2})\to B({{{{\mathcal{H}}}}}_{A}^{i})$ (injection map) and $\Lambda :B({{{{\mathcal{H}}}}}_{A}^{i})\to B({{\mathbb{C}}}^{2})$ (extraction map) such that

$$\Lambda \,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, V\,\approx \,{{{{\rm{id}}}}}_{2},$$

(12)

where the approximate sign refers to a bound on the Choi fidelity between the two maps ${{{\mathcal{F}}}}({{{\mathcal{E}}}},{{{{\mathcal{E}}}}}^{{\prime} })=F\left(({{{\rm{id}}}}\otimes {{{\mathcal{E}}}})[{\Phi }^{+}],({{{\rm{id}}}}\otimes {{{{\mathcal{E}}}}}^{{\prime} })[{\Phi }^{+}]\right)$, where Φ⁺ is a maximally entangled two-qubit state and $F(\rho ,\sigma )={\left({{{\rm{tr}}}}| \sqrt{\rho }\sqrt{\sigma }| \right)}^{2}$ is the fidelity between two states ρ and σ. Note that in the case where ${{{{\mathcal{E}}}}}^{{\prime} }$ is the identity map, Choi fidelity takes a particularly simple form ${{{\mathcal{F}}}}({{{\mathcal{E}}}},{{{\rm{id}}}})=\left\langle {\Phi }^{+}\right\vert ({{{\rm{id}}}}\otimes {{{\mathcal{E}}}})[{\Phi }^{+}]\left\vert {\Phi }^{+}\right\rangle$.

We are concerned with non-deterministic frequency converters. More precisely, our goal is to compare the actual frequency converter to a probabilistic but heralded quantum frequency converter – a device which behaves as an ideal QFC with a certain probability, and otherwise reports a failure. To do so, we can allow the maps Λ and V to be non trace preserving. The quality of an announced QFC is captured by two parameters – the probability that it works and the error it introduces in this case. These are quantified by the following figures of merit. The success probability

$${P}_{{{{\rm{succ}}}}}(\Lambda \,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\,V)={{{\rm{tr}}}}\,\left((\Lambda \,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, V)\otimes {{{\rm{id}}}}\right)[{\Phi }^{+}],$$

(13)

captures the efficiency of the converter. The conditional Choi fidelity

$${{{\mathcal{F}}}}(\Lambda \,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, V)=\left\langle {\Phi }^{+}\right\vert \frac{\left((\Lambda \,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, V)\otimes {{{\rm{id}}}}\right)[{\Phi }^{+}]}{{P}_{{{{\rm{succ}}}}}(\Lambda \,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, V)}\left\vert {\Phi }^{+}\right\rangle ,$$

(14)

bounds the error introduced in the state conditional to a successful frequency conversion. Bounding the quality of the converter thus consists in establishing lower-bounds on both quantities P_succ and ${{{\mathcal{F}}}}$, in addition to guarantee that the carrier frequency of the photons was converted.

Certification of the mapping

We start by discussing how the quality of the qubit mapping realized by the QFC can be assessed, i.e. how the quantities P_succ and ${{{\mathcal{F}}}}$ can be bounded. Following Ref. ²⁹, we do so through the self-testing of the maximally entangled two qubit state Φ⁺ derived in Ref. ³⁷. The latter is based on the Clauser Horne Shimony Holt (CHSH) inequality – a well-known Bell test derived for a setting where two parties Alice and Bob can choose one of two binary measurements at each round. The CHSH score S is given by

$$S=\sum\limits_{a,b,x,z\,=\,0,1}{(-1)}^{a+b+xy}P(a,b| x,y),$$

(15)

where a, b = 0, 1 are the parties’ measurement outcomes, and x, y = 0, 1 label their measurement setting. In the quantum framework, the correlation P(a, b∣x, y) is given by $P(a,b| x,y)={{{\rm{tr}}}}\,\rho \,{M}_{a| x}^{A}\otimes {M}_{b| y}^{B}$ where ρ is the measured state and $\{{M}_{a| x}^{A}\}$ ($\{{M}_{b| y}^{B}\}$) are Alice (Bob)’s appropriate POVM elements. We know from Ref. ³⁷ that for any quantum model $(\rho ,{M}_{a| x}^{A},{M}_{b| y}^{B})$ exhibiting a CHSH score S, there exist local extraction maps Λ_A and Λ_B such that $\left\langle {\Phi }^{+}\right\vert ({\Lambda }_{A}\otimes {\Lambda }_{B})[\rho ]\left\vert {\Phi }^{+}\right\rangle \ge f(S)$ for

$$f(S)=\frac{12+(4+5\sqrt{2})(5S-8)}{80}.$$

(16)

Notably, the form of the maps Λ_A(B) does not depend on the measurement performed by the other party.

This result holds for all quantum states and measurement. When applying it to the quantum model of the filtered state ϱ^(f) after the QFC and the binary measurements ${\overline{{{{\mathcal{M}}}}}}_{A}^{(f)}$ and ${\overline{{{{\mathcal{M}}}}}}_{B}$ for instance, it implies that there exist local maps ${\overline{\Lambda }}_{A}^{(f)}$ and ${\overline{\Lambda }}_{B}$ such that

$$\left\langle {\Phi }^{+}\right\vert ({\overline{\Lambda }}_{A}^{(f)}\otimes {\overline{\Lambda }}_{B})[{\varrho }^{(f)}]\left\vert {\Phi }^{+}\right\rangle \ge f(S),$$

(17)

where S is the CHSH score of the binary measurements on the filtered state, i.e. the post-selected CHSH score.

To derive a bound on the quality of the QFC itself rather than of its output state, we need to show that the state before the action of the QFC can be prepared from Φ⁺ with the injection map V_A acting on Alice, i.e. $({{{\rm{id}}}}\otimes {\overline{\Lambda }}_{B})[{\varrho }^{(i)}]\approx ({\mathbb{1}}\otimes {V}_{A})[{\Phi }^{+}]$. We show in the Methods that this can be done perfectly, i.e.

$$({{{\rm{id}}}}\otimes {\overline{\Lambda }}_{B})[{\varrho }^{(i)}]=\frac{({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]}{{{{\rm{tr}}}}\,({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]},$$

(18)

with a probabilistic map V_A associated to the success rate ${{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({V}_{A})={{{\rm{tr}}}}\,({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]\ge 50 \%$. This is possible because the state $({{{\rm{id}}}}\otimes {\overline{\Lambda }}_{B})[{\varrho }^{(i)}]$ is carried by a qubit at Bob’s side. It can therefore be purified to a state of Schmidt rank 2 and any such state can be efficiently obtained from Φ⁺ by a local filter applied by Alice.

Combining the definition of the filtered state ϱ^(f) in Eq. (9) with Eqs. (17) and (18), we conclude that for the probabilistic extraction map ${\Lambda }_{A}={\overline{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}$, the conditional Choi fidelity of Eq. (14) is bounded by

$${{{\mathcal{F}}}}({\Lambda }_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A})\ge f(S).$$

(19)

We emphasize that this bound is valid for all possible underlying state ρ and measurements $\{{M}_{a| x}^{A}\}$, $\{{M}_{b| y}^{B}\}$ subject to Eq. (5). Therefore, the observation of a large value of S after frequency conversion is sufficient to set a lower-bound on the fidelity of the QFC.

It remains to bound the success probability of the map Λ_A∘QFC∘V_A when applied on Φ⁺, that is ${{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({\Lambda }_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A})={{{\rm{tr}}}}\,(({\overline{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}\circ {{{\rm{QFC}}}}\,{\circ}\,{V}_{A})\otimes {{{\rm{id}}}})[{\Phi }^{+}]$. This map is successful if both the injection map V_A and the filter R_A are, hence

$$\begin{array}{rcl}{{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({\Lambda }_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A})&=&{{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({R}_{A}){{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({V}_{A})\\ &\ge &\displaystyle{\frac{1}{2}}{{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({R}_{A}).\end{array}$$

(20)

P_succ(R_A) can be estimated experimentally using Eq. (10).

The results presented above successfully show that the QFC is capable of preserving a two-dimensional subspace up to an error bounded by the Choi fidelity. This certification is done up to a unitary, as is customary in the device-independent framework. This is in line with the experimental reality: in addition to changing the carrier frequency, the QFC may induce a rotation of the photon polarization, similar to the action that a transmission line such as an optical fiber may have on the transported photon. In practice, this rotation can be compensated by the measurement. In fact, since misaligned measurement bases are not able to maximize a CHSH value, one may even suggest that any such rotation has already been compensated in the experiment. The certified fidelity can then be interpreted as a closeness to the identity channel defined with respect to the measurement bases. More broadly, this means that the results can be applied to any channel which ideally behaves as a unitary on a two-dimensional subspace. This includes quantum memories capable of storing a single photon while preserving its polarization, communication links capable of preserving the polarization of a photon over far away locations, or quantum “translators” mapping between the polarization of a single photon and a stationary qubit carried by an ion, a superconducting circuit or a solid state system.

Certification of the frequency conversion

In the case of the QFC, it is important to guarantee that the device also changes the frequency of the photons on which it operates. Note that the frequency of a photonic mode is a physical property defined with respect to a reference frame, and it does not admit a simple device-independent representation. Hence, we require that frequency filters are used at the source and after the QFC to guarantee that the QFC and the detectors receive photons at the frequency ω_i and ω_f, respectively. Therefore on the physical level, the Hilbert spaces ${{{{\mathcal{H}}}}}_{A}^{(i/f)}$ can be associated with some collections of photonic modes at the corresponding carrier frequencies.

Experimental source of entanglement

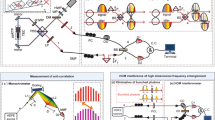
The experimental setup is sketched in Fig. 1. Our source of entanglement is a trapped-ion quantum network node which creates light-matter entanglement between a Zeeman qubit in a single trapped ⁴⁰Ca⁺ ion (Bob) and the polarization state of an emitted single photon at 854 nm (Alice)³⁸. The photons are coupled to a single-mode fiber via a high-aperture laser objective (HALO) and guided to the frequency converter, which is the device we aim to certify.

Fig. 1: Experimental setup.

Light-matter entanglement is generated between a single trapped ⁴⁰Ca⁺ ion and the polarization state of an emitted photon at 854 nm. The photons are collected with a high-aperture laser objective (HALO), coupled to a single-mode fiber and guided to the QFC device. The latter features a PPLN waveguide embedded in a polarization Sagnac interferometer to guarantee polarization-preserving operation. The converted photons pass a series of spectral filters (band-pass filter (BPF), volume Bragg grating (VBG) and etalon) to suppress background stemming from the DFG process. The projection setup at 1550 nm consists of a motorized QWP and HWP, a Wollaston prism to split orthogonally-polarized photons, and two fiber-coupled superconducting-nanowire single-photon detectors (SNSPD). In the lower left part the level scheme of the ⁴⁰Ca⁺ ion including the most relevant states and transitions for entanglement generation and quantum state readout is shown. The atomic qubit is encoded in two Zeeman levels (m = − 3/2 and m = 1/2) of the metastable D_5/2-state.

The entanglement generation sequence is slightly modifed compared to³⁸. The relevant level scheme for the state preparation and detection of the Ca ion is shown in Fig. 1. After Doppler cooling, excitation of the ion on the S_1/2 to P_3/2 transition by a π-polarized, 2 μs long laser pulse at 393 nm creates a spontaneously emitted photon at 854 nm. This photon is collected along the quantization axis, thereby suppressing π-polarized photons, and is entangled with the ion in the state

$$\left\vert \Psi \right\rangle =\sqrt{\frac{2}{3}}\,\left\vert {\sigma }^{+},\downarrow \right\rangle +\sqrt{\frac{1}{3}}\,{e}^{i{\omega }_{L}t}\,\left\vert {\sigma }^{-},\uparrow \right\rangle$$

(21)

with $\vert \downarrow\rangle =\vert {D}_{5/2},m=-3/2\rangle$ and $\vert \uparrow \rangle =\vert {D}_{5/2},m=+1/2\rangle$. The oscillation with frequency ω_L arises from the frequency difference between the $\left\vert \uparrow \right\rangle$ and $\left\vert \downarrow \right\rangle$ states and the asymmetry in the state results from the different Clebsch-Gordan coefficients (CGC) of the transitions between the $\vert {P}_{3/2}\rangle$ and $\vert {D}_{5/2}\rangle$ Zeeman sublevels. We compensate for this by means of a partial readout of the trapped-ion Zeeman qubit during the state preparation: a π/2-pulse at 729 nm transfers 50 % of the population from $\vert \downarrow\rangle =\vert {D}_{5/2},m=-3/2\rangle$ to the S_1/2 ground state. A subsequent fluorescence detection with the cooling lasers is a projective measurement of this population in the following way. The fluorescence detection discriminates between population in the S_1/2-state which results in scattering of photons from the cooling laser, while population in D_5/2 leaves the ion dark. If it yields a bright result, the measurement is discarded, while a dark result leaves the D-state intact and heralds a successful state preparation. Thus, the ion-photon state after a dark result is maximally entangled

$$\left\vert \Psi \right\rangle =\sqrt{\frac{1}{2}}\,\left(\left\vert {\sigma }^{+},\downarrow \right\rangle +{e}^{i{\omega }_{L}t}\,\left\vert {\sigma }^{-},\uparrow \right\rangle \right).$$

(22)

In this way, maximally-entangled ion-photon pairs are generated at a rate of 720 s⁻¹ and a probability per shot of 0.36 %.

Experimental QFC device

The QFC device transduces the photons at 854 nm to the telecom C-band at 1550 nm via the difference frequency generation (DFG) process 1/854 nm - 1/1904 nm = 1/1550 nm in a periodically-poled lithium niobate (PPLN) waveguide³². The input photons are overlapped with the classical pump field at 1904 nm on a dichroic mirror and guided to the core of the QFC device, an intrinsically phase-stable polarization Sagnac interferometer. The latter ensures polarization-preserving operation since the DFG process is inherently polarization-selective. The interferometer is constructed in a similar way as in³⁹, i.e. a polarizing beam-splitter (PBS) spatially separates the orthogonal components and a HWP rotates the not convertible horizontal component of input, pump and output fields by 90^∘. Both components are subsequently coupled to the same waveguide from opposite directions. The converted photons take the same interferometer paths, are recombined in the PBS, separated from the pump and input photons via another dichroic mirror and coupled to a single-mode fiber. Multi-stage frequency filtering down to 250 MHz suppresses pump-induced background photons stemming from anti-Stokes Raman scattering in the waveguide. Note that this stage acts in particular as a strong frequency filter for unconverted photons at 854 nm. Including additional losses from the mirrors and detectors we estimate a suppression of at least 200 dB at 854 nm. The external device efficiency is measured to 57.2 %, independent of the polarization and including all losses between input and output fiber. The QFC-induced background is measured at the operating point to be 24(3) photons/s, being to our knowledge the lowest observed background of a QFC device in this high-efficiency region.

Measurements

To measure the Bell parameter S, we perform joint measurements of the atomic and photonic qubit in the four CHSH basis settings which we choose to lie in the equatorial plane of the Bloch sphere with respect to the basis defined in Eq. (22).

For the atomic qubit, the required basis rotation is implemented by means of a pulsed sequence of two consecutive π-pulses at 729 nm and a radio-frequency (RF) π/2-pulse applied on the S_1/2 ground-state qubit with phase ϕ_RF using a resonant magnetic field coil (Fig. 1). The ground-state qubit states are readout by means of two fluorescence detection rounds yielding bright and dark events depending on whether the state is populated or not, respectively. The phase of the atomic qubit underlies the Larmor precession in D_5/2 with ω_L. The arrival time t of the photon reveals this Larmor phase up to a constant offset which is calibrated with an independent measurement and kept fixed for all following ones (see next section).

For the photonic qubit we employ a set of a motorized quarter- and a half-wave plate for arbitrary basis rotations and a Wollaston prism to split orthogonally polarized photons. Both outputs are connected to fiber-coupled superconducting-nanowire singe-photon detectors (SNSPDs). To fulfill the weak fair sampling assumption we have to balance the efficiencies of both detectors since the error of the post-selected probabilities scales linearly with the imbalance. To this end we use attenuated laser light and adjust the bias current through the SNSPDs to achieve γ = 1 − η_snspd1/η_snspd2 ≤ 0.2% with η_snspd2 = 13.5%. This reduces the deviation of the post-selected probabilities from those obtained with a lossless detector to about 1%³⁰.

To avoid influences of drifts over the measurements, we consecutively acquire runs of data for 5 seconds in each basis and cascade up to 660 runs. The CHSH score is then obtained using the setting choices

$$x=0\to \frac{1}{2}({\sigma }_{x}+1),\quad x=1\to \frac{1}{2}({\sigma }_{y}+1)$$

(23)

in the photonic side and

$$y=0\to \frac{1}{2}\left(\frac{{\sigma }_{x}+{\sigma }_{y}}{\sqrt{2}}+1\right),\quad y=1\to \frac{1}{2}\left(\frac{{\sigma }_{x}-{\sigma }_{y}}{\sqrt{2}}+1\right)$$

(24)

for the ion side.

Experimental results

Figure 2a shows a typical time-resolved coincidence histogram between photonic detection events of one of the detectors (readout base x = 0) and bright events of the atomic state readout (base y = 0). As mentioned previously, the oscillations stem from the Larmor precession of the atomic qubit resulting in a time-dependent entangled state, Eq. (22). From the histograms of all readout bases we calculate the CHSH Bell parameter according to Eq. (15), which is consequently also detection-time dependent (see Fig. 2b). Thus, by postselecting coincidences in a certain time window, we perform a readout in the correct CHSH basis. These windows are located at the top of each oscillation, they are calibrated from an independent measurement and kept fixed during the analysis.

Fig. 2: Measurement results.

a Time-resolved coincidences between photonic detection events of one of the detectors (readout base A₀) and bright events of the atomic state readout from both orthogonal states of the readout base B₀. The oscillations with the Larmor frequency of the atomic qubit stem from the time-dependency of the entangled state. b The average Bell parameter in dependence of the detection time. For the further analysis we select coincidences at the detection times which correspond to a Larmor phase of ω_L t = π resulting in the Ψ⁻ Bell state. To obtain a feasible SBR, we only select concidences in time windows around the first two maxima, whose positions were determined from an independent measurement. c The optimal Bell value is a tradeoff between number of detected events (favouring large time windows) and phase resolution (favouring small time windows). d Bell value after QFC after a certain number of measurement runs based on the coincidences from the optimal time window.

To certify the unitarity of the QFC from finite experimental data, we view the multi-round experiment as a sequence of rounds, labeled with i = 1, …, n. Note that each round is an experimental trial of atom-photon-state generation, not the previously mentioned runs. At each round i, the final atom-photon state corresponds to some intrinsic CHSH score S_i. By virtue of Eqs. (19) the conditional Choi fidelity of the converter at round i satisfies ${{{{\mathcal{F}}}}}_{i}\ge f({S}_{i})$, with f given in Eq.(16). We are interested to bound the average fidelity

$$\overline{{{{\mathcal{F}}}}}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{{\mathcal{F}}}}}_{i}$$

(25)

over all measurement rounds. By linearity of f, this quantity is bounded by $f(\overline{S})$, where $\overline{S}=\frac{1}{n}\sum\nolimits_{i = 1}^{n}{S}_{i}$ is the average CHSH score. A lower bound on $\overline{S}$ thus lower-bounds $\overline{{{{\mathcal{F}}}}}$ through Eq. (16).

To give a clear lower bound on the CHSH score $\overline{S}$ in presence of a finite number of measurement rounds, we construct a one-sided confidence interval on $\overline{S}$. It can be shown that

$$\hat{S}=8{I}_{\alpha }^{-1}(n\overline{T},n(1-\overline{T})+1)-4$$

(26)

is the tightest such lower bound for a confidence level 1 − α whenever α < 1/4 and $n,n\overline{T}\ge 2$⁴⁰. Note that this conclusion does not rely on the I.I.D. assumption (independent and identically distributed), e.g. it holds true even if the state produced by the setup is not identical at each round. Here, $\overline{T}=\mathop{\sum }\nolimits_{i = 1}^{n}{T}_{i}$ is the experimental mean of the random variables corresponding to the CHSH game

$${T}_{i}=\left\{\begin{array}{ll}1\quad &{A}_{i}\oplus {B}_{i}={X}_{i}{Y}_{i}\\ 0\quad &{A}_{i}\oplus {B}_{i}\ne {X}_{i}{Y}_{i}\end{array}\right.$$

(27)

where X_i/A_i (Y_i/B_i) is Alice’s (Bob’s) measurement setting/outcome in round i. Setting α = 0.01, we obtain 99%-confidence lower bounds $\hat{S}$ on $\overline{S}$ for the state produced in the experiment.

Figure 2(c) show the calculated Bell values $\hat{S}$ – obtained from the independent calibration measurement – for different numbers of time windows (located at each oscillation peak) and different window lengths. The optimal values are a tradeoff between a higher number of events favouring better statistics and thus higher Bell values, the signal-to-background ratio which decreases with an increasing number of peaks due to the exponential decay of the photon wavepacket, and phase resolution being ideal for the smallest possible time window. We choose an optimal time window of 8.125 ns (corresponding to 9 time bins) and the first and second oscillation peak.

The final results of the certification are displayed in Fig. 2(d): we see the Bell value $\hat{S}$ after each measurement run (in each run we measure all four correlators). We find a converging behavior due to the increasing number of events, which reduces the statistical uncertainty. The remaining fluctuations of the Bell values after QFC are most likely caused by drifts of the unitary rotation of the photon polarization state in the fiber connecting the ion trap and QFC setup. After 660 runs (16593 events) we find

$$\hat{S}=2.598$$

(28)

and an average observed CHSH score of $8\overline{T}-4=2.65$. The latter is in good agreement with our known error sources, namely signal-to-background-ratio (0.04), phase resolution (0.028), atomic coherence and fidelity of the atomic state readout (0.085), and polarization drifts in the long fiber (0.028). From $\hat{S}$, we calculate via Eq. (16) and Eq. (19) a certified conversion fidelity of

$$\hat{{{{\mathcal{F}}}}}\ge f(\hat{S})=0.8406$$

(29)

To conclude, we bound the converter’s efficiency. Eq. (20) and Eq. (10) allow us to bound the success probability of the QFC directly as a function of the number of coincidence detection at Alice and Bob n_c and the total number of rounds n as

$${\hat{P}}_{{{{\rm{succ}}}}}=\frac{1}{2}{I}_{\alpha }^{-1}({n}_{c},n-{n}_{c}+1),$$

(30)

where we used the probability estimator free of the I.I.D. assumption from Ref. ⁴⁰. With n_c = 16 593 and n = 2 640 000 000, we obtain the lower bound

$${P}_{{{{\rm{succ}}}}}\ge {\hat{P}}_{{{{\rm{succ}}}}}=3.1\times 1{0}^{-6}$$

(31)

at a confidence level 1 − α = 99%. The limited overall success probability can be attributed to several factors: the success probability to collect a photon at 854 nm from the ion (0.36 %), the external device efficiency of the QFC, i.e. the probability to get a 1550 nm photon in the output fiber per 854 nm photon at the input of the QFC (57 %), the quantum efficiency of the single-photon detectors (13.5 %), further optical losses in the whole experimental setup (60 %) and the ratio between the post-selected time window and the total photon wavepacket (3.9 %).

Discussion

We have presented the first recipe leveraging device-independent techniques to certify the unitarity of an operation without assuming that the certification devices are perfectly calibrated. Although not fully device-independent, the proposed recipe requires no assumption on the underlying Hilbert space dimension and is widely tolerant to loss. This is achieved by assuming that the occurrence of no-detection events is independent from the choice of measurement, which is both more general and more realistic than independence from the measured state. This allows in particular to guarantee the certification independently of the action of filters and other devices used in the experiment having no access to the choice of measurement setting.

As an illustration, we focused on the performance of a state-of-the-art polarization-preserving quantum frequency converter. Our calibration-independent method was used in this framework to quantify the performance of the device in terms of conversion efficiency and fidelity of the transmitted photonic polarization qubit. Frequency filters at the source and the detector were used in order to ensure that the device changes the carrier frequency of the transmitted photons.

The proposed recipe could be used to certify quantum storage and processing devices among others. Given the interesting balance between its practical feasibility and high level of trust, we believe that the method is well suited to become a reference certification technique to ensure the suitability of devices for their integration in quantum networks.

Note added

While writing this manuscript we became aware of a related experimental work by Neves et al.⁴¹.

Methods

In this section we present a detailed derivation of the Eqs. (19), (20)) of the main text. We start by recalling the context in which they apply.

Consider a scenario where Alice and Bob control quantum systems, described by unknown finite dimensional Hilbert spaces ${{{{\mathcal{H}}}}}_{A}^{(i)}$ and ${{{{\mathcal{H}}}}}_{B}$, prepared in a global state ϱ⁽ⁱ⁾. In addition, Alice has access to a probabilistic channel modeled by some completely positive trace non increasing map ${R}_{A}\,{\circ}\, {{{\rm{QFC}}}}:B({{{{\mathcal{H}}}}}_{A}^{(i)})\to B({{{{\mathcal{H}}}}}_{A}^{(f)})$. When successfully applied on Alice’s system the channel outputs the state

$${\varrho }^{(f)}=\frac{\left(({R}_{A}\,{\circ}\, {{{\rm{QFC}}}})\otimes {{{\rm{id}}}}\right)[{\varrho }^{(i)}]}{{{{\rm{tr}}}}\,\left(({R}_{A}\,{\circ}\, {{{\rm{QFC}}}})\otimes {{{\rm{id}}}}\right)[{\varrho }^{(i)}]},$$

(32)

which is self-tested to be close to a maximally entangled two qubit state $\left\vert {\Phi }^{+}\right\rangle =\frac{1}{\sqrt{2}}(\left\vert 00\right\rangle +\left\vert 11\right\rangle )$. That is, there exist completely positive trace preserving maps ${\bar{\Lambda }}_{A}^{(f)}:B({{{{\mathcal{H}}}}}_{A}^{(f)})\to B({{\mathbb{C}}}^{2})$) and ${\bar{\Lambda }}_{B}:B({{{{\mathcal{H}}}}}_{B})\to B({{\mathbb{C}}}^{2})$) such that

$$\left\langle {\Phi }^{+}\right\vert ({\bar{\Lambda }}_{A}^{(f)}\otimes {\bar{\Lambda }}_{B})[{\varrho }^{(f)}]\left\vert {\Phi }^{+}\right\rangle \ge f(S).$$

(33)

Let us now show that these predicates are sufficient to guarantee the results of Eqs. ((19),(20)) discussed in the main text.

State preparation

First, let us define the states

$${\bar{\varrho }}^{(i)}=({{{\rm{id}}}}\otimes {\bar{\Lambda }}_{B})[{\varrho }^{(i)}]$$

(34)

$${\bar{\varrho }}^{(f)}=\frac{\left(({R}_{A}\,{\circ}\, {{{\rm{QFC}}}})\otimes {{{\rm{id}}}}\right)[{\bar{\varrho }}^{(i)}]}{{{{\rm{tr}}}}\,\left(({R}_{A}\,{\circ}\, {{{\rm{QFC}}}})\otimes {{{\rm{id}}}}\right)[{\bar{\varrho }}^{(i)}]},$$

(35)

which are positive semi-definite operators on the Hilbert space ${{{{\mathcal{H}}}}}_{A}^{(i)}\otimes {{\mathbb{C}}}^{2}$ and ${{{{\mathcal{H}}}}}_{A}^{(f)}\otimes {{\mathbb{C}}}^{2}$, respectively. These definitions allow us to rewrite the Eq. (33) in the form

$$\left\langle {\Phi }^{+}\right\vert ({\bar{\Lambda }}_{A}^{(f)}\otimes {{{\rm{id}}}})[{\bar{\varrho }}^{(f)}]\left\vert {\Phi }^{+}\right\rangle \ge f(S),$$

(36)

with the map ${\bar{\Lambda }}_{B}$ absorbed in the state. To be able to interpret this bound as Choi fidelity let us now show that the initial state ${\bar{\varrho }}^{(i)}$ can be prepared from Φ⁺ with the help of a local probabilistic map applied by Alice.

To do so, introduce an auxilliary quantum system ${A}^{{\prime} }$ and consider a purification of the state

$${\bar{\varrho }}^{(i)}={{{{\rm{tr}}}}}_{{A}^{{\prime} }}\left\vert \Psi \right\rangle \left\langle \Psi \right\vert ,$$

(37)

where $\left\vert \Psi \right\rangle \left\langle \Psi \right\vert$ is a pure state on ${{{{\mathcal{H}}}}}_{A}^{(i)}\otimes {{{{\mathcal{H}}}}}_{{A}^{{\prime} }}\otimes {{\mathbb{C}}}^{2}$. Since Bob’s system is a qubit by Schmidt theorem this state is of the form

$$\left\vert \Psi \right\rangle =\sum\limits_{k=0}^{1}{\lambda }_{k}{\left\vert {\xi }_{k}\right\rangle }_{A{A}^{{\prime} }}{\left\vert {b}_{k}\right\rangle }_{B},$$

(38)

with λ₀ ≥ λ₁ and orthogonal states 〈b₀∣b₁〉 = 〈ξ₀∣ξ₁〉. There is thus a qubit unitary u_B and an isometry ${v}_{A{A}^{{\prime} }}:{{\mathbb{C}}}^{2}\to {{{{\mathcal{H}}}}}_{A}^{(i)}\otimes {{{{\mathcal{H}}}}}_{{A}^{{\prime} }}$ such that

$$\left\vert \Psi \right\rangle =({v}_{A{A}^{{\prime} }}\otimes {u}_{B})\left({\lambda }_{0}\left\vert 00\right\rangle +{\lambda }_{1}\left\vert 11\right\rangle \right).$$

(39)

In addition, it is straightforward to see that the following qubit filter (completely positive trace non increasing map) with

$$\begin{array}{r}{R}_{A}^{{\prime} }:B({{\mathbb{C}}}^{2})\to B({{\mathbb{C}}}^{2})\\ \rho \mapsto K\rho K\\ {{{\rm{with}}}}\quad K=\left(\begin{array}{cc}1&\\ &\frac{{\lambda }_{1}}{{\lambda }_{0}}\end{array}\right)\end{array}$$

(40)

satisfies

$$\frac{({v}_{A{A}^{{\prime} }}\,{\circ}\, {R}_{A}^{{\prime} }\otimes {u}_{B})[{\Phi }^{+}]}{{{{\rm{tr}}}}({v}_{A{A}^{{\prime} }}\,{\circ}\, {R}_{A}^{{\prime} }\otimes {u}_{B})[{\Phi }^{+}]}=\Psi$$

(41)

and has success probability

$${{{\rm{tr}}}}({v}_{A{A}^{{\prime} }}\,{\circ}\, {R}_{A}^{{\prime} }\otimes {u}_{B})[{\Phi }^{+}]=\frac{1}{2}+\frac{1}{2}\left(\frac{{\lambda }_{1}}{{\lambda }_{0}}\right)\ge \frac{1}{2}.$$

(42)

Combining with Eq. (37) and using $({{{\rm{id}}}}\otimes {u}_{B})[{\Phi }^{+}]=({u}_{B}^{T}\otimes {{{\rm{id}}}})[{\Phi }^{+}]$ we conclude that the probabilistic map

$$\begin{array}{rcl}{V}_{A}:B({{\mathbb{C}}}^{2})&\to &B({{{{\mathcal{H}}}}}_{A}^{(i)})\\ \rho &\mapsto &{{{{\rm{tr}}}}}_{{A}^{{\prime} }}({v}_{A{A}^{{\prime} }}\,{\circ}\, {R}_{A}^{{\prime} }\,{\circ}\, {u}_{B}^{T})[\rho ]\end{array}$$

(43)

fulfills

$$\frac{({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]}{{{{\rm{tr}}}}({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]}={\bar{\varrho }}^{(i)}$$

(44)

and has success probability at least 50% when acting on Φ⁺. Demonstrating the desired result.

Bounding the quality of the QFC

Combining Eqs. (35),(36),(44)) we obtain the following bound

$$\left\langle {\Phi }^{+}\right\vert \frac{({\bar{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]}{{{{\rm{tr}}}}({\bar{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]}\left\vert {\Phi }^{+}\right\rangle \ge f(S).$$

(45)

Which has the form of a bound on the Choi fidelity of the channel ${\bar{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A}$ with respect to the identity channel. To get the expression of the main text it we to define a single probabilistic extraction map ${\Lambda }_{A}={\bar{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}$ in order to obtain

$${{{\mathcal{F}}}}({\Lambda }_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A})\ge f(S).$$

(46)

It remains to argue about the minimal possible value of the success probability. By virtue of $({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]={\bar{\varrho }}^{(i)}\,{{{\rm{tr}}}}({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]$ we get

$$\begin{array}{l}{{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({\Lambda }_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A})\\ ={{{\rm{tr}}}}({\bar{\Lambda }}_{A}^{(f)}\,{\circ}\,{R}_{A}\,{\circ}\, {{{\rm{QFC}}}}\,{\circ}\, {V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}]\\ =({{{\rm{tr}}}}\,({\bar{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}\,{\circ}\, {{{\rm{QFC}}}}\otimes {{{\rm{id}}}})[{\bar{\varrho }}^{(i)}])({{{\rm{tr}}}}({V}_{A}\otimes {{{\rm{id}}}})[{\Phi }^{+}])\\ \ge \frac{1}{2}{{{\rm{tr}}}}\,({\bar{\Lambda }}_{A}^{(f)}\circ {R}_{A}\,{\circ}\, {{{\rm{QFC}}}}\otimes {{{\rm{id}}}})[{\bar{\varrho }}^{(i)}]\\ =\frac{1}{2}{{{\rm{tr}}}}\,({\bar{\Lambda }}_{A}^{(f)}\,{\circ}\, {R}_{A}\,{\circ}\, {{{\rm{QFC}}}}\otimes {\bar{\Lambda }}_{B})[{\varrho }^{(i)}]\\ =\frac{1}{2}{{{\rm{tr}}}}\,({R}_{A}\,{\circ}\,{{{\rm{QFC}}}}\otimes {{{\rm{id}}}})[{\varrho }^{(i)}]\\ =\frac{1}{2}{{{{\rm{P}}}}}_{{{{\rm{succ}}}}}({F}_{A})=\frac{1}{2}{{{\rm{P}}}}(\,{{\mbox{click at Alice}}}| {{\mbox{click at Bob}}})\end{array}$$

where we used the fact that the maps ${\bar{\Lambda }}_{A}^{(f)}$ and ${\bar{\Lambda }}_{B}$ are trace preserving. We thus conclude that the success probability of the map (Λ_A ∘ QFC ∘ V_A) is at most twice lower than the conditional click probability of Alice P(click at Alice∣click at Bob), which can be directly estimated from experimental data.