Quantum autoencoders using mixed reference states

Abstract

One of the fundamental tasks in quantum information theory is quantum data compression, which can be realized via quantum autoencoders that first compress quantum states to low-dimensional ones and then recover to the original ones with a reference state. When taking a pure reference state, there exists an upper bound for the encoding fidelity, which limits the compression of states with high entropy. To overcome the entropy inconsistency, we allow the reference state to be a mixed state and propose a cost function that combines the encoding fidelity and the quantum mutual information. We consider the reference states to be a mixture of maximally mixed states and pure states and propose three strategies for setting the ratio of mixedness. Numerical simulations of different states and experimental implementations on IBM quantum computers illustrate the effectiveness of our approach.

Introduction

Quantum machine learning which combines machine learning and quantum computation has grown into a booming research topic^{1,2,3,4,5,6,7}. Quantum autoencoders (QAEs) inherit the spirit of classical autoencoders to compress information into a latent space such that the original data can be recovered from a reduced-dimension representation^8,9. They have the potential to reduce the requirements of quantum communication channels¹⁰ and the size of quantum gates^11,12 and thus have a practical value for various applications including quantum simulation¹³, quantum communication and distributed computation in quantum networks^10,11.

Owing to the potential of QAEs in quantum information processing, there is a growing interest in designing different schemes to complete state compression tasks. An early work proposed a quantum generalization of a classical neural network¹⁴ and another work designed an autoencoder framework using programmable circuits¹⁵. An enhanced QAE that encodes the feature vector of the input data into single-qubit rotation gates has been implemented in variational quantum circuits¹⁶. There have also been achievements in the implementation of QAEs on photonic systems^12,17,18. Apart from data compression, QAEs have also been applied to other applications, such as state denoise^19,20 and error mitigation²¹. A novel method based on QAEs has been devised to prepare the quantum Gibbs state and estimate the quantum Fisher information²². A hybrid QAE has been proposed to identify the emergence of order in the latent space that can be utilized for clustering and semi-supervised classification²³. Recently, the execution of a QAE-facilitated teleportation protocol has been implemented on a silicon photonic chip²⁴. Furthermore, the exploration of QAEs to analyze datasets originating from industrial contexts demonstrates their potential in processing real-world data²⁵.

In traditional QAE schemes^15,17,18,26, pure states are utilized as reference states for recovering the initial state. For each state to be compressed, there exists an upper bound (hereafter, we call it QAE-pure bound) for the encoding fidelity, i.e., the overlap between the trash state and the reference state. Such a bound limits the compression of states with high entropy. To compensate for the entropy inconsistency between the initial state and the recovered state²⁷, we allow the reference state to be a mixed one. Instead of a fixed mixed state, we configure different reference states for effective compression of different states. To achieve this, we take advantage of quantum mutual information that measures the disentanglement to guide the optimization of the encoding transformation. Meanwhile, the conventional cost function in standard QAEs aims to decouple the initial states into two parts and provides information about the inner structure of initial states, which can be useful for setting the reference state. Hence, we design a novel cost function that combines the above two factors to guide the training of QAEs towards better performance. Inspired by the compression of tensor products of identical states on IBM quantum computers²⁸, we experimentally realize QAEs with mixed reference states on the IBM quantum simulator ibmq_qasm_simulator and quantum computer ibmq_quito.

In this work, we leverage mixed reference states to break the upper bound of compression rate imposed by conventional QAEs²⁶. In particular, we use a mixture of a pure state and the maximally mixed state, with pure reference states being a special case. Similarly, our proposed cost function considers both quantum mutual information and the existing function in conventional QAEs that favor pure reference states. Consequently, our protocol exhibits flexibility, enabling its application to various quantum states. We have observed the direct relationship between the optimal value of the purity ratio in the reference state and the QAE-pure bound. This discovery empowers us with the insights gained from the training of QAEs to adaptively configure mixed reference states for compressing different unknown states. Our experimental implementations on IBM quantum computers demonstrate the potential of the proposed protocol in saving valuable quantum resources for real applications.

Results

QAEs using mixed reference states

Schematic

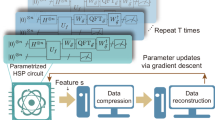
As illustrated in Fig. 1, we define the trash qubits as subsystem A and the latent qubits as subsystem B, respectively. We denote the dimensions of the original space, the latent space, and the trash space as d, d_B, and d_A, respectively. The goal of a QAE is to compress (n_A + n_B)-qubit state ρ₀ into n_B-qubit state ρ_latent via an encoder map U_e and then recover to (n_A + n_B)-qubit state ρ_f via a decoder map U_d. After the encoding operation U_e, the trash state and the latent state are obtained as ${\rho }_{{\rm{trash}}}={{\rm{Tr}}}_{B}({U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger })$ and ${\rho }_{{\rm{latent}}}={{\rm{Tr}}}_{A}({U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger })$, respectively. Denote F(ρ₁, ρ₂) as the state fidelity between ρ₁ and ρ₂²⁹. The efficiency of this task can be quantified by the decoding fidelity between the original state and the recovered state, i.e., ${{\mathcal{F}}}_{{\rm{d}}}=F({\rho }_{0},{\rho }_{f})$ and the scheme is considered reliable when ${{\mathcal{F}}}_{{\rm{d}}}$ approaches 1. During the whole process, a reference state is utilized for two aspects: (i) measure the encoding fidelity between the trash state and the reference state, denoted as ${{\mathcal{F}}}_{{\rm{e}}}=F({\rho }_{{\rm{trash}}},{\rho }_{{\rm{ref}}})$; (ii) reproduce the initial states with the combination of the latent state and the reference state. When the unitary operation U_e perfectly disentangles ρ₀ into two parts as ${U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger }={\rho }_{{\rm{latent}}}\otimes {\rho }_{{\rm{ref}}}$, the overlap between the trash state and the reference state can achieve unity^15,26 and the decoding fidelity ${{\mathcal{F}}}_{{\rm{d}}}$ can also achieve unity. In this work, the unitary transformation U_e is realized through Hamitonian-based control (see Section Methods for detailed information).

Fig. 1: Quantum circuit representation of a QAE using a mixed reference state.

The network includes two parts: (i) The encoder U_e reorganizes the (n_A + n_B)-qubit initial state ρ₀ into two parts, i.e., n_B-qubit state ρ_latent contains the useful information (blue lines) that represent the latent qubits and n_A-qubit state ρ_trash contains the superfluous information (green lines) that represent the trash qubits. Here, the trash state is obtained by tracing out the latent space of n_B qubits. The latent state is obtained by tracing out the trash space of n_A qubits. (ii) The decoder U_d recovers the state ρ_f by using the combination of the latent state and ancillary fresh qubits (initialized to the reference state). The goal of QAEs is to maximize the overlap between the recovered state ρ_f and the original state ρ₀. Note that, we use the common practice of taking the decoding as the inverse of the encoding of ${U}_{{\rm{d}}}={U}_{{\rm{e}}}^{\dagger }$^17,26.

When taking a pure state as reference states ${\rho }_{{\rm{ref}}}=\left\vert {\psi }_{{\rm{ref}}}\right\rangle \left\langle {\psi }_{{\rm{ref}}}\right\vert$ for compressing the initial state ρ₀. There exists an upper bound (i.e., QAE-pure bound, abbreviated as ${Q}_{{\rm{pure}}}^{{\rm{bound}}}$) for the encoding fidelity between ρ_trash and ρ_ref. From the previous work²⁶, we have

$${Q}_{{\rm{pure}}}^{{\rm{bound}}}({\rho }_{0})=\mathop{\max }\limits_{{U}_{{\rm{e}}}}F({{\rm{Tr}}}_{A}({U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger }),\vert {\psi }_{{\rm{ref}}}\rangle )=\mathop{\sum }\limits_{k=1}^{{d}_{B}}{\lambda }_{k}({\rho }_{0}),$$

(1)

where λ_k(ρ) is the k-th (in descending order) eigenvalue of ρ. This bound is determined by eigenvalues of the initial state ρ₀, with no dependency on the pure reference state $\left\vert {\psi }_{{\rm{ref}}}\right\rangle$²⁶. Hence, in traditional QAEs, a common practice is to utilize a fixed pure state as the reference state, e.g., $\left\vert 0\right\rangle \left\langle 0\right\vert$. According to Eq. (1), if ρ₀ has a rank larger than d_B, the optimal encoder U_e can only decouple the largest d_B eigenvalues of ρ₀, whose sum is less than one^26,27. As such, a high-rank state in this work means the rank of its density matrix is larger than d_B.

When compressing ρ₀ with high entropy, the trash state ρ_trash tends to have high entropy and consequentially have low overlap with a pure reference state (e.g., setting ${\rho }_{{\rm{ref}}}=\left\vert 0\right\rangle \left\langle 0\right\vert$). In the decoding stage, the low entropy of a pure state may also limit the entropy of the recovered state (see ρ_f in Fig. 1). To overcome the entropy inconsistency between the initial state ρ₀ and the recovered state ρ_f²⁷, we remove the limitation of a pure reference state and allow the reference state ρ_ref to be mixed. The limitation of the conventional QAEs also motivates us to adopt different mixed states rather than a fixed state for compressing different initial states. In this way, the entropy in the reference state can assist the decoder in achieving a high fidelity for the recovered state. Here, the introduction of entropy offers an intuitive strategy for setting mixed reference states. To ensure that the recovered state ρ_f has high fidelity with ρ₀, additional efforts are required to optimize U_e. Instead of searching U_e and ρ_ref together (a full encoding and decoding procedure is required), we accomplish the task of QAEs with mixed reference states within two stages.

Cost function

In conventional QAEs, the reference state is fixed as a pure state, and ${{\mathcal{F}}}_{{\rm{e}}}$ is utilized as the cost function to train QAEs^15,17,18,26. However, ${{\mathcal{F}}}_{{\rm{e}}}$ is different from ${{\mathcal{F}}}_{{\rm{d}}}$ which characterizes the effectiveness of QAEs in compressing and recovering quantum data. When allowing the reference state to be a mixed state, ${{\mathcal{F}}}_{{\rm{e}}}$ can achieve one by setting ρ_ref = ρ_trash, whereas ${{\mathcal{F}}}_{{\rm{d}}}$ is usually less than one and can reach one only when perfect disentanglement is realized¹⁵. Given that quantum mutual information (QMI) measures the correlation between subsystems of quantum states^30,31, it quantifies the amount of noise that is required to erase (destroy) the correlations completely. To facilitate QAEs using mixed reference states, we aim to disentangle ${U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger }$, which is achieved by minimizing the QMI, i.e., ${\mathcal{I}}({U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger })$ or equivalently maximizing

$${J}_{{\rm{qmi}}}=-{\mathcal{I}}({U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger }),$$

(2)

where ${\mathcal{I}}(\rho )=S({{\rm{Tr}}}_{A}(\rho ))+S({{\rm{Tr}}}_{B}(\rho ))-S(\rho )$ denotes the QMI of ρ and $S(\rho )=-{\rm{Tr}}(\rho \ln (\rho ))$ denotes the von Neumann entropy of ρ. Generally ${\mathcal{I}}(\rho )\ge 0$, and ${\mathcal{I}}(\rho )=0$ when $\rho ={{\rm{Tr}}}_{A}(\rho )\otimes {{\rm{Tr}}}_{B}(\rho )$.

According to existing research²⁶, when training QAEs using the overlap between the trash state and a pure reference state (e.g., taking the reference state as ${\rho }_{{\rm{ref}}}=\left\vert 0\right\rangle \left\langle 0\right\vert$), ${J}_{{\rm{pure}}}=F({{\rm{Tr}}}_{B}({U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger }),\left\vert 0\right\rangle \left\langle 0\right\vert )$ as the cost function, the compression rate of QAEs can approach the theoretical QAE-pure bound. Under that scheme, a high compression rate can be realized for low-rank states²⁶. Although this cost function fails to disentangle a high-rank state with satisfactory performance, the optimization of ${J}_{{\rm{pure}}}$ leads to a direction of reorganizing the information of initial states into two parts. To combine the cases of low-rank states and high-rank states, we propose a cost function,

$$\Phi ({\rm{w}})={\rm{w}}{J}_{{\rm{pure}}}+(1-{\rm{w}}){J}_{{\rm{qmi}}},$$

(3)

where w ∈ [0, 1] controls the ratio of different factors. This protocol is termed QAE-qmi in this paper. Considering the potential of evolutionary strategy (ES) in conventional QAEs²⁶, we employ it to optimize the parameters of U_e.

Reference states

Recall the nature of QAEs lies in disentangling¹⁵. The encoding fidelity that measures the overlap between the trash states and the reference states can reach one (i.e., ${{\mathcal{F}}}_{{\rm{e}}}=1$) by setting ρ_ref = ρ_trash. Although ${{\mathcal{F}}}_{{\rm{d}}}\le {{\mathcal{F}}}_{{\rm{e}}}$, in the general case, ${{\mathcal{F}}}_{{\rm{d}}}$ can approach ${{\mathcal{F}}}_{{\rm{e}}}$ and they both achieve one when perfect disentangling is realized²⁶. When there is no limitation for the reference state, it is helpful to investigate the performance of QAE-qmi with ρ_ref = ρ_trash.

In practical applications, it may be useful to utilize reference states with some physical constraints. According to our previous study, a pure reference state, e.g., $\left\vert 0\right\rangle \left\langle 0\right\vert$ is effective in compressing low-rank states, with the compression rate approaching the QAE-pure bound²⁶, whose value is usually high for low-rank states. For high-rank states with high entropy, the introduction of mixed reference states helps increase the entropy of the recovered states²⁷. While the maximally mixed states I/d_A has the highest entropy among all states in ${{\mathcal{H}}}_{A}$ and is effective for increasing the entropy in the decoding stage. To achieve a good QAE for different quantum states, we take the following reference state

$${\rho }_{{\rm{mix}}}={p}_{r}\left\vert 0\right\rangle \left\langle 0\right\vert +(1-{p}_{r})I/{d}_{A},$$

(4)

where p_r represents the ratio of the pure state and (1 − p_r) represents the ratio of the mixed state in the reference state. I denotes the d_A-dimensional identity matrix. Different initial states with different inner structures may have different optimal reference states following the form of Eq. (4). When compressing initial states with high entropy, it is preferable to use low p_r that generates high entropy for ρ_mix. As such, it is desirable to specify an optimal p_r for different quantum states. Although mixed reference states cost additional memories, our method aims to achieve high fidelity between the recovered state and the initial state. This is particularly important for initial states with low QAE-pure bound. By constraining the mixed reference state in the form of Eq. (4), one can transmit the compressed latent representation and p_r to facilitate the subsequent recovery.

Now, we focus on determining a good p_r to recover quantum states with high decoding fidelity. Intuitively, quantum states with different inner structures (entropy) require different optimal p_r to achieve optimal decoding fidelity. Before deciding the optimal p_r for recovering the state, we first propose a grid-search strategy for setting p_r (marked as grid). Under a fixed cost function (e.g., $\Phi =0.5({J}_{{\rm{pure}}}+{J}_{{\rm{qmi}}})$), we define a candidate set (e.g., {0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0}) for p_r. Then, following the optimized U_e during the encoding process, the decoding process is performed with different p_r selected from the candidate pool. Eventually, the optimal one is determined regarding its decoding fidelity, and this value is defined as ${p}_{r}^{{\rm{grid}}}$. In the following, we also introduce another two strategies: (i) bound: to leverage the QAE-pure bound when prior knowledge of the initial state is available; (ii) guess: to infer from the training process of QAEs. The guess strategy acts as a practical solution that can be implemented in different cases.

In summary, the optimization of QAEs using a mixed reference state is accomplished within two stages. Firstly, the training of QAEs using $\Phi ({\rm{w}})={\rm{w}}{J}_{{\rm{pure}}}+(1-{\rm{w}}){J}_{{\rm{qmi}}}$ is implemented in the encoding stage, while the mixed reference state is introduced in the decoding stage. After the optimization of U_e is finished by maximizing Φ, we determine a reference state for recovery to maximize the overlap between the initial state and the recovered state.

Numerical results

Quantum state settings

For the compression task, we consider three classes of quantum states. Firstly, we consider thermal states as

$$\rho =\frac{{e}^{-\beta H}}{{\rm{Tr}}({e}^{-\beta H})},$$

(5)

where β is the inverse temperature and H denotes the Hamitonian. Let ${\sigma }_{z}^{j}$(${\sigma }_{x}^{j}$) denote the composite value of σ_z(σ_x) on the j-th qubit with identity matrices for the other qubits. For example, we investigate thermal states with the Hamiltonian of the one-dimensional transverse-field

$$H=-\left(\sum _{j}{\sigma }_{z}^{j}{\sigma }_{z}^{j+1}+\sum _{j}{\sigma }_{x}^{j}\right),$$

(6)

with couplings set to 1. Then, we investigate Werner states, which are bipartite and are invariant under any unitary operator in the form of U ⊗ U³². Let $\left\vert k\right\rangle$ and $\left\vert j\right\rangle$ be the computational basis for two bipartite subspaces, respectively. A Werner state can be parameterized by

$$\rho (\alpha )=\frac{1}{{d}^{2}-d\alpha }\left(I-\alpha \sum _{kj}\left\vert kj\right\rangle \left\langle jk\right\vert \right),$$

(7)

where I denotes the d²-dimensional identity matrix and α varies between -1 and 1. Additionally, we also consider the initial states that have a similar form to ρ_mix as

$$\rho ({p}_{0})={p}_{0}\vert \psi \rangle \langle \psi \vert +(1-{p}_{0})I/d,$$

(8)

where I denotes the d-dimensional identity matrix and the value of p₀ controls the purity of the initial states. In this work, we randomly generate a pure state $\vert \psi \rangle$ and utilize it for different values of p₀. By computation, we find that states with high p₀ have a high QAE-pure bound. In this work, we consider compressing 2-qubit states into 1-qubit states and 4-qubit states into 2-qubit states. The density matrices of 2-qubit thermal states and Werner states are presented in Supplementary Discussion 1.

Investigation of different w

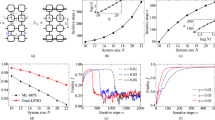
Firstly, we investigate the performance of ρ_ref = ρ_trash. In particular, we consider three different cases: (i) w = 1 considers the fidelity between the trash state and a fixed pure state; (ii) w = 0 considers QMI of the encoding state ${U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger }$; (iii) w = 0.5 considers both factors and acts as a more general function. Comparsion results for 2/4-qubit thermal states and 2/4-qubit Werner states are provided in Figs. 2 and 3, respectively. These results demonstrate that Φ = J_qmi and $\Phi =0.5({J}_{{\rm{pure}}}+{J}_{{\rm{qmi}}})$ achieve a similar decoding fidelity, higher than that of $\Phi ={J}_{{\rm{pure}}}$. The gaps between w = 0.5 and w = 1 suggest that introducing quantum mutual information to the cost function Φ(w) helps enhance the decoding fidelity for 4-qubit states. These results suggest that the introduction of QMI is effective in compressing and recovering quantum states, especially for states with low QAE-pure bounds (i.e., thermal states with β approaching 0 and Werner states with ∣α∣ approaching 0). The training curves of QAE-qmi under different w are summarized in Supplementary Discussion 2.

Fig. 2: Comparison of QAE-qmi under different w using ρ_ref = ρ_trash.

a for 2-qubit states, b for 4-qubit states. β controls the entropy of the thermal states, i.e., an increase of β leads to a decrease of entropy in quantum states. ${{\mathcal{F}}}_{{\rm{d}}}$ represents the decoding fidelity between the initial state and the recovered state. w denotes the ratio of ${J}_{{\rm{pure}}}$ in the cost function Φ(w). The blue dashed line represents the theoretical upper bound of compression rate when only considering pure reference states²⁶.

Fig. 3: Comparison of QAE-qmi under different w for Werner states under ρ_ref = ρ_trash.

a for 2-qubit states, b for 4-qubit states. w denotes the ratio of ${J}_{{\rm{pure}}}$ in the cost function Φ(w). ${{\mathcal{F}}}_{{\rm{d}}}$ denotes the fidelity between the initial state and the recovered state. The blue dashed line represents the theoretical upper bound of compression rate when only considering pure reference states²⁶.

Then we turn to the case of setting reference states as Eq. (4). Although the disentanglement evaluation of J_qmi naturally follows the nature of QAEs, this function fails to achieve a perfect value of 1 for non-separable initial states. When considering ρ_ref = ρ_mix for low-rank states, the optimization of J_qmi tends to bring the trash state far away from a pure state, in conflict with the intuition that pure reference states are enough for low-rank states. To combine the two scenarios together, w = 0.5 is a good solution.

We implement an example of low-rank states (with high QAE-pure bound) using ρ_ref = ρ_mix under different values of p_r, with results in Fig. 4. While, the best solution under w = 0 corresponds to a large p_r (indicating high entropy in ρ_mix) and the best solution under w = 0.5 corresponds to a small p_r (indicating low entropy in ρ_mix). The latter case is in line with our conjecture that compressing states with low entropy and high QAE-pure bound requires a reference state with high purity. As such, we consider $\Phi =0.5({J}_{{\rm{pure}}}+{J}_{{\rm{qmi}}})$ to be useful for both ρ_ref = ρ_trash and ρ_ref = ρ_mix. Hereafter, without specific notation. QAE-qmi refers to the case of $\Phi =0.5({J}_{{\rm{pure}}}+{J}_{{\rm{qmi}}})$.

Fig. 4: An example of QAE-qmi with ρ_ref = ρ_mix under different p_r for 2-qubit thermal states.

a for w = 0, b for w = 0.5. p_r represents the ratio of the pure state in the reference state ρ_mix and (1 − p_r) represents the ratio of the mixed state in the reference state ρ_mix. ${{\mathcal{F}}}_{{\rm{d}}}$ represents the decoding fidelity between the initial and recovered states. The red dashed line represents the theoretical upper bound of compression rate when only considering pure reference states²⁶. In this figure, some selected values of p_r from the candidate pool are used to clearly demonstrate the trends of different values.

The cost function in Eq. (3) can be applied to compress initial states with different purities. According to Eq. (1), states with high purity tend to have eigenvalues close to 0 or 1, and have a high QAE-pure bound²⁶, suggesting that the conventional QAE approach (with only ${J}_{{\rm{pure}}}$) still works. In the unified approach, it is preferable to adopt a large w for compressing initial states with high purities (e.g., thermal states with large β or Werner states with ∣α∣ approaching 1). Furthermore, when compressing initial states with high purity, for example, ρ(p₀) with high p₀, the existence of QMI in the cost function with ratio w = 0.5 brings in a negative effect, which can be overcome by reducing the ratio of J_qmi e.g., w = 0.99. This originates from the two stages of our protocol: firstly optimize U_e via Φ(w) and then determine a reference state for recovering. A large ratio of J_qmi tends to conflict with the mechanism of setting reference states as ${p}_{r}\left\vert 0\right\rangle \left\langle 0\right\vert +(1-{p}_{r})I/{d}_{A}$. This conflict increases with the purity of states, as initial states with high purities favor a high ratio of ${J}_{{\rm{pure}}}$ and a high value of p_r. Nevertheless, we can avoid this by adjusting w. Please refer to Supplementary Discussion 4 for detailed information.

Investigation of different p _r

The introduction of mixed states aims to bring in appropriate entropy for recovering different states. Intuitively, high-rank states with high entropy and low QAE-pure bounds require more entropy for recovery, i.e., a low p_r. Recall that each state has its inner structure, and can be characterized by a QAE-pure bound²⁶. Initially, we tested ${Q}_{{\rm{pure}}}^{{\rm{bound}}}$ but found that its value does not align well with ${p}_{r}^{{\rm{grid}}}$, and their performance regarding ${\mathcal{F}}d$ exhibits a significant gap. Subsequently, we find the square of ${Q}_{{\rm{pure}}}^{{\rm{bound}}}$ aligns more closely with ${p}_{r}^{{\rm{grid}}}$, and their decoding fidelities are comparably close. Hence, we propose a second strategy (marked as bound) for setting p_r by leveraging the QAE-pure bound of the initial state ρ₀, and we have ${p}_{r}^{{\rm{bound}}}={({Q}_{{\rm{pure}}}^{{\rm{bound}}}({\rho }_{0}))}^{2}$.

To validate our conjecture that the optimal ${p}_{r}^{{\rm{grid}}}$ tends to approach the square of the QAE-pure bound, we compare the two strategies, with their actual values of p_r and the associated decoding fidelity ${{\mathcal{F}}}_{{\rm{d}}}$ in one figure. From the results in Figs. 5, 6, it is clear that ${p}_{r}^{{\rm{grid}}}$ has the same trend as ${p}_{r}^{{\rm{bound}}}$, and their decoding fidelities are close to each other under different parameters. For states in the form of ρ(p₀), we observe that the best p_r found using the grid strategy (i.e., ${p}_{r}^{{\rm{grid}}}$) tends to be approaching p₀. The comparison of the two strategies (grid vs bound) regrading p_r and ${{\mathcal{F}}}_{{\rm{d}}}$ is summarized in Fig. 7. The two curves are close to each other with increasing p₀. The decoding fidelities for the two strategies of setting p_r achieve similar values.

Fig. 5: Comparison of two strategies of setting p_r for compressing and recovering thermal states.

a for 2-qubit states, b for 4-qubit states. p_r represents the ratio of the pure state and (1 − p_r) represents the ratio of the mixed state in the reference state. ${{\mathcal{F}}}_{{\rm{d}}}$ represents the fidelity between the initial state and the recovered state. The solid blue line (dashed blue line) corresponds to the actual value of p_r. The solid red line (dashed red line) represents the value of ${{\mathcal{F}}}_{{\rm{d}}}$ through the bound information (grid searching from a set of values).

Fig. 6: Comparison results of two strategies of setting p_r when compressing and recovering Werner states.

a for 2-qubit states, b for 4-qubit states. ${{\mathcal{F}}}_{{\rm{d}}}$ represents the fidelity between the initial and recovered states. p_r represents the ratio of the pure state and (1 − p_r) represents the ratio of the mixed state in the reference state. The solid blue line (dashed blue line) corresponds to the actual value of p_r. The solid red line (dashed red line) represents the value of ${{\mathcal{F}}}_{{\rm{d}}}$ through the bound information (grid searching from a set of values).

Fig. 7: Comparison of two strategies of setting p_r for compressing maximally mixed states blended with pure states.

a for 2-qubit states, b for 4-qubit states. p_r represents the ratio of the pure state and (1 − p_r) represents the ratio of the mixed state in the reference state. ${{\mathcal{F}}}_{{\rm{d}}}$ represents the fidelity between the initial state and the recovered state. The solid blue line (dashed blue line) corresponds to the actual value of p_r. The solid red line (dashed red line) represents the value of ${{\mathcal{F}}}_{{\rm{d}}}$ through the bound information (grid searching from a set of values).

Based on the observation that taking p_r as the square of QAE-pure bound achieves good performance, ${J}_{{\rm{pure}}}$ among the unified cost function is approaching the QAE-pure bound during the training process²⁶. We propose a third strategy (marked as guess) for adaptively configuring the reference states as ${p}_{r}^{{\rm{guess}}}={J}_{{\rm{pure}}}^{2}$. The comparison results of different strategies of setting p_r are summarized in Supplementary Discussion 3, demonstrating that the manual and automatic ways of setting p_r are effective in compressing and recovering different quantum states. By now, we have three strategies for setting p_r, and their comparsion for compressing thermal states and Werner states is summarized in Supplementary Discussion 3. Under the strategy of ${p}_{r}={p}_{r}^{{\rm{guess}}}$, we further compare the performance of QAE-qmi under different w, with results shown in Supplementary Discussion 4. The decline of ${{\mathcal{F}}}_{{\rm{d}}}$ when p₀ approaches one reveals that $\Phi =0.5({J}_{{\rm{pure}}}+{J}_{{\rm{qmi}}})$ hinders the compression of quantum states with high p₀.

Experimental results

Generally, it is assumed that quantum circuits deal with pure states. We need to find a solution to generate mixed states, which is essential in preparing initial states and reference states for encoding and decoding, respectively. We use the technique of purification²⁹ to associate a mixed state with a pure state in a large space. Given a state ρ_K of a quantum system K, it is possible to introduce another system R, and define a pure state ${\vert \psi \rangle }_{KR}$ for the joint system KR such that ${\rho }_{K}={{\rm{Tr}}}_{R}(\vert \psi \rangle {\langle \psi \vert }_{KR})$. The pure state ${\vert \psi \rangle }_{KR}$ reduces to ρ_K when we look at the system K alone. This mathematical procedure can be done for any state. Please refer to Supplementary Discussion 5 for detailed information about the construction of ${\left\vert \psi \right\rangle }_{KR}$ for arbitrary ρ_K.

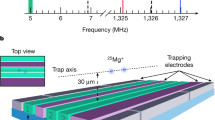
The quantum circuit for compressing 2-qubit states into 1-qubit states is depicted in Fig. 8, where four qubits q₀q₁q₂q₃ are utilized to generate mixed states on q₂q₃, on which the encoding gate and the decoding gate are performed. The circuit can be divided into five parts: (a) prepare the initial state, (b) perform the encoding operation, (c) prepare the reference state, (d) perform the decoding operation, (e) perform quantum measurements to obtain the density matrix of the recovered state. A set of complete measurements is required to specify the density matrix of a quantum state⁷. In Fig. 8, only a special case of local measurement of σ_z ⊗ σ_z on q₂q₃ is performed. Adding some gates (such as the Hadamard gate and the S^† gate) before the measurement part (i.e., between (d) and (e)) helps realize other measurements. Hence, the quantum circuits are repeated several times until a complete measurement is accomplished. Feeding the measured data to the built-in function for quantum state tomography in qiskit³³, the density matrix of the recovered state is finally obtained.

Fig. 8: Quantum circuits for compressing 2-qubit states into 1-qubit states and recovering to 2-qubit states using mixed reference states.

Firstly, four qubits are required to generate a 4-qubit pure state in a, whose partial trace on q₀q₁ leads to a mixed state ρ₀ on q₂q₃. Hereafter, the encoding operation in b and the decoding operation are performed on q₂q₃, where q₂ contains the trash state ρ_trash and q₃ contains the latent state ρ_latent. Then, q₁q₂ are reused to generate a pure state whose partial trace on q₁ leads to a reference state ρ_ref on q₂ in c. Then, the decoding operation in d is performed on the combination of q₂ with ρ_ref and q₃ with ρ_latent. In e, measurements are performed on q₂q₃ for quantum state tomography to obtain the density matrix of the recovered state.

In this work, we do not perform the optimization loops on quantum computers. Instead, we take the encoding transformation U_e and the reference state in the form of Eq. (4) that are learned numerically on classical computers, and then deploy them on IBM quantum simulators and quantum computers, respectively. Note that, each green block in Fig. 8 represents quantum circuits composed of a sequence of quantum gates to achieve unitary operations. Please refer to Supplementary Discussion 5 for the transpiled circuits for the green blocks.

We implement the procedure of compressing and recovering 2-qubit states on ibmq_qasm_simulator and ibmq_quito, with 8192 shots. Each compression task is run 6 times on ibmq_quito. The comparison results are summarized in Fig. 9. The results of the simulators are in agreement with the theoretical results obtained from classical computers. However, gaps exist between the results of ibmq_qasm_simulator and ibmq_quito. In particular, the gap becomes apparent for thermal states with increasing β and Werner states with α approaching -1 or 1. The underlying reason may be that compressing states close to maximally mixed states with a low QAE-pure bound, presents a large space for improvement through the introduction of mixed reference states. By contrast, initial states closer to pure states can achieve a high compression rate by utilizing pure reference states, while pure states can be affected by various noise sources, e.g., CNOT noise. Then, we visualize the density matrices of the initial states and the recovered states obtained from ibmq_quito for Werner states in Supplementary Discussion 5.

Fig. 9: Results for QAEs on ibmq_qasm_simulator and ibmq_quito for encoding and decoding 2-qubit states.

a for thermal states, b for Werner states. ${{\mathcal{F}}}_{{\rm{d}}}$ represents the fidelity between the initial state and the recovered state. The blue dashed line represents the upper bound of compression rate when only considering pure reference states²⁶. The orange line represents the theoretical results of simulating QAEs on classical computers. The green line represents the numerical results obtained from the IBM simulator ibmq_qasm_simulator. The red line with error bars represents the average results of 6 times together with standard deviation when quantum circuits are sampled with 8192 shots on IBM Quantum computer ibmq_quito.

Discussion

In this paper, we have investigated the performance of QAEs with mixed reference states. One may consider employing a fixed mixed state as the reference state as in conventional QAEs. However, it is challenging to decide on a fixed reference state for different initial states, and the proof that arbitrary mixed reference states yield similar bounds remains elusive. The way of merging all the operations into the encoder fails to reveal features of QAEs with mixed reference states. By comparsion, the adaptive configuration of mixed reference states provides a clear clue about improving fidelity via appropriate entropy compensations. Then, we summarize the characteristics of our protocol as follows.

(i) The proposed function of $\Phi ({\rm{w}})={\rm{w}}{J}_{{\rm{pure}}}+(1-{\rm{w}}){J}_{{\rm{qmi}}}$ combines the approximate QAE-pure bound function that reflects the inner structure of the initial states and the quantum mutual information that measures the correlation between subsystems. It is a general function that can be applied to both low-rank states and high-rank states. As demonstrated by the numerical results, training QAEs using Φ(w) achieves high decoding fidelity under different reference setting rules including ρ_ref = ρ_trash and ρ_ref = ρ_mix. In addition, it has been found that for initial states with high QAE-pure bounds (e.g., large p₀ in Eq. (8)), it is preferable to increase w in $\Phi ({\rm{w}})={\rm{w}}{J}_{{\rm{pure}}}+(1-{\rm{w}}){J}_{{\rm{qmi}}}$, giving more importance to the approximate QAE-pure bound. This is consistent with the fact that pure reference states together with ${J}_{{\rm{pure}}}$ can realize a good compression rate for low-rank states²⁶. However, it is crucial to recognize the inherent limitation of employing QMI, whose value depends on the von Neumann entropy that is not an observable. Consequently, this limitation restricts its applications in experimental settings. In our future work, we will explore an approximate function that can be more readily implemented in experimental contexts.

(ii) The numerical results demonstrate that setting the reference state in the form of Eq. (4) helps enhance the decoding fidelity for high-rank states. Due to the special form of the reference states, it is intuitive that different initial states may rely on different optimal purity ratios p_r that help maintain the entropy consistency between the initial states and the recovered states. As demonstrated by the numerical results in Figs. 5, 6, and 7, the optimal p_r using via the grid strategy is close to the square of QAE-pure bound for thermal states, Werner states and maximally mixed states blended with pure states. Such findings provide hints for adaptively setting reference states for different quantum states.

(iii) When limiting the reference states to the form of Eq. (4), we can take advantage of the prior information of the initial states to determine a mixed reference state that achieves a high ${{\mathcal{F}}}_{{\rm{d}}}$. For example, ${({Q}_{{\rm{pure}}}^{{\rm{bound}}}({\rho }_{0}))}^{2}$ can be determined before the training process of QAEs. If no prior knowledge is available, we can also approximate the QAE-pure bound by inferring from the training process and taking $F{({\rho }_{{\rm{trash}}},\left\vert 0\right\rangle )}^{2}$. From this perspective, our protocol may have wide applications in practical quantum applications. For example, the compressed latent representations can be utilized to effectively denoise errors in the original states¹⁹, or act as intermediate states to facilitate high-dimensional subspace teleportation²⁴.

Our work illustrates the effectiveness of QAEs using mixed reference states under different constraints and thus provides implications for practical applications. More work remains to be investigated in the future. For example, other forms of mixed reference states are worthy of further exploration. Imperfections in quantum system models are not considered in this work. Our future work will also include general quantum channels to deal with decoherence for mixed quantum states.

Methods

Quantum control model

Here, we use the density matrix ρ(t) (which is a Hermitian, positive semidefinite matrix satisfying ${\rm{Tr}}(\rho (t))=1$ to describe the state of a closed quantum system. The evolution equation for ρ(t) can be described by the quantum Liouville equation³⁴

$${\rm{i}}\dot{\rho }(t)=\rho (t)H(t)-H(t)\rho (t).$$

(9)

When we use control fields ${\{{u}_{j}(t)\}}_{j = 1}^{M}$ to manipulate the system, the system Hamiltonian in Eq. (9) can be divided into two parts, i.e., $H(t)={H}_{0}+{H}_{c}(t)={H}_{0}+\mathop{\sum }\nolimits_{j = 1}^{M}{u}_{j}(t){H}_{j},$ where H₀ is the time-independent free Hamiltonian of the system, H_c(t) is the control Hamiltonian representing the interaction of the system with the control fields. For such a control system, its solution is given as ρ(t) = U(t)ρ₀U^†(t) with U(0) = I, where the propagator U(t) is formulated as follows:

$$\frac{d}{dt}U(t)=-{\rm{i}}\left({H}_{0}+\mathop{\sum }\limits_{j=1}^{M}{u}_{j}(t){H}_{j}\right)U(t).$$

(10)

For the compression task, we consider spin chain models with

$${H}_{0}=\mathop{\sum }\limits_{i=0}^{{n}_{A}+{n}_{B}-1}{\sigma }_{i}^{x}{\sigma }_{i+1}^{x}+{\sigma }_{i}^{y}{\sigma }_{i+1}^{y}+{\sigma }_{i}^{z}{\sigma }_{i+1}^{z}.$$

Chains with Heisenberg coupling are known to be controllable given at least two noncommuting controls acting on the first or the last spin in the chain^35,36, we exert control fields on the first two qubits towards X and Y directions³⁷, with the control Hamiltonian as

$${H}_{c}=\sum _{k=0,1}{u}_{k}^{x}{\sigma }_{k}^{x}+{u}_{k}^{y}{\sigma }_{k}^{y}.$$

As such, there are four control fields to be designed. We use piece-wise control fields, which means that the total control time T is equally divided into different periods, with each having dt = T/N duration times. In this work, the total control time T = 20 is equally divided into 100 pieces. The bound of control fields is set as [− 10, 10]. Then, the encoding map for QAEs can be obtained by U_e = U(T) following Eq. (10).

Training QAEs using learning algorithms

In this work, the training of QAEs is reduced to searching for an optimal U_e that maximizes $\Phi ({\rm{w}})={\rm{w}}{J}_{{\rm{pure}}}+(1-{\rm{w}}){J}_{{\rm{qmi}}},{\rm{w}}\in [0,1]$. After the training is completed, injecting a mixed state ρ_ref to the decoder helps maintain the entropy consistency between the initial state ρ₀ and the recovered state ${\rho }_{f}={U}_{{\rm{e}}}^{\dagger }({\rho }_{{\rm{latent}}}\otimes {\rho }_{{\rm{ref}}}){U}_{{\rm{e}}}$. Finally, the overlap between the recovered states and the original states is measured to evaluate the efficiency of QAEs. Denote the parameters for the encoder as a vector θ. The procedure of QAE-qmi using mixed reference states is as follows:

• 1. Randomly initialize θ, where θ represents the control fields for the systems

• 2. Apply U_e(θ) to the initial states ρ₀

• 3. Measure ρ_trash and ρ_latent and compute the cost function $\Phi ({\rm{w}})={\rm{w}}F({\rho }_{{\rm{trash}}},\left\vert 0\right\rangle \left\langle 0\right\vert )-(1-{\rm{w}}){\mathcal{I}}({U}_{{\rm{e}}}{\rho }_{0}{U}_{{\rm{e}}}^{\dagger })$

• 4. Perform the optimization of Φ(w) using a learning algorithm and obtain a better control parameter θ

• 5. Repeat steps 2-4 until convergence

• 6. Report the classical information θ and store the latent state ρ_latent

• 7. Determine a suitable reference state ρ_ref using different strategies (e.g., ρ_ref = ρ_trash or ρ_ref = ρ_mix) and prepare the reference state

• 8. Perform ${U}_{{\rm{e}}}^{\dagger }({\boldsymbol{\theta }})$ on the combined state ρ_latent ⊗ ρ_ref and obtain the recovered state as ρ_f

The key is to optimize the cost function of Φ using learning algorithms. Evolutionary strategy (ES) methods exhibit an advantage in exploring unknown environments in games³⁸ and have been applied in optimizing quantum control issues³⁹. The comparison results in our previous work suggest that ES has the potential to optimize QAEs towards the theoretical upper bounds with high efficiency²⁶. In this work, we utilize ES to optimize the cost function Φ(w).

ES is a black-box optimization method that utilizes heuristic search procedures inspired by natural evolution. At every iteration ("generation”), a population of parameter vectors ("genotypes”) is perturbed ("mutated”) and their objective function value ("fitness”) is evaluated. The highest-scoring parameter vectors are then recombined to form the population for the next generation, and this procedure is iterated until convergence³⁸. The detailed description for the ES method is provided in Supplementary Method 1.

It is worth noting that, the initialization process in Step 1 can be formulated as ${\boldsymbol{\theta }}={{\bf u}}_{\min }+{\rm{Rand}}[0,1]({{\bf u}}_{\max }-{{\bf u}}_{\min })$, where Rand[0, 1] is a function to generate random numbers uniformly distributed between 0 and 1 to meet the physical restriction of control fields. In addition, boundary checks and resetting values are required for every step that involves new parameters to guarantee that newly generated parameters lie in the constrained field. For the parameter setting of the ES method, we set the population size as NP = 40 for 2-qubit states and NP = 50 for 4-qubit states. The perturbation factor is set as δ = 0.01. The learning rate is set as χ₁ = 0.5. The momentum factor is set as χ₂ = 0.9. The perturbation factor is decayed as δ ← 0.98δ every 100 training iterations.