Introduction

The effectiveness of information security protocols, whether quantum or classical, relies on specific assumptions. Classical protocols typically make considerations about the computational capabilities of adversaries. On the contrary, the security of quantum protocols is based solely on the validity of quantum theory. However, to leverage this validity in practice, certain assumptions about the implementation are necessary, making the protocol device-dependent. Efforts towards minimizing assumptions for enhanced security evaluation give rise to the device-independent approach in quantum information. A protocol is deemed device-independent when its security remains guaranteed without assumptions about the internal workings of the devices used in its implementation. In these schemes, a physical system prepared in an entangled state is shared and measured by different users, who choose their measurements randomly. Entanglement is necessary to produce correlations that are not reproducible by any local hidden variable theory and are hence referred to as nonlocal. The outcomes serve the dual purpose of manifesting nonlocality and providing a useful classical resource, such as a key or random bit. In principle, the security of this resource is guaranteed by nonlocality even if the devices implementing the protocols are entirely untrusted or controlled by adversaries.

A major drawback of these schemes is the low rate of resource extraction. This is mainly due to the challenges of creating and preserving entanglement, which is degraded by the coupling of the system with the environment. Instead of relying on faster entanglement generation, which may be feasible in the future, we study how to optimize the extraction of useful resources from each single entangled system. A way of doing so proposed in the scientific literature uses weak measurements to realize sequential protocols, in which each quantum system is measured more times1,2,3,4,5,6,7,8,9. Often, they are direct extensions of schemes that use projective measurements, adding further intermediate measurements, and improving the performance in terms of resources extracted from the same quantum system. With the strategy proposed in ref. 4, it is even possible, in principle, to produce an unlimited amount of device-independent randomness for each generated bipartite entangled state. However, the robustness to noise of this protocol is limited and therefore requires great accuracy of realization9.

At the same time, the appeal of sequential protocols lies in the correlations they can create, for instance, for the possibility of sharing nonlocality among multiple users10,11,12. A geometric approach is useful for characterizing quantum correlations. However, although the geometry of quantum correlations has been the subject of several studies13,14,15, its extension to the sequential setting is little known. Most previous analyses focus only on the correlations between each sequential user and the remote one, finding a monogamy trade-off: stronger correlations for one user imply weaker ones for the others1,4,7,8. A detailed investigation of the trade-off, its geometry, and its implications could help formulate better quantum protocols that could overcome this compromise16,17. Moreover, the literature lacks a general mathematical framework that is useful for characterizing sequential quantum correlations.

In this paper, we characterize sequential quantum correlations with a geometric approach. First, we provide a general mathematical framework useful for describing any sequential quantum scenario. Then, we extend the common two-user, two-measurement, two-outcome scenario with a sequential user on one side and study the geometry of the obtainable correlations, identifying a Tsirelson-like quantum boundary that also serves as monogamy trade-off. This trade-off provides further insights about the sharing of nonlocality between sequential users.

Furthermore, we show that the correlations on the boundary can be used to certify the maximum amount of local randomness obtainable for our scenario, that is, two bits. This is possible regardless of how nonlocality, quantified as violation of a given Bell inequality, is divided between the sequential pairs, meaning that the trade-off for nonlocality is not a trade-off for randomness. Contrary to intuition, the maximal number of bits is attained even if the correlations generated by one of the pairs are entirely local. This is in contrast to previous results in which randomness was generated from nonlocal pairwise correlations4, and offers a perspective for future works. We also propose an explicit protocol that can generate boundary correlations using states and measurements similar to those that maximally violate the CHSH inequality. Compared to the protocol of ref. 4, which can also achieve two bits of randomness with two dichotomic measurements, ours is simpler as it requires fewer different settings. Furthermore, we show numerically through semidefinite programming techniques that it is more robust to noise, because it is insensitive to the nonlocality trade-off. Our protocol is also simpler than the two proposals of ref. 18, which can also certify two bits of randomness, since it requires fewer measurements, allowing for easier experimental implementation.

Finally, to demonstrate the feasibility and noise resilience of our protocol, we performed a proof-of-concept experimental test based on polarization-entangled photon pairs that generate the correlations required by the protocol. From these correlations, we could certify 39% more random bits than those obtainable with standard non-sequential CHSH protocols in the same noise conditions.

The paper is structured as follows. In the sequential scenario, we introduce a convenient formalism to describe the sequential quantum scenario. In Bounds on the sequential quantum correlations, we show some inequalities in the values of the correlations. In Sequential-CHSH protocol, we propose a protocol to saturate these inequalities: This will lead us to identify part of the boundary of the sequential quantum correlation. In Randomness from correlations, we show how the saturation of the inequalities can be used to certify randomness, supporting the discussion with numerical simulations for some non-ideal cases. Finally, in Experiment, we describe a proof-of-concept sequential quantum experiment based on quantum optics.

Methods

The sequential scenario

We work in the sequential scenario defined in ref. 16, and specifically in a scenario that includes three users: Alice, Bob1, Bob2. A scheme is depicted in Fig. 1. A common source prepares an unknown physical system that is shared and then measured by the untrusted devices operated by the three users. Each user randomly chooses a measurement identified by a binary input x, y1, y2 ∈ {0, 1} and obtains as a result a binary output a, b1, b2 ∈ { ± 1}. We assume all inputs to be independent of one another, and forbid any communication during data collection between Alice and the Bobs, but we allow unidirectional communication from Bob1 to Bob2 between the production of their respective outputs: This characterizes the sequential correlation scenario that we formally define below.

Fig. 1: Schematic of the sequential scenario.
figure 1

Above, the framework with Kraus operators. Bottom, the projective framework with the operators introduced in the sequential scenario.

Full size image

The main goal of this work is to study the properties of the correlations between inputs and outputs p(a, b∣x, y) = p(a, b1, b2∣x, y1, y2) that can be generated in this scenario and to see how they can be used to produce device-independent random numbers from the Bobs outputs. We assume that after sufficiently many independent and identically distributed runs, the correlations are known perfectly, neglecting the effects of finite statistics. Moreover, we do not have requirements on the probabilities of the inputs, as long as they allow for the entire reconstruction of the correlations p(a, b∣x, y).

The absence of communication means that Alice’s marginal probabilities are independent of Bobs’ inputs and vice versa. Formally, the correlations must satisfy the no-signaling conditions13:

$$\begin{array}{l}\mathop{\sum}\limits_{a}p(a,{\bf{b}}| x,{\bf{y}})=\mathop{\sum}\limits_{a}p(a,{\bf{b}}| x^{\prime} ,{\bf{y}})\quad \forall {\bf{b}},x,x^{\prime} ,{\bf{y}}\\ \mathop{\sum}\limits_{{\bf{b}}}p(a,{\bf{b}}| x,{\bf{y}})=\mathop{\sum}\limits_{{\bf{b}}}p(a,{\bf{b}}| x,{\bf{y}}^{\prime} )\quad \forall a,x,{\bf{y}},{\bf{y}}^{\prime} \end{array}$$
(1)

Furthermore, sequentiality implies that Bob2’s input cannot influence Bob116:

$$\sum _{{b}_{2}}p(a,{b}_{1},{b}_{2}| x,{y}_{1},{y}_{2})=\sum _{{b}_{2}}p(a,{b}_{1},{b}_{2}| x,{y}_{1},y^{{\prime} }_{2})\quad \forall a,{b}_{1},x,{y}_{1},{y}_{2},y^{{\prime} }_{2}$$
(2)

As is common in the context of device-independent protocols, we focus on the set of sequential quantum correlations QSEQ, i.e. those sequential correlations that can be written using Born rule as

$$p(a,{\bf{b}}| x,{\bf{y}})= \mathop{\sum}\limits_{\mu ,{\mu }_{1},{\mu }_{2}}{\rm{Tr}}\left[({K}_{a,\mu }^{x}\otimes {K}_{{b}_{2},{\mu }_{2}}^{{y}_{2}}{K}_{{b}_{1},{\mu }_{1}}^{{y}_{1}})\rho {({K}_{a,\mu }^{x}\otimes {K}_{{b}_{2},{\mu }_{2}}^{{y}_{2}}{K}_{{b}_{1},{\mu }_{1}}^{{y}_{1}})}^{\dagger }\right]$$
(3)

where we have imposed the standard tensor product form to separate Alice and the Bobs19, and the measurements are described in terms of Kraus operators such that \({\sum }_{a,\mu }{{K}_{a,\mu }^{x}}^{\dagger }{K}_{a,\mu }^{x}={\sum }_{{b}_{1},{\mu }_{1}}{{K}_{{b}_{1},{\mu }_{1}}^{{y}_{1}}}^{\dagger }{K}_{{b}_{1},{\mu }_{1}}^{{y}_{1}}={\sum }_{{b}_{2},{\mu }_{2}}{{K}_{{b}_{2},{\mu }_{2}}^{{y}_{2}}}^{\dagger }{K}_{{b}_{2},{\mu }_{2}}^{{y}_{2}}={\mathbb{1}}\) for any input17. We note that the sequentiality is reflected in the order of the Kraus operators.

Expression (3) considers that a real implementation of a protocol can be generally described in terms of mixed states and non-projective measurements. However, the shared state can be assumed to be pure because even if the actual is not, it is always possible to consider its purification in a larger Hilbert space without changing the correlations. Similarly, through the Stinespring20 dilation, the right-hand side of (3) can be rewritten in terms of orthogonal projective measurements satisfying additional constraints in order to guarantee (2) (see Supplementary Methods A and refs. 17,21 for details).

The description in terms of pure states and projective measurements is more convenient for studying the geometry of sequential quantum correlations and we will adopt it in the following. Moreover, as shown in Supplementary Methods A, it can also be rephrased in terms of unitary and hermitian operators (namely measurement operators with only ± 1 eigenvalues) \({B}_{{y}_{1}}\) and \({B}_{{y}_{1},{y}_{2}}\) that satisfy the following constraints:

$$\begin{array}{l}[{B}_{{y}_{1}},{B}_{{y}_{1},{y}_{2}}]=0\\ {B}_{{y}_{1}}^{\dagger }={B}_{{y}_{1}},\,{B}_{{y}_{1},{y}_{2}}^{\dagger }={B}_{{y}_{1},{y}_{2}}\quad \quad \forall {y}_{1},{y}_{2}\\ {B}_{{y}_{1}}^{\dagger }{B}_{{y}_{1}}={B}_{{y}_{1},{y}_{2}}^{\dagger }{B}_{{y}_{1},{y}_{2}}={\mathbb{1}}\,.\end{array}$$
(4)

They can be understood as the observables measured by Bob1 and Bob2. Indeed, the operators \({B}_{{y}_{1}}\) reproduce the statistics of Bob1, while the operators \({B}_{{y}_{1},{y}_{2}}\) reproduce the statistics of Bob2 given that Bob1 has chosen the input y1. See Fig. 1 for a schematic of the scenario. Similar considerations can be applied to Alice’s side to define two unitary and hermitian operators Ax. Without the sequentiality requirement, Alice has no commutation relation analogue to that of (4).

With these definitions, the correlations in the sequential scenario can always be written as

$$p(a,{\bf{b}}| x,{\bf{y}})=\left\langle \psi \right\vert {\Lambda }_{a}^{x}\otimes {\Pi }_{{b}_{1}}^{{y}_{1}}{\Pi }_{{b}_{2}}^{{y}_{1},{y}_{2}}\left\vert \psi \right\rangle$$
(5)

where \({\Lambda }_{a}^{x}\), \({\Pi }_{{b}_{1}}^{{y}_{1}}\) and \({\Pi }_{{b}_{2}}^{{y}_{1},{y}_{2}}\) are the projectors on the eigenspaces of hermitian operators Ax, \({B}_{{y}_{1}}\) and \({B}_{{y}_{1},{y}_{2}}\) respectively (i.e., \({B}_{{y}_{1}}={\Pi }_{+}^{{y}_{1}}-{\Pi }_{-}^{{y}_{1}}\) and similarly for Alice and Bob2). The commutation relation in (4) guarantees that the product of the Bobs’ projectors can be used to compute a well-defined probability.

Results

Bounds on the sequential quantum correlations

Having introduced the notation, we now present a Tsirelson-like bound satisfied by the sequential quantum correlations.

In our specific case, we are not interested in the operations of Bob2 after Bob1 has chosen the input y1 = 1. This means that we will only consider the marginal probability distribution \(p(a,{b}_{1}| x,{y}_{1}=1)={\sum }_{{b}_{2}}p(a,{b}_{1},{b}_{2}| x,{y}_{1}=1,{y}_{2})\). We are allowed to do this because of sequentiality: Bob2 cannot influence Bob1 and hence p(a, b1∣x, y1 = 1) is well-defined and does not depend on y2. Our results are valid regardless of what Bob2 does in this case, we can even think that he does not perform any measurement at all. With this simplification, the association of inputs and measurements is as follows:

$$\begin{array}{rl}Input\,sequence&Measurements\\ {y}_{1},{y}_{2}=0,0&{B}_{0}\,\,\text{and}\,\,{B}_{0,0}\\ {y}_{1},{y}_{2}=0,1&{B}_{0}\,\,\text{and}\,\,{B}_{0,1}\\ {y}_{1},{y}_{2}=1,0\,\,\text{or}\,\,1,1&{B}_{1}\,.\end{array}$$
(6)

Consequently, we consider the following operators:

$$\begin{array}{l}{S}_{1}\equiv ({A}_{0}+{A}_{1}){B}_{0}+({A}_{0}-{A}_{1}){B}_{1}\\ {S}_{2}\equiv ({A}_{0}+{A}_{1}){B}_{0,0}+({A}_{0}-{A}_{1}){B}_{0,1}\,.\end{array}$$
(7)

These are two CHSH-like operators relative to Alice-Bob1 and Alice-Bob2, respectively, and their mean values can be measured in our scenario from the correlations p(a, b∣x, y) by selecting the values of the inputs that correspond to the relevant observables. Hence, the usual results about CHSH operators also apply, so that in a quantum setting \(\langle {S}_{i}\rangle \le 2\sqrt{2}\). Moreover, from conceptually similar results in the literature1,4,8, one can expect a trade-off between 〈S1〉 and 〈S2〉, therefore it is meaningful to consider an expression that combines the two:

$${S}_{\theta }\equiv \cos 2\theta ({S}_{1}-\sqrt{2}{\mathbb{1}})+\sin 2\theta ({S}_{2}-\sqrt{2}{\mathbb{1}})\,.$$
(8)

Furthermore, we introduce the operator

$${S}_{c}\equiv ({A}_{0}+{A}_{1}){B}_{0,0}+({A}_{0}-{A}_{1}){B}_{1}$$
(9)

whose expected value is a function of part of the statistic of Alice-Bob1 and part of the statistic of Alice-Bob2. This is a well-defined CHSH-like operator, as the relevant observables on the Bobs’ side are measured with different inputs: y1, y2 = 1, 0 or 1, 1 for B1 and y1, y2 = 0, 0 for B0,0. Therefore, in a quantum experiment \(\langle {S}_{c}\rangle \le 2\sqrt{2}\).

We can express now our main result (proven in Supplementary Methods B) on the geometry of the sequential correlations, which is a bound on 〈S1〉 and 〈S2〉 in the specific case in which 〈Sc〉 takes its maximum value \(2\sqrt{2}\).

Result 1

For any sequential quantum correlation in our scenario, it holds that

$$\langle {S}_{c}\rangle =2\sqrt{2}\quad \Rightarrow \quad \langle {S}_{\theta }\rangle \le \sqrt{2}\,,\quad \forall \theta \,,$$
(10)

and there exist correlations that saturate the inequality.

This upper bound on 〈Sθ〉 can be interpreted as a monogamy relation between the correlations of Alice-Bob1 and Alice-Bob2. This is different from the trade-offs already present in the literature because S2 considers Bob1’s input, since B0,0 and B0,1 are measured only if y1 = 0. Instead, in ref. 1, the quantity similar to S2 is calculated ignoring the actions of Bob1, while the protocols of refs. 4,8 calculate separate CHSH quantities for each of Bob1’s outputs, adapting Alice’s measurements to obtain the highest values.

Sequential-CHSH protocol

In the following, we will provide state and operators that generate correlations for which \(\langle {S}_{c}\rangle =2\sqrt{2}\) and \({S}_{\theta }=\sqrt{2}\) for any given value of θ, proving that the inequality (10) is tight and identifies a boundary of QSEQ in our scenario.

In the scheme, Alice and Bob1 share the maximally entangled Bell state \({\left\vert {\phi }^{+}\right\rangle }_{AB}=(\left\vert 00\right\rangle +\left\vert 11\right\rangle )/\sqrt{2}\), where \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\) are the eigenstates of the σz Pauli matrix.

Alice randomly chooses between two inputs x ∈ {0, 1}, corresponding to the two observables

$${A}_{0}=\frac{{\sigma }_{z}+{\sigma }_{x}}{\sqrt{2}}\,,\ {A}_{1}=\frac{{\sigma }_{z}-{\sigma }_{x}}{\sqrt{2}}\,.$$
(11)

Bob1 randomly chooses between two inputs y1 ∈ {0, 1}, the latter corresponding to a projective measurement of σx and the former to the non-projective measurement realized by the two Kraus operators depending on the parameter θ:

$$\begin{array}{l}{K}_{+}(\theta )=\cos \theta \left\vert 0\right\rangle \left\langle 0\right\vert +\sin \theta \left\vert 1\right\rangle \left\langle 1\right\vert \,,\\ {K}_{-}(\theta )=\cos \theta \left\vert 1\right\rangle \left\langle 1\right\vert +\sin \theta \left\vert 0\right\rangle \left\langle 0\right\vert \,.\end{array}$$
(12)

In this expression, the parameter θ is taken to be the same as the one appearing in (8) in order to achieve correlations that saturate the inequality in (10). Its value has a clear physical meaning: it controls the strength of the measurement, in the sense that \(\theta =n\frac{\pi }{2}\) leads to a projective measurement of ±σz, while for \(\theta =\frac{\pi }{4}+n\pi\) correspond to a non-interactive measurement. At \(\theta =\frac{\pi }{4}+n\frac{\pi }{2}\) the two Kraus operators are equal, up to a sign.

After these operations, if y1 = 1, the protocol ends. Otherwise, for y1 = 0, Bob1 sends the post-measurement state to Bob2, who randomly chooses between the projective measurements of σz or σx, each corresponding to one of the two inputs y2 ∈ {0, 1}.

As discussed in Supplementary Methods D, in terms of projective operators, this protocol can be formulated by leaving unchanged A0 and A1, while introducing the operators

$$\begin{array}{rcl}{B}_{0}&=&{\sigma }_{z}\otimes {\sigma }_{z}\\ {B}_{1}&=&{\sigma }_{x}\otimes {{\mathbb{1}}}_{{B}^{\prime\prime}}\\ {B}_{0,0}&=&{\sigma }_{z}\otimes {{\mathbb{1}}}_{{B}^{{\prime\prime}}}\\ {B}_{0,1}&=&{\sigma }_{x}\otimes {\sigma }_{x}\end{array}$$
(13)

on the Bobs’ side. These act on an Hilbert space \({{\mathcal{H}}}_{B^{\prime} }\otimes {{\mathcal{H}}}_{B^{\prime\prime} }={{\mathbb{C}}}^{2}\otimes {{\mathbb{C}}}^{2}\). The shared state is now

$$\left\vert \psi \right\rangle ={\left\vert {\phi }^{+}\right\rangle }_{AB^{\prime} }\left[\cos \theta {\left\vert 0\right\rangle }_{B^{\prime\prime} }+\sin \theta {\left\vert 1\right\rangle }_{{B}^{{\prime\prime}}}\right]$$
(14)

One can verify, using Eqs. (3) and (5), that the sequential and projective formulations give the same correlations, and that the operators \({B}_{{y}_{1}}\) and \({B}_{{y}_{1},{y}_{2}}\) respect all the constraints in Eq. (4). Moreover the relations \(\langle {S}_{c}\rangle =2\sqrt{2}\) and \(\langle {S}_{\theta }\rangle =\sqrt{2}\) hold with the above defined state and operators, proving that the inequality on Sθ is tight and define a boundary, as claimed.

A geometric depiction of this boundary is shown in Fig. 2 and can be deduced by Eq. (8): For each θ, when \(\langle {S}_{\theta }\rangle =\sqrt{2}\), this equation describe the tangent to a circumference in the 〈S1〉〈S2〉 plane, centered at \((\sqrt{2},\sqrt{2})\) and of radius \(\sqrt{2}\). The points on the circumference are spanned by the protocol just discussed, while the interior of the circle is filled with sequential quantum correlations satisfying \(\langle {S}_{c}\rangle =2\sqrt{2}\) and \(\langle {S}_{\theta }\rangle < \sqrt{2}\).

Fig. 2: Cross-section of the set of sequential quantum correlations, \({{\mathcal{Q}}}_{SEQ}\), at \(\langle {S}_{c}\rangle =2\sqrt{2}\).
figure 2

The dashed lines denote the maximum values achievable by 〈S1〉 and 〈S2〉 in the local and non-sequential quantum scenarios, without restrictions on 〈Sc〉. The red dots mark the geometric location of the correlations achievable with the protocol explained in Sequential-CHSH protocol.

Full size image

Randomness from correlations

We can now move to our second main result, which is a statement on the randomness that can be obtained from correlations on the aforementioned boundary of QSEQ. In this work, we consider only local randomness, originating solely from the side of the Bobs. Given a sequential probability distribution that is observed experimentally Pexp(a, b∣x, y), the quantity of device-independent random numbers that can be extracted from the outcomes corresponding to a specific input sequence yr can be measured by the (quantum conditional) min-entropy \({H}_{\min }=-{\log }_{2}G\)22, where G is the maximum guessing probability that an adversary Eve has on the Bobs’ outcomes when the input sequence is yr:

$$G=\mathop{\max }\limits_{{p}{ABE}}\sum _{{\bf{b}}}{p}_{BE}({\bf{b}},{\bf{b}}| {{\bf{y}}}_{{\bf{r}}})$$
(15)
$$\begin{array}{c}\,{\text{s.t.}}\,\quad \sum _{{\bf{e}}}{p}_{ABE}(a,{\bf{b}},{\bf{e}}| x,{\bf{y}})={P}_{\exp }(a,{\bf{b}}| x,{\bf{y}})\,,\\ {p}_{ABE}(a,{\bf{b}},{\bf{e}}| x,{\bf{y}})\in {{\mathcal{Q}}}_{SEQ}\,.\end{array}$$
(16)

The first condition of Eq. (16) compels Eve to use a strategy pABE that is compatible with the experimental correlations \({P}_{\exp }(a,{\bf{b}}| x,{\bf{y}})\). The second means that the strategy is also quantum in the sense explained in the sequential scenario and the sequentiality requirement applies only to the Bobs.

With this definition, we can express the second main result of our work:

Result 2

For any sequential quantum correlation in our scenario such that \(\langle {S}_{c}\rangle =2\sqrt{2}\) and \(\langle {S}_{\theta }\rangle =\sqrt{2}\) for a given \(\theta \,\ne\, n\frac{\pi }{4}\), the min-entropy is

$${H}_{\min }=2\,\,\text{bits}\,$$
(17)

when evaluated with the input sequence yr = (0, 1). If \(\langle {S}_{\theta }\rangle =\sqrt{2}\) for some \(\theta =n\frac{\pi }{4}\), it reduces to \({H}_{\min }=1\) bit.

The proof, provided in Supplementary Methods C, is based on the self-testing properties of the CHSH inequality23, which are valid because \(\langle {S}_{c}\rangle =2\sqrt{2}\), and on the additional necessary conditions that the quantum state and measurements must satisfy in order to saturate also Eq. (10). We emphasize that the demonstration is conducted in a device-independent scenario, and it remains valid regardless of the dimension and specific details of the sequential quantum realization. Examples of states and operators capable of producing 2 bits of randomness are those described in Sequential-CHSH protocol.

Two dichotomic measurements can provide, at most, two random bits. The fact that they achieve this bound, certifies the complete unpredictability of their outcomes. This descends from the features of the entire correlation Pexp(a, b∣x, y) and not just from the pairwise ones. Indeed 〈S1〉 and 〈S2〉 cannot be maximized simultaneously, and the situations in which one is maximized are exactly those for which the randomness drops to one bit. By compromising on their respective nonlocality, Bob1 and Bob2 achieve the best results in terms of randomness. There are even regions on the boundary in which either the correlations between Alice and Bob1 or those between Alice and Bob2 are entirely local, as can be checked by verifying that all CHSH inequalities involving their paired results are respected. Yet, thanks to the three-party correlations, the min-entropy is still maximal at two bits.

However, due to unavoidable experimental imperfections, a real implementation cannot generate ideal correlations that sit exactly at the boundary, therefore it is important to study the amount of device-independent randomness in the interior of QSEQ. We address this problem numerically using the Navascués-Pironio-Acín (NPA) hierarchy24,25, and its sequential generalization17. This tool replaces the usually difficult-to-verify second condition in (16) with an ordered series of increasingly stringent necessary conditions on linear combinations of the probabilities pABE(a, b, e∣x, y). The constraint \({p}_{ABE}(a,{\bf{b}},{\bf{e}}| x,{\bf{y}})\in {{\mathcal{Q}}}_{SEQ}\) is retrieved when all conditions are satisfied, but stopping to a finite order k of the series allows casting the problem to a practical semi-definite program (SDP)26 and restricts pABE to belong to a set \({{\mathcal{Q}}}_{SEQ}^{k}\supseteq {{\mathcal{Q}}}_{SEQ}\)17. This means that the optimization is performed over a larger set of correlations than what is allowed by quantum mechanics and gives Eve more power than she actually has. The solution of the program is then an upper bound of the actual guessing probability: Finding a value G through the SDP certifies in a device-independent way that the min-entropy of the two outcomes is at least \(-{\log }_{2}G\) bits.

Numerical issues could in principle overestimate the min-entropy, but this can be prevented by giving tolerances to the constraints of Eq. (16). These tolerances always benefit Eve and, if chosen much larger than the machine precision, overwhelm its the potentially dangerous effect27.

Rather than computing the min-entropy for all possible values of 〈Sc〉 and 〈Sθ〉, we do it in the context of the protocol explained in Sequential-CHSH protocol, so as to study also its noise robustness. We numerically generate the experimental correlations using the maximally entangled state \(\left\vert {\phi }^{+} \right\rangle \) mixed with random noise, namely \({\rho }_{AB}=(1-p)\left\vert {\phi }^{+}\right\rangle \left\langle {\phi }^{+}\right\vert +p{\mathbb{1}}/4\), and the measurements required by the protocol. We then set these correlations as constraint in the optimization problem (15). We perform such computation for different values of the strength parameter θ, since, for noisy states, different values of θ could influence the performance of the protocol by imposing different limitations on Eve’s strategies. Because of the symmetry of the protocol, it is sufficient to restrict the analysis to \(\theta \in [0,\frac{\pi }{4}]\). For such numerical computations we adopt Ncpol2sdpa28 and the solver SDPA-DD29, setting a minimal solver precision of 10−12 for all the theoretical simulations. The NPA order is 1 + AB17, which is enough for retrieving the analytical result in the ideal case scenario.

In Fig. 3 we plot the simulation result, which confirms that, in the ideal case (p = 0), the min-entropy of the measurements of the protocol is two bits for each value of \(\theta \in (0,\frac{\pi }{4})\). When the strength parameter θ is at one of the two extremes, the min-entropy drops to one bit, in agreement with our theoretical result. With the help of the sequential protocol, it is straightforward to understand the drop by observing the state after the measurement of Bob1. For θ = 0, Bob1 measures projectively, hence the state sent to Bob2 is separable and Eve can easily guess the second bit. For \(\theta =\frac{\pi }{4}\), the measurements of Bob1 produce no useful correlations and their outcomes are also easily predictable by Eve. Yet, because the measurement is non-interactive, Bob2 still receives a portion of a maximally entangled pair and generates with Alice the perfect correlations that allow him to certify that his outcomes are unpredictable. In both cases, one outcome (and hence one bit) is securely random, and the other is known to Eve.

Fig. 3: Min-entropy from the sequential protocol proposed in Sequential-CHSH protocol as a function of the strength θ for several values of the noise p.
figure 3

Simulations achieved with the NPA order 1 + AB. For p = 0 we retrieve the results obtained analytically.

Full size image

Figure 3 also shows the impact that the noise quantified by p has on the performance. Intermediate values of θ are optimal, as they are farthest from the extremal points that reduce the randomness even in the ideal case. The approximate flatness of the curve also means that inaccuracies in the setting of θ reduce performance only slightly, simplifying the requirements for the experimental implementation. This descends from the fact that the performance of the noiseless protocol is independent of θ (except for the extremal points). This is in contrast with all other protocols present in the literature, whose optimal performance is obtained for specific values of θ which are close to pathological points4,9,17.

In Fig. 4, we show the best min-entropy achievable with the sequential protocol as a function of the parameter p. It indicates that it is possible to generate more than one random bit per state even if p ≈ 1.8 × 10−2. This value is fairly typical for sources of polarization-entangled photon pairs based on spontaneous parametric down-conversion, and can be reduced with state-of-the-art equipment30,31,32,33,34. For comparison, we also plot the min-entropy achievable with a non-sequential protocol that works in the CHSH scenario and uses the NPA hierarchy35. We find that the threshold value of p at which the two curves begin to split is approximately 8.5 × 10−2, meaning that for any smaller value, the sequential protocol performs better than its non-sequential counterpart. The equivalent threshold for the protocol of ref. 4 is a much smaller 3.7 × 10−3 9.

Fig. 4: Best min-entropy achievable with three different protocols as a function of the depolarization parameter.
figure 4

Our proposal, explained in Sequential-CHSH protocol, the standard CHSH protocol based on numerical optimization (NPA at order 4)35, and the sequential protocol proposed by ref. 4. The experimental data are subjected to additional type of noise not considered by the curves simulations, such as the c parameter discussed in Experiment.

Full size image

We point out that this value is in general affected by the finite orders of the NPA hierarchy set in the maximization (15) of the two protocols, which are 1 + AB and 4 respectively.

In a realistic implementation of the sequential scheme (which still neglects finite-size effects), Alice and the Bobs would generate random inputs to select the measurements to be performed on each state. Their choices should be unbalanced, favoring y = yr = (0, 1) for the Bobs, and arbitrarily one of the two observables for Alice. This is to reduce the randomness cost to select the inputs, which, in the asymptotic limit, can be made arbitrarily close to zero bits per state. Alice and the Bobs’ devices should receive the inputs and produce the outputs while outside of one another’s light cones, to avoid the locality loophole. From the complete list of inputs and outputs gathered in a time interval, Alice and the Bobs should calculate the experimental correlations \({P}_{\exp }(a,{\bf{b}}| x,{\bf{y}})\) to use in the SDP (15) with the help of the NPA hierarchy. The string of outputs of the Bobs corresponding to y = yr should be considered as consisting of pairs of bits (one from Bob1 and one from Bob2). The average min-entropy corresponding to each pair would be calculated from the guessing probability G resulting from the problem. Finally, the Bobs should reduce the string using a randomness extractor and the knowledge of the min-entropy, producing a shorter but uniform and secure sequence of random bits36. The post-processing, consisting of the SDP and the extraction, could be executed during the acquisition of further outputs for a subsequent experimental run, thus reducing its impact on performance. However, the SDP for this protocol can typically be solved in seconds on average personal computers if tackled at level 1 + AB of the NPA hierarchy. This holds independently of the number of samples, as only probabilities are used. The extraction scales at worst quadratically with the length of the raw key, but can be efficiently parallelized37.

Experiment

We evaluated the protocol presented above with a proof-of-concept experiment, with the goal of verifying the feasibility of meeting the required quality for the entangled state and measurements. For this purpose, we did not create an actual random number generator, but only a setup that reproduces all the quantum operations needed by the protocol, to observe the correlations. Furthermore, we did not include the random inputs but only scanned all the measurement settings one by one. Hence, our setup did not require any randomness source, which would be needed by a true generator. As mentioned before, we can only infer probabilities from our experiment by assuming that the results for each quantum state are independent and identically distributed and neglecting the effects of a finite dataset. We did not close either the detection or the locality loophole, relying instead on fair sampling and on the assumption that Alice and the Bobs do not communicate while producing outcomes (although Bob1 is allowed to send information to Bob2). All of this can only be valid at the proof-of-concept level of our experiment and should be improved for a true implementation of the scheme. Yet, our observations are critical to show the feasibility and experimental robustness of the proposed protocol.

The experimental setup is the same as our previous works and uses polarization-entangled photon pairs and Mach-Zehnder interferometers to implement the Kraus operators (12)8,9 (see also Supplementary Methods E for a detailed description). Most of the imperfections in this setup can be modeled by a bipartite state of the form

$${\rho }_{AB}=(1-p-c)\left\vert{\phi}^+\right\rangle \left\langle {\phi}^+\right\vert{+}p\frac{{\mathbb{1}}}{4}+c\frac{\left\vert 00\right\rangle \left\langle 00\right\vert +\left\vert 11\right\rangle \left\langle 11\right\vert }{2}\,,$$
(18)

where p ∈ [0, 1], as above, accounts for the depolarization caused by mixing with random noise, whereas c ∈ [0, 1] induces decoherence by reducing the extreme antidiagonal terms of the density matrix with respect to the diagonal ones. In optical experiments, this is caused by alignment inaccuracies that increase the distinguishability between the two photons in each pair. The two parameters p and c can be easily estimated experimentally by measuring the visibilities in the \({\mathcal{Z}}\) and \({\mathcal{X}}\) bases, indeed \(p=1-{V}_{{\mathcal{Z}}}\) and \(c={V}_{{\mathcal{Z}}}-{V}_{{\mathcal{X}}}\)9.

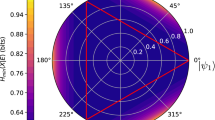
We performed three experiments, labeled by an ID ∈ {1, 2, 3}. Each of them attempts to reproduce the correlations required by the sequential-CHSH protocol described in Sequential-CHSH protocol and by the standard CHSH protocol. For each experiment, we measured the correlations between Alice and the Bobs and we used them as constraints in an NPA hierarchy but instead of setting the whole statistic \({P}_{\exp }(a,{\bf{b}}| x,{\bf{y}})\), we constrained only the single-observable mean values 〈Ax〉, \(\langle {B}_{{y}_{1}}\rangle\) and \(\langle {B}_{{y}_{1},{y}_{2}}\rangle\), and the two-observable mean values \(\langle {A}_{x}{B}_{{y}_{1}}\rangle\) and \(\langle {A}_{x}{B}_{{y}_{1},{y}_{2}}\rangle\), which are all obtainable from the experiment. Doing so allowed us to get around the fact that our simplified experiment can produce results that do not strictly meet the requirements of the protocol. Indeed, during the experiment, the state produced by the source changes slightly. This is mainly due to temperature variations that lead to the movement of the optical components. This affects the interferometers and fiber couplings and, eventually, the experimental probability distribution. Since we are scanning the measurements one by one, we are effectively using different states for each measurement, in contrast with Eq. (3). Constraining all correlations would have prevented the SDP from finding a proper solution, whereas our relaxed constraints allowed us to find one with a small solver tolerance of 10−12 29. In general, this approach does not introduce security issues, since having a smaller number of constraints only gives more power to Eve and finds a min-entropy that is lower than what could be achieved by considering all the correlations. The execution of the SDP was carried out on a personal computer and took less than 10 s.

We also compared the results with those predicted by our model using the same constraints, with the values of p, c, and θ that best fit the experimental data. We calculated the statistical errors on the experimental results as standard deviations of a sample of 300 simulated experiments. In each of these, the photon counts descend from a Poisson distribution whose mean value is the experimental datum.

Tables 1 and 2 summarize the results of all three experiments, reporting the min-entropies and the mean values of the CHSH quantities 〈S1〉, 〈S2〉, 〈Sc〉, and 〈S〉 (which is measured in the non-sequential scenario). They show that our protocol not only is feasible but can overcome the rate of the standard CHSH scheme in real world implementations. Indeed, we found min-entropies between 0.82 and 0.90 bits, or between 23% and 39% higher than those obtained in the non-sequential scenario with the same states, even with visibilities \({V}_{{\mathcal{Z}}}\approx 98 \%\) and \({V}_{{\mathcal{X}}}\approx 97 \%\), which are readily accessible to entangled-photon sources built with commercial components.

Table 1 Experimental results of the sequential CHSH experiment
Full size table
Table 2 Experimental results of the CHSH experiment
Full size table

In addition, the comparison between our results and the predictions of the model show that the latter can be used to evaluate the performance of this type of schemes. The discrepancies can be attributed to other static imperfections in the setup which are not considered by the model and to the aforementioned changes of the state from one measurement to the next.

Discussion

In this work, we studied the set of sequential quantum correlations through a geometric perspective. Initially, we presented a general mathematical framework applicable to describing any sequential quantum scenario. Using this framework in the context of one party on one side and two sequential parties on the other, we identified a Tsirelson-like quantum boundary. This boundary can be interpreted as a monogamy trade-off between the amounts of nonlocality of the sequential users shared with the remote one. Despite this trade-off, we proved analytically that the correlations on the boundary certify the maximal amount of randomness in our device-independent scenario, specifically, two bits (excluding exceptional cases). This result introduces a fundamental perspective: a trade-off for nonlocality does not necessarily translate into one for randomness. In simpler terms, even if the correlations of one sequential user with the spatially separated one are explicable through local hidden variable theories, they can contribute to the generation of secure randomness when considered jointly with the correlations of the other users.

We also proposed an explicit simple qubit-based protocol to generate the correlations on the boundary in the ideal case, and we numerically studied its noise robustness, finding that it can beat the non-sequential CHSH protocol for depolarization p ≲ 8.5 × 10−2 and produce more than one random bit for p ≲ 1.8 × 10−2, values that are feasible to achieve with current technologies.

Finally, we implemented a proof-of-concept experiment, demonstrating not only the feasibility of our protocol, but also that it can perform better than the non-sequential CHSH-based scheme with real-world systems. Indeed, we overcame the min-entropy of the latter by 23% to 39%, and produced 0.90 ± 0.01 bits in our best run. To the best of our knowledge, this is the first experimental observation of the advantage of a sequential protocol with respect to its one-step counterpart in terms of randomness generation.

On the basis of this work, we envisage further steps as follows. When correlations lie on a quantum boundary, it may happen that they identify, or self-test, a unique (up to local isometries) quantum representation that realizes them23,38. It would be interesting to understand if this can happen also in the sequential case and whether the correlations of our protocol can self-test the state and measurements that produce them.

In addition, other portions of the boundary in this scenario might prove useful. A possible avenue is to relax the condition \(\langle {S}_{c}\rangle =2\sqrt{2}\) and study the bounds for 〈Sθ〉. Our formalization of quantum sequential correlations in terms of commuting projective measurements might be helpful, but if boundary features cannot be analytically probed, the sequential extension of the NPA hierarchy can be used17. It could also be meaningful to consider other parameterizations of the boundary. For example, the upper bound of Eq. (10) can equivalently be written in terms of

$${S^{\prime}}_{\alpha }\equiv \cos \alpha \,{S}_{+}+\sin \alpha \,{S}_{-}$$
(19)

as

$$\langle {S^{\prime}}_{\alpha }\rangle \le 2\,,$$
(20)

with S± = (A0 + A1)B0 ± (A0 − A1)B0,1. This expression, detailed in Supplementary Methods B, gives the boundary represented in Fig. 5. Without constraining \(\langle {S}_{c}\rangle =2\sqrt{2}\) and without the commutation relations of Eq. (4) (derived from sequentiality), the Tsirelson-like bound of \(\langle {S^\prime} \rangle\) is relaxed to \(2\sqrt{2}\), leading to a relation similar to the one in14. Due to this greater similarity with the existing literature, \({S^{\prime}}_{\alpha }\) might be easier to investigate than Sθ.

Fig. 5: Cross-section of the sequential quantum set at \(\langle {S}_{c}\rangle =2\sqrt{2}\) in the parametrization 〈S±〉.
figure 5

The dashed circumference denotes the maximum values achievable in non-sequential quantum scenarios, without restrictions on 〈Sc〉. The red dots mark the geometric location of the correlations achievable with the protocol explained in Sequential-CHSH protocol.

Full size image

Our protocol could also be more thoroughly investigated in its robustness to losses. The standard way to treat losses in device-independent schemes is to assign the no-output events to one of the legitimate outputs. In our case, this would cause the correlations to fall from the boundary and into the interior of QSEQ. Could this be partially compensated for with a different set of states and measurements?

It would also be interesting to study whether the protocol can be extended to more Bobs. This stems from the intuition that the independence of the min-entropy from the strength parameter is due to the sequence of two mutually unbiased measurements, σz and σx. This opens up the possibility of adding a third sequential party measuring σy: In this case, the bits would be extracted from a sequence of three mutually unbiased observables. Is it then possible to achieve three bits regardless of the strength parameters under ideal conditions? Could the noise robustness of such a protocol be enough for real-world implementations? A limitation might be the complexity of the SDP, which grows considerably with the number of Bobs.

In conclusion, this work offers tools and results that can improve our understanding of sequential quantum correlations and the performance of randomness generation protocols. The formulation in terms of products of commuting measurements might provide a more intuitive description and suggest interesting points of view from which to analyze a given scenario. For example, it can be used for the investigation of the sharing of nonlocality10,11,12. The boundary correlations we studied highlight that the greatest quantum advantage is reached using the entire set of experimental probabilities, and not just the pairwise ones. This paves the way for further studies on the complex relationship between nonlocality and randomness and can improve the performance of device-independent random number generators with present-day technologies.