Introduction

Gibbs states are mixed quantum states that describe quantum systems at thermodynamic equilibrium with their environment at a finite temperature. Such states play a central role in several fields and applications, such as the study of several quantum statistical mechanics phenomena like thermalization1,2,3,4,5,6,7, out-of-equilibrium thermodynamics8,9,10,11 and open quantum systems5,7,12,13,14,15,16, quantum simulation17, quantum machine learning18,19,20, and quantum optimization21,22,23,24. Moreover, sampling from well-prepared Gibbs states can be used to tackle several problems, such as semi-definite programming25, combinatorial optimization problems21,22, and training quantum Boltzmann machines18,26.

The task of preparing Gibbs states and computing the expectation values of its observables has been proven to be quite cumbersome; at arbitrarily low temperatures, Gibbs state preparation can be considered a QMA-hard problem27,28. Existing algorithms used for such an implementation can require large overhead in resources and/or calibration even in the simplest of cases, as well as the fact that the implementation might be limited to only a specific set of systems.

Algorithms that have been proposed consist of implementing the Davies generators which rapidly converge to the Gibbs distribution29,30,31,32,33,34, the quantum Metropolis algorithm16,31,35,36,37,38, and preparing thermal quantum states through quantum imaginary time evolution (QITE)39,40,41,42,43,44,45,46,47,48. Another popular approach amongst near term devices is that of variational quantum algorithms (VQAs)49,50,51,52,53,54,55,56,57,58,59,60,61,62,63, where a quantum-classical hybrid approach of minimizing a cost function, using a parameterized quantum circuit (PQC) as a variational ansatz to prepare a Gibbs state is implemented. Despite the prominence of VQAs for Gibbs state preparation, they can require many experimental measurements for each optimization step and may suffer from barren plateaus64,65. To bypass the need to find an ansatz and optimize its parameters could significantly reduce the resources needed for Gibbs state preparation.

In certain regimes of locally interacting Hamiltonians on a lattice, with temperatures above any critical point, properties such as the Markov property and uniform clustering property66 enable classical methods such as linked cluster expansions67,68,69 and tensor networks to estimate local observables with respect to the underlying high-temperature Gibbs state69,70. Additionally, these allow for Gibbs states to be prepared with local constant depth channels via expansions of Quantum Belief Propagation (QBP)33,66,71,72,73,74,75. However, the implementation of these channels in practice may be difficult for near-term devices.

Inspired by the methods used with QBP and linked cluster expansions, we propose a method based on sampling from a quasi-distribution of local partitions clusters of mixed states, i.e., expanding the full Gibbs state into a sum of products of local “Gibbs-cumulant” type states easier to implement and sample from on quantum hardware. These short-depth circuits come at the cost of a sampling overhead proportional negativity induced by sampling from this pseudo-mixed state. Our algorithm is analogous to circuit cutting (also known as circuit knitting)76,77,78,79, where a large circuit is cut down to smaller circuits that can be implemented on a smaller number of qubits with the tradeoff of larger sampling overhead and a larger number of shots. The subcircuit results can then be recombined through classical post-processing to produce the outcome of executing the original quantum circuit. Instead of cutting the circuit, we “cut" the global Gibbs state into smaller local clusters that are easier to prepare and sample from. With our method, we outline three different use cases: (1) static observables, (2) dynamical correlation functions, and (3) its value as a warm start for other quantum algorithms, such as VQAs or QITE. While our main contribution would generally be aimed towards points 2 and 3, we do provide a hardware experimental example for point 1 to show convergence with exact numerical results. This work can be considered as a quantum algorithm that makes use of known linked-cluster expansions to prepare the Gibbs state80,81,82,83,84.

We will be discussing the development of our algorithm and use cases for it in measuring different observables for prepared Gibbs states on quantum hardware (specifically, IBM quantum hardware) in this manuscript. In Sec. II, we present the mathematical analysis of our algorithm along with the mathematical description of the different observables we want to measure. In Sec. III A, we illustrate the applications we implement our sampling algorithm for. In Sec. III, we specify the expansion of our Gibbs states of choice and present the results of the measurement of the different observables on IBM quantum hardware, followed by a discussion of the overall work in Sec. IV as well as that of future plans.

Methods

Definitions and notation

In the same spirit as circuit cutting methods, our goal in this paper is to make use of linked cluster expansions to “cut" a Gibbs state into 2 pieces and then reconstruct the full Gibbs state as an initial product state plus a series of correction terms with increasing cluster size. The mathematical definition of a general Gibbs state on N sites is

$${\rho }_{N}(\beta )=\frac{{e}^{-\beta {H}_{N}}}{{{\mathcal{Z}}}_{N}}\,,$$
(1)

where HN is a spin Hamiltonian of N sites, β is the inverse temperature, and \({{\mathcal{Z}}}_{N}={\rm{Tr}}[{e}^{-\beta {H}_{N}}]\) is the partition function over N sites. This series we form for the Gibbs state can be realized as a quasi-distribution over products of local mixed states. This method has the benefit of reducing the circuit depth in preparing each sample state on quantum hardware as long the correlation length of the target Gibbs state is small enough.

Let’s start by defining our base cluster \({{\mathcal{C}}}_{0}\), which in the most fine-grained scenario would be a single qubit and we use the notation \({\rho }_{{{\mathcal{C}}}_{0}}(\beta )\) to define the Gibbs state on the base cluster at inverse temperature β. For convenience, we will drop the β in the expression. Similarly, we use the notation \({\mathcal{C}}\) to represent an arbitrary cluster with it’s corresponding Gibbs state defined as \({\rho }_{{\mathcal{C}}}\). \({\mathcal{C}}\) can be thought of as a graph with \({\mathcal{C}}=({\Lambda }_{{\mathcal{C}}},{E}_{{\mathcal{C}}})\), where \({\Lambda }_{{\mathcal{C}}}\) defines the set of base clusters in the graph, and \({E}_{{\mathcal{C}}}\) represents the bonds between pairs of base clusters. Let \(| {\Lambda }_{{\mathcal{C}}}|\) represent the total number of base clusters in \({\mathcal{C}}\) and \(| {E}_{{\mathcal{C}}}|\) represent the total number of bonds in \({\mathcal{C}}\).

We can now define a cluster correlator as:

$${\Delta }_{{\mathcal{C}}}=\mathop{\sum }\limits_{k=0}^{| {E}_{{\mathcal{C}}}| }{(-1)}^{k}\sum _{{{\mathcal{C}}}^{{\prime} }\in ({\Lambda }_{{\mathcal{C}}},| {E}_{{\mathcal{C}}}| -k)}{\rho }_{{{\mathcal{C}}}^{{\prime} }}\,,$$
(2)

where the second sum represents a sum over all subclusters on the same set of base clusters containing \(| {E}_{{\mathcal{C}}}| -k\) bonds. The last term in this series will always be \({\rho }_{{{\mathcal{C}}}_{0}}^{\otimes | {\Lambda }_{{\mathcal{C}}}| }\). The correlator terms can be considered as the cumulants of the Gibbs states. Alternatively, we can define any \({\rho }_{{\mathcal{C}}}\) as a sum over all possible tensor products of \({\Delta }_{{{\mathcal{C}}}^{{\prime} }}\)’s that can be embedded in \({\mathcal{C}}\):

$${\rho }_{{\mathcal{C}}}={\Delta }_{{\mathcal{C}}}+\mathop{\sum }\limits_{j=2}^{| {\Lambda }_{{\mathcal{C}}}| }\sum _{\begin{array}{c}{{\mathcal{C}}}_{1},{{\mathcal{C}}}_{2},\ldots ,{{\mathcal{C}}}_{j}\\ {\Lambda }_{1}\cup {\Lambda }_{2}\cup \ldots \cup {\Lambda }_{j}={\Lambda }_{C}\end{array}}{\Delta }_{{{\mathcal{C}}}_{1}}\otimes {\Delta }_{{{\mathcal{C}}}_{2}}\ldots \otimes {\Delta }_{{{\mathcal{C}}}_{j}}\,.$$
(3)

The outer sum over j represents the number of partitions of \({\Lambda }_{{\mathcal{C}}}\) and the inner sum represents the sum over all possible j-partitions. The structure of each \({E}_{{{\mathcal{C}}}_{j}}\) is connected such that there are no partitions in the graph \({{\mathcal{C}}}_{j}\).

It should also be noted that we will use the notation ∥O∥1 to represent the Hiblert-Schmitt norm or the sum of the absolute value of the eigenvalues of O and ∥O∥2 to represent the largest eigenvalue of O.

1-D chain notation

In the case where we are working with a 1-D chain of qubits with open boundary conditions where the base cluster is a single qubit we will use a simplified notation where ρN represents the Gibbs state on N-qubits and Δn represents the cluster correlator on n-qubits. In this scenario, there is only one cluster correlator on any contiguous set of n-qubits.

Setting up the algorithm

The first property we take note of is for k-local Hamiltonians in the high-temperature limit, below the system’s critical temperature (β < βc), the cluster correlators \(\Vert{\Delta }_{{{\mathcal{C}}}_{j}}{\Vert }_{1}\), decay exponentially with \(| {E}_{{C}_{j}}|\). This allows us to truncate terms in Eq. (3) above a given threshold.

The second property we take advantage of is the fact that any traceless operator can be expressed as a linear combination of two density matrices:

$${\Delta}_{{\mathcal{C}}}=\frac{\Vert{\Delta }_{{\mathcal{C}}}{\Vert}_{1}}{2}({\sigma }_{+}^{{\mathcal{C}}}-{\sigma}_{-}^{{\mathcal{C}}})\,,$$
(4)

where σ± represents the normalized positive/negative spectrum of \({\Delta }_{{\mathcal{C}}}\). Inserting Eq. (4) into Eq. (3) gives us a linear combination of mixed states with positive and negative coefficients. While one could now use this expression to express \({\rho }_{{\mathcal{C}}}\) as a quasi-distribution of mixed states, the sampling overhead would be proportional to the sum of \(\Vert{\Delta }_{{{\mathcal{C}}}_{1}}\otimes {\Delta }_{{{\mathcal{C}}}_{2}}\ldots \otimes {\Delta }_{{{\mathcal{C}}}_{j}}{\Vert}_{1}\) for each term in the in Eq. (3).

Instead, we use the assumption that due to hardware constraints we only have the capability to prepare or sample from a Gibbs state on half our target system size. Let us start with the state \({\rho }_{{\mathcal{A}}}\otimes {\rho }_{{\mathcal{B}}}\) as an approximation to \({\rho }_{{\mathcal{C}}}\) such that:

$$\begin{array}{l}{\Lambda }_{{\mathcal{A}}}\cup {\Lambda }_{{\mathcal{B}}}={\Lambda }_{{\mathcal{C}}}\\ {E}_{{\mathcal{C}}}-\left({E}_{{\mathcal{A}}}\cup {E}_{{\mathcal{B}}}\right)={E}_{{\partial }_{{\mathcal{A}}{\mathcal{B}}}}\,,\end{array}$$
(5)

where \({E}_{{\partial }_{{\mathcal{A}}{\mathcal{B}}}}\) represents bonds across the boundary of graphs \({\mathcal{A}}\) and \({\mathcal{B}}\). From Eq. (3) we see that we can now represent \({\rho }_{{\mathcal{C}}}\) as:

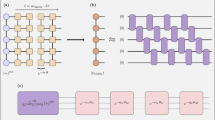
$$\begin{array}{l}{\rho }_{{\mathcal{C}}}={\rho }_{{\mathcal{A}}}\otimes {\rho }_{{\mathcal{B}}}\\ +\mathop{\sum}\limits_{j=1}^{| {\Lambda }_{{\mathcal{C}}}| }\sum\limits_{\begin{array}{c}{{\mathcal{C}}}_{1},{{\mathcal{C}}}_{2},\ldots ,{{\mathcal{C}}}_{j}\\ {\Lambda }_{1}\cup {\Lambda }_{2}\cup \ldots \cup {\Lambda }_{j}={\Lambda }_{C}\\ {E}_{{\partial }_{{\mathcal{A}}{\mathcal{B}}}}\subset {E}_{1}\cup {E}_{2}\cup \ldots \cup {E}_{j}\end{array}}{\Delta }_{{{\mathcal{C}}}_{1}}\otimes {\Delta }_{{{\mathcal{C}}}_{2}}\ldots \otimes {\Delta }_{{{\mathcal{C}}}_{j}}\,,\end{array}$$
(6)

where the sum only includes Δ’s that have bonds connecting systems \({\mathcal{A}}\) and \({\mathcal{B}}\). We highlight this procedure of obtaining the expansion in Fig. 1. We can again re-express this formula as:

$$\begin{array}{c}{\rho }_{{\mathcal{C}}}=\sum\limits_{{{\mathcal{A}}}^{{\prime} }\subseteq {\mathcal{A}},{{\mathcal{B}}}^{{\prime} }\subseteq {\mathcal{B}}}\sum\limits_{j}\sum\limits_{\begin{array}{c}{{\mathcal{C}}}_{1},\ldots ,{{\mathcal{C}}}_{j}\\ {\Lambda }_{1}\cup \ldots \cup {\Lambda }_{j}={\Lambda }_{C}-({\Lambda }_{{{\mathcal{A}}}^{{\prime} }}\cup {\Lambda }_{{{\mathcal{B}}}^{{\prime} }})\end{array}}\\ {\rho }_{{{\mathcal{A}}}^{{\prime} }}\otimes {\Delta }_{{{\mathcal{C}}}_{1}}\otimes \ldots \otimes {\Delta }_{{{\mathcal{C}}}_{j}}\otimes {\rho }_{{{\mathcal{B}}}^{{\prime} }}\end{array}$$
(7)

where the density matrices \(({\rho }_{{{\mathcal{A}}}^{{\prime} }},{\rho }_{{{\mathcal{B}}}^{{\prime} }})\) are supported on \(| {\Lambda }_{{{\mathcal{A}}}^{{\prime} },{{\mathcal{B}}}^{{\prime} }}| \leqslant | {\Lambda }_{{\mathcal{A}},{\mathcal{B}}}|\) base clusters and the tensor product of cluster correlators are supported on \(| {\Lambda }_{{\mathcal{C}}}| -| {\Lambda }_{{{\mathcal{A}}}^{{\prime} }}| -| {\Lambda }_{{{\mathcal{B}}}^{{\prime} }}|\) base clusters. In Supplementary Fig. 4, we introduce the use of different base clusters for the same system and the effect it has on the n − Reduced Density Matrix (RDM) error convergence. More comment on this in Supplementary Note II A.

Fig. 1: The Gibbs state preparation algorithm for linear spin chains.
figure 1

a From the input Hamiltonian H2N of a 2N − spin site chain, b we can define the global Gibbs state of the system via its density of states \({\rho }_{2N}={e}^{-\beta {H}_{2N}}/{\mathcal{Z}}\), where β is the inverse temperature 1/kBT and \({\mathcal{Z}}\) is the partition function of the system. c A local cluster expansion is devised to prepare the Gibbs state. We begin with a half-cut expansion of the Gibbs state, going from ρ2N to ρN ⊗ ρN, leaving us with an expansion of order \({\mathcal{O}}(\beta )\). We define the cluster cumulant terms Δn as described in Eq. (2). They are considered to be classically simulatable as they are not mixed states. They are used to include the cross-boundary interaction terms missing from the expansion after the half-cut. d By writing out the expansion with both the half-cut approximation and the cross-boundary cumulant terms, we can obtain an expansion of higher accuracy in β (i.e., \({\mathcal{O}}({\beta }^{n})\), where n is the chain length of the largest Δn term included) without needing to sample from larger clusters. Different considerations would be needed in the case of going beyond 1D, as we would need to instead define the cumulant terms as ΔT(n), accounting for the different topologies T(n) that could be embedded across the boundary of the half-cut of said lattice.

Full size image

Now, again assuming we are in a regime where correlators decay exponentially with the number of bonds they support, we can truncate Eq. (7) to only include terms in the sum that have correlators support on a number of bonds less than a given threshold. One should also keep in mind that truncating Eq. (7) does preserve the unit trace but does not guarantee positive definiteness. Ideally, one chooses a threshold such that the negative eigenvalues of the truncated equation are exponentially small. We also note that if one wanted to start with multiple partitions the process can be iterated to accommodate any initial partition.

Sampling Algorithm

Our ultimate goal is to sample from different products of local mixed states. To do so we need to express Eq. (7) as a quasi-distribution. The first step is to normalize Eq. (7) which is done by:

$$\begin{array}{c}\lambda =\mathop{\sum}\limits_{{{\mathcal{A}}}^{{\prime} }\subseteq {\mathcal{A}},{{\mathcal{B}}}^{{\prime} }\subseteq {\mathcal{B}}}\mathop{\sum}\limits_{j}\mathop{\sum}\limits_{\begin{array}{c}{{\mathcal{C}}}_{1},\ldots,{{\mathcal{C}}}_{j}\\ {\Lambda }_{1}\cup \ldots \cup {\Lambda }_{j}={\Lambda }_{C}-({\Lambda }_{{{\mathcal{A}}}^{{\prime} }}\cup {\Lambda }_{{{\mathcal{B}}}^{{\prime} }})\end{array}}\\ \Vert {\rho }_{{{\mathcal{A}}}^{{\prime} }}{\Vert}_{1}\Vert{\Delta }_{{{\mathcal{C}}}_{1}}{\Vert }_{1}\ldots \Vert{\Delta }_{{{\mathcal{C}}}_{j}}{\Vert}_{1}\Vert {\rho }_{{{\mathcal{B}}}^{{\prime} }}{\Vert}_{1}\\ \\ =\mathop{\sum}\limits_{{{\mathcal{A}}}^{{\prime} }\subseteq {\mathcal{A}},{{\mathcal{B}}}^{{\prime} }\subseteq {\mathcal{B}}}\mathop{\sum}\limits_{j}\mathop{\sum}\limits_{\begin{array}{c}{{\mathcal{C}}}_{1},\ldots,{{\mathcal{C}}}_{j}\\ {\Lambda }_{1}\cup \ldots \cup {\Lambda }_{j}={\Lambda }_{C}-({\Lambda }_{{{\mathcal{A}}}^{{\prime} }}\cup {\Lambda }_{{{\mathcal{B}}}^{{\prime} }})\end{array}}\\ \Vert {\Delta }_{{{\mathcal{C}}}_{1}}{\Vert}_{1}\ldots \Vert {\Delta}_{{{\mathcal{C}}}_{j}}{\Vert}_{1},\end{array}$$
(8)

so that the probability of sampling any specific term is given by

$$p\left({\rho }_{{{\mathcal{A}}}^{{\prime} }},{\rho }_{{{\mathcal{B}}}^{{\prime} }},{\Delta }_{{{\mathcal{C}}}_{1}},\ldots ,{\Delta }_{{{\mathcal{C}}}_{j}}\right)=\frac{\Vert{\Delta }_{{{\mathcal{C}}}_{1}}{\Vert}_{1}\ldots \Vert{\Delta }_{{{\mathcal{C}}}_{j}}{\Vert}_{1}}{\lambda },$$
(9)

and any observable that is eventually measured is then scaled by a factor of λ. We can call this λ factor as the negativity of our quasi-distribution.

With this term now sampled, we assume that \({\rho }_{{{\mathcal{A}}}^{{\prime} }},{\rho }_{{{\mathcal{B}}}^{{\prime} }}\) can be prepared with any known Gibbs state preparation or sampling algorithm. We also assume that all the correlators, \({\Delta }_{{{\mathcal{C}}}_{k}}\), that remain in our truncated series can be classically diagonalized and each eigenstate can be compiled into a quantum circuit. Now, for each \({\Delta }_{{{\mathcal{C}}}_{k}}\) we will sample an eigenstate from either \({\sigma }_{+}^{{{\mathcal{C}}}_{k}}\) or \({\sigma }_{-}^{{{\mathcal{C}}}_{k}}\) with even probability leaving:

$$p\left({\rho }_{{{\mathcal{A}}}^{{\prime} }},{\rho }_{{{\mathcal{B}}}^{{\prime} }},{\sigma }_{\pm }^{{{\mathcal{C}}}_{1}},\ldots ,{\sigma }_{\pm }^{{{\mathcal{C}}}_{j}}\right)=\frac{\Vert{\Delta }_{{{\mathcal{C}}}_{1}}{\Vert}_{1}\ldots \Vert{\Delta }_{{{\mathcal{C}}}_{j}}{\Vert}_{1}}{\lambda {2}^{j}}.$$
(10)

We also note that samples containing an odd number of \({\sigma }_{-}^{{{\mathcal{C}}}_{k}}\) carry an overall negative sign. The negative sign is then pushed onto the observable that is measured at the end of the circuit. We highlight the sampling algorithm of a 1D Gibbs state in Figs. 1 and 3. In Fig. 2, we demonstrate how λ, which is proportional to the sampling overhead, scales with β for both (A) a 16-spin linear chain case and (B) a 4 × 4 spin 2D square lattice case, where it is evident how drastically the sampling overhead increases. In fact, we see about an order of magnitude increase in λ just from going from the 1D linear chain case to the 2D square lattice case. More comment on these results in Supplementary Note II C.

Fig. 2: Scaling of sampling overhead of Gibbs state sampling, 1D vs 2D case.
figure 2

We present two plots showing how the negativity λ, which is proportional to the sampling overhead, scales with the inverse temperature β, for the two cases (a) a 16-spin linear chain case and (b) a 4 × 4-spin lattice case. The results shown are for Gibbs states for the XY Hamiltonian model and the approximation terms included in this analysis include up to the Δ4 correlator term. Due to the possibility of more nonequivalent topologies and ways of embedding the correlator terms across the half-cut boundary in the 2D case, we see λ drastically scaling up with respect to β as opposed to the 16-spin linear chain case. We see about an order of magnitude increase in λ from going from the 1D linear chain case to the 2D square lattice case. c Illustrates the 1D and 2D topologies of Δn used in the expansions. d Illustrates the spin lattices for which we obtained the results in a and b, respectively. Moreover, we write out the expression for λ in each case.

Full size image

Performance Trade-offs

There is an array of performance trade-offs with our method. As previously mentioned, each of the cluster correlators that are kept for the approximation is first classically diagonalized, and then eigenstates are sampled for these operators and classically compiled into quantum circuits. Here, the classical diagonalization costs scale exponentially in the cluster size and the depth of the compiled circuits for sampled eigenstates can be upper bounded by an exponential in cluster size. This limits the clusters we use to be a constant size, hence limiting us to the short correlation length/high-temperature regime.

Our algorithm also has a bias-variance trade-off. By truncating the clusters that we keep in Eq. (7), we introduce an inherent bias upper bound by the Hilbert-Schmitt norm of our omitted terms. If we include clusters up to size proportional to the correlation length of the exact Gibbs state this bias should be exponentially small.

At the same time, the variance of a measured observable will increase by a factor of λ2. Generally, when starting with an equal bi-partition of the system, λ will loosely scale exponentially with the number of bonds that are cut to create the partition. This makes the algorithm more appealing for 1-D systems as λ is constant in system size for a given fixed truncation size. On the other hand, for systems of dimensionality d > 1, we will start to see exponential scaling. In general for topologically distinct clusters, \({\mathcal{C}}\), on a general lattice, λ can be defined as:

$$\lambda =1+\sum _{{\mathcal{C}}}\alpha ({\mathcal{C}})\Vert{\Delta }_{{\mathcal{C}}}{\Vert}_{1},$$
(11)

where \(\alpha ({\mathcal{C}})\) represents the number of ways a topologically distinct cluster can be embedded across the boundary of the partition. In 1D, using our simplified notation, λ can be expressed as:

$${\lambda }_{1-d}=1+\mathop{\sum}\limits_{j=2}^{{L}_{cutt-off}}(j-1)\Vert{\Delta }_{j}{\Vert }_{1}\,,$$
(12)

where an example of such a case is illustrated in Fig. 3, where we write out an expansion for a linear chain up to the Δ4 term, and hence, λ is written as:

$$\lambda =1+\Vert{\Delta }_{2}{\Vert}_{1}+2\Vert{\Delta }_{3}{\Vert}_{1}+3\Vert{\Delta }_{4}{\Vert}_{1}.$$
(13)
Fig. 3: Variance and bias of a linear spin chain Gibbs state expansion.
figure 3

We illustrate in this figure the different sampling probabilities of the terms of the expansion truncating after the Δ4 term. Moreover, we calculate the value of the negativity λ in this case. When truncating the expansion, one must take into account the variance-bias tradeoff that arises. We define \({\sigma }_{0}^{2}\) as the variance of measuring observable O with respect to the full Gibbs state at inverse temperature β. The variance scales as λ2 in the case of the approximated Gibbs state using the linked cluster expansion, where λ increases with the more terms included in the expansion. On the other hand, the bias increases when including a smaller number of terms in the expansion. Hence, it is important to optimize the number of expansion terms in the approximation.

Full size image

Results

Applications

While the application of our sampling procedure can be used in any situation, its utility lies in calculating high-temperature response functions or serving as a warm-start for other quantum algorithms such as quantum imaginary time evolution methods39,40,41,42,43,44,45,46,47,48.

Moreover, our cluster sampling algorithm can be used to calculate static observables, but would be sub-optimal compared to using standard numerical linked cluster approaches, as explained in Sec., where one would use quantum algorithms/hardware to add larger clusters in the expansion. With that said, we do employ our sampling algorithm on hardware for a specific heat calculation, with the sole intent of showing the convergence of our method at high temperatures for observables that contain non-local terms.

We now illustrate the different applications we use our sampling algorithm for in this manuscript.

Dynamical spin-spin correlation functions

In the case of T = 0, the dynamical spin-spin correlation function can be written as:

$$\begin{array}{ll}{C}_{i,j}^{\alpha \gamma }(t):\,=\,{\langle {s}_{i}^{\alpha }(t){s}_{j}^{\gamma }(0)\rangle }_{0}\\\qquad\quad\,\,=\,\mathop{\sum}\limits_{p}\left\langle 0\right\vert {s}_{i}^{\alpha }\left\vert p\right\rangle \left\langle p\right\vert {s}_{j}^{\gamma }\left\vert 0\right\rangle {e}^{-i{E}_{p}t}\,.\end{array}$$
(14)

For the case of α = γ = z and measuring the correlation function of the Gibbs state, we can write out the ZiZj correlation function as follows:

$${\langle {Z}_{i}(t){Z}_{j}(0)\rangle }_{\beta }={\rm{Tr}}[\rho (\beta ,H){Z}_{i}(t){Z}_{j}(0)]\,,$$
(15)

where i, j are the indices of the spins.

In our work in ref. 85, we work on measuring T = 0 correlation functions for dimers. We use similar methods to measure the ZZ correlation functions of the Gibbs states, with the local Gibbs clusters set as the initial state in this case and the correlation functions being weighed accordingly (further details in Sec. “ρ4 Gibbs state results”). With this, we calculate the transverse dynamical structure factor

$$\begin{array}{l}{S}^{Z,Z}({\bf{Q}},\omega )=\frac{1}{2\pi \hslash }{\int_{-\infty }^{\infty }}dt\,{e}^{-i\omega t}\\ \qquad\qquad\qquad\times \frac{1}{N}\mathop{\sum}\limits_{i,j}{\langle {Z}_{i}(t){Z}_{j}(0)\rangle}_{\beta }{e}^{-i{\bf{Q}}\cdot {{\bf{R}}}_{ij}}.\end{array}$$
(16)

Specific heat

We also aim to measure the specific heat of the Gibbs states. We define it as so:

$$\begin{array}{l}{C}_{\nu }=\frac{1}{| \Lambda | }\frac{\partial \langle H\rangle }{\partial T}\\ =\frac{1}{| \Lambda | {T}^{2}}\left[\langle {H}^{2}\rangle -{\langle H\rangle }^{2}\right]\,,\end{array}$$
(17)

where ∣Λ∣ = N1 × ⋯ × ND is the volume of the lattice Λ and D is the dimensionality. Finding the expectation value of the Hamiltonian, 〈H〉, is equivalent to finding the expectation value of each of the terms of the Hamiltonian and weighing them accordingly.

ρ 4 Gibbs state results

We approximate the global Gibbs state ρ4 of the 4-spin chain as follows:

$${\rho }_{4}\,\approx \,{\rho }_{2}\otimes {\rho }_{2}+{\rho }_{1}\otimes {\Delta }_{2}\otimes {\rho }_{1}+{\Delta }_{3}\otimes {\rho }_{1}+{\rho }_{1}\otimes {\Delta }_{3},$$
(18)

which is illustrated in Fig. 4.

Fig. 4: ρ4 approximation.
figure 4

Approximation of ρ4 with error given by \(\Vert{\rho }_{4}-{\rho }_{4}^{{\prime} }{\Vert}_{1}=\Vert{\Delta }_{4}{\Vert}_{1}\).

Full size image

Hence, to calculate a thermodynamic observable of ρ4, we calculate the following:

$${\rm{Tr}}[{\rho }_{4}O]\,\approx\, {\rm{Tr}}[{\rho }_{2}\otimes {\rho }_{2}O]+{\rm{Tr}}[{\rho }_{1}\otimes {\Delta }_{2}\otimes {\rho }_{1}]+\cdots$$
(19)

and so on.

For our results, we prepare Gibbs states with the Hamiltonian H being set as the 1D XY model Hamiltonian,

$${H}_{XY}=J\left(\mathop{\sum }\limits_{i=1}^{n}{X}_{i}{X}_{i+1}+{Y}_{i}{Y}_{i+1}\right)\,,$$
(20)

where J is the interaction coupling strength. We set J = 1 in all our calculations to obtain our results.

We define H2 for the XY dimer,

$${H}_{2}={X}_{1}{X}_{2}+{Y}_{1}{Y}_{2}\,.$$
(21)

We can explicitly write the first two terms of the approximation in Eq. (19) in terms of the eigenstate basis of H2 and the computational basis,

$$\begin{array}{c}{\rm{Tr}}[{\rho }_{2}\otimes {\rho }_{2}O]=\mathop{\sum }\limits_{n=0}^{3}\mathop{\sum }\limits_{m=0}^{3}{p}_{n}{p}_{m}\left\langle nm\right\vert O\left\vert nm\right\rangle \\ {\rm{Tr}}[{\rho }_{1}\otimes {\Delta }_{2}\otimes {\rho }_{1}O]=\mathop{\sum }\limits_{x=0}^{1}\mathop{\sum }\limits_{n=0}^{3}\mathop{\sum }\limits_{y=0}^{1}\frac{1}{4}({p}_{n}-\frac{1}{4})\left\langle xny\right\vert O\left\vert xny\right\rangle \,,\end{array}$$
(22)

where n, m ∈ the eigenstate basis of H2, x, y ∈ the computational basis, and the probabilities p0, p1, p2, p3 can be written as:

$$\left\{\begin{array}{ll}{p}_{0}=\frac{{e}^{2\beta }}{2(1+\cosh (2\beta ))}\\ {p}_{1}={p}_{2}=\frac{1}{2(1+\cosh (2\beta ))}\\ {p}_{3}=\frac{{e}^{-2\beta }}{2(1+\cosh (2\beta ))}\end{array}\right.$$
(23)

with \({Z}_{2}=2+{e}^{2\beta }+{e}^{-2\beta }=2(1+\cosh (2\beta ))\) being the partition function of the system. As for the Δ3 terms, each simulation result is weighted by the eigenvalue of the corresponding eigenvector the state maps to (which is essentially what is done for the first and second-order terms as well).

Similar to what we have done for our work in ref. 85, we implement the direct measurement scheme to measure the ZZ correlation functions as we set the initial state as the different local Gibbs clusters we prepare to be able to approximately measure the ZZ correlation functions of the full ρ4 Gibbs state. All of our hardware results were run on Qiskit Runtime86 using the Estimator primitive, where we applied twirled readout error extinction (T-REx)87. In Fig. 5, we illustrate examples of the different circuits implemented to measure the ZZ correlation functions of (A) the ρ2 ⊗ ρ2 term and (B) the Δ3 ⊗ ρ1 term in the expansion.

Fig. 5: Sampling circuit examples.
figure 5

a An example of one of the circuits used for the sampling of the ρ2 ⊗ ρ2 term of the approximation of ρ4 and measuring the Z1Z1 correlation function. The computational basis can be implemented by applying different combinations of X gates, amounting to 16 different combinations representing the 16 computational bases of 4-spin 1/2 systems. b An example of one of the circuits used for the sampling of the Δ3 ⊗ ρ1 term of the approximation of ρ4 and measuring the Z1Z1 correlation function. The correlation function obtained from this circuit is weighted by the eigenvalue of the Δ3 ⊗ ρ1 state implemented as the initial state. The direct measurement scheme is employed in all cases.

Full size image

We first demonstrate how well our sampling algorithm performs compared to preparing the full Gibbs state when implemented on quantum hardware. In Fig. 6, we show the results of simulating the imaginary part of the correlation function \({C}_{2,1}^{zz}(t)\) over time t at β = 0.8, having the system initialized with the different orders of the approximation in Eq. (18), along with also showing the full Gibbs state ρ4 simulation of the same correlation function. When implementing on quantum hardware, we see that all of the orders of the approximation perform better than the full Gibbs state compared to the expected analytical result. This goes back to the fact that the approximation terms are all simulated with shorter circuit depths compared to the long circuit depth of the circuit implementation of the full Gibbs state. Hence, we are able to establish that we make better use of our sampling algorithm when wanting to measure the required correlation functions to calculate the dynamical structure factor. Moreover, in Supplementary Figure 3, we present the result of calculating the Root Mean Squared (RMS) errors of the results presented in Fig. 6. Compared to the average 24% RMS error we obtain with the hardware simulation of the full Gibbs state result, we are able to obtain an average RMS error of 6.5% with the implementation of the third order of the approximation on hardware. Hence, a significant increase in accuracy is quantified. In Fig. 7, we present the hardware simulation results of measuring the real part of the correlation functions \({C}_{1,1}^{zz}(t)\), \({C}_{1,2}^{zz}(t)\), \({C}_{1,3}^{zz}(t)\), and \({C}_{0,3}^{zz}(t)\). We further show the accuracy of the simulation results of each order of the approximation compared to the analytical result of the full ρ4 Gibbs state simulation.

Fig. 6: Comparison of accuracy of the approximation vs. the full Gibbs state.
figure 6

Results of measuring the imaginary part of the correlation function \({C}_{2,1}^{zz}(t)\) against Jt, where t is time, for the ρ4 Gibbs state are presented. The Hamiltonian employed is the XY model at the inverse temperature β = 0.8. Results were obtained using ibm_algiers, with the qubits' initial layout of [2,1,4,7] for the direct measurements, along with setting t = 5, the number of time steps = 51, dt ≈ 0.1, and the number of shots = 4000. In panel (a), the analytical result of each order of the approximation as illustrated in Eq. (18) is presented, as well as the analytical result of simulating the full Gibbs state (gray). In panel (b), the corresponding quantum hardware results are presented. The implementation of the full Gibbs state simulation on hardware is shown in orange. In both panels, the first order is in blue, the second order is in green, and the third order is in pink. We observe that all orders of the approximation we have developed with our sampling algorithm perform significantly better than simulating the full Gibbs state on hardware. It should be noted that the analytical result of the second order of the approximation in (a) demonstrates an overshoot, especially compared to the third order. We can see there is a general amplitude damping caused by the noisy hardware with the hardware results in (b). Hence, it would seem that the second-order result on hardware is more accurate than the third, but it is just a coincidence for this correlation function. In general, the third-order results on hardware and analytically are more accurate.

Full size image
Fig. 7: Different correlation functions on hardware.
figure 7

Results of measuring the real part of the correlation function (a)\({C}_{1,1}^{zz}(t)\), (b)\({C}_{1,2}^{zz}(t)\), (c)\({C}_{1,3}^{zz}(t)\), and (d)\({C}_{0,3}^{zz}(t)\) against Jt for the approximation of the ρ4 Gibbs state are presented. The Hamiltonian employed is the XY model at the inverse temperature β = 0.8. Results were obtained using ibm_algiers, with the qubits' initial layout of [2,1,4,7] for the direct measurements, along with setting t = 5, the number of time steps = 51, dt ≈ 0.1, and the number of shots = 4000. The analytical result of the full ρ4 Gibbs state (gray) is plotted with the hardware simulation result of each order of the approximation against time t. The first (blue), second (green), and third (pink) order hardware results are all plotted. An increase in accuracy is observed with each order of the approximation.

Full size image

The goal was to calculate the zz dynamical structure factor Szz(Q, ω). Hence, it was required to measure all of the correlation functions \({C}_{i,j}^{zz}(t)\),

$${C}_{i,j}^{zz}(t)=\left[\begin{array}{cccc}{C}_{0,0}^{zz}(t)&{C}_{0,1}^{zz}(t)&{C}_{0,2}^{zz}(t)&{C}_{0,3}^{zz}(t)\\ {C}_{1,0}^{zz}(t)&{C}_{1,1}^{zz}(t)&{C}_{1,2}^{zz}(t)&{C}_{1,3}^{zz}(t)\\ {C}_{2,0}^{zz}(t)&{C}_{2,1}^{zz}(t)&{C}_{2,2}^{zz}(t)&{C}_{2,3}^{zz}(t)\\ {C}_{3,0}^{zz}(t)&{C}_{3,1}^{zz}(t)&{C}_{3,2}^{zz}(t)&{C}_{3,3}^{zz}(t)\end{array}\right]\,,$$
(24)

where all of the spin index combinations are spanned. In Fig. 8, the results of calculating the dynamical structure factor using all of the correlation functions we measured on quantum hardware are presented in panels (A), (B), (C) and (D) for different values of Q (\({\boldsymbol{Q}}=[0,\frac{\pi }{2},\pi ,\frac{3\pi }{2}]\) respectively). We achieve increasingly greater levels of accuracy with the different orders of the approximation.

Fig. 8: Dynamical structure factor measurements.
figure 8

Results of measuring the dynamical structure factor S(Q, ω) plotted against frequency ω, where the measuring units of ω is that of ∣J∣, for the approximation of the ρ4 Gibbs state are presented. The Hamiltonian employed is the XY model at the inverse temperature β = 0.8. Results were obtained using ibm_algiers, with the qubits' initial layout of [2,1,4,7] for the direct measurements, along with setting t = 5, the number of time steps = 51, dt ≈ 0.1, and the number of shots = 4000 to obtain all of the correlation functions needed to calculate the dynamical structure factor (as illustrated in Eq. (16)). S(Q, ω) is calculated for the values (a) Q = 0, (b) \({\boldsymbol{Q}}=\frac{\pi }{2}\), (c) Q = π, and (Dd)\({\boldsymbol{Q}}=\frac{3\pi }{2}\).

Full size image

ρ 8 Gibbs state results

We approximate the global Gibbs state ρ8 of the 8-spin chain as follows:

$${\rho }_{8}\,\approx \,{\rho }_{4}\otimes {\rho }_{4}+{\rho }_{3}\otimes {\Delta }_{2}\otimes {\rho }_{3}+{\rho }_{2}\otimes {\Delta }_{3}\otimes {\rho }_{3}+{\rho }_{3}\otimes {\Delta }_{3}\otimes {\rho }_{2}\,,$$
(25)

where ρ1, ρ2, ρ3, Δ2, Δ3 all are computed identically to the case of the ρ4 results. ρ4 is written as:

$${\rho }_{4}=\frac{{e}^{-\beta {H}_{4}}}{{\rm{Tr}}[{e}^{-\beta {H}_{4}}]}\,.$$
(26)

An illustration of the expansion is shown in Fig. 9.

Fig. 9: ρ8 approximation.
figure 9

Approximation of ρ8 with error bounded by \(\Vert{\rho }_{8}-{\rho }_{8}^{{\prime} }{\Vert}_{1}\leqslant 3\parallel {\Delta }_{4}{\Vert }_{1}+4\Vert{\Delta }_{5}{\Vert}_{1}+3\Vert{\Delta }_{6}{\Vert}_{1}+2\Vert{\Delta }_{7}{\Vert }_{1}+\Vert {\Delta }_{8}{\Vert}_{1}\).

Full size image

For ρ8, we measure the specific heat Cν. The process of measuring it consists of (i) preparing the different expansion terms and (ii) measuring the expectation values 〈H〉 and 〈H2〉 on the quantum circuits as per the definition of Cν in Eq. (17), which is equivalent to measuring the expectation values of the individual terms of H and H2. The Hamiltonian in this case is still the 1D XY model. The Givens rotations used in the state preparation of the Gibbs clusters in this case do not change. For a Hamiltonian H of the form

$$H=\mathop{\sum }\limits_{i=1}^{n-1}{h}_{i,i+1}\,,$$
(27)

where hi,i+1 = XiXi+1 + YiYi+1 in the case of the 1D XY model and n = 8 in the case of ρ8, we can prove that H2 is written as

$$\begin{array}{ll}{H}^{2}=\mathop{\sum }\limits_{i=1}^{7}{({h}_{i,i+1})}^{2}\,+\,\mathop{\sum }\limits_{i=1}^{6}\{{h}_{i,i+1},{h}_{i+1,i+2}\}\\ \qquad\qquad\qquad\qquad+\mathop{\sum }\limits_{\begin{array}{c}i,j\\ | i-j| > 1\end{array}}^{7}\{{h}_{i,i+1},{h}_{j,j+1}\}\,,\end{array}$$
(28)

And hence evaluate the expectation values of these individual terms.

In Fig. 10, we present the analytical results of calculating the specific heat Cν for the different orders of the approximation illustrated in Eq. (25), as well as the full Gibbs state ρ8, for different values of β. Our algorithm was developed on the basis of being implemented for systems of exponentially decaying correlation length, i.e., systems at higher temperature ranges. Hence, the orders of the approximation start to diverge at larger values of β (i.e., lower temperature range). More orders of the approximation can be taken to increase the accuracy of the approximation at larger values of β. In Fig. 11, we obtain the hardware results of measuring the first three orders of the approximation, specifically on ibm_algiers on qubits [1,4,7,10,12,13,14,11]. Up until β ≈ 0.4, the results of implementing the first three orders of the approximation show great accuracy, but all start to diverge afterward. In Supplementary Figure 4, we present the result of calculating the Root Mean Squared (RMS) errors of the results presented in Figs. 10-11. We were able to produce the hardware results of the three orders of the approximation all within an average RMS error < 2.2% compared to the analytical calculation of the full Gibbs state result.

Fig. 10: Analytical results of measuring the specific heat of the ρ8 Gibbs state.
figure 10

Results of calculating the specific heat of ρ8 approximated by ρ4 ⊗ ρ4 with corrections up to Δ6 plotted against the inverse temperature β. The specific heat is evaluated at β = {0, 0.1, 0.2, 0.3, 0.4, 0.5}. With larger-sized systems, our approximation is predicted to diverge at larger values of β.

Full size image
Fig. 11: Hardware results of measuring the specific heat of the ρ8 Gibbs state.
figure 11

Results of measuring the specific heat of ρ8 on quantum hardware, approximated by ρ4 ⊗ ρ4 with corrections up to Δ3 plotted against the inverse temperature β. The specific heat is evaluated at β = {0, 0.1, 0.2, 0.3, 0.4, 0.5}. Results were obtained using ibm_algiers, with the qubits' initial layout of [1,4,7,10,12,13,14,11]. The gray curve represents the analytical result of measuring the specific heat at these points of β, while the blue points represent the first order of the approximation, the green points represent the second order of the approximation, and the pink points represent the third order of the approximation. As shown analytically in Fig. 10, the orders of the approximation start to diverge at higher values of β. The gate noise introduces a bias in the results, and hence the discrepancy between the analytical results shown in Fig. 10 and the hardware results. We sampled each eigenstate in our expansion with 4000 shots per observable measurement, leaving the error bars too small to make out on the plot.

Full size image

Discussion

We have developed an algorithm to prepare Gibbs states via cluster expansions and utilize them for different simulation applications, such as simulating the dynamical structure factors and specific heats of the systems of these states. Our algorithm is more suited to be used for systems with exponentially decaying correlation length, i.e., stable short-range order/higher temperature ranges. The application test cases we presented in this manuscript were all 1D systems with the XY model Hamiltonian, however, the algorithm is not limited to these cases. The next step would be to move onto a 2D system with a different Hamiltonian model. An obstacle we would face is the fact that the number of clusters per approximation order scales with the size of the boundary, meaning that the computational expense would immensely grow. Steps that would greatly help with circumventing such a problem would be identifying the symmetries and equivalent topologies of the different clusters as well as exploring other possible ways to further reduce the sampling overhead. To circumvent the problem of the temperature range spanned by our algorithm, it can be used in tandem and as a warm-start for other algorithms that would be more suited for lower temperature ranges, such as QITE.