Scaling whole-chip QAOA for higher-order ising spin glass models on heavy-hex graphs

Abstract

We show that the quantum approximate optimization algorithm (QAOA) for higher-order, random coefficient, heavy-hex compatible spin glass Ising models has strong parameter concentration across problem sizes from 16 up to 127 qubits for p = 1 up to p = 5, which allows for computationally efficient parameter transfer of QAOA angles. Matrix product state (MPS) simulation is used to compute noise-free QAOA performance. Hardware-compatible short-depth QAOA circuits are executed on ensembles of 100 higher-order Ising models on noisy IBM quantum superconducting processors with 16, 27, and 127 qubits using QAOA angles learned from a single 16-qubit instance using the JuliQAOA tool. We show that the best quantum processors find lower energy solutions up to p = 2 or p = 3, and find mean energies that are about a factor of two off from the noise-free distribution. We show that p = 1 QAOA energy landscapes remain very similar as the problem size increases using NISQ hardware gridsearches with up to a 414 qubit processor.

Introduction

The quantum alternating operator ansatz (QAOA)¹, and the predecessor quantum approximate optimization algorithm^2,3, is a quantum algorithm that is intended to be a heuristic solver of combinatorial optimization problems. QAOA is typically considered to be a variational hybrid quantum-classical algorithm because there is a set of parameters (usually called angles) that must be tuned in order for QAOA to perform well—and typically, the standard tuning approach is to use a classical processor to perform iterative gradient descent learning on the QAOA angles, using the quantum computer to evaluate the expectation value of the algorithm at a different angles. The motivation for this approach, typically, is that because quantum computers are very difficult to engineer to have low error rate gate operations, current technologies have fairly high error rates—but by using variational algorithms, part of the computation can be off-loaded onto the classical part of the computation. Unfortunately, the task of learning good QAOA angles (and learning variational parameters for hybrid quantum-classical algorithms in general), is computationally hard and only made harder by the presence of noise in the quantum computation^4,5. For these reasons, the suitability of QAOA for Noisy Intermediate-Scale Quantum (NISQ)⁶ computers is unclear, and is being actively studied using a variety of different approaches^{7,8,9,10,11,12,13}.

The quantum alternating operator ansatz consists of the following components: an initial state $\left\vert \psi \right\rangle$, a phase separating cost Hamiltonian H_C, a mixing Hamiltonian H_M (here the standard transverse field mixer ${H}_{M}=\mathop{\sum }\nolimits_{i = 1}^{N}{\sigma }_{i}^{x}$), a number of rounds p ≥ 1 to apply H_C and H_M (also referred to as the number of layers), and two real vectors of angles$\overrightarrow{\gamma }=({\gamma }_{1},...,{\gamma }_{p})$ and $\overrightarrow{\beta }=({\beta }_{1},...,{\beta }_{p})$, each with length p. Note that because we use the standard initial state, mixer, and phase separator, this algorithm is the original quantum approximate optimization algorithm—in particular we do not use more complex mixers.

There exist a large number of QAOA variants because there are a variety of choices of initial states, phase separating cost Hamiltonians (for many different combinatorial optimization problems), mixer Hamiltonians, and tuning methods for the QAOA angles^{14,15,16,17,18,19}. The central question of all QAOA variants is how will QAOA scale in terms of obtaining optimal solutions of combinatorial optimization problems as the number of variables increases. This question has different components, including the angle-finding problem, how many p rounds need to be applied in order to be competitive with existing classical methods, and how the algorithm performs as problem size increases. It is known that, in general, reasonably high p (e.g., more than p = 1 or p = 2) will need to be applied in order for QAOA to perform well at solving combinatorial optimization problems^{20,21,22,23,24}. For this reason, the task of increasing p on larger problem sizes is of particular interest, and this is the primary question that is studied in this paper, using state-of-the-art quantum computing hardware.

Using the whole-chip heavy-hex tailored QAOA circuits that are targeting hardware-compatible Ising models proposed in refs. ^25,26, we investigate the task of scaling these QAOA circuits to higher rounds, and to larger heavy-hex chip quantum processors. Notably, this class of random spin glasses contains higher order terms, which increases the problem difficulty, and can be natively addressed by QAOA. The primary challenge with implementing these extremely large QAOA circuits up to higher p is the angle-finding task. refs. ^25,26, utilized the brute-force approach of full angle gridsearches on the quantum hardware in order to compute good angles for p = 1 and p = 2. Unfortunately, this approach scales exponentially with p if the grid resolution is held constant, and in practice, on-device angle gridsearch learning with p = 3 is already computationally prohibitive. refs. ^25,26 observed that problem instances of the same sizes, but with different random coefficient choices, had nearly identical low-round QAOA energy landscapes. Our approach in this study to overcome these angle-finding challenges is to make use of parameter concentration in QAOA angles in order to transfer high-quality fixed angles from small (16 qubit instances) to larger instances. Parameter concentration has been observed analytically and numerically for a number of different QAOA problem types^{12,22,25,26,27,28,29,30,31,32,33}. We show that training on only a single problem instance provides good angles that can be used for much larger instances. This makes the computation of these parameters very efficient, but previous studies have also used a more computationally intensive approach of training on ensembles of problem instances to obtain good average case parameters.

The goal of this study is to investigate the ideal scaling of QAOA on current quantum computing hardware (with respect to increasing p and increasing the number of variables), using the largest problem sizes that can be feasibly programmed on the hardware. This study uses two critical components:

• 1. The angle-finding procedure is not performed in a variational outer loop classical optimization procedure, but we rather rely on heuristically computed good QAOA angles found on smaller problem instances and then apply parameter transfer. The angle-finding technique with quantum hardware in the inner loop has been studied before on NISQ hardware^10,11, but there are a number of limitations with making this technique feasible—including the computational overhead of the angle learning due to challenges such as local minima, and the noise in the computation making the learning task more difficult. Ideally, good QAOA angles would be able to be computed off-chip (classically), and then be used on large-scale quantum hardware. This is what the parameter transfer has enabled us to do for qubit system sizes that cannot be addressed using brute-force computation.

• 2. Because of the relatively high error rates on the current quantum computers, implementing optimization problems whose structure matches the underlying hardware graph reduces the overhead of gate-depth and gate-count. In particular, on quantum processors that have a sparse hardware graph, implementing long range interactions can be quite costly in terms of SWAP gates. Therefore, defining the combinatorial optimization problems that we sample to be compatible with the IBM Quantum processor heavy-hex graph^25,26 allows the QAOA circuits to be extremely short depth.

We briefly describe our methods and approach in the section “Methods” by giving a description of the higher-order Ising (minimization) optimization problems (subsection “Heavy-hex compatible ising models”), the QAOA circuits to sample these optimization problems (subsection “Whole-chip QAOA circuit description”); we describe the angle finding and parameter transfer methods (subsection “QAOA angle finding with JuliQAOA and parameter transfer”), and give a brief description of the matrix product state (MPS) simulation methods (subsection “MPS simulations”) and the use of CPLEX to classically find the optimal solutions to the optimization problems (subsection “Heavy-hex compatible ising models”). Lastly, the implementation details on IBM quantum computers are given in subsection “IBM quantum hardware implementation details”.

In the section “Results”, the first set of results shows (subsection “Numerical simulations of parameter transfer of QAOA angles“) parameter transfer works very well for these classes of problems up to p = 5 in a noise-free environment as we show through numerical simulation for upto 127 qubits, when trained only on a single 16-qubit instance. In particular, mean expectation values improve consistently with increasing p for all of 100 randomly chosen problem instances at 16, 27, and 127 qubits. These results are enabled by classical simulation techniques. As these problem classes grow entanglement relatively slowly grows with increasing p, MPS simulations enable us to classically produce the solution distributions that QAOA would achieve on an error-corrected quantum computer for up to p = 5 and 127 qubits. Our confidence in the accuracy of these simulations is due to the convergence of the solution values as we increase the MPS bond dimension parameter. Having established that parameter transfer works in a noise-free computation, we then examine to what extent parameter transfer works on actual NISQ computers.

In a second set of results (subsection “Scaling p on 16, 27, and 127 qubit IBM quantum processor hardware”), we execute the 100 problem instances (for each qubit count) on cloud-accessed IBM quantum processors with 16, 27, and 127 qubits using the numerically obtained fixed angles from a single 16 qubit instance. These results are some of the largest quantum hardware experimental QAOA results reported to date, and include an evaluation of the effectiveness of a relatively simple dynamical decoupling scheme for circuits that make use of the entire NISQ processor. We find the following:

• 1. Performance varies significantly among different processors, even if they are from the same hardware generation.

• 2. The digital dynamical decoupling sequences we evaluated (pairs of Pauli X gates) improved the performance of three out of four 127 qubit devices, two out of six 27-qubit devices, and the single 16 qubit device.

• 3. Averaged over 100 instances, the best 127 qubit processors improve until p = 2 and start degrading at higher values of p. For 27 qubits, the best processors improve up to p = 3. Thus, noise appears to effect the higher qubit count devices slightly more than lower qubit count devices despite equal CNOT depth at the same p.

Overall, our second set of results shows that QAOA parameter transfer works for this class of hardware-compatible optimization problems on current NISQ superconducting qubit processors, albeit we can only verify up to p = 3 as the devices succumb to noise at larger p. We thus revisit the question of parameter transferability on quantum hardware in a more systematic fashion in a third set of results limited to p = 1. We find that parameter concentration remains stable for p = 1 energy landscapes, run on actual quantum hardware. We show mean energy QAOA angle landscapes for the two parameters at p = 1 for four different 27 qubit and one 414 qubit systems (subsection “p = 1 QAOA hardware angle gridsearch results”) that are nearly identical. For the 127-qubit backends, we show that the best solution distributions are of similar shape on different backends but shifted linearly to account for better average expectation values (subsection “p = 1 QAOA hardware angle gridsearch results”).

Results

Subsection “Numerical simulations of parameter transfer of QAOA angles” presents numerical simulations showing that under noiseless conditions QAOA parameter transfer works well and can be applied to significantly larger problem sizes than what was trained on. Subsection “Scaling p on 16, 27, and 127 qubit IBM quantum processor hardware” then uses these fixed angles to execute QAOA circuits on a variety of IBM Quantum hardware. Subsection “p = 1 QAOA hardware angle gridsearch results” presents a low p comparison between 127 qubit quantum processors, showing a clear improvement on newer generations of IBM quantum computers. Subsection “p = 1 QAOA hardware angle gridsearch results” show p = 1 QAOA energy landscapes, on whole-chip higher order Ising models, computed on various IBM quantum computers with qubit counts ranging from 27 qubits up to 414 qubits showing consistent parameter transfer as the problem sizes increase but the energy landscapes remain relatively unchanged. Subsection “CPLEX classical compute time” reports the classical compute time required for CPLEX to optimally solve (minimize) the given combinatorial optimization problem instances.

Numerical simulations of parameter transfer of QAOA Angles

As introduced in subsection “QAOA angle finding with JuliQAOA and parameter transfer”, parameter concentration is the following property of a QAOA problem: QAOA parameter (angle) values that are optimized for an instanceIof a particular combinatorial optimization problem (such as random spin glasses or maximum cut) are transferable to other instances of similar structure, but potentially of significantly different size from the original I. Parameters from an instance I are transferable to an instance ${I}^{{\prime} }$ if the quality of the solutions found by fixed QAOA angles are similar for both I and ${I}^{{\prime} }$. While more formal definitions of transferability are possible, we pragmatically define that parameters transfer from I to ${I}^{{\prime} }$ up to a maximum number of rounds ${p}_{\max }$ if the mean solution quality for both I and ${I}^{{\prime} }$ improves with increasing number of rounds p up to and including ${p}_{\max }$. Figure 1 presents the numerical simulation results for the scaling of increasing p QAOA using the fixed parameter transfer angles on 100 random ensembles for 16, 27, and 127 qubit instances, using the methods described in subsection “QAOA angle finding with JuliQAOA and parameter transfer” specifically, the same $\overrightarrow{\beta },\overrightarrow{\gamma }$ (for each p) are used for all numerical simulations in these plots (Section “QAOA angle finding with JuliQAOA and parameter transfer” explicitly gives what these fixed angles are). The 16 and 27 qubit data is the mean energy taken from 10,000 samples per circuit with no noise model, simulated classically using Qiskit³⁴. Simulations of 127-qubit system are performed with MPS. Here we quote expectation values of H_C computed by direct tensor contraction. That computation is equivalent to the limit of an infinite number of shots. Figure 1 shows that the parameter transfer succeeded, and in particular allows us to obtain good angles for up to p = 5, verified by classical MPS simulations. Figure 16 studies the errors in MPS simulations for all 100 random 127 qubit hardware-compatible instances, as a function of χ, including the largest QAOA circuit depth we tested (which is p = 5). Figure 17 shows distributions of samples for the QAOA circuits, computed using the MPS simulation method (with a bond dimension of χ = 2048), which shows what the expected performance of QAOA is under noiseless conditions, for a subset of the 127 variable problem instances.

Fig. 1: Classical simulations of mean energies demonstrating (noiseless) concentration of QAOA parameters.

We simulate 100 random instances for each circuit size using fixed QAOA angles (trained on a single 16-qubit instance): (left) The angles for 1 ≤ p ≤ 5 are used to execute QAOA on 100 random 16-qubit higher-order heavy-hex instances, (center) The same angles are used for 100 random 27-qubit instances, (right) MPS simulation with bond dimension χ = 2048 is used for 100 random 127-qubit instances. For growing circuit sizes 16, 27, 127, for every random higher-order Ising model, as p increases the mean energy strictly improves, showing that parameter transfer succeeds in a noiseless setting. In each plot, also the mean energy across the instance ensemble is plotted as a dashed black line.

Scaling p on 16, 27, and 127 qubit IBM quantum processor hardware

The results presented in this section are reported as the mean energy of the samples of the problem Ising models, from a total of 20,000 shots per parameter and device. The plots in this section use the angles learned from a 16 qubit instance, giving good approximation ratios as p increases for the ideal computation. Figure 1 in subsection “Numerical simulations of parameter transfer of QAOA angles” shows the scaling in p under noiseless conditions obtained with these angles. In particular, these numerical simulations show that in the noiseless setting, we would get improving energy for each step of p. In this section, we execute the whole-chip QAOA circuits on various IBM Quantum computers, specifically using the fixed angles discussed in subsection “Numerical simulations of parameter transfer of QAOA angles” for p = 1 up to p = 5. This is, therefore, an evaluation of how well the transfer-learned angles perform on the heavy-hex graph hardware.

The bare QAOA circuits results are plotted in Fig. 2 for four 127 qubit backends and Fig. 5 for six 27 qubit devices and a single 16 qubit device (ibmq_guadalupe). Recall that without noise, these figures (if represented in terms of Hamiltonian energy, instead of approximation ratio) would look identical to the corresponding energy plots from Fig. 1. Figures 3, 7 show the hardware-executed mean energy for the QAOA circuits using ALAP-scheduled dynamical decoupling QAOA circuits for the 127 and 27 qubit systems respectively. Figures 4, 6 show the same, but with ASAP-scheduled digital dynamical decoupling sequences.

Fig. 2: Mean experimental QAOA approximation ratios of 100 hardware-compatible instances without dynamical decoupling.

Each gray line is an instance shared across devices with experiments run for p = 1, 2, 3, 4, 5. Each green “ ×” marker gives the p that achieves the lowest mean energy for the corresponding instance. The black dashed line shows the average mean QAOA energy across all 100 random spin glass instances with cubic terms. Each data point is computed from 20,000 shots on a 127-qubit device. For each p, angles are fixed across all devices and instances.

Fig. 3: Mean experimental QAOA approximation ratios of 100 random instances with ALAP-scheduled dynamical decoupling.

Each gray line is an instance shared across devices; each green “×” marker gives its corresponding p that achieves the lowest mean energy. The black dashed line shows the average mean QAOA energy across all instances. Cf. Fig. 2.

Fig. 4: Mean experimental QAOA energies of 100 random instances with ASAP-scheduled dynamical decoupling.

Each gray line is an instance shared across devices; each green “×” marker gives its corresponding p that achieves the lowest mean energy. The black dashed line shows the average mean QAOA energy across all instances. Cf. Fig. 2.

For the 127 qubit device from Fig. 2, we see that NISQ reality does indeed look different: As a first observation, three out of four quantum processors (ibm_brisbane,ibm_nazca,ibm_sherbrooke)at least improve the mean approximation ratio as averaged over the 100 instances until p = 2, as indicated by the black dashed line, but fail to improve for higher p, due to noise. The green crosses indicate for each instance the p at which the minimum energy (maximum approximation ratio) was achieved; we see that some instances are sampled best at p = 3, 4, or also p = 1 for a few of the instances. The remaining backend ibm_cusco performs best at p = 1. Secondly, despite all backends featuring an Eagle r3 QPU, performance differences are significant with ibm_brisbane achieving best average approximation ratios of almost 0.7 and ibm_cusco only achieving about 0.6. Overall, these differences are consistent with the reported two qubit gate fidelities for these devices.

In a fourth observation, we look at the two corresponding 127 qubit plots with digital dynamical decoupling sequences, i.e., Fig. 3 for ALAP, and Fig. 4 for ASAP. Overall, the two different scheduling schemes seem to perform similarly. However, both ALAP and ASAP have a positive effect on the performance of three of the quantum processors: ibm_brisbane improves to ~0.72 values and almost achieves a maximum approximation ratio at p = 3 instead of at p = 2, but not quite. The two lower-performing devices ibm_cusco and ibm_nazca, also see significant improvements. Strikingly, however, ibm_sherbrooke’s performance takes a significant hit with both ALAP and ASAP scheduled dynamical decoupling.

Our observations are similar for the 16 and 27 qubit systems from Fig. 5: While most backends still have their average minimum performance at p = 2, in most cases, many instances find their minimum energy (maximum approximation ratio) at p = 3. ibmq_mumbai is a notable exception as it reaches the minimum average at p = 3 and in fact remains nearly flat even to p = 4. Secondly, we again see performance differences among the 27 qubit systems ranging from a mean across the ensemble of 100 instances of 0.70 for ibmq_mumbai to a 0.60 mean value for ibm_auckland, which actually achieves its maximum at p = 1.

Fig. 5: Mean approximation ratio of the samples measured from the whole-chip QAOA circuits, without dynamical decoupling.

Each gray line is an instance run for 1 ≤ p ≤ 5, with its green “×” marker the p that achieves the lowest mean energy. The black dashed line shows the average mean QAOA energy taken across all 100 random higher-order instances. Each data point is computed from 20,000 shots. The same 100 problem instances were executed on a total of six 27-qubit devices, and 100 16-qubit instances were executed on ibmq_guadalupe; with angles shared for any given p.

Our fourth observation with respect to dynamical decoupling for the 27 qubit backends (see Figs. 6 and 7) is less optimistic than for the 127 qubit count: dynamical decoupling only helps two out of six backends, namely ibm_algiers and ibm_cairo, which actually matches ibmq_mumbai’s performance without dynamical decoupling. ASAP-scheduled digital dynamical decoupling shows an average increase of the mean energy up to p = 3 for ibm_auckland, albeit at relatively poor performance. The 16 qubit backend ibmq_guadalupe profits from dynamical decoupling with minimum mean energy up to p = 3. In summary, the particular dynamical decoupling scheme that we applied did not uniformly improve these NISQ QAOA computations, but in some cases it did clearly improve the computation.

Fig. 6: Mean approximation ratio of the samples from the QAOA circuits run with ASAP-scheduled dynamical decoupling.

Each gray line is an instance run for 1 ≤ p ≤ 5, with its green “×” marker the p that achieves the lowest mean energy. The black dashed line shows the average mean QAOA energy taken across all 100 random instances. Cf. Fig. 5.

Fig. 7: Mean approximation ratio of the samples from the QAOA circuits run with ALAP-scheduled dynamical decoupling.

Each gray line is an instance run for 1 ≤ p ≤ 5, with its green “×” marker the p that achieves the lowest mean energy. The black dashed line shows the average mean QAOA energy taken across all 100 random instances. Cf. Fig. 5.

Appendix D contains tables showing the exact optimal energy for all 300 fixed higher-order problem instances studied in this section, along with the minimum energies sampled across the QAOA circuits when executed on hardware. The tables also include the maximum energies of the problem instances, which gives a quantification of the range of the energy spectrum of these higher order Ising models. Notably, these tables show that the IBM Quantum processors were able to find the optimal solution with at least one sample for the 27 and 16 variable problem instances, but were never able to find the optimal solution to the 127 variable problem instances. Figure 8 reports CDF distributions for the gate-level calibrated error rates on the four 127 qubit IBM processors, reported by the vendor, at the time these circuits were executed. These gate error rate distributions show that some device clearly have higher gate error rates than other devices, and the QAOA result quality can be compared to these gate level error rates —where we see that the lower error rate device generally perform better.

Fig. 8: Gate level error rates for the four 127 qubit IBM processors, as measured by the vendor at the time the circuits were run.

These measures are aggregated from all of the executed circuits and all gate operations for each device (including all qubits and two qubit gate operations), and presented as CDFs. Note that error rates of 1 are in the ECR gates are not actually calibrated error rates of 1, but instead placeholder values from the backend denoting that the connection has not been calibrated.

p = 1 QAOA hardware angle gridsearch results

414 qubit p = 1 QAOA on ibm_seattle

Figure 9 shows p = 1 angle gridsearch on ibm_seattle (ibm_seattle was decommissioned before more complete whole-chip QAOA experiments could be executed) for a random Ising model instance with cubic terms and without cubic terms. The angle gridsearch is presented in terms of the mean energy computed from the distribution of 10,000 samples drawn for each β₁, γ₁ angle. A total of 7200 linearly spaced β₁, γ₁ are evaluated, as in refs. ^25,26. The higher-order Ising model is comprised of 475 quadratic terms, 414 linear terms, and 232 ZZZ terms (e.g., hyperedges). The Ising model with no higher order terms is comprised of 475 quadratic terms and 414 linear terms.

Fig. 9: Experimental mean energy landscapes for a p = 1 QAOA on ibm_seattle for two 414 qubit instances.

(left) A higher-order Ising model with up to cubic terms. (right) An Ising model with linear and quadratic terms.

Notably, the hardware-computed p = 1 energy landscape on these 414 qubit instances are very similar to the p = 1 energy landscapes shown in ref. ²⁶. Figure 10 shows the full energy distribution (of 10,000 samples) for the best p = 1 angles on the hardware-gridsearch, along with the optimal energy. Note that the minimum energies found from the p = 1 sampling are far away from the optimal solution energy.

Fig. 10: Experimental sample energy distribution for a p = 1 QAOA on ibm_seattle for two 414 qubit instances, for optimal angles found in the hardware angle gridsearch that minimize the mean energy (shown in Fig. 9).

(left) The higher-order model with cubic terms, with a mean energy of −89.14 for angles β = 0.415, γ = 2.856. (right) The model with linear and quadratic terms, with a mean energy of −87.72 for angles β = 0.467, γ = 2.83. The mean energies are marked with vertical dashed blue lines. The vertical solid lines mark the minimum sample energy found among the 10,000 samples at these angles; however, during the whole angle gridsearch, the overall minimum sample energies lie at −241 for the higher-order Ising model and −221 for the Ising model on the right. For context, the energy spectra of the instances range from −637 (ground state) to +623 (maximum) for the higher-order model on the left and from −567 (ground-state) to +565 (maximum) for the Ising model on the right.

27 qubit p = 1 gridsearch

Figure 11 shows hardware p = 1 angle gridsearch mean energy heatmaps on several IBM Quantum processors. Notably, the energy landscapes are very similar to the 414 qubit whole-lattice heavy-hex QAOA in subsection “p = 1 QAOA hardware angle gridsearch results”, and the previously reported 127 qubit whole-lattice heavy-hex QAOA results from ref. ²⁶. Notice that the energy landscape from ibm_geneva is considerably more noisy compared to the other device energy heatmaps.

Fig. 11: Mean energy landscapes for p=1 QAOA on a single 27-qubit instance sampled using 4 different IBM quantum processors that have the same heavy-hex hardware graph.

The energy landscapes show how the different QAOA angles perform - blue denotes better optimization of the Ising models, since we are solving them as minimization optimization problems. Notably, these search landscapes show the variability of the different quantum processors, where some clearly have noisier search landscapes than others. Each region of the heatmaps are average energies computed over a large distribution of hardware measurements.

Comparison of difference 127 qubit IBMQ Processors with whole-chip p = 1 QAOA circuits

A straightforward question that can be asked using whole-chip circuits is how different processors compare, when executing the same circuit. This offers a clear way to benchmark device performance, using all available hardware components. In this section, we use the short depth QAOA circuits to compare three of the 127 qubit IBM Quantum superconducting qubit processors; ibm_washington, ibm_brisbane, and ibm_sherbrooke. We do this using a focused QAOA angle gridsearch for p = 1 QAOA depth, using higher order Ising models that are compatible with all three of these processors - which in particular means hardware compatible with ibm_washington, as its hardware graph is a subgraph of the other two. The angle gridsearch is performed on-device, using β₁ = 0.4 and γ₁ = 2.9 as the center of the grid (based on the observed parameter concentration, especially of the p = 1 angle gridsearch heatmaps in ref. ²⁶), and a grid of 81 linearly spaced points ±0.15. 10,000 shots are taken for each angle. Figure 12 shows the energy distributions from using these three quantum computers to sample four different random higher-order ising models, where the reported distribution is of the 10,000 samples with the lowest mean energy among the focused angle gridsearch. This distribution shows that the newer generation of the 127 qubit processors (see Table 1) performed definitely better than the previous generation ibm_washington device. Notably, the best angles varied slightly depending on the device, due to the noise in the computation.

Fig. 12: Experimental sample energy distributions for a p = 1 QAOA for four random 127-qubit instances executed across three IBMQ devices, for the best device-specific angles found by a focused angle gridsearch.

The minimum sample energies and mean energies from these distributions are marked with solid and dashed vertical lines, respectively.

Table 1 QPU and Instance summary. Numbers of available qubits and two qubit gates are accurate at the time in which the experiments of this study were executed

CPLEX classical compute time

Here we report the classical compute time from CPLEX that is required to optimally solve all of the optimization problem instances. This time is reported in seconds from the Python CPLEX module; this time does not include the compute time used to perform the order reduction, or datastructure parsing. Note that the order reduction procedure that is used to solve the problem instances using CPLEX introduces auxiliary variables and, therefore, inflates the total number of decision variables that must be solved by CPLEX²⁶.

Figure 13 shows the distributions of CPLEX solve times for the 100 problem instances for the three problem sizes. These timing statistics show the level of computation time that hardware runs of QAOA would need to achieve to be competitive with state-of-the-art classical optimization solvers (albeit, specifically for the class of sparse optimization problems used in this study).

Fig. 13: CPLEX compute times required to exactly solve all 300 heavy-hex compatible problem instances with geometrically local cubic terms.

Note that the actual optimization problem being solved by CPLEX is the order-reduced version of the original problem, meaning that there are added auxiliary variables compared to the original problem.

The heavy-hex 414 qubit problem instance with cubic terms (used in section “p = 1 QAOA hardware angle gridsearch results”) was solved exactly with CPLEX in 3.129 s, and without cubic terms was solved exactly in 0.074 s.

Discussion

We have demonstrated that parameter transfer of QAOA angles up to p = 5 can be successfully applied to large (up to 127 qubit) systems using training on a single small (16 qubit) instance. This provides evidence—in addition to what has been presented in the literature on various other optimization problems—that parameter concentration can be used as an efficient method for computing high-quality (although not necessarily optimal) QAOA angles. We used converged classical MPS simulations with up to a bond dimension of χ = 2048 to calculate the noiseless mean expectation values, as well as the sample distributions, of the 127 qubit QAOA circuits sampling these hardware-compatible higher-order Ising model instances using the transfer-learned angles.

We also demonstrated the scaling of whole-chip QAOA on heavy-hex hardware-native spin glass models, with respect to p, on several IBM Quantum superconducting qubit processors. This demonstration comprises large circuits that fully evaluate the current performance of these IBM Quantum processors using highly NISQ-friendly and short-depth QAOA circuits. We find that the peak of QAOA performance on hardware is at p = 2, 3 on most of the IBM Quantum processors. This result shows the current state of competition between the error inherent in the computation, and the improving approximation ratios from larger p (and good angles learned at higher p). These types of sparse short-depth circuits are in contrast to dense circuits, such as quantum volume circuits^35,36, but allow probing of usage of an entire hardware graph. We observed that the relatively simple Pauli X pair digital dynamical decoupling sequences improved the mean QAOA computation on some of the IBM Quantum processors, but on other devices it actually made the computation worse.

While the scale of the number of qubits used in these QAOA simulations far exceeds what can be exactly classically simulated using full-state vector simulations, the sparsity of the underlying hardware graph means that simulating the mean expectation value for low QAOA rounds is possible. At high rounds, we expect the classical simulation of such QAOA circuits to also begin to struggle, and an interesting future avenue of study is to determine where this point is. In this work, we have used MPS simulations in order to simulate the QAOA circuits up to p = 5 in order to verify that the parameter transfer procedure was successful, but is unclear how classically simulate-able higher round QAOA is when targeting Ising models defined on heavy-hex graphs. For example, a Hamiltonian dynamics simulation was performed on a 127 qubit heavy-hex IBM Quantum device³⁷, the experiments for which were then classically simulated efficiently using a number of different approaches^{38,39,40,41,42,43,44,45,46,47}. This suggests that perhaps even extremely high round QAOA circuits (e.g., where p is significantly higher than what was used in this study) for these sparse heavy-hex Ising models may be easy to simulate when the number of qubits is small. It is also of interest to evaluate how well MPS simulations can be applied to these QAOA circuits when the angles are optimal (or nearly-optimal), as opposed to, for example, random QAOA angles. This is a very interesting regime to investigate since it is approaching the boundary of what is classically verifiable - we leave these high p heavy-hex compatible QAOA simulation questions open for future work. Future work could also study the effects of different choices of the polynomial coefficients, besides +1/−1, or even different distributions of the random coefficients and how that impacts the parameter transfer. There are also interesting variants of QAOA, such as warm-start QAOA^48,49,50, where parameter transfer could also be tested in future studies.

The optimization problems studied here are computationally quite easy to solve, for example standard combinatorial optimization software can exactly solve these problems on the order of less than two seconds of CPU time. These problem instances are used specifically because they are designed to be highly hardware compatible with the heavy-hex connectivity, not because they are significantly computationally challenging for classical algorithms.

Our findings show that QAOA parameter transfer can be used in order to obtain good angles for QAOA circuits that are very high in qubit count, using a computationally efficient learning of only a single small (in this case 16) qubit problem instance. We expect that these types of parameter transfer protocols will be useful in future implementations of QAOA. However, there is an important aspect of this which has not been studied up to this point. This is the case where the QAOA angles computed at a small problem size are so good that they reach an approximation ratio that is effectively 1—in other words, the QAOA performance plateaus (as a function of increasing p) to optimality. Once this occurs, good angles at higher p can no longer be meaningfully computed for the small problem instance^8,24,51, and thus good angles cannot be computed to be used for the larger problem instance. This is related to the question of QAOA scaling (how many p rounds we need in order to obtain good approximation ratios) as a function of increasing N. Succinctly, the task of investigating QAOA angle parameter transfer for extremely high p should be investigated in future research.

Methods

First we outline the hardware-compatible combinatorial optimization problems in subsection “Heavy-hex compatible ising models”. The QAOA algorithm is described in subsection “Whole-chip QAOA circuit description”; subsection “QAOA angle finding with JuliQAOA and parameter transfer” describes the optimized angle-finding and parameter transfer procedure that allows high-quality angles to be computed for 127-qubit QAOA circuits, and subsection “MPS simulations” describes the MPS simulations. Lastly, subsection “IBM quantum hardware implementation details” describes the hardware implementation.

Heavy-hex compatible ising models

The class of minimization combinatorial optimization problems that we consider are heavy-hex graph native spin glasses, and were introduced and described in refs. ^25,26. This class of models was designed specifically to be heavily optimized for a heavy-hex hardware graph⁵², and can include higher order terms (specifically geometrically local cubic terms), thus making the optimization problem more difficult. Importantly, although refs. ^25,26 used these problems for sampling 127 qubit heavy-hex native problems, this problem type is well defined for any heavy-hex hardware graph size. Here, we consider random instances of these problem types defined on 16, 27, 127, and 414 qubit IBM Quantum hardware graphs.

For a heavy-hex graph G = (V, E) and a vector of spins z = (z₀, …, z_n−1) ∈ {+1, −1}ⁿ we define a cost function

$$C(z)=\sum _{v\in V}{d}_{v}\cdot {z}_{v}+\sum _{(i,j)\in E}{d}_{i,j}\cdot {z}_{i}\cdot {z}_{j}+\sum _{l\in W}{d}_{l,{n}_{1}(l),{n}_{2}(l)}\cdot {z}_{l}\cdot {z}_{{n}_{1}(l)}\cdot {z}_{{n}_{2}(l)},$$

(1)

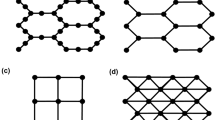
and a QAOA cost Hamiltonian H_C by replacing spin variables z_i with Pauli operators ${\sigma }_{z}^{i}$. Equation (1) defines a random spin glass problem with specific cubic terms: Any subgraph of a heavy-hex lattice is a bipartite graph with vertices V = {0, …, n − 1} is uniquely bipartitioned as V = V₂⊔V₃ with E ⊂ V₂ × V₃, where V_i consists of vertices of maximum degree i. W is the set of vertices l ∈ V₂ of exactly equal to 2, with neighbors denoted by n₁(l) and n₂(l), see Fig. 14. Thus d_v, d_i,j, and ${d}_{l,{n}_{1}(l),{n}_{2}(l)}$ are the linear, quadratic and cubic coefficients, respectively. The coefficients are chosen randomly from { + 1, −1} with probability 0.5, see Fig. 14. Figure 14 (bottom) shows an example problem instance defined on a 127 qubit heavy-hex graph.

Fig. 14: Examples of higher-order ising models that are hardware-compatible with a heavy-hex hardware graph.

(left) A 27-qubit device: Nodes correspond to linear terms, edges to quadratic terms, and hyperedges encircling three neighboring nodes to cubic terms. Ising coefficients of −1 and +1 are depicted in red and green, respectively. (right) A 16-qubit device: Illustrating the terminology of Equation (1), we have W = {2, 4, 5, 10, 11, 13}, with the remaining nodes in V₂ being V₂⧹W = {0, 6, 9, 15}. For node 4 ∈ W, we have neighbors {n₁(l), n₂(l)} = {1, 7} ⊂ V₃. (bottom) A 127-qubit device: Higher order Ising model comprised of 127 linear, 144 quadratic, and 71 cubic terms.

Instance generation and assessment

In Table 1, we give a summary of the studied hardware devices as well as the problem instances generated to run on these QPUs. For each group of QPUs sharing the same hardware graph, we generate 100 random problem instances according to Equation (1), which are shared across these devices.

One additional problem type we evaluate on a subset of the hardware experiments is Equation (1) without cubic terms, i.e., random spin glass problems with only linear and quadratic terms. To assess the achieved QAOA performances in context, we additionally compute for each instance the minimum (ground state) energy and the maximum energy. This is done with CPLEX⁵³ after pre-processing order reduction, which introduces auxiliary variables, as outlined in ref. ²⁶. These problems are solved by CPLEX as Mixed Integer Quadratic Programming (MIQP) problems where the decision variables are all binary.

Whole-chip QAOA circuit description

The quantum alternating operator ansatz consists of preparing the initial state $\left\vert \psi \right\rangle$, then for p rounds applying alternatingly the phase separating Hamiltonian H_C parameterized by the real number γ_i and the mixing Hamiltonian H_M parameterized by the real number β_i:

$$\left|{\vec{\gamma}},{\vec{\beta}}\right\rangle = \mathop{\underbrace{e^{-i\beta_p H_M} e^{-i\gamma_p H_C}}}\limits_{{\rm{round}}\,p}\cdots \mathop{\underbrace{e^{-i\beta_1 H_M} e^{-i\gamma_1 H_C}}}\limits_{{\rm{round}}\,1} \left|{\psi}\right\rangle$$

(2)

In each round, H_C is first applied which separates out the basis states of the state vector by phases e^−iγC(z). Next, H_M gives parameterized interference between solutions with different cost values. After p rounds, the state $\vert\overrightarrow{\gamma },\overrightarrow{\beta }\rangle$ is measured in the computational basis and thus finds a sample z of cost value C(z) with probability $| \langle z| \overrightarrow{\gamma },\overrightarrow{\beta }\rangle {| }^{2}$. Notably, the QAOA cost Hamiltonian can include higher order polynomial terms^54,55, without requiring ancilla qubit overhead. We make use of this property of QAOA in order to sample higher-order Ising models that are heavy-hex hardware-compatible, introduced in refs. ^25,26.

Figure 15 shows the QAOA circuit construction algorithm used in this study for one layer of the algorithm (p = 1), which is the same for all layers, specifically targeting the Ising model type defined in Equation (1). The transverse field mixer QAOA implementation is used in all circuits. A greedy Breadth-first search (BFS) three-edge-coloring is computed each time a circuit is constructed, and that same edge coloring is then used for all p layers in that circuit.

Fig. 15: From refs. ^25,26.

QAOA circuit description for heavy-hex graph compatible higher order Ising models of arbitrary size. The graph is bipartite and has an arbitrary three-edge-coloring given by Kőnig’s line coloring theorem. (left) Three-edge-coloring and bipartite gray-shading of the nodes. Adjacent purple lines denote the cubic terms. (right) Any quadratic term (colored edge) gives rise to a combination of two CNOTs and an Rz-rotation in the phase separator, giving a CNOT depth of 6 due to the degree-3 nodes. When targeting the degree-2 nodes with the CNOT gates, these constructions can be nested to implement the cubic terms with just one additional Rz-rotation.

The operators ${e}^{-i\beta {H}_{M}}$ and ${e}^{-i\gamma {H}_{C}}$ are 2π-periodic, hence we can restrict the QAOA angle search space to β_i, γ_i ∈ [0, 2π) for each round 1 ≤ i ≤ p. However, careful consideration of the parity of solution values as well as symmetries when starting in the state $\left\vert \psi \right\rangle =\left\vert {+}^{n}\right\rangle$ and measuring in the computational basis allows us to further restrict the search space to β₁, …, β_p−1 ∈ [0, π), ${\beta }_{p}\in [0,\frac{\pi }{2})$, and γ₁, …, γ_p ∈ [0, π), see Ref. ²⁶.

QAOA angle finding with JuliQAOA and parameter transfer

Arguably the most difficult aspect of implementing most variants of QAOA is determining good angles. Specifically, it is known that, in general, QAOA needs to be applied for a reasonably high number of rounds (p)^20,21 in order to get to high-quality solutions of combinatorial optimization problems. However, this requires high-quality angles (since, in almost all cases, there are no analytical solutions for optimal QAOA angles) for each p, and there are a total of 2p parameters that need to be optimized. The standard variational hybrid quantum-classical approach to this is to repeatedly evaluate the expectation value of the cost Hamiltonian H_C for different sets of angles on a quantum computer, using a classical algorithm to guide exploration in angle space. This approach is quite costly, however, with respect to total compute time. Moreover, because current quantum computers are quite noisy, learning good angles in this manner is, in general, hard, and, in particular, infeasible for a 127 qubit instance. A promising approach to mitigate some of these problems is to find good angles on smaller, more tractable instances and then use those same angles on larger instances. This technique, often referred to as parameter transfer or parameter concentration, has been shown to be effective, both analytically and numerically, for a number of different problem types^{12,22,25,26,27,28,29,30,31,32,33,56}. Motivated by the existing evidence for parameter transfer working for different problem sizes, and by the experimental evidence for parameter concentration across different random heavy-hex native Ising models observed in refs. ^25,26, we utilize parameter transfer in order to obtain good fixed angles for this class of random Ising models with higher-order terms. Specifically, we obtain good angles for p = 1, 2, 3, 4, 5 on a single random 16 qubit instance, and then validate that those angles transfer to other random 16 qubit instances, and random 27 qubit, as well as random 127 qubit instances. These angles are not optimal QAOA angles, rather they are high-quality heuristic angles, in particular meaning that we obtain reliable improvements in the mean energy as a function of p increasing.

The method we use to compute these good angles is the high-performance, QAOA-specific quantum simulator JuliQAOA⁵⁷ with 1000 basin hopping iterations and angle extrapolation (fixing the angles found at previous p-steps and initializing at those angles when proceeding to the next p). This allows us to find very high-quality angles, in this case, running O(10⁵) exact state vector simulations on one 16 qubit instance (derived from the ibmq_guadalupe architecture) with higher order terms for p = 1, …, 5. The QAOA angles are computed on one arbitrary 16 qubit instance so as to determine how well the parameters transfer for just one instance—and moreover, performing this computation once is much more efficient than repeating this for an entire ensemble of problems (although, this is a likely more robust approach that could be investigated in future study). Having trained on only one problem instance also allows us to evaluate how well the parameters transfer to the other 99 random 16 qubit instances. JuliQAOA has been used in several previous QAOA publications, with the goal of computing very high quality QAOA angles on general types of combinatorial optimization problems^8,16,24,51. The fixed angles used for the experiments shown in subsection “Scaling p on 16, 27, and 127 qubit IBM quantum processor hardware” are given explicitly below.

The trained QAOA angles up to p = 5 on a single 16 qubit problem instance (with cubic terms) using JuliQAOA⁵⁷, which were used for the parameter transfer onto much larger problem instances, are:

• p₁: β = [0.38919], γ = [6.04302]

• p₂: β = [0.48912, 0.27367], γ = [6.09758, 5.95396]

• p₃: β = [0.50502, 0.35713, 0.19264], γ = [6.14054, 6.01729, 5.94123]

• p₄: β = [0.54321, 0.41806, 0.28615, 0.16041], γ = [6.16242, 6.05959, 5.98417, 5.9299]

• p₅: β = [0.53822, 0.44776, 0.32923, 0.23056, 0.12587], γ = [6.16555, 6.08373, 6.01445, 5.9616, 5.93736]

These exact QAOA angles for p = 1 and p = 2 can be directly compared to the angles that were computed using high resolution grid-searches for this same class of optimization problems in refs. ^25,26; this comparison shows that the p = 1, 2 angles agree reasonably well, but are not exactly the same (note that there are angle symmetries that must be accounted for in order to compare these angles).

MPS simulations

We use MPS formalism to compute approximations to $\vert \overrightarrow{\gamma },\overrightarrow{\beta }\rangle$ in Equation (2). Specifically, a version of time-evolving block decimation⁵⁸ has been used to simulate the action of ${e}^{-i{\gamma }_{k}{H}_{C}}$ and ${e}^{-i{\beta }_{k}{H}_{M}}$ for k = 1, …, p. MPS tensors are ordered in the same way as the qubits are labeled in Fig. 14. The accuracy of MPS simulations is determined by bond dimension, denoted by χ here. In general, the accuracy is improved with increasing χ. Significant portion of the terms in ${e}^{-i{\gamma }_{k}{H}_{C}}$ are non-local and accurate simulation with MPS requires the bond dimension to grow quickly.

The Hamiltonian H_C is a sum of ${\sigma }_{i}^{z}$, ${\sigma }_{i}^{z}{\sigma }_{j}^{z}$ and ${\sigma }_{i}^{z}{\sigma }_{j}^{z}{\sigma }_{k}^{z}$ interactions. All those terms commute and ${\sigma }_{i}^{z}{\sigma }_{j}^{z}{\sigma }_{k}^{z}$ terms span the entire graph, so ${e}^{-i{\gamma }_{k}{H}_{C}}$ can be written as ${\prod }_{\overrightarrow{\alpha }}{e}^{-i{h}_{{\alpha }_{1},{\alpha }_{2},{\alpha }_{3}}}$, where $\overrightarrow{\alpha }=({\alpha }_{1},{\alpha }_{2},{\alpha }_{3})$ and each ${h}_{{\alpha }_{1},{\alpha }_{2},{\alpha }_{3}}$ is a three-body term acting on qubits (α₁, α₂, α₃). Importantly, each ${e}^{-i{h}_{{\alpha }_{1},{\alpha }_{2},{\alpha }_{3}}}$ can be written as a Matrix Product Operator with bond dimension 2. This is achieved by standard tensor network methods⁵⁹ that include series of tensor reshapes and SVDs of the original 8 × 8 matrix constructed from ${e}^{-i{h}_{{\alpha }_{1},{\alpha }_{2},{\alpha }_{3}}}$.

Further, three-body interactions are divided into groups such that gates ${e}^{-i{h}_{{\alpha }_{1},{\alpha }_{2},{\alpha }_{3}}}$ and ${e}^{-i{h}_{{\alpha }_{1}^{{\prime} },{\alpha }_{2}^{{\prime} },{\alpha }_{3}^{{\prime} }}}$ belong to the same group if and only if the sets {α₁, α₁ + 1, …, α₃} and $\{{\alpha }_{1}^{{\prime} },{\alpha }_{1}^{{\prime} }+1,\ldots ,{\alpha }_{3}^{{\prime} }\}$ are disjoint. This step is needed, so that the exact simulation of all gates ${e}^{-i{h}_{{\alpha }_{1},{\alpha }_{2},{\alpha }_{3}}}$ in a given group increases the MPS bond dimension by at most factor of 2, for some MPS tensors. After all the gates in a given group are applied, MPS is compressed, so the bond dimension does not increase beyond the predefined maximal value. The above manipulations of ${e}^{-i{\gamma }_{k}{H}_{C}}$ are performed to decrease the cost of MPS simulations and in turn, to increase the accuracy of the simulation. As a result, simulations with small p can be performed exactly and accuracy is expected to gradually deteriorate as p is increased.

We perform MPS simulations with χ = 2^m, for m = 4, …, 11 to estimate the impact of errors imposed by finite bond dimension. The summary of our results is presented in Fig. 16. All the panels show the error in the energy ΔE as a function of bond dimension. It is measured as ΔE = ∣E_χ − E₂₀₄₈∣, where ${E}_{\chi }=\langle {\psi }_{\chi }^{{\rm{MPS}}}\vert {H}_{C}\vert {\psi }_{\chi }^{{\rm{MPS}}}\rangle$. Here, $\vert {\psi }_{\chi }^{{\rm{MPS}}}\rangle$ is an MPS approximation to $\vert \overrightarrow{\gamma },\overrightarrow{\beta }\rangle$ in Equation (2) obtained by a simulation with maximum bond dimension of χ. Our most accurate simulations are performed with χ = 2048, and hence we treat E₂₀₄₈ as the best approximation to the exact energy. Solid, black lines in Fig. 16 represent ΔE averaged over one hundred instances of H_C. All simulation errors, for all instances of H_C, are within gray areas shown in Fig. 16.

Fig. 16: Error analysis performed for MPS simulations.

Here, we show the error in the energy ∣E_χ − E₂₀₄₈∣ as a function of bond dimension χ for different values of p. Solid black lines represent the error in the energy averaged over one hundred instances of H_C. All computed errors, for all instances, are contained within gray areas around black lines. The gray areas are relatively small, especially at large χ. This indicates that different instances of H_C result in similar errors. Errors are small; they are all below 0.1, which is observed in the hardest case of p = 5. Simulations with p < 5 incur smaller errors.

MPS simulations become exact for p = 1 and p = 2 at χ = 64 and χ = 1024, respectively. As pointed out above, the proper treatment of ${e}^{-i{\gamma }_{k}{H}_{C}}$ allows us to perform exact simulations at relatively small values of χ. The error ΔE drops to zero in those cases. Those values are not shown in p = 1 and p = 2 panels of Fig. 16. Simulations with p > 2 are no longer exact, but the errors are small and do not exceed 0.1 for p = 5. Note that ΔE is an absolute error in the energy. In relative terms, the error is below 10⁻³, given E₂₀₄₈ ≈−150 on average. It is important to note that all simulation errors, for all instances of H_C are similar to each other, especially in the large χ limit. This is indicated by very thin gray error areas around the mean values of the error in all panels. Our error analysis strongly suggests that our MPS simulation is dependable and sufficiently accurate (for considered values of p) to represent results that would have been obtained on a quantum computer in the limit of vanishingly small noise.

Since MPS is a unitary tensor network, one can draw bitstrings z from the probability distribution $P(z)=| \langle z| {\psi }_{\chi }^{{\rm{MPS}}}\rangle {| }^{2}$⁶⁰. That is, one can approximately calculate samples that would have been drawn from $\vert \overrightarrow{\gamma },\overrightarrow{\beta }\rangle$ in Equation (2), assuming that the quantum computer has been executing operations noiselessly. We use that fact to generate samples shown in Fig. 17.

Fig. 17: MPS simulation sample distributions, using a bond dimension of χ = 2048 for 127-qubit QAOA circuits sampling eight of the higher-order Ising model problem instances.

For each p, a total of 8192 samples are computed. The ground state energy is marked in all plots with a dashed vertical black line, and the minimum energy found within each p energy distribution is marked with a vertical solid line. In addition to the means of the distributions improving as a function of p (shown for all 100 problem instances in Fig. 1), we see here that the minimum energy sampled also improves as p increases. Notably, none of the distributions sampled the optimal energy, although the minimum energies from p = 4 and p = 5 are close to the optimal energy. These distributions show the ideal QAOA sampling capabilities, using the classical simulation method of MPS, if the quantum computation was noiseless.

On average, computing $\left\vert {\psi }_{\chi }^{{\rm{MPS}}}\right\rangle$ for p = 5 and χ = 2048 took less than 1.5 h on a 48-core computational node.

IBM quantum hardware implementation details

The quantum circuits are passed through the Qiskit³⁴ transpiler in order to adapt the circuits to the hardware native gateset, such as adapting the circuits to use the two qubit unidirectional echoed cross-resonance ECR⁶¹ gate. The QAOA circuits are heavily optimized for the heavy-hex hardware graph, so the compilation uses the fixed hardware graph and the compiler optimization is not able to reduce the two qubit gate count.

We also evaluate a relatively simple, and hardware gate-native, digital dynamical decoupling scheme of pulses of pairs of Pauli X gates, scheduled both as soon as possible (ASAP) and as late as possible (ALAP). This is implemented in Qiskit using the digital dynamical decoupling pass⁶². Dynamical decoupling is an open loop quantum control error suppression technique for mitigating decoherence on idle qubits^{63,64,65,66,67}, which can be approximated using digital sequences of single-qubit gates that are mathematically equivalent to applying the identity gate. Section 4.6 contains detailed compiled circuit renderings for p = 1 whole-chip 127 qubit QAOA circuits. Dynamical decoupling is used for these QAOA circuits specifically because it can mitigate errors on idle qubits encountered in the processor under some noise conditions, but importantly does not introduce compute overhead of additional samples or circuit executions since it is a compilation procedure that adds gates during idle periods of time for qubits.

The hardware results are reported in terms of the mean approximation ratio, which for random Ising models is defined over the full range of unconstrained energy values for a specific problem instance denoted as Min and Max, which for a specific energy sample e is defined as:

$${\text{Approximation}}\,{\text{Ratio}}=\frac{\text{Max}-e}{\text{Max}-\text{Min}}$$

(3)

The goal is to get the approximation ratio of the samples to be as close to 1 as the combinatorial optimization solver can get—an approximation ratio of 1 means that the sampled solutions are optimal.

Note that this definition of approximation ratio is consistent with the standard usage of approximation ratio - but it also means that random samples can, on average, have an approximation ratio of 0.5. Typically we will report the approximation ratio as the mean approximation ratio over a large distribution of samples—this is computed by taking the mean approximation ratio for each individual sample and then taking the mean over all of the approximation ratios for all of the samples.

Compiled whole-chip QAOA circuit diagram

Figure 18 shows the compiled and scheduled 127 qubit whole-chip QAOA circuits (p = 1) with dynamical decoupling sequences inserted, drawn using Qiskit³⁴. The rz gates are virtual gates⁶⁸, meaning they have no error rate, and the rz gates are represented as black circular arrow markers. The x gates are represented as vertical green lines, the sx gates are represented as vertical red lines, and the cx gates (e.g., CNOT gates) are represented by vertical blue lines that connect two qubit lines, and the ECR gates are represented by vertical purple lines that connect two qubit lines. The width of the gate instructions represent the time duration of the gates. The state of all qubits are measured at the end of the circuit, represented by dark gray blocks. The ASAP scheduling inserts more pairs of Pauli X gates compared to the ALAP scheduling.

Fig. 18: p = 1 timeline QAOA circuit for sampling Ising models that contain higher order terms.

Compiled to (both left)ibm_sherbrooke with native two qubit gate ECR and (both right)ibm_washington with native gate CX. For both devices, we compile with Pauli X gate pair dynamical decoupling passes inserted and scheduled ALAP(sub left) or ASAP(sub right). Gate times of ECR are more uniform, resulting in a denser gate scheduling, compared to the CX gate times, whose heterogeneity was not considered in the layered circuit design of Fig. 15. The ASAP scheduled circuits contain more overall idle qubit time, after a qubit has had at least one gate applied, resulting in more dynamical decoupling sequences being inserted compared to ALAP-scheduled circuits.

The timeline circuit diagrams proceed as a function of time on the x-axis, and this representation of the circuits shows that the ibm_washington compiled circuits in Fig. 18 used more time per circuit to execute a single circuit compared to the ibm_sherbrooke compiled circuits.

Note that the ibm_washington compiled circuits in Fig. 18 correspond to QAOA circuits that sample ibm_washington topology native Ising models (see refs. ^25,26), which means that there are two missing CNOTs in the hardware graph compared to the ibm_sherbrooke hardware graph.