Characterizing coherent errors using matrix-element amplification

Abstract

Repeating a gate sequence multiple times amplifies systematic errors coherently, making it a useful tool for characterizing quantum gates. However, the precision of such an approach is limited by low-frequency noise, while its efficiency is hindered by time-consuming scans required to match up the phases of the off-diagonal matrix elements being amplified. Here, we overcome both challenges by interleaving the gate of interest with dynamical decoupling sequences in a protocol we call Matrix-Element Amplification using Dynamical Decoupling (MEADD). Using frequency-tunable superconducting qubits from a Google Sycamore quantum processor, we experimentally demonstrate that MEADD surpasses the accuracy and precision of existing characterization protocols for estimating systematic errors in single- and two-qubit gates. We use MEADD to estimate coherent parameters of CZ gates with 5 to 10 times the precision of existing methods and to characterize previously undetectable coherent crosstalk, reaching a precision below one milliradian.

Introduction

Scalable quantum computation suffers from systematic errors, such as over-rotation and crosstalk. Characterizing these errors often requires coherently amplifying them by repeating the same gate sequence n times in a quantum circuit, a core principle of many schemes^1,2,3,4,5. This approach also allows one to distinguish errors in the gate of interest from state preparation and measurement (SPAM) errors; while gate errors accumulate linearly in n, SPAM errors only introduce a constant offset that is independent of n. However, in practice, noise in certain nuisance parameters often overshadows small, systematic, coherent errors of interest, limiting the extent to which they can be amplified and characterized precisely. In particular, frequency-tunable superconducting qubits suffer from fluctuations and drift in qubit frequencies^6,7, imposing a noise floor that limits the precision of standard characterization approaches.

In this work, we introduce matrix-element amplification using dynamical decoupling (MEADD)—a protocol to amplify coherent errors for their characterization, even in the presence of low-frequency noise. This is achieved by interleaving the gate of interest with carefully chosen single-qubit gates that implement a dynamical decoupling (DD) sequence^8,9,10,11,12, selecting a single target parameter by echoing away the noisy and irrelevant parameters. We experimentally demonstrate its accuracy, reliability, and efficiency for characterizing single- and two-qubit gates in superconducting qubits.

When only a few parameters need to be characterized, MEADD saves time by focusing on the specified parameters. Learning one parameter at a time makes data processing much easier and more reliable, especially when there are unmodeled errors. When measuring small off-diagonal transitions, MEADD also eliminates costly scans needed for identifying the resonance conditions, i.e., phase matching the transition matrix elements so that they add up constructively in a gate sequence. This gives MEADD greater efficiency in the number of experiments to run, which need only scale logarithmically in the maximum circuit depth, compared to similar noise-robust methods based on signal processing¹³, which scale linearly in circuit depth. In contrast to a hardware-agnostic method like gate set tomography (GST)⁵, MEADD is a special-purpose method that leverages knowledge of the noise and systematic errors in the hardware, which is often important to achieving high-quality results and efficient implementations. We expect that insights making MEADD useful in characterizing superconducting qubits can be applied to other qubit platforms, including leveraging the most precise control parameters for estimating less precise ones, isolating stable parameters from less stable and noisy ones, and targeting only a few parameters at a time. That being said, it will likely require domain expertise.

The MEADD protocol combines ideas from several established gate-characterization techniques. Like robust phase estimation (RPE)^1,2 and floquet characterization (FC)^3,4, MEADD measures eigenvalue differences, which can be amplified by repeating the same gate sequence n times. If the procedure works, the measured total phase fits a linear function of n well. The eigenvalue difference can be extracted from the slope of the linear function, while SPAM errors only contribute to the offset. The additional ingredient of MEADD over FC is to use DD sequences to ensure the eigenvalue difference only depends on one gate parameter at a time, much like what is done in Hamiltonian learning¹⁴ and Hamiltonian error amplifying tomography¹⁵. This isolation simplifies data processing, making it easy to debug and relatively robust to processes such as stray couplings and leakage.

An essential requirement of MEADD is robustness to systematic errors in the DD implementation, such as over rotations. These errors can also be amplified coherently, ultimately spoiling the estimation of the intended parameter. In Section “Robustness to implementation errors”, we present a systematic approach to constructing DD sequences such that these types of errors cancel each other to the first order, ensuring accuracy and reliability in practice. Such constructions depend on the gate of interest, and MEADD is most suitable for characterizing gates whose errors can be thought of as perturbations of the ideal gate. Therefore, a typical use of MEADD is to refine gates that are already calibrated with less precise but more versatile methods, such as cross-entropy benchmarking (XEB)^16,17. In practice, MEADD can tolerate gates with angle errors at least as large as several hundred milliradians, as one can see by the distributions of gate angles successfully characterized in Supplementary Information C.

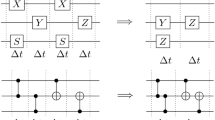
We illustrate the MEADD protocol using the CZ gate as an example in Fig. 1. To describe systematic errors in implemented CZ gates, we consider an arbitrary excitation-preserving two-qubit unitary W that is native to our hardware¹⁸. Up to an overall phase, such a unitary can be parameterized as

$$W=\left(\begin{array}{cccc}{e}^{i\gamma }&0&0&0\\ 0&{e}^{-i\zeta }\cos \theta &-i\,{e}^{i\chi }\sin \theta &0\\ 0&-i\,{e}^{-i\chi }\sin \theta &{e}^{i\zeta }\cos \theta &0\\ 0&0&0&{e}^{-i(\gamma +\phi )}\end{array}\right)\,,$$

(1)

where 0 ≤ θ ≤ π/2 is the swap angle, χ the swap azimuthal phase, ϕ the controlled phase, ζ the 10−01 Z phase, and γ the 00−11 Z phase. Here, we use the lexicographically ordered basis $\{\left\vert 00\right\rangle ,\left\vert 01\right\rangle ,\left\vert 10\right\rangle ,\left\vert 11\right\rangle \}$, where the left bit corresponds to the left qubit in tensor products and the top wire in circuit diagrams. The ideal CZ gate takes the parameters

$$\theta =\zeta =\gamma =0\,,\quad \phi =\pi \,,$$

(2)

and χ is indefinite for θ = 0. The swap angle θ and controlled phase ϕ determine the entangling properties of the two-qubit gate. The swap azimuthal phase χ can be regarded as a basis change of the two-qubit unitary, corresponding to a relative Z rotation of the two qubits; therefore, it must be considered in reference to those of the surrounding gates. The Z phases ζ and γ are especially susceptible to flux noise and drift in the control electronics present in our system. This ultimately hinders one’s ability to characterize precisely the entangling gate parameters, as shown schematically in Fig. 1c.

Fig. 1: Schematic of the working principle of MEADD.

a Standard gate repetition amplifies the matrix elements to estimate but also amplifies other coherent and incoherent (noise) processes. b Making use of single-qubit dynamical decoupling sequences, MEADD filters out specific matrix elements while additionally echoing out the noisy time-varying single-qubit phases. The parameter we are estimating—together with other matrix elements commuting with the DD gates—then builds up linearly with depth and can be fitted from the slope, with Heisenberg scaling in precision with circuit depth. All MEADD circuits possess this simple structure, with a preparation and pre-measurement layer containing at most a single entangling operation together with at most four single-qubit gates, and terminated by standard single-qubit Z-basis measurement. c Fluctuations in a noisy parameter γ (red), representing single-qubit phases, for example, can overshadow the estimation of a stable parameter ϕ (black) in a simple gate repetition scheme that provides estimates depending on both of these parameters (purple). Note that a separate and necessarily noisy estimation of γ is therefore required to find ϕ. In contrast, MEADD provides a direct estimate of the stable parameter ϕ as illustrated at the bottom, thus yielding more precise and accurate characterization information.

In Section “Theory on characterizing two-qubit gate”, we discuss how to use MEADD for characterizing general two-qubit excitation-preserving gates, including CZ, iSWAP, and $\sqrt{{\rm{iSWAP}}}$.

Results and discussion

In this section, we discuss how to characterize both single- and two-qubit gate parameters using MEADD. Remarkably, MEADD can estimate the entangling parameters of CZ gates with 5× and 10× higher precision than previous methods for the controlled-phase and swap angle, respectively. This characterization identifies systematic errors in the implemented quantum operations which can then be corrected for by adjusting the control parameters. In addition, we present experimental results of MEADD on characterizing unwanted crosstalk couplings that were too small to measure previously.

Characterizing CZ

Before describing the MEADD protocol, we first benchmark it against other methods with the CZ gates calibrated using our existing procedure, which can be regarded as excitation-preserving two-qubit gates (1) close to the ideal CZ. In Fig. 2, we compare MEADD to cross-entropy benchmarking (XEB)¹⁷, unitary tomography (UT)¹⁸, and the phase method (PM)⁴. XEB uses random circuits to scramble errors into an effective depolarizing channel and infers unitary parameters by fitting the observed outcome probabilities to those predicted by the unitary in Eq. (1) combined with depolarizing noise. Unitary tomography measures observables whose expectation values correspond to the real and imaginary parts of the matrix elements of an excitation-preserving two-qubit gate. This is achieved by using the eigenstate $\left\vert 00\right\rangle$ as a phase reference. The phase method uses the same initial states and observables as unitary tomography while repeating the gate to be characterized along with additional Z phases for various cycle numbers to amplify coherent errors. By varying these Z phases, one can determine all the matrix elements of the gate of interest by merely estimating the eigenvalue differences of the cycle unitary.

Fig. 2: Experimental results of MEADD on CZ gates (excitation-conserving two-qubit gates close to the ideal CZ).

All data are collected from a 69-qubit Google Sycamore processor, see Supplementary Information in ref. ¹⁷ for details of the processor. a Fidelities obtained using the context-aware fidelity estimation (CAFE) protocol¹⁹. These fidelities indicate how well a particular unitary characterization corresponds to the implementation of the CZ gate, and are presented for unitaries characterized by MEADD (blue), cross-entropy benchmarking (XEB, orange), and the perfect CZ unitary (gray). Solid lines with markers are the median over 85 different CZ gates of a single Sycamore device, and the shaded regions are the inner quartile regions. A higher CAFE fidelity corresponds to a more accurate unitary characterization of the gate, see text for details. The inset shows the empirical cumulative distribution functions (CDF) of the coherent errors inferred from the CAFE curves of every CZ gate, with median values reported in the legend. Also shown are the results obtained using the unitary tomography (UT, green) and the phase method (PM, red) characterization protocols. b Empirical CDFs of run-to-run standard deviations in the characterized controlled phase ϕ, and c swap angle θ, measured over 12 sequential characterizations of the 85 CZ gates. The different protocols were interleaved with one another over several hours to average out device inconsistencies. The median standard deviations of the different methods are reported in milliradian in the plots.

In Fig. 2a, we use a recently introduced protocol named context-aware fidelity estimation (CAFE)¹⁹ to assess the accuracy of the different characterization methods, where the average gate fidelity between the learned unitary and the physical gate implemented is estimated. CAFE estimates this fidelity from an ensemble of circuits with an average expectation value dependent only on the fidelity. Much like direct fidelity estimation²⁰ and randomized benchmarking²¹, this provides an estimate of fidelity that is simultaneously independent of any characterization scheme and more efficient than process tomography. Using different numbers of gate repetitions n gives the protocol robustness to SPAM errors and allows for error budgeting in terms of incoherent and coherent contributions, as these errors build up linearly and quadratically with n to lowest order¹⁹.

The unitaries extracted with MEADD outperform all other unitary characterization techniques as measured by CAFE. Specifically, looking at the inset of Fig. 2a, we see that MEADD captures significantly more of the coherent error budget (80% of the difference to the ideal gate), resulting in a median of 2.5 × 10⁻⁴ uncharacterized coherent error across the 85 CZ gates characterized, 3–5× smaller than the other methods. The remaining 20% unaccounted coherent error derives from statistical noise and qubit-frequency fluctuations that CAFE does not echo away. We note that a variant of CAFE with DD gates, called DECAF¹⁹, can provide a more fine-grained benchmark of errors that excludes qubit-frequency fluctuations, though we exclusively cite CAFE numbers in this work to demonstrate the holistic utility of using MEADD.

In Fig. 2b, c, we compare the precision of MEADD to the other methods by repeating the different unitary characterization techniques and reporting the run-to-run standard deviation of the estimated controlled phase ϕ and swap angle θ for all 85 CZ gates of the device. MEADD provides significantly more consistent characterizations than any other method, with 5× and 10× improvements over XEB for the controlled phase ϕ and swap angle θ, respectively. Remarkably, MEADD achieves a 3.4 × 10⁻⁴ rad standard deviation for estimating the residual swap angle θ of our CZ gates. Such precision, below one milliradian, promises to be a key asset in the calibration of stable high-fidelity two-qubit gates as required for scalable quantum error correction applications. The actual values of θ and ϕ characterized by the various protocols are presented in Supplementary Information C.

Having presented the benchmarking results for our CZ gates, we now overview the four main steps of the MEADD protocol:

1. Precalibrate the CZ gates to be close to the ideal CZ, with a more generic method.

2. Characterize the controlled phase ϕ using the circuits illustrated in Fig. 3a.

Fig. 3: MEADD circuits used to characterize the entangling parameters of CZ gates.

a The circuits are composed of three steps. Prepare $\left\vert +0\right\rangle$ with a microwave gate (blue), or similarly $\left\vert 0+\right\rangle$ (not shown), interleave X ⊗ X dynamical decoupling gates (yellow) with the repeated CZ gates for even repetitions 2n, and finally measure both qubits in the X and Y bases (green). As explained in the main text, combining the resulting measurement bits for different depths n yields an estimate of the controlled phase ϕ that is robust to both low-frequency noise and DD gate imperfections. b Similarly, for the swapping angle θ and phase χ, we prepare $\left\vert 10\right\rangle$ (or $\left\vert 01\right\rangle$, not shown), use X ⊗ X and Y ⊗ X as DD gates, and measure either in the computational basis of both qubits (top circuit) or in the Bell basis of the odd parity subspace (bottom circuit), where ${X}_{{\rm{odd}}}=\left\vert 10\right\rangle \left\langle 01\right\vert +\left\vert 01\right\rangle \left\langle 10\right\vert$ and ${Y}_{{\rm{odd}}}=i\left\vert 10\right\rangle \left\langle 01\right\vert -i\left\vert 01\right\rangle \left\langle 10\right\vert$.

3. Characterize the swap angle θ and azimuthal phase χ using the circuits illustrated in Fig. 3b.

4. Characterize the Z phases ζ and γ using the method introduced in our previous work^3,4, also see Supplementary Information A.

Section “Theory on characterizing two-qubit gate” covers the details behind characterizing ϕ and θ. Measuring the expectation values 〈X〉 + i〈Y〉 on each qubit for the different initial states gives one the matrix elements for the evolution matrix (non-unitary due to decoherence) in the single-excitation (odd-parity) subspace. Taking the determinant of these matrices and fitting the complex angle as a function of n to a line allows one to extract ϕ from the slope.

The estimation of θ can be broken down into two independent measurements of the real and imaginary part of the swap matrix element ${e}^{i\chi }\sin \theta$. The real and imaginary parts are selected by choosing the relative phase of the DD gates that echo away the unwanted part. By preparing a single-excitation state and measuring both population transfer between the two qubits and coherence in different Bell bases, one extracts both Bloch-vector components in the plane of rotation. Fitting the angle of this Bloch vector as a function of n allows one to extract the swap around each axis from the slopes.

Supplementary Information A details how to extract the Z phases ζ and γ by getting matrix elements from the expectation values 〈X〉 + i〈Y〉 like is done for characterizing ϕ, though using circuits without DD. The Z phase γ is extracted by fitting the complex angle of the determinant of the evolution matrix in the odd-parity subspace, while ζ is extracted by fitting phases of the singular-value decomposition of the same matrix.

For the analysis to carry through in the DD circuits for measuring θ and ϕ, the CZ gate must be repeated an even number of times. The robustness analysis of Section “Robustness to implementation errors” reveals that microwave errors are canceled to first order when the CZ repetitions are a multiple of 4, though the fact that these errors do not coherently build up means that simply using multiples of 2 works in practice. For the circuits characterizing ζ and γ, one can use arbitrary repetitions of the CZ gate.

Choosing the maximum number of repetitions in practice depends on the coherence of the device and precision of the microwave gates, see Supplementary Information F. One can evaluate this by running a single experiment with many depths and observing when the data starts deviating significantly from linearity. We find that a maximum depth of 14 repetitions on our device yields reliable data and produces the precision we cite in this work. The same arguments advanced for RPE^1,2 for using logarithmically-spaced depths apply to our method, though for modest maximum depths taking linearly spaced data adds little overhead and produces datasets that are more informative for diagnosing failure modes.

After learning the deviations of the CZ gate parameters, we can correct them by fine-tuning the control pulses in our quantum processors. Here, we briefly discuss this procedure. The exact details are beyond the scope of this work, as they are necessarily implementation dependent and often involve making trade offs among multiple parameters^18,22.

One can separate the entangling parameters θ and ϕ from the rest using a special case of the KAK decomposition²³, as shown in Fig. 4. Therefore, we can zero out the Z phases ζ and γ by applying compensating single-qubit Z rotations before and after the CZ gate. This can be implemented by simply changing the phases of the microwave pulses, without introducing any additional flux pulses, see virtual single-qubit Z rotations in Section “Single-qubit gates”. We can also zero out the swap azimuthal angle χ using the same method. However, it is inconsequential for θ ≪ 1.

Fig. 4: Two equivalent ways to decompose the arbitrary excitation-preserving two-qubit gate defined in Eq. (1) into single-qubit Z rotations and the fundamental entangler F(θ, ϕ) = e^{−iθ(X⊗X+Y⊗Y)/2−iϕZ⊗Z/4}.

While the differential phases ζ_± = (ζ ± χ)/2 do not commute with F(θ, ϕ), the symmetric phase ${\gamma }^{{\prime} }=\gamma +\phi /2$ does and can be placed either before or after the entangling operation.

Correcting θ and ϕ involves adjusting the pulses used for generating entanglement between the qubits. Our diabatic CZ gates are performed by a triplet of control pulses²². Two flux pulses on both qubits bring the two interacting levels, 02 and 11, into resonance. At the same time, a third pulse on the coupler activates a tunable excitation-preserving interaction between the two qubits. The controlled phase ϕ is sensitive to the detuning between the two interacting levels controlled by the first two pulses, while the swap angle θ can be fine-tuned by adjusting the rise time of the third pulse. Synchronized minimization of the leakage and swap errors can be achieved by tuning the hold time (duration of the plateau) and height of the third pulse.

Crosstalk

In our hardware, crosstalk between qubits can arise due to unwanted charge-charge (capacitive) couplings, which results in a qubit-subspace Hamiltonian of the form

$${H}_{{\rm{xtalk}}}\propto {e}^{i\chi }\,{\sigma }_{+}\otimes {\sigma }_{-}+{\rm{h.c.}},$$

(3)

where ${\sigma }_{+}={\sigma }_{-}^{\dagger }=\left\vert 0\right\rangle \left\langle 1\right\vert$ and we neglect the counter-rotating terms. This coupling produces an excitation swapping between the two qubits with angle θ_xtalk. These terms are typically on the order of 100 kHz, much smaller than the detuning of the two qubits on the order of 100 MHz. Therefore, they are suppressed and often hard to measure. The errors this incurs for typical gate times (10s of nanoseconds) yield average gate infidelities between 1 × 10⁻⁵ and 1 × 10⁻⁴, which while small, can be particularly damaging due to their nonlocal nature within error-correcting circuits²⁴.

A typical strategy for measuring θ_xtalk is to tune the qubits to resonance. Since the qubit frequency uncertainty is typically on the order of 100 kHz, such a strategy requires scanning over the qubit-frequency control to find the resonance, which is time-consuming to perform in practice. In contrast, we can use MEADD to directly estimate the unwanted crosstalk without any qubit frequency tuning.

Experimental results are shown in Fig. 5. In (a), we plot data with an unambiguous signal for a crosstalk swapping angle on the order of 1 mrad. We can fit this data to reliably characterize the angle with a precision below 0.1 mrad, as shown in panel (c), which corresponds to an uncertainty on the effective swapping coupling strength of less than 0.5 MHz. Note that this protocol can readily be used to characterize long-range crosstalk across distant qubits on the processor.

Fig. 5: Experimental results of MEADD for characterizing crosstalk.

a Evolution of the components of the Bloch vector in the odd-parity sector, ${X}_{{\rm{odd}}}=\left\vert 10\right\rangle \left\langle 01\right\vert +\left\vert 01\right\rangle \left\langle 10\right\vert$, ${Y}_{{\rm{odd}}}=i\left\vert 10\right\rangle \left\langle 01\right\vert -i\left\vert 01\right\rangle \left\langle 10\right\vert$, and ${Z}_{{\rm{odd}}}=\left\vert 01\right\rangle \left\langle 01\right\vert -\left\vert 10\right\rangle \left\langle 10\right\vert$, for two neighboring qubits involved in 2n parallel CZ gates. The corresponding crosstalk angle is about 4 mrad per cycle. Error bars correspond to the standard deviation over 2000 shots and are smaller than the data markers. Distributions of b the median crosstalk swap angle θ_xtalk and c the run-to-run standard deviation in this estimate after repeating the measurement 10 times over 1 h for 24 neighboring CZ gates on the Sycamore processor, revealing a median signal 6 times larger than the median noise. As shown in the inset, the 34 ns CZ gates (gray) are performed simultaneously on neighboring qubit pairs (green and yellow), and we use MEADD to characterize the residual swap angle produced by these operations, yielding θ_xtalk = (0.42 ± 0.07) mrad on median.

This kind of crosstalk cannot be calibrated away by simply tuning the control pulse and has to be tackled at the hardware level. That being said, we can minimize their effect by putting the involved qubits at frequencies that are far apart from each other during idling and gates.

Single-qubit gates

Leveraging the hierarchy of precision in the different controls available on a quantum device is central to designing highly accurate, reliable, and efficient characterization protocols. To that end, we present the considerations for calibrating single-qubit gates in tunable-frequency superconducting qubits, highlighting the principal noise sources therein^7,25,26,27.

We first describe the way that single-qubit gates are implemented in our hardware. Understanding these details is crucial to designing efficient characterization protocols for our device. Consider a qubit driven by a microwave pulse, where we ignore leakage errors into energy levels lying outside of the qubit subspace. Under the rotating wave approximation (RWA), the Hamiltonian for this two-level system is (ℏ = 1)

$${H}_{{\rm{RWA}}}(t)=-\frac{1}{2}\,{\omega }_{01}(t)\,Z+\left(\Omega (t)\,{e}^{-i\nu t}{\sigma }_{-}+{\rm{h.c.}}\right),$$

(4)

where $Z=\left\vert 0\right\rangle \left\langle 0\right\vert -\left\vert 1\right\rangle \left\langle 1\right\vert$, $\left\vert 0\right\rangle$ and $\left\vert 1\right\rangle$ representing the ground and first excited states of the qubit, respectively. The terms with ${\sigma }_{-}=\left\vert 1\right\rangle \left\langle 0\right\vert$ and its Hermitian conjugate ${\sigma }_{+}=\left\vert 0\right\rangle \left\langle 1\right\vert$ capture the microwave control field, where Ω(t) is an envelope function with bandwidth ~100 MHz and ν/2π is the nominal microwave frequency, sitting at several GHz. The parameter ω₀₁(t) is the angular frequency of the qubit, adjustable via the SQUID loop flux. Ideally, ω₀₁(t) matches ν during idle periods and rotations about axes in the XY plane. However, noise in the flux control line and surrounding electromagnetic environment can cause ω₀₁(t) to drift, leading to various errors when performing qubit operations. This can be seen directly by moving to the interaction frame of the microwave frequency $\left\vert {\psi }_{I}(t)\right\rangle ={e}^{-i\nu tZ/2}\left\vert \psi (t)\right\rangle$, which eliminates the rapidly oscillating phase e^−iνt in Eq. (4) as follows

$${H}_{{\rm{I}}}(t)={e}^{-i\nu tZ/2}{H}_{{\rm{RWA}}}(t)\,{e}^{i\nu tZ/2}+\frac{1}{2}\,\nu Z\,$$

(5)

$$=-\frac{1}{2}\,\delta {\omega }_{01}(t)\,Z+\left(\Omega (t)\,{\sigma }_{-}+{\rm{h.c.}}\right).$$

(6)

Here, one can directly see how any non-zero detuning δω₀₁(t) = ω₀₁(t) − ν ≪ ν can lead to unwanted Z rotations. The resulting unitary produced by this drive can be formally written as

$${U}_{I}={\mathcal{T}}\exp \left(-i\mathop{\int}\nolimits_{\!{t}_{i}}^{{t}_{f}}{H}_{I}(t)\,dt\right)\,,$$

(7)

where ${\mathcal{T}}$ is the time ordering operator and t_i (t_f) is the initial (final) time of the pulse.

We now discuss how to implement quantum logical circuits in the above interaction picture, i.e. control H_I(t) such that U_I corresponds to the desired quantum gate. Note that as we always initialize and measure the qubits in the Z basis, there is no need to implement the unitary e^−iνtZ/2 for the frame change before the final measurement. However, any gate operation that is not diagonal in the Z basis needs to account for the frame change, a process known as phase tracking or matching.

Single-qubit XY rotations (microwave gates)

An arbitrary SU(2) matrix can be parameterized using three angles as

$$R(\mu ,\zeta ,\chi )=\left(\begin{array}{cc}{e}^{-i\zeta }\cos \frac{\mu }{2}&-i\,{e}^{i\chi }\sin \frac{\mu }{2}\\ -i\,{e}^{-i\chi }\sin \frac{\mu }{2}&{e}^{i\zeta }\cos \frac{\mu }{2}\end{array}\right)\,,$$

(8)

where we have recycled some Greek letters used in the single-excitation subspace of the two-qubit gate (1), which shares the same SU(2) structure. This parametrization directly leads to an Euler decomposition of arbitrary single-qubit gates as an X rotation sandwiched by two Z rotations:

$$R(\mu ,\zeta ,\chi )=Z(\zeta -\chi )\,X(\mu )\,Z(\zeta +\chi )\,,$$

(9)

where

$$X(\varphi )={e}^{-i\varphi X/2},\qquad Z(\varphi )={e}^{-i\varphi Z/2}.$$

(10)

The rotation X(μ) can be achieved by applying a microwave pulse to the qubit, e.g., Ω(t) = μ C(t), where C(t) is the shifted cosine function

$$C(t)=\left\{\begin{array}{ll}\frac{1}{2T}\left(1+\cos \frac{2\pi t}{T}\right),\quad &\,{\text{for}}\,-\frac{T}{2}\le t\le \frac{T}{2}\,,\\ 0,\quad &\,{\text{for}}\,| t| > \frac{T}{2},\end{array}\right.$$

(11)

where the pulse time T is around 15 ns in our system. As such, the parameter μ of the single-qubit gate is directly determined by the amplitude of the microwave drive, which can be controlled to a high precision using standard arbitrary waveform generators.

More generally, we consider a rotation along an arbitrary axis in the XY plane, which we notate as a phased-X rotation

$${\rm{PhX}}(\mu ,\vartheta )\equiv Z(\vartheta )\,X(\mu )\,Z(-\vartheta )\,,$$

(12)

where μ and ϑ specify the angle and axis of the rotation, respectively. It can be implemented by simply changing the phase of the microwave pulse

$$\Omega (t)=\mu {e}^{i\vartheta }C(t)\,.$$

(13)

This microwave phase can be used to control χ much more precisely than the uncertainties on the qubit phase, making it an ideal control knob to use in designing characterization protocols. Additionally, the freedom we have in the microwave phase allows us to eliminate one Z rotation from our single-qubit gate

$$R(\mu ,\zeta ,\chi )=Z(2\zeta ){\rm{PhX}}(\mu ,-\zeta -\chi )\,,$$

(14)

which can save time and reduce errors.

In practice, we additionally make corrections to the pulse, such as compensating for the AC Stark effect by introducing a detuning Δ(μ),

$$\Omega (t)=\mu {e}^{i\vartheta }{e}^{-i\Delta (\mu )t}C(t)\,,$$

(15)

which can also be used to adjust the gate parameter ζ. Finally, we make use of derivative removal by the adiabatic gate (DRAG)²⁸ pulses to mitigate leakage errors, which consist of mixing the original pulse Ω(t) with its first-time derivative; see Supplementary Information E for a simple derivation. Impedance mismatches in the control lines can reflect microwave pulses, which cause delayed tails after the main pulses. Here we assume that these tails do not bleed into the entangling pulses such as to preserve the independence of consecutive gates.

Physical and virtual single-qubit Z rotations

Rotations around the z-axis can be implemented simply by moving the qubit frequency away from ν for some duration using a flux pulse while leaving Ω(t) = 0. This can be seen directly by considering the evolved qubit state in the interaction frame under the propagator of Eq. (7)

$$\left\vert {\psi }_{I}({t}_{f})\right\rangle ={e}^{i\varphi ({t}_{f},{t}_{i})Z/2}\left\vert {\psi }_{I}({t}_{i})\right\rangle \,,$$

(16)

where the Z-rotation angle reads

$$\varphi ({t}_{f},\,{t}_{i})=\mathop{\int}\nolimits_{\!{t}_{i}}^{{t}_{f}}\delta {\omega }_{01}(t)\,dt\,.$$

(17)

This type of Z rotation typically takes ~20 ns to implement on our hardware (including a ~10 ns pulse and two 5 ns paddings before and after the pulse), regardless of the angle, with a corresponding gate infidelity of about 10⁻³. However, these physical Z pulses typically have nonzero tails lasting much longer than the gate time^29,30,31, on the order of hundreds of ns in our devices, which can disturb many subsequent operations.

For quantum circuits consisting of only single-qubit gates and diagonal two-qubit gates, such as the CZ gate, the Z rotations can be implemented in software without actually sending flux pulses to the qubits²⁶. This is because Z rotations commute with diagonal two-qubit gates, and when commuted through a microwave gate, only change its phase χ, which we can control with high precision relative to physical Z rotations.

In more detail, one can push single-qubit Z rotations from the beginning of the circuit down—through any two-qubit gates—and combine them with other Z rotations along the way until they hit single-qubit gates that are not Z rotations. One can then use Eq. (14) to put the Z rotations after the XY rotations and repeat the same procedure until all the single-qubit Z rotations are pushed to the end of the circuit. Finally, they can be directly eliminated because the qubits are measured in the Z basis. The above process also works for two-qubit gates that are diagonal up to a SWAP, such as iSWAP. However, physical Z rotations are still required for most other two-qubit gates, and they are typically applied before every two-qubit pulses in these cases.

Relative axes of XY rotations

Consider a circuit consisting of only XY rotations and diagonal two-qubit gates, such as CZ. One can implement the following gauge transformation on all the XY rotations without affecting the measurement results

$${\chi }_{j}\to {\chi }_{j}+\,\text{constant}\,,$$

(18)

where χ_j is the rotation axis of the jth XY gate. Therefore, the absolute value of χ has no physical significance and cannot be measured using such circuits. The relative χ between two different XY rotations, however, is physical and needs to be calibrated. For example, we consider the relative χ between a π gate and a π/2 gate, which is nonzero due to effects such as ac-Stark shifts imparting χ differently for different values of μ. Suppose one has a well calibrated −π/2 pulse, meaning μ = −π/2 and ζ has been removed through virtual Z phase updates,

$$R(-\pi /2,0,{\chi }_{\pi /2})=Z(-{\chi }_{\pi /2})\,X(-\pi /2)\,Z({\chi }_{\pi /2})\,,$$

(19)

and a π pulse with well well-calibrated rotation angle μ

$$R(\pi ,0,{\chi }_{\pi })=Z(-{\chi }_{\pi })\,X(\pi )\,Z({\chi }_{\pi })\,.$$

(20)

One can characterize the relative phase χ_π/2 − χ_π by considering the composite gate:

$$R(\pi ,0,{\chi }_{\pi })R(-\pi /2,0,{\chi }_{\pi /2})$$

(21)

$$=Z({\chi }_{\pi /2}-2{\chi }_{\pi })\,X(\pi /2)\,Z({\chi }_{\pi /2})$$

(22)

$$=R(\pi /2,\zeta ,\chi )\,,$$

(23)

where

$$\zeta ={\chi }_{\pi /2}-{\chi }_{\pi }\,,\qquad \chi ={\chi }_{\pi }\,.$$

(24)

The relative phase is now ζ of the composite gate and can be estimated using our characterization circuits.

In Fig. 6, we present experimental results for interleaved single-qubit X(−π/2) and X(π) gates over the 69 qubits of the device. This can be regarded as an example of MEADD for single-qubit gates, where low-frequency flux noise is echoed away by the X(π) gates. In panel (a), we compare the CAFE results obtained using the unitaries constructed from the MEADD estimates (blue) of the relative axis ζ = χ_π/2 − χ_π in Eq. (24) to the ones assuming perfect gates (gray). The higher fidelities obtained from the MEADD unitaries indicate that these characterizations accurately describe the implemented gates. In panels (b) and (c), we compare the MEADD characterization results to a direct 4-axis tomography protocol which consists of preparing an equatorial state, applying an X(π) pulse, and then measuring expectation values of X and Y. Since the state preparation and measurements use X(−π/2) gates, this protocol measures the relative axes of the X(π) and X(−π/2) gates just like MEADD with interleaved X(−π/2) and X(π) gates does, as described at the end of Section “Theory on characterizing single-qubit gate”. MEADD achieves a median run-to-run standard deviation of 6.11 × 10⁻⁴ rad on estimating ζ, a 6× improvement over the tomography protocol, which is the single-qubit equivalent of unitary tomography. This is illustrated in panel (b) for a representative qubit, showing the tight distribution of repeated MEADD characterizations. We do not compare with XEB, as the single-qubit implementation only reports the gate fidelity, not a unitary characterization.

Fig. 6: Experimental results of MEADD for interleaved single-qubit X(−π/2) and X(π) gates.

a CAFE results for the single-qubit unitaries characterized by MEADD (blue) compared to assuming a perfect gate (gray) for 69 qubits of a single Sycamore device. The cycle circuit being repeated in CAFE is the same as in the MEADD protocol, namely a X(−π/2) rotation followed by a X(π) rotation, performed in parallel on all qubits. Solid lines with markers are the median over the 69 qubits, and the shaded regions are the inner quartile regions. b Distributions of the characterized relative rotation axis parameter ζ = χ_π/2 − χ_π defined in Eq. (24) for a representative single-qubit gate characterized 32 times interleaved between MEADD (blue) and 4-axis tomography (orange), using the same number of measurements for both methods. c Distributions of run-to-run standard deviations in ζ estimates for the two methods over the 32 sequential characterizations of the 69 qubits. The median standard deviations of the two methods are reported in milliradian.

Methods

In this section, we first discuss the theoretical framework for characterizing single-qubit gates using matrix-element amplification. We then extend this framework to characterize general two-qubit excitation-preserving gates, including CZ, iSWAP, and $\sqrt{{\rm{iSWAP}}}$. Finally, we discuss how to construct MEADD protocols that are robust to implementation errors in the DD gates.

Theory on characterizing single-qubit gates

Having presented the experimental results of MEADD, we now describe the theory behind the protocol, starting with the single-qubit version. The single-qubit protocol bears similarity to RPE^1,2, though we are able to simplify the protocol by taking advantage of the high precision with which microwave phases can be set relative to other errors in the system, as discussed in Section “Single-qubit gates”.

For the arbitrary single-qubit gate R(μ, ζ, χ) in Eq. (8), we set μ = 2θ to draw an explicit connection to the two-qubit parametrization (1),

$$R(\mu ,\zeta ,\chi )=I\cos \Omega (\theta ,\zeta )-i\,\sigma (\theta ,\zeta ,\chi )\sin \Omega (\theta ,\zeta )\,,$$

(25)

where

$$\cos \Omega =\cos \theta \cos \zeta \,,\quad \Omega \in [\theta ,\pi -\theta ]\,,$$

(26)

and the spin-1/2 operator

$$\sigma =\frac{\sin \theta }{\sin \Omega }\left(X\cos \chi -Y\sin \chi +Z\cot \theta \sin \zeta \right)\,.$$

(27)

In matrix form, we have

$$\sigma (\theta ,\zeta ,\chi )=\left(\begin{array}{cc}\cos \varrho &{e}^{i\chi }\sin \varrho \\ {e}^{-i\chi }\sin \varrho &-\cos \varrho \end{array}\right)\,,$$

(28)

where the polar angle ϱ is defined by

$$\varrho ={\rm{arccot}}(\cot \theta \sin \zeta )\,,\quad \varrho \in [\theta ,\pi -\theta ]\,.$$

(29)

For example, we have Ω = π/2, ϱ = π/2, and χ = 0 for the ideal X(π) gate.

We can measure the eigenvalues ±Ω(θ, ζ) of R precisely by preparing and measuring uniform superpositions of the eigenstates of R,

$$\left\vert {\sigma }^{+}\right\rangle ={e}^{i\chi /2}\cos (\varrho /2)\,\left\vert 0\right\rangle +{e}^{-i\chi /2}\sin (\varrho /2)\,\left\vert 1\right\rangle$$

(30)

$$\left\vert {\sigma }^{-}\right\rangle ={e}^{i\chi /2}\sin (\varrho /2)\,\left\vert 0\right\rangle -{e}^{-i\chi /2}\cos (\varrho /2)\,\left\vert 1\right\rangle \,,$$

(31)

where $\sigma \left\vert {\sigma }^{\pm }\right\rangle =\pm \left\vert {\sigma }^{\pm }\right\rangle$. We parametrize these superpositions by the relative phase τ between them

$$\left\vert \Phi (\tau )\right\rangle =\frac{1}{\sqrt{2}}\left({e}^{-i\tau /2}\left\vert {\sigma }^{+}\right\rangle +{e}^{i\tau /2}\left\vert {\sigma }^{-}\right\rangle \right)\,.$$

(32)

After applying the cycle unitary n times to the initial state, we have

$${R}^{n}\left\vert \Phi ({\tau }_{0})\right\rangle =\left\vert \Phi ({\tau }_{0}+2n\Omega )\right\rangle \,.$$

(33)

We then measure the probability of finding $\left\vert \Phi (0)\right\rangle$,

$${P}_{0}=| \langle \Phi (0)| \Phi ({\tau }_{0}+2n\Omega )\rangle {| }^{2}$$

(34)

$$=\frac{1+\cos ({\tau }_{0}+2n\Omega )}{2}\,,$$

(35)

and the probability to find $\left\vert \Phi (\pi /2)\right\rangle$ is

$${P}_{\pi /2}=| \langle \Phi (\pi /2)| \Phi ({\tau }_{0}+2n\Omega )\rangle {| }^{2}$$

(36)

$$=\frac{1+\sin ({\tau }_{0}+2n\Omega )}{2}\,.$$

(37)

Estimating these two measurement probabilities for a sequence of repetitions will give us the measurement record

$$2{P}_{0}-1+i(2{P}_{\pi /2}-1)=\exp \left[i({\tau }_{0}+2n\Omega )\right],$$

(38)

from which we can extract Ω by fitting the complex argument as a linear function of repetitions. This procedure is robust to SPAM errors. In particular, the initial states can be prepared assuming ideal microwave gates since errors in these gates result in nonuniform superpositions of the eigenstates $\left\vert {\sigma }^{\pm }\right\rangle$ that merely reduce the contrast of the oscillations in P₀ and P_π/2.

To extract the gate parameters μ and ζ, we perform a set of similar experiments, where we add different virtual Z rotations between the gates, giving us unitaries

$$Z(z)R(\mu ,\zeta ,\chi )=Z(\zeta +z-\chi )\,X(\mu )\,Z(\zeta +\chi )$$

(39)

$$=R\left(\mu ,\zeta +z/2,\chi -z/2\right)\,.$$

(40)

By measuring Ω(θ, ζ + z/2) as a function of z, one can fit the curve to the form given in Eq. (26), obtaining μ and ζ. Note this technique is identical to the technique for extracting two-qubit gate parameters within the single-excitation subspace given in³. Like there, the angle χ does not manifest in the eigenphase Ω(θ, ζ), and so we cannot coherently amplify errors in that parameter without additional interventions. In other words, χ corresponds to a gauge transformation

$$R{(\mu ,\zeta ,\chi )}^{n}=Z(-\chi )\,R{(\mu ,\zeta ,0)}^{n}\,Z(\chi )\,,$$

(41)

which does not add up when the same gate is repeated. That being said, the relative axis of two different single-qubit gates can be estimated with amplified precision. For example, we amplify the relative axis between X(π) and X(−π/2) defined in Eq. (24) by interleaving them many times. Any low-frequency noise in the qubit frequency that would cause the phase to accumulate between the gates will be echoed away, since the time padding on either side of the X(π) gate is the same, making the measurement of this relative phase robust to these fluctuations.

Theory on characterizing two-qubit gates

The entangling parameters ϕ and θ of our two-qubit gates in Eq. (1) are more consistent over time than the single-qubit phases that are susceptible to low-frequency flux noise. It would, therefore, be useful to design characterization circuits that are sensitive only to the stable entangling parameters. To that end, we introduce microwave gates that are interleaved with the repeated two-qubit gate, as illustrated in Fig. 1. To remove flux noise, MEADD is designed to be insensitive to the Z phases ζ and γ in Eq. (1); we use an adapted Floquet characterization technique without DD to estimate these parameters, as described in Supplementary Information A.

For the simple case of interleaving an excitation-preserving two-qubit unitary W in Eq. (1) with X gates, one obtains the cycle unitary

$$C=(X\otimes X)W\,.$$

(42)

A useful representation for the following discussion is given by decomposing the two-qubit unitary W into the even and odd parity subspaces ${{\mathcal{H}}}_{{\rm{even}}}\oplus {{\mathcal{H}}}_{{\rm{odd}}}$,

$$W=\left({e}^{-i\phi /2}\,{W}_{{\rm{even}}}\right)\oplus {W}_{{\rm{odd}}}$$

(43)

$$\begin{array}{rcl}&=&\left[{e}^{-i\phi /2}\left(\begin{array}{cc}{e}^{i(\gamma +\phi /2)}&0\\ 0&{e}^{-i(\gamma +\phi /2)}\end{array}\right)\right]\\ &&\oplus \left(\begin{array}{cc}{e}^{-i\zeta }\cos \theta &-i\,{e}^{i\chi }\sin \theta \\ -i\,{e}^{-i\chi }\sin \theta &{e}^{i\zeta }\cos \theta \end{array}\right)\,.\end{array}$$

(44)

This decomposition is a direct sum of two SU(2) unitaries with a relative phase e^−i(ϕ/2) between the even and odd parity sectors. Conveniently, X ⊗ X decomposes into the direct sum X ⊕ X in this representation, giving the decomposition for the cycle unitary

$$C=\left({e}^{-i\phi /2}{C}_{{\rm{even}}}\right)\oplus {C}_{{\rm{odd}}}\,,$$

(45)

where C_even = XW_even and C_odd = XW_odd. The 2-cycle unitary is trivial in the even-parity subspace

$${C}_{{\rm{even}}}^{2}=X{W}_{{\rm{even}}}X{W}_{{\rm{even}}}=I\,,$$

(46)

a feature we use to design our characterization protocol.

Controlled phase

For measuring ϕ, we need to measure a relative phase between the even- and odd-parity subspaces. Because the 2-cycle unitary is trivial on the even-parity subspace, we can choose any state such as $\left\vert 00\right\rangle$ to serve as our even-parity reference.

To measure the relative phase −ϕ/2, we will therefore prepare states of the form

$$\left\vert {\psi }_{0}\right\rangle =\frac{1}{\sqrt{2}}\left(\left\vert 00\right\rangle +\vert {\psi }_{0,{\rm{odd}}}\rangle \right)$$

(47)

$$=\frac{1}{\sqrt{2}}\left(\left\vert 00\right\rangle +\alpha \left\vert 01\right\rangle +\beta \left\vert 10\right\rangle \right)\,,$$

(48)

where $\vert {\psi }_{0,{\rm{odd}}}\rangle \in {{\mathcal{H}}}_{{\rm{odd}}}$. Applying even powers of the cycle unitary to this initial state puts a phase on $\left\vert 00\right\rangle$ and transforms the odd-parity part of the state separately

$${C}^{2n}\left\vert {\psi }_{0}\right\rangle =\frac{1}{\sqrt{2}}\left({e}^{-in\phi }\left\vert 00\right\rangle +{\alpha }^{{\prime} }\left\vert 01\right\rangle +{\beta }^{{\prime} }\left\vert 10\right\rangle \right),$$

(49)

where

$${\alpha }^{{\prime} }=\alpha \langle 01| {C}_{{\rm{odd}}}^{2n}| 01\rangle +\beta \langle 01| {C}_{{\rm{odd}}}^{2n}| 10\rangle \,,$$

(50)

$${\beta }^{{\prime} }=\alpha \langle 10| {C}_{{\rm{odd}}}^{2n}| 01\rangle +\beta \langle 10| {C}_{{\rm{odd}}}^{2n}| 10\rangle \,.$$

(51)

We will make separable measurements on the qubits to infer ϕ, which one can understand by looking at the final density matrix ${C}^{2n}\left\vert {\psi }_{0}\right\rangle \left\langle {\psi }_{0}\right\vert {C}^{2n\dagger }$ and taking partial traces. Tracing out the right qubit gives

$$\left(\begin{array}{cc}1+| {\alpha }^{{\prime} }{| }^{2}&{e}^{-in\phi }{\beta }^{{\prime} * }\\ {e}^{in\phi }{\beta }^{{\prime} }&| {\beta }^{{\prime} }{| }^{2}\end{array}\right)\,,$$

(52)

and tracing out the left qubit gives

$$\left(\begin{array}{cc}1+| {\beta }^{{\prime} }{| }^{2}&{e}^{-in\phi }{\alpha }^{{\prime} * }\\ {e}^{in\phi }{\alpha }^{{\prime} }&| {\alpha }^{{\prime} }{| }^{2}\end{array}\right)\,.$$

(53)

Observe that by going between choosing α or β to be 1 (and the other 0), one engineers the amplitudes ${\alpha }^{{\prime} }$ and ${\beta }^{{\prime} }$ takes on the values of all the odd-parity cycle matrix elements. By preparing the states $\left\vert 0+\right\rangle$ and $\left\vert +0\right\rangle$ and measuring X and Y on each qubit to reconstruct the off-diagonal reduced-density-matrix elements, one obtains the matrix of values ${e}^{in\phi }{C}_{{\rm{odd}}}^{2n}$, as illustrated in Fig. 3a. As pointed out earlier, C_odd is a special unitary, with a determinant one, and we have

$$\det \left({e}^{in\phi }{C}_{{\rm{odd}}}^{2n}\right)={e}^{i2n\phi }\det \left(\mathop{C}\nolimits_{\rm{odd}}^{2n}\right)={e}^{i2n\phi }\,.$$

(54)

This procedure amplifies ϕ coherently 2n times, suppressing the variance of our estimates of ϕ by a factor of n². The ability to repeat this measurement for multiple depths n and fit the slope of the accumulated phase makes us robust to SPAM errors. Fluctuations in single-qubit phases are also swept away; identically within the even-parity subspace, and to a large extent within the odd-parity subspace as well. The extent to which they survive will be discussed in more detail when considering the swap angle θ. Decoherence errors are also mitigated because they tend to affect only the magnitude of the determinant, not its phase. Altogether, this simple protocol yields highly accurate and precise estimates of the controlled phase of the CZ gates, as demonstrated experimentally in Fig. 2.

Swap angle and axis

We now show how the circuits illustrated in Fig. 3b can be used to estimate θ and χ. The 2-cycle unitary in the odd-parity subspace $\{\left\vert 01\right\rangle ,\left\vert 10\right\rangle \}$ reads

$${C}_{{\rm{odd}}}^{2}=X{W}_{{\rm{odd}}}X{W}_{{\rm{odd}}}$$

(55)

$$\begin{array}{rcl}&=&Z(-\zeta )\,{e}^{-i\theta (\cos \chi X+\sin \chi Y)}Z(-\zeta )\\ &&\times Z(\zeta )\,{e}^{-i\theta (\cos \chi X-\sin \chi Y)}Z(\zeta )\end{array}$$

(56)

$$\approx Z(-\zeta )X(4\theta \cos \chi )\,Z(\zeta )\,,$$

(57)

where the approximation applies for θ ≪ 1, which is relevant when implementing controlled-phase gates like CZ (we discuss larger θ to conclude the section). The dynamical decoupling sequence ensures that the only part of the swap that remains is around the x-axis in the odd-parity sector. The corresponding cycle Rabi angle $\Omega \approx | \theta \cos \chi |$ can be estimated by observing the population transfer rate between $\left\vert 01\right\rangle$ and $\left\vert 10\right\rangle$. To determine the swap around the y-axis, we also introduce the complementary cycle unitary

$$\bar{C}=(Y\otimes X)W={\bar{C}}_{{\rm{even}}}\oplus {\bar{C}}_{{\rm{odd}}}\,,$$

(58)

where the second equation is a result of Y ⊗ X = Y ⊕ Y. For θ ≪ 1, we have

$${\bar{C}}_{{\rm{odd}}}^{2}=Y{W}_{{\rm{odd}}}Y{W}_{{\rm{odd}}}$$

(59)

$$\approx Z(-\zeta )Y(-4\theta \sin \chi )Z(\zeta )\,,$$

(60)

which can be used to estimate $\bar{\Omega }\approx | \theta \sin \chi |$. Again, the estimation error of $\bar{\Omega }$ due to finite sample sizes scales as O(1/n), while the small-angle approximation introduces an additional deterministic error on top of that. Measuring only the population transfer between $\left\vert 01\right\rangle$ and $\left\vert 10\right\rangle$ leaves $\cos \chi$ and $\sin \chi$ with ambiguous signs. By additionally measuring on the Bell-type basis

$${\left\vert \pm \right\rangle }_{{\rm{odd}}}=\frac{1}{\sqrt{2}}\left(\left\vert 01\right\rangle \pm \left\vert 10\right\rangle \right)\,,$$

(61)

$${\left\vert \pm i\right\rangle }_{{\rm{odd}}}=\frac{1}{\sqrt{2}}\left(\left\vert 01\right\rangle \pm i\left\vert 10\right\rangle \right)\,,$$

(62)

one resolves these ambiguities and also mitigates the effect of dephasing errors, since one is effectively measuring the complete odd-parity Bloch vector and can distinguish shrinkage (such as comes from dephasing) from rotation. Since both C and $\bar{C}$ preserve the parity, we can also mitigate single-qubit relaxation errors to first order by postselecting on parity.

For the case of large θ, we can estimate θ and χ using the relations

$$\Omega =\arccos \left(1-2{(\sin \theta \cos \chi )}^{2}\right)/2\,,$$

(63)

$$\bar{\Omega }=\arccos \left(1-2{(\sin \theta \sin \chi )}^{2}\right)/2\,,$$

(64)

where the Rabi angles Ω and $\bar{\Omega }$ can be learned similarly as in the case where θ ≪ 1.

A subtle but important point for measuring unwanted swapping in superconducting qubits is that one must pay attention to how phase tracking is implemented for single-qubit XY rotations (see Section “Single-qubit gates”). For two-qubit gates with θ = 0 (or π) such as CZ, in normal phase tracking one “commutes” Z phases coming from qubit idle evolution through the CZ gate to update the phases of subsequent microwaves. However, the small swap matrix element to be measured does not commute with these Z rotations. As pointed out in ref. ³², this causes it to acquire an artificial phase during phase tracking that is linear in the cycle number n, preventing it from being amplified and measured. To keep the swap phase constant, one must modify phase tracking such that the microwave phases do not follow the qubit idle evolution during the circuit. The same problem also exists in characterizing the crosstalk discussed in Section “Crosstalk”, and it needs to be tackled with care.

In Fig. 7, we compare in simulation MEADD to previously employed techniques for measuring the swap angle: the phase method⁴ and unitary tomography¹⁸. The phase method differs from unitary tomography primarily in that it repeats the gate being characterized to amplify errors. As seen in Fig. 7, this coherent amplification gives the phase method a higher signal-to-noise ratio (SNR) than unitary tomography, even when keeping the total number of measurement results constant across both characterization methods. However, one sees that the advantage of coherent amplification is washed out once ζ is on the same order as θ. In comparison, MEADD exhibits significantly higher SNR and maintains the advantage from coherent amplification even when ζ is significantly larger than θ, as the dynamical-decoupling sequence cancels the swap-suppressing effects of ζ.

Fig. 7: Numerical simulation results on signal-to-noise ratio (SNR) for measuring the swap angle.

Variance is measured over 100 different realizations for each parameter point. The number of simulated measurements is normalized so that the total number of measurements per parameter inferred is the same across the methods (see Supplementary Information B for details). The phase method⁴ has an advantage over unitary tomography in that it coherently amplifies errors. However, this amplification is suppressed as the value of the differential single-qubit phase ζ becomes comparable to θ. In contrast, MEADD exhibits strong SNR through coherent amplification with no visible dependence on the detuning ζ.

Robustness to implementation errors

The dynamical decoupling sequences used by MEADD will unavoidably contain systematic errors, so we must design sequences that are robust to these imperfections. It is well known that the so-called XY4 sequence (XY)²ⁿ is robust to any small systematic errors in X and Y^10,33, whereas the Carr–Purcell–Meiboom–Gill (CPMG) sequence X²ⁿ is susceptible to over-rotation errors in X⁹. Similar to XY4, we require our characterization sequence to be robust to any systematic errors in the single-qubit gates, though the exact robust sequence will depend on the two-qubit gate to be characterized. These errors can lead to non-zero matrix elements between the even and odd-parity subspaces, which destroy the direct sum structure in Eq. (45) that we rely on.

In Fig. 8, we demonstrate the importance of using a robust DD sequence to characterize the entangling parameters of a CZ gate with MEADD. We simulate the protocol to estimate the controlled phase detailed in Section “Theory on characterizing two-qubit gate”, both with the robust CPMG and the non-robust XY4 DD sequences; note how the robustness of the sequences is reversed when being interleaved with CZ gates. Using the robust DD sequence in panel (a), we see that the phase builds up linearly even if we introduce microwave over rotation errors on one of the qubits. Even for an overrotation of 10% (0.314 rad), we still get linear phase accumulation to a good approximation that gives us an estimate of ϕ to sub-milliradian precision, as shown in panel (c) with the blue curve.

Fig. 8: Numerical simulation results for characterizing the controlled phase of a CZ gate with ϕ = π − 0.01, using MEADD and imperfect DD gates.

a Using the robust DD sequence described in Section “Theory on characterizing two-qubit gate”, the angle of the determinant in Eq. (54), which corresponds to −2nϕ, builds up linearly even if we introduce microwave over-rotation errors on one of the qubits. The strength of the over-rotation, a factor multiplying the π rotation around X, is varied between 0 and 10% and illustrated with the different colors. b Similar simulations now use the XY4 DD sequence, which is not robust to implementation errors in this protocol. c Resulting ϕ-estimate error obtained from fitting the slope of the MEADD data for the different over-rotation errors. The dashed line indicates milliard precision.

On the other hand, using the nonrobust DD sequence gives unusable data as we introduce microwave overrotation errors on one of the qubits, as shown in panel (b). For overrotation of just 2% (0.063 rad), the phase accumulation is so distorted from being linear that the error in the ϕ estimate is larger than the value we are trying to measure (0.01 rad). With this sequence, even a 1% over-rotation error introduces errors in the ϕ estimate larger than a milliradian, i.e., it is more than an order of magnitude more sensitive to implementation errors than the robust DD sequence.

In the following, we will first demonstrate how to design robust MEADD protocols for the case of a CZ gate, while general excitation-preserving two-qubit gates are addressed in Supplementary Information D. We consider small arbitrary systematic errors of the X gate as

$$\widetilde{X}({\boldsymbol{\epsilon }})={e}^{-i({\epsilon }_{X}X+{\epsilon }_{Y}Y+{\epsilon }_{Z}Z)}X$$

(65)

$$\approx (I-i{\boldsymbol{\epsilon }}\cdot {\boldsymbol{\sigma }})X\,,$$

(66)

where ϵ = (ϵ_X, ϵ_Y, ϵ_Z) and σ = (X, Y, Z). Since the errors are assumed to be small, we will consider their effect to first order, which allows us to treat errors on the individual qubits separately in the following.

The perfect 2-cycle unitary for W = CZ reads

$${C}^{2}=(X\otimes X){\rm{CZ}}(X\otimes X){\rm{CZ}}$$

(67)

$$=-Z\otimes Z\,.$$

(68)

Noticing that C⁴ = I ⊗ I, we have

$${\left[(X\otimes X){\rm{CZ}}\right]}^{3}=(Y\otimes Y){\rm{CZ}}={\rm{CZ}}(X\otimes X)\,.$$

(69)

Considering errors on the right qubit, the noisy 2-cycle unitary is

$${\widetilde{C}}^{2}=(X\otimes \widetilde{X}){\rm{CZ}}(X\otimes \widetilde{X}){\rm{CZ}}$$

(70)

$$\begin{array}{rcl}&\approx &{C}^{2}-i\left[(I\otimes {\boldsymbol{\epsilon }}\cdot {\boldsymbol{\sigma }})(X\otimes X){\rm{CZ}}(X\otimes X){\rm{CZ}}\right.\\ &&\left.+(X\otimes X){\rm{CZ}}(I\otimes {\boldsymbol{\epsilon }}\cdot {\boldsymbol{\sigma }})(X\otimes X){\rm{CZ}}\right]\,,\end{array}$$

(71)

With the identities in Eq. (69), we have

$${\widetilde{C}}^{2}=V{C}^{2}\,,$$

(72)

where

$$V=I-i\left[(I\otimes {\boldsymbol{\epsilon }}\cdot {\boldsymbol{\sigma }})+{\rm{CZ}}\,(I\otimes Y{\boldsymbol{\epsilon }}\cdot {\boldsymbol{\sigma }}\,Y)\,{\rm{CZ}}\right]\,.$$

(73)

Since X and Y interact with the CZ gate in similar ways, we first consider ϵ_X, ϵ_Y ≠ 0, and ϵ_Z = 0, for which we have the anticommutation relations

$$\{(I\otimes {\boldsymbol{\epsilon }}\cdot {\boldsymbol{\sigma }}),Z\otimes Z\}=0\,,$$

(74)

$$\{{\rm{CZ}}(I\otimes Y{\boldsymbol{\epsilon }}\cdot {\boldsymbol{\sigma }}Y){\rm{CZ}},Z\otimes Z\}=0\,.$$

(75)

Both generator terms in error unitary V in Eq. (73) anticommute with C² = −Z ⊗ Z. Therefore, the noisy 4-cycle unitary ${\widetilde{C}}^{4}=V{C}^{2}V{C}^{2}$ is identical to the noiseless 4-cycle unitary C⁴ to first order, and the sequence is robust to small errors in X and Y for a 4-cycle.

For ϵ_Z ≠ 0 and ϵ_X = ϵ_Y = 0, we have

$${\widetilde{C}}^{2}={e}^{-i{\epsilon }_{Z}(I\otimes Z-I\otimes Z)}{C}^{2}={C}^{2}\,,$$

(76)

and the error ϵ_Z cancels itself in a 2-cycle. The complementary sequence $\bar{C}$ from Eq. (58) is robust in exactly the same way, the only difference being the Y operators in Eq. (73) may be replaced by X, which does not affect their anticommutation with ${\bar{C}}^{2}=-Z\otimes Z$.

One subtlety here is the gauge freedom related to the position assigned to Z errors around microwave gates. It turns out that it can be totally ignored here because one can always commute half of ϵ_Z to the right of the X gate, leaving a pair of ϵ_Z/2 and −ϵ_Z/2 errors conjugating the CZ gate. This gauge has thus no impact at all on the characterization of the controlled phase ϕ or swap angle θ but is indistinguishable from a change in the swapping phase χ. For the current case of CZ characterization, this is acceptable, as for an ideal CZ gate, there is no swapping between the qubits (θ = 0), at which point χ has no meaning.

We use MEADD to measure the crosstalk (stray coupling) by treating the Hamiltonian Eq. (3) integrated over a given time period as a gate and executing the dynamical decoupling sequence to measure the small swap angle, exactly as one does for CZ gates. The main difference is that because there is no CZ gate interleaving the microwaves, we use XY4 sequences on both qubits, which are robust to microwave over-rotation errors.