Simultaneous discovery of quantum error correction codes and encoders with a noise-aware reinforcement learning agent

Abstract

In the ongoing race towards experimental implementations of quantum error correction (QEC), finding ways to automatically discover codes and encoding strategies tailored to the qubit hardware platform is emerging as a critical problem. Reinforcement learning (RL) has been identified as a promising approach, but so far it has been severely restricted in terms of scalability. In this work, we significantly expand the power of RL approaches to QEC code discovery. Explicitly, we train an RL agent that automatically discovers both QEC codes and their encoding circuits for a given gate set, qubit connectivity and error model, from scratch. This is enabled by a reward based on the Knill-Laflamme conditions and a vectorized Clifford simulator, showing its effectiveness with up to 25 physical qubits and distance 5 codes, while presenting a roadmap to scale this approach to 100 qubits and distance 10 codes in the near future. We also introduce the concept of a noise-aware meta-agent, which learns to produce encoding strategies simultaneously for a range of noise models, thus leveraging transfer of insights between different situations. Our approach opens the door towards hardware-adapted accelerated discovery of QEC approaches across the full spectrum of quantum hardware platforms of interest.

Introduction

Quantum error correction^1,2 (QEC) protects quantum information by encoding the state of a logical qubit into several physical qubits and is crucial to ensure that quantum technologies such as quantum communication or quantum computing can achieve their groundbreaking potential.

The past few years have witnessed dramatic progress in experimental realizations of QEC on different platforms^3,4,5,6,7 (this includes especially various superconducting qubit architectures, ion traps, quantum dots, and neutral atoms), reaching a point where the lifetime of qubits has been extended by applying QEC⁸. Given the strong differences in native gate sets, qubit connectivities, and relevant noise models, there is a strong need for a flexible and efficient scheme to automatically discover not only codes but also efficient encoding circuits, adapted to the platform at hand.

In particular, in the field of quantum communication and networking, third-generation quantum repeaters rely on QEC to correct errors during transmission⁹. The use of QEC permits very high communication rates, since only one-way signaling is involved, in contrast to earlier generations of quantum repeaters. In this setting, we may in a first approximation assume that errors happen mainly during transmission over the noisy channel and treat the encoding circuits themselves as noiseless. This is the scenario we will adopt here.

Since Shor’s original breakthrough¹⁰, different qubit-based QEC codes have been constructed, both analytically and numerically, leading to a zoo of codes, each of them conventionally labeled [[n, k, d]], where n is the number of physical qubits, k the number of encoded logical qubits, and d the code distance that defines the number d − 1 of detectable errors. The first examples are provided by the [[5, 1, 3]] perfect code¹¹, the [[7, 1, 3]] Steane¹² and the [[9, 1, 3]] Shor¹⁰ codes, which encode one logical qubit into 5, 7, and 9 physical qubits, respectively, being able to detect up to 2 physical errors and correct up to 1 error on any physical qubit. The most promising approach so far is probably the family of the so-called toric or surface codes¹³, which encode a logical qubit into the joint entangled state of a d × d square of physical qubits. More recently, examples of quantum Low-Density Parity Check (LDPC) codes that are competitive with the surface code have been discovered¹⁴.

However, knowledge of a code does not automatically translate to knowing how to encode the logical states of that code in an efficient way. Standard approaches are unconstrained, meaning that an all-to-all connectivity between qubits is assumed as well as a set of gates that are not necessarily native to the hardware platform of interest^15,16. This then leads to larger-than-necessary circuits when implementing them on specific devices.

Numerical techniques have already been employed to construct QEC codes. Often, this has involved greedy algorithms, which may lead to sub-optimal solutions but can be relatively fast^17,18,19,20.

The recent advent of powerful tools from the domains of Artificial Intelligence (AI), are transforming scientific approaches²¹. From these, Reinforcement Learning (RL), which is designed to solve complex decision-making problems by autonomously following an action-reward scheme²², is a promising artificial discovery tool for QEC strategies. The task to solve is encoded in a reward function, and the aim of RL training algorithms is to maximize such a reward over time. RL can provide new answers to difficult questions, in particular in fields where optimization in a high-dimensional search space plays a crucial role. For this reason, RL can be an efficient tool to tackle the problem of QEC code construction and encoding under hardware-specific constraints.

The first example of RL-based automated discovery of QEC strategies²³ did not rely on any human knowledge of QEC concepts. While this allowed exploration without any restrictions, e.g., going beyond stabilizer codes, it was limited to only small qubit numbers. More recent works have moved towards optimizing only certain QEC subtasks, injecting substantial human knowledge. For example, RL has been used for optimization of given QEC codes²⁴, and to discover tensor network codes²⁵ or codes based on “Quantum Lego” parametrizations^26,27. Additionally, RL has been used to find efficient decoding processes^28,29,30,31 and self-correcting control protocols³².

In our work, we significantly expand the scaling capabilities of RL code discovery by introducing two critical components:

• 1. An efficiently computable and general RL reward based on the Knill-Laflamme error correction conditions.

• 2. A highly parallelized custom-built Clifford circuit simulator that runs entirely on modern AI chip accelerators such as GPUs or TPUs.

The main results that are enabled by this strategy are the following:

• 1. A state-of-the-art scheme based on deep RL that simultaneously discovers QEC codes together with the encoding circuit from scratch, tailored to specific noise models, native gate sets, and connectivities, minimizing the circuit size for improved hardware efficiency.

• 2. Effortless discovery of both stabilizer and CSS codes and encoders with code distances from 3 (found in tens of seconds) to 5 (found in tens of minutes to a few hours) with up to 25 physical qubits.

• 3. A general RL agent that is trained only once but afterwards is able to adapt and switch its encoding strategy based on the specific noise that is present in the system. We call this a noise-aware RL agent.

• 4. A scalable platform for artificial scientific discovery of QEC strategies based on RL that potentially allows discovery of distance 8-10 codes on a single GPU, while offering further scaling opportunities on distributed machines.

Regarding applications to quantum computing, the discovered circuits are in general not fault-tolerant. However, strategies to build fault-tolerant versions out of non-fault-tolerant circuits exist³³, and these can even be automated with RL³⁴.

While the authors of ref. ³⁵ also set themselves the task of finding both codes and their encoding circuits, this was done using variational quantum circuits involving continuously parametrized gates, which leads to much more costly numerical simulations and eventually only an approximate QEC scheme. By contrast, our RL-based approach does not rely on any human-provided circuit ansatz, can use directly any given discrete gate set, is able to exploit highly efficient Clifford simulations, and produces a meta-agent able to cover strategies for a range of noise models. In particular, their approach was not able to scale to d = 5 codes due to prohibitive computational costs.

The paper is organized as follows: In Section “Results” we detail the RL strategy, its numerical results and estimations on how far this strategy can be scaled in principle. In Section “Methods” we give a reminder on stabilizer codes and the Knill-Laflamme conditions, provide background describing the RL methods used in this work and give all details of our implementation.

Results

Section “Reinforcement Learning Approach to QEC Code Discovery” describes our approach to build a noise-aware RL agent. Section “Reinforcement Learning Results” details the numerical results found with our strategy. Section “Scaling automated QEC discovery” explains how our approach can be scaled up to larger code parameters.

Reinforcement learning approach to QEC code discovery

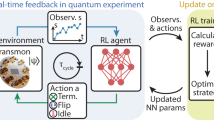
The main objective of this work is to automatize the discovery of QEC codes and their encoding circuits using RL. We exclusively focus on stabilizer codes due to their efficient simulability with classical computers. We will consider a scenario where the encoding circuit is assumed to be error-free (non fault-tolerant encoding). This is applicable to quantum communication or quantum memories, where the majority of errors happen during transmission over a noisy channel or during the time the memory is retaining the information. Nevertheless, we remark that there exist techniques to make circuits fault-tolerant such as flag fault-tolerance³³, and the code itself would anyway be discovered with our strategy. A scheme of our approach can be found in Fig. 1, and the following sections are dedicated to explain its different constituent parts.

Fig. 1: QEC code and encoding discovery using a noise-aware RL meta-agent.

A set of error operators, a gate set, and qubit connectivity are chosen. Different error models can be considered by varying some noise parameters, which are fed as an observation to the agent. The agent then builds a circuit using the available gate set and connectivity that detects the most likely errors from the target error model by using a reward based on the Knill-Laflamme QEC conditions according to Eq. (2). After training, a single RL agent is able to find suitable encodings for different noise models, which are able to encode any state $\left\vert \psi \right\rangle$ of choice.

Encoding circuit

In order to encode the state of k logical qubits on n physical qubits one must find a sequence of quantum gates that will entangle the quantum information in such a way that QEC is possible with respect to a target noise channel. Initially, we imagine the first k qubits as the original containers of our (yet unencoded) quantum information, which can be in any state $\left\vert \psi \right\rangle \in {({{\mathbb{C}}}_{2})}^{\otimes k}$. The remaining n − k qubits are chosen to each be initialized in the state $\left\vert 0\right\rangle$. These will be turned into the corresponding logical state ${\left\vert \psi \right\rangle }_{L}\in {({{\mathbb{C}}}_{2})}^{\otimes n}$ via the application of a sequence of Clifford gates on any of the n qubits. In the stabilizer formalism, this means that initially, the generators of the code stabilizer group are

$${Z}_{k+1},{Z}_{k+2},\ldots ,{Z}_{n}.$$

(1)

The task of the RL agent is to discover a suitable encoding sequence of gates for the particular error model under consideration. After applying each gate, the n − k code generators (1) are updated. The agent then receives a representation of these generators as input (as its observation) and suggests the next gate (action) to apply. In this way, an encoding circuit is built up step by step, taking into account the available gate set and connectivity for the particular hardware platform. This process terminates when the Knill-Laflamme conditions are satisfied for the target error channel and the learned circuit can then be used to encode any state $\left\vert \psi \right\rangle$ of choice.

Reward

The most delicate matter in RL problems is building a suitable reward for the task at hand. Our goal is to design an agent that, given a list of (Pauli) errors {E_μ} with associated occurrence probabilities {p_μ}, is able to find an encoding sequence that protects the quantum information from such noise.

Ideally, one would like to maximize the probability of successful recovery of the initial encoded state after decoding. Unfortunately, optimizing for this task is computationally too expensive. A much cheaper alternative is to use a scheme where the cumulative reward (which RL optimizes) simply is maximized whenever all the Knill-Laflamme conditions are fulfilled. One implementation of this idea uses what we call the (negative) weighted Knill-Laflamme sum as an instantaneous reward, which we define as:

$${r}_{t}=-\sum _{\mu }{\lambda }_{\mu }{K}_{\mu },$$

(2)

where K_μ = 0 if the corresponding error operator E_μ satisfies the Knill-Laflamme conditions, and K_μ = 1 otherwise, and where λ_μ are real positive hyperparameters weighting each error. If all errors in {E_μ} can be detected, the reward is zero, and is negative otherwise, thus leading the agent towards short gate sequences. In particular, note that the agent is not explicitly incentivized to minimize circuit depth or to place gates in parallel. However, reinforcing short gate sequences may sometimes also lead to a small circuit depth. The range of the index μ is found by counting the number of Pauli strings of weight w < d, which is

$${\left\vert \{{E}_{\mu }\}\right\vert }_{w < d}=\mathop{\sum }\limits_{w=0}^{d-1}{3}^{w}\left(\begin{array}{l}n\\ w\end{array}\right),$$

(3)

where the factor of three is for X, Y, Z Pauli errors. Thus, the fact that (3) grows exponentially with d will impose the most severe limitation in our approach (as is the case in any QEC application). Later, we will also be interested in situations where not all errors can be corrected simultaneously and a good compromise has to be found. In that case, one simple heuristic choice for the reward (2) would be λ_μ = p_μ, giving more weight to errors that occur more frequently. While we will later see that maximizing the Knill-Laflamme reward given here is not precisely equivalent to maximizing the state recovery probability, one can still expect a reasonable performance at this task, and indeed this is what we find in our work.

Noise-aware meta-agent

Regarding the error channel to be targeted, here there are in principle several choices that can be made. The most straightforward one is choosing a global depolarizing channel (see “Methods” (8)). This still allows for asymmetric noise, i.e., different probabilities p_X, p_Y, p_Z. One option would be to train an agent for any given, fixed choice of these probabilities, necessitating retraining if these characteristics change. However, we want to go beyond that and build a single agent being capable of deciding what is the optimal encoding strategy for any level of bias in the noise channel (11). For instance, we want this noise-aware agent to be able to understand that it should prioritize detecting more Z errors than X ones when the channel is biased towards Z, yet it should do the opposite when X errors become more likely. This translates into two aspects: The first one is that the agent has to receive the noise parameters as input. In the illustrative example further below, we will choose to supply the bias parameter ${c}_{Z}=\log {p}_{Z}/\log {p}_{X}$ (see “Methods”) as an extra observation, while keeping the overall error probability fixed. The second aspect is that the list of error operators will have to contain more operators than the total number that can actually be detected reliably since it is now part of the agent’s task to prioritize some of those errors while ignoring the least likely errors. All in all, the list of operators participating in the reward (2) will be fixed, and we will vary c_Z during training.

Vectorized Clifford simulator

RL algorithms exploit guided trial-and-error loops until a signal of a good strategy is picked up and convergence is reached, so it is of paramount importance that simulations of our RL environment are extremely fast. Thanks to the Gottesman-Knill theorem, the Clifford circuits needed here can be simulated efficiently on classical computers. Optimized numerical implementations of Clifford circuits exist, e.g., Stim³⁶. However, in an RL application we want to be able to run multiple circuits in parallel in an efficient, vectorized way that is compatible with modern machine learning frameworks. For that reason, we have implemented our own special-purpose vectorized GPU Clifford simulator (described in detail in Methods), which is publicly available in our repository³⁷. When compared to Stim, we find a ~50 × speedup at simulating random Clifford circuits and a ~450 × speedup when restricted to the simulation of Calderbank-Shor-Steane (CSS) codes (see “Methods”). In particular, we can simulate 8000 random Clifford circuits of 1000 gates on 49 qubits in under a second. However, note that our simulator is not capable of sampling noisy circuits, which is the main application of Stim.

Reinforcement learning results

We will first illustrate the basic workings of our approach for a symmetric noise channel before showing the noise-aware meta-agent that is able to simultaneously discover strategies for a range of noise models.

Codes in a symmetric depolarizing noise channel

We now show the versatility of our approach by discovering a library of different [[n, k, d]] codes and their associated encoding circuits.

We fix the error model to be a symmetric depolarizing channel and consider different target code distances (from 3 to 5). The corresponding target error set is E_μ = {I, X_i, Y_i, Y_j, X_iX_j, …, Z_iZ_j} for d = 3, and likewise for d = 4, 5, with the set for d = 5 including all Pauli string operators of up to weight 4. For illustrative purposes, we start by taking the gateset to be {H_i, CNOT(i < j)}, i.e., a directed all-to-all connectivity, which is sufficient given that our unencoded logical state is at the first k qubits by design. Nevertheless, we will also see examples with other connectivities and alternative gatesets. The error probability p is fixed, meaning p_I = 1 − 3p, p_X = p_Y = p_Z = p, and thus no noise parameter is needed as an observation to the agent.

For d = 3 and d = 4 codes we proceed as follows: for any given target [[n, k, d]], we launch a few training runs. Once the codes are collected, we categorize them by calculating their quantum weight enumerators (see “Methods”), leading to a certain number of non-degenerate and degenerate code families. We repeat this process and keep launching new training runs until no new families are found. In this way, our strategy presumably finds all stabilizer codes that are possible for the given parameters n, k, d, together with a suitable encoding circuit. Note that this statement is based on empirical observations. While successive training runs do not yield new code families, this does not exclude the possibility of there being more. This total number of families is shown in Fig. 2, with labels (x, y) for each [[n, k, d]], where x is the number of non-degenerate families and y is the number of degenerate ones. It should be stressed that categorizing all stabilizer code families is in general an NP-complete problem³⁸, yet our framework is very effective at solving this task. To the best of our knowledge, this work provides the most detailed tabulation of (x, y) populations together with optimal encoding circuits for the code parameters shown here.

Fig. 2: Discovering codes and encoding circuits for various numbers of physical qubits, logical qubits, and distances (see main text and Methods for d = 5).

Families of stabilizer codes tailored to symmetric depolarizing noise channels, found with our RL framework. The labels (x, y) indicate the number of non-degenerate (x) and degenerate (y) code families. The circuit size shown is the absolute minimum throughout all families. In general, different families have different circuit sizes, and even within the same family we find variations in circuit sizes. Since further training runs do not increase family populations, it is likely that there are no more stabilizer codes for the shown code parameters.

This approach discovers suitable encoding circuits, given the assumed gate set, for a large set of codes. Among them are the following known codes for d = 3 (see ref. ³⁹ for explicit constructions of codes [[n, n − r, 3]] with minimal r, for all n): The first one is the five-qubit perfect code¹¹, which consists of a single non-degenerate [[5, 1, 3]] code family and is the smallest stabilizer code that corrects an arbitrary single-qubit error. Next are the 10 families³⁸ of [[7, 1, 3]] codes, one of which corresponds to Steane’s code¹². The smallest single-error-correcting surface code, Shor’s code¹⁰, is rediscovered as one of the 143 degenerate code families with parameters [[9, 1, 3]]. The smallest quantum Hamming code⁴⁰[[8, 3, 3]] is obtained as well. Our approach is efficient enough to discover codes with up to 20 physical qubits in under 10 min, at which point we stopped increasing n. We also include in the Supplementary the encoding circuit for a [[20, 13, 3]] code consisting of a total of 45 gates.

The RL framework presented here easily allows to find encoding circuits for different connectivities. The connectivity affects the likelihood of discovering codes within a certain family during RL training as well as the typical circuit sizes. In Fig. 3 we illustrate this for the case of [[9, 3, 3]] codes, with their 13 families, for two different connectivities: an all-to-all (directed, i.e., CNOT(i < j)) and a nearest-neighbor square lattice connectivity. On average, the agent needs one less gate to prepare the encoding on the all-to-all connectivity than when using the square lattice. This difference in circuit size is likely to become larger for larger qubit numbers. We also include in Methods examples using different gatesets and a larger variety of connectivities.

Fig. 3: Influence of connectivity.

Characteristics of the 13 families of [[9, 3, 3]] codes found with our framework, clustered according to families distinguished by their quantum weight enumerators (13). Families 9 and 13 are degenerate, while the rest are non-degenerate. We have trained a total of 10240 agents for each of both cases. In the all-to-all (directed: CNOT(i < j)) connectivity, 9574 agents were successful, while this number went down to 3808 in the other case. The bars display how these codes are distributed across different families. Codes in the same family found by different agents are not necessarily distinct, so the bars are rather an indication of the likelihood of a training run to find a code within the family. The points show the mean circuit size, averaged within each family, while the error bar is its standard deviation. It is interesting to see that even with different connectivities, families occur with similar likelihoods during training. We explicitly list the corresponding quantum weight enumerators computed with (13) in the Supplementary.

We now move to distance d = 5 codes. These are more challenging to find due to the significantly increased number of error operators (3) to keep track of, which impacts both the computation time and the hardness of satisfying all Knill-Laflamme conditions simultaneously. Nevertheless, our strategy is also successful in this case. It is known that the smallest possible distance—5 code has parameters [[11, 1, 5]], a result that we confirm with our strategy. We find the single family of this code to have weight enumerators,

$$\begin{array}{rcl}A&=&(1,0,0,0,0,0,198,0,495,0,330,0),\\ B&=&(1,0,0,0,0,198,198,990,495,1650,330,234),\end{array}$$

(4)

with an encoding circuit consisting of 32 gates in the minimal example, which we show in the Supplementary.

The largest d = 5 code that we have considered here is [[15, 2, 5]], although we will later show larger codes. We have found a single code family with weight enumerators

$$\begin{array}{rcl}A&=&\left(1,0,0,0,0,0,23,96,361,776,1318,1832,\right.\\ &&\left.1814,1304,579,88\right),\\ B&=&\left(1,0,0,0,0,101,449,1763,5081,12034,\right.\\ &&\left.21722,29366,29622,20489,8661,1783\right).\end{array}$$

(5)

and an encoding circuit consisting of 49 gates shown in the Supplementary. Other successfully discovered d = 5 codes are shown in Methods, Fig. 4.

Fig. 4: Families of d = 5 stabilizer codes found with RL.

The labels (x, y) indicate the number of non-degenerate (x) and degenerate (y) code families. The circuit size shown is the absolute minimum throughout all families using a directed (CNOT(i < j)) qubit connectivity.

Noise-aware meta-agent

We now move on to codes in more general asymmetric depolarizing noise channels. This lets us illustrate a powerful aspect of RL-based encoding and code discovery: One and the same agent can learn to switch its encoding strategy depending on some parameter characterizing the noise channel. This is realized by training this noise-aware agent on many different runs with varying choices of the parameter, which is fed as an additional input to the agent.

In the present example, the parameter in question is the bias parameter ${c}_{Z}=\log {p}_{Z}/\log {p}_{X}$. This allows the same agent to switch its strategy depending on the kind of bias present in the noise channel. The error set E_μ is now taken to be all Pauli strings of weight ≤4, i.e., {E_μ} = {I, X_i, Y_i, Z_i, X_iX_j, …, Z_iZ_jZ_kZ_l}, but their associated error probabilities will vary depending on c_Z. For every RL training trajectory, a new c_Z is chosen and the error probabilities p_μ are updated correspondingly.

We apply this strategy to target codes with parameters n = 9, k = 1 in asymmetric noise channels. We allow a maximum number of 35 gates. Moreover, we consider an all-to-all connectivity, taking as available gate set {H_i, S_i, CNOT(i, j)}, where S_i is the phase gate acting on qubit i.

We discover codes with the following parameters: [[9, 1, d_e(c_Z = 0.5) = 2]], [[9, 1, d_e(c_Z = 0.6) = 3]], [[9, 1, d_e(c_Z = 1.4) = 4]], [[9, 1, d_e(c_Z = 2) = 5]], where d_e is the effective code distance, defined in Methods. To the best of our knowledge, the last two codes are new. Codes inbetween, 0.5 ≤ c_Z < 0.6, have d_e = 2, 0.6 ≤ c_Z < 1.4 have d_e = 3, and so on.

Next, we evaluate the performance of the noise-aware agent trained with this strategy at minimizing the failure probability, defined in “Methods”. The main results are shown in Fig. 5. We start by comparing the two best-performing post-selected agents according to minimizing the weighted Knill-Laflamme sum (green) and minimizing the failure probability (orange), see Fig. 5a, b. There we see that there is a nice correlation between the two tasks, especially in the region c_Z < 1. We also compare the smallest undetected effective weight of the codes found by these two agents in Fig. 5c. Surprisingly, the code found by the best agent according to the weighted Knill-Laflamme sum (green) at c_Z = 2 has d_e = 5, while the best code at minimizing the failure probability (orange) has d_e = 4. However, at the specific point c_Z = 2 these two codes perform equally well in terms of the failure probability (see Fig. 5b).

Fig. 5: Performance of the noise-aware RL agent.

The agent finds n = 9, k = 1 codes and encoding circuits, simultaneously for different levels of noise bias c_Z, with single-qubit fidelity p_I = 0.9. In panels a,b,c, green represents the agent that was post-selected among all trained agents for performing best at minimizing the weighted Knill-Laflamme sum, averaged over all c_Z values. Orange refers to the agent minimizing the failure probability, averaged over c_Z. a Weighted Knill-Laflamme sum as a function of the noise bias parameter c_Z (best agent: green line). b Failure probability as a function of the noise bias parameter c_Z (best agent: orange line) (c) Smallest undetected effective weight (effective code distance is the integer part) as a function of the noise bias parameter c_Z. While there is almost a perfect overlap between both best agents until c_Z = 1.1, the situation changes afterwards, leading at c_Z = 2 to a d_e = 5 code (green) or a d_e = 4 code (orange) that perform equally well in terms of the failure probability, as seen in b. d Evaluation of the failure-probability of the best-performing agent (orange in the other panels) for larger values of p_I (smaller errors) than the ones it was trained on.

Now we focus on the agent that performs best at minimizing the failure probability (orange) since it is the one of most interest in practical scenarios. We begin by evaluating the performance of the same agent on different values of p_I. This is shown in Fig. 5d. There where we see that the failure probability asymptotically follows a power law with exponent ≳2 depending on the specific value of c_Z. Thus, the strategies found during training at a fixed value of p_I are readily usable in other situations.

We continue by analyzing the encoding circuits and code generators for some selected values of c_Z. These are chosen after computing the quantum weight enumerators (see “Methods”), which we show in Fig. 6a. There we see that the same code family is kept for 0.5 ≤ c_Z < 0.9, where Z errors are more likely than X/Y. From that point onward, the agent switches to a new code family that is kept until the end (c_Z = 2). We thus choose to analyze the encoding circuits and their associated code generators for the values c_Z = {0.5, 0.9, 1.4, 2}. However, we remark that this particular code switching only occurs for the best post-selected agent and there is a large variety of strategies observed for the 714 meta-agents that we have trained, both in terms of where the switching occurs and the number of switches.

Fig. 6: Characteristics of the 9-qubit codes and encodings found by the noise-aware meta-agent post-selected for minimizing the failure probability.

a Associated code family according to their (symmetric) weight enumerators A, B. The same code family is used from 0.5 ≤ c_Z < 0.9, while a family switching occurs at c_Z = 0.9, and it is kept until c_Z = 2. b Encoding circuits: Here we see that many small gate sequences (highlighted with different colors) are reused across different values of c_Z. This is an indication of transfer learning, i.e., the power of the meta-agent. We remark that the agent does not place gates in parallel, the circuits shown here show gates in parallel for compactness. c Corresponding code generators. To aid visualization, we have chosen different colors for different Pauli matrices. However, since our scenario is by construction symmetric in X/Y, we choose to represent X and Y by the same color. Code generators g_i corresponding to the encoding circuits, where we do not make a distinction between X or Y. Here we see that the code generators g_i vary across different values of c_Z.

We begin by showing the encoding circuits in Fig. 6b, highlighting common motifs that are re-used across various values of c_Z with different colors, indicative of transfer learning. Another interesting behavior is that S gates are used more prominently at small values of c_Z, in particular in the combination S ⋅ H. This gate combination implements a permutation: X → Y, Y → Z, Z → X (ignoring signs), which is very useful to exchange Y by Z efficiently. In situations where Z errors are more likely than X/Y, (c_Z < 1), this operation is beneficial. While we have been able to identify and interpret this simple combination of gates with the naked eye, extracting general principles from the discovered codes remains challenging but is nonetheless a valuable and important area that deserves further analysis.

Next, we show the code generators of such encoding circuits in Fig. 6c. Since the code used at c_Z = 0.5 is the only one from a different code family, it is natural that its code generator pattern is the most distinct. However, we see that the generators of the remaining values of c_Z have similar structures.

So far we have shown that a single meta-agent trained on different values of the noise bias parameter can find suitable strategies for all values of such a parameter. Now, we want to compare the performance of such meta-agent against an ensemble of agents that each have been trained on a single value of the noise bias parameter. The settings of this comparison are explained in Methods. The results are shown in Fig. 7. The first stark result is that the simple agents perform rather bad at the extreme values c_Z = 1.9 and c_Z = 2. Outside of these two points, they perform comparably to the best meta-agent, even though the meta-agent strategy yields better performance overall. This advantage is enabled by transfer learning, i.e., the idea that patterns that work in one situation can be reused in other places effectively (recall the common motifs from Fig. 6b). In our case, the meta-agent switched the code family as early as c_Z = 0.9 (recall Fig. 6a), and all the experiences between c_Z = 0.9 and c_Z = 2 were useful in providing a superior performance to that of the simple agents. Moreover, the noise-aware meta-agent is able to provide predictions for all continuous values in the considered range, while the simple agents cannot.

Fig. 7: Noise-aware meta-agent vs ensemble of agents trained on fixed single values of noise.

They have comparable performance at minimizing the failure probability (smaller is better), but the simple agents perform badly at larger values of c_Z. The noise-aware meta-agent reaches a superior performance by reusing useful sub-circuits across different values of c_Z and can provide encoding circuits for all continuous values of c_Z.

Scaling automated QEC discovery

In this final section we explore to which extent our RL-based strategy can be scaled up. We will see that by restricting to CSS^10,12 codes (which are a subclass of stabilizer codes) we are able to reduce the computational demands of our algorithms, leading to an estimated better scaling with larger code parameters.

In order to exclusively target CSS codes, it is sufficient to constrain the structure of the circuit to contain an initial layer of Hadamard gates applied to a subset of the qubits followed by CNOT gates thereafter (see “Methods” for a proof).

There are several possible modifications that we could do to our RL strategy in order to target CSS codes, which we discuss in Methods. In this work, we choose a mixed human-AI strategy where we are the ones deciding the content of the Hadamard layer (i.e., how many and where they are placed) and where the agent has to discover suitable CNOT blocks. In this way, we simplify the task of the agent as much as possible.

We have tested this approach by targeting weakly self-dual codes (meaning the Hadamard layer contains num(H) = (n − k)/2 gates) of distance d = 5 using next-to-nearest neighbor CNOT connectivity and where we place the initial Hadamard gates in alternating qubit indices.

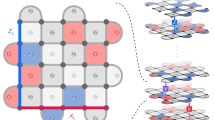
We have found that we can discover [[17, 1, 5]] codes (with num(H) = 8), from scratch and with their encoding circuit. An example of such a discovered circuit is shown in Fig. 8. It consists of 8 Hadamard gates (that we chose) and a remaining sequence of 46 CNOT gates discovered by the agent. The few CNOTs that connect seemingly distant qubits are due to allowing periodic boundary conditions. An interesting strategy that the agent uses is first building Bell pairs between adjacent qubits (which are [[2, 0, 2]] codes) and then entangling these pairs with each other to gradually build up a d = 5 code. We remind the reader that the largest (non-CSS) code that we had shown in previous sections was [[15, 2, 5]] and it needs roughly 4 h of computing. The [[17, 1, 5]] code presented here only needs around 20 min of compute time.

Fig. 8: CSS code and encoding discovery in a next-to-nearest neighbor connectivity with periodic boundary conditions.

The initial layer of Hadamard gates was chosen by us and fixed. We considered two scenarios: Starting from just that initial Hadamard layer (as in [[17, 1, 5]]) or also providing the first layer of CNOTs to start from neighboring Bell pairs (as in [[25, 1, 5]]). The rest of the circuit is successfully discovered by the RL agent. We remark that the agent does not place gates in parallel, the circuits shown here show gates in parallel for compactness.

An interesting observation is that the strategy of initially creating Bell pairs is persistent. We thus consider a final scenario where we initialize the circuit with neighboring Bell pairs and ask the agent to complete the encoding circuit.

Now we focus on [[25, 1, 5]] due to these parameters being compatible with the first d = 5 surface code. We present an example of such a discovered code with its encoding circuit in a next-to-nearest neighbor connectivity in Fig. 8. It uses a total of 83 gates, where the last 59 CNOT gates were discovered by the agent and took around 2 h to train. If we instead ask the agent to start from a circuit where only the Hadamard layer is provided, it still finds good encodings. The drawback is that it takes longer to train, and the agent still prepares the Bell pairs (but has to learn it). We remark that these code parameters are by no means the upper limit of what is possible with our strategy. However, we defer the exploration of effective scaling strategies to future work.

Finally, we make some estimations on the practical limits of CSS code discovery using a Knill-Laflamme-based reward. As we have seen, a crucial ingredient of efficient QEC code discovery driven by RL is being able to both simulate the environment and train the RL agent with GPUs. With this in mind, we estimate the amount of memory that would be needed to store all error operators for some code parameters n and d (this calculation is independent of k, see Methods). We show the results of this estimation in Fig. 9 for code distances from 5 to 10 and physical qubit numbers of 20–100. In particular, we consider what fraction of memory they would occupy in an NVIDIA A100 GPU, which is the modern GPU model standard. The results shown in Fig. 9 indicate that our approach can be extended to ~100 physical qubits (d = 6) and to ~40 physical qubits and d = 10 in a single GPU. Moreover, we identify a region of opportunity that could potentially lead to new codes surpassing the performance of the smaller qLDPC codes found in ref. ¹⁴ since we do not have an ansatz that limits the families of codes that we could find. Exploring this region of opportunity is an exciting endeavor that we leave for future work. We emphasize that not only would we discover the code, but a hardware-efficient encoding circuit would also be simultaneously discovered, which is something currently lacking.

Fig. 9: Scaling CSS code and encoding discovery to larger code parameters.

We show the fraction of the 80 GB of GPU memory needed (NVIDIA A100 GPU) to store all the error operators that are required to reward the agent. We also show for comparison the memory load of stabilizer (non-CSS) code discovery for code distance d = 10. We identify a region of opportunity where our RL strategy could outperform some of the qLDPC codes found in ref. ¹⁴ in the near future.

Discussion

We have presented an efficient RL framework that is able to simultaneously discover QEC codes and their encoding circuits from scratch, given a qubit connectivity, gate set, and error operators. It learns strategies simultaneously for a range of noise models, thus re-using and transferring discoveries between different noise regimes. We have been able to discover codes and circuits up to 25 physical qubits and code distance 5, while presenting a roadmap to scale this approach much further. This is thanks to our formulation in terms of stabilizers, which serve both as compact input to the agent as well as the basis for rapid Clifford simulations, which we implemented in a vectorized fashion using a modern machine-learning framework.

In the present work, we have focused on the quantum communication or quantum memory scenario, where the encoding circuit itself can be assumed error-free since we focus on errors happening during transmission. As a result, our encoding circuits are not fault tolerant, i.e., single errors, when introduced, might sometimes proliferate to become incorrigible. Flag-based fault tolerance³³ added on top of our encoding circuits would be an effective strategy to make them fault tolerant.

We have also shown how to efficiently scale up this strategy by exclusively targeting CSS codes, potentially being able to outperform the recent quasi-cyclic codes from ref. ¹⁴ in the near future. To achieve such a milestone, one should be able to target LDPC codes directly. As a starting point, one could add an additional term in the reward that penalizes stabilizers with large weights. This would not be guaranteed to work out of the box, as one would need to tune the importance between the original Knill-Laflamme term and this new term through some new hyperparameter. In addition, stabilizer generators of LDPC codes must also be local, meaning that their weight must be distributed along neighboring qubits for efficient measurement cycles. Finally, there is a large degeneracy in how the code generators are chosen: there are many possible choices of which n − k Pauli strings out of the 2^n−k elements of the stabilizer group are the stabilizer generators, leading to different stabilizer weights. All in all, we believe that, while promising, substantial innovations are needed in order to discover LDPC codes with such an RL-based strategy. However, the payoff would be quite substantial: a strategy based on RL would not be restricted to the particular ansatz of quasi-cyclic codes. In addition, not only would the codes be discovered, but their encoding circuits would also be automatically known.

One of the limits of our approach is GPU memory. However, this could be circumvented through different means. While it is always possible to trade performance by memory load, the tendency to train very large AI models is thrusting both the development of novel hardware with increased memory capabilities and the integration of distributed computing options in modern machine learning libraries. These developments makes us envision scenarios where the framework presented in this work could be scaled up straightforwardly to multiple GPU machines. This makes us optimistic about the future of AI-discovered QEC in the very near future.

Methods

Stabilizer codes

The stabilizer formalism

Some of the most promising QEC codes are based on the stabilizer formalism¹⁵, which leverages the properties of the Pauli group G_n on n qubits. The basic idea of the stabilizer formalism is that many quantum states of interest for QEC can be more compactly described by listing the set of n operators that stabilize them, where an operator O stabilizes a state $\left\vert \psi \right\rangle$ if $\left\vert \psi \right\rangle$ is an eigenvector of O with eigenvalue + 1: $O\left\vert \psi \right\rangle =\left\vert \psi \right\rangle$. The Pauli group on a single qubit G₁ is defined as the group that is generated by the Pauli matrices X, Y, Z under matrix multiplication. Explicitly, G₁ = { ±I, ±iI, ±X, ±iX, ±Y, ±iY, ±Z, ±iZ}. The generalization to n qubits consists of all n-fold tensor products of Pauli matrices (called Pauli strings).

A code that encodes k logical qubits into n physical qubits is a 2^k-dimensional subspace (the code space${\mathcal{C}}$) of the full 2ⁿ-dimensional Hilbert space. It is completely specified by the set of Pauli strings ${S}_{{\mathcal{C}}}$ that stabilize it, i.e., ${S}_{{\mathcal{C}}}=\{{s}_{i}\in {G}_{n}| {s}_{i}\left\vert \psi \right\rangle =\left\vert \psi \right\rangle ,\forall \left\vert \psi \right\rangle \in {\mathcal{C}}\}$. ${S}_{{\mathcal{C}}}$ is called the stabilizer group of ${\mathcal{C}}$ and is usually written in terms of its group generators g_i as ${S}_{{\mathcal{C}}}=\left\langle {g}_{1},{g}_{2},\ldots ,{g}_{n-k}\right\rangle$, where each g_i is a Pauli string.

Quantum noise

Noise affecting quantum processes can be represented using the so-called operator-sum representation⁴¹, where a quantum noise channel ${\mathcal{N}}$ induces dynamics on the state ρ according to

$${\mathcal{N}}(\rho )=\sum _{\alpha }{E}_{\alpha }\rho {E}_{\alpha }^{\dagger },$$

(6)

where E_α are Kraus operators, satisfying ${\sum }_{\alpha }{E}_{\alpha }^{\dagger }{E}_{\alpha }=I$. The most elementary example is the so-called depolarizing noise channel,

$${{\mathcal{N}}}_{{\rm{DP}}}(\rho )={p}_{I}\rho +{p}_{X}X\rho X+{p}_{Y}Y\rho Y+{p}_{Z}Z\rho Z,$$

(7)

where p_I + p_X + p_Y + p_Z = 1 and the set of Kraus operators are ${E}_{\alpha }=\{\sqrt{{p}_{I}}I,\sqrt{{p}_{X}}X,\sqrt{{p}_{Y}}Y,\sqrt{{p}_{Z}}Z\}$. When considering n qubits, one can generalize the depolarizing noise channel by introducing the global depolarizing channel,

$${{\mathcal{N}}}_{{\rm{GDP}}}(\rho )=\mathop{\bigotimes }\limits_{j=1}^{n}{{\mathcal{N}}}_{\,\text{DP}\,}^{(j)}({\rho }_{j}),$$

(8)

consisting of local depolarizing channels acting on each qubit j independently. Taken as is, this error model generates all 4ⁿ Pauli strings by expanding (8). A commonly used simplification is the following. Assume that all error probabilities are identical, i.e., p_X = p_Y = p_Z ≡ p (and p_I = 1 − 3p). Then, the probability that a given error occurs decreases with the number of qubits it affects. For instance, if we consider 3 qubits, the probability associated with XII is p(XII) = p(1−3p)², and in general, the leading order contribution to the probability of an error affecting m qubits is p^m. This leads to the concept of the weight of an operator as the number of qubits on which it differs from the identity and to a hierarchical approach to building QEC codes. In particular, stabilizer codes are described by specifying what is the minimal weight in the Pauli group that they cannot detect.

The Knill-Laflamme conditions

The fundamental theorem in QEC is a set of necessary and sufficient conditions for quantum error detection discovered independently by Bennett, DiVincenzo, Smolin and Wootters⁴², and by Knill and Laflamme in ref. ⁴³ (Knill-Laflamme conditions from now on). These state that a code ${\mathcal{C}}$ with associated stabilizer group ${S}_{{\mathcal{C}}}$ can detect a set of errors {E_μ} ⊆ G_n, if and only if for all E_μ we have either

$$\{{E}_{\mu },{g}_{i}\}=0,$$

(9)

for at least one g_i, or the error itself is harmless, i.e.,

$${E}_{\mu }\in {S}_{{\mathcal{C}}}.$$

(10)

The smallest weight in G_n for which none of the above two conditions hold is called the distance of the code. For instance, a distance − 3 code is capable of detecting all Pauli strings of up to weight 2, meaning that Knill-Laflamme conditions (9), (10) are satisfied for all Pauli strings of weights 0, 1 and 2. Moreover, the smallest weight for which these are not satisfied is 3, meaning that there is at least one weight − 3 Pauli string violating both (9) and (10). However, some weight − 3 Pauli strings (and higher weights) will satisfy the Knill-Laflamme conditions, in general.

While these conditions are framed in the context of quantum error detection, there is a direct correspondence with quantum error correction. Indeed, a quantum code of distance d can correct all errors of up to weight t = ⌊(d − 1)/2⌋¹⁵. If all the errors that are detected with a weight smaller than d obey (9), the code is called non-degenerate. On the other hand, if some of the errors satisfy (10), the code is called degenerate.

Asymmetric codes

The default weight-based [[n, k, d]] classification of QEC codes implicitly assumes that the error channel is symmetric, meaning that the probabilities of Pauli X, Y, and Z errors are equal. However, this is usually not the case in experimental setups: for example, dephasing (Z errors) may dominate bit-flip (X) errors. In our work, we consider an asymmetric noise channel where p_X = p_Y but p_X ≠ p_Z. To quantify the asymmetry, we use the bias parameter c_Z³⁵, defined as

$${c}_{Z}=\frac{\log {p}_{Z}}{\log {p}_{X}}.$$

(11)

For symmetric error channels, c_Z = 1. If Z-errors dominate, then 0 < c_Z < 1, since ${p}_{Z}={p}_{X}^{{c}_{Z}}$ and p_X, p_Z ≪ 1; conversely c_Z > 1 when X/Y errors are more likely than Z errors.

The weight of operators and the code distance can both be generalized to asymmetric noise channels^44,45,46,47. Consider a Pauli string operator E_μ and denote as w_X the number of Pauli X inside E_μ (likewise for Y, Z). Then one can introduce the c_Z − effective weight³⁵ of E_μ as

$${w}_{e}({E}_{\mu },{c}_{Z})={w}_{X}({E}_{\mu })+{w}_{Y}({E}_{\mu })+{c}_{Z}{w}_{Z}({E}_{\mu }),$$

(12)

which reduces to the symmetric weight for c_Z = 1, as expected. The c_Z − effective distance of a code d_e(c_Z) is then defined³⁵ as the largest possible integer such that the Knill-Laflamme conditions (9), (10) hold for all Pauli strings E_μ with w_e(E_μ, c_Z) < d_e(c_Z). Like in the symmetric noise case, the meaning of this effective distance is that all error operators with an effective weight smaller than d_e can be detected.

Code classification

It is well known that there is no unique way to describe quantum codes. For instance, there are multiple sets of code generators that generate the same stabilizer group, hence describing the same code. Moreover, the choice of logical basis is not unique, and qubit labeling is arbitrary. While such redundancies are convenient for describing quantum codes in a compact way, comparing and classifying different codes can be rather subtle. Fortunately, precise notions of code equivalence have been available in the literature since the early days of this field. In this work, we refer to families of codes based on their quantum weight enumerators (QWE)⁴⁸, A(z), and B(z), which are polynomials with coefficients

$$\begin{array}{ll}{A}_{j}=\frac{1}{{({2}^{k})}^{2}}\mathop{\sum}\limits_{w({E}_{\mu })=j}{\rm{Tr}}\,\left({E}_{\mu }{P}_{{\mathcal{C}}}\right){\rm{Tr}}\,\left({E}_{\mu }^{\dagger }{P}_{{\mathcal{C}}}\right),\\ {B}_{j}=\frac{1}{{2}^{k}}\mathop{\sum}\limits_{w({E}_{\mu })=j}{\rm{Tr}}\,\left({E}_{\mu }{P}_{{\mathcal{C}}}{E}_{\mu }^{\dagger }{P}_{{\mathcal{C}}}\right),\end{array}$$

(13)

where w is the operator (c_Z = 1) weight, j runs from 0 to n and ${P}_{{\mathcal{C}}}$ is the orthogonal projector onto the code space. Intuitively, A_j counts the number of error operators of weight j in ${S}_{{\mathcal{C}}}$ while B_j counts the number of error operators of weight j that commute with all elements of ${S}_{{\mathcal{C}}}$. Logical errors are thus the ones that commute with ${S}_{{\mathcal{C}}}$ but are not in ${S}_{{\mathcal{C}}}$, and these are counted with B_j − A_j.

Such a classification is especially useful in scenarios with symmetric noise channels, where it is irrelevant whether the undetected errors contain a specific Pauli operator at a specific position. However, such a distinction can in principle be important in asymmetric noise channels. One could in principle generalize (13) to asymmetric noise channels substituting the weight w by the effective weight w_e of operators, but then comparing codes across different values of noise bias becomes cumbersome. Hence, in the present work we always refer to (symmetric) code families according to (13) for all values of c_Z, i.e., we will effectively pretend that c_Z = 1 when computing the weight enumerators of asymmetric codes.

Reinforcement learning

Reinforcement Learning (RL)⁴⁹ is designed to discover optimal action sequences in decision-making problems. The goal in any RL task is encoded by choosing a suitable rewardr, a quantity that measures how well the task has been solved, and consists of an agent (the entity making the decisions) interacting with an environment (the physical system of interest or a simulation of it). In each time step t, the environment’s state s_t is observed. Based on this observation, the agent takes an action a_t which then affects the current state of the environment. A trajectory is a sequence of state and action pairs that the agent takes. An episode is a trajectory from an initial state to a terminal state. For each action, the agent receives a reward r_t, and the goal of RL algorithms is to maximize the expected cumulative reward (return), ${\mathbb{E}}\left[{\sum }_{t}{r}_{t}\right]$. The agent’s behavior is defined by the policy π_θ(a_t∣s_t), which denotes the probability of choosing action a_t given observation s_t, and that we parameterize by a neural network with parameters θ. Within RL, policy gradient methods²² optimize the policy by maximizing the expected return with respect to the parameters θ with gradient ascent. One of the most successful algorithms within policy gradient methods is the actor-critic algorithm⁵⁰. The idea is to have two neural networks: an actor network that acts as the agent and that defines the policy, and a critic network, which measures how good was the action taken by the agent. In this paper, we use a state-of-the-art policy-gradient actor-critic method called Proximal Policy Optimization (PPO)⁵¹, which improves the efficiency and stability of policy gradient methods.

Implementation and hyperparameters

We use the PPO implementation of⁵², which we break down in more detail here (see also Fig. 10 and Table 1 for a list of hyperparameters). In our implementation, the RL environment is vectorized, meaning that the agent interacts with multiple different quantum circuits at the same time. The hyperparameter that determines this number of RL environments is called NUM_ENVS. The learning algorithm consists of two processes: collect and update. During collection, the agent interacts with the environments and a total of NUM_STEPS sequences of (observation, action, reward) are collected per environment. Following the collection, the update process begins. Here, we have a total of NUM_ENVS * NUM_STEPS individual steps that are shuffled and reshaped into NUM_MINIBATCHES minibatches (each of size NUM_ENVS * NUM_STEPS // NUM_MINIBATCHES). These are used for updating the weights of the neural networks through gradient ascent, which happens a number UPDATE_EPOCHS times during every update process. The whole collection-update cycle gets repeated NUM_EPOCHS times.

Fig. 10: Structure of the PPO algorithm used in this work, focusing on its structural and operational aspects.

In the Collect phase, the agent interacts with the environments to extract triples (observation, action, reward) that are then used in the Update phase to update the parameters of the neural networks via gradient ascent.

Table 1 Hyperparameters that were used during training with some typical range of values that we have seen to lead to good performance (see Methods for a description of each hyperparameter)

The neural networks that we have chosen are standard feedforward fully-connected neural networks with ReLU activation functions and with identical architectures for both the actor and value networks, except for the output layer. In particular, they both consist of an input layer of size 2n(n − k) given by the observation from the environment, followed by two hidden layers of size h (we have experimented with sizes 16 to 400) and an output layer of size n_A (number of actions) in the case of the actor network and of size 1 for the value network (see Fig. 10). The number of actions n_A is determined by the number of physical qubits, available gate set and qubit connectivity.

Other hyperparameters that participate in the PPO implementation which we include for completeness (but that we refer to ref. ⁵¹ for further explanations) are the discount factor γ, the generalized advantage estimator (GAE) parameter λ, the actor loss clipping parameter ε, the entropy coefficient and the value function (VF) coefficient (see Table 1 for typical values that we have found to work well).

Regarding the optimizer itself, we use ADAM with a clipping in the norm of the gradient (MAX_GRAD_NORM) and some initial learning rate (LR) that gets annealed (ANNEAL_LR) using a linear schedule as the training evolves, see Table 1 for specific numerical values of these hyperparameters.

Next, we show an example of a typical training trajectory in Fig. 11 together with all the hyperparameter numerical values that were used and the execution time on a single NVIDIA Quadro RTX 6000 GPU. There, 4 agents are tasked to find [[7, 1, 3]] codes, which each of them completes successfully running in parallel in 20 s. The error channel is chosen to be global symmetric depolarizing with p_I = 0.9 (i.e., p_X = p_Y = p_Z = 1 − p_I/3). The average circuit size starts being 20 by design, i.e., if no code has been found after 20 gates, the circuit gets reinitialized. This number starts decreasing when codes start being found and it saturates to a final value, which is in general different for each agent. As a final remark, running the same script on a CPU node with two Xeon Gold 6130 processors takes 7 min 40 s.

Fig. 11: Example of a training run for [[7, 1, 3]] code discovery.

a Return and circuit size during training, b Details of the data calculation pipeline and complete set of hyperparameters used for this run. Here, 4 parallel agents each interact with batches of 64 circuits processed in parallel. Each agent finds a different encoding circuit, and the training finishes in 20 s on a single GPU. The meaning of every hyperparameter is explained in Methods.

Finally, we show how the runtime scales when increasing the number of physical qubits n and the code distance d in Fig. 12. In order to get a meaningful comparison, we fix all other hyperparameters to be identical to those shown in Fig. 11. We remark that in general the agents will not have converged to a successful encoding sequence given the allotted resources.

Fig. 12: Time to reach 1 million training steps.

Execution time of training trajectories of 4 parallel agents (in a single GPU) with identical hyperparameters as those shown in Fig. 11 with different number of physical qubits n and code distance d (but keeping the number of logical qubits k = 1).

Clifford simulator

Here we give more details on the implementation of our simulations, which are based on the binary symplectic formalism¹⁶ of the Pauli group and that have been optimized to be compatible with modern vectorized machine learning frameworks running on Graphical Processing Units (GPU). All the operations that are required for both simulating the quantum circuits and to compute the reward have been implemented using binary linear algebra. Our Clifford simulator is implemented using JAX⁵³, a state-of-the-art modern machine learning framework with good vectorization and just-in-time compilation capabilities. On top of that, we also train multiple RL agents in parallel on a single GPU. This is achieved by interfacing with PUREJAXRL⁵², a library that offers a high-performance end-to-end JAX RL implementation. The source code for our project is available on GITHUB under the name QDX³⁷, which is an acronym for Quantum Discovery with JAX. It includes both the Clifford simulator, the PPO algorithm and demo Jupyter notebooks to reproduce some of our main results.

A stabilizer generator g_i is formally represented as a Pauli string P₁ ⊗ P₂ ⊗ ⋯ ⊗ P_n, where P_i ∈ {I, X, Y, Z} is any Pauli operator, and numerically as a binary vector of size 2n. For example, the Pauli matrices are represented as I = (0, 0), X = (1, 0), Y = (1, 1), Z = (0, 1), and a general Pauli string is represented as (x₁, …, x_n, z₁, …, z_n), where all x_i and z_i are either 0 or 1. For instance, the binary vector (1, 1, 0, 0, 0, 1, 1, 0) represents the Pauli string XYZI. Matrix multiplication gets mapped to binary sum (ignoring global phases), e.g.,

$$X\cdot Y=Z\leftrightarrow (1,0)+(1,1)=(0,1)(\,\text{mod}\,2).$$

(14)

A stabilizer code is specified by n − k stabilizer group generators ${S}_{{\mathcal{C}}}=\langle {g}_{1},{g}_{2},\ldots ,{g}_{n-k}\rangle$ and is therefore represented by a check matrixG¹⁶, which is a (n − k) × 2n binary matrix where each row i represents the Pauli string g_i from ${S}_{{\mathcal{C}}}$. Clifford gates map Pauli strings to Pauli strings, meaning that a check matrix G gets mapped to a different check matrix $G{\prime}$ under the action of any Clifford gate. It is sufficient to consider the action of the Clifford gates H,S,CNOT on X/Z stabilizers. For instance, the action of H is the well-known

$$HXH=Z,\ HZH=X,$$

(15)

meaning that it exchanges X by Z. More generally, H_i exchanges columns i and i + n of a check matrix G. We implement this transformation by representing H_i with a binary matrix H(i)_b and by performing binary matrix multiplication between G and H(i)_b. Explicitly, H(i)_b is the 2n × 2n identity matrix with columns i and i + n exchanged,

$$H{(i)}_{b}=\left(\begin{array}{cccccccc}1&0&\cdots \,&0&\cdots \,&0&\cdots \,&0\\ 0&1&\cdots \,&0&\cdots \,&0&\cdots \,&0\\ 0&0&\cdots \,&0&\cdots \,&0&\cdots \,&0\\ \vdots &\vdots &&\vdots &&\vdots &&\vdots \\ 0&0&\cdots \,&0&\cdots \,&{\underbrace{1}}\atop{i}&\cdots \,&0\\ \vdots &\vdots &&\vdots &&\vdots &&\vdots \\ 0&0&\cdots \,&{{\underbrace{1}}\atop{i+n}}&\cdots \,&0&\cdots \,&0\\ \vdots &\vdots &&\vdots &&\vdots &&\vdots \\ 0&0&\cdots \,&0&\cdots \,&0&\cdots \,&1\end{array}\right),$$

(16)

and matrix multiplication must be done from the right, i.e., $G{\prime} =G\cdot H{(i)}_{b}(\,\text{mod}\,2)$. Binary matrix representations can be built for all S_i and CNOT(i, j) gates in a similar manner and can be explicitly found in our repository³⁷.

When simulating CSS circuits, the check matrix G splits into two non-overlapping block submatrices: G_X and G_Z. An advantage of working with CSS circuits is that we can make the binary representation of Pauli strings even more compact. Specifically, we will never encounter a Pauli string with a Y in it, and all Pauli strings will contain either only X’s or only Z’s. Thus, it suffices to represent Pauli strings with arrays of n bits. Possible ambiguities (e.g., both XX and ZZ would be represented by (1, 1)) are avoided by labeling which code generators are in G_X and which ones are in G_Z. We can thus represent an [[n, k]] code with n(n − k) bits, getting an improvement of a factor of 2 with respect to generic stabilizer codes.

In practice, we only need to implement the CNOT gate (H only decides the splitting between G_X and G_Z). Here we show how to implement a simple CNOT gate on a system of two qubits for illustrative purposes. The CNOT transformation rules are the following:

(17)

(18)

Crucially, exchange of control and target labels turns an X transformation rule into a Z transformation rule. We can thus use a single binary matrix per CNOT (we choose the one that implements the X transformation rule) and use the binary matrix representation of the CNOT with exchanged control and target to transform Z-type stabilizers.

We benchmark the performance of our simulator against Stim³⁶, a fast simulator for Clifford circuits. In particular, we compare the time needed to generate random Clifford circuits of 1000 gates on 40 qubits (generic stabilizer) and on 49 qubits (CSS), which is shown in Fig. 13. The gap in simulation time decreases as the number of qubits scales up, yet we retain a competitive advantage for all qubit numbers considered in this work and that will likely be considered in follow-up works.

Fig. 13: Comparison between our stabilizer simulator and Stim.

Compute time required to generate random Clifford circuits of 1000 gates for 40 qubits (upper, generic stabilizer) and for 49 qubits (lower, CSS restriction) with Stim (green) and with our simulator (orange).

Two Pauli strings P₁ and P₂ either commute or anticommute. We compute this by evaluating the binary symplectic bilinear

$${P}_{1}\cdot \Omega \cdot {P}_{2}^{T}=\left\{\begin{array}{ll}0&{\rm{if}}\,{P}_{1}\,{\rm{and}}\,{P}_{2}\,{\rm{commute}},\\ 1&{\rm{if}}\,{P}_{1}\,{\rm{and}}\,{P}_{2}\,{\rm{anticommute}}\end{array}\right.$$

where P₁ and P₂ are the corresponding binary representations and Ω is the 2n × 2n symplectic metric

$$\Omega =\left(\begin{array}{rc}{{\mathbb{0}}}_{n}&{{\mathbb{1}}}_{n}\\ {{\mathbb{1}}}_{n}&{{\mathbb{0}}}_{n}\\ \end{array}\right).$$

(19)

In our problem, we want to determine whether a list of operators {E_μ} anticommute with any of the code generators g_i. We group the error operators inside a binary matrix E_M, where each row corresponds to the binary representation of a different operator, and we compute

$${E}_{M}\cdot \Omega \cdot {G}^{T}.$$

(20)

The result is a binary matrix with dimensions (num(E_μ), n − k). The first Knill-Laflamme condition Eq. (9) requires checking whether at least one code generator g_i anticommutes with any given error operator. This means that the result has to be transformed into a binary vector of size num(E_μ), where a 1 means that the first Knill-Laflamme condition Eq. (9) is satisfied for the corresponding operator E_μ and that is zero otherwise.

The second Knill-Laflamme condition Eq. (10) requires checking whether any error operator ${E}_{\mu }\in {S}_{{\mathcal{C}}}$. In principle, the full stabilizer group of 2^n−k elements must be built at every time step of our simulations. For the physical qubit numbers that we have considered in our work, this computation is still fast enough, becoming more challenging as n − k ≥ 13. In practice, not many error operators end up being in ${S}_{{\mathcal{C}}}$, which we leverage by introducing a softness parameter s such that only a subgroup of ${S}_{{\mathcal{C}}}$ is built. More precisely, s = 0 means that this subgroup is empty, s = 1 means taking only the generators g_i as the subgroup, s = 2 means taking the generators g_i and all pairwise combinations of generators g_ig_j, and so on for larger s.

Different connectivities and gatesets

Here we present results for some other selected gatesets and connectivities to show the flexibility of our approach. We choose to target stabilizer codes with parameters [[7, 1, 3]] and show the shortest encoding circuit for each case. More concretely, we pick three different gatesets and three different connectivities according to Fig. 14. We have trained 640 agents in every case.

Fig. 14: Different connectivities and gatesets.

Description of the three different (a) connectivities and (b) gatesets that we consider.

Line connectivity:

G1:

G2:

G3:

Brick connectivity:

G1:

G2:

G3:

Square connectivity:

G1:

G2:

G1:

Distance 5 stabilizer codes

Here we show the code families that were found for d = 5, with number of physical qubits varying between 11 and 15. In order to reduce computational effort, for n ≥ 14 we ignored the second Knill-Laflamme condition (10), and as a result the codes found in Fig. 2n ≥ 14 are only non-degenerate. Moreover, the increased memory requirements from keeping track of more error operators (3) means that the number of agents that can be trained in parallel on a single GPU decreases. Each of these training runs needs 1–4 h, depending on the code parameters and whether degenerate codes are also targeted.

Noise-aware meta-agent

Here we provide further details on the more general meta-agent that switches its encoding strategy depending on the kind of noise present in the system, characterized by the bias parameter c_Z, according to (11).

Training setup and hyperparameters

During training, the meta-agent collects experiences with different values of c_Z, which we sample from the set c_Z ∈ {0.5, 0.6, 0.7, …, 1.9, 2} with a uniform probability distribution. Once a particular value of c_Z is picked, the error probabilities characterizing the noise channel are $({p}_{I},{p}_{X},{p}_{X},{p}_{X}^{{c}_{Z}})$. Normalization of the error probabilities imposes a relationship between p_I and p_X, which means that there is only one other free parameter besides c_Z, either p_I or p_X. It is more beneficial for training and generalization to keep p_I fixed and solve for p_X; otherwise the magnitude of the probabilities {p_μ} changes a lot when varying c_Z, leading to poorer performance.

The hyperparameters λ_μ of the reward (2) are defined as

$${\lambda }_{\mu }={\left.\frac{{p}_{\mu }}{\text{max}({p}_{\mu })}\right| }_{{c}_{Z}},$$

(21)

by which we mean that for every c_Z, the corresponding set of p_μ’s gets normalized by the maximal value of p_μ in that set. We choose p_I = 0.9, even though both slightly smaller and larger values around p_I ≈ 0.9 perform equally well. However, going below p_I ≲ 0.8 or above p_I ≳ 0.95 comes with different challenges. In the former (for large errors), we lose the important property that the sum of p_μ’s decreases as a function of weight, ${({\sum }_{\mu }{p}_{\mu })}_{w = 1} > {({\sum }_{\mu }{p}_{\mu })}_{w = 2} > \ldots \,$. In the latter (small errors), the range of values of p_μ is so large that one would need to use a 64-bit floating-point representation to compute the reward with sufficient precision. Since both RL algorithms and GPUs are currently designed to work best with 32-bit precision, we decide to avoid this range of values for p_I during training, but we will still evaluate the strategies found by the RL agent on different values of p_I.

We allow a maximum of 35 gates before the trajectory gets reinitialized. Even though all encodings that the meta-agent outputs have circuit size 35, we notice that trivial gate sequences are applied at the last few steps, effectively reducing the overall gate count. We remark that this feature is not problematic: it means that the agent is done well before a new training run is launched, and the best thing it can do is collecting small negative rewards until the end. We manually prune the encodings to get rid of such trivial operations, and the resulting circuit sizes vary from 22 to 35, depending on the value of c_Z.

Failure probability

As is the case for most RL learning procedures, every independent learning run will typically result in a different learned strategy by the agent. We thus train many agents and post-select the few best-performing ones. Now, there are in principle two different ways to make this selection: The first one is based on how well they minimize the weighted Knill-Laflamme sum (which is what they were trained for). The second one is by evaluating the probability that a single error correction cycle will end in failure, i.e., the probability that the wrong correction would be applied based on the detected syndrome. Typically, this metric would require a decoder. In practice, we implement a simple maximum likelihood decoder as follows. First, since we work with a probabilistic model of errors, we have a representation of the probability that each type of error occurs. Then, we iterate through all possible non-zero syndromes (undetectable errors in degenerate codes belong to the zero syndrome class and don’t lead to an error), so that for each non-zero syndrome:

• We identify all errors that could have caused this syndrome.

• We extract the probabilities of these errors based on our probabilistic model of errors.

• We find the maximum probability among these errors, which corresponds to the most likely error for this syndrome.

• Finally, we calculate the failure probability as the sum of all error probabilities except the most likely one in that given syndrome.

If the code is degenerate there could still be the possibility that the actual error was misidentified and after correction one could still have ended up with an “error” that is inside the stabilizer group. The contribution from these cases are negligible in our case and are thus ignored. However, one would in principle still have to consider them in a general scenario. In practice one could still evaluate the codes discovered with our RL approach by substituting the decoder accordingly.

Noise-aware meta-agent vs an ensemble of simple agents

Here we explain the settings of this experiment (shown in Fig. 7) in order to make a fair comparison. There are 16 possible values of the bias parameter, c_Z = {0.5, 0.6, …, 1.9, 2}. Since each meta-agent has seen instances of all 16 values, we will only allow the single-c_Z agents to be trained on one sixteenth of the total timesteps than the ones used for each meta-agent. In addition, the best post-selected meta-agent was selected out of 714 training runs. Therefore, we train 714 × 16 = 11424 single − c_Z agents to make the comparison. All other hyperparameters are kept fixed.

We also include an extended statistical analysis over the entire ensemble of both meta-agents and simple agents in Fig. 15. There, we average over their respective ensembles and show the average performance of agents of each class, together with their standard deviations. There we see that all simple agents consistently fail at minimizing the failure probability at large values of c_Z. The larger error bars at smaller values of c_Z for the meta-agents can also be interpreted as these class of more general agents allocating a larger effort in both exploration and generalization to other values of c_Z.

Fig. 15: Comparison between the performance of the noise-aware meta agent vs simple agents.

The results shown are averaged over their respective ensembles. Error bars are one standard deviation.

CSS codes

A particularly useful subclass of stabilizer codes are CSS codes^10,12. They are defined by their stabilizer generators containing either only X or only Z Pauli operators. This restriction is useful because X-type and Z-type errors are detected independently, thereby implying the detection of Y-type errors when the corresponding X and Z-type stabilizers fire simultaneously. Moreover, strong contenders for implementation in large-scale quantum computations such as surface codes or color codes are of the CSS type.

Alternative strategies using RL

In the main text we have argued that CSS codes can be constructed by constraining the encoding circuit to be built from an initial layer of Hadamard gates and CNOTs thereafter.

In order to adapt our RL strategy to CSS code discovery we have considered a mixed human-AI strategy where we decide the Hadamard layer and where the RL agent decides the content of the CNOT block. Here we comment on other possibilities.

The first one would be to keep as actions both H and CNOT gates for the agent to use, but penalize the agent every time that a Hadamard gate is used after a CNOT gate. This would in principle lead to an agent that would know what is the correct architecture to be used for CSS codes at expenses of having to fine-tune this new penalty term in the reward. We avoided this strategy because we did not want to introduce further hyperparameters. The second option would be to have a multi-agent scenario with two agents: one that only places Hadamards and another one that only places CNOTs. While interesting, multi-agent tasks are typically harder to train and would involve redesigning our entire framework.

Circuit structure of CSS codes

Here we give a proof of the claim that codes resulting from circuits with an initial block of Hadamard gates on a subset of the qubits and followed by CNOT gates thereafter can only be CSS.

Let us label physical qubits with index 1 ≤ q ≤ n and target a CSS code with parameters [[n, k, d]]. Let’s assume for simplicity that the initial block of Hadamard gates is applied to qubits k + 1, …, k + n_H, with n_H < n − k. The initial tableau of the would-be code reads

$$\begin{array}{lll}{g}_{1} & = & {X}_{k+1}, \\ {g}_{2} & = & {X}_{k+2}, \\ & \cdots \\ {g}_{{n}_{H}} & = & {X}_{k+{n}_{H}},\\ {g}_{{n}_{H}+1} & = & {Z}_{k+{n}_{H}+1},\\ & \cdots \\ {g}_{n-k} & = & {Z}_{n}.\end{array}$$

(22)

From this moment forward, only CNOT gates are allowed. Let’s start by considering what is the effect of a CNOT gate with control qubit inside the H-block, i.e., control ∈ {k + 1, …, k + n_H}. For whatever target qubit, what such a CNOT does is populate the target position of the corresponding stabilizer g_control with an X. Subsequent CNOT gates affecting those positions, either as control or target qubits, will either introduce additional X’s or simply do nothing. Since X² = 1, the stabilizers ${g}_{1},{g}_{2},\ldots {g}_{{n}_{H}}$ will only ever contain either X’s or 1’s. Similarly, the effect of CNOTs on stabilizers ${g}_{{n}_{H}+1},\ldots ,{g}_{n-k}$ is simply populating them with Z’s or 1’s. Since the set of stabilizer generators can be clearly separated into a subset built with only X’s and 1’s and another one with only Z’s and 1’s, such a tableau describes a CSS code.

GPU memory estimation

The independence of X and Z-type error detection in CSS codes means that the number of error operators that we have to keep track of drastically reduces from (3) to

$$| {\{{E}_{\mu }\}}^{{\rm{CSS}}}{| }_{w\le d-1}=2\mathop{\sum }\limits_{w=0}^{d-1}\left(\begin{array}{l}n\\ w\end{array}\right),$$

(23)

where the overall factor of 2 counts both X and Z-type errors.

Thanks to the separability of X and Z in the stabilizer generators, the tableaus that we have to simulate are block-diagonal,

$$\left(\begin{array}{rc}{g}_{X}&0\\ 0&{g}_{Z}\\ \end{array}\right),$$

(24)

where g_X is a binary matrix of size num(H) × n containing the X-type stabilizer generators, and g_Z is of size (n − k − num(H)) × n and it contains the representation of the Z-type generators. Here, num(H) is the number of Hadamard gates that are applied at the very beginning.

Separability of X- and Z-type error detection implies that g_X must detect all Z-type errors (by the first Knill-Laflamme condition (9)), and correspondingly for g_Z with X-type errors. If the code is degenerate, it must happen that some X-type errors are elements of the stabilizer subgroup generated by g_X and likewise for Z.

All in all, this means that we can reduce the number of error operators (23) by a factor of 2 (since we use the same representation for both X and Z-type errors). Each of such error operator is a binary array of size n, which amounts to 8n bits of memory.

We therefore estimate the memory usage by counting the number of error operators (23) (divided by 2, as argued above), times the amount of binary digits that have to be specified for each of them, i.e., 8n.