Introduction

Triggered by many proof-of-principle experiments over the past decades1,2,3,4,5, quantum key distribution (QKD) has reached a level of maturity that allows building large-scale networks over standard telecommunication fiber6,7. However, due to absorption of photons, long-distance transmission still requires the use of trusted nodes8, even though QKD has recently been reported over 1000 km using an idealized laboratory setting with spooled fiber9. To enable information-theoretic secure QKD and entanglement-based applications, these trusted nodes have to be replaced by (untrusted) quantum repeaters, which promise the creation of distant entanglement with improved scaling compared to direct transmission10,11.

In many quantum repeater schemes, long-lived entanglement is established between multi-mode quantum memories positioned at the opposite ends of “elementary links” of limited length, e.g., 10–100 km12. Each attempt is probabilistic, but the use of a sufficiently large number of modes ensures success with large probability in at least one of them13– which one being indicated by a “heralding signal”. In turn, this allows extending entanglement by means of entanglement swapping across neighboring elementary links after photons have been retrieved from their memories and their modes shifted to make them indistinguishable. Such feed-forward control has been implemented using various degrees-of-freedom (DOF) of the electromagnetic field13,14,15,16,17,18,19,20.

To enable the required multi-mode operation of an elementary link, all its elements—sources of entangled photon pairs, optical quantum memory, and single-photon detectors—must allow, respectively, emitting, storing, and detecting photons in a multi-mode or mode-selective manner. However, while the creation, storage and detection of temporally multiplexed photon pairs is common, the other DOFs have received much less attention, and their practical value—including the joint operation of all components—remains to be assessed. This is particularly important for spectral modes since their use simplifies the quantum memory—no readout-on-demand is required13—but, at the the same time, imposes new constraints on sources and detectors.

In 2014, Sinclair et al. proposed a repeater scheme that exploits frequency multiplexing, and demonstrated spectrally multimode photon storage in a cryogenically-cooled Tm3+:LiNbO3 crystal together with mode shifting after feed-forward control13. To complement this work, here we focus on the demonstration of the multiplexed photon pair source, demultiplexed detection of photons in different spectral modes, and, as a precursor to frequency-multiplexed quantum memory, a programmable spectral filter based on the same crystal as in ref. 13. More precisely, we implement a novel alignment-free, frequency multiplexed photon pair source that is based on fiber-pigtailed, cavity-enhanced spontaneous parametric down-conversion (SPDC) in a nonlinear crystal and is easy to integrate within a practical quantum repeater. Our work builds on previous demonstrations of cavity-enhanced SPDC21,22,23,24,25,26,27, but extends them from the characterization of either a single pair of spectrally-resolved modes or a large number of unresolved modes to many pairs of spectrally-resolved modes, as required for a quantum repeater.

Furthermore, as a simple spectral filter does not allow one to distinguish between different spectral modes (only one mode can be selected at a time), we also study a novel approach to frequency-demultiplexed photon detection based on a Virtually Imaged Phased Array (VIPA)28,29,30,31 connected to an array of 8 fibers out of which, we use 5. The demultiplexer provides a system efficiency up to 17%, superior spectral resolution compared to standard diffraction gratings32, and cross-talk below—25 dB. See the Supplemental Materials (SM) for details.

Next, to filter the 795 nm photons, we create a spectral trench through persistent spectral hole burning of an inhomogeneously broadened transition of Tm in LiNbO333. This approach is closely related to atomic-frequency-comb (AFC)-based quantum memory for light34, differing only in the creation of a spectral bin with uniformly low optical depth instead of a periodic modulation (an AFC). Coincidence measurements reveal non-classical correlations between spectrally correlated photon pairs and strongly reduced correlations between photons belonging to non-matched spectral channels.

Finally, we note that the demonstration by Sinclair et al.13 was based on time-bin qubits, however, that the proposed scheme can be generalized to any type of entanglement. This includes energy-time entanglement, as done in the present investigation.

Results

Experimental setup

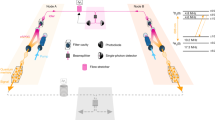
Figure 1 depicts a schematic of the experimental setup, and its integration into a quantum repeater is described in the SM. To create spectrally multiplexed photon pairs, we exploit SPDC in an 1 cm long, type-0, quasi-phase-matched, periodically poled LiNbO3 (PPLN) crystal waveguide. At a temperature of 44.5 °C, the poling period of 6.9 μm enables the interaction between 523.5 nm continuous-wave pump light and “signal” and “idler” photons with spectra centered at 795 nm and 1532 nm, respectively. To enable future use of this source in a quantum repeater, the signal wavelength matches the absorption line of Tm-doped crystals13,35,36, which are promising platforms for spectrally multiplexed quantum storage. Furthermore, the idler photon wavelength of 1532 nm allows low-loss transmission through fiber networks.

Fig. 1: Schematic of the experimental setup including a spectrally-multiplexed photon pair source, a VIPA-based demultiplexer for mapping spectral modes to distinct spatial channels, and a Tm3+:LiNbO3-based spectral filter: APD - avalanche photodiode; DDG - digital delay generator; SNSPD - superconducting nanowire single photon detector; AD - achromatic Doublet (focusing lens coupling the output beam into collection fiber).
figure 1

CyL1, CyL2 and CyL3 are cylindrical lenses with f = –50 mm, 200 mm and 150 mm, respectively.

Full size image

The PPLN is part of a monolithic Fabry–Pérot cavity, created by reflection coatings at its input and output facets (R ≈ 99% at 1532 nm, T > 99% at 523.5 nm and 795 nm, HC Photonics Corp). The cavity resonances restrict the spectrum of the idler photons to discrete spectral intervals. In turn, energy conservation also modifies the signal spectrum. Indeed, assuming a coherent pump laser with frequency ωp, we find that ωs = ωp−ωi (where s, i, label signal and idler photons, respectively), and thus perfect energy correlations between pairs of signal and idler spectral modes. Note that the cavity is singly resonant at 1532 nm to avoid clustering27,37.

To ease the use of the SPDC cavity in a practical setting, its input is pigtailed to a single-mode fiber for 523 nm wavelength, and the output is fiber-coupled to a 1:2 demultiplexer that separates signal and idler photons into two separate fiber pigtails. The rate of emitted 1532 nm photons, calculated from detection rates, is around 6 times smaller than that of the 795 nm photons, suggesting a misaligned pigtail. After filtering out all residual pump light, the width of the signal and idler spectra are reduced using frequency tunable Fabry–Pérot étalons of 6.1 GHz and 16 GHz bandwidths, respectively.

The 795 nm signal photons are directed to a spectral filter based on a trench in the absorption profile of a Tm3+:LiNbO3 crystal cooled to ≈600 mK. This trench is created by means of persistent spectral hole-burning, i.e., the transfer of Tm ions using a 795 nm laser over a 100 MHz bandwidth from the ground state to an excited state. From the excited state, ions subsequently decay spontaneously to a long-lived state—a second ground-state that arises under the application of a 400 Gauss magnetic field—that does not interact with the laser light anymore. A typical trench is depicted in Fig. 3c. The central frequency of this spectral filter can easily be tuned by changing the wavelengths over which the laser is swept during hole burning. The filtered photons are subsequently detected using a Silicon avalanche photodiode (APD)-based single-photon detector featuring a detection efficiency of 55%, a dark count rate of around 60 Hz, and ~600 ps detection time jitter.

Demultiplexing of idler spectral modes

To spectrally demultiplex the idler modes at around 1532 nm, we use a VIPA (Light Machinery Inc.) with resolving power λ/Δλ ≃ 2.5 × 105, free spectral range (FSR) of ~60.8 GHz and bandwidth of ~0.76 GHz (FWHM). The input light exits a single-mode fiber via a series of beam shaping lenses, and is focused onto the entrance slit of the VIPA. A telescopic lens system with an effective focal length of 60 mm maps the exiting spectral modes onto distinct spatial modes that are matched to the position and the numerical aperture of five standard single-mode fibers in a fiber array (PHIX Photonics Assembly). For the initial characterization of the VIPA we use a single collection fiber instead of the fiber array and a lens with fixed focal length of 45 mm instead of the telescopic system. See SM for more information. The idler photons are detected by WSi Superconducting Nanowire Single Photon Detectors (SNSPDs) featuring detection efficiencies around 65%, dark count rates around 70 Hz, and ~250 ps detection time jitter.

Finally, the signals from the single-photon detectors—one for the 795 nm photons and five for those at 1532 nm—are sent to a time tagger that outputs coincidence detection rates.

As a first step, we demonstrate the demultiplexing capability of our VIPA-setup using a tunable continuous-wave laser, a single collection fiber, and a linear photodetector instead of the photon pair source, the fiber array, and the SNSPDs, respectively. For light at λ0 = 1532.71 nm, we couple the brightest order of the VIPA into the collection fiber, and measure the transmitted intensity as a function of laser detuning. We find a 1.53 GHz-wide (FWHM) Gaussian shape with no discernible background, see SM Fig. 7a (note that the broadening compared to the VIPA specifications is due to the finite core size of the single mode collection fiber). This yields a system resolving power λ/Δλ ≃ 1.28 × 105, in good agreement with the limit imposed by the VIPA. Differently stated, the cross-talk from a 5 GHz detuned spectral channel is below—25 dB. See SM for more information.

Next, we create 8 spectral modes by frequency detuning the laser in steps of 6.5 GHz (equal to the idler mode spacing, see below) and measure their spatial profiles by displacing the collection fiber. Figure 2a shows the recorded intensity variations for each of these modes. The figure also shows the expected intensity distribution, calculated by taking into account the spectral broadening imposed by the finite linewidth of the laser and the spatial broadening due to the finite size of the core of the collection fibers, see SM for details. The result is in good agreement with the measured data.

Fig. 2: Spectroscopy using the VIPA.
figure 2

a Measured signal intensity as a function of the position of the VIPA output fiber for eight spectral modes separated by Δν = 6.5 GHz (dots) created by shifting the laser frequency, and simulation results (solid lines). b Spectrum for twenty idler modes created by the SPDC source (dots) as measured using the VIPA setup, and simulation results (solid line). c Transmission profile of the Fabry–Pérot filter cavity operating in the range of 795 nm (dots: measured data; solid line: fit). d Spectrum of the 795 nm signal photons measured by detuning the 6.1 GHz filter cavity (dots), simulated frequency comb with 6.5 GHz mode spacing (light blue line), and its convolution (dark blue line) with the cavity profile shown in (c) (green curve). e A table mentions which specific parts of the setup shown in Fig. 1 were used for the different measurements shown in this figure.

Full size image

After reverting to the SPDC source and the SNSPD, we assess the spatial distribution of the idler modes in the back focal plane of the lens behind the VIPA. To do this, we displace again the collection fiber, but now we record the single photon detection rates. To avoid that several spectral modes are mapped onto the same spatial position, we reduce the bandwidth of the idler photons to less than the VIPA’s FSR using the 16 GHz-linewidth Fabry–Pérot filter depicted in Fig. 1. In order to capture a broad spectrum, we detune the filter cavity over a total spectral range of 130 GHz so that the transmission is always maximized. Using the calibration curve in SM Fig. 7e, we convert spatial positions of the fiber into frequency, and after subsequent normalization with respect to the system efficiency (SM Fig. 7f), we obtain the spectrum of 20 idler modes plotted in Fig. 2b. As expected from the length of the cavity, we find a mode spacing of 6.5 GHz. Note that the total number of modes is only limited by phase matching. Estimating the total idler bandwidth to be 1.3 THz, this yields 200 modes.

Next, we simulate an optical comb of identical Lorentzian peaks with the same spacing of 6.5 GHz, and calculate the spatial intensity distribution for different linewidth values by taking into account the response functions of the Fabry–Pérot filter and the demultiplexer (see SM, Section V and Fig. 6). The solid blue line in Fig. 2b shows the resulting spectrum for a linewidth of 1.48 GHz (FWHM). This is in good agreement with the experimentally measured spectrum and yields an approximate value of the linewidth of the idler modes produced by the source.

To complete the characterization of the cavity-enhanced SPDC emission, we also measure the detection rate of signal photons at a wavelength around 795 nm as a function of detuning of the filter cavity (its transmission profile is shown in Fig. 2c). The recorded spectrum, plotted in Fig. 2d, shows a mode spacing of 6.5 GHz, equivalent to that of the idler photons. The low contrast is due to the similarity between the mode spacing and the cavity linewidth of 6.1 GHz. To deduce the spectrum of the signal photons prior to filtering, we fit the measured data using the convolution of the cavity transmission profile in Fig. 2c with a comb of identical Lorentzian peaks spaced by 6.5 GHz and varying their linewidth. We find good agreement for the expected linewidth of 1.48 GHz, calculated after taking into account the (quasi perfect) energy correlations between signal and idler photons due to the spectrally narrow pump of less than 10 MHz width.

Spectrally resolved joint measurements of signal and idler photons

We now assess the quantum nature of the cavity-based SPDC source. Towards this end, we first measure the 2nd order auto-correlation coefficients \({g}_{s,s}^{(2)}(0)\) and \({g}_{i,i}^{(2)}(0)\) for the individual signal and idler modes. For instance, for the signal mode, this coefficient is defined as \({g}_{s,s}^{(2)}(0)={p}_{s,s}/{p}_{s}^{2}\), where ps,s is the probability of detecting two signal photons in coincidence, and ps is the detection probability for individual signal photons. The correlation coefficient is measured using the time tagger (see SM and ref. 38). We obtain \({g}_{s,s}^{(2)}\,=\,1.299\,\pm \,0.032\) and \({g}_{i,i}^{(2)}=1.362\,\pm \,0.150\), indicating classical fields for which 1 ≤ g(2) ≤ 239. Due to accidental coincidences and a finite coincidence window, the auto-correlation coefficients are reduced compared to their expected value of 240,41. See SM for details.

Second, we also measure cross-correlation coefficients \({g}_{s,i}^{(2)}(0)={p}_{s,i}/({p}_{s}\cdot {p}_{i})\) between signal and idler photons for various combinations of spectral channels. Here, ps,i is the coincidence detection probability of signal and idler photons, and ps and pi are defined above. For classical fields, the Cauchy–Schwarz parameter \(R={({g}_{s,i}^{(2)})}^{2}/({g}_{s,s}^{(2)}\cdot {g}_{i,i}^{(2)})\) is upper bounded by 142. Taking into account the upper limit of 2 for \({g}_{s,s}^{(2)}\) and \({g}_{i,i}^{(2)}\), we find for the cross-correlation coefficient \({g}_{s,i}^{(2)}\le 2\), again under the assumption of classical fields. Initial optimization for the coincidence measurements is performed using a single optical fiber in our demultiplexer (see “Methods” for details). Later, our measurements are performed after replacing the fiber by the fiber array, using 5 SNSPDs instead of one, and employing the Tm3+:LiNbO3 -based spectral filter to narrow down the spectral widths of the signal photons, as shown in Fig. 1.

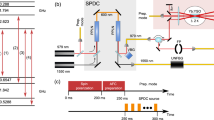
The energy levels employed for creating the spectral filter, the measurement sequence and the spectral transmission profile through the Tm-based filter are shown in Fig. 3a, b and c, respectively. We retained the Fabry–Pérot filter cavities with linewidths of 6.1 GHz and 16 GHz for the signal and idler photons, respectively, as mentioned earlier and shown in Fig. 1. These filter cavities provide additional selectivity for the spectral measurements of the signal and idler photons. Prior to the coincidence measurements for each pair of correlated signal-idler spectral modes, we maximize the coincidence counts by spectrally tuning these Fabry–Pérot cavities. For details see the Methods. Note that an actual quantum repeater implementation would take advantage of customized Fabry–Pérot filter cavities with optimized spectral widths that cover the entire bandwidths of all signal and all idler spectral modes, in which case no such optimization would be required. In this case, the Fabry–Pérot cavity for the idler photons should have a smaller bandwidth than the FSR of the VIPA in order to ensure that only a single spectral channel is mapped onto each spatial mode (see SM for more details).

Fig. 3: Measurements of cross-correlation coefficients.
figure 3

a Simplified Tm level scheme. b Measurement sequence. c A trench in the Tm absorption profile used to filter the signal modes. d 5 × 5 cross correlation coefficients measured with a VIPA array, 5 SNSPDs and a Tm:LiNbO3 filter e 89 cross correlation coefficients on a 20 × 20 grid of signal and idler spectral modes, measured using a single collection fiber and only the 6.1 GHz cavity filter for the 795 nm photons. Panels (d) and (e) use the same heatmap to indicate the value of \({{\rm{g}}}_{s,i}^{(2)}\).

Full size image

Figure 3d shows 25 cross-correlation coefficients, obtained using a laser power of 1.8 mW at the input of the SPDC cavity, on a grid composed of 5 × 5 signal and idler spectral modes. The desired spectral channels were selected using a specific SNSPD (for the 1532 nm photons) and after tuning the Tm3+:LiNbO3 filter and adjusting the angle of the Fabry–Pérot cavity that filters the 795 nm photons.

The results of these measurements confirm our expectations. We find strong quantum correlations for energy-correlated pairs of signal/idler modes with correlation coefficients up to 10, significantly above the maximum classical value of 2. All measurements relied on a coincidence window of approximately three FWHM of the coincidence peak. A threefold reduction of the window width increases \({g}_{s,i}^{(2)}\) from 10 to 20 but at the expense of a larger uncertainty. In addition, when either the signal or the idler mode is changed, the value for \({g}_{s,i}^{(2)}\) drops rapidly below 2. We attribute the small cross talk to the finite rejection of 795 nm photons outside the transmission bandwidth of the Tm3+:LiNbO3 filter, see Fig. 3c.

Finally, we expand the measurements to a grid of 20 × 20 spectral modes out of which 89 combinations were measured using the single collection fiber and no Tm3+:LiNbO3 filter. As depicted in Fig. 3e and described in the SM, we find similar results.

Discussion

Our demonstration combines the key elements of the quantum repeater architecture based on spectral multiplexing proposed in ref. 13, namely a source of spectrally multiplexed quantum-correlated photon pairs, a compatible detection setup based on a VIPA, as well as quantum memory-anticipating spectral filtering in a Tm3+:LiNbO3 crystal.

Given the narrowband pump laser, our fully pigtailed, cavity-based SPDC source is expected to generate energy-time entangled signal and idler photons that allow distributing heralded entanglement across elementary links using a Bell-state measurement43.

The width of the signal modes—currently 1.5 GHz—makes the emitted photons suitable for subsequent storage in Tm-based quantum memories using the AFC protocol34, a development that we anticipate by employing the Tm-based spectral filter. (Note that the line width can be reduced by using a cavity with higher quality factor.) However, the current mode spacing of 6.5 GHz should be decreased to optimize the available memory bandwidth. Furthermore, in order to increase the coincidence rate, the excess loss at 1532 nm wavelength needs to be removed, most likely through better pigtail alignment.

The VIPA-based detection setup allows demultiplexing of spectral modes at 1532 nm wavelength with 1.5 GHz resolution and negligible cross-talk. To improve the setup, a VIPA with higher spectral channel density should be designed, and loss at various interfaces has to be reduced. For instance, one can improve the collection efficiency of the spatial modes into the single-mode fibers by replacing the manual alignment stage of the fiber array by a piezo-controlled multi-axes precision stage. Additionally, the positions of the fibers within the array should be optimized individually. Alternatively, one should investigate the possibility to locate the VIPA inside the cryostat and to map the idler modes directly onto an SNSPD array44, which would remove the need for fiber coupling and eliminate the associated loss.

To demonstrate multimode storage and eventually an elementary quantum repeater link, one should also create a high-efficiency Tm+3:LiNbO3 memory by embedding it into an impedance-matched cavity, which ideally allows 100% efficiency45.

Taken individually, both the source and the use of the VIPA improves the state-of-the art, even before implementing the mentioned improvements. Beyond, the demonstration of both components in conjunction with the hole-burning-based spectral filter has so far been lacking. It has allowed us to reveal strong non-classical correlations between spectrally correlated signal and idler modes, and represents an important step towards a spectrally multiplexed quantum repeater based on feed-forward control.

Methods

Second order cross-correlation measurements

We start by describing the alignment of the spectral filters and demultiplexers for the case of using the VIPA with a single collection fiber. To identify and select energy-correlated frequency modes for signal and idler photons, we first optimize the count rate of the 795 nm signal photons by tuning the FPsignal filter cavity to 795.325 nm wavelength. As the signal modes are spaced by 6.5 GHz, the FPsignal filter cavity with line width of 6.1 GHz allows us to select predominantly a single spectral mode (the two neighboring modes are also transmitted but with significant loss). We then maximize the coincidence count rate by tuning the FPidler filter cavity without the VIPA-based demultiplexer. But since the 16 GHz-large bandwidth of this cavity is much broader than the idler mode spacing of 6.5 GHz, we subsequently add the VIPA-based demultiplexer and maximize the coincidence rate again by optimizing the position of the collecting fiber. This results in the selection of a single idler mode with negligible cross-talk from neighboring modes and allows us to identify pairs of energy-correlated signal/idler modes, i.e., the modes for which the cross correlation coefficient features a maximum.

To move to the neighboring signal mode, we detune the FPsignal filter cavity by 6.5 GHz. Next, to find the corresponding energy-correlated idler mode, we optimize again the coincidence detection rate by shifting the cavity in steps of 6.5 GHz and by adjusting the position of the collection fiber at the VIPA output. Repeating this procedure, we establish correlation coefficients between any pair of signal and idler modes. The results of these measurements are detailed in the SM section VIII.

In the case of using the VIPA together with a fiber array, we proceeded as follows: for achieving high coupling efficiencies, we design the fiber array and the focusing lens system such that the spatial profile of the idler modes, imaged by the lens system, match the mode size and the numerical aperture of the collection fiber, and that the spacings between the adjacent idler modes match the corresponding distances between neighboring fiber cores in the array. We find that a lens with focal distance of 60 mm is optimal for these purposes. We build a telescopic system comprising two achromatic doublets with focal lengths of 100 mm. The telescope has an effective focal length of 60 mm and allows fine tuning the focal distance for optimal coupling to the fibers. For achieving efficient coupling, we mount the fiber array on a tip-tilt stage, which we mount on a 3-axes translational stage. For our proof-of-principle demonstration of frequency-resolved joint spectral measurements, we couple 5 idler modes to 5 fibers. We proceed with the coincidence measurements with the energy correlated signal modes that are sequentially selected using the FPsignal filter cavity and spectral trenches burned into the inhomogeneous absorption line of Tm3+:LiNbO3 (see next section). The details of fiber array design and characterization are given in SM section X.

Spectral filtering of signal modes: burning wide spectral holes in Tm3+:LiNbO3

As a first step towards creating a multimode AFC-based quantum memory that allows storing the spectral modes of the signal photons, we burn spectral holes (trenches) of 100 MHz width into the inhomogeneously broadened 795 nm 3H6 to 3H4 absorption line of Tm3+:LiNbO3, see Fig. 3c. The trenches match the spectral positions of the signal photon modes. We apply a magnetic field of 400 Gauss along the c-axis of the crystal and employ one of the resulting nuclear spin sub-levels of 3H4 (with lifetime >1 s) as a shelving state for persistent hole burning. The experiments are performed at a temperature of 600 mK, and the power of the laser used for hole burning is 300 μW, measured before the Tm3+:LiNbO3 crystal. As shown in Fig. 3b, the burn duration is 50 ms and the measurement time per cycle is 150 ms. Since the excited state lifetime is 160 μs, we wait 2 ms between hole burning and measurement to ensure that no population remains in the 3H4 level and no spontaneously emitted photons can mask the photons created by the SPDC source.