Quantum algorithms for matrix geometric means

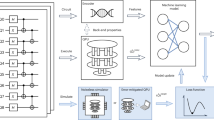
Abstract

Matrix geometric means between two positive definite matrices can be defined from distinct perspectives—as solutions to certain nonlinear systems of equations, as points along geodesics in Riemannian geometry, and as solutions to certain optimisation problems. We devise quantum subroutines for the matrix geometric means, and construct solutions to the algebraic Riccati equation—an important class of nonlinear systems of equations appearing in machine learning, optimal control, estimation, and filtering. Using these subroutines, we present a new class of quantum learning algorithms, for both classical and quantum data, called quantum geometric mean metric learning, for weakly supervised learning and anomaly detection. The subroutines are also useful for estimating geometric Rényi relative entropies and the Uhlmann fidelity, in particular achieving optimal dependence on precision for the Uhlmann and Matsumoto fidelities. Finally, we provide a BQP-complete problem based on matrix geometric means that can be solved by our subroutines.

Introduction

Quantum computation is considered a rapidly emerging technology that has important implications for the development of algorithms. Many quantum algorithms that have theoretically demonstrated potential quantum advantage, however, have been chiefly directed towards linear problems—in part because quantum mechanics is itself linear. These include simulating solutions of linear systems of equations¹, known as quantum linear algebra, and linear ordinary and partial differential equations^2,3,4,5.

However, many problems of scientific interest are nonlinear. While most nonlinear systems of equations of interest for applications only appear after discretising nonlinear ordinary and partial differential equations, there is an important class of nonlinear systems of equations that is not only relevant to partial differential equations but is also of independent interest. This class consists of the algebraic Riccati equations, which are nonlinear matrix equations with quadratic nonlinearity⁶. These are also the stationary states of the Riccati matrix differential equations, which are essential for many applications in applied mathematics, science, and engineering problems. These nonlinear matrix equations are particularly relevant for optimal control, stability theory, filtering (e.g., Kalman filter⁷), network theory, differential games, and estimation problems⁸.

It turns out that solutions to the algebraic Riccati equations are closely connected with the concept of a matrix geometric mean. For example, the unique solution to the simplest algebraic Riccati equation can be precisely expressed as the standard matrix geometric mean, as we will recall later. The matrix geometric means are matrix generalisations of the scalar geometric mean and have a long history in mathematics^9,10; there are diverse approaches to this same concept. For example, the standard matrix geometric mean can be defined as the output of an optimisation problem. The matrix geometric mean between two matrices also has an elegant geometric interpretation as a midpoint along the geodesic joining these two matrices that live in Riemannian space⁶. The Monge map between two Gaussian distributions, appearing in optimal transport, can also be expressed in terms of the matrix geometric mean¹¹. The standard and weighted matrix geometric means appear in quantum information in the form of quantum entropic^12,13 and fidelity^14,15,16 measures.

However, computing the matrix geometric mean involves matrix multiplication and also nonlinear operations like taking inverses and square roots of matrices. Here classical numerical schemes can be inefficient, with costs that are polynomial in the size of the matrix¹⁷. The processing of several matrix multiplications can, under certain conditions, be more efficient through quantum processing. Our aim here is to construct quantum subroutines that embed the standard and weighted matrix geometric means into unitary operators and to determine the conditions under which these embeddings can indeed be conducted efficiently. There are many such possible unitary operators, and we choose a formalism called block-encoding^18,19,20.

The block-encoding of a non-unitary matrix Y is a unitary matrix U_Y whose upper left-hand corner is proportional to Y. The construction of this unitary matrix allows realisation by means of a quantum circuit, which describes unitary evolution. The matrix Y can be subsequently recovered by extracting only the top-left corner through measurement. This provides a convenient building block for constructing sums and (integer and non-integer) powers of matrices Y by concatenating its block-encodings via unitary circuits. This formalism allows us to form the block-encoding of the standard and weighted matrix geometric means, which are products of matrices and their roots. From these block-encodings, one can also recover their expectation values with respect to certain states. These different expectation values are then relevant for various applications, like in machine learning and quantum fidelity estimation.

Under certain assumptions, we show how these can be efficiently implementable on quantum devices. This efficiency arises from the fact that matrix multiplications can be more efficient with quantum algorithms. This observation has an important consequence. It means that a quantum device can efficiently prepare solutions of the (nonlinear) algebraic Riccati equations. The expectation values of these solutions can also be shown to be efficiently recoverable for different applications. Our approach differs from many past works in three key respects: (a) ours is the first quantum subroutine, to the best of our knowledge, to prepare solutions of nonlinear matrix equations without using iterative methods. The solutions themselves are matrices and not vectors, which differs from other quantum algorithms for nonlinear systems of equations, for example^21,22,23; (b) the solutions are not embedded in a pure quantum state, but rather an observable, thus introducing a novel embedding of the solution. This is important when solutions themselves are in matrix form (for matrix equations), which differs from the quantum embeddings of solutions of discretised nonlinear ordinary and partial differential equations (solutions not in matrix form)^21,22,23; (c) we show the efficient recovery of outputs for nonlinear systems of equations directly relevant for applications.

One class of applications is in the area of machine learning. Machine learning algorithms often require an assignment of a metric, or distance measure, in order to compute distances between data points. The values of these distances then become central to the outcome, for instance, in making a prediction for classification. This means that the choice of the metric itself is important, but the best metric can depend on the actual data. Learning the metric from given data —called metric learning—can also be formulated as a learning problem. While most of these metric learning algorithms require iterative techniques like gradient descent to minimise the proposed loss function, a class of metric learning algorithms called geometric mean metric learning²⁴ admits closed-form solutions. It has also been shown to attain higher classification accuracy with greater speed than previous methods. Here we devise efficient quantum algorithms, using our quantum subroutine for the matrix geometric mean, for geometric mean metric learning for both classical and quantum data. For quantum data, we propose new algorithms that can be used for the anomaly detection of quantum states, which differs from previous algorithms²⁵. The applicability extends also to asymmetric cases for which there is a higher cost to be paid for false negatives or true positives. This is, in fact, related to the weighted matrix geometric mean.

There is also an important connection between the solution of the geometric mean metric learning problem and the Fuchs–Caves observable¹⁴, which appears in quantum fidelity estimation. This allows for a re-derivation of quantum fidelity from the point of view of machine learning. We show that our quantum subroutines for the matrix geometric mean can also be used in the efficient estimation of geometric Rényi relative entropies and the quantum fidelity by means of the Fuchs–Caves observable. This new way of estimating quantum fidelity has polynomially better performance in precision than previously known fidelity estimation algorithms. It is also shown to be optimal with respect to precision.

We can also extend our method to a more general class of nonlinear systems of equations of pth-degree. These are pth-degree polynomial generalisations of the simplest algebraic Riccati equations. We show that the unique solutions of these equations are weighted matrix geometric means. We similarly devise quantum subroutines to prepare their block-encodings. The weighted matrix geometric mean for two quantum states has an elegant geometric interpretation as the positive semi-definite operator at (1/p)-th of the length along the geodesic connecting two quantum states in Riemannian space. We also show these are relevant to the weighted version of our new quantum learning algorithm. Furthermore, preparing block-encodings of the weighted matrix geometric means allows us to construct, to the best of our knowledge, the first quantum algorithm for estimating the geometric Rényi relative entropies.

Results

Summary of our results

For convenience, we provide a brief summary of our results here. Our first contribution consists of basic quantum subroutines in the section “Quantum subroutines for matrix geometric means, algebraic Riccati equations, and higher-order nonlinear equations” for matrix geometric means (see Definition 1) and their weighted generalisation (see Definition 2).

Solving algebraic Riccati equations

We then consider the problem of solving the algebraic matrix Riccati equation

$$YAY-{B}^{\dagger }Y-{Y}^{\dagger }B-C=0,$$

(1)

where A, B, and C are d × d complex-valued matrices. We delineate quantum algorithms with time complexity $O\left({\rm{poly}}\log d\right)$ for solving Eq. (1) for well-conditioned matrices, in the section “Quantum subroutine for matrix geometric means” and section “B ≠ 0 algebraic Riccati equation”. Here, we say a matrix A is well-conditioned if $A\ge I/({\rm{poly}}\log d)$. The higher-order case $Y{\left(AY\right)}^{p-1}=C$ is studied in the section “Higher-order polynomial equations”. In section “BQP-hardness”, we show that it is ${\mathsf{BQP}}$-complete to solve the equation YAY = C, a special case of Eq. (1), in which case the solution is Y = A⁻¹#C (see Definition 1 for the meaning of this notation).

Geometric mean metric learning

We introduce quantum algorithms for learning the metric in machine learning, by phrasing this as an optimisation problem using a geometric perspective. Unlike other metric learning algorithms, this optimisation problem has a closed-form solution. This follows the geometric mean metric learning method²⁴. The solution turns out to be expressible in terms of the matrix geometric mean Y = A⁻¹#C. We design quantum algorithms for the learning task for classical data (section “Learning Euclidean metric from data”) as well as for quantum data (section “1-class quantum learning”). We present the conditions under which the quantum algorithm is more efficient than the corresponding classical algorithm. For example, the classical learning task with well-conditioned matrices A and C has time complexity $O({\rm{poly}}(\log d,\log (1/\epsilon )))$. We also show that the quantum learning task with well-conditioned quantum states ρ and σ has time complexity $O({\rm{poly}}(\log d,\log (1/\epsilon )))$. The latter learning task for quantum data is uniquely quantum in nature and has no classical counterpart.

(Uhlmann) fidelity estimation

Based on the Fuchs–Caves observable¹⁴, we design a new quantum algorithm for fidelity estimation in section “Fidelity” via the fidelity formula $F\left(\rho ,\sigma \right)={\rm{Tr}}\left(\left({\sigma }^{-1}\#\rho \right)\sigma \right)$, which involves the matrix geometric mean. We show that our quantum algorithm has query complexity $\tilde{O}\left({\kappa }^{4}/\epsilon \right)$ provided that ρ, σ ≥ I/κ for some known κ > 0, and that the ϵ-dependence is optimal up to polylogarithmic factors.

Geometric Rényi relative entropy

In the section “Geometric fidelity and geometric Rényi relative entropy”, we present the first quantum algorithm for computing the geometric Rényi relative entropy, to the best of our knowledge. In particular, we design a quantum algorithm for computing the geometric fidelity ${\widehat{F}}_{1/2}\left(\rho ,\sigma \right):={\rm{Tr}}\left(\rho \#\sigma \right)$ (also known as the Matsumoto fidelity^15,16) with query complexity $\tilde{O}\left({\kappa }^{3.5}/\epsilon \right)$ provided that ρ, σ ≥ I/κ for some known κ > 0, and we prove that the ϵ-dependence is optimal up to polylogarithmic factors.

Organisation of this paper

In the section “Background”, we begin with a review of the standard matrix geometric mean, weighted matrix geometric mean, the algebraic Riccati equation, and block-encoding. In section “Quantum subroutines for matrix geometric means, algebraic Riccati equations, and higher-order nonlinear equations” we compute the costs required to prepare block-encodings of the solutions of algebraic Riccati equations and their pth-order generalisations. Applications are presented section “Applications”. In section “BQP-hardness” we show how our new quantum subroutines for the matrix geometric mean can solve a ${\mathsf{BQP}}$-complete problem. We end in section “Discussion” with discussions.

Background

In this section, we give a brief overview of the standard and weighted matrix geometric means and their role in solving algebraic Riccati equations (see ref. ²⁶, Chapters 4 & 6 and refs. ^9,10 for more details). We then provide a definition of block-encoding. Throughout the paper, unless otherwise stated, we deal with Hermitian matrices.

Matrix geometric means

Definition 1

(Matrix geometric mean). Fix $D\in {\mathbb{N}}$. Given two D × D positive definite matrices A and C, the matrix geometric mean of A and C is defined as

$$A\#C:={A}^{1/2}{({A}^{-1/2}C{A}^{-1/2})}^{1/2}{A}^{1/2}\, >\, 0.$$

(2)

Note that the matrix geometric mean between A⁻¹ and C is thus defined by

$${A}^{-1}\#C={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{1/2}{A}^{-1/2}\, >\, 0.$$

(3)

Alternatively, the matrix geometric mean A#C can be equivalently be written as

$$A\#C=\max \left\{Y\ge 0:\left(\begin{array}{cc}A&Y\\ Y&C\end{array}\right)\ge 0\right\},$$

(4)

where the ordering of Hermitian matrices is given by the Löwner partial order.

The matrix geometric mean appears in quantum information, for example, like the Fuchs–Caves observable¹⁴, in quantum fidelity and entropy operators like the Tsallis relative operator entropy²⁷, and quantum fidelity measures between states^12,15,16 and channels²⁸. This concept can also be generalised to the weighted matrix geometric mean.

Definition 2

(Weighted matrix geometric mean). Fix p > 0. The weighted matrix geometric mean with a weight 1/p is defined as

$$A{\#}_{1/p}\,C:={A}^{1/2}{({A}^{-1/2}C{A}^{-1/2})}^{1/p}{A}^{1/2}.$$

(5)

The weighted matrix geometric mean between A⁻¹ and C is then equal to

$${A}^{-1}{\#}_{1/p}\,C={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{1/p}{A}^{-1/2}.$$

(6)

The canonical matrix geometric mean corresponds to the weighted geometric mean with weight 1/p = 1/2.

We will use the definitions in Eqs. (3) and (6) here and throughout because, as we will see later on, they are relevant to solutions of classes of nonlinear matrix equations like the algebraic Riccati equations.

For positive definite matrices (which include full-rank density matrices), the standard and weighted matrix geometric means have elegant geometric interpretations. It is known that the inner product on the real vector space formed by the set of Hermitian matrices gives rise to a Riemannian metric²⁶, Chapter 6. This Riemannian metric is defined on the manifold M_H formed by the set of positive definite matrices. Following ref. ²⁶, Eqs. (6.2) & (6.4), a trajectory γ: [a, b] → M_H on this manifold is a piecewise differential path on M_H whose length is defined by $L(\gamma ):=\mathop{\int}\nolimits_{a}^{b}{\left\Vert {\gamma }^{-1/2}(t){\gamma }^{{\prime} }(t){\gamma }^{-1/2}(t)\right\Vert }_{2}\,dt$. Then, the distance $\delta ({A}^{-1},C)=\mathop{\inf }\nolimits_{\gamma }L(\gamma )$ between any two positive definite matrices A⁻¹ and C on this manifold is defined to be the shortest length joining these two points. Then we have the following result.

Lemma 3

(Ref. ²⁶, Theorem 6.1.6). If A⁻¹ and C are two positive definite matrices, then there exists a unique geodesic joining A⁻¹ and C. This geodesic has the following parameterisation with t ∈ [0, 1]:

$${\gamma }_{{\rm{geod}}}(t)={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{t}{A}^{-1/2},\,t\in [0,1].$$

(7)

This geodesic has a length given by

$$\delta ({A}^{-1},C)=L({\gamma }_{{\rm{geod}}})={\left\Vert \log ({A}^{1/2}C{A}^{1/2})\right\Vert }_{2}.$$

(8)

In the above, $\parallel\!\! X{\parallel }_{2}:=\sqrt{{\rm{Tr}}[{X}^{\dagger }X]}$ denotes the Schatten 2-norm, whereas ∥ ⋅ ∥ refers to the operator norm throughout our paper.

From this viewpoint, the matrix geometric mean A⁻¹#C = γ_geod(t = 1/2) can clearly be interpreted as the midpoint along the geodesic joining A⁻¹ and C. Similarly, the weighted geometric mean with weight 1/p can be interpreted as the point along the manifold when t = 1/p.

Algebraic Riccati equations

Let us begin with a general form of the algebraic Riccati equation for the unknown D × D matrix Y:

$${Y}^{\dagger }AY-{B}^{\dagger }Y-{Y}^{\dagger }B-C=0,$$

(9)

where A, B, and C are D × D matrices with complex-valued entries. This can be understood as a matrix version of the famous (scalar) quadratic equation ay² − 2by − c = 0. Solutions of equations like (9) are not always guaranteed to exist, and certain conditions are required to prove the existence of, for instance, Hermitian solutions²⁹. See ref. ³⁰ for conditions on solvability. Even if existence can be shown, the solutions may not be unique or could alternatively be uncountably many^31,32,33. However, there are unique solutions under certain conditions. For instance, if all the matrix entries are real-valued, then for symmetric positive semi-definite A, C and symmetric positive Y, there is a unique positive definite solution if and only if an associated matrix $H=\scriptstyle\left(\begin{array}{cc}-B&A\\ C&{B}^{T}\end{array}\right)$ has no imaginary eigenvalues³⁴.

In this paper, we confine our attention to simpler cases, for example in Lemmas 4 and 5, when there are unique solutions.

Lemma 4

(Solution of simple algebraic Riccati equation). Consider the following algebraic Riccati equation when A and C are positive definite matrices and Y is Hermitian:

$$Y\,AY=C.$$

(10)

This equation has a unique positive definite solution given by the standard matrix geometric mean:

$$Y={A}^{-1}\#C:={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{1/2}{A}^{-1/2}\, >\, 0.$$

(11)

Proof

This lemma is well known from refs. ^35,36, but we provide a brief proof for completeness. Starting from the Riccati equation in (10) and by using the fact that A is positive definite with a unique square root, consider that

$$YAY=C\quad \iff \quad Y{A}^{1/2}{A}^{1/2}Y=C$$

(12)

$$\iff \quad {A}^{1/2}Y{A}^{1/2}{A}^{1/2}Y{A}^{1/2}={A}^{1/2}C{A}^{1/2}$$

(13)

$$\iff \quad {({A}^{1/2}Y{A}^{1/2})}^{2}={A}^{1/2}C{A}^{1/2}.$$

(14)

Since the matrix A^1/2CA^1/2 is positive definite and the equality in the last line above has been shown, both A^1/2CA^1/2 and ${({A}^{1/2}Y{A}^{1/2})}^{2}$ have a unique positive definite square root, implying that

$${A}^{1/2}Y{A}^{1/2}={({A}^{1/2}C{A}^{1/2})}^{1/2}\quad \iff \quad Y={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{1/2}{A}^{-1/2},$$

(15)

thus justifying that Y = A⁻¹#C is the unique positive definite solution as claimed. □

See ref. ³⁷ for a discussion of (10) in the infinite-dimensional case.

If A and C are both positive definite with unit trace ${\rm{Tr}}(A)=1={\rm{Tr}}(C)$, then A and C can also be interpreted as density matrices. Then the operator A⁻¹#C is also known as the Fuchs–Caves observable³⁸, which is of relevance in the study of quantum fidelity. We will return to this point later. See also ref. ³⁹, Section V for an interpretation of (10) when A and C are density matrices.

We can also extend Lemma 4 to the B ≠ 0 case, and the following holds.

Lemma 5

If A and C are positive definite, B is an arbitrary matrix, and $({A}^{-1}B)={({A}^{-1}B)}^{\dagger }$, then a Hermitian solution to Eq. (9) can be expressed as

$$Y={A}^{-1}\#({B}^{\dagger }{A}^{-1}B+C)+{A}^{-1}B.$$

(16)

Proof

See Appendix IV A. □

Classical algorithms for solving algebraic Riccati equations are typically inefficient¹⁷ with respect to the size of the problem, i.e., polynomial in D. We will be looking at conditions for which a quantum algorithm for solving algebraic Riccati equations can be executed with less complexity.

Block-encoding

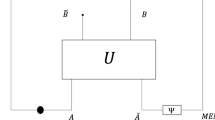
Classical information can be embedded in quantum systems in the form of quantum states, either pure or mixed, or in the form of quantum processes. A closed quantum system evolves under a unitary transformation, represented by a unitary matrix. In this paper, we will be focusing on how a matrix solution to a matrix equation can be embedded in a unitary matrix. Unlike other quantum subroutines that prepare solutions of a linear system of equations embedded in the amplitudes of a pure quantum state, here we first embed the solution Y into a unitary matrix.

There are different ways of embedding an arbitrary matrix into a unitary matrix. For instance, it is guaranteed by the Sz. Nagy dilation theorem (see, e.g., ref. ⁴⁰, Theorem 1.1) that such a unitary matrix should always exist. We choose a flexible dilation known as block-encoding^18,19,20. A unitary matrix U_Y is called a block-encoding of a matrix Y if it satisfies the following definition.

Definition 6

(Block-encoding). Fix $n,a\in {\mathbb{N}}$ and ϵ, α ≥ 0. Let Y be an n-qubit operator. An (n + a)-qubit unitary U_Y is an (α, a, ϵ)-block-encoding of an operator Y if

$$|| Y-\alpha {\left\langle \right.0| }_{a}{U}_{Y}{| 0\left.\right\rangle }_{a}|| \,\le\, \epsilon .$$

(17)

Here ${| 0\left.\right\rangle }_{a}$ consists of all $| 0\left.\right\rangle$ states in the computational basis of the a-ancilla qubits. The block-encoding formalism allows one to construct, for example, block-encodings of sums of matrices, linear combinations of block-encoded matrices, and polynomial approximations of negative and positive power functions of matrices¹⁸. We list several associated lemmas in Appendix IV B for convenience.

Quantum subroutines for matrix geometric means, algebraic Riccati equations, and higher-order nonlinear equations

Let us focus on cases where the solutions to the algebraic Riccati equations can be captured by the matrix geometric mean in Lemmas 4 and 5. The computation of the matrix geometric mean involves the computation of the square roots of matrices and several matrix multiplications. For D × D matrices, typically these costs will scale polynomially with D for a classical algorithm. However, quantum algorithms for matrix multiplications of block-encoded matrices can be performed more efficiently when compared to the number of classical numerical steps. These series of block-encoded matrix multiplications can be achieved in the quantum case via the block-encoding formalism.

Let us begin with the algebraic Riccati equation in Eq. (9):

$$Y\,AY-{B}^{\dagger }Y-{Y}^{\dagger }B-C=0.$$

(18)

It is our goal below first to construct a block-encoding of the solution Y, denoted U_Y, under the conditions obeyed in Lemmas 4 and 5. This we consider as a subroutine that we can then employ in various applications.

Below we assume that we also have access to the block-encodings of A, B, C—denoted U_A, U_B, U_C, respectively—as well as their inverses ${U}_{A}^{\dagger }$, ${U}_{B}^{\dagger }$, ${U}_{C}^{\dagger }$ and controlled versions. For example, if A, B, and C are positive semi-definite matrices with unit trace, these can be considered density matrices. Then, from Lemma 30, we can prepare block-encodings U_A, U_B and U_C by accessing the unitaries that prepare purifications of A, B and C, with only a single query to each purification and $O(\log d)$ gates. In more general scenarios, we can leave the preparation of these block-encodings to a later stage, which also depends on the particular application. Below, κ_A and κ_C denote the condition numbers for A and C, respectively. It is important to clarify that, as assumed in ref. ¹, all of our quantum algorithms for matrix geometric means assume that

$$I\ge A\ge I/{\kappa }_{A},$$

(19)

$$I\ge C\ge I/{\kappa }_{C},$$

(20)

$$I\ge {B}^{\dagger }B.$$

(21)

This means that κ_A and κ_C are really equal to the inverses of the minimum eigenvalues of A and C, respectively, and $\left\Vert A\right\Vert ,\left\Vert B\right\Vert ,\left\Vert C\right\Vert \le 1$. The upper bounds above are automatically satisfied whenever A and C are density matrices.

Quantum subroutine for matrix geometric means

As a warm-up, we present a quantum subroutine for implementing block-encodings of the weighted matrix geometric means.

Lemma 7

(Block-encoding of weighted matrix geometric mean). Suppose that U_A, U_C are (1, a, 0)-block-encodings of matrices A, C, respectively, where A ≥ I/κ_A, C ≥ I/κ_C, and I is the identity matrix. For ϵ ∈ (0, 1/2), one can implement a $(2{\kappa }_{A}^{1/p}{\gamma }_{p},5a+12,\epsilon )$-block-encoding of Y for every fixed real p ≠ 0, where

$${\gamma }_{p}=\left\{\begin{array}{ll}1\qquad\qquad\quad \,p\, >\, 0,\\ {\kappa }_{A}^{-1/p}{\kappa }_{C}^{-1/p}\quad \,p\, <\, 0,\end{array}\right.$$

(22)

and

$$Y=A{\#}_{1/p}C={A}^{1/2}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}{A}^{1/2},$$

(23)

using

• $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_C, $\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{4}\left(1/\epsilon \right)\right)$ queries to U_A;

• $\tilde{O}\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{4}\left(1/\epsilon \right)\right)$ gates; and

• ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

Remark 1

In the above and in what follows, “queries to U” refers to access not only to U, but also to its inverse U^†, controlled-U, and controlled-U^†. Here and in the following, $\tilde{O}(\cdot )$ suppresses logarithmic factors of functions appearing in (⋅). The same convention applies to $\widetilde{\Omega }(\cdot )$ and $\tilde{\Theta }(\cdot )$.

Proof sketch of Lemma 7. See Appendix IV C for a detailed proof. As an illustration for the construction of our quantum subroutines, we outline the basic idea. Other quantum subroutines later presented in this section are obtained using similar ideas. Our approach consists of three main steps:

• 1. Implement a block-encoding of A^−1/2, using roughly $\tilde{O}\left({\kappa }_{A}\right)$ queries to a block-encoding of A (for simplicity, we ignore the ϵ-dependence in our brief explanation here). This is done by applying quantum singular value transformation (QSVT)¹⁸ with polynomial approximations of negative power functions (see Lemma 27).

• 2. Implement a block-encoding of ${\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}$, using roughly $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}\right)$ queries to a block-encoding of A^−1/2CA^−1/2. This is done by applying QSVT with polynomial approximations of positive power functions (see Lemma 28). Note that a block-encoding of A^−1/2CA^−1/2 can be implemented using $O\left(1\right)$ queries to block-encodings of A^−1/2 and C by the method for realising the product of block-encoded matrices (see Lemma 24).

• 3. Similar to Step 2, implement a block-encoding of ${A}^{1/2}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}{A}^{1/2}$, using $O\left(1\right)$ queries to block-encodings of A^1/2 and ${\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}$, where a block-encoding of A^1/2 can be implemented using $\tilde{O}\left({\kappa }_{A}\right)$ queries to a block-encoding of A.

To conclude, the overall query complexity is roughly $\tilde{O}\left({\kappa }_{A}\right)\!\cdot\! \tilde{O}\left({\kappa }_{A}{\kappa }_{C}\right)+\tilde{O}\left({\kappa }_{A}\right)=\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}\right)$. Note that the construction is mainly based on QSVT and thus is also time efficient. So the overall time complexity is equal to the query complexity only up to polylogarithmic factors.

B = 0 algebraic Riccati equation

Let us begin with the unique positive definite solution to the algebraic Riccati equation with B = 0, i.e., Eq. (9), which can be expressed as the matrix geometric mean Y = A⁻¹#C, according to Lemma 4, where A and C are positive definite matrices. Then we have the following lemma, which characterises a block-encoding of the solution in a quantum circuit.

Lemma 8

Suppose that U_A, U_C are (1, a, 0)-block-encodings of matrices A, C, respectively, with A ≥ I/κ_A and C ≥ I/κ_C. For ϵ ∈ (0, 1/2), one can implement a (2κ_A, 5a + 11, ϵ)-block-encoding of Y, where

$$Y={A}^{-1}\#C={A}^{-1/2}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}{A}^{-1/2},$$

(24)

using

• $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_C and

  $\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_A;

• $\tilde{O}\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ gates; and

• ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

Proof

See Appendix IV D. □

B ≠ 0 algebraic Riccati equation

Here we want to construct a block-encoding of a Hermitian solution to the algebraic Riccati equation via the standard matrix geometric mean, according to Lemma 5. We then have the following lemma.

Lemma 9

Suppose that U_A, U_B, U_C are (1, a, 0)-block-encodings of matrices A, B, C, respectively, with A ≥ I/κ_A, C ≥ I/κ_C and ${A}^{-1}B={\left({A}^{-1}B\right)}^{\dagger }$. For ϵ ∈ (0, 1/2), one can implement a $(2{\kappa }_{A}^{3/2},b,\epsilon )$-block-encoding of Y, where $b=O\left(a+\log \left({\kappa }_{A}{\kappa }_{C}/\epsilon \right)\right)$ and

$$Y={A}^{-1}\#\left({B}^{\dagger }{A}^{-1}B+C\right)+{A}^{-1}B$$

(25)

$$={A}^{-1/2}{\left({A}^{1/2}\left({B}^{\dagger }{A}^{-1}B+C\right){A}^{1/2}\right)}^{1/2}{A}^{-1/2}+{A}^{-1}B,$$

(26)

using

• $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_B and U_C, and $\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_A;

• $\tilde{O}\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ gates; and

• ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

Proof

See Appendix IV E. □

Higher-order polynomial equations

Algebraic Riccati equations are second-order nonlinear equations whose solutions are given by the second-order matrix geometric mean, i.e., p = 2. We can also generalise our formalism to particular pth-order nonlinear matrix equations, whose solutions involve p ∈ {3, 4, …} weighted matrix geometric means. For example, consider the following p^th-order nonlinear matrix equations, which we call the pth-order YAY algebraic equations

$$Y{(AY)}^{p-1}=C,$$

(27)

where p is the highest order polynomial in Y. It is straightforwardly checked that the solutions can be written in terms of the weighted geometric mean from Definition 2:

$$Y={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{1/p}{A}^{-1/2}={A}^{-1}{\#}_{1/p}C.$$

(28)

See ref. ⁴¹ for a discussion of this kind of equation in the infinite-dimensional case.

Lemma 10

(Solution of simple pth-order algebraic YAY equation). Fix p ∈ {2, 3, 4, …}. Consider the pth-order algebraic YAY equation when A and C are positive definite matrices:

$$Y{(AY)}^{p-1}=C.$$

(29)

This equation has a unique positive definite solution given by the following weighted geometric mean:

$$Y={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{1/p}{A}^{-1/2}={A}^{-1}{\#}_{1/p}C \,>\, 0.$$

(30)

Proof

The proof is a generalisation of that for Lemma 4, and we provide it for completeness. Starting from the equation in (29) and by using the fact that A is positive definite with a unique square root, consider that

$$Y{(AY)}^{p-1}=C\quad \iff \quad Y{({A}^{1/2}{A}^{1/2}Y)}^{p-1}=C$$

(31)

$$\iff \quad {({A}^{1/2}Y{A}^{1/2})}^{p}={A}^{1/2}C{A}^{1/2},$$

(32)

where the last line is obtained by left and right multiplying the previous line by A^1/2. Since the matrix A^1/2CA^1/2 is positive definite and the equality in the last line above has been shown, both A^1/2CA^1/2 and ${({A}^{1/2}Y{A}^{1/2})}^{p}$ have a unique positive definite p-th root, implying that

$${A}^{1/2}Y{A}^{1/2}={({A}^{1/2}C{A}^{1/2})}^{1/p}\quad \iff \quad Y={A}^{-1/2}{({A}^{1/2}C{A}^{1/2})}^{1/p}{A}^{-1/2},$$

(33)

thus justifying that Y = A⁻¹#_1/pC is the unique positive definite solution as claimed. □

To construct a block-encoding for the weighted geometric mean (and thus the solution of (27)), we have proven the following lemma, which holds for every non-zero real number p.

Lemma 11

Suppose that U_A, U_C are (1, a, 0)-block-encodings of matrices A, C, respectively, with A ≥ I/κ_A and C ≥ I/κ_C and let p ≠ 0 be any fixed non-zero real number. For ϵ ∈ (0, 1/2), one can implement a (2κ_Aγ_p, 5a + 11, ϵ)-block-encoding of Y, where

$$Y={A}^{-1}{\#}_{1/p}C={A}^{-1/2}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/p}{A}^{-1/2},$$

(34)

and

$${\gamma }_{p}=\left\{\begin{array}{ll}1\quad\quad\quad\quad\quad \,p \,>\, 0,\\ {\kappa }_{A}^{-1/p}{\kappa }_{C}^{-1/p}\quad \,p\, <\, 0,\end{array}\right.$$

(35)

using

• $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_C and

  $\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_A;

• $\tilde{O}\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ gates; and

• ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

Proof

See Appendix IV F. □

Applications

Here we explore two classes of applications for preparing block-encodings of the matrix geometric mean. The first class of applications is to learning problems, in particular for metric learning from data, both quantum and classical. Next, we demonstrate how having access to the matrix geometric mean also allows us to compute some fundamental quantities in quantum information, like the quantum fidelity between two mixed states via the Fuchs–Caves observable, as well as geometric Rényi relative entropies.

Quantum geometric mean metric learning

In learning problems, there is typically a loss function L that we want to optimise. Suppose we have D × D positive definite matrices Y, A, and C. We note that here the uniqueness result in Lemma 4 continues to hold. Consider the following optimisation problem:

$$\mathop{\min }\limits_{Y\ge 0}L(Y),\,L(Y):={\rm{Tr}}(YA)+{\rm{Tr}}({Y}^{-1}C).$$

(36)

It turns out that, for given A and C, the unique Y minimising L(Y) is Y = A⁻¹#C. In ref. ²⁴, this result was proven for real positive definite matrices A and C, and here we extend it to positive definite Hermitian matrices. In ref. ⁴², the same optimisation problem was considered in the context of quantum fidelity, where it was shown that the optimal value of (36) is equal to ${\rm{Tr}}[{({A}^{1/2}C{A}^{1/2})}^{1/2}]$.

Lemma 12

Fix A and C to be positive definite matrices. The unique solution to $\mathop{\min }\limits_{Y\ge 0}L(Y)$ where $L(Y)={\rm{Tr}}(YA)+{\rm{Tr}}({Y}^{-1}C)$ is the matrix geometric mean Y = A⁻¹#C.

Proof

If L(Y) is both strictly convex and strictly geodesically convex, then the solution to ∇ L(Y) = 0 will also be a global minimiser. For the proof of strict convexity and strict geodesic convexity, see Appendix IV G. Now ∇ L(Y) = A − Y⁻¹CY⁻¹ = 0 implies the algebraic Riccati equation YAY = C or Y = A⁻¹#C, which is the unique solution for positive definite matrices A and C. □

We will use this property and map two learning problems—one for classical data and another for quantum data—onto this optimisation problem. Using the block-encoding for the matrix geometric mean in Lemma 8, we then devise quantum algorithms for learning a Euclidean metric from data, as well as a 1-class classification algorithm for quantum states. We also extend to the case of weighted learning, where there are unequal contributions to the loss function in Eq. (36) from ${\rm{Tr}}(YA)$ and ${\rm{Tr}}({Y}^{-1}C)$.

Learning Euclidean metric from data

Machine learning algorithms rely on distance measures to quantify how similar one set of data is to another. Naturally, different distance measures can give rise to different results, and so choosing the right metric is crucial for the success of an algorithm. The distance measure itself can, in fact, be learned, for example, in a weakly supervised scenario, and this is called metric learning⁴³. Here we are provided with the following two sets ${\mathcal{S}}$ (similar) and ${\mathcal{D}}$ (dissimilar) of pairs (training data)

$${\mathcal{S}}:=\{({\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} })\,| \,{\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} }\,\,{\text{are}}\, {\rm{in}}\, {\rm{the}}\, {\rm{same}\, class}\,\},$$

(37)

$${\mathcal{D}}:=\{({\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} })\,| \,{\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} }\,\,{\text{are}}\, {\rm{in}}\, {\rm{different}}\, {\rm{classes}}\,\},$$

(38)

and ${(({{\boldsymbol{x}}}^{(k)},{{\boldsymbol{x}}}^{{\prime} (k)}))}_{k}$ are the data points, where k labels all the pairs that either belong to ${\mathcal{S}}$ or ${\mathcal{D}}$. An important example in metric learning is learning the Euclidean metric from data, which can be reformulated as a simple optimisation problem with a closed-form solution. Learning a Euclidean metric is a common form of metric learning, where we can learn a Mahalanobis distance d_Y

$${d}_{Y}({\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} })\, := \,{({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} })}^{T}Y({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} })={\rm{Tr}}(Y({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} }){({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} })}^{T}),$$

(39)

with Y a real D × D symmetric positive definite matrix. To identify a suitable Y, one requires a suitable cost function.

In geometric mean metric learning²⁴, we want d_Y to be minimal between data in the same class, i.e., ${\mathcal{S}}$. At the same time, when the data are in different classes, i.e., ${\mathcal{D}}$, we want ${d}_{{Y}^{-1}}$ to be minimal instead. Thus we want to minimise the sum ${\sum }_{{\mathcal{S}}}{d}_{Y}+{\sum }_{{\mathcal{D}}}{d}_{{Y}^{-1}}$. This leads to an optimisation problem of the form in Eq. (36)

$$\mathop{\min }\limits_{Y\ge 0}L(Y),\,L(Y):={\rm{Tr}}(YA)+{\rm{Tr}}({Y}^{-1}C),$$

(40)

$$A=\sum _{({\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} })\in {\mathcal{S}}}({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} }){({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} })}^{T},$$

(41)

$$C=\sum _{({\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} })\in {\mathcal{D}}}({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} }){({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} })}^{T},$$

(42)

where we assume A and C are positive definite. From Lemma 12, we see that the optimal solution to Eq. (40) is the matrix geometric mean Y = A⁻¹#C. We see that this is also, in fact, the solution of the B = 0 algebraic Riccati equation YAY = C. In Lemma 8, we saw that, given access to the block-encodings of U_A, U_C, their inverses, and controlled versions, we can construct the block-encoding of Y, denoted U_Y. Lemma 8 also shows that the query and gate complexity costs are efficient in D, i.e. $O(\,\text{poly}\,\log d)$, when the condition numbers for A and C are also polynomial in $\log d$.

While we see that it is possible to efficiently recover U_Y, it is not sufficient for a direct application to machine learning. Learning Y is part of the learning stage, but reading off the classical components of Y directly from U_Y is inefficient. However, if we consider the testing stage in machine learning, then we need to compute the actual distance d_Y if we are given a new data pair $({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })$, known as testing data. For this testing data, we do not know its classification into ${\mathcal{S}}$ or ${\mathcal{D}}$ a priori. Thus the task is to show that, having access to U_Y, it is then sufficient to compute d_Y without needing to read out the elements of Y. For example, a large value of ${d}_{Y}({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })$ means that we should classify $({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })\in {\mathcal{D}}$, whereas a small value of ${d}_{Y}({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })$ means that we should classify $({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })\in {\mathcal{S}}$. We discuss later the preparation of the block-encodings of U_A and U_C.

Before proceeding, we first discuss the preparation of a quantum state that we later require. Given a new data pair (testing data) $({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })$ for which we want to compute d_Y, where we use the optimal Y, we can define a corresponding pure quantum state with $m=O(\log d)$ qubits ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}=(1/{{\mathcal{N}}}_{\psi })\mathop{\sum }\nolimits_{i = 1}^{d}{({\boldsymbol{y}}-{{\boldsymbol{y}}}^{{\prime} })}_{i}| i\left.\right\rangle$, with normalisation constant ${{\mathcal{N}}}_{\psi }^{2}=\mathop{\sum }\nolimits_{i = 1}^{d}{({\boldsymbol{y}}-{{\boldsymbol{y}}}^{{\prime} })}_{i}^{2}$. Its amplitudes are proportional to ${\boldsymbol{y}}-{{\boldsymbol{y}}}^{{\prime} }$ for any pair $({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })$. We say that the state ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$ has sparsity σ if σ is the number of non-zero entries in the amplitude. We can use optimal state preparation schemes^44,45,46 to prepare ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$.

Lemma 13

(Quantum state preparation,^44,45,46). A quantum circuit producing an m-qubit state $| z\left.\right\rangle =\mathop{\sum }\nolimits_{i = 1}^{{2}^{m}}{z}_{i}| i\left.\right\rangle$ from $| 0\left.\right\rangle$ with given classical entries ${\{{z}_{i}\}}_{i = 1}^{{2}^{m}}$ can be implemented by using O(mσ) CNOT gates, $O(\sigma (\log \sigma +m))$ one-qubit gates, and O(1) ancilla qubits, where the circuit description can be classically computed with time complexity $O(m{\sigma }^{2}\log \sigma )$. Further, the gate depth complexity can be reduced to $\Theta (\log (m\sigma ))$, if $O(m\sigma \log \sigma )$ ancilla qubits are used.

Since here $m=O(\log d)$, we see that as long as σ is small, e.g., $\sigma =O({\rm{poly}}\log d)$, then the total initial state preparation cost, in either gate complexity and number of ancillas is $O({\rm{poly}}\log d)$. Next we compute d_Y.

Theorem 14

Suppose we are given U_A, U_C, which are $(1,\log d,0)$-block-encodings of $A={\sum }_{({\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} })\in {\mathcal{S}}}({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} }){({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} })}^{T}$ and $C={\sum }_{({\boldsymbol{x}},{{\boldsymbol{x}}}^{{\prime} })\in {\mathcal{D}}}({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} }){({\boldsymbol{x}}-{{\boldsymbol{x}}}^{{\prime} })}^{T}$, respectively. We also assume access to their inverses and controlled versions. We assume that the data obeys ${\kappa }_{A},{\kappa }_{C}=O({\rm{poly}}\log d)$. Given a testing data pair $({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })$, we assume that the corresponding state ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$ has sparsity $O({\rm{poly}}\log d)$ and ${{\mathcal{N}}}_{\psi }=O({\rm{poly}}\log d)$. Then computing ${d}_{Y}({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })$ to precision ϵ has a query and gate complexity $O({\rm{poly}}(\log d,1/\epsilon ))$.

Proof

We first make the observation that, for optimal Y,

$${d}_{Y}({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })={{\mathcal{N}}}_{\psi }^{2}{\langle \psi \vert }_{y,{y}^{{\prime} }}Y{| \psi \rangle }_{y,{y}^{{\prime} }}\approx 2{{\mathcal{N}}}_{\psi }^{2}{\kappa }_{A}{\rm{Tr}}(\langle 0\vert {U}_{Y}| 0\rangle {| \psi \rangle }_{y,{y}^{{\prime} }}{\langle \psi \vert }_{y,{y}^{{\prime} }}),$$

(43)

where Y = A⁻¹#C and U_Y is a (2κ_A, 5a + 11, ϵ) block-encoding of Y. The proportionality constant of 2κ_A comes from Lemma 8, which shows that $|| Y-2{\kappa }_{A}{\left\langle 0\right\vert }_{5a+11}{U}_{Y}{| 0\left.\right\rangle }_{5a+11}||\, \le\, \epsilon$, where $a=\log d$. For simplicity, we neglect the subscript on the $| 0\left.\right\rangle$ states. This trace can be interpreted as an expectation value of ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$ with Y as the observable, and comes from the definition of d_Y and ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$.

To compute this trace given U_Y, we observe that ${\rm{Tr}}((S\otimes T)X)={\rm{Tr}}({X}_{T}S)$, where if $T={\sum }_{n}{\lambda }_{n}| {u}_{n}\left.\right\rangle \,\langle {v}_{n}\vert$, then ${X}_{T}={\sum }_{n}{\lambda }_{n}\langle {v}_{n}\vert X\vert {u}_{n}\rangle$. So we can rewrite

$${d}_{Y}({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })\approx 2{{\mathcal{N}}}_{\psi }^{2}{\kappa }_{A}{\rm{Tr}}(\langle 0\vert {U}_{Y}| 0\left.\right\rangle {| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}{\langle \psi \vert }_{y,{y}^{{\prime} }})$$

(44)

$$=2{{\mathcal{N}}}_{\psi }^{2}{\kappa }_{A}{\rm{Tr}}(({| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}{\langle \psi \vert }_{y,{y}^{{\prime} }}\otimes | 0\left.\right\rangle \langle 0\vert ){U}_{Y})$$

(45)

$$=2{{\mathcal{N}}}_{\psi }^{2}{\kappa }_{A}{\langle \Psi \vert }_{y,{y}^{{\prime} }}{U}_{Y}{| \Psi \left.\right\rangle }_{y,{y}^{{\prime} }},$$

(46)

where ${| \Psi \left.\right\rangle }_{y,{y}^{{\prime} }}={| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}\otimes | 0\left.\right\rangle$. The last expectation value can be realised with a conventional swap test^47,48 between the states ${| \Psi \left.\right\rangle }_{y,{y}^{{\prime} }}$ and ${U}_{Y}{| \Psi \left.\right\rangle }_{y,{y}^{{\prime} }}$. One can also use the destructive SWAP test (i.e., Bell measurements and classical post-processing)⁴⁹. Alternatively, ${\rm{Tr}}(({| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}{\langle \psi \vert }_{y,{y}^{{\prime} }}\otimes | 0\rangle\langle 0\vert ){U}_{Y})$ can also be computed through a Hadamard test (Lemma 31), where one is given the controlled-U_Y and state ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}\otimes | 0\left.\right\rangle$. For example, applying the unitary U_Y to ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}\otimes | 0\left.\right\rangle$ and using the swap test with ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}\otimes | 0\left.\right\rangle$, we recover ${\langle \psi \vert }_{x,{x}^{{\prime} }}Y{| \psi \left.\right\rangle }_{x,{x}^{{\prime} }}$ to precision ϵ with query and gate complexity $O({\rm{poly}}(\log d,1/\epsilon ))$, when ${\kappa }_{A}=O({\rm{poly}}\log d)$. Now, ${d}_{Y}({\boldsymbol{y}},{{\boldsymbol{y}}}^{{\prime} })={{\mathcal{N}}}_{\psi }^{2}{\langle \psi\vert }_{y,{y}^{{\prime} }}Y{| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$. Since we only have $\sigma =O(\,\text{poly}\,\log d)$ non-zero entries in ${\boldsymbol{y}}-{{\boldsymbol{y}}}^{{\prime} }$, the cost in the classical computation of the normalisation constant is also of order $O({\rm{poly}}\log d)$. Assuming that ${{\mathcal{N}}}_{\psi }^{2}=O({\rm{poly}}\log d)$, then we recover d_Y efficiently when given access to U_Y and ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$.

We saw that preparing the state ${| \psi \left.\right\rangle }_{y,{y}^{{\prime} }}$ according to Lemma 13 incurs a cost $O({\rm{poly}}\log d)$. From Lemma 8 we can construct a $(2{\kappa }_{A},O(\log d),\epsilon )$-block-encoding of Y with gate and query complexity $O({\rm{poly}}({\kappa }_{A},{\kappa }_{C},\log (1/\epsilon )))$. Since ${\kappa }_{A},{\kappa }_{C}=O(\,{\text{poly}}\,\log d)$, then the theorem is proved. □

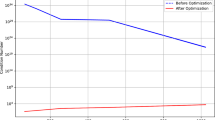
Thus, if our assumptions are obeyed, the quantum cost for computation of d_Y can be $O(\,\text{poly}\,\log d)$, whereas classical numerical algorithms for computing the matrix geometric mean alone has cost O(polyd) for d × d matrices^50,51.

In Theorem 14, we also assumed access to U_A, U_C. We show below the preparation of a block-encoding of density matrices, which are proportional to A and C and how this can be used to compute d_Y efficiently. First consider Lemma 30, which shows how to create a block-encoding of a density matrix. We first observe that we can define density matrices ρ_A and ρ_C where rewrite

$$\begin{array}{rcl}{\rho }_{A}=\frac{A}{{\rm{Tr}}(A)},&&A=\mathop{\sum}\limits _{k\in {\mathcal{S}}}{{\mathcal{N}}}_{{\psi }_{k}}^{2}| {\psi }_{k}\left.\right\rangle \,\left\langle \right.{\psi }_{k}| ,\,{\rm{Tr}}(A)=\mathop{\sum}\limits _{k\in {\mathcal{S}}}{{\mathcal{N}}}_{{\psi }_{k}}^{2},\\ {\rho }_{C}=\frac{C}{{\rm{Tr}}(C)},&&C=\mathop{\sum}\limits _{k\in {\mathcal{D}}}{{\mathcal{N}}}_{{\psi }_{k}}^{2}| {\psi }_{k}\left.\right\rangle \,\left\langle \right.{\psi }_{k}| ,{\rm{Tr}}(C)=\mathop{\sum}\limits _{k\in {\mathcal{D}}}{{\mathcal{N}}}_{{\psi }_{k}}^{2},\end{array}$$

(47)

where $| {\psi }_{k}\left.\right\rangle =(1/{{\mathcal{N}}}_{{\psi }_{k}})\mathop{\sum }\nolimits_{i = 1}^{d}{({{\boldsymbol{x}}}^{(k)}-{{\boldsymbol{x}}}^{{\prime} (k)})}_{i}| i\left.\right\rangle$ and ${{\mathcal{N}}}_{{\psi }_{k}}^{2}=\mathop{\sum }\nolimits_{i = 1}^{d}{({{\boldsymbol{x}}}^{(k)}-{{\boldsymbol{x}}}^{{\prime} (k)})}_{i}^{2}$ is the corresponding normalisation. Then from Lemma 30, if we are given unitaries V_A and V_C that prepare purifications of ρ_A and ρ_C, respectively, it is possible to create ${U}_{{\rho }_{A}}$ and ${U}_{{\rho }_{C}}$ using one query to V_A and V_C respectively and $O(\log d)$ gates. One such class of states purifying ρ_A and ρ_C are

$$| {\Sigma }_{A}\left.\right\rangle :=\sum _{k\in {\mathcal{S}}}\sqrt{{p}_{k}^{(A)}}| k\left.\right\rangle | {\psi }_{k}\left.\right\rangle ,$$

(48)

$$| {\Sigma }_{C}\left.\right\rangle :=\sum _{k\in {\mathcal{D}}}\sqrt{{p}_{k}^{(C)}}| k\left.\right\rangle | {\psi }_{k}\left.\right\rangle ,$$

(49)

where

$${p}_{k}^{(A)}:={{\mathcal{N}}}_{{\psi }_{k}}^{2}/\sum _{l\in {\mathcal{S}}}{{\mathcal{N}}}_{{\psi }_{l}}^{2},$$

(50)

$${p}_{k}^{(C)}:={{\mathcal{N}}}_{{\psi }_{k}}^{2}/\sum _{l\in {\mathcal{D}}}{{\mathcal{N}}}_{{\psi }_{l}}^{2}.$$

(51)

To prepare $| {\Sigma }_{A}\left.\right\rangle$ and $| {\Sigma }_{C}\left.\right\rangle$ we require the controlled unitaries ${V}_{A}={\sum }_{k\in {\mathcal{S}}}| k\left.\right\rangle \,\left\langle \right.k\left.\right\vert \otimes {W}_{k}^{(A)}$ and ${V}_{C}={\sum }_{k\in {\mathcal{D}}}| k\left.\right\rangle \,\left\langle \right.k| \otimes {W}_{k}^{(C)}$ acting on states ${\sum }_{k\in {\mathcal{S}}}\sqrt{{p}_{k}^{(A)}}| k\left.\right\rangle | 0\left.\right\rangle$ and ${\sum }_{k\in {\mathcal{D}}}\sqrt{{p}_{k}^{(A)}}| k\left.\right\rangle | 0\left.\right\rangle$ respectively. Here ${W}_{k}^{(A)}$ and ${W}_{k}^{(C)}$ are the state preparation circuits from Lemma 13 that create $| {\psi }_{k}\left.\right\rangle$ where $k\in {\mathcal{S}}$ and $k\in {\mathcal{D}}$, respectively. Since ${W}_{k}^{(A)}$ and ${W}_{k}^{(C)}$ are known circuits and assuming $\sigma =O({\rm{poly}}\log d)$, it is similarly efficient and also straightforward to realise V_A and V_C. Then, from Lemma 30, it is possible to create $(1,O(\log d),0)$-block-encodings of ρ_A and ρ_C with gate and query complexity $O({\rm{poly}}\log d)$, denoted ${U}_{{\rho }_{A}}$ and ${U}_{{\rho }_{C}}$, respectively. In the case where ${\rm{Tr}}(A)=1={\rm{Tr}}(C)$, then this automatically gives us the unitaries U_A and U_C required in Theorem 14.

For general classical data, ${\rm{Tr}}(A)=1={\rm{Tr}}(C)$ does not hold in general. However, since $A={\rm{Tr}}(A){\rho }_{A}$ and $C={\rm{Tr}}(C){\rho }_{C}$, the proof in Theorem 14 holds in the same way if we began with ${U}_{{\rho }_{A}}$ and $U_{{\rho }_{C}}$, from which we can create ${U}_{{Y}^{{\prime} }}$ where ${Y}^{{\prime} }\equiv {\rho }_{A}^{-1}\#{\rho }_{C}={({\rm{Tr}}(C)/{\rm{Tr}}(A))}^{1/2}Y$. This implies

$$\left\langle 0\right\vert {U}_{Y}| 0\left.\right\rangle \approx Y={({\rm{Tr}}(A)/{\rm{Tr}}(C))}^{1/2}{Y}^{{\prime} }\approx {({\rm{Tr}}(A)/{\rm{Tr}}(C))}^{1/2}\left\langle 0\right\vert {U}_{{Y}^{{\prime} }}| 0\left.\right\rangle .$$

(52)

Following through the same proof idea as in Theorem 14 allows us to extract ${d}_{Y}^{{\prime} }$. To recover d_Y, we just use ${d}_{Y}\approx {({\rm{Tr}}(A)/{\rm{Tr}}(C))}^{1/2}{d}_{Y}^{{\prime} }$. These normalisations can be efficiently recovered by assuming the states $| {\psi }_{k}\left.\right\rangle$ have low sparsity ${\sigma }_{k}=O({\rm{poly}}\log d)$ for each k. This also means that the normalisations ${\rm{Tr}}(A)$ and ${\rm{Tr}}(C)$ are efficient to compute. So long as ${({\rm{Tr}}(A)/{\rm{Tr}}(C))}^{1/2}$ is $O({\rm{poly}}\log d)$, then d_Y is efficiently estimable.

1-class quantum learning

Here we propose a new quantum classification problem that is a 1-class problem. This means that given a quantum state, we only want to know whether this state belongs to a class ${\mathcal{A}}$ or not. This problem occurs in many areas in machine learning, in particular in anomaly detection, where ${\mathcal{A}}$ is the class of states that are considered anomalous. Here we can be provided with the following training data:

$$\rho =\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{\rho }_{i},\,{\rho }_{i}\in {\mathcal{A}},$$

(53)

$$\sigma =\frac{1}{M}\mathop{\sum }\limits_{i=1}^{M}{\sigma }_{i},\,{\sigma }_{i}\,\notin\, {\mathcal{A}},$$

(54)

where ${\{{\rho }_{i}\}}_{i}$ and ${\{{\sigma }_{i}\}}_{i}$ are sets of D-dimensional states. In anomaly detection scenarios, there are usually much fewer examples of anomalous states than ‘normal’ states, so that N ≪ M. However, we will not focus on subtleties associated with imbalanced training data here.

Suppose that we have an incoming quantum state ξ and we want to flag this as belonging to the class ${\mathcal{A}}$ or not. Then it is useful to learn an ‘observable’ or a ‘witness’ Y such that its expectation value ${\rm{Tr}}(Y\xi )$ is large when ξ is flagged as anomalous, belonging to ${\mathcal{A}}$, but this value is small when ξ is ‘normal’. Thus we can set up an optimisation problem of the form

$$\mathop{\min }\limits_{Y\ge 0}L(Y),\,L(Y):={\rm{Tr}}(Y\sigma )+{\rm{Tr}}({Y}^{-1}\rho ).$$

(55)

It is sensible in the above to minimise ${\rm{Tr}}({Y}^{-1}\rho )$ in L(Y) above since it is simple to show that a small value of ${\rm{Tr}}({Y}^{-1}\rho )$ implies a large value of ${\rm{Tr}}(Y\rho )$. Since ρ is a density matrix, it can be shown that ${\rm{Tr}}({Y}^{-1}\rho )\ge {\rm{Tr}}{(Y\rho )}^{-1}$, which is a consequence of the operator Jensen inequality (see [⁵², Eqs. (29–35)]). Thus ${\rm{Tr}}({Y}^{-1}\rho )\le \lambda$ implies ${\rm{Tr}}(Y\rho )\ge 1/\lambda$.

When ρ and σ are (positive definite) density matrices, the unique solution to Eq. (55) is given by the matrix geometric mean Y = σ⁻¹#ρ. We can, therefore, proceed as before to compute ${\rm{Tr}}(Y\xi )$, except now we do not need to be concerned with state preparation of ρ and σ, and we can assume that we are given copies of ρ and σ. Thus, given access to U_Y, we can estimate the following expectation:

$${\rm{Tr}}(Y\xi )\approx 2{\kappa }_{\sigma }{\rm{Tr}}((\xi \otimes | 0\left.\right\rangle \,\left\langle 0\right\vert ){U}_{Y}),$$

(56)

where the κ_σ constant follows from Lemma 8 and the error in the above estimate is upper bounded by ϵ. We then have the following result.

Theorem 15

Suppose that we are given the block-encodings U_ρ and U_σ, where $\rho \in {\mathcal{A}}$, $\sigma\, \notin\, {\mathcal{A}}$ and that we are also given access to multiple copies of ξ. Suppose further that ${\kappa }_{\rho },{\kappa }_{\sigma }=O({\rm{poly}}\log d)$. Then computing ${\rm{Tr}}(Y\xi )$ for the optimal Y in Eq. (55) to precision ϵ > 0 has a query and gate complexity $O({\rm{poly}}(\log d,1/\epsilon ))$.

Proof

From Lemma 8 we can construct a $(2{\kappa }_{\sigma },O(\log d),\epsilon )$-block-encoding of Y with gate and query complexity $O({\rm{poly}}({\kappa }_{\rho },{\kappa }_{\sigma },\log (1/\epsilon )))$. Considering that ${\kappa }_{\rho },{\kappa }_{\sigma }=O({\rm{poly}}\log d)$, applying the unitary U_Y to $\xi \otimes | 0\left.\right\rangle \,\left\langle 0\right\vert$, and using the Hadamard test (Lemma 31) with $\xi \otimes | 0\left.\right\rangle \,\left\langle 0\right\vert$, we recover ${\rm{Tr}}(Y\xi )$ to precision ϵ with query and gate complexity $O({\rm{poly}}(\log d,1/\epsilon ))$. □

We emphasise that this problem is entirely quantum in nature as we are given directly only quantum data.

Remark 2

The assumption of U_ρ and U_σ as block-encodings of ρ and σ, respectively, is without loss of generality in practice. There are two quantum input models for quantum states that are commonly employed in quantum algorithms:

• Quantum query access model. In this model, quantum unitary oracles ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ are given such that they prepare purifications of ρ and σ, respectively. By the technique of purified density matrix in ref. ²⁰ (see Lemma 30), we can implement U_ρ and U_σ from ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ with query and gate complexity $\tilde{O}\left(1\right)$. Therefore, Theorem 15 can be adapted to the quantum query access model with query and gate complexity $O({\rm{poly}}(\log d,1/\epsilon ))$.

• Quantum sample access model. In this model, independent and identical copies of ρ and σ are given. By the technique of density matrix exponentiation^53,54, we can implement unitary operators that are block-encodings of ρ and σ using their copies (which was first noted in ref. ⁵⁵ and later investigated in refs. ^56,57,58). In this way, Theorem 15 can be adapted to the quantum sample access model with sample and gate complexity $O({\rm{poly}}(\log d,1/\epsilon ))$.

A very interesting observation to note here is that the matrix geometric mean solution Y to Eq. (55) is precisely the Fuchs–Caves observable¹⁴, which is important for distinguishing two states ρ and σ. From this observation, we can motivate the Fuchs–Caves observable as the observable that gives rise to a kind of ‘optimal witness’ that distinguishes ρ and σ and the value of this ‘witness’ is precisely quantum fidelity, as shown in the next section. This provides an alternative motivation for the form of quantum fidelity between two mixed states from a metric learning viewpoint. In fact, a protocol involving measurement of the Fuchs–Caves observable also achieves an upper bound on sample complexity for the quantum hypothesis testing problem in distinguishing ρ and σ [ref. ⁵⁹, Appendix F]. Thus, up to constant factors, the strategy also minimises the number of copies of each state used for a given tolerated precision in distinguishing the states. We note that the loss function also appears in Eq. (6) in ref. ⁴², but this is motivated from a different perspective.

Extension to weighted geometric mean metric learning

The two terms in the loss function in Eq. (53), involving σ and ρ respectively, have equal weights. This means the learning algorithm deems closeness to ρ and farness to σ of equal ‘importance’. However, there are scenarios, especially in anomaly detection, where asymmetry is preferable. For example, this occurs when there is a higher cost of getting false negatives.

Modifying Eq. (53) by simply multiplying each of the two terms by different constants α, β leads to $L(Y)=\alpha {\rm{Tr}}(Y\sigma )+\beta {\rm{Tr}}({Y}^{-1}\rho )$. However, this only rescales the optimal solution Y → (β/α)^1/2Y by a constant factor, as observed in ref. ²⁴. A new loss function is, therefore, necessary for the asymmetric case.

Following ref. ²⁴, one can first observe that the solution Y = σ⁻¹#ρ is in fact also a solution to the following optimisation problem when t = 1/2:

$$\mathop{\min }\limits_{\tilde{Y}\ge 0}{L}_{t}(\tilde{Y}),\,{L}_{t}(\tilde{Y}):=(1-t)\delta (\tilde{Y},{\sigma }^{-1})+t\delta (\tilde{Y},\rho ),\,t\in [0,1],$$

(57)

where δ is the geodesic distance defined in Eq. (8). While the mathematical proof is more involved, this fact can easily be understood from the geometric viewpoint. Here Y = σ⁻¹#ρ can be understood as the midpoint along the unique geodesic in Riemannian space joining σ⁻¹ and ρ. When t = 1/2, the optimal $\tilde{Y}$ is then the point along this geodesic that simultaneously minimises the distance between $\tilde{Y}$ and σ⁻¹, as well as $\tilde{Y}$ and ρ. This clearly must be the midpoint. Similar geometric reasoning leads one to generalise to t ≠ 1/2 where the solution to Eq. (57) is the weighted matrix geometric mean $\tilde{Y}={\sigma }^{-1}{\#}_{t}\rho$. That this is the unique solution to Eq. (57) is a special case (the n = 2 case) in ref. ⁶⁰ and proofs can also be found in ref. ²⁶, Chapter 6. Also, see ref. ²⁴ for a discussion in the context of geometric mean metric learning.

We can proceed similarly to 1-class quantum learning algorithm with equal weights as described in the previous section. The goal is also to output ${\rm{Tr}}(\tilde{Y}\xi )$ for some input test state ξ. Here, we require instead the construction of block-encodings of the weighted matrix geometric mean, as given in Lemma 11. However, for all t > 0 (p > 0 in Lemma 11), we see that there is no scaling difference for constructing the block-encoding for the weighted version. Thus, the cost, up to constant and logarithmic factors, is identical for the quantum-weighted geometric mean metric learning algorithm as for the unweighted version in Theorem 15.

Estimation of quantum fidelity and geometric Rényi relative entropies

Here, we describe our quantum algorithms for estimating quantum fidelity and geometric Rényi relative entropies using our quantum subroutines for preparing block-encodings of the standard and weighted matrix geometric means.

Fidelity

The fidelity between two mixed quantum states is defined by⁶¹

$$F\left(\rho ,\sigma \right):={\rm{Tr}}\!\left({\left({\sigma }^{1/2}\rho {\sigma }^{1/2}\right)}^{1/2}\right),$$

(58)

which is a commonly considered measure of the closeness of or similarity between two quantum states. Estimating the value of fidelity is a fundamental task in quantum information theory. When given matrix descriptions of the states ρ and σ, it can be calculated directly using the formula above or as the solution to a semi-definite optimisation problem⁴². Recently, several time-efficient quantum algorithms for fidelity estimation have been developed when one has access to state-preparation circuits for ρ and σ ^56,62,63.

Here, we introduce a new approach for fidelity estimation that is based on the Fuchs–Caves observable¹⁴. For two quantum states ρ and σ, this observable is given by M = σ⁻¹#ρ. Then the fidelity between ρ and σ can be represented as the expectation of M with respect to σ (cf. [ref. ³⁸, Eq. (9.159)]):

$$F\left(\rho ,\sigma \right)={\rm{Tr}}\left(M\sigma \right).$$

(59)

Theorem 16

(Fidelity estimation via Fuchs–Caves observable). Suppose that ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ prepare purifications of mixed quantum states ρ and σ, respectively. Then, we can estimate $F\left(\rho ,\sigma \right)$ within additive error ϵ using $\tilde{O}(\min \{{\kappa }_{\rho }^{{2}},{\kappa }_{\sigma }^{2}\}\cdot {\kappa }_{\rho }{\kappa }_{\sigma }/\epsilon )$ queries to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$, where κ_ρ, κ_σ > 0 are such that ρ ≥ I/κ_ρ and σ ≥ I/κ_σ.

Proof

Suppose that ρ and σ are n-qubit mixed quantum states and ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ are $\left(n+a\right)$-qubit unitary operators. By Lemma 30, we can implement two unitary operators U_ρ and U_σ that are $\left(1,n+a,0\right)$-block-encodings of ρ and σ using $O\left(1\right)$ queries to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$, respectively. Then, by applying Lemma 8, we can implement a $\left(2{\kappa }_{\sigma },b,\delta \right)$-block-encoding U_M of M = σ⁻¹#ρ, using $\tilde{O}({\kappa }_{\sigma }{\kappa }_{\rho }{\log }^{2}(1/\delta ))$ queries to U_ρ and $\tilde{O}({\kappa }_{\sigma }^{2}{\kappa }_{\rho }{\log }^{3}(1/\delta ))$ queries to U_σ, where $b=O\left(n+a\right)$, and κ_ρ and κ_σ satisfy ρ ≥ I/κ_ρ and σ ≥ I/κ_σ.

By the Hadamard test (given in Lemma 31), there is a quantum circuit C that outputs 0 with probability $\frac{1}{2}\left(1+{\rm{Re}}\{ {\rm{Tr}}\left({\left\langle \right.0| }_{b}{U}_{M}{| 0\left.\right\rangle }_{b}\sigma \right)\}\right)$, using one query to U_M and one sample of σ. By noting that

$$\left\vert 2{\kappa }_{\sigma }{\rm{Re}} \{ {\rm{Tr}}\left({\left\langle \right.0| }_{b}{U}_{M}{| 0\left.\right\rangle }_{b}\sigma \right)\}-{\rm{Tr}}\left(M\sigma \right)\right\vert \le \Theta \left(\delta \right),$$

(60)

we conclude that an $O\left(\epsilon /{\kappa }_{\sigma }\right)$-estimate of ${\rm{Re}} {\rm{Tr}}\left({\left\langle \right.0| }_{b}{U}_{M}{| 0\left.\right\rangle }_{b}\sigma \right)$ with $\delta =\Theta \left(\epsilon /{\kappa }_{\sigma }\right)$ suffices to obtain an ϵ-estimate of ${\rm{Tr}}\left(M\sigma \right)$ (which is the fidelity according to Eq. (59)). By quantum amplitude estimation (given in Lemma 33), this can be done using $O\left({\kappa }_{\sigma }/\epsilon \right)$ queries to C.

In summary, an ϵ-estimate of $F\left(\rho ,\sigma \right)$ can be obtained by using $\tilde{O}({\kappa }_{\sigma }^{3}{\kappa }_{\rho }/\epsilon )$ queries to ${{\mathcal{O}}}_{\sigma }$ and $\tilde{O}({\kappa }_{\sigma }^{2}{\kappa }_{\rho }/\epsilon )$ queries to ${{\mathcal{O}}}_{\rho }$. The proof is completed by taking the minimum over symmetric cases (i.e., simply flipping the role of ρ and σ since the fidelity formula is symmetric under this exchange). □

The current best quantum query complexity of fidelity estimation is $\tilde{O}\left({r}^{2.5}/{\epsilon }^{5}\right)$, due to⁵⁶, where r is the lower rank of the two input mixed quantum states. In comparison, our quantum algorithm for fidelity estimation based on the Fuchs–Caves observable, as given in Theorem 16, has a better dependence on the additive error ϵ, if κ_ρ and κ_σ are known in advance.

Moreover, we note that the ϵ-dependence of the quantum algorithm given in Theorem 16 is optimal (up to polylogarithmic factors), as stated in Lemma 17 below.

Lemma 17

(Optimal ϵ-dependence of fidelity estimation). Suppose that ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ prepare purifications of mixed quantum states ρ and σ, respectively, satisfying ρ ≥ I/κ_ρ and σ ≥ I/κ_σ for κ_ρ, κ_σ > 0. Then, every quantum algorithm that estimates $F\left(\rho ,\sigma \right)$ within additive error ϵ requires query complexity $\Omega \left(1/\epsilon \right)$ even if ${\kappa }_{\rho }={\kappa }_{\sigma }=\Theta \left(1\right)$.

Proof

See Appendix IV I. □

In addition to the optimal $\epsilon$-dependence of fidelity estimation in Lemma 17, a quantum query algorithm for estimating the fidelity $F(|\psi\rangle, |\varphi\rangle)$ between pure states with query complexity in $\Theta(1/\epsilon)$ was given in⁶⁴.

Remark 3

(Sample complexity for fidelity estimation). Using the method in Theorem 16, we can also estimate the fidelity by using only samples of quantum states, which is achieved by density matrix exponentiation^{53,54,56,58,65}. As analysed in Appendix IV J, the sample complexity for fidelity estimation is shown to be $\tilde{O}(\min \{{\kappa }_{\rho }^{5},{\kappa }_{\sigma }^{5}\}\cdot {\kappa }_{\rho }^{2}{\kappa }_{\sigma }^{2}/{\epsilon }^{3})={\rm{poly}}({\kappa }_{\rho },{\kappa }_{\rho })\cdot \tilde{O}(1/{\epsilon }^{3})$. The prior known sample complexity for fidelity estimation is $\tilde{O}\left({r}^{5.5}/{\epsilon }^{12}\right)$ due to⁵⁶, where r is the lower rank of the two input mixed quantum states.

We also show a sample lower bound $\Omega \left(1/{\epsilon }^{2}\right)$ for fidelity estimation even if ${\kappa }_{\rho }={\kappa }_{\sigma }=\Theta \left(1\right)$ using the method in the proof of Lemma 17; this can be seen as an analogue of the sample lower bound $\Omega \left(1/{\epsilon }^{2}\right)$ for pure-state fidelity estimation in ref. ⁶⁶. In addition, a sample lower bound $\Omega \left(r/\epsilon \right)$ for (low-rank) fidelity estimation is implied in refs. ^67,68.

Currently, quantum algorithms for fidelity estimation with optimal sample complexity are only known for pure states. For estimating the squared fidelity $F^2(|\psi\rangle, |\varphi\rangle)$, the sample complexity $\Theta(1/\epsilon^2)$ can be achieved by the SWAP test⁴⁸. In⁶⁶, they showed that $\Theta(\max\{1/\epsilon^2, \sqrt{d}/\epsilon\})$ samples are sufficient and necessary to estimate $F^2(|\psi\rangle, |\varphi\rangle)$ when only single-copy measurements are allowed. Recently in⁶⁹, the sample complexity of estimating the fidelity $F(|\psi\rangle, |\varphi\rangle)$ was shown to be $\Theta(1/\epsilon^2)$.

Geometric fidelity and geometric Rényi relative entropy

Here we present, to the best of our knowledge, the first quantum algorithm for computing the geometric α-Rényi relative entropy, as introduced in ref. ¹². For $\alpha \in (0,1)\cup \left(1,2\right]$, the geometric α-Rényi relative entropy is defined as (see, e.g., [ref. ¹³, Eq. (9)] and [ref. ⁷⁰, Eq. (7.6.1)])

$${\tilde{D}}_{\alpha }\left(\rho || \sigma \right):=\frac{1}{\alpha -1}\log {\widehat{F}}_{\alpha }\left(\rho ,\sigma \right),$$

(61)

where

$${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right):={\rm{Tr}}\left(\rho {\#}_{1-\alpha }\sigma \right)={\rm{Tr}}\left(\sigma {\#}_{\alpha }\rho \right)$$

(62)

is known as the geometric α-Rényi relative quasi-entropy. When α ∈ (0, 1), we also refer to ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ as the geometric α-fidelity. In particular, for the case of α = 1/2, the quantity ${\widehat{F}}_{1/2}\left(\rho ,\sigma \right)$ is the geometric fidelity (also known as the Matsumoto fidelity)^15,16. The α-geometric Rényi relative entropy has several uses in quantum information theory, especially in analysing protocols involving feedback^13,28,71.

Here we present quantum algorithms in Theorems 18 and 19 for computing the geometric Rényi relative (quasi-)entropy.

Theorem 18

Suppose that ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ prepare purifications of mixed quantum states ρ and σ, respectively. Then, for $\alpha \in \left(0,1\right)\cup \left(1,2\right]$, we can estimate ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ to within additive error ϵ using

• $\tilde{O}(\min {\{{\kappa }_{\rho },{\kappa }_{\sigma }\}}^{\min \left\{1+\alpha ,2-\alpha \right\}}\cdot {\kappa }_{\rho }{\kappa }_{\sigma }/\epsilon )$ queries for α ∈ (0, 1), and

• $\tilde{O}(\min \{{\kappa }_{\rho }{\kappa }_{\sigma }^{\alpha -1},{\kappa }_{\rho }^{\alpha -1}{\kappa }_{\sigma },{\kappa }_{\rho }^{1+\alpha },{\kappa }_{\sigma }^{1+\alpha }\}\cdot {\kappa }_{\rho }{\kappa }_{\sigma }/\epsilon )$ queries for $\alpha \in \left(1,2\right]$

to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$, where κ_ρ, κ_σ > 0 satisfy ρ ≥ I/κ_ρ and σ ≥ I/κ_σ.

In particular, when α = 1/2, ${\widehat{F}}_{1/2}\left(\rho ,\sigma \right)$ is the geometric fidelity (also known as the Matsumoto fidelity), which can be estimated using $\tilde{O}(\min {\{{\kappa }_{\rho },{\kappa }_{\sigma }\}}^{3/2}\cdot {\kappa }_{\rho }{\kappa }_{\sigma }/\epsilon )$ queries to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$.

Proof

See Appendix IV H. □

Theorem 19

Suppose that ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ prepare purifications of mixed quantum states ρ and σ, respectively. Then, for $\alpha \in \left(0,1\right)\cup \left(1,2\right]$, we can estimate ${\tilde{D}}_{\alpha }\left(\rho || \sigma \right)$ within additive error ϵ using

• $\tilde{O}(\min {\{{\kappa }_{\rho },{\kappa }_{\sigma }\}}^{\min \left\{1+\alpha ,2-\alpha \right\}}\cdot {\kappa }_{\rho }{\kappa }_{\sigma }^{2-\alpha }/\epsilon)$ queries for α ∈ (0, 1), and

• $\tilde{O}(\min \{{\kappa }_{\rho }{\kappa }_{\sigma }^{\alpha -1},{\kappa }_{\rho }^{\alpha -1}{\kappa }_{\sigma },{\kappa }_{\rho }^{1+\alpha },{\kappa }_{\sigma }^{1+\alpha }\}\cdot {\kappa }_{\rho }^{\alpha }{\kappa }_{\sigma }/\epsilon )$ queries for $\alpha \in \left(1,2\right]$

to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$, where κ_ρ, κ_σ > 0 satisfy ρ ≥ I/κ_ρ and σ ≥ I/κ_σ.

Proof

See Appendix IV H. □

Notably, we show that our quantum algorithm for estimating the geometric fidelity ${\widehat{F}}_{1/2}\left(\rho ,\sigma \right)$ achieves an optimal ϵ-dependence. The optimality also holds for ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ with α ∈ (0, 1).

Lemma 20

(Optimal ϵ-dependence of geometric α-fidelity estimation). Suppose that ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ prepare purifications of mixed quantum states ρ and σ, respectively, with ρ ≥ I/κ_ρ and σ ≥ I/κ_σ, where κ_ρ, κ_σ > 0. Then, for every constant α ∈ (0, 1), every quantum algorithm that estimates ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ within additive error ϵ requires query complexity $\Omega \left(1/\epsilon \right)$ even if ${\kappa }_{\rho }={\kappa }_{\sigma }=\Theta \left(1\right)$, where $\Omega \left(\cdot \right)$ hides a constant factor that depends only on α.

Proof

See Appendix IV I. □

It remains an open problem to determine whether optimality still holds for $\alpha \in \left(1,2\right]$. However, note that when $\alpha \in \left(1,2\right]$, the inequality ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)\ge 1$ holds, and so ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ cannot be interpreted as a fidelity for these values of α; thus, different techniques are required in order to establish optimality.

Remark 4

Similar to Remark 3, for estimating the corresponding quantities, we can extend Theorems 18 and 19 to quantum algorithms with sample complexity ${\rm{poly}}({\kappa }_{\rho },{\kappa }_{\rho })\cdot \tilde{O}\left(1/{\epsilon }^{3}\right)$, and extend Lemma 20 to a sample complexity lower bound of $\Omega \left(1/{\epsilon }^{2}\right)$.

BQP-hardness

In this section, we consider the hardness of computing the matrix geometric mean. Precisely, we show that our quantum algorithm for matrix geometric means (given in Lemma 8) can be used to solve a ${\mathsf{BQP}}$-complete problem (defined in Problem 1). Roughly speaking, this problem pertains to testing a certain property of the matrix geometric mean of two well-conditioned sparse matrices.

Problem 1 (Matrix geometric mean)

For functions ${\kappa }_{A}:{\mathbb{N}}\to {\mathbb{N}}$ and ${\kappa }_{C}:{\mathbb{N}}\to {\mathbb{N}}$, let ${\rm{MGM}}\left({\kappa }_{A},{\kappa }_{C}\right)$ be a decision problem defined as follows. For a size-n instance of ${\rm{MGM}}\left({\kappa }_{A},{\kappa }_{C}\right)$, let N = 2ⁿ and let $A,C\in {{\mathbb{C}}}^{N\times N}$ be $O\left(1\right)$-sparse positive definite matrices satisfying $I/{\kappa }_{A}\left(n\right)\le A\le I$ and $I/{\kappa }_{C}\left(n\right)\le C\le I$, and given by a ${\rm{poly}}\left(n\right)$-size uniform classical circuit ${{\mathcal{C}}}_{n}$ such that, for every 1 ≤ j ≤ N, the circuit ${{\mathcal{C}}}_{n}\left(j\right)$ computes the positions and values of the non-zero entries in the j-th row of A and C. Let $Y\in {{\mathbb{C}}}^{N\times N}$ be the matrix geometric mean of A and C such that YAY = C. The task is to decide which of the following is the case, promised that one of the two holds:

• Yes: $\left\langle \right.\psi | M| \psi \left.\right\rangle \ge 2/3$;

• No: $\left\langle \right.\psi | M| \psi \left.\right\rangle \le 1/3$,

where $| \psi \left.\right\rangle :=\frac{{Y}^{2}| 0\left.\right\rangle }{\left\vert {Y}^{2}| 0\left.\right\rangle \right\vert }$ and $M=| 0\left.\right\rangle \,\left\langle \right.0| \otimes {I}_{N/2}$ measures the first qubit.

Theorem 21

$\,\text{MGM}\,\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$ is ${\mathsf{BQP}}$-complete.

Proof

The proof consists of two parts: Lemma 22 and Lemma 23.

• 1. In Lemma 22, we state that ${\rm{MGM}}\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$ is ${\mathsf{BQP}}$-hard; the proof employs a reduction of the quantum linear systems problem (QLSP).

• 2. In Lemma 23, we state that ${\rm{MGM}}\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$ is in ${\mathsf{BQP}}$; the proof employs the quantum algorithm for the matrix geometric mean given in Lemma 8.

□

Lemma 22

${\rm{MGM}}\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$ is ${\mathsf{BQP}}$-hard.

Proof

We consider the quantum linear systems problem (QLSP) defined as follows. □

Problem 2 (QLSP)

For functions $\kappa :{\mathbb{N}}\to {\mathbb{N}}$, let ${\rm{QLSP}}\left(\kappa \right)$ be a decision problem defined as follows. For a size-n instance of ${\rm{QLSP}}\left(\kappa \right)$, let N = 2ⁿ and $A\in {{\mathbb{C}}}^{N\times N}$ be an $O\left(1\right)$-sparse Hermitian matrix such that $I/\kappa \left(n\right)\le A\le I$, given by a ${\rm{poly}}\left(n\right)$-size uniform classical circuit ${{\mathcal{C}}}_{n}$ such that for every 1 ≤ j ≤ N, ${{\mathcal{C}}}_{n}\left(j\right)$ computes the positions and values of the non-zero entries in the j-th row of A. The task is to decide which of the following is the case, promised that one of the two holds:

• Yes item: $\left\langle \right.\psi | M| \psi \left.\right\rangle \ge 2/3$;

• No item: $\left\langle \right.\psi | M| \psi \left.\right\rangle \le 1/3$,

where $| \psi \left.\right\rangle :=\frac{{A}^{-1}| 0\left.\right\rangle }{\left\vert {A}^{-1}| 0\left.\right\rangle \right\vert }$ and $M=| 0\left.\right\rangle \,\left\langle \right.0| \otimes {I}_{N/2}$ measures the first qubit.

It was shown in ref. ¹ that ${\rm{QLSP}}\left({\rm{poly}}\left(n\right)\right)$ is ${\mathsf{BQP}}$-complete. Here, we reduce ${\rm{QLSP}}\left({\rm{poly}}\left(n\right)\right)$ to ${\rm{MGM}}\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$, and therefore show the ${\mathsf{BQP}}$-hardness of ${\rm{MGM}}\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$. Consider any instance (matrix) $A\in {{\mathbb{C}}}^{N\times N}$ of ${\rm{QLSP}}\left(\kappa \right)$, where N = 2ⁿ and $\kappa ={\rm{poly}}\left(n\right)$. We choose $C=I\in {{\mathbb{C}}}^{N\times N}$ to be the identity matrix, which is a 1-sparse Hermitian matrix and each of whose rows can be easily computed. Note that the matrix geometric mean Y of A⁻¹ and C is Y = A⁻¹#C = A^−1/2. Then, it can be seen that Y² = A⁻¹ and thus $| {\psi }_{Y}\left.\right\rangle ={Y}^{2}| 0\left.\right\rangle /\left\Vert {Y}^{2}| 0\left.\right\rangle \right\Vert ={A}^{-1}| 0\left.\right\rangle /\left\Vert {A}^{-1}| 0\left.\right\rangle \right\Vert =| {\psi }_{A}\left.\right\rangle$. Consequently, any quantum algorithm that determines whether $\left\langle \right.{\psi }_{Y}| M| {\psi }_{Y}\left.\right\rangle \ge 2/3$ or $\left\langle \right.{\psi }_{Y}| M| {\psi }_{Y}\left.\right\rangle \le 1/3$ with success probability at least 2/3 can be used to determine whether $\left\langle \right.{\psi }_{A}| M| {\psi }_{A}\left.\right\rangle \ge 2/3$ or $\left\langle \right.{\psi }_{A}| M| {\psi }_{A}\left.\right\rangle \le 1/3$. In summary, ${\rm{QLSP}}\left(\kappa \right)$ can be reduced to ${\rm{MGM}}\left(\kappa ,1\right)$ through the above encoding. Therefore, ${\rm{MGM}}\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$ is ${\mathsf{BQP}}$-hard.

Lemma 23

MGM(poly(n), poly(n)) is in BQP.

Proof

See Appendix IV K. □

Discussion

We constructed efficient block-encodings of the matrix geometric mean (and the weighted matrix geometric mean). These are unique solutions to the simplest algebraic Riccati equations—quadratically nonlinear system of matrix equations. Unlike the output of most quantum algorithms for linear systems of equations, these solutions of the nonlinear matrix equations are not embedded in pure quantum states, but rather in terms of observables from which we can extract expectation values.

This allows us to introduce a new class of algorithms for quantum learning, called quantum geometric mean metric learning. For example, this can be applied in a purely quantum setting for picking out anomalous quantum states. This can also be adapted to the case of flexible weights on the cost of flagging an anomaly. The new quantum subroutines can also be used for the first quantum algorithm, to the best of our knowledge, to compute the geometric Rényi relative entropies and new quantum algorithms to compute quantum fidelity by means of the Fuchs–Caves observable. In the latter case, we demonstrate optimal scaling Ω(1/ϵ) in precision.

While most of the applications introduced above are for quantum problems for which there is no direct classical equivalent (although the quantum learning algorithm can also be applied to learning Euclidean distances for classical data), there are potential benefits that the new quantum subroutine can have over purely classical methods. This could be exploited for future applications. For example, classical numerical algorithms to compute the matrix geometric mean have cost O(polyD) for D × D matrices^50,51. The same is also true for solving the differential matrix Riccati equation and algebraic matrix Riccati equation¹⁷ through iterative methods and other methods based on finding the eigendecomposition of a larger matrix⁷². For quantum processing on the other hand, we showed conditions under which the block-encodings of some of these solutions can be obtained with cost $O({\rm{poly}}\log d)$.

For example, there are many classical problems for which it is important to compute the matrix geometric mean between two matrices. They appear in imaging^73,74 and in the analysis of multiport electrical networks⁷⁵. The algebraic Riccati equation of the form in Eq. (9) also appears in optimal control and Kalman filters. Under the assumptions in Lemma 5 when uniqueness of its solution is also satisfied, it can be possible to construct its block-encoding in Lemma 9. Although these assumptions are not generally satisfied, this still gives an idea of the extent and reach of the matrix geometric mean. Extensions of our algorithms to the matrix geometric mean consisting of more than two matrices can also be explored, which already find applications in areas like elasticity and radars^76,77. It is also intriguing to consider purely quantum extensions of these problems. The main difficulty associated with constructing block-encodings of multivariate geometric means is that they are not known to have an analytical form as they do in the bivariate case; rather, they are constructed as the solutions of nonlinear equations generalising the simple algebraic Riccati equation¹⁰. It is worth mentioning that there are many other quantum algorithms for learning problems with different loss functions and the solutions to these problems do not have general analytical forms. Examples include semi-definite programming^78,79,80,81, linear programming^82,83,84, and general matrix games⁸⁵. It is interesting to ask whether the techniques developed in this paper can be used in these problems.

In addition to usefulness in applications, the standard and weighted matrix geometric means also have an elegant interpretation in terms of geodesics in Riemannian space. Despite the importance and beauty of Riemannian geometry in mathematics and other areas in physics, sensing, and machine learning, it has not appeared too much in quantum computation yet, apart from very notable exceptions like⁸⁶. This geometric perspective is useful in understanding the weighted quantum learning algorithm, and we showed how it provided an alternative motivation for the form of quantum fidelity via the Fuchs–Caves observable. There is more potential here for the matrix geometric mean to bring the ideas of geometry closer to quantum information and computation.

Methods

Proof of Lemma 5

This follows by observing that (9) is a matrix version of the quadratic equation and by following an argument similar to what is well known as completing the square. Consider that

$${\left(Y-{A}^{-1}B\right)}^{\dagger }A\left(Y-{A}^{-1}B\right)=({Y}^{\dagger }-{\left({A}^{-1}B\right)}^{\dagger })A\left(Y-{A}^{-1}B\right)$$

(63)

$$=({Y}^{\dagger }-{B}^{\dagger }{\left({A}^{-1}\right)}^{\dagger })A\left(Y-{A}^{-1}B\right)$$

(64)

$$=\left({Y}^{\dagger }-{B}^{\dagger }{A}^{-1}\right)A\left(Y-{A}^{-1}B\right)$$

(65)

$$={Y}^{\dagger }AY-{Y}^{\dagger }A{A}^{-1}B-{B}^{\dagger }{A}^{-1}AY+{B}^{\dagger }{A}^{-1}A{A}^{-1}B$$

(66)

$$={Y}^{\dagger }AY-{Y}^{\dagger }B-{B}^{\dagger }Y+{B}^{\dagger }{A}^{-1}B.$$

(67)

Then

$$\begin{array}{l}{Y}^{\dagger }AY-{B}^{\dagger }Y-{Y}^{\dagger }B-C\\\,={\left(Y-{A}^{-1}B\right)}^{\dagger }A\left(Y-{A}^{-1}B\right)-{B}^{\dagger }{A}^{-1}B-C,\end{array}$$

(68)

and so (9) is equivalent to

$${X}^{\dagger }AX=D,$$

(69)

where

$$X=Y-{A}^{-1}B,$$

(70)

$$D={B}^{\dagger }{A}^{-1}B+C.$$

(71)

Observe that D is positive definite because B^†A⁻¹B is positive semi-definite and C is positive definite. So this is a reduction to the original simplified form of the algebraic Riccati equation in (10), which we know from Lemma 4 has the following unique positive definite solution:

$$X={A}^{-1}\#D$$

(72)

$$={A}^{-1}\#\left({B}^{\dagger }{A}^{-1}B+C\right).$$

(73)

This implies that

$$Y=X+{A}^{-1}B$$

(74)

$$={A}^{-1}\#\left({B}^{\dagger }{A}^{-1}B+C\right)+{A}^{-1}B$$

(75)

is a solution of (9).

Remark 5

Contrary to what is stated in the proof of [ref. ⁸⁷, Corollary 4], the solution of (9), under the assumptions stated in Lemma 5, is not unique. Indeed,

$$Y=-\left({A}^{-1}\#\left({B}^{\dagger }{A}^{-1}B+C\right)\right)+{A}^{-1}B$$

(76)

is also a legitimate solution. In fact, the following is a matrix version of the famous quadratic formula:

$${A}^{-1}B\pm \left({A}^{-1}\#\left({B}^{\dagger }{A}^{-1}B+C\right)\right),$$

(77)

for which the scalar version is $\scriptstyle\frac{b}{a}\pm \sqrt{\frac{1}{a}\left(\frac{{b}^{2}}{a}+c\right)}$ corresponding to a solution of ay² − 2by − c = 0 (stated after (9)), under the assumption that a, c > 0.

Preliminary lemmas of the block-encoding formalism and other useful results

Let us introduce several preliminary lemmas of the block-encoding formalism, which enable us to implement various arithmetic operations on the block-encoded matrices. The first lemma states that, given block-encodings of two matrices, we can obtain a block-encoding of their product.

Lemma 24

(Product of block-encoded matrices [ref. ¹⁸, Lemma 30]). If U is an (α, a, δ)-block-encoding of A and V is a (β, b, ϵ)-block-encoding of B, then there is a unitary W that is an (αβ, a + b, αϵ + βδ)-block-encoding of AB, and can be implemented by one query to U and V.

Taking the linear combination of several block-encoded matrices is also useful and is stated in the following lemma.

Lemma 25

(Linear combination of block-encoded matrices [ref. ¹⁸, Lemma 29]). Let $m\in {\mathbb{N}}$ and β > 0 be constant, and let ${\boldsymbol{x}}=({x}_{1},\ldots ,{x}_{m})\in {{\mathbb{R}}}^{m}$ be a vector such that ${\left\Vert {\boldsymbol{x}}\right\Vert }_{1}\le \beta$. Suppose that each U_j is a (1, a, ϵ)-block-encoding of A_j for j = 1 to m. Then there is a unitary U that is a $(1,a+\eta \log (1/\epsilon ),2{\beta }^{-1}\epsilon )$-block-encoding of ${\beta }^{-1}\mathop{\sum }\nolimits_{j = 1}^{m}{x}_{j}{A}_{j}$, where η is some constant, and U can be implemented by one query to each U_j and ${\rm{polylog}}(1/\epsilon )$ gates.

To construct our quantum algorithms for matrix geometric means, we need to deal with the nonlinear terms in the matrix geometric means. The tool to be used is quantum singular value transformation¹⁸, which, in our case, is an (approximate) polynomial transformation of the block-encoded matrix, as stated in the following lemma.

Lemma 26

(Polynomial eigenvalue transformation [ref. ¹⁸, Theorem 31]). Let U be a (1, a, ϵ)-block-encoding of a Hermitian matrix A. If δ ≥ 0 and $q(x)\in {\mathbb{R}}[x]$ is a polynomial of degree d such that $\left\vert q(x)\right\vert \le 1$ for x ∈ [− 1, 1], then there is a unitary $\widetilde{U}$ that is a $(1,a+2,4d\sqrt{\epsilon }+\delta )$-block-encoding of q(A)/2, and can be implemented by d queries to U and O((a + 1)d) gates. A description of such an implementation can be computed classically in time $O\left({\rm{poly}}\left(d,\log (1/\delta )\right)\right)$.

We also need two polynomial approximation results for applying Lemma 26 in our scenario. The following two lemmas show low-degree polynomials for approximating the negative and positive power functions, respectively.

Lemma 27

(Polynomial approximations of negative power functions [ref. ¹⁸, Corollary 67 in the full version]). Let $f(x)={\left(x/\delta \right)}^{-c}/2$. For δ, ϵ ∈ (0, 1/2) and c > 0, there is a polynomial q(x) of degree $O\left((c+1){\delta }^{-1}\log (1/\epsilon )\right)$ such that

• $\left\vert q(x)-f(x)\right\vert \le \epsilon$ for x ∈ [δ, 1];

• $\left\vert q(x)\right\vert \le 1$ for x ∈ [− 1, δ).

Lemma 28

(Polynomial approximations of positive power functions [ref. ¹⁹, Lemma 10]). Let f(x) = x^c/2. For δ, ϵ ∈ (0, 1/2) and c ∈ (0, 1), there is a polynomial q(x) of degree $O\left({\delta }^{-1}\log (1/\epsilon )\right)$ such that

• $\left\vert q(x)-f(x)\right\vert \le \epsilon$ for x ∈ [δ, 1];

• $\left\vert q(x)\right\vert \le 1$ for x ∈ [− 1, δ).

In practice, how to encode the desired matrices into block-encodings and how to extract useful (classical) information from the block-encodings are of great concern. For the encoding, a typical scenario is that we are given sparse oracle access to a sparse matrix, and we can construct a block-encoding of the matrix, as stated in the following lemma.

Lemma 29

(Block-encoding of sparse matrices, [ref. ¹⁸, Lemma 48 in the full version]). Suppose $A\in {{\mathbb{C}}}^{N\times N}$ is an s-sparse matrix such that every entry A_j,k satisfies $\left\vert {A}_{j,k}\right\vert \le 1$. Suppose sparse oracles ${{\mathcal{O}}}_{s}$ and ${{\mathcal{O}}}_{A}$ are given such that

$${{\mathcal{O}}}_{s}| j\left.\right\rangle | k\left.\right\rangle =| j\left.\right\rangle | {l}_{j,k}\left.\right\rangle ,$$

(78)

$${{\mathcal{O}}}_{A}| j\left.\right\rangle | k\left.\right\rangle | 0\left.\right\rangle =| j\left.\right\rangle | k\left.\right\rangle | {A}_{j,k}\left.\right\rangle ,$$

(79)

where l_j,k denotes the column index of the k-th non-zero entry in the j-th row. Here, we assume that the exact value of the entry A_j,k is given in a binary representation. Then, we can implement a quantum circuit that is an $(s,{\log }_{2}N+3,\epsilon )$-block-encoding of A, using two queries to ${{\mathcal{O}}}_{s}$, two queries to ${{\mathcal{O}}}_{A}$, and $O(\log N+{\log }^{2.5}(s/\epsilon ))$ one- and two-qubit quantum gates.

Another useful case of encoding commonly considered is that we are given purified access to a density operator, and we can construct a block-encoding of the density operator.

Lemma 30

(Block-encoding of density operators [ref. ²⁰, Lemma 7], [ref. ¹⁸, Lemma 25]). Let ρ be an n-qubit density operator, and let V_ρ be an (n + a)-qubit unitary that prepares a purification of ρ such that ${{\rm{tr}}}_{a}({V}_{\rho }{| 0\left.\right\rangle }_{n+a}\,\left\langle \right.0| {V}_{\rho }^{\dagger })=\rho$. Then there is a (2n + a)-qubit unitary $\widetilde{V}$ that is a (1, n + a, 0)-block-encoding of ρ, and it can be implemented by one query to V and O(n) gates.

To extract classical information from the block-encodings, one needs to perform quantum measurements. The Hadamard test is a useful and efficient way to estimate the expectation value of a quantum observable on a given quantum state. The following lemma shows a Hadamard test for block-encodings.

Lemma 31

(Hadamard test for block-encodings, [ref. ⁵⁶, Lemma 9]). Suppose that U is a unitary operator that is a $\left(1,a,0\right)$-block-encoding of an n-qubit operator A. Then, there is a quantum circuit that outputs 0 with probability $\frac{1+{\rm{Re}} \{ {\rm{Tr}}\left(A\rho \right) \}}{2}$, using one query to U and one sample of the mixed quantum state ρ.

The success probability of extracting classical information from a block-encoding often depends on the scaling factor of the block-encoding. For our purpose, we need the following up-scaling lemma for block-encoded operators adapted from ref. ⁵⁷.

Lemma 32

(Up-scaling of block-encoded operators, adapted from [ref. ⁵⁷, Lemma 2.8]). Let unitary operator U be an $\left(\alpha ,a,\epsilon \right)$-block-encoding of A with α = Ω(1), $\epsilon \in \left(0,1\right)$ and $\left\vert A\right\vert \le 1$. Then, we can implement a quantum circuit ${U}^{{\prime} }$ that is a $\left(2,a+1,\tilde{\Theta }\left(\sqrt{\alpha \epsilon }\right)\right)$-block-encoding of A, using $\tilde{O}\left(\alpha \log \left(1/\epsilon \right)\right)$ queries to U, $\tilde{O}\left(a\cdot \alpha \log \left(1/\epsilon \right)\right)$ gates, and ${\rm{poly}}\left(\alpha ,\log (1/\epsilon )\right)$ classical time.

Apart from the block-encoding formalism, let us introduce other useful results. Quantum amplitude estimation allows one to estimate the amplitude of a specific component of a quantum state, stated as follows.

Lemma 33

(Quantum amplitude estimation [ref. ⁸⁸, Theorem 12]). Suppose that unitary operator U is given by

$$U| 0\left.\right\rangle | 0\left.\right\rangle =\sqrt{p}| 0\left.\right\rangle | {\phi }_{0}\left.\right\rangle +\sqrt{1-p}| 1\left.\right\rangle | {\phi }_{1}\left.\right\rangle ,$$

(80)

where $| {\phi }_{0}\left.\right\rangle$ and $| {\phi }_{1}\left.\right\rangle$ are normalised pure quantum states, and $p\in \left[0,1\right]$. Then, we can obtain an estimate $\widetilde{p}$ of p such that

$$\left\vert \widetilde{p}-p\right\vert \le \frac{2\pi \sqrt{p(1-p)}}{M}+\frac{{\pi }^{2}}{{M}^{2}}$$

(81)

with probability ≥8/π² using $O\left(M\right)$ queries to U. In particular, if we take $M=\Theta \left(1/\delta \right)$, then $\widetilde{p}$ is a δ-estimate of p with high probability.

Finally, the following two lemmas give relevant bounds on the condition number of matrices, which will be useful in the complexity analysis of our algorithms.

Lemma 34

Let A, B > 0 be two positive definite matrices such that $\left\Vert A\right\Vert =\left\Vert B\right\Vert =1$. Then ${\kappa }_{A+B}^{-1}\ge {\kappa }_{A}^{-1}+{\kappa }_{B}^{-1}$.

Lemma 35

Let A > 0 be a positive definite matrix, and let B be a matrix of full rank, such that $\left\Vert A\right\Vert =\left\Vert B\right\Vert =1$. Then ${\kappa }_{{B}^{\dagger }AB}\le {\kappa }_{A}{\kappa }_{{B}^{\dagger }B}$.

Proof

First note that B^†B > 0 and B^†CB > 0 for every C > 0. Since A ≥ I/κ_A, it follows that

$${B}^{\dagger }AB\ge {\kappa }_{A}^{-1}{B}^{\dagger }IB\ge {\kappa }_{A}^{-1}{\kappa }_{{B}^{\dagger }B}^{-1}I.$$

(82)

It immediately follows that ${\kappa }_{{B}^{\dagger }AB}^{-1}\ge {\kappa }_{A}^{-1}{\kappa }_{{B}^{\dagger }B}^{-1}$. □

Proof of Lemma 7

In this appendix, we prove Lemma 7. Let us first prove the following lemma, which shows that we can implement a block-encoding of the matrix ${\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}$.

Lemma 36

Suppose that U_A, U_C are (1, a, 0)-block-encodings of matrices A, C, respectively, such that A ≥ I/κ_A and C ≥ I/κ_C. For ϵ ∈ (0, 1/2), one can implement a (2, 3a + 7, ϵ)-block-encoding of ${\kappa }_{A}^{-1/p}{\gamma }_{p}^{-1}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}$ for any fixed real p ≠ 0, where

$${\gamma }_{p}=\left\{\begin{array}{ll}1\quad\quad\quad\quad\quad \,p \,>\, 0,\\ {\kappa }_{A}^{-1/p}{\kappa }_{C}^{-1/p}\quad \,p \,<\, 0,\end{array}\right.$$

(83)

using

• $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_C, $\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_A;

• $\tilde{O}\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ gates; and

• ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/{\epsilon }_{2}\right)\right)$ classical time.

Proof

We first consider the case p > 0. Let us construct ${U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$, a block-encoding of ${\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}$, step by step as follows. Along the way, we also analyse the resources for each step. In the remainder of the paper, we use the notation ${\tilde{O}}_{{a}_{1},\ldots ,{a}_{n}}(f)$ to denote $O(f{\rm{polylog}}({b}_{1},\ldots ,{b}_{n}))$, where a_i, b_i are parameters, f is a function, and ${b}_{i}={a}_{i}+{a}_{i}^{-1}$. Similarly, we use ${\widetilde{\Omega }}_{{a}_{1},\ldots ,{a}_{n}}(f)$ to denote $\Omega (f/{\rm{polylog}}({b}_{1},\ldots ,{b}_{n}))$. In context without ambiguity, we just omit the subscripts as usual.

• 1. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1/2}/4}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={\kappa }_{A}^{-1}$, and ϵ = ϵ₁ in Lemma 27, we have a polynomial q₁(x) of degree ${d}_{1}=O\left({\kappa }_{A}\log (1/{\epsilon }_{1})\right)$ that approximates ${({\kappa }_{A}x)}^{-1/2}/2$.

    • (b) Taking U = U_A, q = q₁(x), ϵ = 0, and δ = ϵ₁ in Lemma 26, we have ${U}_{{\left({\kappa }_{A}A\right)}^{-1/2}/4}$, a (1, a + 2, ϵ₁)-block-encoding of q₁(A)/2, which is therefore a (1, a + 2, 2ϵ₁)-block-encoding of ${\left({\kappa }_{A}A\right)}^{-1/2}/4$.

  • Resources: O(d₁) queries to U_A, O(ad₁) quantum gates, and ${\rm{poly}}({d}_{1},\log (1/{\epsilon }_{1}))$ classical time.

• 2. ${U}_{C},{U}_{{({\kappa }_{A}A)}^{-1/2}/4}\to {U}_{{2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}}$:

  • Construction: by Lemma 24, given U_C and ${U}_{{({\kappa }_{A}A)}^{-1/2}/4}$, we have ${U}_{{2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}}$, a (1, 3a + 4, 4ϵ₁)-block-encoding of ${2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}$.

  • Resources: O(1) queries to U_C and ${U}_{{({\kappa }_{A}A)}^{-1/2}/4}$.

• 3. ${U}_{{2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}}\to {U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$:

  • Construction:

    • (a) Taking c = 1/p, $\delta ={2}^{-4}{\kappa }_{A}^{-1}{\kappa }_{C}^{-1}\le {2}^{-4}{\kappa }_{A}^{-1}{\kappa }_{{A}^{-1/2}C{A}^{-1/2}}^{-1}$ (by Lemma 35 and noting ${\kappa }_{{A}^{-1}}\le 1$), and ϵ = ϵ₂ in Lemma 28, we have a polynomial q₂(x) of degree ${d}_{2}=O\left({\kappa }_{A}{\kappa }_{C}\log (1/{\epsilon }_{2})\right)$ that approximates x^1/p/2.

    • (b) Taking $U={U}_{{2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}}$, q = q₂(x), ϵ = Θ(ϵ₁), and δ = ϵ₂ in Lemma 26, we have ${U}_{{2}^{2-4/p}{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$, a $(1,3a+6,\Theta ({d}_{2}{\epsilon }_{1}^{1/2})+{\epsilon }_{2})$-block-encoding of ${q}_{2}\left({2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}\right)/2$, which is therefore a $(1,3a+10,\Theta ({d}_{2}{\epsilon }_{1}^{1/2}+{\epsilon }_{2}))$-block-encoding of ${\left({2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}/4$.

    • (c) Taking $U={U}_{{2}^{2-4/p}{\kappa }_{A}^{-1/p}{({A}^{-1/2}C{A}^{-1/2})}^{1/p}}$, α = 2^2−4/p in Lemma 32, we obtain ${U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$, a $(2,3a+7,\tilde{\Theta }({d}_{2}^{1/2}{\epsilon }_{1}^{1/4}+{\epsilon }_{2}^{1/2}))$-block-encoding of ${\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}$, where we use $\sqrt{x+y}\le \sqrt{x}+\sqrt{y}$.

  • Resources: $\tilde{O}\left({d}_{2}\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1})\right)$ queries to ${U}_{{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}}$, $\tilde{O}\left(a{d}_{2}\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1})\right)$ gates, and ${\rm{poly}}\left({d}_{2},\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1})\right)$ classical time.

To bound the final approximation error $\tilde{\Theta }({d}_{2}^{1/2}{\epsilon }_{1}^{1/4}+{\epsilon }_{2}^{1/2})$ in $\scriptstyle{U}_{{\kappa }_{A}^{-1/p}{({A}^{-1/2}C{A}^{-1/2})}^{1/p}}$ by ϵ, it is sufficient to take

• ${\epsilon }_{2}=\tilde{\Theta }({\epsilon }^{2})$; and

• ${\epsilon }_{1}=\tilde{\Theta }\left({\epsilon }^{4}{d}_{2}^{-2}\right)=\tilde{\Theta }\left({\kappa }_{A}^{-2}{\kappa }_{C}^{-2}{\epsilon }^{4}{\log }^{-2}\left(1/{\epsilon }_{2}\right)\right)=\tilde{\Theta }\left({\kappa }_{A}^{-2}{\kappa }_{C}^{-2}{\epsilon }^{4}\right)$.

The number of ancilla qubits for constructing ${U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$ is 3a + 7.

Finally, let us calculate the complexities of each step.

• 1. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1/2}/4}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 2. ${U}_{C},{U}_{{({\kappa }_{A}A)}^{-1/2}/4}\to {U}_{{2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}}$: O(1) queries to U_C, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 3. ${U}_{{2}^{-4}{\kappa }_{A}^{-1}{A}^{-1/2}C{A}^{-1/2}}\to {U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_C, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

For the case p < 0, the analysis is the same except that in Step 3a, we can use Lemma 27 instead of Lemma 28. This only incurs an additional scaling factor ${\kappa }_{A}^{1/p}{\kappa }_{C}^{1/p}$ into the final block-encoded matrix, without significantly changing the complexity. □

Now we are ready to prove Lemma 7, which gives an implementation of a block-encoding of the weighted matrix geometric mean in Eq. (2).

Proof of Lemma 7

We first consider the case p > 0. Let us construct ${U}_{{\kappa }_{A}^{-1/p}Y}$, a (2, 5a + 12, ϵ)-block-encoding of ${\kappa }_{A}^{-1/p}Y$, step by step as follows, where

$$Y=A{\#}_{1/p}C={A}^{1/2}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}{A}^{1/2}.$$

(84)

Along the way, we also analyse the resources for each step.

• 1. ${U}_{A}\to {U}_{{A}^{1/2}/4}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={\kappa }_{A}^{-1}$, and ϵ = ϵ₁ in Lemma 28, we have a polynomial q₁(x) of degree ${d}_{1}=O\left({\kappa }_{A}\log (1/{\epsilon }_{1})\right)$ that approximates x^1/2/2.

    • (b) Taking U = U_A, q = q₁(x), ϵ = 0, and δ = ϵ₁ in Lemma 26, we have ${U}_{{A}^{1/2}/4}$, a (1, a + 2, ϵ₁)-block-encoding of q₁(A)/2, which is therefore a (1, a + 2, 2ϵ₁)-block-encoding of A^1/2/4.

  • Resources: O(d₁) queries to U_A, O(ad₁) quantum gates, and ${\rm{poly}}({d}_{1},\log (1/{\epsilon }_{1}))$ classical time.

• 2. ${U}_{A},{U}_{C}\to {U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$:

  • Construction:

    Taking ϵ = ϵ₂ in Lemma 36, we can construct ${U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$, a (2, 3a + 7, ϵ₂)-block-encoding of ${U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$.

  • Resources:

    According to Lemma 36, the resources for the above construction are:

    • $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/{\epsilon }_{2}\right)\right)$ queries to U_C, $\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/{\epsilon }_{2}\right)\right)$ queries to U_A;

    • $\tilde{O}\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/{\epsilon }_{2}\right)\right)$ gates; and

    • ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/{\epsilon }_{2}\right)\right)$ classical time.

• 3. ${U}_{{A}^{1/2}/4},{U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}\to {U}_{{\kappa }_{A}^{-1/p}Y}$:

  • Construction:

    • (a) By Lemma 24, given ${U}_{{A}^{1/2}/4}$ and ${U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$, we have ${U}_{{2}^{-5}{\kappa }_{A}^{-1/p}Y}$, a (1, 5a + 11, Θ(ϵ₁ + ϵ₂))-block-encoding of ${2}^{-5}{\kappa }_{A}^{-1/p}Y$.

    • (b) Taking ${U}_{{2}^{-5}{\kappa }_{A}^{-1/p}Y}$, α = 2⁵ in Lemma 32, we obtain ${U}_{{\kappa }_{A}^{-1/p}Y}$, a $\scriptstyle(2,5a+12,\tilde{\Theta }({\epsilon }_{1}^{1/2}+{\epsilon }_{2}^{1/2}))$-block-encoding of ${\kappa }_{A}^{-1/p}Y$.

  • Resources: $\tilde{O}\left(\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1})\right)$ queries to ${U}_{{A}^{1/2}/4}$ and ${U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$, $\tilde{O}\left(a\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1})\right)$ gates, and ${\rm{poly}}(\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1}))$ classical time.

To bound the final approximation error $\tilde{\Theta }({\epsilon }_{1}^{1/2}+{\epsilon }_{2}^{1/2})$ in ${U}_{{\kappa }_{A}^{-1/p}Y}$ by ϵ, it is sufficient to take ${\epsilon }_{1}=\tilde{\Theta }\left({\epsilon }^{2}\right)$ and ${\epsilon }_{2}=\tilde{\Theta }\left({\epsilon }^{2}\right)$. The number of ancilla qubits for constructing ${\kappa }_{A}^{-1/p}Y$ is 5a + 11. Finally, let us calculate the complexities of each step.

• 1. ${U}_{A}\to {U}_{{A}^{1/2}/4}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 2. ${U}_{A},{U}_{C}\to {U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}$: $\tilde{O}({\kappa }_{A}{\kappa }_{C}{\log }^{2}(1/\epsilon))$ queries to U_C, $\tilde{O}({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}(1/\epsilon))$ queries to U_A, $\tilde{O}(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}(1/\epsilon))$ gates, and ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/{\epsilon }_{2}\right)\right)$ classical time.

• 3. ${U}_{{A}^{1/2}/4},{U}_{{\kappa }_{A}^{-1/p}{\left({A}^{-1/2}C{A}^{-1/2}\right)}^{1/p}}\to {U}_{{\kappa }_{A}^{-1/p}Y}$: $\tilde{O}({\kappa }_{A}{\kappa }_{C}{\log }^{3}(1/\epsilon))$ queries to U_C, $\tilde{O}({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{4}(1/\epsilon))$ queries to U_A, $\tilde{O}\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{4}\left(1/\epsilon \right)\right)$ gates, and ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/{\epsilon }_{2}\right)\right)$ classical time.

By Definition 6, $\scriptstyle{U}_{{\kappa }_{A}^{-1/p}Y}$ is also a $(2{\kappa }_{A}^{1/p},5a+12,{\kappa }_{A}^{1/p}\epsilon )$-block-encoding of Y. Replacing the precision parameter immediately yields the results for the case p > 0 in Lemma 7. For the case p < 0, the analysis is similar and is omitted. □

Proof of Lemma 8

In this appendix we prove Lemma 8.

Proof of Lemma 8

Let us construct $\scriptstyle{U}_{{\kappa }_{A}^{-1}Y}$, a (2, 5a + 11, ϵ)-block-encoding of ${\kappa }_{A}^{-1}Y$, step by step as follows, where

$$Y={A}^{-1}\#C={A}^{-1/2}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}{A}^{-1/2}.$$

(85)

Along the way, we also analyse the resources for each step.

• 1. ${U}_{A}\to {U}_{{A}^{1/2}/4}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={\kappa }_{A}^{-1}$, and ϵ = ϵ₁ in Lemma 28, we have a polynomial q₁(x) of degree ${d}_{1}=O\left({\kappa }_{A}\log (1/{\epsilon }_{1})\right)$ that approximates x^1/2/2.

    • (b) Taking U = U_A, q = q₁(x), ϵ = 0, and δ = ϵ₁ in Lemma 26, we have ${U}_{{A}^{1/2}/4}$, a (1, a + 2, ϵ₁)-block-encoding of q₁(A)/2, which is therefore a (1, a + 2, 2ϵ₁)-block-encoding of A^1/2/4.

  • Resources: O(d₁) queries to U_A, and O(ad₁) gates, and ${\rm{poly}}({d}_{1},\log (1/{\epsilon }_{1}))$ classical time.

• 2. ${U}_{C},{U}_{{A}^{1/2}/4}\to {U}_{{2}^{-4}{A}^{1/2}C{A}^{1/2}}$:

  • Construction: by Lemma 24, given U_C and ${U}_{{A}^{1/2}/4}$, we have $\scriptstyle{U}_{{2}^{-4}{A}^{1/2}C{A}^{1/2}}$, a (1, 3a + 4, 4ϵ₁)-block-encoding of 2⁻⁴A^1/2CA^1/2.

  • Resources: O(1) queries to U_C and ${U}_{{A}^{1/2}}$.

• 3. ${U}_{{2}^{-4}{A}^{1/2}C{A}^{1/2}}\to {U}_{{2}^{-4}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={2}^{-4}{\kappa }_{A}^{-1}{\kappa }_{C}^{-1}\le {2}^{-4}{\kappa }_{{A}^{1/2}C{A}^{1/2}}^{-1}$ (by Lemma 35), and ϵ = ϵ₂ in Lemma 28, we have a polynomial q₂(x) of degree ${d}_{2}=O\left({\kappa }_{A}{\kappa }_{C}\log (1/{\epsilon }_{2})\right)$ that approximates x^1/2/2.

    • (b) Taking $U={U}_{{2}^{-4}{A}^{1/2}C{A}^{1/2}}$, q = q₂(x), ϵ = Θ(ϵ₁), and δ = ϵ₂ in Lemma 26, we have ${U}_{{2}^{-4}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}}$, a $(1,3a+6,\Theta ({d}_{2}{\epsilon }_{1}^{1/2})+{\epsilon }_{2})$-block-encoding of ${q}_{2}\left({2}^{-4}{A}^{1/2}C{A}^{1/2}\right)/2$, which is therefore a $(1,3a+6,\Theta ({d}_{2}{\epsilon }_{1}^{1/2}+{\epsilon }_{2}))$-block-encoding of ${\left({2}^{-4}{A}^{1/2}C{A}^{1/2}\right)}^{1/2}/4$.

  • Resources: O(d₂) queries to ${U}_{{2}^{-4}{A}^{1/2}C{A}^{1/2}}$, and O(ad₂) gates, and ${\rm{poly}}({d}_{2},\log (1/{\epsilon }_{2}))$ classical time.

• 4. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1/2}/4}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={\kappa }_{A}^{-1}$, and ϵ = ϵ₃ in Lemma 27, we have a polynomial q₃(x) of degree ${d}_{3}=O\left({\kappa }_{A}\log (1/{\epsilon }_{3})\right)$ that approximates ${({\kappa }_{A}x)}^{-1/2}/2$.

    • (b) Taking U = U_A, q = q₃(x), ϵ = 0, and δ = ϵ₃ in Lemma 26, we have ${U}_{{\left({\kappa }_{A}A\right)}^{-1/2}/4}$, a (1, a + 2, ϵ₃)-block-encoding of q₃(A)/2, which is therefore a (1, a + 2, 2ϵ₃)-block-encoding of ${\left({\kappa }_{A}A\right)}^{-1/2}/4$.

  • Resources: O(d₃) queries to U_A, and O(ad₃) gates, and ${\rm{poly}}({d}_{3},\log (1/{\epsilon }_{3}))$ classical time.

• 5. ${U}_{{({\kappa }_{A}A)}^{-1/2}/4},{U}_{{2}^{-4}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}}\to {U}_{{\kappa }_{A}^{-1}Y}$:

  • Construction:

    • (a) By Lemma 24, given ${U}_{{({\kappa }_{A}A)}^{-1/2}/4}$ and ${U}_{{2}^{-4}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}}$, we have ${U}_{{2}^{-8}{\kappa }_{A}^{-1}Y}$, a $(1,5a+10,\Theta ({d}_{2}{\epsilon }_{1}^{1/2}+{\epsilon }_{2}+{\epsilon }_{3}))$-block-encoding of ${2}^{-8}{\kappa }_{A}^{-1}Y$.

    • (b) Taking ${U}_{{2}^{-8}{\kappa }_{A}^{-1}Y}$, α = 2⁸ in Lemma 32, we obtain ${U}_{{\kappa }_{A}^{-1}Y}$, a $(2,5a+11,\tilde{\Theta }({d}_{2}^{1/2}{\epsilon }_{1}^{1/4}+{\epsilon }_{2}^{1/2}+{\epsilon }_{3}^{1/2}))$-block-encoding of ${\kappa }_{A}^{-1/p}Y$.

    Resources: $\tilde{O}\left(\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1}{\epsilon }_{3}^{-1})\right)$ queries to ${U}_{{({\kappa }_{A}A)}^{-1/2}/4}$ and ${U}_{{2}^{-4}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}}$, $\tilde{O}\left(a\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1}{\epsilon }_{3}^{-1})\right)$ gates, and ${\rm{poly}}(\log ({\epsilon }_{1}^{-1}{\epsilon }_{2}^{-1}{\epsilon }_{3}^{-1}))$ classical time.

To bound the final approximation error $\scriptstyle\tilde{\Theta }({d}_{2}^{1/2}{\epsilon }_{1}^{1/4}+{\epsilon }_{2}^{1/2}+{\epsilon }_{3}^{1/2})$ in ${U}_{{\kappa }_{A}^{-1}Y}$ by ϵ, it is sufficient to take

• ${\epsilon }_{3}=\tilde{\Theta }({\epsilon }^{2})$.

• ${\epsilon }_{2}=\tilde{\Theta }({\epsilon }^{2})$.

• ${\epsilon }_{1}=\tilde{\Theta }({\epsilon }^{4}{d}_{2}^{-2})=\tilde{\Theta }\left({\kappa }_{A}^{-2}{\kappa }_{C}^{-2}{\epsilon }^{4}{\log }^{-2}\left(1/{\epsilon }_{2}\right)\right)=\tilde{\Theta }\left({\kappa }_{A}^{-2}{\kappa }_{C}^{-2}{\epsilon }^{4}\right)$.

The number of ancilla qubits for constructing ${U}_{{\kappa }_{A}^{-1}Y}$ is 5a + 11.

Finally, let us calculate the complexities of each step.

• 1. ${U}_{A}\to {U}_{{A}^{1/2}/4}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 2. ${U}_{C},{U}_{{A}^{1/2}/4}\to {U}_{{2}^{-4}{A}^{1/2}C{A}^{1/2}}$: O(1) queries to U_C, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }({\kappa }_{A}\log(1/\epsilon))$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 3. ${U}_{{2}^{-4}{A}^{1/2}C{A}^{1/2}}\to {U}_{{2}^{-4}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }({\kappa }_{A}{\kappa }_{C}\log(1/\epsilon))$ queries to U_C, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{2}(1/\epsilon))$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

• 4. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1/2}/4}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${\rm{poly}}\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 5. ${U}_{{({\kappa }_{A}A)}^{-1/2}/4},{U}_{{2}^{-4}{\left({A}^{1/2}C{A}^{1/2}\right)}^{1/2}}\to {U}_{{\kappa }_{A}^{-1}Y}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_C, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

By Definition 6, ${U}_{{\kappa }_{A}^{-1}Y}$ is also a (2κ_A, 5a + 11, κ_Aϵ)-block-encoding of Y. Replacing the precision parameter immediately yields the results in Lemma 8. □

Proof of Lemma 9

In this appendix, we prove Lemma 9.

Proof of Lemma 9

Let D = B^†A⁻¹B + C and E = A^1/2DA^1/2. As B^†A⁻¹B ≥ 0, we have

$${\kappa }_{D}^{-1}\ge {\kappa }_{C}^{-1}$$

(86)

by Lemma 34.

Similar to the proof of Lemma 8 in Appendix IV D, let us construct ${U}_{{\kappa }_{A}^{-3/2}Y}$, a (2, b, ϵ)-block-encoding of ${\kappa }_{A}^{-3/2}Y$, step by step as follows, where $b=O\left(a+\log \left({\kappa }_{A}{\kappa }_{C}/\epsilon \right)\right)$ and

$$Y={A}^{-1}\#D+{A}^{-1}B={A}^{-1/2}{E}^{1/2}{A}^{-1/2}+{A}^{-1}B.$$

(87)

Along the way, we also analyse the resources for each step.

• 1. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1}/4}$:

  • Construction:

    • (a) Taking c = 1, $\delta ={\kappa }_{A}^{-1}$, and ϵ = ϵ₁ in Lemma 27, we have a polynomial q₁(x) of degree ${d}_{1}=O\left({\kappa }_{A}\log (1/{\epsilon }_{1})\right)$ that approximates ${({\kappa }_{A}x)}^{-1}/2$.

    • (b) Taking U = U_A, q = q₁(x), ϵ = 0, and δ = ϵ₁ in Lemma 26, we have ${U}_{{\left({\kappa }_{A}A\right)}^{-1}/4}$, a (1, a + 2, ϵ₁)-block-encoding of q₁(A)/2, which is therefore a (1, a + 2, 2ϵ₁)-block-encoding of ${\left({\kappa }_{A}A\right)}^{-1}/4$.

  • Resources: O(d₁) queries to U_A, and O(ad₁) gates, and ${\rm{poly}}({d}_{1},\log (1/{\epsilon }_{1}))$ classical time.

• 2. ${U}_{B},{U}_{{\left({\kappa }_{A}A\right)}^{-1}/4}\to {U}_{{2}^{-2}{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B}$:

  • Construction: Note that given U_B, one can construct ${U}_{{B}^{\dagger }}={U}_{B}^{\dagger }$, a (1, a, 0)-block-encoding of B^†, using 1 query to U_B. By Lemma 24, given U_B and ${U}_{{\left({\kappa }_{A}A\right)}^{-1}/4}$, we have ${U}_{{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B}$, a (1, 3a + 2, 2ϵ₁)-block-encoding of ${2}^{-2}{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B$.

  • Resources: O(1) queries to U_B and ${U}_{{\left({\kappa }_{A}A\right)}^{-1}/4}$.

• 3. ${U}_{C},{U}_{{2}^{-2}{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B}\to {U}_{{2}^{-3}{\kappa }_{A}^{-1}D}$:

  • Construction: Taking m = 2, ${\boldsymbol{x}}=(1,{2}^{-2}{\kappa }_{A}^{-1})$, β = 2, ${U}_{1}={U}_{{2}^{-2}{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B}$, U₂ = U_C and ϵ = Θ(ϵ₁) in Lemma 25, we obtain ${U}_{{2}^{-3}{\kappa }_{A}^{-1}D}$, a $\left(1,3a+2+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right),\Theta ({\epsilon }_{1})\right)$-block-encoding of ${2}^{-3}{\kappa }_{A}^{-1}D$, for some constant η₁.

  • Resources: O(1) queries to U_C and ${U}_{{2}^{-2}{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B}$, and ${\rm{polylog}}\left(1/{\epsilon }_{1}\right)$ gates.

• 4. ${U}_{A}\to {U}_{{A}^{1/2}/4}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={\kappa }_{A}^{-1}$, and ϵ = ϵ₂ in Lemma 28, we have a polynomial q₂(x) of degree ${d}_{2}=O\left({\kappa }_{A}\log (1/{\epsilon }_{2})\right)$ that approximates x^1/2/2.

    • (b) Taking U = U_A, q = q₂(x), ϵ = 0, and δ = ϵ₂ in Lemma 26, we have ${U}_{{A}^{1/2}/4}$, a (1, a + 2, ϵ₂)-block-encoding of q₂(A)/2, which is therefore a (1, a + 2, 2ϵ₂)-block-encoding of A^1/2/4.

  • Resources: O(d₂) queries to U_A, and O(ad₂) gates, and ${\rm{poly}}({d}_{2},\log (1/{\epsilon }_{2}))$ classical time.

• 5. ${U}_{{2}^{-3}{\kappa }_{A}^{-1}D},{U}_{{A}^{1/2}/4}\to {U}_{{2}^{-7}{\kappa }_{A}^{-1}E}$:

  • Construction: By Lemma 24, given ${U}_{{2}^{-3}{\kappa }_{A}^{-1}D}$ and ${U}_{{A}^{1/2}/4}$, we have ${U}_{{2}^{-7}{\kappa }_{A}^{-1}E}$, a $(1,5a+6+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right),\Theta ({\epsilon }_{1}+{\epsilon }_{2}))$-block-encoding of ${2}^{-7}{\kappa }_{A}^{-1}E$.

  • Resources: O(1) queries to ${U}_{{2}^{-3}{\kappa }_{A}^{-1}D}$ and ${U}_{{A}^{1/2}/4}$.

• 6. ${U}_{{2}^{-7}{\kappa }_{A}^{-1}E}\to {U}_{{2}^{-5.5}{\kappa }_{A}^{-1/2}{E}^{1/2}}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={2}^{-7}{\kappa }_{A}^{-2}{\kappa }_{C}^{-1}\le {2}^{-7}{\kappa }_{A}^{-2}{\kappa }_{D}^{-1}\le {2}^{-7}{\kappa }_{A}^{-1}{\kappa }_{E}^{-1}$ (by Lemma (86) and Lemma 35), and ϵ = ϵ₃ in Lemma 28, we have a polynomial q₃(x) of degree ${d}_{3}=O\left({\kappa }_{A}{\kappa }_{C}\log (1/{\epsilon }_{3})\right)$ that approximates x^1/2/2.

    • (b) Taking $U={U}_{{2}^{-7}{\kappa }_{A}^{-1}E}$, q = q₃(x), ϵ = Θ(ϵ₁ + ϵ₂), and δ = ϵ₃ in Lemma 26, we have ${U}_{{2}^{-2.5}{\kappa }_{A}^{-1/2}{E}^{1/2}}$, a $(1,5a+8+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right),\Theta ({d}_{3}{\epsilon }_{1}^{1/2}+{d}_{3}{\epsilon }_{2}^{1/2})+{\epsilon }_{3})$-block-encoding of ${q}_{3}\left({2}^{-7}{\kappa }_{A}^{-1}E\right)/2$, which is therefore a $(1,5a+8+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right),\Theta ({d}_{3}{\epsilon }_{1}^{1/2}+{d}_{3}{\epsilon }_{2}^{1/2}+{\epsilon }_{3}))$-block-encoding of ${2}^{-5.5}{\kappa }_{A}^{-1/2}{E}^{1/2}$.

  • Resources: O(d₃) queries to ${U}_{{2}^{-7}{\kappa }_{A}^{-1}E}$, and $O\left(\left(a+\log \left(1/{\epsilon }_{1}\right)\right){d}_{3}\right)$ gates, and ${\rm{poly}}({d}_{3},\log (1/{\epsilon }_{3}))$ classical time.

• 7. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1/2}/4}$:

  • Construction:

    • (a) Taking c = 1/2, $\delta ={\kappa }_{A}^{-1}$, and ϵ = ϵ₄ in Lemma 27, we have a polynomial q₄(x) of degree ${d}_{4}=O\left({\kappa }_{A}\log (1/{\epsilon }_{4})\right)$ that approximates ${({\kappa }_{A}x)}^{-1/2}/2$.

    • (b) Taking U = U_A, q = q₄(x), ϵ = 0, and δ = ϵ₄ in Lemma 26, we have ${U}_{{({\kappa }_{A}A)}^{-1/2}/4}$, a (1, a + 2, ϵ₄)-block-encoding of q₄(A)/2, which is therefore a (1, a + 2, 2ϵ₄)-block-encoding of ${\left({\kappa }_{A}A\right)}^{-1/2}/4$.

  • Resources: O(d₄) queries to U_A, and O(ad₄) gates, and ${\rm{poly}}({d}_{4},\log (1/{\epsilon }_{4}))$ classical time.

• 8. ${U}_{{({\kappa }_{A}A)}^{-1/2}/4},{U}_{{2}^{-5.5}{\kappa }_{A}^{-1/2}{E}^{1/2}}\to {U}_{{2}^{-9.5}{\kappa }_{A}^{-3/2}{A}^{-1}\#D}$:

  • Construction: By Lemma 24, given ${U}_{{({\kappa }_{A}A)}^{-1/2}/4}$ and ${U}_{{2}^{-5.5}{\kappa }_{A}^{-1/2}{E}^{1/2}}$, we have ${U}_{{\kappa }_{A}^{-3/2}{A}^{-1}\#D}$, a $\scriptstyle(1,7a+12+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right),\Theta ({d}_{3}{\epsilon }_{1}^{1/2}+{d}_{3}{\epsilon }_{2}^{1/2}+{\epsilon }_{3}+{\epsilon }_{4}))$-block-encoding of ${2}^{-9.5}{\kappa }_{A}^{-3/2}{A}^{-1}\#D$.

  • Resources: O(1) queries to ${U}_{{({\kappa }_{A}A)}^{-1/2}/4}$ and ${U}_{{2}^{-5.5}{\kappa }_{A}^{-1/2}{E}^{1/2}}$.

• 9. ${U}_{{({\kappa }_{A}A)}^{-1}/4},{U}_{B}\to {U}_{{2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B}$:

  • Construction: By Lemma 24, given ${U}_{{({\kappa }_{A}A)}^{-1}/4}$ and U_B, we have ${U}_{{2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B}$, a (1, 2a + 2, 2ϵ₁)-block-encoding of ${2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B$.

  • Resources: O(1) queries to ${U}_{{({\kappa }_{A}A)}^{-1}/4}$ and U_B.

• 10. ${U}_{{2}^{-9.5}{\kappa }_{A}^{-3/2}{A}^{-1}\#D},{U}_{{2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B}\to {U}_{{\kappa }_{A}^{-3/2}Y}$:

  • Construction:

    • (a) Taking m = 2, ${\boldsymbol{x}}=(1,{2}^{-7.5}{\kappa }_{A}^{-1/2})$, β = 2, ${U}_{1}={U}_{{2}^{-9.5}{\kappa }_{A}^{-3/2}{A}^{-1}\#D}$, ${U}_{2}={U}_{{2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B}$ and $\epsilon ={\epsilon }_{5}=\Theta ({d}_{3}{\epsilon }_{1}^{1/2}+{d}_{3}{\epsilon }_{2}^{1/2}+{\epsilon }_{3}+{\epsilon }_{4})$ in Lemma 25, we obtain ${U}_{{2}^{-10.5}{\kappa }_{A}^{-3/2}Y}$, a $\left(1,7a+12+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right)+{\eta }_{2}\log \left(1/{\epsilon }_{5}\right),{\epsilon }_{5}\right)$-block-encoding of ${2}^{-10.5}{\kappa }_{A}^{-3/2}Y$, for some constant η₂.

    • (b) Taking $U={U}_{{2}^{-10.5}{\kappa }_{A}^{-3/2}Y}$ and α = 2^10.5 in Lemma 32, we obtain ${U}_{{\kappa }_{A}^{-3/2}Y}$, a $\left(2,7a+13+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right)+{\eta }_{2}\log \left(1/{\epsilon }_{5}\right),\tilde{\Theta }({\epsilon }_{5}^{1/2})\right)$-block-encoding of ${\kappa }_{A}^{-3/2}Y$.

  • Resources: $\tilde{O}\left(\log \left({\epsilon }_{5}^{-1}\right)\right)$ queries to ${U}_{{2}^{-9.5}{\kappa }_{A}^{-3/2}{A}^{-1}\#D}$ and ${U}_{{2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B}$, $\tilde{O}\left(a{\log }^{2}\left({\epsilon }_{1}^{-1}{\epsilon }_{5}^{-1}\right)\right)$ gates and ${\rm{poly}}(\log ({\epsilon }_{5}^{-1}))$ classical time.

To bound the final approximation error $\tilde{\Theta }({\epsilon }_{5}^{1/2})$ in ${U}_{{\kappa }_{A}^{-3/2}Y}$ by ϵ, it is sufficient to take

• ${\epsilon }_{5}=\tilde{\Theta }({\epsilon }^{2})$.

• ${\epsilon }_{4}={\epsilon }_{3}=\tilde{\Theta }({\epsilon }^{2})$.

• ${\epsilon }_{2}={\epsilon }_{1}=\tilde{\Theta }({d}_{3}^{-2}{\epsilon }^{4})=\tilde{\Theta }\left({\kappa }_{A}^{-2}{\kappa }_{C}^{-2}{\epsilon }^{4}{\log }^{-2}\left(1/{\epsilon }_{3}\right)\right)=\tilde{\Theta }\left({\kappa }_{A}^{-2}{\kappa }_{C}^{-2}{\epsilon }^{4}\right)$.

The number of ancilla qubits for constructing ${U}_{{\kappa }_{A}^{-3/2}Y}$ is

$$7a+13+{\eta }_{1}\log \left(1/{\epsilon }_{1}\right)+{\eta }_{2}\log \left(1/{\epsilon }_{5}\right)=O\left(a+\log \left({\kappa }_{A}{\kappa }_{C}/\epsilon \right)\right).$$

(88)

Finally, let us calculate the complexities of each step.

• 1. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1}/4}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 2. ${U}_{B},{U}_{{\left({\kappa }_{A}A\right)}^{-1}/4}\to {U}_{{2}^{-2}{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B}$: O(1) queries to U_B, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 3. ${U}_{C},{U}_{{2}^{-2}{\kappa }_{A}^{-1}{B}^{\dagger }{A}^{-1}B}\to {U}_{{2}^{-3}{\kappa }_{A}^{-1}D}$: O(1) queries to U_C and U_B, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 4. ${U}_{A}\to {U}_{{A}^{1/2}/4}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 5. ${U}_{{2}^{-3}{\kappa }_{A}^{-1}D},{U}_{{A}^{1/2}/4}\to {U}_{{2}^{-7}{\kappa }_{A}^{-1}E}$: O(1) queries to U_C and U_B, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 6. ${U}_{{2}^{-7}{\kappa }_{A}^{-1}E}\to {U}_{{2}^{-5.5}{\kappa }_{A}^{-1/2}{E}^{1/2}}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}{\kappa }_{C}\log \left(1/\epsilon \right)\right)$ queries to U_C and U_B, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

• 7. ${U}_{A}\to {U}_{{({\kappa }_{A}A)}^{-1/2}/4}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${\rm{poly}}\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 8. ${U}_{{({\kappa }_{A}A)}^{-1/2}/4},{U}_{{2}^{-5.5}{\kappa }_{A}^{-1/2}{E}^{1/2}}\to {U}_{{2}^{-9.5}{\kappa }_{A}^{-3/2}{A}^{-1}\#D}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}{\kappa }_{C}\log \left(1/\epsilon \right)\right)$ queries to U_C and U_B, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

• 9. ${U}_{{({\kappa }_{A}A)}^{-1}/4},{U}_{B}\to {U}_{{2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B}$: O(1) queries to U_B, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}\log \left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}\log \left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},\log \left(1/\epsilon \right)\right)$ classical time.

• 10. ${U}_{{2}^{-9.5}{\kappa }_{A}^{-3/2}{A}^{-1}\#D},{U}_{{2}^{-2}{\kappa }_{A}^{-1}{A}^{-1}B}\to {U}_{{\kappa }_{A}^{-3/2}Y}$: ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\epsilon \right)\right)$ queries to U_C and U_B, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ queries to U_A, ${\tilde{O}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left(a{\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\epsilon \right)\right)$ gates, and ${{\rm{poly}}}_{{\kappa }_{A},{\kappa }_{C},\epsilon }\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\epsilon \right)\right)$ classical time.

By Definition 6, ${U}_{{\kappa }_{A}^{-3/2}Y}$ is also a $(2{\kappa }_{A}^{3/2},b,{\kappa }_{A}^{3/2}\epsilon )$-block-encoding of Y. Replacing the precision parameter immediately yields the results in Lemma 9. □

Proof of Lemma 11

In this appendix we prove Lemma 11.

Proof of Lemma 11

The proof is similar to that of Lemma 8. For p > 0, we can simply take c = 1/p instead in Step 3a, without significantly changing the complexity.

For p < 0, in Step 3a, we can use Lemma 27 instead of Lemma 28, and take c = − 1/p. This only incurs an additional scaling factor ${\kappa }_{A}^{1/p}{\kappa }_{C}^{1/p}$ into the final block-encoded matrix, without significantly changing the complexity. □

Proof of Lemma 12

Although in ref. ²⁴ the lemma was stated only for real, symmetric positive definite matrices (SPDs), each step in the proof is also applicable to positive definite Hermitian matrices as we show below.

To find the global minimum of L(Y), it is sufficient to find the solution to ∇ L(Y) = 0 when L(Y) is strictly convex and is also strictly geodesically convex on the manifold of positive definite Hermitian matrices. For the definition of distances on this manifold and the geometric interpretation for the matrix geometric mean, see the section “Matrix geometric means”.

The strict convexity of Y ↦ L(Y) can be proved for the two terms separately since strict convexity is preserved in a sum. The term ${\rm{Tr}}(YA)$ is clearly strictly convex since it is linear and A is positive definite. For strict convexity of the second term ${\rm{Tr}}({Y}^{-1}C)$, it follows directly from the fact that Y → Y⁻¹ is strictly operator convex and C is positive definite. As an alternative proof, we evoke the following relationship. It is known that a twice-differentiable function L: V → R on an open subset ${\mathcal{Y}}$ of a vector space ${\mathcal{Z}}$ is convex if and only if for all $Y\in {\mathcal{Y}}$ and $Z\in {\mathcal{Z}}$

$$\frac{{d}^{2}L(Y+tZ)}{d{t}^{2}}{| }_{t = 0} \,>\, 0.$$

(89)

Using the Woodbury matrix identity, we can rewrite

$$\begin{array}{ll}{(Y+tZ)}^{-1}\,={(Y(I+t{Y}^{-1}Z))}^{-1}={Y}^{-1}-t{Y}^{-1}{(I+tZ{Y}^{-1})}^{-1}Z{Y}^{-1}\\\qquad\qquad\quad\;={Y}^{-1}-t{Y}^{-1}Z{Y}^{-1}+{t}^{2}{Y}^{-1}Z{Y}^{-1}Z{Y}^{-1}+O({t}^{3}).\end{array}$$

(90)

Therefore the condition in Eq. (89) for ${\rm{Tr}}({Y}^{-1}C)$ is equivalent to showing that

$${\rm{Tr}}(DC) \,>\, 0,\,D={Y}^{-1}Z{Y}^{-1}Z{Y}^{-1}.$$

(91)

Y is positive definite Hermitian and let Z be Hermitian so D = D^†. We note that DC is similar to the matrix D^−1/2(DC)D^1/2 = D^1/2CD^1/2, so they have identical eigenvalues. Then it suffices to show that D^1/2CD^1/2 only has positive eigenvalues. Since D^1/2 is also Hermitian and C is positive definite Hermitian, then ${\rm{Tr}}({D}^{1/2}C{D}^{1/2})={\rm{Tr}}(CD) > 0$.

By strictly geodesically convex, it means that for all positive definite Hermitian matrices Y₁, Y₂, we have

$$\begin{array}{r}L({Y}_{1}{\#}_{t}{Y}_{2})\, <\, tL({Y}_{1})+(1-t)L({Y}_{2}),\,t\in [0,1].\end{array}$$

To show geodesic convexity, we also need the following two facts. From ref. ⁸⁹, there is the fundamental operator inequality for positive definite matrices for t ∈ [0, 1]

$${Y}_{1}{\#}_{t}{Y}_{2}\le (1-t){Y}_{1}+t{Y}_{2}.$$

(92)

For Y₁ ≠ Y₂ for t = 1/2, this is a strict inequality. From the definition, it can also be shown that²⁶

$${({Y}_{1}{\#}_{t}{Y}_{2})}^{-1}={Y}_{1}^{-1}{\#}_{t}{Y}_{2}^{-1}.$$

(93)

Since midpoint convexity (convexity at t = 1/2) and continuity imply convexity, we have

$$\begin{array}{lll}L({Y}_{1}{\#}_{1/2}{Y}_{2}) & = & {\rm{Tr}}(({Y}_{1}{\#}_{1/2}{Y}_{2})A)+{\rm{Tr}}({({Y}_{1}{\#}_{1/2}{Y}_{2})}^{-1}C)\\&& < \displaystyle\frac{1}{2}({\rm{Tr}}({Y}_{1}A)+{\rm{Tr}}({Y}_{2}A))+{\rm{Tr}}({({Y}_{1}{\#}_{1/2}{Y}_{2})}^{-1}C)\\ && =\displaystyle\frac{1}{2}({\rm{Tr}}({Y}_{1}A)+{\rm{Tr}}({Y}_{2}A))+{\rm{Tr}}(({Y}_{1}^{-1}{\#}_{1/2}{Y}_{2}^{-1})C)\\&& < \displaystyle\frac{1}{2}({\rm{Tr}}({Y}_{1}A)+{\rm{Tr}}({Y}_{2}A)+{\rm{Tr}}({Y}_{1}^{-1}C)+{\rm{Tr}}({Y}_{2}^{-1}C))\\ && = \displaystyle\frac{1}{2}(L({Y}_{2})+L({Y}_{1})).\end{array}$$

(94)

Thus we have strict geodesic convexity.

Proof of Theorems 18 and 19

Here we provide details of the proofs of Theorems 18 and 19.

Proof of Theorem 18

By Eq. (62), the definition of ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$, we have

$${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)={\rm{Tr}}\left(\rho {({\rho }^{-1/2}\sigma {\rho }^{-1/2})}^{1-\alpha }\right)={\rm{Tr}}\left(\sigma {({\sigma }^{-1/2}\rho {\sigma }^{-1/2})}^{\alpha }\right).$$

(95)

Suppose that ρ and σ are n-qubit mixed quantum states and ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ are $\left(n+a\right)$-qubit unitary operators. By Lemma 30, we can implement two unitary operators U_ρ and U_σ that are $\left(1,n+a,0\right)$-block-encodings of ρ and σ using $O\left(1\right)$ queries to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$, respectively. We consider two approaches via the first and second formulas in Eq. (95) separately. □

Via the first formula

By Lemma 36, we can implement a $\left(2,b,\delta \right)$-block-encoding W of ${\kappa }_{\rho }^{\alpha -1}{\gamma }_{\alpha }{\left({\rho }^{-1/2}\sigma {\rho }^{-1/2}\right)}^{1-\alpha }$ using $\tilde{O}({\kappa }_{\rho }^{2}{\kappa }_{\sigma }{\log }^{2}\left(1/\delta \right))$ queries to U_ρ and $\tilde{O}({\kappa }_{\rho }{\kappa }_{\sigma }\log \left(1/\delta \right))$ queries to U_σ, where b = 3a + 7, and

$${\gamma }_{\alpha }=\left\{\begin{array}{ll}1,\quad\quad\quad\quad \,\alpha \in \left(0,1\right),\\ {\kappa }_{\rho }^{1-\alpha }{\kappa }_{\sigma }^{1-\alpha },\quad \,\alpha \in (1,2].\end{array}\right.$$

(96)

By the Hadamard test (given in Lemma 31), there is a quantum circuit C that outputs 0 with probability $\frac{1}{2}\left(1+{\rm{Re}} \{ {\rm{Tr}}\left(\rho {\left\langle \right.0| }_{b}W{| 0\left.\right\rangle }_{b}\right) \} \right)$, using one query to W and one sample of ρ. By noting that

$$\left\vert 2{\kappa }_{\rho }^{1-\alpha }{\gamma }_{\alpha }^{-1}{\rm{Re}} \{ {\rm{Tr}}\left(\rho {\left\langle \right.0| }_{b}W{| 0\left.\right\rangle }_{b}\right) \} -{\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)\right\vert \le \Theta \left({\kappa }_{\rho }^{1-\alpha }{\gamma }_{\alpha }^{-1}\delta \right),$$

(97)

we conclude that an $O({\kappa }_{\rho }^{\alpha -1}{\gamma }_{\alpha }\epsilon )$-estimate of ${\rm{Re}} {\rm{Tr}}(\rho {\left\langle \right.0| }_{b}{U}_{M}{| 0\left.\right\rangle }_{b})$ with $\delta =\Theta ({\kappa }_{\rho }^{\alpha -1}{\gamma }_{\alpha }\epsilon )$ suffices to obtain an ϵ-estimate of ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$. By quantum amplitude estimation (given in Lemma 33), this can be done using $O\left(1/\delta \right)=O({\kappa }_{\rho }^{1-\alpha }{\gamma }_{\alpha }^{-1}{\epsilon }^{-1})$ queries to C.

To conclude, an ϵ-estimate of ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ can be obtained by using

$$\tilde{O}\left({\kappa }_{\rho }^{2}{\kappa }_{\sigma }{\log }^{2}\left(1/\delta \right)\right)\cdot O\left({\kappa }_{\rho }^{1-\alpha }{\gamma }_{\alpha }^{-1}{\epsilon }^{-1}\right)=\left\{\begin{array}{ll}\tilde{O}\left({\kappa }_{\rho }^{3-\alpha }{\kappa }_{\sigma }/\epsilon \right),\quad &\alpha \in \left(0,1\right),\\ \tilde{O}\left({\kappa }_{\rho }^{2}{\kappa }_{\sigma }^{\alpha }/\epsilon \right),\quad &\alpha \in (1,2],\end{array}\right.$$

(98)

queries to ${{\mathcal{O}}}_{\rho }$ and

$$\tilde{O}\left({\kappa }_{\rho }{\kappa }_{\sigma }\log \left(1/\delta \right)\right)\cdot O\left({\kappa }_{\rho }^{1-\alpha }{\gamma }_{\alpha }^{-1}{\epsilon }^{-1}\right)=\left\{\begin{array}{ll}\tilde{O}\left({\kappa }_{\rho }^{2-\alpha }{\kappa }_{\sigma }/\epsilon \right),\quad &\alpha \in \left(0,1\right),\\ \tilde{O}\left({\kappa }_{\rho }{\kappa }_{\sigma }^{\alpha }/\epsilon \right),\quad &\alpha \in (1,2],\end{array}\right.$$

(99)

queries to ${{\mathcal{O}}}_{\sigma }$.

Via the second formula

By Lemma 36, we can implement a $\left(2,b,\delta \right)$-block-encoding W of ${\kappa }_{\sigma }^{-\alpha }{\left({\sigma }^{-1/2}\rho {\sigma }^{-1/2}\right)}^{\alpha }$ using $\tilde{O}\left({\kappa }_{\sigma }^{2}{\kappa }_{\rho }{\log }^{2}\left(1/\delta \right)\right)$ queries to U_σ and $\tilde{O}\left({\kappa }_{\rho }{\kappa }_{\sigma }\log \left(1/\delta \right)\right)$ queries to U_ρ, where b = 3a + 7. By the Hadamard test (given in Lemma 31), there is a quantum circuit C that outputs 0 with probability $\frac{1}{2}\left(1+{\rm{Re}} \{ {\rm{Tr}}\left(\rho {\left\langle \right.0| }_{b}W{| 0\left.\right\rangle }_{b}\right) \} \right)$, using one query to W and one sample of ρ. By noting that

$$\left\vert 2{\kappa }_{\sigma }^{\alpha }{\rm{Re}} {\rm{Tr}}\left(\rho {\left\langle \right.0| }_{b}W{| 0\left.\right\rangle }_{b}\right)-{\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)\right\vert \le \Theta \left({\kappa }_{\sigma }^{\alpha }\delta \right),$$

(100)

we conclude that an $O\left({\kappa }_{\sigma }^{-\alpha }\epsilon \right)$-estimate of ${\rm{Re}} {\rm{Tr}}\left(\rho {\left\langle \right.0| }_{b}{U}_{M}{| 0\left.\right\rangle }_{b}\right)$ with $\delta =\Theta \left({\kappa }_{\sigma }^{-\alpha }\epsilon \right)$ suffices to obtain an ϵ-estimate of ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$. By quantum amplitude estimation (given in Lemma 33), this can be done using $O\left(1/\delta \right)=O\left({\kappa }_{\sigma }^{\alpha }{\epsilon }^{-1}\right)$ queries to C.

To conclude, an ϵ-estimate of ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ can be obtained by using $\tilde{O}({\kappa }_{\sigma }^{2}{\kappa }_{\rho }{\log }^{2}\left(1/\delta \right))\cdot O\left(1/\delta \right)=\tilde{O}({\kappa }_{\sigma }^{2+\alpha }{\kappa }_{\rho }/\epsilon )$ queries to ${{\mathcal{O}}}_{\sigma }$ and $\tilde{O}({\kappa }_{\sigma }{\kappa }_{\rho }\log (1/\delta ))\cdot O(1/\delta )=\tilde{O}({\kappa }_{\sigma }^{1+\alpha }{\kappa }_{\rho }/\epsilon )$ queries to ${{\mathcal{O}}}_{\rho }$.

Conclusion

Combining the above cases (and their symmetrical cases), the query complexity is

• $\scriptstyle\tilde{O}\left({\kappa }_{\rho }{\kappa }_{\sigma }/\epsilon \cdot \min {\{{\kappa }_{\rho },{\kappa }_{\sigma }\}}^{\min \{1+\alpha ,2-\alpha \}}\right)$ for α ∈ (0, 1),

• $\tilde{O}\left({\kappa }_{\rho }{\kappa }_{\sigma }/\epsilon \cdot \min \{{\kappa }_{\rho }{\kappa }_{\sigma }^{\alpha -1},{\kappa }_{\rho }^{\alpha -1}{\kappa }_{\sigma },{\kappa }_{\rho }^{1+\alpha },{\kappa }_{\sigma }^{1+\alpha }\}\right)$ for $\alpha \in \left(1\right.,\left.2\right]$.

Proof of Theorem 19

Note that I/κ_σ ≤ ρ^−1/2σρ^−1/2 ≤ κ_ρI. Thus ${\kappa }_{\sigma }^{\alpha -1}I\le {({\rho }^{-1/2}\sigma {\rho }^{-1/2})}^{1-\alpha }\le {\kappa }_{\rho }^{1-\alpha }I$ for α ∈ (0, 1) and ${\kappa }_{\rho }^{1-\alpha }I\le {({\rho }^{-1/2}\sigma {\rho }^{-1/2})}^{1-\alpha }\le {\kappa }_{\sigma }^{\alpha -1}I$ for $\alpha \in \left(1,2\right]$. By Eq. (95), we have ${\kappa }_{\sigma }^{\alpha -1}\le {\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)\le {\kappa }_{\rho }^{1-\alpha }$ for α ∈ (0, 1) and ${\kappa }_{\rho }^{1-\alpha }\le {\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)\le {\kappa }_{\sigma }^{\alpha -1}$ for $\alpha \in \left(1,2\right]$.

For α ∈ (0, 1), to estimate ${\tilde{D}}_{\alpha }\left(\rho \parallel \sigma \right)$ within additive error ϵ, we can estimate ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ to relative error ϵ (i.e., within additive error ${\kappa }_{\sigma }^{\alpha -1}\epsilon$). By Theorem 18, this can be done by using using $\tilde{O}({\kappa }_{\rho }{\kappa }_{\sigma }^{2-\alpha }/\epsilon \cdot \min {\{{\kappa }_{\rho },{\kappa }_{\sigma }\}}^{\min \{1+\alpha ,2-\alpha \}})$ queries to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$.

For $\alpha \in \left(1,2\right]$, to estimate ${\tilde{D}}_{\alpha }\left(\rho \parallel \sigma \right)$ within additive error ϵ, we can estimate ${\widehat{F}}_{\alpha }\left(\rho ,\sigma \right)$ to relative error ϵ (i.e., within additive error ${\kappa }_{\rho }^{1-\alpha }\epsilon$). By Theorem 18, this can be done by using using $\tilde{O}({\kappa }_{\rho }^{\alpha }{\kappa }_{\sigma }/\epsilon \cdot \min \{{\kappa }_{\rho }{\kappa }_{\sigma }^{\alpha -1},{\kappa }_{\rho }^{\alpha -1}{\kappa }_{\sigma },{\kappa }_{\rho }^{1+\alpha },{\kappa }_{\sigma }^{1+\alpha }\})$ queries to ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$. □

Proof of Lemmas 17 and 20

To prove the lower bound, we need the quantum query lower bound for distinguishing probability distributions given in ref. ⁹⁰.

Lemma 37

([Ref. ⁹⁰ Theorem 4]). Let $p,q:\left\{1,2,\ldots,n\right\}\to\left[0,1\right]$ be two probability distributions on a sample space of size n. Let

$${U}_{p}| 0\left.\right\rangle =\mathop{\sum }\limits_{j=1}^{n}\sqrt{{p}_{j}}| j\left.\right\rangle | {\varphi }_{j}\left.\right\rangle ,$$

(101)

$${U}_{q}| 0\left.\right\rangle =\mathop{\sum }\limits_{j=1}^{n}\sqrt{{q}_{j}}| j\left.\right\rangle | {\psi }_{j}\left.\right\rangle ,$$

(102)

where ${\{| {\varphi }_{j}\left.\right\rangle\}}_{j = 1}^{n}$ and ${\{| {\psi }_{j}\left.\right\rangle\}}_{j = 1}^{n}$ are orthonormal bases. Then, given an unknown unitary operator U, any quantum query algorithm that determines whether U = U_p or U = U_q with probability at least 2/3, promised that one or the other holds, has query complexity $\Omega \left(1/{d}_{{\rm{H}}}\left(p,q\right)\right)$, where

$${d}_{{\rm{H}}}\left(p,q\right):=\sqrt{\frac{1}{2}\mathop{\sum }\limits_{j=1}^{n}{\left(\sqrt{{p}_{j}}-\sqrt{{q}_{j}}\right)}^{2}}$$

(103)

is the Hellinger distance.

Lemma 37 was also used to prove quantum query lower bounds in [ref. ⁹¹, Section 4.2], [ref. ⁹², Theorem 13], and [ref. ⁶⁴, Section V].

Proof of Lemma 17

Let ϵ ∈ (0, 1/4). Consider the discrimination of the two probability distributions $p,q:\left\{0,1\right\}\to \left[0,1\right]$ on a sample space of size two such that for each $j\in \left\{0,1\right\}$,

$${p}_{j}=\frac{1+{\left(-1\right)}^{j}\epsilon }{2},$$

(104)

$${q}_{j}=\frac{1+{\left(-1\right)}^{j}2\epsilon }{2}.$$

(105)

It can be verified that their Hellinger distance is upper bounded by

$${d}_{{\rm{H}}}\left(p,q\right)=\sqrt{1-\frac{\sqrt{\left(1+\epsilon \right)\left(1+2\epsilon \right)}+\sqrt{\left(1-\epsilon \right)\left(1-2\epsilon \right)}}{2}}\le \epsilon .$$

(106)

Suppose that two unitary operators U_p and U_q are given such that

$${U}_{p}| 0\left.\right\rangle =\sqrt{{p}_{0}}| 0\left.\right\rangle | {\varphi }_{0}\left.\right\rangle +\sqrt{{p}_{1}}| 1\left.\right\rangle | {\varphi }_{1}\left.\right\rangle ,$$

(107)

$${U}_{q}| 0\left.\right\rangle =\sqrt{{q}_{0}}| 0\left.\right\rangle | {\psi }_{0}\left.\right\rangle +\sqrt{{q}_{1}}| 1\left.\right\rangle | {\psi }_{1}\left.\right\rangle ,$$

(108)

where $\{| {\varphi }_{0}\rangle ,| {\varphi }_{1}\rangle \}$ and $\{| {\psi }_{0}\rangle ,| {\psi }_{1}\rangle \}$ are orthonormal bases.

Let ${\mathcal{A}}({{\mathcal{O}}}_{\rho },{{\mathcal{O}}}_{\sigma },{\kappa }_{\rho },{\kappa }_{\sigma },\epsilon )$ be any quantum query algorithm that estimates the fidelity $F\left(\rho ,\sigma \right)$ between two mixed quantum states ρ and σ within additive error ϵ, where ${{\mathcal{O}}}_{\rho }$ and ${{\mathcal{O}}}_{\sigma }$ prepare purifications of ρ and σ, respectively, with ρ ≥ I/κ_ρ and σ ≥ I/κ_σ. In the following, we use ${\mathcal{A}}({{\mathcal{O}}}_{\rho },{{\mathcal{O}}}_{\sigma },{\kappa }_{\rho },{\kappa }_{\sigma },\epsilon )$ to distinguish U_p and U_q. We first note that U_p and U_q can be understood as quantum unitary oracles that prepare purifications of the following two quantum states:

$$\rho =\frac{1+\epsilon }{2}| 0\left.\right\rangle \,\left\langle 0\right\vert +\frac{1-\epsilon }{2}| 1\left.\right\rangle \,\left\langle \right.1\left.\right\vert ,\quad \sigma =\frac{1+2\epsilon }{2}| 0\left.\right\rangle \,\left\langle 0\right\vert +\frac{1-2\epsilon }{2}| 1\left.\right\rangle \,\left\langle \right.1\left.\right\vert .$$

(109)

Then, one can set ${\kappa }_{\rho }={\kappa }_{\sigma }=4=\Theta \left(1\right)$. Consider the quantum state

$$\eta =\frac{1}{4}| 0\left.\right\rangle \,\left\langle 0\right\vert +\frac{3}{4}| 1\left.\right\rangle \,\left\langle \right.1\left.\right\vert ,$$

(110)

and let ${{\mathcal{O}}}_{\eta }$ be a quantum oracle that prepares a purification of η. We note that

$$F\left(\rho ,\eta \right)=\frac{\sqrt{1+\epsilon }+\sqrt{3\left(1-\epsilon \right)}}{\sqrt{8}}.$$

(111)

$$F\left(\sigma ,\eta \right)=\frac{\sqrt{1+2\epsilon }+\sqrt{3\left(1-2\epsilon \right)}}{\sqrt{8}}.$$

(112)

By simple calculation, we have

$$F\left(\rho ,\eta \right)-F\left(\sigma ,\eta \right)\ge \frac{\epsilon }{16}.$$

(113)

Let U be the unitary oracle to be tested, promised that either U = U_p or U = U_q. For convenience, suppose that U prepares a purification of ϱ, promised that either ϱ = ρ or ϱ = σ. Our algorithm for determining which is the case is given as follows.

1. Apply ${\mathcal{A}}(U,{{\mathcal{O}}}_{\eta },4,4,\epsilon /64)$ to obtain an ϵ/64-estimate $\tilde{x}$ of $F\left(\varrho ,\eta \right)$.

2. If $\left\vert \tilde{x-F\left(\rho ,\eta \right)}\right\vert \le \epsilon /32$, then return that U = U_p; otherwise, return that U = U_q.

It can be verified that the above algorithm determines whether U = U_p or U = U_q with high probability, where the correctness is mainly based on Eq. (113).

On the other hand, by Lemma 37, any quantum query algorithm that distinguishes U_p and U_q has query complexity $\Omega \left(1/{d}_{{\rm{H}}}\left(p,q\right)\right)=\Omega \left(1/\epsilon \right)$. Therefore, the algorithm ${\mathcal{A}}(U,{{\mathcal{O}}}_{\eta },4,4,\epsilon /64)$ should use at least $\Omega \left(1/\epsilon \right)$ queries to U, which completes the proof. □

Using the same hard instance, we can prove Lemma 20.

Proof of Lemma 20

Note that under the choice of ρ, σ, η the same as the proof of Lemma 17, we still have

$${\widehat{F}}_{1/2}\left(\rho ,\eta \right)-{\widehat{F}}_{1/2}\left(\sigma ,\eta \right)\ge \frac{\epsilon }{16},$$

(114)

which is similar to Eq. (113).

Such an observation can be generalised to the general case when 0 < α < 1, which, however, becomes a bit more complicated. We first note that

$${\widehat{F}}_{\alpha }\left(\rho ,\eta \right)={\left(\frac{1}{4}\right)}^{1-\alpha }{\left(\frac{1+\epsilon }{2}\right)}^{\alpha }+{\left(\frac{3}{4}\right)}^{1-\alpha }{\left(\frac{1-\epsilon }{2}\right)}^{\alpha },$$

(115)

$${\widehat{F}}_{\alpha }\left(\sigma ,\eta \right)={\left(\frac{1}{4}\right)}^{1-\alpha }{\left(\frac{1+2\epsilon }{2}\right)}^{\alpha }+{\left(\frac{3}{4}\right)}^{1-\alpha }{\left(\frac{1-2\epsilon }{2}\right)}^{\alpha }.$$

(115)

To make the construction in the proof of Lemma 17 applicable to ${\widehat{F}}_{\alpha }\left(\cdot ,\cdot \right)$ for 0 < α < 1, we only have to show that there is a constant c > 0 and ϵ₀ > 0 (which depends only on α) such that for all 0 < ϵ < ϵ₀, it holds that

$${\widehat{F}}_{\alpha }\left(\rho ,\eta \right)-{\widehat{F}}_{\alpha }\left(\sigma ,\eta \right)\ge c\epsilon .$$

(117)

To complete the proof, we show that this is achievable by noting that

$$\mathop{\lim }\limits_{\epsilon \to 0}\frac{{\widehat{F}}_{\alpha }\left(\rho ,\eta \right)-{\widehat{F}}_{\alpha }\left(\sigma ,\eta \right)}{\epsilon }={\left(\frac{1}{2}\right)}^{\alpha }\left[{\left(\frac{3}{4}\right)}^{1-\alpha }-{\left(\frac{1}{4}\right)}^{1-\alpha }\right]\alpha\, >\, 0.$$

(118)

□

Sample complexity for fidelity estimation

In this section, we show how to extend our quantum query algorithm in Theorem 16 to a quantum algorithm that only uses samples of quantum states as input. To this end, we need the technique of density matrix exponentiation^53,54. Here, we use the extension given in ref. ⁵⁸ that is easy to use for quantum query algorithms.

Lemma 38

(Samplizer,⁵⁸, Theorem 1.3). Let ${{\mathcal{A}}}^{U}$ be a quantum query algorithm that uses Q queries to the unitary oracle U. Then, for any $\delta \in \left(0,1\right)$ and quantum state ρ, we can implement a quantum channel ${{\mathsf{Samplize}}}_{\delta }\langle {{\mathcal{A}}}^{U}\rangle [\rho ]$ by using $\tilde{O}\left({Q}^{2}/\delta \right)$ samples of ρ, such that there is a unitary operator U_ρ that is a $\left(1,a,0\right)$-block-encoding of ρ/2 for some a > 0 satisfying

$$||{{{\mathcal{A}}}^{{U}_{\rho }}-{{\mathsf{Samplize}}}_{\delta }\left\langle {{\mathcal{A}}}^{U}\right\rangle \left[\rho \right]||}_{\lozenge }\le \delta .$$

(119)

Now let ${{\mathcal{A}}}^{{U}_{A},{U}_{C}}$ be the quantum query algorithm in Lemma 8, where U_A and U_C are supposed to be $\left(1,a,0\right)$-block-encodings of matrices A and C, respectively. Assume that if it is known that A ≥ I/κ_A and C ≥ I/κ_C, then ${{\mathcal{A}}}^{{U}_{A},{U}_{C}}$ uses ${Q}_{A}=\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\delta \right)\right)$ queries to U_A and ${Q}_{C}=\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\delta \right)\right)$ queries to U_C. Here, ${{\mathcal{A}}}^{{U}_{A},{U}_{C}}$ is a $\left(2{\kappa }_{A},b,\delta \right)$-block-encoding of A⁻¹#C, where b = 5a + 11.

Let ${\delta }_{A},{\delta }_{C}\in \left(0,1\right)$ be parameters to be determined. By Lemma 38, we can implement a quantum query algorithm (using queries to U_C)

(120)

that uses ${S}_{A}=\tilde{O}\left({Q}_{A}^{2}/{\delta }_{A}\right)$ samples of σ such that there is a unitary operator U_σ that is a $\left(1,{a}_{\sigma },0\right)$-block-encoding of σ/2 for some a_σ > 0 satisfying

$$|| {{{\mathcal{A}}}^{{U}_{\sigma },{U}_{C}}-{{\mathcal{B}}}^{{U}_{C}}}||_{\lozenge }\le {\delta }_{A},$$

(121)

Here, the boxed oracle denotes the oracle to be samplized.

Again, by Lemma 38, we can implement a quantum channel

$${\mathcal{C}}:={{\mathsf{Samplize}}}_{{\delta }_{C}}\left\langle {{\mathcal{B}}}^{{U}_{C}}\right\rangle \left[\rho \right]$$

(122)

that uses additional ${S}_{C}=\tilde{O}\left({Q}_{C}^{2}/{\delta }_{C}\right)$ samples of ρ such that there is a unitary operator U_ρ that is a $(1,{a}_{\rho },0)$-block-encoding of ρ/2 for some a_ρ > 0 satisfying

$$|| {{{\mathcal{B}}}^{{U}_{\rho }}-{\mathcal{C}}}||_{\lozenge }\le {\delta }_{C}.$$

(123)

By Eq. (121) and Eq. (123), we have

$$|| {{{\mathcal{A}}}^{{U}_{\sigma },{U}_{\rho }}-{\mathcal{C}}}||_{\lozenge }\le {\delta }_{A}+{\delta }_{C}.$$

(124)

By taking A: = σ/2 and C: = ρ/2, we know that ${{\mathcal{A}}}^{{U}_{\sigma },{U}_{\rho }}$ is a $\left(4{\kappa }_{\sigma },b,\delta \right)$-block-encoding of ${\left(\sigma /2\right)}^{-1}\#\left(\rho /2\right)={\sigma }^{-1}\#\rho$. Then, following the analysis of Theorem 16, by the Hadamard test (given in Lemma 31), there is a quantum circuit C that outputs 0 with probability

$$p=\frac{1}{2}\left(1+{\rm{Re}} \left\{{\rm{Tr}}\left({\left\langle \right.0| }_{b}{{\mathcal{A}}}^{{U}_{\sigma },{U}_{\rho }}{| 0\left.\right\rangle }_{b}\sigma \right)\right\}\right),$$

(125)

using one query to ${{\mathcal{A}}}^{{U}_{\sigma },{U}_{\rho }}$ and one sample of σ. Note that

$$\left\vert 4{\kappa }_{\sigma }{\rm{Re}} {\rm{Tr}}\left({\left\langle \right.0| }_{b}{{\mathcal{A}}}^{{U}_{\sigma },{U}_{\rho }}{| 0\left.\right\rangle }_{b}\sigma \right)-{\rm{Tr}}\left(\left({\sigma }^{-1}\#\rho \right)\sigma \right)\right\vert \le \Theta \left(\delta \right).$$

(126)

If we construct another quantum circuit ${C}^{{\prime} }$ by replacing ${{\mathcal{A}}}^{{U}_{\sigma },{U}_{\rho }}$ by ${\mathcal{C}}$ in the implementation of C, then ${C}^{{\prime} }$ outputs 0 with probability ${p}^{{\prime} }$ such that

$$\left\vert p-{p}^{{\prime} }\right\vert \le \Theta \left({\delta }_{A}+{\delta }_{C}\right)$$

(127)

because of Eq. (124). By $O\left(1/{\epsilon }_{H}^{2}\right)$ repetitions of ${C}^{{\prime} }$, we can obtain an ϵ_H-estimate $\tilde{p}$ of ${p}^{{\prime} }$, i.e.,

$$| \tilde{p}-{p}^{{\prime} }\le {\epsilon }_{H}.$$

(128)

By Eqs. (125), (126), (127), and (128), we have

$$\left\vert 4{\kappa }_{\sigma }\left(2\tilde{p}-1\right)-F\left(\rho ,\sigma \right)\right\vert \le \Theta \left(\delta +{\kappa }_{\sigma }\left({\delta }_{A}+{\delta }_{C}+{\epsilon }_{H}\right)\right).$$

(129)

By taking $\delta =\Theta \left(\epsilon \right)$ and ${\delta }_{A}={\delta }_{C}={\epsilon }_{H}=\Theta \left(\epsilon /{\kappa }_{\sigma }\right)$, we can estimate $F\left(\rho ,\sigma \right)$ to within additive error ϵ. The number of samples of σ used is

$$O\left(\frac{1}{{\epsilon }_{H}^{2}}\right)\cdot \left({S}_{A}+1\right)=\tilde{O}\left(\frac{{\kappa }_{\sigma }^{7}{\kappa }_{\rho }^{2}}{{\epsilon }^{3}}\right),$$

(130)

and the number of samples of ρ used is

$$O\left(\frac{1}{{\epsilon }_{H}^{2}}\right)\cdot {S}_{C}=\tilde{O}\left(\frac{{\kappa }_{\sigma }^{5}{\kappa }_{\rho }^{2}}{{\epsilon }^{3}}\right).$$

(131)

Therefore, the total number of samples of ρ and σ used is $\tilde{O}({\kappa }_{\sigma }^{7}{\kappa }_{\rho }^{2}/{\epsilon }^{3})$. By considering the symmetric case, the sample complexity for fidelity estimation is $\tilde{O}\left(\min \left\{{\kappa }_{\rho }^{5},{\kappa }_{\sigma }^{5}\right\}\cdot {\kappa }_{\rho }^{2}{\kappa }_{\sigma }^{2}/{\epsilon }^{3}\right)$.

Lemma 39

(Sample complexity for fidelity estimation). Suppose that two quantum states ρ and σ satisfy ρ ≥ I/κ_ρ and σ ≥ I/κ_σ for some known parameters κ_ρ, κ_σ ≥ 1. Then, we can estimate their fidelity by using $\tilde{O}\left(\min \left\{{\kappa }_\rho ^{5},\,{\kappa }_{\sigma }^{5}\right\}\cdot {\kappa }_\rho ^{2}{\kappa }_{\sigma }^{2}/{\epsilon }^{3}\right)$ samples of them.

We can also derive a sample lower bound for fidelity estimation.

Lemma 40

(Sample lower bound for fidelity estimation). Suppose that two quantum states ρ and σ satisfy ρ ≥ I/κ_ρ and σ ≥ I/κ_σ for some known parameters κ_ρ, κ_σ ≥ 1. Then, every quantum algorithm that estimates $F\left(\rho ,\sigma \right)$ within additive error ϵ requires sample complexity $\Omega \left(1/{\epsilon }^{2}\right)$ even if ${\kappa }_{\rho }={\kappa }_{\sigma }=\Theta \left(1\right)$.

Proof

Using the same instance in the proof of Lemma 17, we can distinguish the following two quantum states ρ and σ defined by Eq. (109) by estimating the fidelity $F\left(\rho ,\eta \right)$ and $F\left(\sigma ,\eta \right)$, where η is defined by Eq. (110). On the other hand, distinguishing ρ and σ requires sample complexity $\Omega \left(1/{\epsilon }^{2}\right)$ by the Helstrom–Holevo bound^93,94. □

Proof of Lemma 23

We consider how to solve ${\rm{MGM}}\left({\kappa }_{A},{\kappa }_{C}\right)$ in quantum time ${\rm{poly}}\left(n\right)$ for ${\kappa }_{A}={\rm{poly}}\left(n\right)$ and ${\kappa }_{C}={\rm{poly}}\left(n\right)$. It is straightforward that the given uniform classical circuit ${{\mathcal{C}}}_{n}$ implies the quantum implementations of the sparse oracles of A and C, which are (uniform) quantum circuits of size ${\rm{poly}}\left(n\right)$. By Lemma 29, we can implement U_A and U_C such that U_A and U_C are $\left(O\left(1\right),{\rm{poly}}\left(n\right),\epsilon \right)$-block-encodings of A and C, respectively, using $O\left(1\right)$ queries to the sparse oracles of A and C and $O\left({\rm{poly}}\left(n\right)+{\rm{polylog}}\left(1/\epsilon \right)\right)$ one- and two-qubit quantum gates. Here, we choose $\epsilon =1/\exp \left(n\right)$ for convenience, and we assume that U_A and U_C are $\left(O\left(1\right),{\rm{poly}}\left(n\right),0\right)$-block-encodings of $\hat{A}$ and $\hat{C}$ such that $|| {\hat{A}-A}|| \le \epsilon$ and $|| {\hat{C}}-C|| \le \epsilon$.

Let $\delta =O\left({\kappa }_{A}^{-5}{\kappa }_{C}^{-5}\right)=1/{\rm{poly}}\left(n\right)$. By Lemma 8, we can implement an $\left(O\left(1\right),{\rm{poly}}\left(n\right),\delta \right)$-block-encoding U_Y of ${\kappa }_{A}^{-1}\hat{Y}$ using $\tilde{O}\left({\kappa }_{A}{\kappa }_{C}{\log }^{2}\left(1/\delta \right)\right)={\rm{poly}}\left(n\right)$ queries to U_C, $\tilde{O}\left({\kappa }_{A}^{2}{\kappa }_{C}{\log }^{3}\left(1/\delta \right)\right)={\rm{poly}}\left(n\right)$ queries to U_A, and ${\rm{poly}}\left(n\right)\cdot {\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\delta \right)\right)={\rm{poly}}\left(n\right)$ one- and two-qubit quantum gates, where $\hat{Y}={\hat{A}}^{-1}\#\hat{C}$. Moreover, the quantum circuit description of U_Y can be computed in classical time ${\rm{poly}}\left({\kappa }_{A},{\kappa }_{C},\log \left(1/\delta \right)\right)={\rm{poly}}\left(n\right)$. By Lemma 24, we can implement an $\left(O\left(1\right),{\rm{poly}}\left(n\right),O\left(\delta \right)\right)$-block-encoding ${U}_{{Y}^{2}}$ of ${\kappa }_{A}^{-2}{\hat{Y}}^{2}$ using $O\left(1\right)$ queries to U_Y. Here, we assume that ${U}_{{Y}^{2}}$ is an $\left(O\left(1\right),{\rm{poly}}\left(n\right),0\right)$-block-encoding of

$$Z={\left\langle \right.0| }^{\otimes a}{U}_{{Y}^{2}}{| 0\left.\right\rangle }^{\otimes a}$$

(132)

such that $|| Z-{\kappa }_{A}^{-2}{\hat{Y}}^{2}|| \le O\left(\delta \right)$, and it can be easily shown that $|| {\hat{Y}-Y}|| \le O\left(\epsilon \right)$. Then,

$$|| Z-{\kappa }_{A}^{-2}{Y}^{2}|| \le O\left(\delta +{\kappa }_{A}^{-2}\epsilon \right),$$

(133)

$$\left({\kappa }_{A}^{-3}{\kappa }_{C}^{-1}-O\left(\epsilon \right){\kappa }_{A}^{-2}-O\left(\delta \right)\right)I\le Z\le I.$$

(134)

The latter can be seen by noting that ${\kappa }_{A}^{-1}{\kappa }_{C}^{-1}I\le {Y}^{2}\le {\kappa }_{A}^{2}I$.

Now we prepare the quantum state $| \psi \left.\right\rangle ={U}_{{Y}^{2}}| 0\left.\right\rangle ={| 0\left.\right\rangle }^{\otimes a}\otimes Z| 0\rangle +|\!\!\perp \rangle$ where $|\!\!\perp\!\! \left.\right\rangle$ is orthogonal to ${| 0\left.\right\rangle }^{\otimes a}\otimes | \varphi \left.\right\rangle$ for any $| \varphi \left.\right\rangle$. By measuring the first a qubits of $| \psi \left.\right\rangle$, the outcome will be 0^a with probability

$${|| Z| 0\rangle || }^{2}\ge \Theta \left({\kappa }_{A}^{-6}{\kappa }_{C}^{-2}\right)=\frac{1}{{\rm{poly}}\left(n\right)}$$

(135)

and $| \psi \left.\right\rangle$ will become the state $|{u}_{Z}\rangle:=Z| 0\rangle /|| Z| 0\rangle ||$. Let $| {u}_{Y}\rangle :={Y}^{2}| 0\rangle /|| {Y}^{2}| 0\rangle ||$. We have

$$\Vert | {u}_{Z}\rangle -| {u}_{Y}\rangle \Vert \le \left|\left| \frac{Z| 0\rangle }{\left|\left| Z| 0\rangle \right|\right| }-\frac{{\kappa }_{A}^{-2}{Y}^{2}| 0\rangle }{\left|\right| Z| 0\rangle} \right|\right| +\left|\left| \frac{{\kappa }_{A}^{-2}{Y}^{2}| 0\rangle }{\left|\left| Z| 0\rangle\right|\right| }-\frac{{\kappa }_{A}^{-2}{Y}^{2}| 0\rangle }{\left|\left| {\kappa }_{A}^{-2}{Y}^{2}| 0\rangle \right|\right| }\right|\right|$$

(136)

$$\le O\left(\frac{\left|\left| Z-{\kappa }_{A}^{-2}{Y}^{2}\right|\right| }{\left|\left| Z| 0\left.\right\rangle \right|\right| }\right)$$

(137)

$$\le O\left(\frac{\delta +{\kappa }_{A}^{-2}\epsilon }{{\kappa }_{A}^{-3}{\kappa }_{C}^{-1}}\right)=\frac{1}{{\rm{poly}}\left(n\right)}.$$

(138)

Let p_Z (resp. p_Y) be the probability that outcome 0 will be obtained by measuring the first qubit of $| {u}_{Z}\left.\right\rangle$ (resp. $| {u}_{Y}\left.\right\rangle$). Note that ${p}_{Z}=\left\langle \right.{u}_{Z}| M| {u}_{Z}\left.\right\rangle$ and ${p}_{Y}=\left\langle \right.{u}_{Y}| M| {u}_{Y}\left.\right\rangle$, where $M=| 0\left.\right\rangle \,\left\langle 0\right\vert \otimes I$ measures the first qubit of $| {u}_{Z}\left.\right\rangle$ and $| {u}_{Y}\left.\right\rangle$. Then, $\left\vert {p}_{Z}-{p}_{Y}\right\vert \le 1/{\rm{poly}}\left(n\right)$ by Eq. (138).

Finally, we can estimate p_Z to precision, say 0.1, by repeating the above procedure for $O\left(1\right)$ times; in this way, we can determine whether p_Y ≥ 2/3 or p_Y ≤ 1/3 with high probability. As all the procedures mentioned above take ${\rm{poly}}\left(n\right)$ time, we obtain a polynomial-time quantum algorithm for ${\rm{MGM}}\left({\kappa }_{A},{\kappa }_{C}\right)$ if ${\kappa }_{A}={\rm{poly}}\left(n\right)$ and ${\kappa }_{C}={\rm{poly}}\left(n\right)$. Therefore, we conclude that ${\rm{MGM}}\left({\rm{poly}}\left(n\right),{\rm{poly}}\left(n\right)\right)$ is in ${\mathsf{BQP}}$.