Landau–Zener without a qubit: multiphoton sidebands interaction and signatures of dissipative quantum chaos

Abstract

Landau–Zener–Stückelberg–Majorana (LZSM) interference occurs when qubit parameters are periodically modulated across avoided level crossings. We explore this phenomenon in nonlinear multilevel bosonic systems, where interference is influenced by multiple energy levels. We fabricate two superconducting resonators with flux-tunable Josephson junction arrays. The first device, exhibiting weak nonlinearity, behaves like a linear resonator under weak driving but shows LZSM interference akin to two-level systems. With stronger driving, nonlinear effects alter the interference pattern. We theoretically demonstrate that merging LZSM peaks can lead to dissipative quantum chaos. In the second device, where nonlinearity exceeds photon-loss rates, we observe additional LZSM peaks from Kerr multiphoton resonances. Under Floquet theory, these resonances represent synthetic modes of coupled nonlinear cavities, revealing effective coupling as modulation parameters vary. Our findings advance the understanding of LZSM physics and emphasize the control of nonlinear Floquet states and the emergence of chaos in engineered systems, with significant implications for novel applications in quantum dynamics and quantum control.

Introduction

Qubits—two-level systems—are the building blocks of digital quantum computers and simulators, as well as an essential paradigm for describing many quantum systems^1,2. Understanding and controlling their dynamics is thus pivotal to the progress of quantum technologies. When the qubit’s energy-level splitting is varied in such a way that the two levels become almost degenerate, the Landau–Zener–Stückelberg–Majorana (LZSM)^3,4,5,6 transition probability dictates the likelihood of non-adiabatic transitions between the ground and excited states. When the variation of the splitting is periodic in time, a rich LZSM interference pattern arises, as schematically shown in Fig. 1a (see ref. ⁷ for a recent overview of the field). At each oscillation period, the transition paths can interfere constructively or destructively to determine the final probability of the qubit to reach the excited state, as observed in, e.g., superconducting qubit architectures^8,9, semiconductor quantum dots^10,11, and nitrogen-vacancy center in diamond¹².

Fig. 1: LZSM interference mechanisms in bosonic systems.

For cases studied in this article, we show the level structure of the undriven system (left); the photon number n of the driven, but not-modulated, system as a function of the pump-to-cavity detuning Δ (center); and the LZSM pattern emerging when the cavity eigenfrequency is periodically modulated with strength ζ and frequency Ω (right). a In the qubit regime of infinite nonlinearity, the system consists only of the ground and excited states. This level structure gives rise to a single excitation peak ($\left\vert 0\right\rangle \to \left\vert 1\right\rangle$) at detuning Δ = 0. Thus, the standard LZSM interference pattern emerges. b In the Kerr regime, where the anharmonicity is larger than the loss (∣χ∣ > κ), the system consists of many uneven-spaced states with different numbers of excitations. When Δ = nχ, multiphoton transitions $\left\vert 0\right\rangle \to \left\vert n\right\rangle$ occur for a large enough drive. This multi-photonic transition structure is periodically repeated around each standard LZSM peak. c In the Duffing regime, where the anharmonicity is smaller than the loss (∣χ∣ < κ), the uneven-spaced states are broadened by dissipation and cannot be distinguished. The drive excites multiple levels, resulting in a deviation from a Lorentzian shape, and the Kerr nonlinearity competes with detuning, giving rise to bistability. Such a deviation and the presence of bistability are imprinted in each LZSM peak. d In the linear regime (χ = 0), all levels are equispaced. When driven, only a Lorentzian peak appears at Δ = 0, similar to the qubit regime. Upon modulation of the resonator frequency, the LZSM interference is also indistinguishable from that in the qubit regime.

Historically, the understanding of LZSM transitions was a foundational step in the development of non-relativistic quantum mechanics^3,4,5,6. Recently, LZSM interference gained also considerable attention, as a versatile tool for the study of quantum systems. Examples include the characterization of the frequency noise of superconducting resonators¹³ and the decoherence properties of charge states from steady-state measurements^11,14,15. LZSM interferometry was also employed for the fast coherent control of charge^16,17 and spin^18,19,20 qubits, and to mediate and control the coupling of two flux qubits²¹ or of a single qubit to multiple mechanical modes²². Finally, LZSM interferometry has also been proposed as a tool for efficient quantum parameter estimation²³ and for the preparation of exotic quantum states, such as two-level systems with tunable absorption properties²⁴, correlated photons²⁵ and Schrödinger-cat states^26,27. The physics of LZSM interference beyond the two-level approximation has been marginally investigated, and often focuses on isolated avoided level crossing within a larger multilevel structure⁷. Furthermore, coupled classical oscillators have been proposed²⁸ and studied^29,30 as classical systems displaying LZSM interference. Indeed, in the presence of tailored modulation, these multimode classical systems display the same equation of motion of a qubit³¹, and thus exhibit LZSM interference due to the presence of an effective two-level system.

In bosonic systems, the qubit limit can be reached by the introduction of a Kerr nonlinearity (anharmonicity) χ, permitting, in principle, to address only the ground and first excited states¹. This description applies to several platforms, including superconducting circuits³², polaritonic microcavities³³, mechanical resonators³⁴, and the vibration of trapped ions³⁵. A realistic description of these systems must include the effects of dissipative processes, which blur the distinction between energy levels and thus hinder the possibility of addressing them singularly. Depending on the magnitude of the total loss rate κ, one can thus determine two distinct regimes that we dub the Kerr (∣χ∣ > κ) and Duffing (∣χ∣ < κ) regimes^36,37. In the Kerr regime, depicted in Fig. 1b, the energy quantization of the bosonic mode is still accessible despite the presence of dissipation³⁸. The system can absorb n photons from a drive and transition to the nth excited level, in a process known as Kerr multiphoton resonance (or multiphoton transition). Note that here multiphoton resonance refers to the fact that absorbing n photons leads to the nth excited state of the resonator. This is not the multiphoton Rabi resonance, where n driving photons are absorbed to populate the excited level of the qubit. In the Duffing regime (Fig. 1c), instead, dissipation blurs these multiphoton resonances, giving rise to a single spectral feature, where the energy quantization of the underlying bosonic mode can’t be resolved. The effect of the nonlinearity, in this case, is to shift this resonance, leading to phenomena such as bistability and hysteresis^39,40,41. Multimodal Duffing oscillators, where multiple bistabilities are present, display emergent phenomena, such as the formation of domain walls and dissipative phase transitions^42,43,44, as well as dissipative quantum chaos⁴⁵. The latter is triggered by the combined presence of classical and quantum fluctuations and the competition of unitary dynamics and dissipative processes^46,47.

In general, the study of periodically modulated systems through all regimes of nonlinearity is a topic attracting growing attention in the community of superconducting circuits⁴⁸. These studies sit within the broader context of Floquet physics, which has proven crucial in describing periodically-modulated quantum systems, finding diverse applications such as quantum control^48,49 and band topology engineering^50,51,52,53. This approach enables the construction of synthetic lattices^54,55,56, allowing, for example, the implementation of controllable LZSM transitions between Floquet states^57,58. Recent research focused on expanding Floquet theory to encompass open quantum systems^59,60, and investigating its effects in nonlinear systems^61,62,63,64.

In this article, we extend the paradigm of LZSM physics, through the study of two nonlinear superconducting resonators, one in the Kerr and one in the Duffing regime, investigating strongly driven and dissipative nonlinear Floquet systems. Given the high degree of tunability of the drive, the modulation, and the other system parameters, we determine the whole LZSM interference diagram for nonlinear bosonic systems. We present a simple unified model that captures the relevant features of the system under consideration.

The main results of this work can be summarized as follows.

First, we experimentally demonstrate and theoretically clarify that, at low driving amplitude, the LZSM interference pattern is independent of the nonlinearity of the system [c.f. the rightmost panels of Fig. 1a, d]. Namely, there is no distinction in the LZSM interference pattern between a completely linear resonator and a qubit.

Second, we show novel effects due to the competition between the modulation and the nonlinearity at larger pumping power, demonstrating the role of dissipation (Fig. 1b, c). In particular (i) In the Kerr regime, we observe how Kerr multiphoton resonances add structure to the LZSM interference. These resonances and the associated quasi-energy (Floquet) states can be interpreted as the modes of a multimode synthetic cavity array, with effective interference between these multiple transitions resulting in avoided level crossings. (ii) In the Duffing regime, we show how bistability and hysteresis come into play in determining the state of the system, suggesting the emergence of dissipative quantum chaos in a Floquet regime, i.e., Floquet-dissipative quantum chaos.

Our work establishes a comprehensive framework for understanding LZSM and Floquet physics, clarifying the role of nonlinearity and dissipation in determining the interference patterns. It paves the way to their control, with perspectives for synthetic dimension engineering in Floquet configurations. This platform can be used as a quantum simulator to investigate quantum chaos and critical phenomena in highly controllable superconducting systems.

The article begins with a presentation of the experimental system and the model used to describe it. It then explores LZSM interference in the qubit and linear regimes, followed by an analysis of photon-resolved effects in the Kerr regime, where multiphoton resonances influence the emergent LZSM interference. The discussion continues with an examination of the Duffing regime, characterized by weak nonlinearity, highlighting the emergence of Floquet dissipative quantum chaos. The methods section provides details on device fabrication, measurement setup, and parameter extraction. Supplementary Material includes theoretical insights and additional experimental data that enhance the understanding of our findings.

Results

Experimental system and model

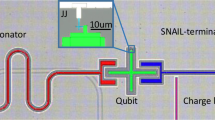
We aim to investigate all regimes of nonlinearity and dissipation, namely, qubit, Kerr, Duffing, and linear, as shown in Fig. 1a–d, respectively. To this extent, we design and fabricate two frequency-tunable nonlinear resonators that can operate in these different regimes according to the driving amplitude. These are superconducting SQUID arrays^65,66,67, galvanically connected to the ground on one side, and capacitively shunted to the ground on the other side, as shown in Fig. 2a, b, and f. A detailed summary of their parameters is reported in Table 1.

Fig. 2: SQUID array characterization.

a Equivalent lumped electrical circuit of the device composed of N SQUIDs in series. The static flux is controlled via an external coil and a microwave signal can be applied to the flux line (purple) for fast frequency modulation. The resonator is coupled to a feedline in a notch configuration. b, f Optical micrograph of the two SQUID array resonators studied in this work with N = 10 (red) and N = 32 (blue) SQUIDs, with details on the Josephson junction shown in the inset where the white scale bar represents 5 μm. c, d For the Kerr case (N = 10), the magnitude and phase of the transmission coefficient through the feedline as a function of drive power at the sample. The black dashed curve indicates where the phase of S₂₁ is zero according to numerical simulations, highlighting the position of the multiphoton resonances. e Selected traces of the data reported in (d). Experimental data are shown with circle markers whose colors correspond to the ticks in (d). Numerical fits to a full quantum model are shown in black solid lines. The gray dotted vertical lines indicate the position of the multiphoton resonances obtained from numerical simulations. g–i Same measurement as in (c–e), but for the Duffing case. The dashed curves in (g, h) indicate the minima of ∣S₂₁∣ obtained from a full quantum simulation.

Table 1 Summary of the relevant SQUID array parameters at flux operating point Φ_wp

The frequency of the resonators can be tuned by a dedicated flux line that uniformly threads the magnetic fields in each SQUID loop (in purple) and an external superconducting coil. The two resonators differ in the number of SQUIDs in each array, as highlighted by red and blue false colors, determining the two orders of magnitude difference in their Kerr nonlinearity χ. Increasing the number of SQUIDs in an array leads to a decrease in nonlinearity due to the reduced Josephson inductance required to maintain a fixed frequency and the diminished phase fluctuations across each junction⁶⁸. Hereafter, the red and blue color schemes will always indicate measurements of the devices in the Kerr/qubit and Duffing/linear regimes, respectively. Each resonator is also capacitively coupled to a feedline (in green) in a notch configuration, resulting in an external coupling κ_ext close to the internal dissipation rate κ_int (critically coupled regime). We define the total dissipation rate as κ = κ_ext + κ_int.

Each device is thermally and mechanically anchored at the mixing chamber plate of a dilution refrigerator, reaching an average base temperature of 15 mK. The devices are probed by a coherent drive with amplitude F at the sample, and injected in the feedline through highly attenuated coaxial lines. The drive amplitude is related to the input power P_in by $F=\sqrt{{P}_{{\rm{in}}}{\kappa }_{{\rm{ext}}}/\hslash {\omega }_{{\rm{d}}}}$, where ω_d is the drive frequency. Although the frequency of the untuned cavity is ω_c, through the paper, the frequency working point of the resonators, ω_wp, is set by a static flux generated by direct current through an external superconducting coil. The flux operating point is Φ_wp = 0.45Φ₀ for the N = 10 device, while Φ_wp = 0.32Φ₀ for the N = 32 one, where Φ₀ = h/2e is the magnetic flux quantum. Finally, driving the fluxline at a frequency Ω periodically modulates the frequency of the resonator, approximately between ω_wp ± ζ, with ζ representing the strength of the modulation. The single-tone spectroscopy of the resonators at low-driving power as a function of the external magnetic flux is reported in the Supplementary Information.

As explained in the Supplementary Information, both devices can be modeled as a bosonic mode with the following time-dependent Hamiltonian:

$$\hat{H}/\hslash =-\Delta {\hat{a}}^{\dagger }\hat{a}+\chi {\hat{a}}^{\dagger }{\hat{a}}^{\dagger }\hat{a}\hat{a}+F\,(\hat{a}+{\hat{a}}^{\dagger })+\zeta \cos (\Omega \,t){\hat{a}}^{\dagger }\hat{a}\,,$$

(1)

where Δ = ω_d − ω_wp is the detuning between the working point of the devices (ω_wp) and the drive frequency (ω_d). Beyond the total dissipation rate κ, the system is subject to dephasing with rate κ_ϕ. We include them in the time evolution of the density matrix $\hat{\rho }$ using the Lindblad master equation

$$\hslash \,{\partial }_{t}\hat{\rho }=-i\left[\hat{H},\hat{\rho }\right]+\kappa {\mathcal{D}}[\hat{a}]\hat{\rho }+{\kappa }_{\phi }{\mathcal{D}}[{\hat{a}}^{\dagger }\hat{a}]\hat{\rho }\,.$$

(2)

Here, ${\mathcal{D}}[\hat{L}]\hat{\rho }\equiv \hat{L}\hat{\rho }{\hat{L}}^{\dagger }-\{{\hat{L}}^{\dagger }\hat{L},\hat{\rho }\}/2$ is the Lindblad dissipator⁶⁹.

In Fig. 2 we characterize the coherent response of the resonators in the absence of modulation (i.e., ζ = 0) and use it to determine the parameters of the two devices. In Fig. 2c, d we report the magnitude and phase of the transmission coefficient S₂₁ (see “Methods”) as a function of the driving power P_in ∝ F² in the Kerr regime. At low power, only a single dip around Δ = 0 is visible, representing the transition to the first excited state (noted as $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$, where $\left\vert n\right\rangle$ is the photon number state of the resonator). At larger values of the drive, several dips appear, representing the so-called Kerr multiphoton transitions between the ground state and the higher-excited levels ($\left\vert 0\right\rangle \to \left\vert n\right\rangle$), highlighted in the single traces shown in Fig. 2e. According to Eq. (1), all the dips should appear at Δ ≃ (n − 1)χ. Small deviations from this prediction are due to higher-order nonlinearities (see “Methods”). For even larger powers, the nonlinearity suppresses the intracavity photon number with respect to the input power, resulting in an almost unitary transmission S₂₁.

We report the same measurements for the resonator in the Duffing regime in Fig. 2g–i. In this case, dissipation smears the multiphoton resonances, resulting in an indistinguishable level structure. Increasing the drive, the single dip of S₂₁ originally at Δ = 0 moves to negative detunings, indicating that the drive is exciting higher levels. Scanning the detuning from negative to positive values, as done in Fig. 2i, reveals the presence of a sharp jump, where the resonator passes from a highly- to a lowly-populated phase. This behavior is associated with optical bistability, i.e., the presence of two metastable states that require a long time to decay to the steady state^42,43. This phenomenon gives rise to hysteresis^40,41 and makes it difficult to properly resolve the exact detuning where the transition occurs.

Linear and qubit LZSM interference

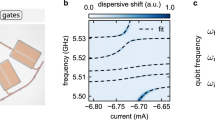
We can investigate the linear and qubit regimes using the N = 10 and N = 32 resonators described above. Indeed, for the N = 10 resonator, the second-excited level is not significantly populated if F² ≪ ∣χ∣κ (see Eq. (21) “Methods”). For the N = 10 device parameters and the drive F/2π ≃ 1.6 MHz considered here, the third level is predicted to be populated less than 0.03%. For the values used in this first part of the experiment, the system effectively behaves like an ideal qubit subject to dissipation and dephasing. We report the experimental data in Fig. 3b, c. In Fig. 3b we show the norm of the scattering coefficient S₂₁ sweeping the detuning Δ, for a fixed modulation frequency Ω, and varying the modulation strength ζ. One observes the LZSM pattern emerging, with populated regions at Δ = mΩ, for integer m. Fixing ζ and scanning Ω, in Fig. 3c we observe again the interference pattern at Δ = mΩ. We thus confirm the presence of LZSM interference and the control over the modulation of the resonator in the Kerr regime.

Fig. 3: LZSM interference patterns.

a–c (red) Analysis of the N = 10 device, with input power P_in = −138.8 dBm, ensuring that we are in the qubit regime. b The transmission coefficient ∣S₂₁∣ as a function of the detuning Δ and the modulation strength ζ, for fixed modulation frequency Ω/2π = 30 MHz [see Eq. (1)]. a Comparison of the experimental and theoretical data for ∣S₂₁∣. Solid lines represent the results of the numerical simulations of the full quantum model obtained at Δ = 0, Δ = −Ω, and Δ = −2Ω (see Supplementary Information). The circles are the experimental data obtained from panel (b), in which Δ is slightly re-scaled to account for the nonlinear flux-dependency of the resonator frequency (see Supplementary Information). c ∣S₂₁∣ as a function of Δ and Ω. d–f (blue) As in (a–c), but for the N = 32 device, with P_in = −133.3 dBm to ensure that the system is in the linear regime. From these plots, the two regimes appear almost indistinguishable. g The photon number vs Δ and ζ is obtained from a simulation using the effective model of Eq. (3) that reproduces the interference pattern in (b, e). h–j Depiction of the time evolution of the energy level $\left\vert 1\right\rangle$, in the frame rotating at the drive frequency ω_d, if F = 0. A finite drive F opens gaps at each crossing between $\left\vert 0\right\rangle$ and $\left\vert 1\right\rangle$, allowing a non-adiabatic passage between the two. The parameters Δ and ζ are indicated by green markers in (g). h At Δ = 0, the level $\left\vert 1\right\rangle$ becomes resonant with $\left\vert 0\right\rangle$ (they form a level crossing, see the inset). The values of ζ, F, and κ then determine the probability of transitioning out of the vacuum. i For non-zero detuning (e.g., ∣Δ∣ = Ω) and small modulation (ζ ≪ Ω), the level $\left\vert 1\right\rangle$ is never resonant with $\left\vert 0\right\rangle$ and it cannot be populated. j For strong enough modulation ζ > ∣Δ∣, the level $\left\vert 1\right\rangle$ can form again an avoided level crossing, and constructive interference is possible again.

We now consider the N = 32 device. In this case, the oscillator approximately behaves as a purely linear resonator if $F < \sqrt{{\kappa }^{3}/| \chi | }$ (see Eq. (24) in Methods). For the N = 32 device parameters and the drive F/2π ≃ 3 MHz considered here, we estimate a relative photon-number deviation from a completely linear resonator of less than 3%. Within this regime, we repeat the previous measurements and report them in Fig. 3e, f. Surprisingly, we observe the same interference pattern emerging, with no distinguishable differences between the qubit and the completely linear case. This feature indicates that only the energy difference between $\left\vert 0\right\rangle$ and $\left\vert 1\right\rangle$ determines the interference pattern in both the qubit and the linear regimes (c.f. Fig. 3g–j). This similarity may be expected from linear response theory; indeed, weakly driven nonlinear oscillators should behave similarly even if they have widely different anharmonicities. The presence of LZSM interference seems even more general, as it should be observable even in a purely linear cavity and for an arbitrarily large number of photons. We remark that the frequency modulation of almost linear oscillators has been used to perform mode-conversion⁷⁰, parametric amplification⁷¹, and squeezing⁷². However, to the best of our knowledge, LZSM interferences were not studied in linear oscillators, and this discussion is missing from recent reviews on the topic^7,73.

To provide more quantitative reasoning, we choose $\bar{m}$ minimizing $\Delta -\bar{m}\Omega$ and, following the procedure derived in the Supplementary Information, and passing in the frame rotating at the frequency $\bar{m}\Omega$, we have

$${\hat{H}}_{\bar{m}}/\hslash \simeq -{\Delta }_{\bar{m}}{\hat{a}}^{\dagger }\hat{a}+\chi {\hat{a}}^{\dagger }{\hat{a}}^{\dagger }\hat{a}\hat{a}+{F}_{\bar{m}}\left(\hat{a}+{\hat{a}}^{\dagger }\right)\,,$$

(3)

where the renormalized detuning ${\Delta }_{\bar{m}}$ and renormalized drive ${F}_{\bar{m}}$ are

$${\Delta }_{\bar{m}}=(\Delta -\bar{m}\Omega ),\quad {F}_{\bar{m}}=F\,{J}_{\bar{m}}\left(\frac{\zeta }{\Omega }\right),$$

(4)

with ${J}_{\bar{m}}\left(\zeta /\Omega \right)$ indicating the Bessel function of the first kind. All dissipative terms maintain their form as in (2). In other words, when we can single out a single relevant frequency ${\Delta }_{\bar{m}}$ for each of the LZSM interference dips, the devices behave as a collection of independent nonlinear resonators, whose driving amplitudes ${F}_{\bar{m}}$ are modulated via Bessel functions. For the parameters we consider here, and if we also assume a weak enough drive to be in the linear and qubit regime (see Eq. (21), Eq. (24) “Methods”), we obtain

$$\langle {\hat{a}}^{\dagger }\hat{a}\rangle \simeq \frac{4{F}_{\bar{m}}^{2}}{\kappa }\frac{\kappa +\beta {\kappa }_{\phi }}{4{\Delta }_{\bar{m}}^{2}+{(\kappa +\beta {\kappa }_{\phi })}^{2}}\,,$$

(5)

with β = 1 for a linear resonator regime and β = 4 in the weakly driven qubit limit. Namely, the two regimes have identical interference patterns, only slightly modulated by the dephasing rate κ_ϕ. To further demonstrate the validity of these results, additional LZSM interference patterns are reported in the Supplementary Information, highlighting the precise control of the number and frequency spacing of modes over a broad range of modulation strengths and frequencies.

The approximation of the effective model correctly captures the value of the photon number, but not that of the field $\hat{a}$ (and thus cannot be used to quantitatively study S₂₁). As is discussed in the Supplementary Information, to correctly capture this feature, one has to resort to a full quantum simulation of the Floquet model. This is shown in Fig. 3a, d, where we plot ∣S₂₁∣ of the first three LZSM lobes, comparing the experimental data with the theoretical predictions both for the qubit and linear regimes. In both cases, we find an excellent agreement between theory and experiments. We note that the maxima and the minima of ∣S₂₁∣ of the $\bar{m}{\rm{th}}$ LZSM mode coincide with the extremes of the associated Bessel function ${J}_{\bar{m}}$, showing the qualitative validity of Eq. (3) in describing also S₂₁.

We remark here that the Hamiltonian in Eq. (3) could be obtained by approximating the response of an array of nonlinear resonators, each at a frequency ${\Delta }_{\bar{m}}$. Therefore, we can interpret each of the LZSM dips as the response of a different Floquet synthetic mode. As we show below, by increasing the drive, these initially non-interacting modes will begin to interact.

LZSM beyond the qubit approximation: Kerr regime

We now focus on those phenomena emerging due to the simultaneous presence of the multilevel structure of nonlinear resonators and the modulation of their eigenenergies, studying the devices beyond their qubit and linear regimes.

In the Kerr regime and for strong enough drives to probe the multiphoton transitions (see Eq. (21)), we investigate how the frequency and amplitude of the modulation modifies the multiphoton resonances.

The system’s behavior around the multiphoton resonance $\left\vert 0\right\rangle \to \left\vert n\right\rangle$ occurring for Δ ≃ χ(n − 1) can be described by a 2 × 2 matrix. For instance, the $\left\vert 0\right\rangle \to \left\vert 2\right\rangle$ multiphoton transition can be described as

$$\begin{array}{l}{\hat{H}}^{(2)}/\hslash =2[-\Delta +\chi +\zeta \cos (\Omega \,t)]\left\vert 2\right\rangle \left\langle 2\right\vert \\ \qquad\qquad+\,{G}^{(2)}(\left\vert 0\right\rangle \left\langle 2\right\vert +{\rm{h.c.}}),\end{array}$$

(6)

where G⁽²⁾ represents the effective drive between the vacuum and the state $\left\vert 2\right\rangle$. For ζ = 0, one has G⁽²⁾ = F²/χ for Δ = χ. This formula can be generalized to obtain G⁽ⁿ⁾ for arbitrary $\left\vert 0\right\rangle \to \left\vert n\right\rangle$ transitions⁷⁴. The dissipation maintains its form, instead. As we show below, the fundamental parameter to describe these phenomena is the ratio between the modulation frequency Ω, determining the position of the LZSM sidebands, and the nonlinearity χ, determining the position of the multiphoton resonance.

Strong modulation case

We first choose Ω ≫ ∣χ∣ (strongly modulated case). In Fig. 4a–c we report the scattering coefficient ∣S₂₁∣ as a function of the detuning Δ and the strength ζ of the modulation. As the drive amplitude F is increased, several additional dips appear, signaling the transitions between the photon number states $\left\vert 0\right\rangle$ and $\left\vert n\right\rangle$ of the resonator. These dips occur at a frequency lower than each main LZSM dip associated with the transition $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$. Each new additional dip is detuned by the same frequency as the unmodulated multiphoton resonances shown in Fig. 2c–e. Within a first approximation, this effect is due to the interplay between the modulation in Eq. (3) and the nonlinearity of the system, as shown in Fig. 4d reporting the result of a numerical simulation.

Fig. 4: LZSM interferometry for the N = 10 device, in the Kerr regime and strongly-modulated case Ω ≫ ∣χ∣.

a–c The magnitude of S₂₁ is measured vs Δ and ζ for fixed modulation frequency Ω/2π = 150 MHz. As the drive power P_in is increased, Kerr multiphoton resonances from $\left\vert 0\right\rangle$ to $\left\vert n\right\rangle$ appear detuned by (n − 1)χ on the left of bare LZSM resonances. For large ζ, notice the shift of the pattern to negative detuning, due to the nonlinear dependence of the SQUID array frequency on the flux, as explained in the Supplementary Information. d Photon-number simulation using the effective model of Eq. (3) for the same parameters as in (b), recovering the same interference pattern. e–g In the drive frame, energy vs time for different values of ζ and Δ including the first three levels of an undriven Kerr resonator (F = 0). Green markers indicate the corresponding value of Δ and ζ in (d). e For Δ = 0, although multiple levels cross with $\left\vert 0\right\rangle$, only the level $\left\vert 1\right\rangle$ forms a constructive interference. f For Δ = χ, the second level $\left\vert 2\right\rangle$ crosses $\left\vert 0\right\rangle$, and an appropriate choice of parameters leads to constructive interference. g For Δ = χ + Ω, similar LZSM interference can be constructive again and the level $\left\vert 2\right\rangle$ can be populated. We verified that both the data and full numerical simulations recover that the interference patterns are fully constructive at Δ = Ω and ζ ≈ 1.84Ω, where the Bessel function J₁(ζ/Ω) is at a maximum, confirming the prediction of the effective model in Eq. (3).

To explain this behavior, we can assume that, around each of the LZSM dips, we again have a drive of the same form as Eq. (3). When we then match the condition for a multiphoton resonance, it is this effective drive that leads to the excitation of the state $\left\vert 2\right\rangle$. One then obtains

$${\hat{H}}_{\bar{m}}^{(2)}/\hslash =2[-{\Delta }_{\bar{m}}^{(2)}+\chi ]\left\vert 2\right\rangle \left\langle 2\right\vert +{G}_{\bar{m}}^{(2)}(\left\vert 0\right\rangle \left\langle 2\right\vert +{\rm{h.c.}}),$$

(7)

where⁷⁴

$${\Delta }_{\bar{m}}^{(2)}=\Delta -\bar{m}\Omega ,\quad {G}_{\bar{m}}^{(2)}\simeq \frac{{F}_{\bar{m}}^{2}}{\chi }=\frac{{F}^{2}}{\chi }{\left[{J}_{\bar{m}}\left(\frac{\zeta }{\Omega }\right)\right]}^{2}.$$

(8)

This formula can be generalized to arbitrary n-photon resonances with ${\Delta }_{\bar{m}}^{(n)}=\Delta -\bar{m}\Omega$ and ${G}_{\bar{m}}^{(n)}\propto {({J}_{\bar{m}}\left(\zeta /\Omega \right))}^{n}$. We conclude that when the rescaled detuning matches the condition for the nth multiphoton resonance, and if the rescaled drive ${F}_{\bar{m}}$ is strong enough, an additional dip appears. Therefore, we can treat each of the multiphoton resonances for each LZSM dip as a yet separate phenomenon.

As sketched in Fig. 4e–g, at the multiphoton resonance, i.e., at Δ = mΩ + (n − 1)χ, the states $\left\vert 0\right\rangle$ and $\left\vert 2\right\rangle$ can satisfy the conditions for the development of constructive interference. In other words, around each of the main LZSM dips, and for large enough drive amplitude, several multiphoton resonances emerge with the same characteristics as those shown in Fig. 2c–e.

Weak modulation case

When Ω ≪ ∣χ∣ (weakly modulated case), instead, one can capture the system’s behavior around the second multiphoton resonance via the Hamiltonian in Eq. (6), with G⁽²⁾ = F²/χ representing the effective drive between the vacuum and the state $\left\vert 2\right\rangle$ if ζ = 0. Removing the modulation using the same approximation as in Eq. (3) leads to an equation identical to Eq. (7), where now

$${\Delta }_{\bar{m}}^{(2)}=(\Delta -\bar{m}\Omega /2)\,,\quad {G}_{\bar{m}}^{(2)}=\frac{{F}^{2}}{\chi }{J}_{\bar{m}}\left(\frac{2\zeta }{\Omega }\right).$$

(9)

This formula can be generalized to arbitrary n-photon resonances, with ${\Delta }_{\bar{m}}^{(n)}=\Delta -\bar{m}\Omega /n$ and ${G}_{\bar{m}}^{(n)}\propto {J}_{\bar{m}}\left(n\zeta /\Omega \right)$. Thus, for detunings close to the nth multiphoton transition, a new LZSM interference pattern should emerge, characterized by an effective modulation frequency Ω/n. It is this scaling that differentiates the weakly and strongly modulated cases, c.f. Figs. 5a, e and 4d. While previously, for Ω ≫ ∣χ∣, the standard LZSM sidebands were dressed by Kerr multiphoton resonances, we now find that, for Ω ≪ ∣χ∣, each Kerr n-th multiphoton resonance is dressed by LZSM sidebands with effective modulation frequency Ω/n.

Fig. 5: Controllable Floquet states with the N = 10 device in the Kerr regime.

Through the figure, we set the drive input power to P_in = −128 dBm. a–d Both modulation strength ζ and frequency Ω are swept together to maintain a constant ratio ζ/Ω. This choice ensures that the effective drives in Eqs. (3) and (7) are kept constant. This allows enhancing the visibility of the transition between the strongly- and weakly-modulated cases. a Sketch of the results of Eq. (7) for the transition $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$ (purple, labeled $\left\vert 1\right\rangle$) and $\left\vert 0\right\rangle \to \left\vert 2\right\rangle$ (green, labeled $\left\vert 2\right\rangle$). For $\left\vert 1\right\rangle$, the pattern radiates from Δ = 0 with frequency modulation Ω. For the multiphoton transition to $\left\vert 2\right\rangle$, the LZSM interference pattern is centered at Δ = χ and scales with Ω/2. b Simulation of ∣S₂₁∣ as a function of Δ and Ω with the full quantum model in Eq. (2) (see Supplementary Information for details on the simulation method), having fixed ζ/Ω = 0.86. The corresponding measurement is shown in (c) and perfectly overlaps with the results of the numerical simulation. The black arrows in (a–d) mark the position of two avoided crossings, where the “bare levels” in (a) interact and hybridize in (b–d). The crossings are further highlighted by the solid (associated with $\left\vert 1\right\rangle$) and dashed ($\left\vert 2\right\rangle$) lines in (b). The amplitude of the different avoided crossings can be controlled by modulating the Bessel functions ${J}_{\bar{m}}(n\zeta /\Omega )$ as shown in (d), where a larger ratio ζ/Ω is chosen. e As in panel (a), the sketch of the results of Eq. (7) for Ω = ∣χ∣ and as a function of Δ and ζ. In this “bare picture”, the two independent LZSM interference patterns scale with Ω and Ω/2 for $\left\vert 1\right\rangle$ and $\left\vert 2\right\rangle$, respectively. f Full quantum simulation and g corresponding measurement of ∣S₂₁∣ for Ω = ∣χ∣. The position of some LZSM resonances in the bare picture is superimposed in (f) as a guideline for the eye. h Repeating the measurement for Ω = 1.5∣χ∣, we observe line splittings, indicating a modulation of the coupling between different Floquet states.

For the device under consideration, accessing the weakly modulated case would require κ ≪ Ω/n to distinguish between the different LZSM dips. To better resolve this feature, we propose the following driving scheme. We fix the ratio ζ/Ω to have a constant effective drive, according to both effective theories in Eqs. (3) and (7). We then increase Ω and ζ, to cross from the weakly modulated ∣χ∣ > Ω to the strongly modulated case ∣χ∣ < Ω. This is shown in Fig. 5b–d where, for small Ω, we distinctly see the expected LZSM dips associated with the second multiphoton resonance $\left\vert 0\right\rangle \to \left\vert 2\right\rangle$ and with a slope Ω/2. We note that such two-photon LZSM transitions were recently reported in a linearly-modulated three-level system⁷⁵, with a similar factor two in the LZSM velocity compared to regular single-photon LZSM transitions.

Non-perturbative regime

The weak- and strong-modulation regimes have very different scales from each other [c.f. the effective models in Eqs. (8) and (9)]. We thus expect that there is a non-perturbative passage from weak- to strong modulation through some effective interaction, and the transition between these two regimes cannot be explained using any of the two effective theories alone.

Particularly interesting are the values of Ω ≃ n∣χ∣, where the system passes from the weak- to the strong-modulated case for a specific state $\left\vert n\right\rangle$. At these values, it is possible for a n-photon resonance to exactly match the LZSM dips of a different m-photon resonance. We observe the signatures of avoided level crossings between resonances in Fig. 5b, c, indicating that the $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$ and $\left\vert 0\right\rangle \to \left\vert 2\right\rangle$ resonances interact through the action of an effective emergent coupling. In this sense, these different resonances constitute a controllable synthetic Floquet space, where changing Ω and ζ allows selecting an effective interaction between these multiphoton resonances. This is also evident in Fig. 5d, where the ratio Ω/ζ is changed, leading both to different interference patterns and different splittings between the Floquet states.

To further highlight an example of these non-perturbative effects, in Fig. 5f, g we fix Ω = ∣χ∣. First, we numerically simulate the interplay of these effects in Fig. 5f. We predict a partial overlap between the second multiphoton transition $\left\vert 0\right\rangle \to \left\vert 2\right\rangle$ with the first LZSM dip associated with the $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$ transition at Δ = −Ω. For increasing modulation strength ζ, the LZSM structure predicted by Eq. (7) is observed, although strongly deformed compared to the prediction of the effective model due to the presence of the LZSM lobe associated with the $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$ resonance. These theoretical predictions are completely recovered in the data in Fig. 5g. Finally, in Fig. 5h we fix Ω = 1.5∣χ∣, and we observe a line splitting of several resonances, indicating again the merging and interaction between $\left\vert 0\right\rangle \to \left\vert 2\right\rangle$ and $\left\vert 0\right\rangle \to \left\vert 1\right\rangle$ transitions. For larger drive amplitudes (not shown), the system shows an extremely rich structure that cannot be simply assigned to any of these original phenomena. Note also the asymmetric nature of the interference pattern, determined by the negative sign of the Kerr nonlinearity.

LZSM beyond the qubit approximation: Duffing regime

Finally, we investigate the Duffing regime κ > ∣χ∣ for a drive amplitude sufficiently large to deviate from the linear regime (see Eq. (24)). For the intermediate drive amplitudes shown in Fig. 6a, b, the various dips are well separated despite showing an asymmetric bending of ∣S₂₁∣. When compared with Fig. 2g, h, we observe a similar deformation of the transmission dips. Therefore, we assign this feature to the emergence of bistability triggered by the competition between detuning and Kerr nonlinearity. For these parameters, we find that the formula in Eq. (3) captures the deformation of the dips, as discussed more in detail in the Supplementary Information. Thus, the system behaves as a collection of independent Duffing oscillators and the overall effect of the modulation is to rescale the drive amplitude F of each sideband.

Fig. 6: LZSM interferometry with the N = 32 device in the Duffing regime.

a–c Measured magnitude of S₂₁ vs Δ and ζ for increasing drive power P_in. The dashed color lines refer to the values of ζ chosen for panels (d–f). The star in (c) indicates the value where the analysis of chaos is performed in Fig. 7d. d–f Measured S₂₁ as a function of detuning and for three specific values of ζ/2π: 41.3 MHz (green curve), 101.1 MHz (orange curve), and 161.2 MHz (purple curve). The black superimposed curves are the results of the numerical simulation of the full quantum model for the parameters in Table 1 (detailed in “Methods”). The modulation frequency is set to Ω/2π = 30 MHz. The systematic discrepancy in the position of the dips between theory and experiments is due to the nonlinear dependence of the modulation of the flux amplitude discussed in the Supplementary Information.

When the driving power is further increased in Fig. 6c, several of the neighboring LZSM dips eventually overlap. This case cannot be simply captured as separated LZSM interferences, and it is qualitatively different from all the previously studied cases. The simplified picture of Eq. (3) thus breaks down, and the system becomes multimodal and behaves as a set of interacting nonlinear cavities. Nonetheless, the full simulation of the quantum Floquet model matches the data in all regimes, as shown in Fig. 6d–f.

As detailed in the methods section, the merging of several modes and the qualitative change in the system’s behavior can be associated with the emergence of dissipative quantum chaos. At weak pump power, the LZSM dips correspond to distinct Fourier modes, each characterized by its own frequency. As the pump power increases, these modes begin to interact and merge, analogous to phenomena observed in strongly driven resonators^45,46, thereby suggesting the onset of chaos in the Floquet system. Classical chaos is characterized by a system’s sensitive dependence on initial conditions, often quantified by a positive Lyapunov exponent⁷⁶. On the other hand, the characterization of quantum chaos often relies on the spectral properties predicted by random matrix theory^77,78,79,80. In open quantum systems, quantum chaos can be extended through the analysis of the Liouvillian superoperator, which governs the dynamics of the density matrix and provides insights into integrability and chaos. The complex spacing ratio is an efficient criterion for distinguishing between integrable and chaotic regimes, as it assesses the distribution of spacings between eigenvalues⁸¹. However, as shown in the Methods section, applying the usual complex spacing ratio criterion to Floquet systems fails to capture the nuances of dissipative quantum chaos. Instead, we generalize the spectral statistics of quantum trajectories (SSQT) criteria introduced in ref. ⁴⁵ to Floquet systems, demonstrating its relevance and correctness in identifying chaotic behavior (see Fig. 9). This refined approach allows for a precise analysis of the system’s dynamics, accurately pinpointing the transition to chaotic phases.

Merging of sidebands: signature of dissipative quantum chaos

Utilizing the novel criterion developed in the methods for Floquet dissipative quantum systems, we demonstrate that the parameters predicting chaos in the model correspond precisely with those where the sidebands merge.

We investigate LZSM interference for three values of modulation strength ζ as a function of the driving power P_in, as shown in Fig. 7a–c. As in all the other experiments presented in this work, measurements are done in a steady state and are thus independent of the initial conditions of the system. At low driving power, we find a linear regime where m dips appear separated by the frequency Ω/2π = 30 MHz and with visibility given by Bessel functions ${J}_{\bar{m}}(\zeta /\Omega )$. This regime is remarkably similar to that of several nonlinear modes separated by the same frequency Ω. As the driving power increases, each of these dips initially follows the typical Duffing behavior of a single resonator, as already mentioned. For high enough input power, however, these individual dips disappear and merge, leading to a very broad response of the system. At this point, one completely loses the notion of individual synthetic modes and their bistability.

Fig. 7: Multimodal-like behavior in the Duffing regime.

a–c Measurement of ∣S₂₁∣ for increasing drive power, fixed frequency modulation Ω/2π = 30 MHz and increasing ratios ζ/Ω ≈ 1.4 (a), ζ/Ω ≈ 2.6 (b), and ζ/Ω ≈ 3.8 (c). For low input powers the system behaves as a collection of noninteracting nonlinear modes, each one well separated from the others. For larger values of P_in, the system enters a phase characterized by a single broad response where the notion of isolated mode is lost. Such a response can be observed in multimode nonlinear systems and has been associated with a transition from integrability to dissipative quantum chaos⁴⁵. To show that this is indeed a dissipative quantum chaotic phase we plot in (d) the histogram of the probability density p(s) of the level spacings s obtained by diagonalizing the Floquet Liouvillian in the broad-response region indicated by the star in (a). Parameters are set to ζ/2π = 41.3 MHz, Ω/2π = 30 MHz, Δ = −1.1Ω and F/2π = 49.5 MHz (P_in ≈ −105 dBm). The cutoff in the Hilbert space is set to 90. The solid black (orange) curve represents the ideal Poisson (Ginibre) distribution given by Eqs.(15) and (16) associated with integrability (chaos).

The merging and broadening of the dips of the scattering coefficient ∣S₂₁∣ in Fig. 7a occur for an input power P_in ≈ −108 dBm, which coincides with the point where dissipative quantum chaos emerges according to our theory, as reported in Fig. 9 of the Methods section. In Fig. 7d, we plot the probability density of the level spacings obtained by diagonalizing the Floquet Liouvillian for the parameters indicated by a star in Fig. 7a where LZSM dips have merged. It has been shown that integrable systems exhibit Poisson-distributed level spacings, indicating no level repulsion, while chaotic systems follow Ginibre statistics, characterized by level repulsion and non-Hermitian random matrix behavior^45,80. We find that, upon the merging of the Floquet modes, the Floquet Liouvillian level statistics conform to the Ginibre distribution [see Eq. (16)], indicating a clear transition to the dissipative quantum chaos regime.

The onset of the chaotic phase can also be controlled by tuning the spacing between LZSM resonances through the modulation frequency Ω, as shown in the Supplementary Information. For instance, the separated bistable regions of Fig. 6b would start overlapping by decreasing Ω, potentially resulting in a chaotic state.

Discussion

This article investigates the physics of LZSM interference beyond the conventional two-level approximation. By employing two nonlinear superconducting resonators—one in the Kerr (nonlinearity larger than dissipation rate) and the other in the Duffing (nonlinearity smaller than dissipation rate) regime—we have established a general paradigm for studying LZSM interference in bosonic systems. We have developed a unified model that accurately describes the observed phenomena across all parameter regimes before the onset of many-body-like effects.

At low driving powers, we have shown that interference patterns remain independent of the system's nonlinearity, preventing the distinction between linear and nonlinear resonators. However, at higher driving powers, we have uncovered novel effects arising from the interplay between modulation and nonlinearity, with the dissipation rate playing a crucial role in shaping the emergent features. For large enough modulation frequency Ω with respect to the nonlinearity ∣χ∣, the sidebands remain well separated and the standard LZSM picture can be extended to account for nonlinear effects. The nonlinearity of the resonator dresses each LZSM interference lobe by the nonlinear features observed in Fig. 2. For ∣χ∣ < κ, we observe continuous bending of the LZSM interference pattern. On the other hand, for ∣χ∣ > κ, we observe how multiphoton resonances are reproduced all through the LZSM interference pattern. For Ω ≪ ∣χ∣, we observed a different regime of multiphoton LZSM interferences. For instance, when ∣χ∣ > κ, each Kerr multiphoton resonance is dressed by LZSM sidebands. The resulting pattern is determined by an effective n-photon absorption equivalent to an n-photon drive that is dressed by the modulation. This results in a characteristic Ω/n modulation of the n-photon LZSM interference pattern, similar to those recently observed in ref. ⁷⁵ for a single passage through the avoided crossing.

All of these diverse phenomena occurring across a wide range of device parameters are effectively captured by our extension of the standard LZSM transition paradigm, see Eq. (3). This demonstrates the efficiency of the LZSM formalism in predicting nonlinear resonator dynamics in Floquet regimes.

Beyond this paradigm, we investigated regimes where different sidebands begin to overlap and interact. All observed features in this regime are quantitatively reproduced through full quantum simulations of the Floquet model, which is detailed in section I. of the Supplementary Information. In the Kerr regime, we demonstrated that when the modulation frequency is commensurate with the nonlinearity, level crossings form between LZSM sidebands. Moreover, the interaction between these Floquet states can be tuned via drive and modulation parameters. Conversely, in the Duffing regime, we theoretically predicted and experimentally observed the overlap and merging of different sidebands, and how it coincides with quantum chaotic behavior. The significance of this finding is twofold. Theoretically, it contributes to recent efforts to provide an operational definition of chaos tied to measurable quantities. Our extension of dissipative quantum chaos to Floquet systems is general and can be applied to other periodically modulated quantum systems. Experimentally, our work is relevant to superconducting quantum circuits, a leading platform for quantum computing and error correction. Recent studies predict that quantum chaos can impair quantum information storage and manipulation^45,47,82,83. Our work provides one of the first indirect observations of DQC in a fundamental component of superconducting quantum hardware.

From a fundamental point of view, the time features of the system remain to be investigated. Indeed, in the absence of frequency modulation, switching dynamics of conventional Duffing oscillators in the bistable regime have been thoroughly studied, including phenomena such as the quantum-to-classical transition^36,40 and the two-photon driven case^41,84,85. Applying frequency modulation is expected to modify the critical phase diagram, potentially offering new ways to control and shape dissipative phase transitions with possible applications in quantum sensing^43,86,87. Additionally, in a regime where sidebands merge and lead to chaos, the system dynamics may become significantly richer and depart from standard bistable behaviors. Furthermore, while our current analysis primarily utilizes spectral statistics to investigate chaos, other tools such as out-of-time-order correlations (OTOCs) could be developed within an open and dissipative formalism to investigate even more general features, such as quantifying quantum information scrambling and sensitivity to initial conditions^88,89,90. While the open system formulation of OTOCs to dissipative Kerr resonators has been used^45,46, extending these techniques to Floquet systems requires a robust definition of time reversion in the presence of periodic modulations.

Overall, our work significantly advances the current understanding of LZSM and Floquet physics, shedding light on the intricate interplay between interference and nonlinear effects. While many studies have demonstrated the applications of LZSM phenomena in two-level systems⁷, we anticipate our work enabling similar benefits for multilevel nonlinear bosonic systems. Our findings offer exciting perspectives for controlling and engineering Floquet states and synthetic dimensions^70,91, with potential extensions to systems involving multiple cavities^92,93,94,95 and higher-dimensional synthetic spaces^54,96. Moreoever, our platform is well-suited to investigate the rich interplay between Floquet physics and topology^50,51, with potential extensions to nonlinear topology^62,97,98. The merging of multiple interference peaks, both in the Kerr and Duffing regimes, offers several potential applications. In the Kerr regime, we show the presence of an “effective interaction” between Floquet states⁹⁹, that can be either enabled or suppressed by tuning the modulation parameters. These could be used to, e.g., engineer transition and interaction between states with different decay rates, and provide opportunities to simulate non-Markovian baths¹⁰⁰. Conversely, in the Duffing regime, this Floquet approach to dissipative chaos has reduced susceptibility to disorder and fabrication mismatches when compared to alternative implementations in extended systems^101,102,103. This opens possibilities to use this LZSM interference to simulate emergent chaotic features in engineered dissipative and time-dependent configurations, such as ultrastrongly coupled light-matter systems^104,105, devices in the noisy intermediate-scale quantum (NISQ) era^46,47, and two-photon driven systems^41,75,106. Finally, LZSM protocols have been used as quantum simulators of Kibble–Zurek mechanisms^107,108. The extension of a similar protocol to multilevel phenomena is still lacking.

Methods

Device fabrication

The devices are fabricated on a 525 μm thick high-resistivity intrinsic 4-inch silicon wafer. The substrate is cleaned using piranha solution, followed by the removal of native oxide via a 1% hydrofluoric acid treatment. Immediately after, a 150 nm thick layer of aluminum is deposited by e-beam evaporation at a rate of 0.2 nm s⁻¹. Alignment markers are defined through photolithography, e-beam evaporation of a 5 nm thick Ti layer and a 55 nm thick Pt layer, and subsequent lift-off. The waveguide and control lines are patterned via photolithography and wet etching for 2 min 30 s in TechniEtch Alu80 etchant. E-beam lithography is employed to define the Josephson junctions of the SQUID array. The wafer is coated with a bilayer resist stack consisting of 500 nm of MMA EL9 and 450 nm of PMMA 495K A8. The mask is then patterned using e-beam lithography (Raith EBPG5000+ at 100 keV) and developed in a 1:3 MIBK:IPA solution for 2 min. The Josephson junctions have a square shape with a width of approximately 350 nm. The Josephson junctions are formed by double-angle evaporation in an ultra-high vacuum Plassys MEB550SL3 system using the Manhattan technique¹⁰⁹. This involves the deposition of 50 nm of aluminum at 0.5 nm s⁻¹ at +45° tilt angle, followed by an oxidation step of 10 min in 0.15 Torr of pure dioxygen, a second aluminum deposition of 120 nm at 0.5 nm s⁻¹ and 45° tilt angle, and a capping oxidation layer formed during 10 min in 4 Torr of pure O₂. Lift-off is performed in 80 °C 1165 remover for 4–h. A final patching step is carried out to close the loops of the isolated Josephson junctions formed with the Manhattan technique and to connect one side of the SQUID array to the ground plane. The same bilayer resist stack is used, and e-beam lithography is employed to expose the patch areas. The native oxide of the bottom aluminum layer is removed in the Plassys system by argon ion plasma milling, and a 200 nm thick aluminum layer is deposited directly after at a rate of 0.5 nm s⁻¹. Finally, the wafer is diced into 4 × 7 mm² chips using a nickel-bonded diamond blade.

Measurement setup

A schematic of the measurement setup is shown in Fig. 8. The 4 × 7 mm² die is wire bonded with aluminum wire on custom-printed circuit board. The die is then glued directly on a high-purity copper sample holder that is thermally anchored at the mixing chamber stage of a LD Bluefors cryostat with a typical base temperature of 15 mK. The sample holder is protected against external magnetic fields using two mu-metal shields. The SQUID array is coupled to a 50 Ohm coplanar waveguide in a notch configuration. The input signal is generated by a vector network analyzer (VNA) R&S ZNB20 and transmitted via a heavily attenuated coaxial line to the device feedline. The output signal passes through two double-circulators before being amplified at 4K by a LNF-LNC4_8C HEMT amplifier and at room temperature by an Agile AMT-A0284 low-noise amplifier. The signal is collected and demodulated in the VNA. Six-port Radiall R591723605 coaxial switches are placed on the mixing chamber plate on both sides of the feedline to allow switching between different devices. Both N = 10 and N = 32 devices presented in this work were connected between the same switches and thus shared the same input and output lines. The static flux of the SQUID array is controlled by applying a direct current to an NbTi external coil mounted underneath the sample holder. The direct current is applied via twisted NbTi pairs using a Yokogawa GS200 source. The frequency modulation of the SQUID array is performed by applying a signal generated by an R&S SGS 100A signal generator to the local flux line of the device. The DC noise is attenuated using a high-pass filter with a cutoff frequency of 100 kHz at room temperature. The line is further attenuated and filtered at the mixing chamber stage with a Minicircuits VLFX-300+ low-pass filter (LPF). We found that without this LPF, the internal loss rate of the SQUID arrays was increased by up to a factor of ten. We also included an additional 20 dB of attenuation between the LPF and the flux line to eliminate spurious standing wave modes between the LPF and the on-chip ground termination of the flux line. Devices N = 10 and N = 32 were housed in different sample holders in separate shields and thus did not share the same external coil and flux lines.

Fig. 8

Schematics of the full wiring of the cryostat and room-temperature electronics.

Estimation of device parameters

We then carefully characterize the two devices at their chosen flux operating points. The parameters of the devices, reported in Table 1, are obtained by fitting S₂₁ without modulating the frequency. The SQUID array is modeled as a Kerr resonator according to the Hamiltonian of (1) with ζ = 0. First we fit the transmission at low enough power to ensure an average occupation of less than one photon. This allows us to neglect the Kerr nonlinearity and the dephasing. The expression of the linear transmission coefficient S₂₁ is obtained from standard notch configuration input-output theory^41,110 as

$${S}_{21}=1-\frac{{\kappa }_{{\rm{ext}}}}{{\kappa }_{{\rm{ext}}}+{\kappa }_{{\rm{int}}}+2i\Delta }\times \frac{{e}^{i\phi }}{\cos \phi }.$$

(10)

Following the diameter correction method¹¹¹, we add the last term to compensate for impedance mismatch. To fit the measured transmissions to this expression, we first normalize the data by a background transmission measured with the SQUID threaded by a different flux, such that its frequency lies outside of the measurement range. All experimental data reported in this work are normalized this way. We then extract the precise operating frequency, as well as the internal and external loss rates of each device.

To determine the Kerr nonlinearity χ and the dephasing rate κ_ϕ, we need to fit the power dependence of the transmission which is reported in Fig. 2. A simple analytical model could be used for weakly anharmonic devices satisfying ∣χ∣ ≪ κ^41,112. Instead we directly solve the Lindblad master equation (2) to find the intra-cavity field α, again setting ζ = 0 in the Hamiltonian. This model is valid for both devices studied in this work and accounts for dephasing. Using input-output theory, we convert α to the transmission scattering parameter using the following relation

$${S}_{21}=1-i\frac{{\kappa }_{{\rm{ext}}}\,\alpha }{2F}.$$

(11)

The drive amplitude F is related to the input power P_in as

$$F=\sqrt{\frac{{P}_{{\rm{in}}}{\kappa }_{{\rm{ext}}}}{\hslash {\omega }_{d}}}.$$

(12)

We start by fitting the device N = 10 in the Kerr regime. We perform a global simultaneous fit of approximately ten frequency sweeps at different driving powers. We use the parameters obtained from the low-power fit and keep three independent fitting parameters: κ_ϕ, χ, and the attenuation of the input drive line. Because single multiphoton transitions are well-resolved with the Kerr device, we can obtain all three parameters without prior calibration of the input attenuation. The Kerr multiphoton resonances reported in Fig. 2c–e are not equispaced by χ, instead the spacing increases for larger $\left\vert n\right\rangle$. We attribute this effect to non-negligible higher-order nonlinearities from the expansion of the Josephson cosine potential. To accurately reproduce the experimental data of the N = 10 device, we also include a term of the form ${\chi }^{(5)}{({\hat{a}}^{\dagger })}^{3}{\hat{a}}^{3}$ in the model, and find a value of χ⁽⁵⁾ ≈ 5%χ≈ −2π × 1.1 MHz.

Finding the Kerr nonlinearity of the Duffing device, however, requires knowing the input attenuation. But the feedline of the Kerr and Duffing devices are connected on the same microwave switch, as depicted in Fig. 8. Therefore we assume that the input attenuation obtained from the fit of the Kerr device is also valid for the Duffing device. We perform a similar global fit of the power dependence of the transmission of the Duffing device, this time with only two free fitting parameters: χ and κ_ϕ. Simulations of the Kerr shift of both devices are shown in Fig. 2.

Analysis of dissipative quantum chaos

Classical chaos is defined by the sensitivity of a system’s dynamics to initial conditions, often characterized by a positive Lyapunov exponent⁷⁶. Quantum chaos, in both isolated and open systems, is typically described through the quantum chaos conjecture^77,78,79,80, i.e., assuming the system has a meaningful classical limit that exhibits chaos, one can conjecture that the spectral properties of the time evolution generator align with the universal predictions of random matrix theory. For models without a classical limit, random matrix theory predictions are still employed to define quantum chaos^81,113,114 due to their success in forecasting the properties of quantum systems without a classical counterpart^115,116,117.

A criterion for dissipative quantum chaos in Floquet systems

For time-independent Liouvillian systems, integrability and dissipative quantum chaos in the open quantum system are often characterized via the spectral properties of the Liouvillian. For a time-independent system, the equation of motion reads $\partial \hat{\rho }/\partial t={\mathcal{L}}\hat{\rho }$ where ${\mathcal{L}}$ is the non-Hermitian Liouvillian superoperator. As $\hat{\rho (t)}=\exp ({\mathcal{L}}t)\hat{\rho }(0)$, the eigendecomposition of ${\mathcal{L}}$ fully characterizes the dynamics of the density matrix. The right eigenoperators ${\hat{\eta }}_{j}$ and left eigenoperators ${\hat{\sigma }}_{j}$ of ${\mathcal{L}}$¹¹⁸ are defined by

$${\mathcal{L}}{\hat{\eta }}_{j}={\lambda }_{j}{\hat{\eta }}_{j},\qquad {{\mathcal{L}}}^{\dagger }{\hat{\sigma }}_{j}={\lambda }_{j}^{* }{\hat{\sigma }}_{j},$$

(13)

where λ_j are complex, ${\rm{Re}}({\lambda }_{j})\le 0$, and $\,{\text{Tr}}\,({\hat{\sigma }}_{j}^{\dagger }{\hat{\eta }}_{k})={\delta }_{jk}$.

Chaos is then characterized through the statistical distribution of the spacings of the complex Liouvillian eigenvalues {λ_j}⁸⁰. In particular, one studies the distribution of nearest-neighbor eigenvalue spacings

$$p(s)=\sum _{j}\delta ({s}_{j}-s),$$

(14)

where ${s}_{j}=| {\lambda }_{j}-{\lambda }_{j}^{{\rm{NN}}}|$, with ${\lambda }_{j}^{{\rm{NN}}}$ the eigenvalue closest to λ_j in the complex plane. In integrable dissipative systems, s follows a 2D Poisson distribution

$${p}_{2{\rm{D}}}(s)=\frac{\pi }{2}s{e}^{-\frac{\pi }{4}{s}^{2}},$$

(15)

while for chaotic dissipative systems, the level spacing distribution follows the Ginibre distribution of Gaussian non-Hermitian random matrices ensembles

$${p}_{{\rm{GinUE}}}(s)=\left(\mathop{\prod }\limits_{k=1}^{+\infty }\frac{\Gamma (1+k,{s}^{2})}{k!}\right)\mathop{\sum }\limits_{j=1}^{+\infty }\frac{2{s}^{2j+1}{e}^{-{s}^{2}}}{\Gamma (1+j,{s}^{2})}.$$

(16)

An unfolding procedure, in which the uncorrelated part is removed from p(s) in Eq. (14), is required to evaluate the level statistics from the spectrum and for the proper characterization of chaos¹¹⁹. We adopt that described in ref. ¹¹⁴.

An alternative, efficient way to perform this analysis is the complex spacing ratio⁸¹

$${z}_{j}=\frac{{\lambda }_{j}^{{\rm{NN}}}-{\lambda }_{j}}{{\lambda }_{j}^{{\rm{NNN}}}-{\lambda }_{j}}={r}_{j}{e}^{i{\theta }_{j}},$$

(17)

with ${\lambda }_{j}^{{\rm{NN}}}$ the eigenvalue closest to λ_j in the complex plane, and ${\lambda }_{j}^{{\rm{NNN}}}$ the second-nearest neighbor to λ_j. The average values 〈r〉 of r_j and $\langle \cos \theta \rangle$ of $\cos {\theta }_{j}$, can be used as indicators of dissipative quantum chaos. For a 2D Poisson distribution, associated with an integrable system, 〈r〉 = 0.66, and $-\langle \cos \theta \rangle =0$. For the Ginibre distribution, i.e., chaos, 〈r〉 = 0.74, and $-\langle \cos \theta \rangle =0.24$.

The spectral definition of DQC presented above can be extended to Floquet systems through the introduction of the Floquet Liouvillian superoperator ${{\mathcal{L}}}_{{\rm{F}}}$. Also ${{\mathcal{L}}}_{{\rm{F}}}$ can be diagonalized obtaining its right (left) eigenvectors ${\hat{\eta }}_{j}$ (${\hat{\sigma }}_{j}$) and the Liouvillian spectrum {λ_j}

$${{\mathcal{L}}}_{{\rm{F}}}{\hat{\eta }}_{j}={\lambda }_{j}{\hat{\eta }}_{j},\qquad {{\mathcal{L}}}_{{\rm{F}}}^{\dagger }{\hat{\sigma }}_{j}={\lambda }_{j}^{* }{\hat{\sigma }}_{j},$$

(18)

which satisfy the bi-orthonormality condition $\,{\text{Tr}}\,\{{\hat{\sigma }}_{j}^{\dagger }{\hat{\eta }}_{l}\}={\delta }_{jl}$. The very same spectral criteria can then be applied to the Floquet eigenvalues.

Extending the spectral statistics of quantum trajectories for Floquet systems

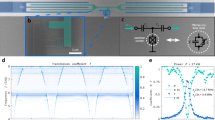
The above spectral signatures alone, however, do not correctly capture the emergence of dissipative quantum chaos in the system considered in this work. For instance, in Fig. 9a we plot the indicator $\langle \cos \theta \rangle$ as a function of the input power P_in. For these input powers, the prediction of the spectral analysis of the Floquet Liouvillian is that the system is always in a chaotic phase, despite it being almost a pure state for weak P_in [c.f. Fig. 9b]. We conclude that this straightforward analysis of chaos cannot capture the relevant features of the model under consideration.

Fig. 9: Analysis of dissipative quantum chaos using the SSQT criterion detailed in ref. ⁴⁵ and generalized to Floquet states here.

a Theoretical indicator of chaos $\langle \cos \theta \rangle$ introduced in ref. ⁸¹ computed on the full Floquet-Liouvillian spectrum (red line and circles) and on the eigenvalues selected by the SSQT criterion (green line and squares). While the spectral analysis on the full Liouvillian indicates the presence of chaos independently of the drive amplitude for the parameters considered in the plot, the SSQT criterion identifies the broadening of the Duffing peaks in Fig. 7a–c (gray rectangle) with a dissipative quantum chaotic phase for the Floquet steady state ${\hat{\rho }}_{{\rm{ss}}}^{F}$. When the number of selected eigenvalues is smaller than 100 a statistically significant analysis can not be carried out, and we set $\langle \cos \theta \rangle =0$. b Purity $\,{\text{Tr}}\,({[{\hat{\rho }}_{{\rm{ss}}}^{{\rm{F}}}]}^{2})$ of the Floquet steady state ${\hat{\rho }}_{{\rm{ss}}}^{{\rm{F}}}$. The onset of steady-state quantum chaos in (a) coincides with the drop of the purity of the steady state below 0.1. We use the parameters of Fig. 7a, the cutoff in the Hilbert space is fixed to 90, and ${c}_{\min }$ is selected as discussed in the text.

Given the lack of predictive results, here we generalize the theoretical framework of the spectral statistics of quantum trajectories (SSQT) introduced in ref. ⁴⁵. First, one remarks that the Lindblad master equation admits also a stochastic unraveling in terms of quantum trajectories $\left\vert \psi (t)\right\rangle$, combining the Hamiltonian dynamics with a continuous monitoring of the environment^120,121. The wave function $\left\vert \psi (t)\right\rangle$ can be interpreted as a single stochastic realization of the dissipative dynamics whose average reproduces the predictions of the Lindblad master equation (2). As discussed in ref. ⁴⁵, since the system discussed in this article does not have any weak or strong Liouvillian symmetry, all the possible unravelings are expected to give the same information about steady-state integrability and chaos. We can therefore assume a diagonal unraveling which we can write down considering the spectral decomposition of the Floquet steady state

$${\hat{\rho }}_{{\rm{ss}}}^{{\rm{F}}}=\sum _{k}{p}_{k}\left\vert {\psi }_{k}\right\rangle \left\langle {\psi }_{k}\right\vert .$$

(19)

Using the spectral decomposition introduced in Eq. (18), one can then define

$${\hat{\rho }}_{k}=\left\vert {\psi }_{k}\right\rangle \left\langle {\psi }_{k}\right\vert =\sum _{j}{c}_{k,j}(t)\,\,{\hat{\eta }}_{j}.$$

(20)

This procedure allows associating to each eigenvalue λ_j the relative spectral weight c_k,j. We select the Liouvillian eigenvalues λ_j, for which $| {c}_{k,j}(t)|\, > \,{c}_{\min }$. We set the cutoff ${c}_{\min }=\bar{C}/1000$ where $\bar{C}$ is the average of the spectral weights in Eq. (20), as detailed in ref. ⁴⁵. For the Floquet Liouvillian, we found that some of the ∣c_j∣ were very large (order of magnitudes bigger than one). As the average procedure of the spectral weights would have been affected by those outliers, we restrict the mean to the ones such that ∣c_j∣ ≤ 1. Such a choice is justified as a spectral coefficient ∣c_j∣ > 1 will be for sure chosen with the SSQT protocol, and we get a meaningful ${c}_{\min }$ as in ref. ⁴⁵. On each ${\hat{\rho }}_{k}$ we perform the spectral analysis by computing, e.g., the complex spacing ratio for the selected eigenvalues ${\langle \cos \theta \rangle }_{k}$. We finally obtained $\langle \cos \theta \rangle ={\sum }_{k}{p}_{k}{\langle \cos \theta \rangle }_{k}$.

In Fig. 9a, the green curve represents the results of the SSQT criterion. Compared to the spectral statistics applied to the full Floquet Liouvillian spectrum, we see a profoundly different behavior of the system as a function of the drive amplitude. Notably, comparing the results of Fig. 9a with the purity of ${\hat{\rho }}_{{\rm{ss}}}^{{\rm{F}}}$ Fig. 9b, this time we observe that it drops below 0.1 only when we enter the steady-state chaotic region. This result ultimately demonstrates the necessity of the SSQT criterion to correctly interpret the onset of chaos in open quantum systems.

Linear and qubit regime approximations

Under sufficiently weak drive, the two devices can be approximated as respectively qubit and linear resonators. It is in this regime that we observed standard LZSM interferences as shown in Fig. 3. We now give explicit conditions for the linear approximation to hold.

For the strongly nonlinear N = 10 resonator, one can show that, assuming at most two photons in the system, the maximum of the two-photon population occurs at the multiphoton resonance Δ = χ, where

$$\left\langle 2\left\vert {\hat{\rho }}_{{\rm{s}}s}\right\vert 2\right\rangle =\frac{2{F}^{4}}{9{F}^{4}+2{\kappa }^{2}\left[2\left({\kappa }^{2}+{\chi }^{2}\right)-5{F}^{2}\right]}\simeq \frac{{F}^{4}}{2{\kappa }^{2}{\chi }^{2}}.$$

(21)

It follows that F² ≪ ∣χ∣κ ensures the validity of the qubit approximation

For the weakly nonlinear N = 32 resonator, we consider the semiclassical (coherent state approximation) ${\hat{\rho }}_{{\rm{s}}s}=\left\vert \alpha \right\rangle \left\langle \alpha \right\vert$. One finds that the photon number n = ∣α∣² satisfies

$$\begin{array}{rcl}&&\left[\frac{{\kappa }^{2}}{4}+{(\Delta +n\chi )}^{2}\right]n-{F}^{2}\\ &&\simeq 2\Delta {n}^{2}\chi +n\left({\Delta }^{2}+\frac{{\kappa }^{2}}{4}\right)-{F}^{2}=0.\end{array}$$

(22)

The solution to this equation can be expanded in powers of χ as

$$n={n}_{0}\left(1-{n}_{0}\frac{8\Delta \chi }{4{\Delta }^{2}+{\kappa }^{2}}\right),\,\,{\text{with}}\,\,{n}_{0}=\frac{{F}^{2}}{{\Delta }^{2}+{\kappa }^{2}/4}.$$

(23)

The deviation from the linear regime, defined as δn = 1 − n/n₀ is then maximal for $\Delta =\kappa /(2\sqrt{3})$, which leads to

$$\delta n=\frac{3\sqrt{3}{F}^{2}\chi }{{\kappa }^{3}}.$$

(24)

Since we are interested in the regime δn ≪ 1, we recover the condition $F < \sqrt{{\kappa }^{3}/| \chi | }$ for the linear approximation, as given in the main text.