Introduction

Quantum key distribution (QKD) enables the generation of information-theoretic security keys between two parties over insecure quantum channels, with the security of these shared keys guaranteed by the fundamental laws of quantum mechanics1,2,3,4,5. The QKD protocol can be categorized into two distinct series. Firstly, the discrete variable (DV) protocol utilizes discrete quantum degrees of freedom to encode information, such as polarization in free-space and phase coding in fiber-based scheme6,7,8. Alternatively, the continuous-variable (CV) protocol represents a natural alternative to the QKD protocol. Compared to DV systems, it can transmit more information per signal and utilize cheaper technology implementations9,10,11,12,13,14.

The backscattering of solar radiation in the atmosphere is much higher when the QKD is running during the daytime, which leads to much stronger stray light. The impact of daylight operations on QKD has been examined for over two decades, with several successful demonstrations of free-space QKD in daylight having been conducted15,16,17. Recently, using single-mode fiber coupling as spatial filtering, wavelength division multiplexing filtering technology as spectral filtering, and telecommunication wavelengths to minimize external photo noise, QKD systems can be completed during the daytime18,19,20,21. However, to overcome strong background light, it is often necessary to simultaneously use spatial, spectral, and temporal filtering techniques to reduce background noise. In previous daytime QKD experimental demonstrations, it was found that the theoretical limit of a single spatial-spectral-time mode needed to be approached to maximize the suppression of background noise21. This discovery highlights the necessity and challenge of integrating multiple filtering techniques in practical applications. First, spatial filtering needs to be implemented by collecting photons into the single-mode fiber and suppressing the corresponding field of view of the receiving telescope. However, this usually greatly increases the difficulty of tracking alignment and increases system transmission losses. In addition, the time-bandwidth product limitation between spectral filtering and time filtering prevents both spectral width and pulse width from being infinitely small simultaneously. Too narrow a spectrum will have a high requirement for the wavelength stability of the QKD light source, and will also limit the system repetition rate. However, a pulse width that is too short makes system time synchronization very difficult, especially in field experiments. All these factors significantly increase the cost and difficulty of experiments, especially in practical applications. For CV-QKD protocol, we can theoretically reduce the external background light noise by using the pattern matching of signal and bright local oscillator (LO) in homodyne detection, so that the LO (transmitted or locally generated) acts as an effective and natural noise filter in frequency22. This provides a new direction for implementing the QKD protocol under daytime conditions. Although the study of the existing free space CV-QKD mostly chooses a 700-900 nm band of light, although the band has a good atmosphere transmission efficiency, its application is limited to a quiet night usually23,24. Therefore, CV-QKD protocol has great application potential in the daytime environment, can effectively cope with the challenge of background light noise, and improves the practicality and flexibility of QKD.

In this paper, we introduce a robust free-space Gaussian modulated coherent state (GMCS) CV-QKD for intense daytime background light combined with active beam tracking and classical laser communication services to achieve daylight CV-QKD over a free-space link of 860 m for the first time. We demonstrate that daytime QKD can achieved by choosing an operating wavelength of 1550 nm to reduce the background noise caused by solar radiation and Rayleigh scattering, and by using LO polarisation-multiplexed with the signal light as spatial and spectral filters, which significantly reduces the system complexity. Combined with classical laser communication for real-time post-processing, we obtained an average SKR of about 317 kbps in real-time during the daytime and about 40 kbps after finite-key analysis. Based on this, we also implemented the GMCS CV-QKD for rainy days. Overall, our experiments verify the robustness of the GMCS CV-QKD protocol to external environmental noise, demonstrating its potential for practical applications. This work not only provides a new solution for quantum key distribution under daytime conditions but also significantly improves the reliability and efficiency of the system by incorporating classical communication techniques.

Results

Protocol

In quantum mechanics, polarization can be described by the quantum Stokes operators which read as25:

$$\begin{array}{l}\hat{{S}_{0}}={\hat{a}}_{H}^{\dagger }{\hat{a}}_{H}+{\hat{a}}_{V}^{\dagger }{\hat{a}}_{V},\quad \hat{{S}_{1}}={\hat{a}}_{H}^{\dagger }{\hat{a}}_{H}-{\hat{a}}_{V}^{\dagger }{\hat{a}}_{V},\\ \hat{{S}_{2}}={\hat{a}}_{H}^{\dagger }{\hat{a}}_{V}+{\hat{a}}_{V}^{\dagger }{\hat{a}}_{H},\quad \hat{{S}_{3}}=i({\hat{a}}_{V}^{\dagger }{\hat{a}}_{H}-{\hat{a}}_{H}^{\dagger }{\hat{a}}_{V}).\end{array}$$
(1)

in terms of the creation and annihilation operators \({\hat{a}}^{\dagger }\) and \(\hat{a}\) for orthogonal polarization modes. In our experiment, where the LO is \(\hat{{S}_{1}}\) and the signal states are measured by heterodyne detection of the \({\hat{S}}_{2,3}\), the result of the uncertainty relation is:

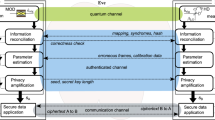
$$Var(\hat{{S}_{2}})Var(\hat{{S}_{3}})\ge {\left\vert \langle {S}_{1}\rangle \right\vert }^{2},$$
(2)

For coherent states, this equality holds, and the variances of \(\hat{{S}_{2}}\) and \(\hat{{S}_{3}}\) are equal. The preparation and measurement scheme of the GG02 protocol26 based on polarization coding is briefly described as follows. Firstly, Alice prepares displaced coherent states with quadrature components X and P, which are realizations of two random variables obeying the same zero-centered normal distribution. We use fiber-based Sagnac interferometers to modulate the polarization quantum Stokes parameter with the Gaussian distribution27. Subsequently, Alice sends her coherent states to Bob through a quantum channel. Bob simultaneous measurement of two orthogonal components by heterodyne detection without additional random basis selection. Finally, Alice and Bob perform parameter estimation, data reconciliation, and privacy amplification over an authenticated public channel to generate the final keys.

Experimental setup

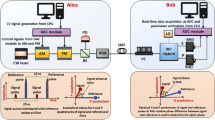
We implement a daylight free-space CV-QKD over an 860 m urban atmosphere between Alice and Bob, and the experimental setup is presented in Fig. 1. In our experiment, the acquisition, pointing, and tracking (APT) system is mainly responsible for establishing a stable channel link between two points (Alice and Bob), where the classical signals and the quantum signals of QKD are transmitted using wavelength division multiplexers (WDM). The QKD between the two points is realized with the help of the stable channel link and the classical communication service provided by classical laser communication. Alice’s transmitting telescope (Fig. 1c) is an achromatic refractor with an aperture diameter of 60 mm, mounted in a ball machine. Bob’s receiving telescope (Fig. 1d) is a Keplerian telescope with an equivalent focal length of 259 mm, including a 250 mm diameter primary mirror, mounted in a fixed mount.

Fig. 1: Setup of free-space CV-QKD.
figure 1

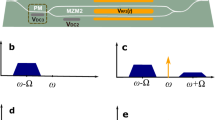
a Top view of the experimental layout at the Guilin City of China. Alice and Bob at a distance of 860 m. b The compact modulation device for polarization encoded GMCS CV-QKD. A CW laser of 1550 nm produces a repetition rate of 10 MHz and a pulse width of 20 ns through Sagnac-1. According to the Box-Muller tansform38, the generated optical pulses are injected into Sagnac-2,3 to modulate the desired Rayleigh distribution and uniform distribution, respectively. c The transmitting antenna. A fast steering mirror (FSM) and a two-axis rotary table are used for fine and coarse tracking. A dichroic mirror (DM) is used to separate the signal and classical light. A 785 nm pulsed laser shooting from Alice to Bob for classical optical communication while also providing beam position information for fine tracking. d The receiving antenna. A similar APT system to the transmitter is implemented. A polarization analyzer consisting of QWP, HWP, and PBS is used, followed by two homodyne detectors (HOM1 and HOM2). Note LD laser diode, CIR circulator, BS beam splitter, PBS polarizing beam splitter, PM phase modulator, FR Faraday rotator, NPBS non-polarizing beam splitter, QWP quarter-wave plate, HWP half-wave plate, FSM faster steering mirror, DM dichroic mirror, IF interference filter, APD avalanche photodiode.

Full size image

In general, the background noise during daytime is more than five magnitudes higher than that of a full moon at midnight under the same meteorological and geographical conditions18,28. Therefore, spectral filtering is a key to free-space QKD during the daytime. However, narrow-band filters typically incur additional losses to the signal light and require more accurate frequency calibration between the source and the filter20. Interestingly, the GMCS CV-QKD protocol is robust to incoherent background noise and can effectively suppress ambient light in free space29, thus tolerating considerable background noise without additional spectral filtering23. In our experiment, we use the polarization degree to multiplex the signal and LO in the same spatial mode which auto-compensates for atmospheric phase fluctuations and obtains excellent interference. Furthermore, atmospheric turbulence on a sunny day is considerably more severe than at night. This atmospheric turbulence has to be taken into special consideration because it not only affects the signal state but also leads to fluctuations in the LO and undesired classical excess noise. We address this issue through the use of APT, which consists of a fast steering mirror (FSM) and a two-axis turntable for fine and coarse tracking, respectively.

The detailed diagram of the transmitter side is shown in Fig. 1b. To implement the polarization-encoded GMCS CV-QKD, we use an earlier proposed polarization coding scheme based on the Sagnac interferometer27. The QKD system uses a continuous wave (CW) distributed feedback (DFB) laser diode with a wavelength of 1550 nm and a linewidth of 3 MHz. The Sagnac-1 generates pulsed light with a pulse repetition rate of 10 MHz and a pulse duration of 20 ns, and subsequent Sagnac-2 and Sagnac-3 achieve the Gaussian modulation with coherent states in the polarization degree which are connected using polarization-maintaining fibers (PMF) (see Methods for details). The classical laser communication system uses a laser with a wavelength of 785 nm for intensity modulation at the transmitter side and an avalanche photodiode (APD) with a photosensitive surface of ϕ = 0.5 mm to receive the classical signal light with a wavelength of 808 nm from the Bob side. Therefore, the received field of view is 2.26 mrad when the focal length of the signal-receiving optical system is 108 mm. The classical and quantum signals were collimated to free space by a collimator and then coupled by a dichroic mirror (DM) before being sent to the telescope (mounted in a ball machine with two-dimensional motion), Fig. 1c. We have a quantum emission optical focal length of 173 mm and a minimum divergence angle of 0.06 mrad, a classical emission optical focal length of 117 mm, and a minimum divergence angle of 1.1 mrad.

Bob’s receiving device, is shown in the inset of Fig. 1d. Classical optical communication uses an 808 nm light to transmit to Alice, and a Keplerian telescope collects the signal light with a 250 mm receiving aperture, using an APT system similar to the transmitting terminal. The 808 nm laser is output to the transmitter optics via a multimode fiber, which is defocused in front of the fiber end to achieve full aperture beams with a large dispersion angle, and the transmitter optics have a focal length of 320 mm, with a minimum divergence angle can reach 0.33 mrad. For the quantum signal receiving system, the effective aperture is 246 mm, the system focal length is 259 mm, and the maximum receiving field of view is about ± 0.03 mrad, considering that the photosensitive surface of the quantum signal receiving detector is ϕ = 0.3 mm. For the classical signal-receiving optical system with a focal length of 193 mm, a detector with a photosensitive surface of ϕ = 0.5 mm is used for reception, so the received field of view is about ± 0.07 mrad. The quantum light at 1550 nm and the classical light at 785 nm are separated by a DM. Then the quantum light passes through a 95/5 non-polarizing beam splitter (NPBS) separating a small portion for LO monitoring, and the remainder passes through a polarization analyzer consisting of the QWP, HWP, and PBS, followed by two homodyne detectors (Thorlabs, PDB230C). The classical light passes through a beam splitter into a fine-tracking CCD and a signal APD for APT and classical laser communication, respectively. All detected signals are sent into FPGA for analysis.

Experimental analysis

In Fig. 2, we show the statistical distribution of the transmission T monitored simultaneously with the quantum signals in direct detection at different times. The bin width (ΔT) is 0.1%. In addition, the mean values of atmospheric channel transmittance (Tmean) measured on the night of 15 June 2023 and at noon on 16 June were 45.4% and 44.5%, respectively. It is worth noting that the difference between the Tmean at night and during the day is not significant, but the atmospheric turbulence is stronger during the day than at night, resulting in a wider transmission distribution during the day. To further analyze the effect of the atmospheric channel on CV-QKD at different periods, we randomly select half of the data blocks each time we obtain a data block (106) for parameter estimation to obtain transmission (T) and excess noise (ξ) in our experiments, and then carry out finite-size analyses after accumulating 10 data blocks (N = 107). In Fig. 3, we compare ξ and T at different times. Figure 3(a) and (b) show the data at 20:00 on 15 June and noon on 16 June, respectively. It can be noticed that both transmittance and excess noise fluctuate in a sharper range during the daytime than during the nighttime, which is due to stronger atmospheric turbulence and background noise during the daytime compared to the nighttime.

Fig. 2: Probability distribution of the fluctuating channel transmission T, including attenuation of receiver optics.
figure 2

The bin width (ΔT) is 0.1%. a The Tmean measured on the evening of 15 June 2023 was 45.4%. b The Tmean measured at noon on 16 June 2023 was 44.5%.

Full size image
Fig. 3: T and ξ results were obtained during QKD operation at different times in two days.
figure 3

a The quiet night at 20:00 on June 15th, and b the sunny noon at 12:00 on June 16th. The left blue axis represents T and the right red axis represents ξ.

Full size image

After analyzing the data samples for the secure key rate (SKR) in both the asymptotic and finite size regimes (see Methods for details), we obtain Fig. 4. In the quiet atmosphere of the night, we can achieve relatively stable values for T and ξ, as depicted in Fig. 3a. Consequently, we can achieve stable SKR in both asymptotic and finite-size regimes, as shown in Fig. 4a. It is evident that when T remains stable, the fluctuation of ξ plays a significant role in the SKR. Due to the tranquil atmosphere of the night, we can generate an SKR of over 100 kilobits/s and 10 kilobits/s in two scenarios, respectively. Conversely, under strong atmospheric perturbations during the day, the experimentally obtained values of T and ξ, as depicted in Fig. 3b, cannot remain stable for an extended period, which could negatively impact the SKR in the finite-size regimes. As shown in Fig. 4b, the red squares representing the SKR in the finite-size regimes are lost in two cases: (1) when T is normal, there is a sharp fluctuation of ξ, and (2) when T decreases resulting in a rise of ξ. Overall, to achieve daylight operation of CV-QKD, we need to reduce the extra noise of the system while ensuring the stability of the free-space channel. It is worth noting that our system achieves SKR of over 4 kilobits/s in both asymptotic and finite-size regimes, despite the intense atmospheric perturbations at midday.

Fig. 4: CV-QKD running results obtained during the day and at night.
figure 4

a The stable SKR on the evening of 15 June 2023. b The SKR at noon on 16 June 2023. Blue dots represent SKR under asymptotic regimes, and red squares represent SKR under finite-size regimes.

Full size image

It is worth noting that our homodyne system can operate in the daytime with stronger atmospheric turbulence without any spectral or spatial filters. However, in the field experiments, we found that the FR in the modulated system would produce modulation errors due to temperature variations, which would lead to an increase in excess noise27. To solve this problem and make the system stable, we first add a temperature control unit, and then add a global scan voltage (PM2) to evaluate the modulation offset and use PM3 to compensate for the corresponding phase. To synchronize the two terminals, we use FPGA to modulate a specific optical signal as the synchronization frame of the system at the transmitter and design a synchronization window whose window size is equal to the length of the synchronization frame at the receiver. The detection results in the window are compared to a pre-agreed synchronization frame. It should be noted that the optical link between Alice and Bob will be affected by atmospheric disturbance and other factors will lead to the loss of optical signal, if the loss is near the synchronization frame will lead to synchronization failure and the loss of a large amount of data, so it is necessary to optimize the length of synchronization frame in different situations to reduce the probability of synchronization failure.

Our experiments are carried out on sunny days, but it is also interesting to study the performance of our system in rainy weather conditions. In the previous literature19,30, some models are proposed to estimate the link attenuation of different levels of rainfall or snow rates, usually expressed in millimeters per hour (mm/h). However, these works only stop at the simulation step and do not complete the QKD in a real rainy environment. We show the statistical distribution of the transmission from 19:03 to 19:33 on June 17, with moderate rainfall (around 6 mm/h) from 19:13 to 19:33 in Fig. 5. Comparison Fig. 5a with b shows that rain causes a decrease in the transmittance. In Fig. 5c, we observe that even under rainfall conditions, the APT system maintains transmission stability, yielding a more narrow transmission distribution. By analyzing the data collected during this period, we can discern trends in T and ξ and the corresponding SKR, as illustrated in Figs. 6 and 7, respectively. We observe that rain causes a reduction in transmittance, but it does not significantly affect the excess noise. Within the same ten-minute period, the least amount of data is gathered when it rains and APT is not activated (Fig. 6b), yielding only 167 sets. Conversely, when it does not rain and APT is switched off (Fig. 6a), 233 sets of data are obtained. Similarly, when it rains and APT is activated (Fig. 6c), 203 sets of data are collected. Rainfall increases the likelihood of signal loss, necessitating the use of an APT system to track the beam’s position in real time. We calculated the SKR for the three sets of data mentioned above. The results show that the probability of successfully obtaining the SKR under progressive conditions is 68.2%, 66.4%, and 75.3%, respectively, but when it rains and APT is closed, the SKR is one order of magnitude less than the other two cases, which is 10 kilobits/s. Under the finite-size N = 107, a SKR greater than 10 kilobits/s can be achieved with the help of the APT system, even though it rains, as shown in Fig. 7c. Rainfall can diminish the SKR, but we can still generate secret keys even under moderate rainfall conditions. This result demonstrates the robustness of the GMCS CV-QKD protocol under free-space ambient noise thereby offering a new choice for the practical realization of low-cost, highly robust free-space quantum communication.

Fig. 5: Probability distribution of fluctuating channel transmission under different turbulence conditions.
figure 5

a Channel transmission distribution from 19:03 to 19:13 on June 17, when APT was off and the weather was clear. b Channel transmission distribution from 19:13 to 19:23 on June 17, when APT was off and the weather was moderate rain. c Channel transmission distribution from 19:23 to 19:33 on June 17, when APT was on and the weather was moderate rain. The with of one bin is 1%. Sunset was around 17:30. Note that the rain causes a decrease in the transmittance.

Full size image
Fig. 6: T and ξ results were obtained during QKD operation under different turbulence conditions.
figure 6

a Clear weather from 19:03 to 19:13 on June 17. b Moderate rain from 19:13 to 19:23 on June 17. c Moderate rain from 19:23 to 19:33 on June 17. The left blue axis represents \({{\rm{T}}}_{\min }\) and the right red axis represents \({\xi }_{\max }\).

Full size image
Fig. 7: CV-QKD running results obtained during different turbulence.
figure 7

a SKR under clear weather from 19:03 to 19:13 on June 17, with APT off. b SKR under moderate rain from 19:13 to 19:23 on June 17, with APT off. c SKR under moderate rain from 19:23 to 19:33 on June 17, with APT on. Blue dots represent SKR under asymptotic regimes, and red squares represent SKR under finite-size regimes. Sunset was around 19:30.

Full size image

Discussion

We successfully demonstrate the application of 860 m free space CV-QKD in daytime and rain for the first time. By using 1550 nm working wavelength and APT system, we provide an innovative solution for quantum communication in sunlight and rainy days. Our research proves the strong robustness of GMCS CV-QKD to background photo noise and provides a new choice for quantum communication between free space and existing terrestrial optical fibers. Nevertheless, in order to further improve the communication distance and SKR of the practical system in the future, there is still a lot of room for improvement in our work. It includes improving pulse repetition rate, optimizing APT technology to improve average channel efficiency and restrain fluctuation, and using more suitable reconciliation protocol to improve reconciliation efficiency. Generally speaking, the robustness of our system to background noise shows that it has great potential in practical applications in the future.

There is significant potential for improvement in our work to enhance the communication distance and SKR of the practical system. Specifically, add a feedback system that adjusts the optimal modulation variance in real-time, as per the channel conditions31. Furthermore, the use of efficient and suitable information reconciliation schemes can boost the system’s overall performance and increase the secure key rate through enhanced error correction efficiency32,33,34,35. For unstable free-space channels, the impact of the finite-key-size effect is significant, necessitating the rapid collection of a large number of symbols. This can be achieved by increasing the repetition rate of the system and employing a high-bandwidth balanced detector that combines high-speed DACs and ADCs36. Simultaneously, for faster real-time implementations, graphics processing unit (GPU)-based decoding schemes can be employed to enhance decoding throughput during post-processing37.

Methods

Experimental details

In the GMCS CV-QKD protocol based on Stokes operators coding, \(\hat{{S}_{2}}\) and \(\hat{{S}_{3}}\) can be generated from a pair of uniformly distributed random numbers (U1 and U2) on the interval [0,1] according to the Box-Muller transform38:

$$\begin{array}{l}\langle \hat{{S}_{2}}\rangle ={x}_{A}=\sqrt{-2{V}_{A}\ln {U}_{1}}\sin (2\pi {U}_{2}),\\ \langle \hat{{S}_{3}}\rangle ={p}_{A}=\sqrt{-2{V}_{A}\ln {U}_{1}}\cos (2\pi {U}_{2}),\end{array}$$

\(\hat{{S}_{2}}\) and \(\hat{{S}_{3}}\) are two independent Guassian variables with the same variance VA in shot-noise units. Perform a polar coordinate transformation on the above equations,

$$\begin{array}{l}| {\alpha }_{A}| =\sqrt{{{x}_{A}}^{2}+{{p}_{A}}^{2}}=\sqrt{-2{V}_{A}\ln {U}_{1}},\\ \theta =\arcsin ({p}_{A}/\sqrt{{{x}_{A}}^{2}+{{p}_{A}}^{2}})=2\pi {U}_{2},\end{array}$$

where θ has a uniform distribution on [0,2π], and ∣αA∣ obeys the Rayleigh distribution

$$P(| {\alpha }_{A}| )=\frac{| {\alpha }_{A}| }{{V}_{A}}{e}^{-| {\alpha }_{A}{| }^{2}/2{V}_{A}}.$$

Therefore, the Sagnac-2,3 can be used together to achieve bivariate Gaussian modulation. We loaded the modulation voltage on PM2 very weakly, making the signal light 40 dB lower than the LO, and the intensity of the LO, ∣〈S1〉∣, remained almost constant. The output light intensity of Alice is 51 μW, the inherent loss caused by the Bob receiving antenna is 1.26 dB (including this loss in the above transmittance T), and the detection efficiency of the two homodyne detectors in heterodyne detection is 64.9%. The transmission power of classical laser communication is 1.5 dBm (1.413mW) with a bit error rate (BER) of 10−7. In the APT system, the geometric center of the spot remains in the same position by adjusting the tracking system. The rapid convergence of tracking is achieved through the adjustment of step size.

In our information reconciliation step, we use slice reconciliation with low-density parity-check (LDPC) codes39,40. The slice reconciliation scheme is a useful reconciliation method in the case of a high signal-to-noise ratio (SNR)41,42. It means that the two communication parties (Alice and Bob) first quantify the Gaussian distribution variables, convert them into multiple binary sequences, and then use binary error correction code for error correction. In reverse reconciliation, Bob divides the real axis into 25 intervals of equal width, and the Gaussian variables distributed in each interval are represented by 5 binary digits43. After quantization, multi-level coding (MLC) and multi-stage decoding (MSD) schemes based on LDPC codes are used to correct the errors. Finally, a hash function is used for privacy amplification.

Secret key generation

The reverse-reconciliation secure key rate obtained for a finite-size analysis is44

$${K}_{finite}=f\frac{n}{N}[\beta I(A:B)-{S}_{{\epsilon }_{PE}}(B:E)-\Delta (n)],$$

where f is the repetition rate, N is the total block size, n is the number of points contributing to the final keys, β is the reconciliation efficiency, I(A: B) is the classical mutual information between Alice and Bob in the case of heterodyne detection, \({S}_{{\epsilon }_{PE}}(B:E)\) is the Holevo information compatible with the statistics except with probability ϵPE, and Δ(n) is the parameter related to the security of the privacy amplification. With security parameters \({\epsilon }_{PE}={\epsilon }_{PA}=\overline{\epsilon }=1{0}^{-10}\). In the asymptotic mechanism, the correction term Δ(n) is ignored, and the real channel parameters η and ξ are assumed to be known and equal to the estimated values. Our system has repetition rate f = 10 MHz, the reverse reconciliation efficiency β = 90%, the efficiency of the homodyne detector η = 0.649, the electronic noise is 0.566 SNU, the modulation variance VA is 3 SNU.

Our daytime measurements at noon on June 16th obtained an average asymptotic SKR of about 317 kbps. After finite-key analysis, the average SKR dropped to about 40 kbps. Figure 8 shows the SKR results obtained from numerical simulations and daytime experiments. The diamond marks in the figure represent our daytime experimental data, which we compared with the results of previous CV-QKD field experiments. It is worth noting that the SKR under asymptotic is cut off at a channel loss of 8.72 dB, while the SKR under finite-size effect is cut off at 3.66 dB. We can theoretically calculate the potential of our system, i.e., the longest distance in free space, using the relevant formula in ref. 22. The overall channel loss of the system can be written as

$$l=10\,{\log }_{10}({\eta }_{d}{\eta }_{atm}{\eta }_{Bob}),$$

where parameter \({\eta }_{d}=1-{e}^{-2{a}_{R}^{2}/{w}_{z}^{2}}\) is the transmissivity of the channel due to the free-space diffraction and the finite-size of the receiver, and wz is the diffraction-limited spot size of the beam at distance z. The parameter ηatm represents the effect of atmospheric extinction, and the parameter ηBob represents the intrinsic loss at the receiver. For our system, the divergence angle of the transmitter is 0.06 mrad, the effective aperture of the receiver (aR) is 246 mm, and assuming that the atmospheric extinction is 1dB/km, it can be calculated that the maximum transmission distance under asymptotic conditions is 5.62 km and 2.39 km under finite-size effect.

Fig. 8: Experimental key rates and numerical simulations of CV-QKD at noon during the day.
figure 8

Blue represents SKR in the asymptotic regime, and red represents SKR in the finite-size regime. For comparison, we also show the previous field experimental results of CV-QKD.

Full size image

Comparison with other free-space QKD experiments

In Table 1, we compare the results of this study with those of existing literature, covering key parameters such as link distance, QDK protocol, weather conditions, and SKR. The relevant data are all from refs. 19,21,24. All experiments in the table were conducted in a real environment rather than under laboratory conditions, which is significant for evaluating the feasibility of daylight QKD. The study found that for CV-QKD, ref. 24 can only achieve an SKR of 0.152 kbps under asymptotic conditions in a 460 m free-space channel on a clear night. For DV-QKD, references refs. 19 and 21 implemented the decoy-state BB84 protocol under clear daytime, and obtained SKR of 30 kbps and 0.495 kbps under finite-size, respectively. Our study achieved CV-QKD under daytime conditions for the first time and QKD under rainy conditions, and we obtained 40 kbps SKR under finite-size in an 860 m free-space channel. Overall, our study has made significant progress in many aspects, such as link distance, weather adaptability, and SKR. It has made important contributions to promoting the practical application of free-space QKD technology.

Table 1 Compare our work with other free-space QKD experiments
Full size table