Introduction

Realizing an efficient interface between light and atoms represents one of the most active research directions in experimental quantum optics. While collective interactions between light and atoms can provide a feasible solution in large atomic ensembles1,2,3, small trapped ensembles of individual atoms or ions typically utilize a complementary approach based on high numerical aperture (NA) collection optics. Diverse optical and trapping designs for efficient coverage of large solid angles with bulk optics 4,5,6,7,8,9,10,11,12,13,14,15,16,17,18 or trap-embedded optical micro-devices19,20,21,22 have been developed and tested. The implementations of such couplings have typically been significantly more challenging for trapped ions due to the high sensitivity of their motion to the proximity of dielectric surfaces, which limits the acceptable working distances of collection optics. At the same time, however, the tight and extremely stable trapping potentials of Paul traps make this platform superior in diverse fundamental tests and a broad range of applications23,24,25,26,27,28,29,30,31. The availability of an efficient interface between internal electronic states and well-defined photonic modes plays a critical role in a majority of their implementations. For example, the limited collection efficiency of light from many trapped ions to a single mode severely hinders the extendability of studies of their interaction with light to measurement of higher photon correlations32,33. Its enhancement would directly provide a required speedup of generation and distribution of entanglement between quantum repeater nodes based on trapped ions34,35,36. Recent progress of interfaces based on optical cavities demonstrated a possible viable solution31,37,38, however, the selection of a particular spatial mode structure and slow cavity decay rates impose limits on applications which rely on inherently fast dynamics39,40. On the other hand, setups employing high-NA collection optics in free space are mostly limited to absolute photon detection efficiencies on the order of a few percent, even in particularly optimized trapping and imaging geometries12,13,15,18,20,21,22. These often result in severe restrictions of other critical implementation parameters, including the trapping potential structure, motional heating rates, or restricted field of view corresponding to only single or few trapped ions.

Here, we devise and demonstrate a scheme for enhancing the collection efficiency of light from linear ion strings by tailoring their far-field scattering patterns in the limit of small collection spatial angles. We consider the realistic spatial structure of trapped ion strings in a single harmonic potential formed along the axial direction of a linear Paul trap. The relative collection enhancements in a given solid angle along the linear trap axis are optimized by scanning the length of the ion string, which can be experimentally controlled by the applied static electric potential. The experimental tests are considered in the elastic scattering limit and build on the demonstrated feasibility of scalable interference from large ion strings41,42. The performed simulations predict that within the typical motional regimes and corresponding position uncertainties of ions, there is no significant disadvantage from the non-equidistant crystal structure compared to idealized regularly spaced chains of atomic scatterers. Following the experimental implementation limited by finite thermal position uncertainties of 40Ca+ ions, we analyze the prospects of further enhancements by employing 138Ba+, which provides a more suitable configuration of longer scattering wavelength and higher spatial localization at comparable trapping frequencies and the Doppler cooling limit. In addition, an analogous collection approach for spontaneously emitted photons from ion strings prepared in an entangled state of electronic excitations can be envisaged, following the methodology demonstrated previously with two-ion crystals43.

We illustrate the capability of the proposed scheme on a generic experimental scenario with broadly feasible ion trapping parameters. The photons scattered from the linear ion string are collected within a spatial angle parameterized by the numerical aperture in a vacuum \({\rm{NA}}=\sin \theta\), where θ is half of the aperture angle. The relevance of the axial optical access along the z-direction emerges from the availability of the smallest angular gradient of the intensity patterns generated by scattering light from linear ion strings along their symmetry axis. The maximization of the coupling in the particular solid angle fraction centered along the axial direction of the trap using far-field interference critically depends on the collective constructive contribution to the coupled mode given by the relative positions of ions in the same linear harmonic potential. The equilibrium position of i-th ion in the laser-cooled string can be found by minimizing the potential energy of the whole n-ion crystal. Since the spatial configuration in a common harmonic potential is effectively determined by a single parameter, ions positions can be conveniently parameterized using a common spatial length scale \(l={({q}^{2}/(4\pi {\epsilon }_{0}m{\omega }_{z}^{2}))}^{(1/3)}\), where ϵ0 is permittivity of free space, such that zi = lvi, and vi is dimensionless equilibrium position of i-th ion found numerically by minimizing the total potential energy of the ion string44. The upper limit on the axial trapping frequency is ultimately given by the requirement on the geometrically linear configuration of ions in the trap, which sets the ratio \(A={({\omega }_{z}/{\omega }_{r})}^{2}\) to be lower than Acrit = cnB, where parameters c = 2.94 and B = −1.845,46,47. However, we note that in the experiment, other factors affecting the stability of the linear crystal and the feasibility of the optimal laser cooling will further restrict the convenient range of axial motional frequencies. The opposite - maximal spatial length scale is set to the frequency of the secular motion in the axial direction \({\omega }_{z}^{\min }={(\frac{\lambda }{4})}^{-2}\frac{\hslash }{2m}\), such that the corresponding position uncertainty at the Doppler cooling limit effectively still allows for resolving optical interference from two scatterers.

Results

Simulations

We access the feasible photon collection enhancements by evaluating the far-field spatial angular dependence of optical intensity resulting from the interference of light scattered elastically from a linear ion string. We consider a scattering of the beam with a plane wavefront and direction given by the excitation angle α. The evaluation of an intensity pattern on a spherical screen represents a generic scenario, which can be applied to comparing the achievable relative collection enhancements irrespective of the particular collection optics and photon detection system. Any linear optical imaging with a corresponding input numerical aperture will merely affect the resulting spatial intensity patterns at the detector. The complex amplitude of light field scattered from the first ion in the far-field can be written as \({U}_{1}={\varepsilon }_{0}{e}^{{\rm{-i}}(kr-{\varphi }_{0})}\), where ε0 is the amplitude, k is the wavenumber, r is the distance traveled by the wave from the first ion to the screen, and φ0 is the phase of the light at the position of the first ion. Here, we omit the residual β-dependent phase offset, as the following evaluation of interference patterns depends only on the relative phase delay of the fields scattered from different ions. The complex amplitude of light scattered from the j-th ion can then be expressed as \({U}_{j}={\varepsilon }_{j}{e}^{{\rm{-i}}(kr-{\varphi }_{0})}{e}^{{\rm{-i}}k{\Delta }_{d}^{j,1}}\), where the path difference \({\Delta }_{d}^{j,1}=l({v}_{j}-{v}_{1})(\cos \alpha -\cos \beta )\) is taken with respect to the first ion. The far-field amplitude resulting from the scattering of the monochromatic light with a plane wavefront and a wavenumber k from a string of n identical two-level scatterers is given by the sum of complex amplitudes from different ions \({U}_{{\rm{tot}}}=\mathop{\sum }\nolimits_{j = 1}^{n}{U}_{j}\). For simplification, we assume identical amplitudes εj = 1, which is an experimentally plausible approximation in the considered axial crystal spatial lengths and feasible excitation beam widths41,48. The spatial intensity pattern I(β) = ∣Utot(β)∣2 can then be evaluated as

$$\begin{array}{ll}I(\beta )\,=\,\left| \mathop{\sum }\limits_{j=1}^{n}{U}_{j}(\beta )\right|^{2}=\left|\mathop{\sum }\limits_{a,b=1}^{n}{U}_{a}(\beta ){U}_{b}(\beta )\right| =\\ \qquad\quad\,=\,\mathop{\sum }\limits_{a,b=1}^{n}\cos (k{\Delta }_{d}^{a,b}),\end{array}$$
(1)

where \({\Delta }_{d}^{a,b}\) is a path difference between fields scattered from the a-th ion and the b-th ion proportional to their mutual distance l(va − vb). We note that this simplified model neglects polarization effects and corresponding orientations of atomic dipoles, as they provide on average the same enhancement for the considered scattering from multi-ion crystals and to the reference average emission from a single emitter.

The optimization of collection enhancements can be quantified by the evaluation of the maximal photon flux ΦNA(n) = ∫ΩIdΩ within a given solid angle \(\Omega =2\pi (1-\cos \theta )\) over experimentally feasible spatial length scales l. Equivalently, parametrization by the corresponding numerical aperture \(\theta =\arcsin ({\rm{NA}})\) can be employed. Due to the circular symmetry of the scattering patterns around the z-axis, the photon flux can be evaluated in a paraxial limit, evaluated in spherical coordinates as \({\Phi }_{{\rm{NA}}}(n)=\mathop{\int}\nolimits_{\phi = 0}^{2\pi }\mathop{\int}\nolimits_{\beta = 0}^{\theta }I\sin \beta {\rm{d}}\beta {\rm{d}}\phi =2\pi \mathop{\int}\nolimits_{0}^{\theta }I(\beta )\sin \beta {\rm{d}}\beta\). Using the overall flux from an n ion string Φ4π(n) = n4π, the collection efficiency can be defined as \({P}_{{\rm{D}}}=\frac{{\Phi }_{{\rm{NA}}}}{{\Phi }_{{\rm{4\pi }}}}\), where ΦNA denotes the conventional parametrization by the numerical aperture NA. For accessing a more direct estimation of the enhancement, the relative enhancement factor PD,rel can be defined as the collection efficiency for the n ion string normalized by the collection efficiency for a single ion

$${P}_{{\rm{D}},{\rm{rel}}}(n)=\frac{{P}_{{\rm{D}}}(n)}{{P}_{{\rm{D}}}(n=1)}=\frac{{\Phi }_{{\rm{NA}}}(n)}{{\Phi }_{{\rm{NA}}}(n=1)n}.$$
(2)

The enhancement of photon collection efficiency by the presented methodology depends on the feasibility of geometrical arrangements providing a close to constructive interference of the scattered light from many ions within the selected solid angle. The practical limits on such configurations in ion traps are imposed by the stability of linear ion crystals. We present the simulations of feasible enhancements for up to n = 10 ions considering experimentally broadly feasible radial secular trapping frequencies ωr = (2π) × 5 MHz for evaluation of the upper limit on \({\omega }_{z}^{\min }\). For higher ion numbers, insufficient axial compression of the string in the harmonic trap prevents further enhancement in the practically useful limit of NA > 0.05. In addition, the finite thermal motion is expected to significantly reduce the practical applicability of the employment of high ion numbers, which require increasingly lower axial trapping frequencies necessary for achieving close to a quasi-periodic structure. The excitation angle α = 45∘ is available in many experimental setups, as this configuration allows for simultaneous efficient cooling of the axial and radial motion of ions in a linear Paul trap. Employment of smaller excitation angles would allow further decrease in the sensitivity to thermal motion, and the optimal setting could correspond to an excitation angle that is slightly larger than the maximal collection angle θ, such that it would closely avoid the contribution of the excitation laser light to the detected photon signal. The presented simulation constraints result in evaluated values of minimal spatial length scales ranging from \({l}_{\min }=1.61\) μm, to \({l}_{\min }=4.23\) μm for n = 2 and 10 ions, respectively. The value of the maximal spatial length scale \({l}_{\max }=81.18\) μm corresponding to \({\omega }_{z}^{\min }\) is kept the same for all simulations. The photon collection enhancements have been numerically optimized over the spatial parameter l.

Figure 2a illustrates the feasibility of significant gains in a broad range of numerical apertures. In the limit of NA << 0.1 and small ion numbers, the enhancement PD,rel becomes close to linear with n. This is a consequence of approaching the scaling of ideal constructive interference from a quasi-periodic array of point scatterers, where \({I}_{\max }\propto {n}^{2}\), as the angular interference pattern does not approach the first destructive node within the corresponding analyzed small spatial angles. The divergence from this idealized scaling for large n is given only by residual deviations from the quasi-periodic ion positions within the available range of axial trapping frequencies. For higher numerical apertures NA >> 0.1, the advantage due to the coherent contributions gradually decreases. The phase of the interference patterns oscillates more rapidly for large scattering angles, and the overall gain vanishes due to the averaging of constructive and destructive interference contributions. More complete understanding of the emergence of enhancement scaling thus must consider the actual behavior of I(β) for different length scales l, as the relative heights of the resulting constructive peaks depend on the integrated spatial angle given by the chosen NA. This results in the sharp transitions between different interference peaks for different NA corresponding to kinks in the curves shown in Fig. 2a. A more detailed analysis of the corresponding behavior of PD,rel can be found in the Supplementary Information.

As becomes emergent from the simulations in Fig. 2a, the considered maximal numerical aperture NA = 0.3 approaches field distributions with large scattering angles β, which result in finite angular distributions of constructive interference lobes. These limit the achievable enhancements for higher numbers of ions n with the corresponding longer spatial lengths of the ion crystal. For n > 3, the dependence of PD,rel on NA displays kinks, which correspond to points of transitions between different optimal maximal constructive lobes, which result in maximal PD,rel at different numerical apertures NA. Generally, lower NA allows for the employment of a narrower angular distribution of the contributing constructive lobe of the interference pattern.

The ideal quasi-periodic ion positions cannot be guaranteed on the axis for the case of four or more ions in a single harmonic trapping potential. The optimized numerical solutions presented in Fig. 2a include many configurations, where mutual ion positions provide significant collection enhancements in a given solid angle despite residual deviations from the fully constructive interference configurations. We quantify the corresponding inefficiency of relative enhancement by analysis of the case with equal mutual distances between neighboring ions. To allow for a physically relevant comparison, the range of the mutual distances was in this case limited to the average distance of the same number of ions in the harmonic trap given by the presented limits on their motional frequencies \({\omega }_{z}^{\min }\) and \({\omega }_{z}^{\max }\). The example of simulation in Fig. 2b for different ion numbers and NA ~0.07 and α = 45∘ corresponding to our experimental setting provides a clear illustration of the emergence of a close-to-linear scaling with n for small ion numbers. The simulation suggests that the ideal equidistant spacing could still allow for further enhancement in this limit. The additional relative enhancement of collection efficiency achievable by employing an equidistant string of atomic scatterers can be quantified as \({P}_{{\rm{D}},{\rm{rel}}}^{{\rm{eq}}}/{P}_{{\rm{D}},{\rm{rel}}}^{{\rm{harm}}}=1.48\) with 9 ions in an ideal periodic lattice. In comparison, the feasible improvement by implementation of excitation at α = 90∘, while keeping the harmonic potential, reaches \({P}_{{\rm{D}},{\rm{rel}}}^{9{0}^{\circ }}/{P}_{{\rm{D}},{\rm{rel}}}^{4{5}^{\circ }}=1.26\) for the same 9 ion string. We note that such perpendicular excitation can be additionally advantageous due to the reflection symmetry of the interference patterns, where simultaneous enhancement of coupling to both opposite axial directions can be achieved.

The particularly high spatial localization, long-term stability, and large mutual distances between ions in Paul traps allow for efficient optical addressing schemes49,50. Excitation of the ion string with an array of tightly focused laser beams with individually controllable n − 1 relative phases allows for maximization of the coupling of scattered light in the given solid angle. Alternatively, such a scenario could also be realized in the inelastic scattering regime by implementing local corrections to phases of light scattered by different ions to the collectively formed far-field interference pattern using the addressable AC-Stark shifts on a string of ions prepared in a collective single-excitation Dicke state of internal electronic levels33,43. An example of a simulation of the optimal phase differences for the given excitation geometry and for the case of n = 5 ions in the single harmonic potential considers n − 1 = 4 independently optimized phases. Eq. (1) can then be modified to

$$I(\beta ) \sim \mathop{\sum }\limits_{a,b=1}^{n}\cos [{\Delta }_{\varphi }^{a,b}+({\varphi }_{a}^{{\prime} }-{\varphi }_{b}^{{\prime} })],$$
(3)

where \({\varphi }_{a}^{{\prime} }\) and \({\varphi }_{b}^{{\prime} }\) are phase shifts for different ions with respect to the initial phase of the first ion in the string. Thus, \({\varphi}_{1}^{\prime}={\rm{0}}\) and \({\varphi}_{2}^{\prime}-{\varphi}_{n}^{\prime}\) are varying from 0 to 2π. Their independent optimization in principle allows for employing the shortest feasible value of the spatial length scales \(l\to {l}_{\min }\) for the given radial confinement. Figure 2c presents an example comparison of the three coupling methods for a linear string of five ions. The green data points depict the results of the approach with numerically optimized independent phase factors in scattering from different contributing ions in a single harmonic trap. The result depicted as the solid line corresponds to the equal initial phase factors for all ions and optimization over a single parameter—the spatial length scale l, and is identical to the result presented in Fig. 2a. The dashed line represents the optimization over the range of distances between ions in a periodic ion string. In the limit of low numerical apertures NA < 0.1, the three approaches provide nearly identical collection enhancements, and the harmonic trapping potential does not present any limitation. For higher solid angles, the possibility of optimization of initial phases allows for significant improvement of enhancements, which can provide PD,rel even beyond the equidistant case. This results from the feasibility of the optimal constructive interference over given solid angles achievable at the smallest distance allowed by the trap \({l}_{\min }\). The employment of the optimization of phases becomes even more beneficial in the limit of a large number of ions, where a close-to-optimal pattern is not feasible for any realistic ranges of spatial length parameter l.

Experimental test

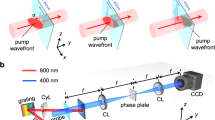
The practical feasibility of the enhancement of collection efficiency has been tested for a crystal of 40Ca+ ions trapped in the linear Paul trap, as illustrated in the example presented in Fig. 1a. The frequency of the radio-frequency (RF) voltage applied to radial electrodes was ωrf = (2π) × 29.9 MHz. The two radial motional modes had close to degenerate secular frequencies of about (2π) × 2.2 MHz. The axial secular frequencies ωz were experimentally optimized by scanning the applied static voltage Utip to confirm the predicted collection enhancements within ranges ωz ≈ (2π) × (0.60 − 1.22) MHz for 2 ions to ωz ≈ (2π) × (0.30 − 0.77) MHz for 9 ions crystal. They correspond to l parameter ranging from 3.9 to 6.2 μm and from 5.3 to 9.6 μm for 2 and 9 ions, respectively. The linear structure of the string was monitored by the camera in the radial trapping direction during the whole experiment.

Fig. 1: Illustration of the coherent enhancement of the collection of light from linear ion crystals in a single harmonic trapping potential.
figure 1

a depicts the principle of employment of far-field angular intensity distributions I(β) of light scattered from the excitation beam with a wave vector \({\vec{k}}_{{\rm{in}}}\) for maximizing the gain in the collection efficiency PD,rel in available axial optical collection numerical aperture \({\rm{NA}}=\sin \theta\) along the ion crystal axis. The optimization over the spatial length scale l of the ion crystal can be tailored by controlling the axial trapping potential, which allows for direct experimental tunability and evaluation of the enhancement. The presented measurement example in (b) with n = 5 trapped 40Ca+ ions illustrates the feasible modification of relative detection efficiency for excitation angle α = 45∘. The corresponding simulated normalized scattering spatial patterns I(β) depict several notable cases, including destructive emission along both axial directions, constructive in the direction of the detector, and constructive in the opposite direction, from left to right, respectively. They illustrate the basic principle of maximization of the relative collection efficiency in a given solid angle along the axial trapping direction by controlling the spatial length scale l of the ion crystal. The normalization of the detected photon rate C(n) to the rate from the same number of ions in a fully incoherent scattering regime nC(n = 1) allows for a direct evaluation of the relative collection enhancement PD,rel.

Full size image

The far-field collection of photons scattered by ion strings in the axial direction has been based on a single plan-convex lens with a focal length of 100 mm. The limit on the effective observation spatial angle was set by the aperture of the axially positioned trapping electrode, which has been estimated from the trap design to NA ≈ 0.07. The collected light passed a polarization beam-splitter, which transmitted the linear polarization oriented perpendicular to the direction of the applied magnetic field, such that it maximizes the portion of the elastically scattered field from the σ-transitions in the detected signal. The precise measurements of the count rate from a single ion and the background count rate were implemented to allow for the exact evaluation of the relative enhancements of the coupling of photons from ions. A count rate from a single trapped ion for the laser excitation settings allowing for the stable continuous measurement and optimal Doppler cooling for all ion crystals was estimated to C(n = 1) = 270 ± 17 counts/s. It corresponds to a saturation parameter of the scattered 397 nm laser of about s397 ≈ 0.65 and detuning Δ397 = −21 MHz, optimized for the maximal crystal stability and visibility of the interference on the largest employed ion string with n = 9. To allow for the reliable experimental estimation of scaling with the number of ions, the laser parameters and radial trapping frequencies were kept identical in all measurements. The excitation laser frequencies were stabilized to an optical frequency comb which provides a long-term stability51. The measured background of Cbg = 24 ± 5 counts/s originated dominantly from the residual scattering of the 397 nm laser off the radial trapping electrodes.

An example of an experimental test in Fig. 1b, illustrates the tunability of the collection enhancement on the scattering from n = 5 ions. The optimization over axial potential strength was performed for all presented experimental values within the feasible ranges of the spatial length scales l. The normalized enhancement of the photon collection efficiency was then evaluated from the measured photon rates as

$${P}_{{\rm{D,rel}}}^{\exp }(n)=\frac{C(n)-{C}_{{\rm{bg}}}}{(C(n=1)-{C}_{{\rm{bg}}})n}.$$
(4)

The measured data were fitted using the model \({P}_{{\rm{D}},{\rm{rel}}}^{{\rm{cal}}}\) considering the ideal interference of the coherently scattered part according to the Eq. (1) with the probability fcoh and the complementary incoherent part of the scattered light fincoh = 1 − fcoh,

$${P}_{{\rm{D,rel}}}^{\exp }={f}_{{\rm{incoh}}}+{f}_{{\rm{coh}}}{P}_{{\rm{D}},{\rm{rel}}}^{{\rm{cal}}}.$$
(5)

The parameter fcoh was evaluated from the local fits of the model (5) to the experimental data around the maximal measured \({P}_{{\rm{D,rel}}}^{\exp }\) to suppress the effect of measurement noise and the residual deviations of the simplified theoretical model from the experimental reality. The resulting local maximum is depicted as a green diamond, and the error bar shows a statistically evaluated single standard deviation corresponding to photon number fluctuations of measured count rate close to the maximal PD,rel.

Figure 3 presents the summary of the measured maximal values of \({P}_{{\rm{D,rel}}}^{\exp }\) (red diamonds) and the estimated fractions of coherently scattered light (black crosses). The values of coherent fraction fcoh estimated from the fit using the Eq. (5) are similar across the whole range of ion numbers, which supports the relevance of the observed scaling of PD,rel with n. We note that its relative decrease by about 20 % of the initial value for n > 5 ions can be mostly attributed to increased spatial position uncertainties, as the optimal working points correspond to larger spatial length scales l for this number of ions. The raw collection enhancements have been measured from about 1.51 ± 0.01 for two ions and monotonously increased to 3.05 ± 0.09 for a nine-ion crystal.

The measured two-ion enhancement value is close to what has been presented previously43. Despite working here in a much smaller NA limit, these values can be directly compared because PD,rel is independent of NA for a very small number of ions in the corresponding effective NA regimes, as illustrated in Fig. 2a. The intrinsic regularity of ion spacing for two and three-ion strings enhances their robustness to various geometrical factors and enables comparison among different experimental regimes and ion trapping platforms. The residual differences can be attributed mostly to thermal motional effects specific to different atomic species. The unique feasibility of testing with a higher number of ions presented in this work allows for the first observation of the scaling of experimental gains for n > 2 trapped ions. We note that the absolute overall detection efficiency of photon scattered from a single trapped ion estimated to PD,abs = 1.7 × 10−2% remains relatively small mostly due to the employment of trap with the axial access corresponding to the optical solid angle of Ω ≈ 0.015 and the finite detection efficiency of employed single-photon counting module of ηSPCM ≈ 50%. However, the relative enhancement for 9 ions gives final PD,abs = 0.051 ± 0.001%, which is close to the optimized value of the overall detection efficiency in radial direction PD,abs = 0.06% measured with the collection objective with much higher NA of ≈ 0.3 covering about 2% of the full solid angle in the same apparatus and in the analogous photon detection settings52. These comparisons provide an experimental validation of the applicability of the proposed approach for diverse applications requiring efficient photon collection from ions, including the implementation of particularly challenging experiments requiring multi-photon detection events from many ions43,53.

Fig. 2: Simulations of the relative enhancement of the collection efficiency PD,rel of light from linear ion crystals in a single harmonic trapping potential.
figure 2

a shows the optimized PD,rel for different numbers of 40Ca+ ions within the practically relevant range of numerical apertures NA of the collection optical mode. The scattering wavelength λ = 397 nm and α = 45∘. b depicts feasible PD,rel for different numbers of ions and the numerical aperture NA = 0.07 corresponding to the employed experimental test. Results of optimization in the harmonic potential for the two angles of incidence α = 45∘, α = 90∘, and for the case with regular ion spacing and α = 45∘ (circles) are shown as full squares, triangles, and circles, respectively. c illustrates the example of different optimization protocols for the string of n = 5 ions. The optimization solely over the single trapping parameter—the spatial length scale l in the harmonic trapping potential is shown as a solid curve. The addressable tunability of individual scattering phases in the single harmonic potential allows for maximization of PD,rel for the lowest feasible mutual distance of ions given by \(l={l}_{\min }\), with resulting enhancements shown as green points. The dashed line depicts the example of optimization for equidistant scatterers.

Full size image

The finite saturation parameter and the multilevel electronic level structure of 40Ca+ reduce the observed enhancements, which amounts to the residual difference between the measured and simulated data points. The contribution of the inelastically scattered light has been estimated to be about 13% using dark resonance spectroscopy. In addition, the steady-state population of the metastable 32D3/2 manifold of about 13% effectively corresponds to a random switching of the contribution of different ions to the interfering signal. However, we remind that these effects are intrinsic to the experimental tests relying on the elastic scattering and should not affect the collection efficiency of photons scattered from the ion crystal prepared in entangled \(| W\left.\right\rangle\) states with coherently shared electronic excitation33,43,54,55.

The reduction of the interference visibility due to the position uncertainty of ions has been estimated to be the most significant deterioration process, similar to previous demonstrations of interference from strings of trapped ions41,42,43,56. The impact of motion increases for low trapping frequencies and corresponding larger spatial length scales l due to the greater mean position uncertainty of ions, which also becomes emergent from the measured maximal enhancements. Considering the position uncertainties of thermal motional states, equation (1) can be modified to

$$I \sim \mathop{\sum }\limits_{a,b=1}^{n}{e}^{-\frac{1}{2}{k}_{{\rm{eff}}}^{2}{\sigma }_{a,b}^{2}}\cos {\Delta }_{\varphi }^{a,b}.$$
(6)

Here \({\vec{k}}_{{\rm{eff}}}={\vec{k}}_{{\rm{out}}}-{\vec{k}}_{{\rm{in}}}\), \({\vec{k}}_{{\rm{out}}}\) and \({\vec{k}}_{{\rm{in}}}\) are the scattered and incident wave vectors, respectively, and σa,b is the standard deviation of the mutual distance between a-th and b-th ions considering full decomposition to n normal axial motional modes. The corresponding simulations of collection enhancements affected by motional dephasing are shown in Fig. 3 as gray squares. The average reduction of the relative enhancement for n = 2 to 6 ion crystals due to the thermal motion at the Doppler cooling limit has been evaluated to around 25 %, while the estimated suppression becomes clearly more significant with the increasing spatial length scale for higher ion numbers. The enhancement for the given trapping parameters is thus expected to be further significantly improved when employing heavier ion species, as the variance of the mutual ion positions is given by \({\sigma }_{a,b}^{2} \sim \frac{\hslash }{2m{\omega }_{z}}\), or by employing a higher scattering wavelength. Figure 3 includes examples of simulations with 138Ba+ considering scattering at the 62S1/2 ↔ 62P1/2 dipole transition with λ ≈ 493 nm, shown as gray circles. The two presented data points represent notable cases of the largest feasible relative enhancement in comparison with the measurements on 40Ca+ for n = 5 and the highest measured \({P}_{{\rm{D}},{\rm{rel}}}^{\exp }\) for n = 9. For n = 5, the simulation predicts additional improvement \({P}_{{\rm{D}},{\rm{rel}}}^{{\rm{Ba}}}/{P}_{{\rm{D}},{\rm{rel}}}^{{\rm{Ca}}}\approx 1.45\), i.e., a total enhancement of about \({P}_{{\rm{D}},{\rm{rel}}}^{{\rm{Ba}}}\approx 3.93\). The predicted optimum for n = 5 is the consequence of the enhanced sensitivity to motion for larger n, which requires longer spatial length scales to approach quasi-periodic crystal structure. At the same time, these longer crystals result in spatial interference patterns with a much smaller angular width of the first constructive lobe. These effects jointly contribute to the decreasing in maximal gain \({P}_{{\rm{D,rel}}}^{\exp }/n\) for high n.

Fig. 3: Summary of the measured enhancements of collection efficiency for a linear chain of 40Ca+ ions for the NA ≈0.07.
figure 3

Values evaluated from the measurements shown as red diamonds can be compared with simulations shown as squares, which consider the thermal motion of ions at the Doppler cooling limit. The coherent fraction fcoh shown in the bottom graph was evaluated from the measured interference dependencies on the spatial length scale l using the Eq. (5). The error bars correspond to a single standard deviation and are smaller than the displayed data point symbols, where not shown. The examples of predictions for 138Ba+ illustrate the expected enhancements for the equivalent excitation configuration.

Full size image

Discussion

The presented scheme for the enhancement of collection efficiency from linear ion strings employs a scattering geometry that is intrinsic to diverse modern linear ion traps. Its simulations confirm the feasibility of the close to an ideal linear gain by a factor of n in the collection efficiency of light scattered from up to n = 5 ions for small numerical apertures NA < 0.1, and predict still significant enhancements even for higher ion numbers and numerical apertures, still within the experimentally feasible position uncertainties and axial motional frequencies. The scheme provides the most attractive enhancements within the range of numerical apertures 0.05 < NA < 0.2, where the maximum gain can be in the ideal case of fully coherent scattering approached already for relatively small ion numbers n ≈ 5. They allow for the employment of small spatial length scales \({l}_{\min }\) for the given radial secular frequency and thus naturally provide optimal enhancement configurations due to the resulting interference patterns with smaller angular gradients. For higher ion numbers, it becomes unfeasible to achieve a sufficient axial compression of the string in a single linear harmonic trapping potential, and the corresponding minimal spatial length scales lead to the lower maximal collection enhancements. Although the optimization in the case of equidistant emitters predicts the feasibility of further enhancements, these gains can be, in principle, fully eliminated by control of individual scattering phases in strings of ions prepared in states possessing a collective coherent spin excitation43.

The realized experiment demonstrated enhancements ranging from ≈ 1.51 for the two-ion crystal to ≈ 3.05 for the nine-ion crystal, limited dominantly by the residual thermal motion, finite saturation parameters, and multilevel effects. While the detrimental impact of the inelastically scattered light and multilevel effects would be practically absent in the schemes employing the collectively shared spin excitation33,43, the position uncertainty can be further improved by employing ions with large atomic mass, employment of transitions with longer wavelengths, further decrease of the input scattering angle, or their combination.

The presented approach enables a broadly applicable, efficient photon collection from ions for small spatial angles. When compared to the free space high-NA collection setups, the considered small solid angle limit provides an inherent advantage for the reduction of wavefront aberrations of the collected light with simple paraxial collection optics, which promises perspectives in diverse interferometric applications using collectively coupled trapped ion crystals57,58,59. Demonstrated methodology with trapped ion strings can be directly extended to implementations of protocols involving the enhanced directionality originally based on forward-scattering of light in cold atomic clouds60,61,62,63. The scaling of the corresponding collective enhancements in a single-mode detection limit is expected to be comparable to the coherent enhancements of the collection efficiency presented here. As the large focus depth of the small-NA fluorescence collection allows for simultaneous observation of light from many ions, the available control of large trapped ion quantum registers64,65 can allow for mapping of the collective internal states of the ion string on the direction of the scattered light33,43.

Methods

Experimental scheme

The scattering wavelength and excitation angle are selected according to the presented experimental tests with 40Ca+, however, the results can be easily adapted to any other combination of atomic ion species and excitation geometries. The experimental demonstration employs a 3D linear Paul trap and collection of the 397 nm photons. This corresponds to several recent experiments on coherent elastic scattering from ion strings41,42,66. The trapping of linear ion strings is achieved by the RF voltage \({U}_{{\rm{rf}}}\cos ({\omega }_{{\rm{rf}}}t)\) applied to radial electrodes and a static voltage Utip at two axial cone-shaped hollow tip electrodes, which together provide a three-dimensional trapping potential. The frequency of the secular motion of ions along the axial direction is given by \({\omega }_{z}=\sqrt{2q{U}_{{\rm{tip}}}\kappa /(m{z}_{0}^{2})}\), where m is the ion mass, q is the ion charge, 2z0 is the distance between the two tip electrodes, Utip is the voltage applied to the tip electrodes, and κ is the geometrical factor. The radial motional frequencies \({\omega }_{r}=q{U}_{{\rm{rf}}}/(m{r}_{0}^{2}{\omega }_{{\rm{rf}}}\sqrt{2})\) depend on the amplitude of the RF potential Urf and its angular frequency ωrf. Figure1a illustrates the excitation and detection geometry, which is similar to that previously employed in both neutral atom and trapped ion interference experiments41,67. The scattering of the 397 nm field with a red-detuned frequency ωl from the 42S1/2 ↔ 42P1/2 electric dipole transitions provides a simultaneous Doppler cooling of ions. The laser scatters off the ion string at an angle α ≈ 45 ∘ with respect to the axial trapping direction in the z−x plane. The 866 nm laser beam with the same direction is used for reshuffling the population of the metastable 32D3/2 manifold back to the cooling transition. The degeneracy of Zeeman states is lifted by applying a static magnetic field with a magnitude \(| \vec{B}| =3.3\) of Gauss along the y-direction. Polarizations of both excitation lasers are considered to be linear with the vector perpendicular to the applied magnetic field.