Introduction

Direct measurement of individual spins is an extremely challenging task given their small magnetic dipole moment. However, in semiconductor nanostructures, the charge dipole associated with electron tunnelling can be sizeable. Such divide in electronic properties is reflected in the vastly different state-of-the-art sensitivities for the spin (~10 spins/\(\sqrt{\,\text{Hz}\,}\)1,2,3) and charge degrees of freedom (~10−6 electrons/\(\sqrt{\,\text{Hz}\,}\)4,5,6), which has pushed researchers to develop spin-to-charge conversion (SCC) techniques in conjunction with charge sensing for electrical spin readout. Energy filtering, for example, uses the difference in tunnel rates to a charge reservoir of Zeeman-split spins states confined to a quantum dot (QD) (or impurity)7 whereas spin blockade (SB) uses quantum selection rules to inhibit tunnelling between two-particle states with different spin numbers8, see Fig. 1. In particular, SB is a more scalable mechanism for SCC requiring only two bound spins for its implementation and has proven instrumental in achieving high fidelity readout of spin qubits9,10,11,12 even at low magnetic fields13 and high temperatures14,15.

Fig. 1: Spin readout using spin-blockade.
figure 1

a Anti-symmetric spins allow for the movement of spins, while (b, c) symmetric spins are blockaded, allowing for the two-particle spin states to be distinguished. At increased detuning, SB can be lifted in the presence of either a large spin-orbit interaction (b) or the presence of low-lying excited orbital states of energy δo (c).

Full size image

Charge sensing, in conjunction with SCC mechanisms as described above, relies on bi-state measurements arising from the charge sensor detecting either charge tunnelling or the lack thereof. This means that only a specific subset of spin measurement outcomes may trigger the charge detector, while the absence of such a trigger may be attributed to the complementary subset16. However, this approach has drawbacks, including potential state leakage or spin mapping errors17. Furthermore, various mechanisms may lift SB, such as strong spin-orbit coupling (SOC) – which allows two-particle states with different spin numbers to couple (Fig. 1b)18,19 – and low valley-orbit level splitting – allowing symmetric spin states to exist in different orbital or valley states of the same confining potential (Fig. 1c)20,21. The former mechanism is particularly relevant to spins III-V materials22,23,24,25 and novel spin qubit systems such as holes in germanium26,27,28,29, and silicon QDs30,31,32 that have come at the forefront of semiconductor-based quantum computing due to their technical ease for spin manipulation via electric fields33,34,35,36,37 and their potential for large-scale integration38,39. A key element in the operation of spin qubits in double QDs is rapid spin projection(separation) pulses through a singlet-triplet anticrossing, which are utilized to read(initialize) the system40. However, the anisotropic nature of SOC on these systems results in magnetic field orientations in which SOC is strongly enhanced, which may compromise satisfying the diabatic condition of the pulses and hence the ultimate achievable readout and initialization fidelity in scaled-up systems (see Supplementary Note 1).

To overcome these challenges, we present a methodology, based on dispersive readout techniques41 and spin-to-charge-polarizability conversion42 that utilizes the very same coupling between states that leads to SB lifting, as a resource for selective readout of the states of a two-spin system. More concretely, our methodology makes use of the energy-detuning-dependent charge polarizability of the two-spin system to positively detect the spin measurement outcome without the need to perform a rapid diabatic pulse through a singlet-triplet anticrossing, minimising SCC mapping errors. The difference in polarizability manifests itself as a state-dependent quantum capacitance that can be detected through the dispersive interaction with a microwave superconducting resonator43. We demonstrate this readout methodology using a hybrid system subject to a strong SOC formed by a hole QD and a Boron acceptor in a silicon nanowire transistor, and measure its spin relaxation time as a function of energy detuning. Finally, we expand the readout methodology to systems with low-lying orbital states, where SB may be lifted by allowed tunnelling to the higher energy orbital. We implement the demonstration in a different charge configuration of our hybrid system, and show that the spin states can be mapped onto signals arising from the orbital ground and excited state charge transitions, allowing for the spin states to be measured selectively.

Results

Spin blockade lifting via spin-orbit coupling

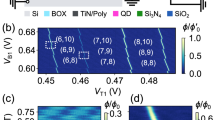
We use a p-type single-gate silicon transistor with light Boron channel doping, a system subject to strong SOC (Fig. 2a)44. By applying a voltage on the top-gate (Vg) and back-gate (Vbg), we accumulate holes in QDs formed in the nanowire, as well as in individual Boron atoms (Fig. 2b). We connect the gate of the transistor to a superconducting microwave(mw) resonator (panel a), to detect quantum capacitance changes arising from mw-driven cyclic charge tunnelling between the QD/Boron and the source and drain charge reservoirs (S,D) as well as between QDs and Boron atoms. We refer to the latter as interdot charge transitions (ICTs).

Fig. 2: Device description and readout concept.
figure 2

a Schematic of silicon nanowire transistor (top-view), labelled with Source (S), Drain (D), and top-gate (G) contacts, embedded in an LCR resonator for charge readout. b Schematic side-view of Si-nanowire with gate stack including gate metal (red), gate oxide (grey), channel (transparent blue), buried oxide (BOX in black), and intrinsic silicon substrate (Si-i, also blue). The corner QD and Boron atom, where holes are confined, are marked in yellow. c Charge stability diagram showing the capacitive signal measured in the Vg-Vbg space near the boron-dot transition (positive slope). A boron-reservoir transition is also visible (negative slope). The charge occupations are annotated in the plot. The approximate location of the dot-reservoir transition is indicated in red dashed lines. Location of Load, Wait and Read voltages for readout measurements are marked in red. d Magneto-spectroscopy measurement near the point labelled R in the stability diagram. The dotted line shows the location of the \({{\rm{T}}}_{1,1}^{-}\)/S2,0 anticrossing. e Simulated magneto-spectroscopy of the same transition. The insert shows a simulation of the same transition with Δsf = 0, showing the emergence of SB. f, h Energy level diagram at two magnetic fields. g, i Capacitive signal of the lowest two states (↑B, ↓D) and (↓B, ↓D) at two magnetic fields. In each case, the excited state is plotted in dashed lines.

Full size image

We tune the device to an ICT between a Boron atom and a QD (ICT A) with nominal charge occupation of (NB,ND) = (1,1)/(2,0) (Fig. 2c) and a gate lever arm asymmetry Δα = 0.26 ± 0.03, a parameter used to convert gate voltage to energy detuning between the QD and Boron atom, see Supplementary Note 2 for the full charge stability map. Throughout this work, we provide state occupations in the form (B,D), where the first refers to the state of the Boron atom and the second to that of the QD. To characterise the spin eigenstates of the system, we perform magneto-spectroscopy45 by measuring the resonator response, which at low temperature (kBT ≪ Δsc, Δsf as defined below) corresponds to the quantum capacitance, Cq, of the ground state of the system, against gate voltage across the ICT and magnetic field strength applied in the plane of the sample (Fig. 2d).

The data reveal an enhancement of the resonator response which shifts up in Vg as the magnetic field is increased above B ≈ 0.2 T. This is the signature of an effective two-spin system subject to strong SOC, where, above 0.2 T, the system is free to tunnel between the polarised triplet state (↓B, ↓D) and the joint singlet (S2,0)46. The enhancement in the signal originates from the reduced tunnel coupling of the ↓B, ↓D (ground state above B ≈ 0.2 T) compared with the ↑B, ↓D (ground state below B ≈ 0.2 T) with the S2,0 state. This is SOC-mediated spin blockade lifting which we describe in detail below.

We consider the two-particle SOC Hamiltonian in Supplementary Note 3 that takes into account the g-factor of the Boron(QD) gB(D) (where in our case gB < gD) and the spin-conserving and spin-flip tunnel coupling, Δsc and Δsf. In Fig. 2e, we plot the simulated magneto-spectroscopy, as well as the eigenenergies and capacitive signals (Fig. 2 f, h and g, i) arising from the lowest two states at B = 0(1) T. For B < 0.2 T, the capacitive signal arises from charge tunnelling between the ground (↑B, ↓D) and S2,0 states, mediated by the finite Δsc, see blue trace in panel g. For B > 0.2 T, however, the signal arises from the tunnelling between the Zeeman split \({{\rm{T}}}_{1,1}^{-}\) = (↓B, ↓D) and the S2,0 state, in this case mediated by Δsf, see the red trace in panel i. The good match between the experiment and simulations confirms the presence of the lifting mechanism since, for systems with low SOC, like few-electron QDs in silicon, such spin-flip tunnelling processes are forbidden resulting in the signal vanishing asymmetrically at high fields (see the simulation in the insert of Fig. 2e)47.

Magneto-spectroscopy allows us to quantify the parameters in the Hamiltonian. First, we obtain the average g-factor of the hole spin in the QD and Boron, \(\overline{g} \sim\) 2, which is given by the slope of the transition in the \({{\rm{T}}}_{1,1}^{-}\)/S2,0 regime (\(\overline{g}=e\alpha \Delta {V}_{{\rm{g}}}/{\mu }_{B}B\)), where e is the electron charge and μB the Bohr magneton (We define the g-factor at a particular magnetic field angle as \(g=| {\boldsymbol{g}}\overrightarrow{B}| /| \overrightarrow{B}|\) where g is the g-tensor.). Further, from the linewidth of the signal at zero and high field (\({{\rm{T}}}_{1,1}^{-}\)/S2,0 regime), we extract the total charge and spin-flip coupling rates, \(\sqrt{2}{\Delta }_{c}=\sqrt{{\Delta }_{\,\text{sc}}^{2}+{\Delta }_{\text{sf}\,}^{2}} \sim\) 10.4 GHz and Δsf~3.4 GHz, respectively. Additionally, by measuring the shift in Vg of the Boron-reservoir transition with magnetic field (not shown), we find the g-factor of the Boron gB ~1.6 making the g-factor of the QD, gD ~ 2.4.

Spin readout under spin-orbit lifted SB

Spin blockade is based on the exclusion principle, in which two fermionic particles cannot possess all the same quantum numbers. It is utilized in DQDs to project the combined spin state of two separated spin-carrying particles into that of a single QD whose ground state is the joint singlet, S2,0. Particularly, the polarized Triplets \({T}_{1,1}^{\pm }\) are blockaded from transitioning into S2,0, a feature that is used for spin parity readout, or for Singlet-Triplet readout if the unpolarized triplet state T0 is also blocked48.

In the presence of SOC, however, Δsf enables tunnelling of the \({T}_{1,1}^{\pm }\) states into the S2,0, eliminating the spin selectivity of SB readout via projective measurements unless a fast diabatic pulse across the Δsf anticrossing can be performed. Such a requirement may be challenging in practice, given that the Δsc anticrossing also needs to be crossed adiabatically, ultimately limiting the fidelity of the SCC mechanism (see Supplementary Note 1).

In this work, we use Δsf to our advantage. The finite spin flip coupling term between the \({{\rm{T}}}_{1,1}^{-}\) and S2,0 spin branches generates a distinct anticrossing at positive energy detuning ε. Most critically, for the purpose of our demonstration, we note that the capacitive signals arising from the anticrossings of the aligned (↓B, ↓D) and anti-aligned (↑B, ↓D) spin outcomes occur at different detuning (see the red and blue traces in Fig. 2i, respectively), a concept that we exploit in the following for spin readout.

We note two additional features of this readout scheme that may be used to distinguish the other spin states, \({{\rm{T}}}_{1,1}^{+}\) = (↑B, ↑D) and (↓B, ↑D), from the \({{\rm{T}}}_{1,1}^{-}\) and (↑B, ↓D) states: First, the \({{\rm{T}}}_{1,1}^{+}\) and (↓B, ↑D) additionally anticross with the S0,2 state at a third and fourth readout point at negative detuning (see Fig. 2h), allowing for these populations to be distinctly measured (Supplementary Note 4). Second, beyond a positive and negative Cq, also a neutral response can be measured. This allows for the spin states producing a Cq to be additionally distinguished from those that do not (see Supplementary Note 5). For example, assuming the spin states were adiabatically transferred from the (1,1), at the anticrossing between the \({{\rm{T}}}_{1,1}^{-}\) and S2,0 states, a positive (or negative) Cq would correspond to a \({{\rm{T}}}_{1,1}^{-}\) (or (↑B, ↓D)) measurement outcome, respectively, while a neutral response indicates either a \({{\rm{T}}}_{1,1}^{+}\) or (↓B, ↑D) state. Together, these two techniques may be used to measure the full spin state of the two-spin system (Supplementary Note 4.1).

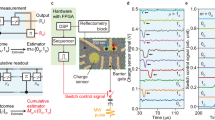
To measure the spin of the Boron, we first randomly initialise the system in either (↑B, ↓D) or \({{\rm{T}}}_{1,1}^{-}\). We do so by starting in the (2B,1D) charge state (point L in Fig. 2c) to then pulse into the (1B,1D) region (point W), which randomly unloads a spin from the Boron atom, as illustrated in Fig. 3a. We then pulse to either of the readout points (RA, RP where the subscripts stand for anti-parallel and parallel) and measure the dispersive signal in the time domain, see Fig. 3d–f. For these preliminary experiments, we set the wait time at W to tW = 0 s. Additionally, we perform a control measurement in which we wait in the (1,1) region to deterministically initialize the system in the \({{\rm{T}}}_{1,1}^{-}\) by relaxation (see pulse sequences in Fig. 3c and Methods).

Fig. 3: Readout protocol with spin-orbit coupling.
figure 3

a Schematic of pulsing scheme. The state is initialised by randomly unloading a spin from the Boron atom starting from a (2,↓) configuration resulting in either a (↓B, ↓D), or a (↑B, ↓D) The measurement is performed either at RA [triggered by the (↑B, ↓D) state] or at RP [triggered by the (↓B, ↓D) state]. b Energy level diagram showing the load (L) and read points for the two states (RA, RP). The black dashed line denotes the Boron-reservoir transition between the (2,1) and the (1,1) charge states. c Schematic of pulse sequence for spin readout. States are initialised at L, and then pulsed to either RA or RP (blue or red lines). The black dashed lines indicates the control pulse where the state is initialised in the (1,1) region. The time at which data acquisition is started is indicated. d Capacitive signal as a function of measurement time and detuning showing two signal arising from the (↓B, ↓D) and (↑B, ↓D) states. RA and RP are indicated with dashed lines. Measurements carried out at B = 1 T. e, f Line-cuts of d at detuning of RA and RP showing the capacitive signal (normalised to the peak value of each trace) against time. Dashed lines are given as a guide to the eye. The black lines are the signals recorded from the control measurement.

Full size image

We observe two signals at different detuning (panel d), the separation of which depends on the magnetic field intensity as anticipated (see Supplementary Note 6). When we take a cut at zero detuning (panel e), we observe the signal from the (↑B, ↓D) - S2,0 anticrossing, i.e., a (↑B, ↓D) measurement outcome. The signal initially rises, due to the finite ring-up of the resonator, before decaying with a time constant T1 ~ 100 ns given by the relaxation time to the T−state (blue trace). We highlight a slower decay in the signal from the (↑B, ↓D) measurement at more negative detuning, which we attribute to a detuning-dependent T1, which we investigate further in the following Section. We note that the short T1 at the readout point prevented us from performing single-shot readout measurements (see Supplementary Note 7 for further discussion).

At finite positive detuning (RP), on the other hand, we observe signals arising from the \({{\rm{T}}}_{1,1}^{-}\)-S2,0 anticrossing, i.e., a \({{\rm{T}}}_{1,1}^{-}\) measurement outcome (Fig. 3f). In this case, the signal (red trace) is delayed with respect to the resonator ring up (black trace). The slower dynamics is caused by the fraction of (↑B, ↓D) shots that carry a negative quantum capacitance at RP, hence reducing the signal at timescales comparable to the relaxation time of 95 ns in this case.

Our result shows that, in spin systems with lifted SB due to SOC, the spin state can be read using the different detuning points at which the dispersive signal of the (↑B, ↓D) and \({{\rm{T}}}_{1,1}^{-}\) measurement outcomes manifest. This measurement is done without the need to perform a perfectly diabatic pulse through the \({{\rm{T}}}_{1,1}^{-}\)-S2,0 anticrossing.

Spin relaxation time

To demonstrate the benefit of this spin readout mechanism, we now study the spin qubit decay constant T1 as a function of detuning. We again initialise randomly in the (↑B, ↓D) or \({{\rm{T}}}_{1,1}^{-}\) state but wait in the (1,1) region (point W(ε)) for a variable time before pulsing to the readout point RA (Fig. 4a–c). For long tW, the initialised state will have a higher chance to decay to the ground state, resulting in a reduction in the average excited state signal (Fig. 4d). We extract T1 by fitting the data to an exponential decay of the form \({P}_{S}({t}_{{\rm{W}}})\propto \exp (-{t}_{{\rm{W}}}/{T}_{1})\) (red dashed line). We repeat this measurement for different detuning points and find that T1 increases exponentially away from the readout point (Fig. 4e) up to 8 μs, increasing its utility as a spin qubit.

Fig. 4: T1 characterisation: measurements carried out at B = 700 mT.
figure 4

a–c Schematic of the measurement protocol: The state is initialised as described in Fig. 3. This is followed by a Wait (W(ε)) period of variable time and pulse depth in which (↑B, ↓D) may relax into \({{\rm{T}}}_{1,1}^{-}\). Finally, the state is read out at the spin anti-parallel readout point (RA). The location of W(ε) is varied to characterise T1 as a function of ε. The time at which data acquisition is started is indicated. d Example capacitive signal [a proxy for the (↑B, ↓D) population] against tw at ε = −92 μeV = −1.12 Δc (red dot, e). The data is taken from the maximum signal of line traces similar to that in Fig. 3d. The data is fitted using an exponential decay to extract T1 (730 ± 80 ns in this case). e T1 against detuning of the wait location W(ε) showing an exponential dependence (black dashed line) with detuning. The location of RA is marked in blue. The data in panel d is marked with a red dot.

Full size image

We hypothesize that the short T1 at the readout point is caused by the coupling of the spin and charge degrees of freedom, i.e., at the anticrossing, the spin-carrying charges have the largest dipole and therefore are most impacted by charge noise. We note that a charge relaxation time, T1 = 100 ns, has been measured in a similar sample49.

To further support the hypothesis, we discard spin-orbit coupling as the dominant source of relaxation at the readout point due to the lack of dependence of T1 on magnetic field50 (see Supplementary Note 6), where we show several time-dependent readout signals similar to that reported in Fig. 3 but recorded at different magnetic fields.

Spin readout under orbitally lifted SB

In projective SB measurements, the presence of low-lying excited orbital or valley states (of energy δo) lifts SB by allowing spin triplets (T0,2) to exist in the (0,2) charge configuration. Hence, when the energy detuning exceeds δo, both triplet and singlet are allowed to transition into the (0,2), eliminating spin selectivity of the charge movement (Fig. 1c). Although techniques are available to increase the energy of the δo, for example by moving to a (1,3) charge occupation to fill the lowest valley in electron systems51 or by reducing the size of the QD to increase orbital energies, the excited states still impact the readout of using projective SB. This mechanism limits the magnetic fields at which SB can be performed in transport measurements to \(B < {\delta }_{o}/(\overline{g}{\mu }_{{\rm{B}}})\)20, while in charge-sensing experiments, it limits the size of the voltage window in which SB can be detected52.

In this Section, we demonstrate that the readout mechanism described in the context of SOC, naturally extends to anticrossings arising from orbital states. In particular, we show that instead of being a constraint, the presence of orbital states can be used as a resource by resulting in two distinct readout locations which can be used to measure the spin state of the hybrid DQD. Such an approach allows for the selective and positive detection of different spin measurement outcomes. While this method does not increase the size of the readout window as compared to standard charge-sensed SB, it provides an alternate methodology to read the spin state dispersively.

For the demonstration, we tune the device to a different ICT comprising a different Boron atom and QD (ICT B) with nominal charge occupation (NB,ND) = (1,1)/(0,2) and differential lever arm Δα = 0.54 ± 0.02 (Fig. 5a). Notably, in the (0,2) configuration the two holes reside within the QD, in contrast to ICT A where they resided in the Boron. The presence of low-energy orbital excited states in the QD allows for an orbital lifting of SB. We perform magneto-spectroscopy and again find an enhancement of the signal at magnetic fields above 300 mT characteristic of a two-spin system with SOC. However, in this case, we additionally find that above 600 mT the signal remains at a fixed Vg point and its intensity is reduced, the signature that a transition from \({{\rm{T}}}_{1,1}^{-}\) to the \({{\rm{T}}}_{0,2}^{-}\) state involving an orbital excitation in the QD is now allowed21.

Fig. 5: Readout utilising orbital states.
figure 5

a Stability diagram of ICT B showing the nominal charge occupation. The readout location is highlighted. b, c Magneto-spectroscopy and simulation at the point marked R in (a). d, f Energy level diagrams showing the energy levels of the transition at two magnetic fields. e, g Capacitive signals from the (↑B, ↓D)/S0,2 (blue) and \({{\rm{T}}}_{1,1}^{-}\)/\({{\rm{T}}}_{0,2}^{-}\) (red) anticrossings marking the two readout locations. In each case the excited state is marked in dashed lines. h, i Capacitive signal measured, used to distinguish (↑B, ↓D) and \({{\rm{T}}}_{1,1}^{-}\) states utilising the orbital \({{\rm{T}}}_{1,1}^{-}\)/\({{\rm{T}}}_{0,2}^{-}\) transition (low magnetic field) or the (↑B, ↓D)/S0,2 transition (high magnetic field) as readout points. The response is normalised to the maximum of each line trace.

Full size image

From magnetospectroscopy (Fig. 5b), we extract Δc ~20 GHz, Δsf ~4 GHz, δo ~20 GHz, where δo is the QD excited state energy. From the slope of the transition in the \({{\rm{T}}}_{1,1}^{-}\)/S0,2 and the \({{\rm{T}}}_{0,2}^{-}\) regimes, we extract the average g-factor, \(\overline{g}=2.1\pm 0.1\), and g-factor difference δg = gB−gD = 0.3 ± 0.1, respectively. We extend the Hamiltonian to include the \({T}_{0,2}^{-}\) state (Supplementary Note 3) and simulate the magnetospectroscopy in Fig. 5c. In the data, we note the additional edges in the signal parallel to the \({{\rm{T}}}_{1,1}^{-}\)/S0,2 anticrossing (white dashed line), see Fig. 5b. These arise due to resonant interactions between the spin system and photons in the mw resonator (2.1 GHz). Although less clear, these can also be observed in Fig. 2d.

We plot the energy-level diagrams and capacitance from the ground and first excited states at B = 0 T and B = 0.75 T in Fig. 5d–g. For ease of readability, we only include the \({{\rm{T}}}_{1,1}^{-}\) and (↑B, ↓D) states in the (1,1) charge region and the \({{\rm{T}}}_{0,2}^{-}\) in the (0,2) region. We further set Δsf = 0, since it is less relevant at fields explored in this section, i.e., outside the intermediate field regime where the T−/S anticrossing occurs. At magnetic fields below and above the T−/S regime, two distinct readout points emerge corresponding to the (↑B, ↓D)/S0,2 anticrossing (ground state at low magnetic field), and the \({{\rm{T}}}_{1,1}^{-}\)/\({{\rm{T}}}_{0,2}^{-}\) anticrossing (ground state at high magnetic fields), separated in detuning by \({\delta }_{o}+([{g}_{B}-{g}_{D}^{* }]/2){\mu }_{{\rm{B}}}B\), where \({g}_{D}^{* }\) is the g-factor of the excited state of the doubly occupied QD.

We now demonstrate readout in each of these regimes. First, at low field (B = 0.15 T), we use the \({{\rm{T}}}_{1,1}^{-}\)/\({{\rm{T}}}_{0,2}^{-}\) anticrossing as the readout point. We start deep in the (1,1) region, where the ground state is \({{\rm{T}}}_{1,1}^{-}\), to then perform a diabatic passage through the \({{\rm{T}}}_{1,1}^{-}\)/S0,2 anticrossing to prepare the system in the excited \({{\rm{T}}}_{1,1}^{-}\) state near zero detuning. Finally, we ramp to the \({{\rm{T}}}_{1,1}^{-}\)/\({{\rm{T}}}_{0,2}^{-}\) anticrossing and gather the time-domain response (red points in Fig. 5h). We observe an initial resonator ring-up followed by a decay with T1~140 ± 50 ns (see Methods). In this case, the signal does not fully decay to zero as it was the case for the SOC experiments. This is a particularity of our concrete experiments since the signal from the ground state can also be detected at the readout point since δo ≲ Δc (note the overlap in the Cq peaks in Fig. 5e and g). We discuss this limitation further in Supplementary Note 9. We compare the signal to a control measurement where we initialise in the ground state deep in the (0,2) region by waiting for relaxation to the S0,2 state. We then ramp to the readout point (black points). In this case, the system remains in the ground state and the signal rises with the ring up of the resonator.

For the high field case (B = 0.75 T), where we use the (↑B, ↓D)/S0,2 anticrossing for readout, we perform a similar sequence but starting deep in the (0,2) region where the ground states is S0,2. Via diabatic pulsing through the T−/S0,2 anticrossing (outside the detuning range of panel f), we prepare the system in the excited S0,2 near zero detuning to then ramp to the readout point. We observe a similar resonator ring-up followed by a decay with now a T1 ~ 270 ± 50 ns. We plot the data and the control in Fig. 5i.

By measuring the decay constant as a function of detuning near the readout points, we find that T1 ranges between 100-200 ns (200-400 ns) in the low (high) magnetic field case, with larger values reported further from the readout point. We hypothesize that the difference in T1 for the two cases is related to the state decay happening primarily between the T0,2 and S0,2 at low fields - a spin decay within the QD - while at high magnetic fields the decay occurs between the (↑B, ↓D) and (↓B, ↓D) states - a decay within the Boron atom.

Overall, our results show that, in spin systems with lifted SB due to orbital states, the spin state can be read selectively and positively by making use of the different detuning points at which the dispersive signal of the (↑B, ↓D) and \({{\rm{T}}}_{1,1}^{-}\) measurement outcomes manifest. While SOC is present in our system, resulting in a finite Δsf and g-factor difference, neither are required for readout using orbital states, allowing the readout mechanism to be extended to systems lacking strong SOC such as electrons in silicon. In such systems (Δsf = 0, gD = gB), the two readout points correspond to a Singlet or Triplet (T±, T0) outcome. We discuss this further in Supplementary Note 4.2.

Discussion

We have presented a novel spin readout methodology based on the detuning-dependent polarizability of the two-spin system in a semiconductor DQD to perform spin readout even when SB lifting mechanisms are present. We demonstrate this readout mechanism in two situations: Readout in the presence of SOC, leading to spin flip tunnel coupling between the T− and S2,0 states, and spin-blockade lifting due to the presence of excited orbital states.

We note that, going beyond the applications presented in the experimental section, our methodology enables three-valued readout, where up to three different spin sub-states can be discerned with a single measurement at a given measurement point (see Supplementary Note 5). This is a consequence of the charge polarization nature of the method, where a positive, negative, and neutral response of the system can be detected. The tri-state and selective nature of our measurements may therefore enable complete readout of the state of two-spin systems more efficiently than what is possible through charge sensing53, reducing the number of necessary repetitive measurements54 (see Supplementary Note 4.1).

Our work and methodology open new opportunities to (i) study the fundamentals of SB, its angular dependence in SOC systems and its impact on the ultimate readout fidelity. We highlight the limit of typical charge-sensed SB protocols to perform SCC due to incomplete diabatic passage of the ↑, ↑/S2,0 anticrossing (see Supplementary Note 1). Since the method presented in this work does not require any diabatic passages, it may be a way to enable high SCC fidelity. (ii) The ability to use the selective and tri-state nature of the readout may be used to enhance the spin readout fidelity, detect state leakage and complete readout of two-spin systems without the need of perturbative tunnel barrier pulses53. In particular, by successively measuring at the various readout points of the spin-orbit coupled system, the full spin state, as well as state leakage out of the computational subspace, may be detected (see Supplementary Note 4.1). (iii) Our work encourages the exploration of hybrid QD-acceptor systems and its interaction with a microwave resonator as a system for quantum information processing. This work shows interesting promise that in these systems, the spin-relaxation time may be improved, increasing their utility as potential qubits. The acceptor (which can be seen as a hole analogue to a phosphorus donor) produces tight confinement, increasing the energy of orbital states.

Methods

Fabrication details. The transistors used in this study consist of a single gate silicon-on-insulator (SOI) nanowire transistor with a channel width of 120 nm, a length of 60 nm, and height of 8 nm on top of a 145-nm-thick buried oxide. The silicon layer has a Boron doping density of 5 ⋅ 1017 cm−3. The silicon layer was patterned to create the channel using optical lithography, followed by a resist trimming process. The transistor gate stack consists of 1.9 nm HfSiON – leading to a total equivalent oxide thickness of 1.3 nm–capped by 5 nm TiN and 50 nm polycrystalline silicon. After gate etching, a Si3N4 layer (10 nm) was deposited and etched to form a first spacer on the sidewalls of the gate, then 18-nm-thick Si raised source and drain contacts were selectively grown before source/drain extension implantation and activation annealing. A second spacer was formed, followed by source/drain implantations, an activation spike anneal and salicidation (NiPtSi). The nanowire transistor and superconducting resonator were connected via Al/Si 1% bond wires.

Measurement set-up

Measurements were performed at the base temperature of a dilution refrigerator (T~10 mK). Low-frequency signals (Vg, Vbg) were applied through Constantan twisted pairs and RC filtered at the MXC plate. Radio-frequency signals were applied through filtered and attenuated coaxial lines to a coupling capacitor at the input of the LC resonator. Fast pulsing signals were applied through attenuated coaxial CuNi lines to an on-PCB (printed circuit-board) bias-T connected to the source of the transistor. The resonator (characteristic frequency 2.1 GHz) consists of a NbTiN superconducting spiral inductor (L ~30 nH), coupling capacitor (Cc ~40 fF) and low-pass filter fabricated by Star Cryoelectronics. For exact details of the superconducting chiplet see ref. 43. The PCB was made from 0.8-mm-thick RO4003C with an immersion silver finish. The reflected rf signal was amplified at 4 K and room temperature, followed by quadrature demodulation (Polyphase Microwave AD0540B), from which the amplitude and phase of the reflected signal were obtained (homodyne detection).

Readout pulse sequence

The data in Fig. 3d consists of 100,000 shots at each detuning point, resulting in an average resonator response of the initialised states. After the readout measurement cycle in Fig. 3c, we wait for 100 microseconds in the (1,1) region to ensure the spin in the QD has decayed to the ↓ ground state. This ensures only the (↑B, ↓D) and (↓B, ↓D) states can be initialised. For the time domain data (Fig. 3d-f), the time constant of the resonator ring-up (τ ~ 80 ns) is in good agreement with the bandwidth of our resonator (κ/2π ~3-4 MHz with the exact value depending on magnetic field, and τ = 2/κ). For readout at RA, we estimate the state decay constant T1 from the exponential decay of the signal after the initial rise. For readout at RP, the initialised signal rises more slowly (τ ~95 ns) as compared to the control (τ ~ 80 ns).

Fit of time traces to extract T 1 at the readout point

To extract the state decay constants from the time-traces in Figs. 3e, 5h and i, we fit the data with a model combining the ring-up of the resonator (determined by τ ~ 80 ns) with capacitive signal contributions arising from the ground (Cgnd) and excited state (Cexc) where the excited state exponentially decays into the ground determined by a time constant T1:

$${C}_{{\rm{total}}}=\left(1-{e}^{\frac{-t}{\tau }}\right)\left[{C}_{{\rm{exc}}}{e}^{\frac{-t}{{T}_{1}}}+{C}_{{\rm{gnd}}}\left(1-{e}^{\frac{-t}{{T}_{1}}}\right)\right],$$
(1)

where t is the measurement time. We use a least square fit to extract T1 and estimate the uncertainty from the covariance of the fit.