Introduction

The recent discoveries of topological semimetals (TSMs) have stimulated intense interest in condensed matter physics and material science.1,2,3,4,5,6 The typical Dirac semimetals such as Na3Bi1,7 and Cd3As2,2 for instance, have four-fold degenerate band crossing points in the momentum space. The existence of these Dirac points or line-like nodes is topologically protected due to the crystal and time reversal symmetries. A Dirac semimetal can transform to a Weyl semimetal when the spin degeneracy is lifted by breaking either time-reversal or spatial inversion symmetry, resulting in paired Weyl points with opposite helicities. The inversion symmetry broken Weyl states have been discovered in a series of transition-metal monopnictide.5,6,8,9,10 When the Dirac or Weyl points are near the Fermi level, the relativistic Dirac or Weyl fermions emerge as low energy quasi-particles, resulting in several exotic transport phenomena such as light effective mass, high carrier mobility, and large magnetoresistance.1,2,3,4,5,6,7,11,12,13,14 In general, topological insulators15 or topological superconductors16,17,18,19,20,21,22,23,24,25,26 can be viewed as a result of gap formation in TSMs7 without or with internal U(1) symmetry breaking. More generic topological materials should include topological metals, the bulk metals with topologically protected surface states or band crossing points. Such metals can be viewed as doped TSMs or doped topological insulators, or the mixtures with additional metallic bands, though a thorough classification has yet to be reached.27,28 Among all these topological materials the two dimensional graphene is known as the simplest Dirac semimetal consisting of a single layer of pure carbons.29,30

Gallium, which was first predicted by Russian chemist Dmitri Mendeleev in 1871, is one of the four pure metals (with other three being Cesium, Rubidium, and Mercury) which are in the liquid phase near room temperature at ambient pressure. Although gallium is a simple metal element, the bulk gallium crystals have a rich phase diagram. Only the orthorhombic α-Ga (space group Cmca) phase is stable at atmospheric pressure. In this phase, each Ga atom has a nearest neighbor at distance 2.44 Å and six others between 2.71 and 2.79 Å.31 The α-Ga has been long considered as a compensated metal with the broadband s2p1 electronic configuration. The Shubnikov de Hass (SdH) and de Haas van Alphen (dHvA) quantum oscillations were measured, indicating a complicated band structure with separated Fermi surface sheets.32,33,34 A signal of superconducting transition below 1.08 K was probed earlier by specific measurement.35,36 However, such transition is hard to be probed by conventional resistivity measurement due to the extremely low resistance.

In this article, we have carried out a comprehensive investigation of bulk properties for the α-Ga single crystals grown by using a super-cooled method. The most prominent new feature we have found is that the magnetoresistance (MR) has a significant enhancement in the low temperature regime, reaching 1.66 × 106% at 2 K under a field of 9 T, and 3.84 × 106% at 4.2 K under a pulse magnetic field of 60 T. The magnitude of MR at this temperature regime is much larger than those in known topological semimetals. Moderately away from this regime, the MR decreases to 500% at 30 K. The measurements of the dHvA oscillations in the isothermal magnetization show very high quantum mobility (up to ∼1.17 × 104 cm2/Vs at 5 K) and very light effective mass (∼0.02–0.05m0, with m0 being the free electron mass) for charge carriers, in addition to a nontrivial Berry phase whose topological origin is evidenced by the first principle calculations. Furthermore, superconductivity in the same α-Ga single crystals is confirmed not only by the specific heat capacity measurement but also by an improved resistivity measurement. All these findings show the coexistence of topological phase and superconducting properties in such a simple pure metal.

Results

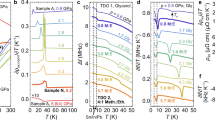
Several α-Ga single crystals were measured showing the similar transport properties. We mainly report the results of “sample 1” in the following. Figure 1a shows the magnetotransport of the longitudinal resistivity ρ (T) at various applied magnetic fields. In a zero magnetic field, the resistivity of the α-Ga single crystal at room temperature is about 16 μΩ cm, nearly one order larger than that of silver, the pure metal with the best conductivity. Lowing the temperature, the zero-field resistivity decreases rapidly, reaching a remarkably low residual resistivity = 8 nΩ cm at 10 K. The data below 10 K is not smooth because the magnitude of resistivity is too small to be within the limit of our PPMS measurements. The residual resistivity of the α-Ga single crystal is comparable with the well-known low resistivity compounds such as PdCoO2 (10 nΩ cm, 2 K), IrO2 (15 nΩ cm, 3 K), and MoP (6 nΩ cm, 2 K),37 and is much smaller than those of topological semimetals reported so far. The detailed information is listed in Table 1. In our measurement, the residual resistivity ratio (RRR) is ρ(300 K)/ρ(10 K) ≈ 2000, implying the high quality of our single crystals.

Fig. 1
figure 1

Results of resistivity measurements in α-Ga. a The log–log plot of resistivity ρ(T) measured at various applied magnetic field H = 0, 0.5, 1, 2, 3, 5, 7, and 9 T for H // b-axis, the current J is within the ac-plane. b ∂ρ (T)/ ∂T plotted as a function of temperature. The minimum in the curve ∂ρ (T)/∂T marks the inflection point Ti, and the sign change in the curve ∂ρ (T)/∂T marks the resistivity minimum at Tm, shown in the upper inset. Tm and Ti plotted as the function of applied magnetic fields is in the low inset in which Ti stays almost unchanged whereas Tm clearly evolves with field. c The normalized magnetoresistance as a function of temperature at various magnetic fields. d Specific heat capacity divided by temperature as a function of T2. The lambda-like peaks indicate a superconducting phase below 0.9 K. e Resistance as a function of temperature at various magnetic fields (0, 0.5, 1.5, 2, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 10, 15, 20, 50, and 100 mT). f Resistance as a function of applied field at 0.5 K. The inset displays the resistance in lower magnetic fields

Full size image
Table 1 Residual resistivity, RRR, MR, and relative effective mass of the typical semimetals extracted from the relevant references
Full size table

The topological characteristic of α-Ga is revealed by the first principle electronic band structure calculations as displayed in SI-Fig. 5. Without the spin–orbit coupling (SOC), the band structure of α-Ga shows numerous degenerate points and Dirac-like features typical for TSMs. The band crossing points at X, between S and R, and between Z and Γ, as well as the energy degenerate point at Z, are close to the Fermi level. Once the SOC is considered, all the features between the bands 12 and 13 are gapped out throughout the whole Brillouin zone. Therefore, the system could be characterized by the Z2 topological invariant. The Z2 classification of the system is (1;110), manifesting the strongly nontrivial property of the system. The topologically protected edge states are thus expected between bands 12 and 13. In addition, there is still a four-fold degenerate point for the bands 11 and 12 near the Fermi surface along the A–Z direction. While the material cannot be simply identified as a clean nodal line semimetal because of the non-integer electron filling and coexisting metallic bands, this feature may lead to the Dirac-like excitations. The detailed information is listed in SI-Table III.

Next, we turn to the results of resistivity measurements. The temperature dependence of resistivity is dramatically changed under the applied magnetic fields. A prominent field-driven resistivity up-turn appears around 20 K as the field increases to 0.5 T, and, a plateau-like saturation develops below = 6 K in ρ(H, T) as shown in Fig. 1a. In fact, this phenomenon can survive at magnetic field as low as 0.05 T as shown in Supplementary Information (SI-Fig. 2a). Figure 1b shows the derivative ∂ρ(T)/∂T curves at various fields. In the insets of Fig. 1b, Tm is the point where ∂ρ(T)/∂T changes sign which is associated with the crossover. Ti is the inflection point of the curve below which the resistivity plateau (plotted in logarithmic scale) sets in. A subtle feature here is that Ti(≈6 K) is nearly independent of the field whereas Tm increases with the field. Such transformative turn-on or metal-insulator-like crossover behavior has also been observed in other materials showing large MR4,5,6 but at relatively high magnetic fields. Its origin is commonly attributed to the strong field and temperature dependence of high mobility of charge carriers,38,39,40 or to a true metal-insulator transition or an electronic structure change driven by the magnetic field.41,42,43,44 In Fig. 1c we show a normalized MR defined as MR(H,T)/MR(H, 2 K) as a function of temperature at various magnetic fields, which collapses into one curve. This implies the fact that the plateau-like saturation observed here is field-independent, in favor of the topological origin.

When further lowing the temperature, a superconducting phase with Tc = 0.9 K is observed by means of the specific heat measurement as shown in Fig. 1d. At low temperatures, Cp/T = γn + βT2, where γn = 0.55 mJ/mol K2 is the Sommerfeld constant and β = 0.055 mJ/mol K4 the Debye constant. The magnitudes of γn and β are consistent with the early reports35,36 although our Tc is a little bit smaller. The slight discrepancy in Tc is likely due to a small residual magnetic field which cannot be removed in our PPMS equipment. It is very hard to directly detect the superconducting transition by means of resistivity measurement because the resistance of the bulk α-Ga is extremely low. To overcome this difficulty, we connect several bars of α-Ga single crystals in series so as to increase the voltage between the contacts. The temperature dependence of electrical resistance down to 0.5 K at ambient pressure is presented in Fig. 1e. Then, a sudden drop in resistance at 0.9 K is observed, in agreement with the specific heat measurement. Therefore, the drop is most reasonably caused by the superconducting transition, while the very small residual resistance down to the lowest temperature is obviously due to the electrical contact resistance between the bulk α-Ga bars. Upon increasing field, Tc shifts firstly to the maximum 1.1 K at 2.5 mT, because of the small residual magnetic field in PPMS, and then to lower temperatures. The critical magnetic field is estimated as about 5 mT at 0.5 K as shown in Supplementary Information (SI-Fig. 2c).

Figure 2 shows the field dependence of the MR at various temperatures. When the current J is in the ac-plane and the magnetic field is out-of-plane (H//b), the MR is positive, reaching about 1,656,500% at 2 K at 9 T. This MR is large compared with the ones in known TSMs. For instances, it is about ten times larger than that measured at the same field in WTe23 and about two times of the one in NbP.45 When temperature increases, the MR decreases quickly, to 500 % at 30 K as shown in the inset of Fig. 2a. The MR follows the typical power-law MR∝H n behavior, with n changing from 1.787 (T = 2 K) to 1.5 (T = 30 K). The power law of MR (with n = 2) behavior may indicate a compensation effect.46 We also measured the angular dependent MR by rotating the applied field from the b-axis to the ac-plane, with θ being the angle between the applied field H and the current J. The MR(H, θ) at 2 K first increases before 17° and then decreases rapidly. For example, MR(9 T, 88°) ≈ 400 %, which is only 0.02% of MR(9 T, 17°). The power law behavior is not very sensitive to θ excepts for θ close to 90° or H //J where n drops to n = 0.4. Overall, as shown in Fig. 2c, the MR(H,θ) curves collapse to a single curve, MR(H, 17°), with a field scaling factor εθ ∝ cos(θ + 52°), indicating open trajectories with a single average direction in the Fermi surface.46 Moreover, as shown in Fig. 2d, the MR increases with the field without saturation. Clear SdH quantum oscillations are observed at high magnetic field as shown in Fig. 2d.

Fig. 2
figure 2

Field and angular dependence of resistivity. a Temperature dependence of the magnetoresistance at various temperatures (T = 2, 3, 6, 7, 8, 9, 13, 20, and 30 K) with the current parallel to ac-plane and the external magnetic field H is parallel to b-axis; it is maximized at 2 K and 9 T with MR = 1.66 × 106%. b Angular dependence of the magnetoresistance at 2 K with the current within the ac-plane, and the field rotates from the b-axis to the ac-plane. The inset shows that the MR tends to saturate under high magnetic field when the direction of the field is close to the ac-plane. c Scaling behavior of the field dependence of the MR at various magnetic field directions. Upper inset: MR shows a power law behavior as MR ∝ H 1.787 at 2 K, lower inset: scaling factor εθ as a function of θ. d The MR of α-Ga up to 60 T at 4.2 K, with the current within the ac-plane and H parallel to the b-axis

Full size image

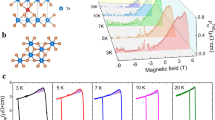
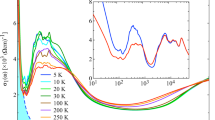
Figure 3 presents the results of isothermal magnetization at various temperatures for H//b, H//a, and H//c, respectively. Very strong oscillations with the amplitudes of 15 emu/mol at T = 2 K and μ0H = 7 T are clearly visible for H//b. For H//a, or H//c, the oscillation amplitude is about 1 emu/mol, comparable to the topological Dirac nodal-line semimetal ZrSiSe.47 Based on the Fast Fourier transformation (FFT) analyses, we found six major low frequencies (19.9, 22.1, 29.1, 38.2, 78.6, and 156.6 T), and five major high frequencies (753, 782, 803, 840, and 865 T) for H//b, see in Fig. 4b. A superposition of low-frequency and high-frequency oscillations indicated by a beat pattern is shown in Fig. 4a. The detailed frequency for H//a and H//c are presented in SI-Figs. 3b and 4b.

Fig. 3
figure 3

Isothermal magnetization for H//b, H//a, and H//c in α-Ga at various temperatures. a, b, c The oscillatory components of magnetization for H//b, a and c, respectively. The inset in a shows the effect of Zeeman split

Full size image
Fig. 4
figure 4

Results of isothermal magnetization without background for H//b. a The oscillatory components for H//b. b FFT spectra of ΔM oscillations. c The normalized FFT amplitude vs. temperature; the solid lines represent the LK fits for effective mass. d The LK fits results at temperatures of 5 K. The blue solid lines represent the multiband LK fits

Full size image

In general, the oscillatory magnetization of a Dirac system can be described by the Lifshitz-Kosevich (LK) formula48,49

$$\Delta M \propto - B^{1/2}R_{\mathrm{T}}R_{\mathrm{D}}R_{\mathrm{S}}\sin \left[ {2{\mathrm{\pi }}\left( {F{\mathrm{/}}B - \varphi _{\mathrm{B}} - {\mathrm{\delta }}} \right)} \right],$$
(1)

here, φB is the Berry’s phase, δ is a phase shift, with δ = ± 1/8 in 3D, RT = αTm*/Bsinh(αTm*/B), RD = exp(−αTD m*/B), RS = cos(πgm*/m0), m* and m0 are the effective cyclotron mass and free electron mass, respectively. Here, TD is Dingle temperature, and α = (2π2kBm0)/(ћe) ≈ 14.7 T/K. The thermal and Dingle damping terms RT and RD are due to the Landau level (LL) broadening driven by the finite temperature effects on the Fermi-Dirac distribution and the electron scattering rate, respectively. The spin reduction factor RS results from the Zeeman effect. We observed the peak splits in oscillations along all three directions as shown in the inset of Fig. 4a (and SI-Figs. 3a, 4a). Raising the temperature above 10 K, the splits gradually merge into a single peak due to the smearing of the Zeeman effect.

The effective electron cyclotron mass m* can be estimated by fitting the temperature dependence of the oscillation amplitude to the thermal damping factor RT, as shown in Fig. 4c (and SI-Figs. 3c and 4c). For all probed oscillation frequencies, the obtained effective mass is in the range of 0.016–0.05m0. Such value is comparable to that of the Dirac semimetal Cd3As2,50,51 whose effective mass is among the smallest one in known Dirac semimetals. Taking the effective mass and the oscillation frequencies derived from the FFT spectra as known parameters, we can further fit the oscillation patterns by the LK formula (Eq. 1), from which the Dingle temperature and Berry phase can be derived. To avoid the influence from the Zeeman splitting, we have fitted the dHvA oscillations at temperatures where the Zeeman effect is minimized by the thermal broadening of the LLs. The results are shown in Fig. 4d (and SI-Figs. 3d, 4d) and several relevant parameters obtained from the LK formula are listed in Table 2. For example, the Dingle temperature TD is estimated as 11 K for Fβ = 22.3 T at 5 K. Therefore, the quantum relaxation time τq = ћ/2πkBTD = 1.12 × 10−12 s, and the quantum mobility μq = eτq/m* is estimated to be 1.17 × 104 cm2/(Vs). The LK fit also yields the Berry phase φB = 0.91π for δ = −1/8, or 1.41π for δ = 1/8. The Berry phase is close to π, thus it plays a topologically non-trivial role in the transport behavior.

Table 2 Parameters obtained from the dHvA oscillations of α-Ga
Full size table

We note that the magnitudes of the calculated effective masses of some bands are relatively larger than that observed by the SdH oscillations. The sharp dependence of Fermi surface cross section, the possible misalignment in experiments, or the magnetic breakdown effect in high magnetic fields may be the cause for the above discrepancy. Nevertheless, such discrepancy is still a puzzle and we will try to clarify it in the near future.

Discussion

Materials with very large MRs are important building blocks of magnetic field sensors or other devices which are perpetually at the frontier of contemporary materials science. Meanwhile, a long-standing interest in condensed matter physics is the interplay between superconductivity and topology of electronic band structures. While the genuine topological superconductivity is expected due to this interplay, the superconductivity paring mechanism in materials with non-trivial topological band structures still remains a major puzzle. The materials exhibiting both superconductivity and topological characteristics are thus desirably attractive but rare. To our best knowledge, such candidate materials discovered so far are binary or more complicated compounds exhibiting moderately large MR. For instances, the nodal-line semimetal PbTaSe2, possessing a nonzero Z2 topological invariant and topologically protected surface states, is a noncentrosymmetric superconductor with Tc = 3.8 K. Its MR is about 40–150% in the normal state at 9 T.25,26 The type-II Dirac semimetal PdTe2 is also a superconductor with Tc = 2 K, the MR is ~900% at 0.36 K under the magnetic field of 30 T with the effect mass of 0.13m0.52 A large unsaturated MR is also discovered in WTe23 at ambient pressure, but the MR is quickly suppressed under high pressure, and then a superconducting state appears at the critical pressure of 10.5 GPa.21,53

It is known that in the type-I Dirac semimetal the density of states near the Fermi level is very small so the appearance of superconductivity usually requires electron or hole doping. The situation is different in the type-II Dirac semimetal where the density of states near the Fermi level is relatively large.23 In the Weyl semimetal, as studied in a theoretical work,53 the superconductivity may be caused by the px + ipy pairing state due to the existing Fermi arc. Combining the experimental results and the theoretical calculations, the present studied material α-Ga has both topological trivial and non-trivial bulk states. Therefore, such topological metal offers a particular interesting platform for understanding the superconducting mechanism in topological materials.

In summary, we have performed a systematic investigation on the high quality α-Ga single crystals, finding a number of fascinating properties which are unexpected for simple pure metals. The resistivity ρ(H,T) of the α-Ga shows a plateau-like saturation at relatively low temperatures after a metal-to-insulator-like crossover. The MR is large at low temperatures obeying the power-law behavior. The very high conductivity and large MR, together with the fitted cyclotron effect mass and the carrier mobility, manifest the α-Ga as a clean system with excellent transport properties among known TSMs. The electronic origin behind these properties is linked to the non-trivial topological band structure of this material, as evidenced by the observed Berry phase and the first principle calculation, suggesting the coexisting doped topological Z2 bands and a nodal line near the Fermi level. We have also demonstrated the phenomenon of bulk superconductivity in this material by improving the resistivity measurement. Therefore, the α-Ga not only represents a pure metal material with interesting transport properties, but also hosts both bulk superconductivity and topological characteristics. Further investigations on the topological and surface state properties are needed in order to clarify whether this superconductivity originates from trivial or nontrivial bands. We expect that the α-Ga will be a new and promising platform not only for the purpose of materials application, but also for the study of the novel physics bridging the topology and superconductivity.

Methods

XRD and single crystal growth of α-Ga

The Ga (99.999%) used in this work were obtained from Alfa Aesar company. The single crystal was prepared from super-cooled gallium. Large single crystals of gallium were grown from the oriented seeds. The XRD experiment was performed at room temperature with a monochromatic Cu Kα1 radiation using a PANalytical x-ray diffractometer (Model EMPYREAN) at Zhejiang University. We employed a conventional θ–2θ scan for the as grown single crystal lying on a sample holder. In order to obtain the powder XRD pattern of gallium we first paste the melted gallium to the sample holder. After cooling there are many micro-single-crystals in the surface and the XRD patterns appear no peaks or only one peak. However, we can successfully obtain the XRD pattern by carefully mixing the Ga powder with the Si powder below its melting temperature which ensures that the surface of Si powder enwraps gallium powder. The information about structure and XRD results are displayed in SI-Fig. 1a. The zero shift of XRD is derived as 0.0255° from SI-Fig. 1b. SI-Fig. 1c displays the polycrystalline XRD pattern which is well indexed by Cmca space group. SI-Fig. 1d shows the single crystal XRD pattern where the crystal surface is normal to the b-axis.

Theoretical calculations

The electronic band structure was calculated using plane-wave basis density functional theory (DFT) as implemented in the Vienna Ab-initio Simulation Package (VASP). Projected augmented wave (PAW) method and the Perdew, Burke, and Ernzerhof parametrization (PBE) of generalized gradient approximation were employed. An energy cut-off of 250 ev and 12 × 12 × 12 Γ-centered K-mesh (over primitive cell) is sufficient to converge the total energy to 1 meV/atom. The density of states (DOS) were obtained with dense Γ-centered K-mesh of 24 × 24 × 24. The DFT band structures were fitted to a tight-binding (TB) model Hamiltonian using the maximally localized Wannier function (MLWF) method with Ga-4p and 4 s orbitals. The Fermi surface was obtained by extrapolating the TB Hamiltonian on a 100 × 100 × 100 K mesh. Since α-Ga has an inversion center, the Z2 topological indices were calculated using the parity-check method.