Abstract
The longstanding view of the zero sound mode in a Fermi liquid is that for repulsive interaction it resides outside the particle-hole continuum and gives rise to a sharp peak in the corresponding susceptibility, while for attractive interaction it is a resonance inside the particle-hole continuum. We argue that in a two-dimensional Fermi liquid there exist two additional types of zero sound: “hidden” and “mirage” modes. A hidden mode resides outside the particle-hole continuum already for attractive interaction. It does not appear as a sharp peak in the susceptibility, but determines the long-time transient response of a Fermi liquid and can be identified in pump-probe experiments. A mirage mode emerges for strong enough repulsion. Unlike the conventional zero sound, it does not correspond to a true pole, yet it gives rise to a peak in the particle-hole susceptibility. It can be detected by measuring the width of the peak, which for a mirage mode is larger than the single-particle scattering rate.
Similar content being viewed by others
Introduction
Zero-sound (ZS) is a collective excitation of a Fermi liquid (FL) associated with a deformation of the Fermi surface (FS)1,2,3,4. The dispersion of the ZS mode ω = vzsq encodes important information about the strength of correlations, as was demonstrated in classical experiments on 3He5. Conventional wisdom holds6 that for a strong enough repulsive interaction in a given charge or spin channel, ZS excitations are anti-bound states which live outside the particle hole continuum (vzs > vF) and appear as sharp peaks in spectroscopic probes, while for attractive interaction they are resonances buried inside the continuum. Possibly the best known example of a resonance is a Landau-overdamped mode near a Pomeranchuk transition1,2,3,4,6,7,8,9,10,11,12,13,14,15,16. These qualitative notions are consistent with rigorous results for a 3D FL1,2,3,4,6.
In this paper we report on two unconventional features of ZS excitations in a clean 2D FL. First, for relatively weak attraction, ZS modes with any angular momentum l are not the expected overdamped resonances but rather sharp propagating modes with vzs > vF. However, a spectroscopic probe will not show a peak at ω = vzsq. Second, for sufficiently strong repulsion, ZS modes with l ≥ 1 appear as peaks in a spectroscopic measurement with vzs > vF, but the modes are not the true poles of the dynamical susceptibility and, as a result, are not the longest lived excitations of the system. We argue that these two features come about because the charge (c) and spin (s) susceptibilities \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) in the angular momentum channel l are nonanalytic functions of complex ω with branch points at ω = ±vFq, which arise from the threshold singularity at the edge of the particle hole continuum. Accordingly, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) is defined on the complex ω plane with branch cuts, located slightly below the real axis in the clean limit (see Fig. 1). In 3D, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) near a branch point has only a weak logarithmic non-analyticity. In 2D, however, the non-analyticity is algebraic (\(\sqrt{x}\)). In this situation, the analytic structure of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) is encoded in a two-sheet genus 0 algebraic Riemann surface (a sphere)17,18,19. It has a physical sheet, on which \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) is analytic in the upper half-plane by causality, and a nonphysical sheet. The ZS modes appear as poles of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\). Both the genus and the number of ZS poles are topological invariants of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\), which remain unchanged as the poles move on continuous trajectories over the complex plane. However, to pass smoothly through a branch cut, a ZS pole must move from the physical to unphysical sheet and vice versa. We show that, for relatively weak attractive interaction, the propagating pole is on the physical sheet, but below the branch cut. Consequently, it cannot be analytically extended to the real ω axis of the physical sheet and does not give rise to a sharp peak in \({\rm{Im}}{\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) above the continuum. We label such a mode as “hidden”. It is similar to the “tachyon ghost” plasmon that appears in an ultra-clean 2D electron gas once retardation effects are taken into account20,21. For sufficiently weak repulsive interaction in channels with l ≥ 1, the pole is located above the branch cut but, when the interaction exceeds some critical value, the pole moves through the branch cut to the unphysical Riemann sheet. Although the pole is now below the branch cut, it does gives rise to a peak in χl(q, ω) because the pole can be continued back through the branch cut to the physical real axis. We label such a mode as “mirage”.
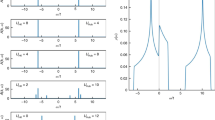
a l = 0 surface. Blue circles: overdamped ZS mode; magenta circles: hidden mode; orange circles: propagating ZS mode. b l = 1 surface. Blue circles: damped ZS mode; magenta circles: hidden mode; orange circles: propagating ZS mode; green circles: mirage mode. For clarity, additional poles on the unphysical sheet are not shown (see the “Methods” section). In both figures, solid (dashed) circles denote the poles on the physical (unphysical) Riemann sheet. Solid (dashed) blue arrows denote the direction of poles’ motion on the physical (unphysical) sheet with increasing \({F}_{l}^{{\rm{c}}({\rm{s}})}\).
Hidden and mirage modes cannot be directly identified spectroscopically by probing \({\rm{Im}}{\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\), as hidden modes do not appear in such a measurement at all, while mirage modes do appear but cannot be distinguished from conventional modes. We argue, however, that they can be identified by studying the transient response of a 2D FL in real time, i.e., by analyzing \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) extracted from pump-probe measurements, which have recently emerged as a powerful technique for characterizing and controlling complex materials22,23,24,25,26,27,28,29,30. At long times, the response function \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) is the sum of contributions from the ZS poles and the branch points. One can readily distinguish a conventional ZS modes from a mirage one via \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) because a conventional ZS mode is located above the branch cut and decays slower than the branch point contribution, while a mirage mode decays faster. As a result, the response of a FL hosting a mirage mode undergoes a crossover from oscillations at the ZS mode frequency to oscillations at the branch point frequency ω = vFq at some t = tcross (see Fig. 2). The detection of a hidden mode is a more subtle issue as this mode does not appear on the real frequency axis, and \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) at large t always oscillates at ω = vFq. However, we show that in the presence of the hidden pole the behavior of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) changes from \(\cos ({v}_{{\rm{F}}}qt+\pi /4)/{t}^{1/2}\) at intermediate t to \(\cos ({v}_{{\rm{F}}}qt-\pi /4)/{t}^{3/2}\) at the longest t, and the location of the hidden pole can be extracted from the crossover scale \({\bar{t}}_{{\rm{cross}}}\) between the two regimes (see Fig. 3a).
The figure depicts the time evolution of \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) for a conventional ZS mode at \({F}_{1}^{{\rm{c}}({\rm{s}})}=0.2\) (orange) and a mirage mode at \({F}_{1}^{{\rm{c}}({\rm{s}})}=8.0\) (green). The modes correspond to the orange and green circles in Fig. 1b. The conventional mode displays an underdamped behavior with decay constant γzs < γ and oscillation period T* = 2π/szs < 2π at all times. The mirage mode decays with γzs > γ and crosses over to oscillations with period T* = 2π at a crossover time \({t}_{{\rm{cross}}}\approx {({\gamma }_{{\rm{zs}}}-\gamma )}^{-1}\). Inset: a zoomed-in view showing the crossover at t* ~ tcross. \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is multiplied by \({{\rm{e}}}^{\gamma {t}^{* }}\) to enhance visibility. The solid line is added to the data points for clarity. The disorder strength is γ = 0.2.
a–c show the time dependence \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) for a system hosting: a A hidden mode at \({F}_{0}^{{\rm{c}}({\rm{s}})}=-0.125\) (magenta circles in Fig. 1a). The gray lines show the characteristic power-law decays ∝ t−1/2, t−3/2. b A damped l = 1 mode at \({F}_{1}^{{\rm{c}}({\rm{s}})}=-0.9\) (blue circles in Fig. 1b). At even longer times (not shown), the period of oscillations approaches 2π. c A hidden l = 1 mode at \({F}_{1}^{{\rm{c}}({\rm{s}})}=-0.121\) (magenta circles in Fig. 1b). d The numerically extracted variation of the phase shift between the two regimes of the hidden mode described in the text (solid), and the analytic prediction (dashed), for \({F}_{0}^{{\rm{c}}({\rm{s}})}=0.03\).
Results
Zero-sound modes in 2D
A generic bosonic excitation of a FL with angular momentum l and dispersion ω(q) is the solution of \({\left({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\right)}^{-1}=0\). ZS excitations are the modes with linear dispersion ω = vzsq in the limit q ≪ kF, where kF is the Fermi momentum. The quasiparticle susceptibility at small ω and q but fixed ω/vFq = s is expressed solely in terms of Landau parameters \({F}_{l}^{{\rm{c}}({\rm{s}})}\) in the charge or spin sectors1,2,3,4,6,7,14,15,16. An explicit form of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) is rather cumbersome but becomes much simpler if one of the Landau parameters, \({F}_{l}^{{\rm{c}}({\rm{s}})}\), is much larger than the others. Up to an irrelevant overall factor, for this case we have
where χl(s) is the quasiparticle contribution from states near the FS, normalized to χl(0) = 1. The general structure of χl(s) can be inferred from the particle-hole bubble of free fermions with propagators \({G}_{0}({\bf{k}},\omega )={\left(\omega +{\rm{i}}\tilde{\gamma }/2-{v}_{{\rm{F}}}(| {\bf{k}}| -{k}_{{\rm{F}}})\right)}^{-1}\) and form-factors fl(θ) at the vertices, where θ is the angle between k and q, f0 = 1, and \({f}_{l}(\theta )=\sqrt{2}\cos l\theta \ (\sqrt{2}\sin l\theta )\) for the longitudinal (transverse) channels with l ≥ 1. (The longitudinal/transverse modes correspond to oscillations of the FS that conserve/do not conserve its area.) However, to properly specify the position of the pole with respect to the branch cut one must include vertex corrections due to the same scattering processes that give rise to the \(i\tilde{\gamma }\) term in G0 (refs 15,31). This is true even in the clean limit \(\tilde{\gamma }\to 0\). To be specific, we assume that extrinsic damping is provided by short-range impurities, and account for the corresponding vertex corrections in all subsequent calculations. We study the case l = 0 as an example of a hidden mode, and the case l = 1, with \({f}_{l}(\theta )=\sqrt{2}\cos \theta\), as an example of a mirage mode. (The l = 1 transverse mode has recently been discussed in refs 15,16).
For l = 0, χ0(s) with vertex corrections due to impurity scattering included is given by15,31
where \(\gamma =\tilde{\gamma }/{v}_{{\rm{F}}}q\). Observe that (i) χ0(s) vanishes at q → 0 and finite ω and γ, as required by charge/spin conservation, and (ii) χ0(s) has branch cuts at s = ±x − iγ, x > 1, see Fig. 1. From Eq. (1), the equation for the pole is \(1+{F}_{0}^{{\rm{c}}({\rm{s}})}{\chi }_{0}(s)=0\). For \({F}_{0}^{{\rm{c}}({\rm{s}})}\, > \, 0\) and γ ≪ 1, the two poles are located at \(\omega ={v}_{{\rm{F}}}q\left(\!\pm\! {s}_{{\rm{zs}}}-{\rm{i}}{\gamma }_{{\rm{zs}}}\right)\), where \({s}_{{\rm{zs}}}=(1+{F}_{0}^{{\rm{c}}({\rm{s}})})/\sqrt{1+2{F}_{0}^{{\rm{c}}({\rm{s}})}}\, > \, 1\) and \({\gamma }_{{\rm{zs}}}=\gamma (1+{F}_{0}^{{\rm{c}}({\rm{s}})})/(1+2{F}_{0}^{{\rm{c}}({\rm{s}})})\, < \,\gamma\). These are conventional ZS poles above the branch cut, which give rise to a peak in \({\rm{Im}}{\chi }_{0}^{{\rm{c}}({\rm{s}})}(q,\omega )\) at ω = vFszsq. For \(-1 \, < \, {F}_{0}^{{\rm{c}}({\rm{s}})}\, < \, -1/2\), the two poles are located along the imaginary s axis, one on the physical Riemann sheet, at \({s}_{{\rm{zs}}}=-{\rm{i}}(1-| {F}_{0}^{{\rm{c}}({\rm{s}})}| )/\sqrt{2| {F}_{0}^{{\rm{c}}({\rm{s}})}| -1}\), and the other on the unphysical Riemann sheet. This is another conventional behavior – the ZS is Landau overdamped, and at \({F}_{0}^{{\rm{c}}({\rm{s}})}\to -1\) its frequency vanishes, signaling a Pomeranchuk instability6,15. The hidden ZS mode emerges at \(-1/2 \, < \, {F}_{l}^{{\rm{c}}({\rm{s}})} \, < \, 0\). Here the two modes are again located near the real axis, at \(\omega ={v}_{{\rm{F}}}q\left(\!\pm\!{s}_{{\rm{h}}}-{\rm{i}}{\gamma }_{{\rm{h}}}\right)\), where \({s}_{{\rm{h}}}=(1-| {F}_{0}^{{\rm{c}}({\rm{s}})}| )/\sqrt{1-2| {F}_{0}^{{\rm{c}}({\rm{s}})}| }\, > \,1\) and \({\gamma }_{{\rm{h}}}=\gamma (1-| {F}_{0}^{{\rm{c}}({\rm{s}})}| )/(1-2| {F}_{0}^{{\rm{c}}({\rm{s}})}| )\, > \, \gamma\). Since sh > 1, the ZS mode is formally outside the continuum, i.e., it is an anti-bound state, even though the interaction is attractive (\({F}_{0}^{{\rm{c}}({\rm{s}})}\, < \,0\)). However, because γh > γ, the pole is located below the branch cut. Since a pole cannot pass smoothly through the cut without moving to a different Riemann sheet, a hidden pole does not give rise to a peak in \({\rm{Im}}{\chi }^{{\rm{c}}({\rm{s}})}(q,\omega )\) at ω = vFshq. The evolution of the poles with \({F}_{0}^{{\rm{c}}({\rm{s}})}\) is depicted in Fig. 1a.
For l = 1 one finds:
In this case too, a hidden pole exists for attractive interaction, in the interval \(-1/9\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 0\). In addition, a new type of behavior emerges for \({F}_{1}^{{\rm{c}}({\rm{s}})}\, > \, 0\). Namely, \({\chi }_{1}^{{\rm{c}}({\rm{s}})}\) has a conventional ZS pole above the branch cut only for a finite range \(0\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, {F}_{1}^{{\rm{m}}}\), where \({F}_{1}^{{\rm{m}}}=3/5\) in the clean limit. At \({F}_{1}^{{\rm{c}}({\rm{s}})}={F}_{1}^{{\rm{m}}}\) the pole merges with the branch cut and, for larger \({F}_{1}^{{\rm{c}}({\rm{s}})}\), it moves below the branch cut and, simultaneously, to the unphysical Riemann sheet. We call this pole a “mirage” one because although it is located on the unphysical Riemann sheet, it can be connected to the physical real axis through the branch cut. As a result, the pole gives rise to a sharp peak in \({\rm{Im}}{\chi }_{1}^{{\rm{c}}({\rm{s}})}(q,\omega )\); however, the width of the mirage mode, γm, is larger than γ.
Detection of hidden and mirage modes
We argue that hidden and mirage modes can be observed experimentally by analyzing the transient response of a FL which, for an instantaneous initial perturbation, is described by the susceptibility in the time domain, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\). At first glance, it seems redundant to study \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\), which is just a Fourier transform of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) for real ω, expressed via \({\rm{Im}}{\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) as \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t\, > \, 0)=(2/\pi )\mathop{\int}\nolimits_{0}^{\infty }\sin (\omega t){\rm{Im}}{\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) by causality. A hidden mode does not give rise to a peak in \({\rm{Im}}{\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) for real ω, while the peak due to a mirage mode is essentially indistinguishable from that due to a conventional ZS mode. However, we will show below that there are subtle features in \({\rm{Im}}{\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) for hidden and mirage modes that manifest themselves in the time evolution of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\).
Our reasoning is based on the argument that \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) can be obtained by closing the contour of integration over ω on the Riemann surface. A choice of the particular contour is a matter of convenience, but a contour can always be decomposed into a part enclosing the poles in the lower half-plane (either on the physical or unphysical sheet) and a part connecting the branch points on the Riemann sphere. For both conventional and mirage modes the second contribution at long times comes from the vicinity of the branch points and behaves as \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\propto \cos ({t}^{* }-\pi /4){{\rm{e}}}^{-\gamma {t}^{* }}{t}^{-3/2}\), where t* = vFqt. The pole contribution behaves as \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\propto \sin ({s}_{{\rm{a}}}{t}^{* }){{\rm{e}}}^{-{\gamma }_{{\rm{a}}}{t}^{* }}\), where a = zs, h, m. For a conventional ZS mode γzs < γ, and the long-t behavior of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) is dominated by oscillations at the ZS frequency. For a mirage mode γm > γ, and the oscillations associated with the mirage mode decay faster than the ones associated with the branch points. We illustrate this behavior in Fig. 2, which depicts \({\chi }_{1}^{{\rm{c}}({\rm{s}})}(q,t)\) at intermediate and long times for \({F}_{1}^{{\rm{c}}({\rm{s}})}=0.2\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}=8\), which correspond to the cases of a conventional and mirage ZS mode, respectively. Alternatively, of course, the mirage mode may be identified from the width of the ZS peak if an independent measurement of γ is available.
For a hidden mode, the situation is more tricky as the pole contribution is cancelled out by a portion of the branch cut contribution and so a hidden pole does not contribute directly to \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(q,t)\). The only oscillations in \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(q,t)\) are due to the branch points, with a period T = 2π/vFq. However, a more careful study shows (see “Methods”) that in the presence of a hidden pole the branch point contribution undergoes a crossover between two types of oscillations with the same period: at intermediate t, \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(q,t)\propto \cos ({t}^{* }+\pi /4)/{({t}^{* })}^{1/2}\), while at longer t, \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(q,t)\propto \cos ({t}^{* }-\pi /4)/{({t}^{* })}^{3/2}\). We illustrate this behavior in Fig. 3a. Note that both the t-dependence of the envelope changes and the phase is shifted by π/2. The crossover scale \({t}_{{\rm{cross}}}^{* }\) is determined by the position of a hidden pole in relation to the branch point. For small \({F}_{0}^{{\rm{c}}({\rm{s}})}\) it is just \({t}_{{\rm{cross}}}^{* }=| {s}_{{\rm{h}}}-(1-{\rm{i}}\gamma ){| }^{-1}\); this relation is verified numerically in the Methods section. Hence, a hidden pole can be extracted from time-dependent measurements even though it does not show up in spectroscopic probes.
For completeness, we also briefly discuss the behavior of \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(q,t)\) in the range \(-1\, < \, {F}_{0}^{{\rm{c}}({\rm{s}})}\, < \, -\!1/2\), where the pole is Landau overdamped even in the absence of disorder, i.e., ω = −ivFqγzs15. In this situation, dynamics at intermediate t is dominated by a non-oscillatory, exponentially decaying pole contribution, while dynamics at longer t is dominated by algebraically decaying oscillations arising from the branch points, with the period T = 2π/(vFq). The crossover time is \({({t}_{{\rm{cross}}}^{* })}^{-1}={({\gamma }_{{\rm{zs}}}-\gamma )}^{-1}\) to logarithmic accuracy. We also present the results for \({\chi }_{1}^{{\rm{c}}({\rm{s}})}(q,t)\) in two representative regimes of \({F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 0\). As shown in Fig. 1b, the l = 1 poles travel in the complex plane, starting from ω = 0 at the Pomeranchuk instability point \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1\) and arriving at the lower edge of the branch cut at \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1/9\). Near \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1\), the poles are close to the real axis and, accordingly, \({\chi }_{1}^{{\rm{c}}({\rm{s}})}(q,t)\) displays weakly damped oscillations (Fig. 3b). When \({F}_{1}^{{\rm{c}}({\rm{s}})}\) crosses the critical value of −1/9, the poles transform into hidden ones, and oscillations are now controlled by the branch points (Fig. 3c). As a final remark, we also verified that the behavior does not change qualitatively for a more realistic case when two Landau parameters, \({F}_{0}^{{\rm{c}}({\rm{s}})}\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}\), have comparable magnitudes.
Discussion
In this work we argued that ZS collective excitations in a 2D FL have two unexpected features. First, for any angular momentum l and for the Landau parameter \({F}_{l}^{{\rm{c}}({\rm{s}})}\) in some negative range, a ZS mode is not a damped resonance inside a particle-hole continuum, as is the case in 3D, but a propagating mode with velocity larger than vF. In the clean limit, a ZS pole of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}\) is located arbitrary close to the real axis, but still below the branch cut, which hides the pole. Such a “hidden” mode does not manifest itself in spectroscopic probes but can be identified by transient, pump-probe techniques. Second, for l ≥ 1 and positive \({F}_{l}^{{\rm{c}}({\rm{s}})}\) above some critical value, a ZS pole moves from the physical Riemann surface to the unphysical one and becomes a “mirage” one. In this situation, \({\rm{Im}}{\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) still has a peak at the pole frequency in the clean limit. However, the long-time behavior of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) is now determined by the branch points rather than by the pole.
The existence of hidden modes in 2D can be traced to the fact that in 2D the branch points associated with the particle-hole threshold are algebraic. The consequence of this is that the poles move continuously on the Riemann surface as \({F}_{l}^{{\rm{c}}({\rm{s}})}\) is varied. This feature is best seen for the case of weak interaction (\(| {F}_{l}^{{\rm{c}}({\rm{s}})}| \ll 1\)) and vanishingly small damping. In this case, the poles of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) are near the branch points: ω = vzsq(±1 − iγ) with vzs ≈ vF and γ ≪ 1. Then the form of branch point singularity determines the trajectory of the pole as \({F}_{l}^{{\rm{c}}({\rm{s}})}\) is varied. For the square-root branch point, the pole’s trajectory is described by \((\omega /{v}_{{\rm{F}}}q)-(1-{\rm{i}}\gamma )\propto -\,{\gamma }^{2}+{({F}_{l}^{{\rm{c}}({\rm{s}})})}^{2}+2i\gamma {F}_{l}^{{\rm{c}}({\rm{s}})}\), which gives rise to hidden modes. (To see this for l = 0 mode, note that the equation for the pole, following from Eqs. (1) and (2), is reduced for small \(| {F}_{0}^{{\rm{c}}({\rm{s}})}| \ll 1\) to \(\sqrt{{(1+z)}^{2}-1}-{\rm{i}}\gamma ={F}_{0}^{{\rm{c}}({\rm{s}})}\), where z = (ω/vFq) − (1 − iγ). For small z, this gives the required trajectory.) In contrast, in 3D the cut is logarithmic and poles move discontinuously15. For example, in the l = 0 channel in 3D the pole position moves from above the branch cut for \({F}_{0}^{{\rm{c}}({\rm{s}})}\, > \, 0\) to the imaginary axis for \({F}_{0}^{{\rm{c}}({\rm{s}})}\, < \,0\) (ref. 6). We also stress that in our calculations we always assumed ω ≫ vFqγ, which corresponds to the collisionless regime. In the opposite limit of ω ≪ γvFq, there is no hidden mode.
The existence of mirage modes for l ≥ 1 but not for l = 0 is a consequence of the fact that the l = 0 channel represents the response function of a conserved quantity (total particle number or spin), while the l ≥ 1 channels represent the response functions of the quantities which are not conserved in the presence of even infinitesimally weak disorder (for example, l = 1 corresponds to the charge or spin current). As a result, the free susceptibility χ0 ≡ χl = 0 in the long wavelength limit (γ ≫ 1) must have a diffusion pole with small magnitude, s = 1/(2iγ). Because of this constraint, the pole in χ0(s) remains above the branch cut for all values of \({F}_{0}^{{\rm{c}}({\rm{s}})}\). For l ≥ 1, there are no constraints limiting the damping term. The result of this is that the imaginary part of the ZS frequency grows with increasing repulsion \({F}_{l}^{{\rm{c}}({\rm{s}})}\), and at some critical \({F}_{l}^{{\rm{c}}({\rm{s}})}\) the pole frequency crosses the branch cut. We note in passing that the difference between the l = 0 and l ≥ 1 channels is not special to 2D, although 2D is a more natural setting to search for a mirage mode, since the pole positions move continuously on the Riemann surface as a function of \({F}_{l}^{{\rm{c}}({\rm{s}})}\). Indeed, it can be shown that there is a mirage mode in the 3D l = 1 longitudinal channel as well. (The calculation is analogous to the one for the 2D case. The pole equation is \(1+{F}_{1}^{{\rm{c}}({\rm{s}})}{\chi }_{1}(s)=0\), where χ1(s) is the particle-hole bubble with vertex corrections from impurities, with a form factor \({Y}_{1}^{0}=\sqrt{3}\cos \theta\). We find that the crossover to a mirage mode occurs for vanishing γ at \({F}_{1}^{{\rm{m}}}=0.44\).)
In more general terms, our work establishes that dynamics of a 2D FL, even of an isotropic and Galilean-invariant one, is determined not just by the poles of its response functions, but also by topological properties encoded in the Riemann surfaces defined by those functions. Here we studied the simplest case, where the Riemann surface is a closed sphere. There exist more complex cases, e.g., for two bands with different Fermi velocities, vF,1 and vF,2, there are four branch points in the complex plane, at ω = ±vF,1q, ±vF,2q, and the associated Riemann surface is a torus. In such cases, one should expect new topological features of ZS excitations.
A few remarks about real systems. First, our results apply to both neutral and charged FLs, with a caveat that for charged FLs the l = 0 charge mode becomes a plasmon32. Second, to observe a ZS mode, one needs to either employ finite-q versions of the pump-probe techniques, e.g., time resolved RIXS33 and neutron scattering34, or spatially modulate/laterally confine 2D electrons. The most readily verifiable prediction is the hidden mode in the spin channel, which occurs for \(0\, < \, {F}_{0}^{{\rm{s}}}\, < \, -\!1/2\). Previous measurements on a GaAs/AlGaAs quantum well35,36 indicate that \({F}_{0}^{{\rm{s}}}\) for this system is exactly in the required range.
Methods
In this section we present the details of our calculations of the charge/spin susceptibility in the time domain, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\), and discuss the analytic structure of the Riemann surface of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\). In Section A we discuss the framework to calculate \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) for a generic l in the charge or spin channel. In Sections B and C we give detailed derivations of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) in the l = 0 and the l = 1 longitudinal channels and briefly discuss how these calculations can be extended to arbitrary l. In Section E we show that the results, discussed in the main text, i.e. the existence of conventional, hidden, and mirage poles, also hold when two Landau parameters, \({F}_{0}^{{\rm{c}}({\rm{s}})}\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}\), have comparable magnitudes.
Throughout this section, we assume an isotropic system, such that at low enough momenta and frequency the fermionic dispersion can be approximated as ω = εk − μ ≈ vF(∣k∣ − kF), where vF is the renormalized Fermi velocity \({v}_{{\rm{F}}}^{(0)}m/{m}^{* }\) and m* is the FL effective mass. We assume that single-particle states are damped by impurity scattering and that the damping rate, \(\tilde{\gamma }\), is small compared to Fermi energy. We also assume that the temperature T is low enough such that the quasiparticle damping rate can be neglected, but still higher than the critical temperature of a superconducting (Kohn-Luttinger) instability.
Dynamical susceptibliities \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) and \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\)
In this section we provide details of our calculations of the response functions in the frequency and time domains, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) and \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\). We assume that typical frequencies and momentum transfers are small, i.e., q ≪ kF and ω ≪ EF. In this limit the response of a FL to a weak external perturbation comes predominantly from quasiparticles near the FS. The quasiparticle contribution to the dynamical susceptibility was obtained by Leggett back in 1965 (ref. 37). To get it diagrammatically, one needs to sum up series of bubble diagrams coupled by quasiparticle interactions. For the case when one Landau parameter dominates, the quasiparticle contribution to \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) has the form
Here the Landau parameter Fl is the properly normalized l’th moment of the antisymmetrized four-fermion vertex, νF is the (renormalized) thermodynamic density of states, and χl(s) is the retarded free-fermion susceptibility in the l’th channel. The subscript qp makes explicit the fact that this is only the quasiparticle response. The full \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\) differs from (4) by an overall factor, which accounts for renormalizations by fermions with higher energies, and also contains (for a non-conserved order parameter) an additional term, which comes solely from high-energy fermions37. These additional terms are relevant for the full form of the susceptibility near Pomeranchuk instabilities towards states with special order parameter13,15,38,39 but not for collective modes studied in this paper. The expression for the free-fermion susceptibility χl(s) in the presence of impurity scattering is obtained by (a) evaluating a particle-hole bubble using propagators of free fermions with fermionic frequency ω shifted to \(\omega +{\rm{i}}\tilde{\gamma }\) and (b) summing up the ladder diagrams for the vertex renormalizations due to impurity scattering. The detailed form of χl(s) depends both on the channel angular momentum l and its polarization (longitudinal/transverse). For a detailed derivation of Eq. (4) and explicit forms of χl(s) we refer the reader to refs 14,15,31. Here we just state the final results for \({\chi }_{{\rm{qp}},l}^{{\rm{c}}({\rm{s}})}(s)\) and focus on calculating its time-domain form. To shorten the notations, henceforth we skip the subindex “qp” in \({\chi }_{{\rm{qp}},l}^{{\rm{c}}({\rm{s}})}\left(q,\omega \right)\), as we did in the main text.
The retarded time-dependent susceptibility is a Fourier transform of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,\omega )\):
where t* = vFqt. In physical terms, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t)\) describes a response of the order parameter in the l’th charge or spin channel to a pulse-like excitation of the form hle−iq⋅rδ(t).
To evaluate Eq. (5), it is convenient to close the integration contour in the complex plane. As discussed in the main text, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(s)\) has two types of singularities in complex s plane, both of which contribute to the result of integration. First, it has a set of poles sj, which can be either on the physical or unphysical sheet. To be concrete, in the subsequent calculations for l = 0, 1 we will label by s1 the pole in the lower-right quadrant of a complex plane of frequency, where Res ≥ 0, Ims < 0. We express the coordinates of the pole s1 as
where a = zs, h, m, and the notations are for three different types of the poles corresponding to a “conventional” ZS mode (either a propagating one, or a resonance within the particle-hole continuum), a hidden mode, and a mirage mode, respectively. These are the same notations that we used in the main text. To make the text less cumbersome, we will refer to each pole according to the mode it gives rise to, i.e. we will call them a “conventional pole”, a “hidden pole”, and a “mirage pole”.
Second, \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(s)\) has branch points at s = ±1 − iγ, where \(\gamma =\tilde{\gamma }/{v}_{{\rm{F}}}q\), and we chose the branch cuts to run along the lines ±x − iγ, 1 < x < ∞. Because of the sign of the argument of the exponential function in Eq. (5), the contour must be closed in the lower half-plane for t > 0, so it traces over the branch cuts in the manner shown in Fig. 4. For t < 0, the contour must be closed in the upper half-plane, where \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(s)\) has no singularities and thus \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(q,t \, < \, 0)=0\) as required by casuality.
The integration contour over (dimensionless) complex frequency s on the physical Riemann sheet from which we obtain \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(t^*)\) in Eq. 7.
The evaluation of the integral over the contour in Fig. 4 yields
Here \({\chi }_{l,{\rm{pole}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is a contribution from the residues of the poles of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(s)\) on the physical sheet:
Since the sum over sj is restricted to the poles on the physical sheet, it includes conventional ZS and and hidden poles, but not mirage poles.
The second term in (7) is the branch-cut contribution
where Δc(s)χl(x) is the discontinuity of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(s)\) at the branch cut:
It is also possible to re-arrange the contour integral into the one depicted in Fig. 5. This is done by (a) closing the integration contour in complex s on the physical sheet along the line x − iγ + iε, where ε is infinitesimal and x =−∞…∞, i.e. along the line which is located right above the branch cuts, (b) adding an integration contour on the unphysical sheet along the line x − iγ + iε, x = −∞…∞, i.e., right below the branch cut, (c) closing this second contour via an infinite half-circle in the unphysical lower half plane, and (d) adding two compensating integration segments along the lines x − iγ − iε, where −1 ≤ x ≤ 1, on the physical sheet, and along x − iγ + iε, −1 ≤ x ≤ 1 on the unphysical sheet (dashed lines in Fig. 5). Because \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(s)\) varies smoothly through the branch cuts if one simultaneously move between physical and unphysical Riemann sheets, the integration segments running above and below the branch cuts cancel out.
We added to the integral over real s the integration segments over s immediately above the branch cuts on the physical sheet and immediately below the branch cuts on the unphysical sheet. These additional integrals then cancel out between the two Riemann sheets. We then added the integral over an infinite semi-circle to the unphysical sheet, and for both sheets added and subtracted the integrals over the range of s between the branch points. The resulting integration contour in each Riemann sheet consists of the closed contour (the solid line) and an additional piece (the dashed line).
The evaluation of the integrals again yields an expression of the form of Eq. (7), but now the sum in Eq. (8) is over the poles on the physical sheet above the branch cut (i.e., conventional poles with damping rate γzs < γ), and over mirage poles:
In addition, the second contribution in Eq. (7) now comes from the difference between the values of \({\chi }_{l}^{{\rm{c}}({\rm{s}})}(s)\) on the two Riemann sheets rather than from a discontinuity at the branch cut:
It can be verified that the integration contour of Fig. 5 is equivalent to a contour on the physical sheet, when the branch cut is chosen to run along the line x − iγ, − 1 < x < 1, see Fig. 6. In this case, the integral for χbranch can be understood as running around the circumference of the contour glueing the two Riemann sheets together into a single sphere.
In what follows, we will present calculations using both integration contours, the one in Fig. 4 and the one in Fig. 5. Although the result, of course, does not depend on the choice of a contour, some details of the calculation are more transparent when using one contour and some are clearer when using the other.
\({\chi }_{l}^{{\rm{c}}({\rm{s}})}({t}^{* })\) for l = 0
In this section we provide detailed calculations for the case of l = 0. First, we use the integration contour in Fig. 4 and then the one in Fig. 5.
The free-fermion susceptibility is given by Eq. (2) of the main text
The quasiparticle susceptibility is obtained by plugging χ0 into Eq. (4). The two poles of \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(s)\) are located at
In Fig. 7 we show a 3D depiction of the poles’ trajectories on the Riemann surface. In what follows, we assume that γ ≪ 1, as we did in the main text.
The figure is obtained by mapping the complex s point of the two Riemann sheets to the 3D set of points \(\{{\rm{Re}}s,{\rm{Im}}s,\pm {\rm{Re}}\sqrt{1-{s}^{2}}\}\) where +(−) maps the physical (unphysical) sheet to the top (bottom) sheet of the figure. On this representation of the surface, the solid and blue red lines denote the pole evolution with increasing \({F}_{0}^{{\rm{c}}({\rm{s}})}\). The evolution of the poles begins at the origin of the physical and unphysical sheets at \({F}_{0}^{{\rm{c}}({\rm{s}})}=-1\). The poles initially move along Im(s) axis down(up) the physical(unphysical) sheets. The pole on the unphysical sheet reaches infinity and crosses to the physical sheet at \({F}_{0}^{{\rm{c}}({\rm{s}})}=-1/2\), and the poles merge and bifurcate at \({F}_{0}^{{\rm{c}}({\rm{s}})}=-(1-{\gamma }^{2})/2\). The regions with yellow shading denote areas where a pole in \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(s)\) either on physical, or on unphysical Riemann sheet, gives rise to a peak in \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(s)\) on the physical real s axis. The areas shaded by peach color are regions where a pole cannot be analytically extended to the physical real axis due to the branch cuts, and \({\chi }_{0}^{{\rm{c}}({\rm{s}})}(s)\) on the physical real frequency axis has no sharp peaks. We set γ = 0.2 for definiteness.
The discontinuity of χ0(s) at the branch cut is
where s1,2 are given by (14), see Eq. (10).
We obtain χ0(q, t*) for the three cases shown in Fig. 1a of the main text, i.e., for a ZS resonance (an overdamped l = 0 mode), hidden mode, and weakly damped ZS mode.
ZS resonance, \(-1\,< \, {F}_{0}^{{\rm{c}}({\rm{s}})}\, < \, -\!1/2\)
An overdamped ZS resonance occurs for \(-1\, < \, {F}_{0}^{{\rm{c}}({\rm{s}})}\, < \, -\!1/2\). The pole contribution can be found directly from Eq. (8). As follows from Eq. (14), there is only one pole in the lower half-plane, at s1 = −iγzs, where
Note γzs ≫ γ everywhere but in the narrow vicinity of the Pomeranchuk instability at \({F}_{0}^{{\rm{c}}({\rm{s}})}=-1\). Evaluating the residue in Eq. (8) we obtain
Now we turn to \({\chi }_{0,{\rm{branch}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\), Eq. (9). One can readily verify that at large t*, the leading contribution to the integral in (9) comes from the vicinity of the branch point s = 1 − iγ. Accordingly, we shift the integration variable in Eq. (9) to y = 1 + x and expand the integrand to leading order in y. We obtain
where
are the pole coordinates measured from the branch point at s = 1 − iγ
Keeping γ only in the exponential, we re-write Eq. (18) as
Comparing \({\chi }_{0,{\rm{pole}}}^{{\rm{c}}({\rm{s}})}\) and \({\chi }_{0,{\rm{branch}}}^{{\rm{c}}({\rm{s}})}\), we see that at \({F}_{0}^{{\rm{c}}({\rm{s}})}\gtrsim -\!1\), where γzs ≪ 1 (but still γzs > γ), the pole contribution dominates up to t* ~ tcross, where
For t* ≫ tcross, the branch-cut contribution becomes the dominant one. At \({F}_{0}^{{\rm{c}}({\rm{s}})}\) not close to −1, tcross ~ 1. In this situation, the branch-cut contribution dominates over the pole one for all t* ≫ 1.
Weakly damped ZS mode, \({F}_{0}^{{\rm{c}}({\rm{s}})}\, > \, 0\)
For \({F}_{0}^{{\rm{c}}({\rm{s}})}\, > \, 0\), ZS excitations are conventional propagating modes. The time-dependent \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is analyzed along the same lines as for the overdamped case. The main difference is that for a propagating mode γzs < γ, and, hence, the pole contribution remains the dominant one at all times, i.e. there is no crossover to oscillations from the branch point (this incidentally is indicated by the divergence of tcross in Eq. (21) as γzs crosses γ). The pole contribution is now obtained by summing up the residues of the two poles at s1,2 = ±szs − iγzs, where \({s}_{{\rm{zs}}}=(1+{F}_{0}^{{\rm{c}}({\rm{s}})})/{(1+2{F}_{0}^{{\rm{c}}({\rm{s}})})}^{1/2}\) and \({\gamma }_{{\rm{zs}}}=\gamma (1+{F}_{0}^{{\rm{c}}({\rm{s}})})/(1+2{F}_{0}^{{\rm{c}}({\rm{s}})})\, < \,\gamma\). Keeping γ only in the exponential, we find
Hidden mode, \(-1/2\, < \,{F}_{0}^{{\rm{c}}({\rm{s}})}\, < \, 0\)
We next consider the range \(-1/2\, < \, {F}_{0}^{{\rm{c}}({\rm{s}})}\, < \, 0\), where the ZS pole is a hidden one: s1 = sh − iγh, where \({s}_{{\rm{h}}}=(1-| {F}_{0}^{{\rm{c}}({\rm{s}})}| )/\sqrt{1-2| {F}_{0}^{{\rm{c}}({\rm{s}})}| }\) and \({\gamma }_{{\rm{h}}}=\gamma (1-| {F}_{0}^{{\rm{c}}({\rm{s}})}| )/(1-2| {F}_{0}^{{\rm{c}}({\rm{s}})}| )\, > \, \gamma\). The pole contribution to \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is up to O(γ) terms
Note that to get the prefactor right, one has to keep γ finite, otherwise the pole and the branch cut would be at the same depth below the real axis, and the prefactor in (23) would be smaller by a factor of two because the angle integration around the pole would be only over a half-circle rather than over a full circle.
The branch cut contribution in Eq. (9) reduces to
where now s1,2 = ±sh − iγh. Evaluating the integral, we find two dominant contributions: one from x ≈ 1, i.e., from the vicinity of the branch point, and another one from x ≈ sh, i.e., from the vicinity of the hidden pole (there is only one such term because Re s2 < 0). Accordingly, we write
To obtain \({\chi }_{0,{\rm{branch}};a}^{{\rm{c}}({\rm{s}})}\), we expand near x = sh as x = sh + ϵ and keep the leading terms in ϵ. We obtain
where \(\bar{\gamma }={\gamma }_{{\rm{h}}}-\gamma \, > \,0\). The integral in (26) yields, by Cauchy theorem
Substituting into (26) we obtain
Observe that the exponential factor in (25) is \({{\rm{e}}}^{-{\gamma }_{{\rm{h}}}{t}^{* }}\), despite that the overall factor in (24) is \({{\rm{e}}}^{-\gamma {t}^{* }}\). The extra factor \({{\rm{e}}}^{-({\gamma }_{{\rm{h}}}-\gamma ){t}^{* }}\) appears after the integration in (27).
Comparing (23) and (28), we see that \({\chi }_{0,{\rm{branch}};a}^{{\rm{c}}({\rm{s}})}({t}^{* })\) cancels out the pole contribution:
Because of the cancellation between \({\chi }_{0,{\rm{branch}};a}^{{\rm{c}}({\rm{s}})}\)(t*) and χ0,pole(t*), there are no oscillations in \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })\) with frequency sh, set by the hidden pole. Note in passing that if we computed \({\chi }_{0,{\rm{branch}};a}^{{\rm{c}}({\rm{s}})}({t}^{* })\) strictly at γ = 0, the overall prefactor would be smaller by the factor of two because then \({\int \nolimits_{-\infty }^{\infty}}d\epsilon {{\rm{e}}}^{-{\rm{i}}\epsilon {t}^{* }}/\epsilon =-{\rm{i}}\pi\). The relation \({\chi }_{0,{\rm{branch}};a}^{{\rm{c}}({\rm{s}})}({t}^{* })={\chi }_{0,{\rm{pole}}}({t}^{* })\) would still hold because the pole contribution at γ = 0 would also be smaller by a factor of two.
The second term in Eq. (25) is the contribution from the vicinity of the branch point. At the largest t*, this contribution has the same form as in Eq. (18):
However, the full form of \({\chi }_{0,{\rm{branch}};b}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is more involved, and the \(1/{({t}^{* })}^{3/2}\) behavior sets in only after some characteristic time tcross,1, which becomes progressively larger as \(| {F}_{0}^{{\rm{c}}({\rm{s}})}|\) decreases and sh approaches 1. To see this, we expand the integrand of (24) in y = x − 1, but do not assume that y is small compared to σh = sh − 1. We obtain, at t* ≫ 1
where z = −iyt* and
where \(\sqrt{-{\rm{i}}}\) in (32) stands for \((1-{\rm{i}})/\sqrt{2}\). Note that both σh and \({({F}_{0}^{{\rm{c}}({\rm{s}})})}^{2}\) vanish in the limit \({F}_{0}^{{\rm{c}}({\rm{s}})}\to 0\), but their ratio remains finite: \({\sigma }_{{\rm{h}}}/{({F}_{0}^{{\rm{c}}({\rm{s}})})}^{2}\approx 1/2\). At small enough \({F}_{0}^{{\rm{c}}({\rm{s}})}\), a = σht* can remain small even when t* is large. Accordingly, we treat a as a variable which can have any value. In the two limits a ≫ 1 and a ≪ 1 we have
Accordingly, in the two limits \({\chi }_{0,{\rm{branch}};b}^{{\rm{c}}({\rm{s}})}({t}^{* })\) behaves as
We see that both the exponent of the power law decay and the phase of oscillations vary between the two regimes. In particular, the phase changes by π/2 between the regimes of σht* ≪ 1 and σht* ≫ 1 (up to corrections O(γ). The crossover between the two regimes occurs at t* ~ tcross,1, where
is related to the coordinate of the hidden pole. This relation provides a way to detect the hidden mode experimentally, particularly for small \({F}_{0}^{{\rm{c}}({\rm{s}})}\), where sh − 1 ≪ 1 and tcross,1 ≫ 1, by either by looking at the crossover in the power-law decay of \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })\) or by studying a variation of the phase shift.
In the intermediate regime of t* ~ tcross,1 (assuming that tcross,1 ≫ 1) the susceptibility behaves as \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* }) \sim A({\sigma }_{{\rm{h}}}{t}^{* })\cos ({t}^{* }-\phi ({t}^{* }))/{({t}^{* })}^{1/2}\). In Fig. 8 we depict ϕ(t*) extracted from numerical evaluation of \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })\) for different \({F}_{0}^{{\rm{c}}({\rm{s}})}\). To obtain the data in the figure, we fit segments of the data at different t* onto a trial function \(A\cos ({t}^{* }-\phi )/{({t}^{* })}^{\alpha }\), where A, ϕ, α are fitting parameters. We then fit ϕ(t*/tcross) to the prediction of Eq. (37). The data shows a good collapse of the phase evolution onto a universal function of σht* = t*/tcross,1, given by Eqs. (31) and (32), even for not-too-small \({F}_{0}^{{\rm{c}}({\rm{s}})}\), and a very good agreement between the numerical value of tcross,1 and the asymptotic expression in Eq. (35).
a Evolution of the phase of the oscillations ϕ(t*) in Eq. (37) with time, for different \({F}_{0}^{{\rm{c}}({\rm{s}})}=-0.03,-0.06,\ldots -\!0.48\) (the rightmost blue dots are for \({F}_{0}^{{\rm{c}}({\rm{s}})}=-0.48\)). Numerical results for ϕ(t*) are plotted as a function of t*/tcross. For t* > tcross the data for different \({F}_{0}^{{\rm{c}}({\rm{s}})}\) collapse onto a universal curve described by Eq. (31). b Evolution of tcross with \({F}_{0}^{{\rm{c}}({\rm{s}})}\). The black curve is the asymptotic expression in Eq. (35).
Calculations using the contour of Fig. 5
We now demonstrate how to evaluate \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })\) in the case of a hidden pole, i.e., at \(-1/2\, < \, {F}_{0}^{{\rm{c}}({\rm{s}})}\, < \, 0\), using the contour of Fig. 5. The advantage of using this contour is that there is no need to account for a partial cancellation between the pole and brunch-cut contributions. Inspecting the integration contours, we note that χ0,pole(t*) = 0 because there are no poles either above the branch cuts on the physical sheet or below it on the unphysical sheet. We are left only with χ0,branch, defined in Eq. (12). We shift the integration variable in (12) to y = 1 − x. At t* ≫ 1 only small y matter, and one can safely extend the limits of integration to ±∞. We then obtain
It is easy to verify that Eq. (36) is the analog of Eq. (24), up to small corrections due to γ. The integral in Eq. (36) can be solved exactly with the result
where Z(a) was defined in Eq. (32). This result is the same as in Eq. (31), but with corrections due to finite γ.
We also note in passing that at small t* < 1, \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is linear in t* for all values of \({F}_{0}^{{\rm{c}}({\rm{s}})}\). In the limit γ → 0 the dependence is given by:
At small but finite γ, the slope at t* → 0 changes to \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })=({t}^{* }/2)(1+\gamma \Phi ({F}_{0}^{{\rm{c}}({\rm{s}})}))\), where Φ(−1) = 0 and \(\Phi (0-)=8/(\pi | {F}_{0}^{{\rm{c}}({\rm{s}})}| )\). For \({F}_{0}^{{\rm{c}}({\rm{s}})}=0\), \({\chi }_{0}^{{\rm{c}}({\rm{s}})}({t}^{* })={J}_{1}({t}^{* })\), where J1 is a Bessel function.
\({\chi }_{l}^{{\rm{c}}({\rm{s}})}({t}^{* })\) in the l = 1 longitudinal channel
In this section we provide a detailed derivation of \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) in the longitudinal channel. The free-fermion susceptibility is
In the limit γ → 0, the pole coordinates are the solutions of
This gives four poles, which are located on both physical and unphysical sheets. In Fig. 9 we present a 2D sketch of the evolution of the four poles on the Riemann surface. As before, we label the pole with Re s > 0, Ims > 0 as s1, We label the pole in the first quadrant of the unphysical sheet as s3 and define \({s}_{2}=-{s}_{1}^{* },{s}_{4}=-{s}_{3}^{* }\). At finite γ, the expressions for the coordinates of the poles are much more involved, but the number of poles remains unchanged, as does their qualitative behavior.
a A sketch of the trajectories of the poles of \({\chi }_{1}^{{\rm{c}}({\rm{s}})}(s)\) on the physical and unphysical Riemann surfaces. Solid (dashed) circles denote the poles on the physical (unphysical) Riemann sheet. Arrows on solid (dashed) blue lines denote the direction of poles' motion on the physical (unphysical) sheet with increasing \({F}_{1}^{{\rm{c}}({\rm{s}})}\). Blue, magenta, orange, and green circles show typical positions of the poles for the cases of an overdamped ZS mode, a hidden mode, a propagating ZS mode, and a mirage mode, respectively. Note the existence of poles (orange and green, on the \({\rm{Im}}(s)\) axis) corresponding to additional overdamped ZS modes for \({F}_{1}^{{\rm{c}}({\rm{s}})}\, > \, 0\). b A crossover in \({\chi }_{1}^{{\rm{c}}({\rm{s}})}(q,t)\) between the regions dominated by the contributions from the visible and hidden poles. The blue (magenta) points denote the numerical result for \({F}_{1}^{{\rm{c}}({\rm{s}})}={F}_{1}^{{\rm{vis}}}+0.05\) (\({F}_{1}^{{\rm{vis}}}-0.05\)), where \({F}_{1}^{{\rm{vis}}}=-0.162\), and the solid lines depict the analytical result. (The significance of \({F}_{1}^{{\rm{vis}}}\) is described in the text around Eq. (61)). It can be seen that the two traces begin in phase, then move out of phase, and finally become in-phase again. This is an indication that \({\chi }_{1}^{{\rm{c}}({\rm{s}})}(q,t)\) oscillates at different frequencies that correspond to poles for different \({F}_{1}^{{\rm{c}}({\rm{s}})}\), until oscillations from the branch points take over at long times.
The discontinuity at the branch cut is
Before proceeding to a calculation of \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) we sketch out the trajectories of s1...4 on the physical and unphysical sheets, see Fig. 9. We start with the limit γ → 0. The two poles on the physical sheet, s1,2, depart from s = 0 at \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1\) and move in the complex frequency plane as \({F}_{1}^{{\rm{c}}({\rm{s}})}\) increases from −1, until approaching the branch cut at \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1/9\). For \({F}_{1}^{{\rm{c}}({\rm{s}})}\) close to −1, the poles are almost propagating, and γzs < γ. Such poles give rise to oscillations in \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) at the pole frequency. For \(-1/9\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 0\), the poles on the physical sheet are hidden. For \(0\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 3/5\), the poles are conventional ZS poles with γzs < γ. For \(3/5\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\), the poles move to the unphysical sheet and become mirage poles. The two poles on the unphysical sheet, s3,4, are the mirror images of the poles on the physical sheet in the range \(-1\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, -\!1/9\), i.e., \({s}_{3}={s}_{1}^{* },{s}_{4}={s}_{2}^{* }\). In the range \(-1/9\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 0\), the two poles move parallel to the real exis, reaching ±∞ at \({F}_{1}^{{\rm{c}}({\rm{s}})}=0\). For positive \({F}_{1}^{{\rm{c}}({\rm{s}})}\), the poles s3, s4 are on the imaginary axis of the lower half plane of the physical sheet, and on the imaginary axis of the upper half-plane of the unphysical sheet. (We recall, that on the Riemann surface the points ±∞, +i∞ on the unphysical sheet, and −i∞ on the physical sheet, are identical). The pole on the physical sheet moves up from −i∞ and the pole on the unphysical sheet moves down from +i∞. At finite γ, the trajectories are slightly deformed, so that, e.g., s1,2 never quite reach the branch cut and s3,4 are never true mirror images, but the qualitative behavior remains the same.
We now evaluate \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\). As we did in the l = 0 case, we first use the contour of Fig. 4. The evaluation proceeds along similar lines as for l = 0, except for two differences related, first, to the existence of mirage poles, and second, to the fact that for some ranges of \({F}_{1}^{{\rm{c}}({\rm{s}})}\) we need to take into account contributions from all four poles.
Weakly damped ZS mode, \({F}_{1}^{{\rm{c}}({\rm{s}})}\gtrsim -\!1\)
Consider first the limiting case \({F}_{1}^{{\rm{c}}({\rm{s}})}\gtrsim -\!1\). Here s1 = szs − iγzs, where \({s}_{{\rm{zs}}}\approx {((1-| {F}_{1}^{{\rm{c}}({\rm{s}})}| )/2)}^{1/2}\) and \({\gamma }_{{\rm{zs}}}\approx (1-| {F}_{1}^{{\rm{c}}({\rm{s}})}| )/4\). The real part of s1 is much larger than the imaginary one (γzs ≪ szs ≪ 1), i.e., the mode is underdamped. The pole and branch contributions to χc(s)(t*) are given by
respectively, where σj = sj − (1 − iγ), similar to Eq. (19). For γ → 0, the pole contribution is
The branch cut contribution has the same form as in the l = 0 case, cf. Eq. (30):
For \({F}_{1}^{{\rm{c}}({\rm{s}})}\approx -1\), the pole contribution is larger than the branch-cut one over a wide range of t* because the pole contributions contains a large prefactor 1/szs while the branch cut contribution is reduced by \(1/{({t}^{* })}^{3/2}\) at large t*. Still, at any \(| {F}_{1}^{{\rm{c}}({\rm{s}})}| < \, 1\), intrinsic γzs is finite and by our construction is larger than extrinsic γ. Then, at large enough t* > tcross,2, the branch-cut contribution becomes larger than the contribution from the pole. The crossover scale is
This tcross,2 is the l = 1 analog of tcross in the l = 0 channel, Eq. (21).
Hidden pole, \(-1/9\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 0\)
In the hidden pole regime, which occurs for \(-1/9\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 0\), the pole contribution is still given by Eq. (42). To leading order in γ, it is
where
The pole frequency is
In the two limits, \({s}_{{\rm{h}}}=2/\sqrt{3}\) for \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1/9\) and sh → 1 for \({F}_{1}^{{\rm{c}}({\rm{s}})}\to 0\).
To leading order in γ, the branch-cut contribution can be expressed as the sum of the two terms:
The first term contains the frequency of the pole s1 on the physical Riemann sheet:
where we recall that s1 = sh − iγh and γh ≥ γ. The second term contains the frequency of the pole s3 on the unphysical Riemann sheet:
where \({s}_{3}={s}_{3}^{\prime}-{\rm{i}}{\gamma }_{3}\) with γ3 < 0 and
As for l = 0, the two largest contributions to \({\chi }_{1,{\rm{branch}};1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) in (51) at t* ≫ 1 come from x ≈ sh and from x ≈ 1. Accordingly, we further split \({\chi }_{1,{\rm{branch}},1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) into two parts as \({\chi }_{1,{\rm{branch}};1}^{{\rm{c}}({\rm{s}})}({t}^{* })={\chi }_{1,{\rm{branch}};1a}^{{\rm{c}}({\rm{s}})}({t}^{* })+{\chi }_{1,{\rm{branch}};1b}^{{\rm{c}}({\rm{s}})}({t}^{* })\). The first contribution is obtained in the same way as for l = 0, by expanding in ϵ = x − sh. The result is
Because γh > γ, the two terms in the last bracket in (54) are of the same sign and add up to a factor of 2. Then
This term exactly cancels out \({\chi }_{1,{\rm{pole}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\) from (47). The second contribution, \({\chi }_{1,{\rm{branch}};b}^{{\rm{c}}({\rm{s}})}\), yields oscillations with frequency equal to one. It evinces a crossover from \({\chi }_{1,{\rm{branch}};b}^{{\rm{c}}({\rm{s}})}\propto \cos (t+\pi /4)/{({t}^{* })}^{1/2}\) behavior at t* < tcross,3 to \({\chi }_{1,{\rm{branch}};b}^{{\rm{c}}({\rm{s}})}\propto \cos (t-\pi /4)/(({s}_{{\rm{zs}}}-1){({t}^{* })}^{3/2})\) behavior at t* > tcross,3, where again
This tcross,3 is the analog of tcross,1 for l = 0, Eq. (35).
The term \({\chi }_{1,{\rm{branch}};2}^{{\rm{c}}({\rm{s}})}({t}^{* })\) can also be split into two contributions, one from \(x\approx {s}_{3}^{\prime}\) and another one from x ≈ 1. Evaluating the first contribution, we find that, up to an overall factor,
Because γ3 < 0, the second term in the round brackets equals −1 and cancel the first one. As a result, there is no \(\sin ({s}_{3}^{\prime}{t}^{* })\) term in \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\). The second contribution, \({\chi }_{1,{\rm{branch}};2b}^{{\rm{c}}({\rm{s}})}({t}^{* })\), has the same structure as \({\chi }_{1,{\rm{branch}};1b}^{{\rm{c}}({\rm{s}})}({t}^{* })\) and just adds up to the prefactor of an oscillation with frequency equal to one.
Damped ZS mode for \({F}_{1}^{{\rm{c}}({\rm{s}})}\le -1/9\)
In this section we consider the range of \(-1\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, <\, -\!1/9\), excluding the immediate vicinity of −1, which has been already considered in Section 1. For \({F}_{1}^{{\rm{c}}({\rm{s}})}\lesssim -1/9\) the pole is close to but somewhat below the branch cut, i.e., in our notations this is a weakly damped conventional ZS pole (by x ≲ y we mean that x is smaller than y by an asymptotically small quantity). Here we have \({s}_{{\rm{zs}}}\approx 2/\sqrt{3},{\gamma }_{{\rm{zs}}}\approx \sqrt{3(| {F}_{1}^{{\rm{c}}({\rm{s}})}| -1/9)/2}\). Up to two leading orders in γzs, the pole contribution is
We verified that both terms in the pole contribution are cancelled out by the corresponding contributions from the branch cut. The branch cut contribution can again be represented as the sum of two terms, like in (50), (51), (52), but now s3 is complex conjugate of s1: s3 = sh + iγh. The term that cancels (58) is obtained by expanding in ϵ = x − sh and evaluating integrals up to two leading orders in γh. The cancellation implies that there are no oscillations in \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) with frequency szs, even when the system is slightly outside the range where the ZS pole is a hidden one. The remaining contribution from the branch cut has the same form as in other regimes: at largest t*,
We now study the crossover from the behavior at \({F}_{1}^{{\rm{c}}({\rm{s}})}\lesssim -\!1/9\), where we just found that the pole contribution is cancelled by the contribution from the branch cut, to the behavior at \({F}_{1}^{{\rm{c}}({\rm{s}})}\gtrsim -\!1\), where we found earlier that there is no such cancellation. As \({F}_{1}^{{\rm{c}}({\rm{s}})}\) decreases, the trajectory of s1 evolves in the complex plane, mirrored by the other s2..4. During this evolution, γzs is finite but numerically small. For this reason, below we restrict ourselves to the leading contribution in γzs.
Within this approximation, the pole contribution is the first term in (58). For the branch cut contribution we find, not requiring szs to be close to \(2/\sqrt{3}\),
For szs < 1, the lower limit of the integral is positive. This happens when
where \({F}_{1}^{{\rm{vis}}}=-0.162\). In this range of \({F}_{1}^{{\rm{c}}({\rm{s}})}\), one can safely set γzs to zero – the integral does not diverge. As a consequence, \({\chi }_{1,{\rm{branch}};1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) does not contain the factor \(\propto\! {\gamma }_{{\rm{zs}}}^{-1}\) and cannot cancel \({\chi }_{1,{\rm{pole}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\propto \cos ({s}_{{\rm{zs}}}{t}^{* })/{\gamma }_{{\rm{zs}}}\) in (58). The leading contribution to the integral in (60) comes from x ≈ 1 − szs, and the integration yields
as in (59). We see that the behavior of \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is qualitatively the same as for F ≥ −1: the pole contribution yields oscillations with frequency szs and remains the largest contribution to \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) up to t* ~ tcross,2. At t* > tcross,2, the branch cut contribution becomes the largest one and \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) oscillates at the (dimensionless) frequency equal to one.
However, when szs > 1, which happens for \({F}_{1}^{{\rm{vis}}}\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\,<\, -\!1/9\), the lower limit of integration in Eq. (60) is negative, and the integral contains a singular contribution from x → 0. Using
we find that this singular piece cancels out the contribution from the pole. Evaluating the other relevant contribution from x ≈ 1 − szs, we find
This result is valid for t*∣szs − 1∣ ≫ 1. The \(\cos ({t}^{* }-\pi /4)/{({t}^{* })}^{3/2}\) is precisely the expected time dependence for the case when the contribution to \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) comes solely from the end points of the branch cut.
We see therefore that oscillations with frequency szs exist as long as \({F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, {F}_{1}^{{\rm{vis}}}\). For \({F}_{1}^{{\rm{vis}}}\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, -\!1/9\) only oscillations, coming from the branch points, with frequency equal to one are present.
In the analysis above we expanded in γzs, i.e., we assumed that the damping remains small in the crossover regime around \({F}_{1}^{{\rm{vis}}}\). The approximation of small γzs would be rigorously valid if the pole trajectory in the complex plane would remain close to the real axis for all \(-1\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, -\!1/9\). In that case we would expect oscillations to persist for a long time, both at \({F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, {F}_{1}^{{\rm{vis}}}\) and at \(-1/9\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, {F}_{1}^{{\rm{vis}}}\). For \({F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, {F}_{1}^{{\rm{vis}}}\) oscillations would occur with frequency szs at intermediate t* (but still t* ≫ 1) and with frequency equal to one at even larger t*. For \({F}_{1}^{{\rm{vis}}}\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\) oscillations would occur with frequency equal to one at all t* ≫ 1. We see therefore that the branch contribution “eats up” the pole contribution once the coordinate of the pole in the complex plane moves to below the branch cut. In reality, γzs is small (or order γ) near \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1/9\), but is of order one at \({F}_{1}^{{\rm{c}}({\rm{s}})} \sim {F}_{1}^{{\rm{vis}}}\). In this situation, the crossover between the behaviors at \({F}_{1}^{{\rm{c}}({\rm{s}})}\gtrsim -\!1\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}\lesssim -\!1/9\) is expected to be obscured by damping. Nevertheless, in numerical calculations, we do see indications of the crossover in the behavior of \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\), when \({F}_{1}^{{\rm{c}}({\rm{s}})}\) is varied around \({F}_{1}^{{\rm{vis}}}\), see Fig. 9 b and its caption.
Calculations using the contour of Fig. 5
We now obtain the same results by using the integration contour of Fig. 5. Again, the use of this contour will allow us to avoid canceling out pole and branch contributions. It also allows one to see more transparently how the poles on the unphysical sheet contribute to the dynamics. We study both the regime of hidden poles and the crossover regime between \({F}_{1}^{{\rm{c}}({\rm{s}})}=-1\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}-1/9\). For consistency we define s1 = szs − iγzs and σzs = s1 − (1 − iγ). With the contour of Fig. 5, the pole contribution is zero for the same reason as for the l = 0 case (cf. Section 4), and the dynamics is determined entirely by the branch-cut contribution, which is given by
where we used Eq. (12) and shifted the integration variable via y = 1 − x. To proceed further, we infer from Eq. (41) that the y integral is dominated by the region y ≪ ∣σi∣, i.e., by whichever pole is nearest to the branch point, see Eq. (19). In our notations, it is σ1 ≡ σzs. For ∣σzs∣ ≪ 1 we may expand the integral in small y and extend the integration limits to infinity. This yields
First, we consider the situation when \({F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 0\) and \(| {F}_{1}^{{\rm{c}}({\rm{s}})}| \ll 1/9\), i.e., when s1,2 reside below the branch cut (see Fig. 9) and are close to the branch point. In this situation ∣s3,4∣ ≫ 1 and the y dependence in the (y + σ3)(y + σ4) factor in Eq. (66) can be neglected. Then Eq. (66) is identical to Eq. (36), up to unimportant constant factors, i.e., the hidden pole behavior for l = 1 is the same as for l = 0. Next, we consider the situation when \({F}_{1}^{{\rm{c}}({\rm{s}})}\) decreases and becomes smaller than −1/9. We evaluate the integral in Eq. (66) exactly by contour integration in the first quadrant of complex y and obtain
where \({A}_{j}={\sum }_{i\ne j}{({\sigma }_{i}-{\sigma }_{j})}^{-1}\) are the partial fraction decompositions of ∏j(x + σj), and
where Z(a) was defined in Eq. (32) and Θ(a) is the Heaviside function. (Note that since s2,3 are not near the branch point at 1 − iγ, they have σj ≈ −2 while the integral is dominated by the region y ~ ∣σ1∣, ∣σ4∣. However, their contribution is included in the complex conjugate term in χ1,branch.)
Equations (67) and (68) are applicable in both the hidden pole regime and the crossover regime, as long as ∣σ1∣ ≪ 1. Let us examine them in the crossover regime. Although the sum in Eq. (67) is over all four poles, the Heaviside functions in Eq. (68) are nonzero only for s1. It can be verified that the sudden appearance of the pole contribution for s1 is mirrored by a jump in ∑jAjZ(σjt), so that the crossover is actually smooth—the pole progressively “emerges” from behind the branch cut. This behavior is the analog of the progressive “eating up” of the poles that we obtained via integration over the contour of Fig. 4, see Eq. (60).
To obtain a qualitative understanding of how the poles emerge, we expand Eqs. (67) and (68) in small γzs − γ. This approximation is analogous to the one we made above when studying the crossover using the contour of Fig. 4, i.e. of keeping only the leading contribution in γzs. Using our results for the contour of Fig. 5, the only necessary step is to take the limit \({\rm{Im}}{\sigma }_{j}\to 0\) in Eqs. (67) and (68), which yields,
i.e. oscillations at a frequency szs ≠ 1 begin to emerge precisely when szs < 1. Eq. (69) is valid when ∣(1 − szs)t*∣ ≪ 1.
Mirage poles
Finally, we discuss the mirage poles. For \(0\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 3/5\), the conventional ZS pole s1 is located outside particle-hole continuum, and its position in the lower half-plane of frequency is between the real frequency axis and the branch cut, i.e., \({\rm{Re}}{s}_{1}\, > \, 1\) and −γ < Ims1 < 0. At \({F}_{1}^{{\rm{c}}({\rm{s}})}=3/5\), \({\rm{Im}}{s}_{1}\) becomes equal to γ, and for larger \({F}_{1}^{{\rm{c}}({\rm{s}})}\), the pole moves to the unphysical Riemann sheet, i.e. in our notations it becomes a mirage pole (see ref. 15).
As before, we first compute \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) using the integration contour in Fig. 4. Because there are no poles on the physical Riemann sheet for \({F}_{1}^{{\rm{c}}({\rm{s}})}\, > \, 3/5\), the whole contribution comes from the branch cut: \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })=-{\chi }_{1,{\rm{branch}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\). The integral over the branch cut has two relevant contributions. The first one, \({\chi }_{1,{\rm{branch}};{a}_{{\rm{m}}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\), comes from the vicinity of branch points. This contribution is computed in the same way as the analogous contributions in other cases considered earlier. The result is
The second contribution, \({\chi }_{1,{\rm{branch}};{b}_{{\rm{m}}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\), comes from the vicinity of the point on the upper edge of the branch cut, s = xm − i(γ − 0+), where there would be a ZS pole in the absence of damping. The real xm is the solution of
At \({F}_{1}^{{\rm{c}}({\rm{s}})}=3/5\), \({x}_{{\rm{m}}}=2/\sqrt{3}\). For larger \({F}_{1}^{{\rm{c}}({\rm{s}})}\), xm increases monotonically with \({F}_{1}^{{\rm{c}}({\rm{s}})}\). For \({F}_{1}^{{\rm{c}}({\rm{s}})}\gg 1\), \({x}_{{\rm{m}}}\approx {(3{F}_{1}^{{\rm{c}}({\rm{s}})}/4)}^{1/2}\). For s near xm − i(γ − 0+),
where
Equation (72) is valid only for s above the branch cut, i.e., for ∣Ims∣ < γ. This is satisfied on the upper branch of the cut, but not on the lower branch.
The function Q2(xm) satisfies \({Q}_{2}(2/\sqrt{3})=1\) and increases with xm for larger xm, which correspond to \({F}_{1}^{{\rm{c}}({\rm{s}})}\, > \, 3/5\). At large \({F}_{1}^{{\rm{c}}({\rm{s}})}\), \({Q}_{2}({x}_{{\rm{m}}})\approx {F}_{1}^{{\rm{c}}({\rm{s}})}/2\). The condition Q2(xm) > 1 implies that there is no pole in (72) above the branch cut, where this expression is valid. Evaluating the branch cut contribution along s = x − i(γ − 0+), we find that the largest piece comes from x ≈ xm and yields
Combining (70) and (74), we see that in the range where a ZS pole is a mirage one, \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })=-({\chi }_{1,{\rm{branch}};{a}_{m}}^{{\rm{c}}({\rm{s}})}({t}^{* })+{\chi }_{1,{\rm{branch}};{b}_{m}}^{{\rm{c}}({\rm{s}})}({t}^{* }))\) has a contribution oscillating with (dimensionless) frequency xm and the contribution oscillating with (dimensionless) frequency equal to one. When \({F}_{1}^{{\rm{c}}({\rm{s}})}=O(1)\), the second contribution is the dominant one in some range of t* > 1, because the first contribution contains \(1/{({t}^{* })}^{3/2}\). However, above a certain t* the contribution from the branch point becomes the dominant one as it contains the smaller factor in the exponent. This crossover from oscillations with frequency xm to oscillations with frequency 1 provides a way to detect a mirage pole experimentally.
For \(0\, < \, {F}_{1}^{{\rm{c}}({\rm{s}})}\, < \, 3/5\), the ZS pole is located in the lower half-plane of frequency on the physical Rieman sheet. In this situation, \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) contains contributions both from the pole and from the branch cut. The combined contribution from the pole and the upper edge of the branch cut is
where now \(0\, < \, {x}_{{\rm{m}}}\, < \, 2/\sqrt{3}\) and Q2(xm) < 1. The contribution from the branch points is still given by (70). There is no crossover in this case because the exponential factor in the pole contribution is smaller than in the branch cut contribution. We note in passing that there is also a sign change between \({\chi }_{1}^{{\rm{c}}({\rm{s}})}({t}^{* })\) and \(-{\chi }_{1,{\rm{branch}};{b}_{m}}^{{\rm{c}}({\rm{s}})}({t}^{* })\) in (74), (i.e., the phase of \(\sin ({x}_{{\rm{m}}}){t}^{* }\)) oscillations changes by π between the regions where a ZS pole is a conventional one and where it is a mirage one.
Calculations using the contour of Fig. 5. The same results can be obtained using the contour in Fig. 5. For the contour of Fig. 5, the pole contribution is non-zero and is given by
where s1 = sm −iγm is the mirage pole according to our conventions. This is just −1 times the result for a conventional ZS mode residing above the branch cut on the physical sheet, Eq. (42). The phase shift is due to the pole being on the unphysical sheet. The contribution of \({\chi }_{1,{\rm{branch}}}^{{\rm{c}}({\rm{s}})}({t}^{* })\) is dominated by the branch points and is given by
The crossover time is
i.e., it is analogous to the crossover time for a conventional pole with γzs < γ, see Eq. (46).
Arbitrary l
Our results for l = 0 and l = 1 can be readily generalized to any channel. Using the contour of Fig. 5, we see that for a given channel with 2n poles on the Riemann surface, the solution is given by the contributions of mirage and conventional poles with γzs < γ, along with the branch points contribution
where Z(a) is given by Eq. (32), \({A}_{j}={\sum }_{i\ne j}{({\sigma }_{i}-{\sigma }_{j})}^{-1}\) and Q0 is a constant, calculated directly from \(\Delta {\chi }_{l}^{{\rm{c}}({\rm{s}})}(x)\) and given by
To study a crossover regime where a pole s1 emerges from behind a branch cut, simply replace eiπ/4Z(σjt*) in (80) by \({\mathcal{Z}}\), given in Eq. (67).
The case of comparable \({F}_{0}^{{\rm{c}}({\rm{s}})}\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}\)
In the main text and in the previous sections, we assumed that one Landau parameter dominates over all others. In this section, we discuss what happens when two Landau parameters are comparable. We focus on the most physically relevant case when \({F}_{0}^{{\rm{c}}({\rm{s}})}\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}\) dominate over all others, as can be expected for a generic interaction which decreases monotonically with momentum transfer. Our results can be readily generalized for the case of more nonzero \({F}_{l}^{{\rm{c}}({\rm{s}})}\)’s.
When both \({F}_{0}^{{\rm{c}}({\rm{s}})},{F}_{1}^{{\rm{c}}({\rm{s}})}\) are nonzero, the expression for the quasiparticle susceptiblity becomes more complex, since there are now cross terms in the ladder series. Resumming the series, we obtain15,38,39
where χ0 and χ1 are given by Eqs. (13) and (39), respectively, while χ01(s) is the fermion bubble with l = 0 and l = 1 form-factors at the vertices
The equations for the poles in the l = 0 and (longitudinal) l = 1 channels are the same because Eqs. (82a) and (82b) have the same denominator. (The pole in the transverse l = 1 channel is different.) The solution of
interpolates smoothly between the limits of \(| {F}_{0}^{{\rm{c}}({\rm{s}})}| \gg | {F}_{1}^{{\rm{c}}({\rm{s}})}|\) and \(| {F}_{0}^{{\rm{c}}({\rm{s}})}| \ll | {F}_{1}^{{\rm{c}}({\rm{s}})}|\), studied in the previous sections. As a result, the behavior of the poles for the case of comparable \({F}_{0}^{{\rm{c}}({\rm{s}})}\) and \({F}_{1}^{{\rm{c}}({\rm{s}})}\) does not change qualitatively. A new element, however, is that the mirage mode occurs both in the l = 0 and l = 1 channels (again, because they have a common pole). Also, the conditions for the existence of the mirage mode become less stringent compared to the \({F}_{0}^{{\rm{c}}({\rm{s}})}=0\) case, when the mirage mode occurs only in the l = 1 channel and for \({F}_{1}^{{\rm{c}}({\rm{s}})}\, > \, 3/5\). If \({F}_{0}^{{\rm{c}}({\rm{s}})}\, \ne \, 0\), the mirage mode occurs already for smaller values of \({F}_{1}^{{\rm{c}}({\rm{s}})}\), e.g., for \({F}_{1}^{{\rm{c}}({\rm{s}})}\, > \, 0.15\) if \({F}_{1}^{{\rm{c}}({\rm{s}})}=1\).
For a charged FL, the situation is somewhat different. The new diagrammatic element are the chains of bubbles connected by the unscreened Coulomb interaction, Uq = 2πe2/q. Such chains are present in the l = 0 charge channel and in the l ≥ 1 longitudinal charge channel, but not in the transverse charge channel and the spin channel. Each bubble in the chain is renormalized by a FL interaction, parameterized by the Landau function. The Landau function comprises infinite series of diagrams containing the screened Coulomb interaction. Resumming the diagrammatic series, one obtains the full charge susceptibilities in the form
where \({\chi }_{l}^{c}(q,\omega )\) is the quasiparticle susceptibility renormalized by the FL interaction and \({\chi }_{l0}^{c}(q,\omega )\) is the “mixed” quasiparticle susceptibility with vertices at the opposite corners given by \(\sqrt{2}\cos l\theta\) and 1, correspondingly. The pole of (85a) is a 2D, \(\sqrt{q}\) plasmon, whose group velocity is renormalized by the FL interaction40. This is the only collective mode in the l = 0 charge channel. In the channels with l ≥ 1 there are two kinds of collective modes: the acoustic ZS modes, which correspond to the pole of the first term in Eq. (85b), and the plasmon mode, which correspond to the pole of the second term in this equation. Note that the longitudinal ZS modes exist for any repulsive FL interaction, as opposed to the case of transverse ZS modes, which occur only if the FL interaction exceeds certain threshold16.
Data availability
All the data in the figures of this paper was produced using Mathematica scripts, available upon request from the corresponding author.
Code availability
The scripts used to produce the figures in this manuscript are available upon request from the corresponding author.
References
Abrikosov, A. A.Gorkov, L. P. & Dzyaloshinski, I. E. Methods of Quantum Field Theory in Statistical Physics. Dover Books on Physics Series (Dover Publications, 1975).
Lifshitz, E. M. & Pitaevskii, L. P. Landau and Lifshitz Course of Theoretical Physics, v. IX: Statistical Physics, Part 2 (Butterworth-Heinemann, 1980).
Baym, G. & Pethick, C. J. Landau Fermi-Liquid Theory: Concepts and Applications (John Wiley and Sons, 1991).
Nozières, P. & Pines, D. Theory of Quantum Liquids (Hachette UK, 1999).
Abel, W. R., Anderson, A. C. & Wheatley, J. C. Propagation of zero sound in liquid He3 at low temperatures. Phys. Rev. Lett. 17, 74–78 (1966).
Pethick, C. & Ravenhall, D. Growth of instabilities in a normal Fermi liquid. Ann. Phys. 183, 131–165 (1988).
Pomeranchuk, I. I. On the stability of a Fermi liquid. Sov. Phys. JETP 8, 361–362 (1959).
Oganesyan, V., Kivelson, S. A. & Fradkin, E. Quantum theory of a nematic Fermi fluid. Phys. Rev. B 64, 195109 (2001).
Dell’Anna, L. & Metzner, W. Fermi surface fluctuations and single electron excitations near Pomeranchuk instability in two dimensions. Phys. Rev. B 73, 045127 (2006).
Wu, C., Sun, K., Fradkin, E. & Zhang, S.-C. Fermi liquid instabilities in the spin channel. Phys. Rev. B 75, 115103 (2007).
Maslov, D. L. & Chubukov, A. V. Fermi liquid near Pomeranchuk quantum criticality. Phys. Rev. B 81, 045110 (2010).
Watanabe, H. & Vishwanath, A. Criterion for stability of Goldstone modes and Fermi liquid behavior in a metal with broken symmetry. Proc. Natl Acad. Sci. USA 111, 16314–16318 (2014).
Kiselev, E. I., Scheurer, M. S., Wölfle, P. & Schmalian, J. Limits on dynamically generated spin-orbit coupling: Absence of l = 1 Pomeranchuk instabilities in metals. Phys. Rev. B 95, 125122 (2017).
Chubukov, A. V., Klein, A. & Maslov, D. L. Fermi-liquid theory and Pomeranchuk instabilities: fundamentals and new developments. JETP 127, 826–843 (2018).
Klein, A., Maslov, D. L., Pitaevskii, L. P. & Chubukov, A. V. Collective modes near a Pomeranchuk instability in two dimensions. Phys. Rev. Res. 1, 033134 (2019).
Khoo, J. Y. & Villadiego, I. S. Shear sound of two-dimensional Fermi liquids. Phys. Rev. B 99, 075434 (2019).
Nehari, Z. Conformal Mapping (New York, McGraw-Hill, 1952).
Farkas, H. M. & Kra, I. Riemann Surfaces (2nd ed., Graduate texts in mathematics; 71). (New York, Springer-Verlag, 1992).
Weyl, H. The Concept of a Riemann surface (3d ed., 1955. ed., ADIWES International Series in Mathematics). (Reading, Mass, Addison-Wesley Pub., 1964).
Fal’ko, V. I. & Khmel’nitskii, D. E. What if the film conductivity is higher than the speed of light? JETP 68, 1150–1152 (1989).
Oriekhov, D. O. & Levitov, L. S. Plasmon resonances and tachyon ghost modes in highly conducting sheets. Phys. Rev. B 101, 245136 (2020).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Mitrano, M. et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature 530, 461–464 (2016).
Giannetti, C. et al. Ultrafast optical spectroscopy of strongly correlated materials and high-temperature superconductors: a non-equilibrium approach. Adv. Phys. 65, 58–238 (2016).
Gandolfi, M. et al. Emergent ultrafast phenomena in correlated oxides and heterostructures. Phys. Scr. 92, 034004 (2017).
Nosarzewski, B., Moritz, B., Freericks, J. K., Kemper, A. F. & Devereaux, T. P. Amplitude mode oscillations in pump-probe photoemission spectra from a d-wave superconductor. Phys. Rev. B 96, 184518 (2017).
Nicoletti, D. & Cavalleri, A. Nonlinear light-matter interaction at terahertz frequencies. Adv. Opt. Photon. 8, 401–464 (2016).
von Hoegen, A., Mankowsky, R., Fechner, M., Först, M. & Cavalleri, A. Probing the interatomic potential of solids with strong-field nonlinear phononics. Nature 555, 79–82 (2018).
Mitra, A. Quantum quench dynamics. Annu. Rev. Condens. Matter Phys. 9, 245–259 (2018).
Zong, A. et al. Dynamical slowing-down in an ultrafast photoinduced phase transition. Phys. Rev. Lett. 123, 097601 (2019).
Zala, G., Narozhny, B. N. & Aleiner, I. L. Interaction corrections at intermediate temperatures: Longitudinal conductivity and kinetic equation. Phys. Rev. B 64, 214204 (2001).
Lucas, A. & Das Sarma, S. Electronic sound modes and plasmons in hydrodynamic two-dimensional metals. Phys. Rev. B 97, 115449 (2018).
Mitrano, M. et al. Ultrafast time-resolved x-ray scattering reveals diffusive charge order dynamics in La2−xBaxCuO4. Sci. Adv. 5, eaax3346 (2019).
Granroth, G. E. et al. Event-based processing of neutron scattering data at the Spallation Neutron Source. J. Appl. Cryst. 51, 616–629 (2018).
Tan, Y.-W. et al. Measurements of the density-dependent many-body electron mass in two dimensional GaAs/AlGaAs heterostructures. Phys. Rev. Lett. 94, 016405 (2005).
Tan, Y.-W. et al. Spin susceptibility of a two-dimensional electron system in GaAs towards the weak interaction region. Phys. Rev. B 73, 045334 (2006).
Leggett, A. J. Theory of a superfluid Fermi liquid. I. General formalism and static properties. Phys. Rev. 140, A1869–A1888 (1965).
Wu, Y.-M., Klein, A. & Chubukov, A. V. Conditions for l = 1 Pomeranchuk instability in a Fermi liquid. Phys. Rev. B 97, 165101 (2018).
Zyuzin, V. A., Sharma, P. & Maslov, D. L. Dynamical susceptibility of a Fermi liquid. Phys. Rev. B 98, 115139 (2018).
Levitov, L. S., Shtyk, A. V. & Feigelman, M. V. Electron-electron interactions and plasmon dispersion in graphene. Phys. Rev. B 88, 235403 (2013).
Acknowledgements
We thank M.H. Christensen, A. Kamenev, L. Levitov and L.P. Pitaevskii for stimulating discussions. This work was supported by the NSF DMR-1834856 (A.K. and A.V.C.), NSF-DMR-1720816 (D.L.M.), and UF DSP Opportunity Fund OR-DRPD-ROF2017 (D.L.M.). A.V.C. is thankful to the Aspen Center for Physics (A.S.P.) for hospitality during the completion of this work. A.S.P. is supported by National Science Foundation grant PHY-1607611.
Author information
Authors and Affiliations
Contributions
All three authors performed the analytical calculations and participated in writing the manuscript. A.K. performed the numerical calculations.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klein, A., Maslov, D.L. & Chubukov, A.V. Hidden and mirage collective modes in two dimensional Fermi liquids. npj Quantum Mater. 5, 55 (2020). https://doi.org/10.1038/s41535-020-0250-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0250-4
This article is cited by
-
Hydrodynamic approach to two-dimensional electron systems
La Rivista del Nuovo Cimento (2022)