Enhancement of superconductivity on the verge of a structural instability in isovalently doped β-ThRh_1−xIr_xGe

Abstract

β-ThRhGe, the high-temperature polymorph of ThRhGe, is isostructural to the well-known ferromagnetic superconductor URhGe. However, contrary to URhGe, β-ThRhGe is nonmagnetic and undergoes an incomplete structural phase transition at 244 K, followed by a superconducting transition below 3.36 K. Here we show that the isovalent substitution of Ir for Rh leads to a strong enhancement of superconductivity by suppressing the structural transition. At x = 0.5, where the structural transition disappears, T_c reaches a maximum of 6.88 K. The enhancement of superconductivity is linked to the proximity to a structural quantum critical point at this Ir concentration, as suggested by the analysis of thermodynamic as well as resistivity data. First principles calculations indicate that the Ir doping has little effect on the electronic band dispersion near the Fermi level. β-ThRh_1−xIr_xGe thus provides an excellent platform to study the interplay between superconductivity and structural quantum criticality in actinide-containing compounds.

Introduction

The interplay between structural instability and superconductivity has attracted sustainable attention over the past few decades. In particular, the superconducting transition temperature T_c is often enhanced as the structural phase transition is suppressed by chemical doping or external pressure, which is of interest from both fundamental and application points of view. Thus far, such enhancement has been observed in a variety of systems, including elements^1,2,3, intermetallic compounds^{4,5,6,7,8,9,10,11,12,13,14,15,16,17}, transition metal dichalcogenides^18,19, cuprates^20,21, and iron pnictides^22,23,24,25. In several cases, the disappearance of structural transition coincides with the maximum in T_c, which is taken as evidence for a structural quantum critical point (QCP)^13,14,26. However, in actinide-containing compounds, where many exotic properties have been found, no such example has been reported to date.

Very recently, a ternary equiatomic germanide ThRhGe has been synthesized and characterized²⁷. Depending on the annealing temperature, two orthorhombic polymorphs are obtained at ambient condition. α-ThRhGe crystallizes in the YPdSi-type structure (Pmmn) and displays a normal metallic behavior down to 1.8 K. On the other hand, β-ThRhGe adopts the same TiNiSi-type structure (Pnma) as URhGe, which exhibits both ferromagnetism and superconductivity²⁸. By contrast, the nonmagnetic β-ThRhGe undergoes an incomplete transition into the monoclinic structure (P2₁/c) on cooling below 244 K and becomes superconducting below T_c = 3.36 K. The structural transition is of first order and accompanied by a bump in resistivity, a drop in magnetic susceptibility and a distinct specific-heat anomaly. Below the transition, the orthorhombic and monoclinic phases are found to coexist, though the precise atomic position in the latter remains to be determined when single crystalline samples become available. Notably, the application of hydrostatic pressure suppresses the structural transition and enhances T_c, whose onset reaches 8.36 K at 2.8 GPa. To our knowledge, β-ThRhGe represents the rare actinide-containing compound that shows the concurrence of structural transition and superconductivity, which provides an emerging platform to study the interplay between the two phenomena. In this respect, it is noted that the TiNiSi-type sister compound ThIrGe is also a superconductor with T_c = 5.25 K and exhibits no structural transition²⁹. Hence a systematic investigation of the isovalently doped β-ThRh_1−xIr_xGe series is worth pursuing.

Motivated by this, we present a systematic study on the structural and superconducting properties of β-ThRh_1−xIr_xGe across the whole x range of 0 ≤ x ≤ 1. It is found that the disappearance of structural transition coincides with the maximum in T_c at x = 0.5. At this x value, extremes in thermodynamic parameters as well as a non-Fermi liquid behavior are also observed, providing evidence for the existence of a structural QCP. Furthermore, we show that Ir doping and application of hydrostatic pressure affect the structural transition and superconductivity in a very similar way. The effect of Ir doping on the electronic band structure is investigated by theoretical calculations, whose results are discussed in comparison with the experimental observations.

Results and discussion

XRD at room temperature

Figure 1a shows the room temperature XRD patterns for the series of β-ThRh_1−xIr_xGe samples. For all x values, the major diffraction peaks can be well indexed on the TiNiSi-type orthorhombic structure with the Pnma space group, and a small amount of ThRh/ThIr impurity is also identified. A schematic structure of β-ThRh_1−xIr_xGe is displayed in Fig. 1b. One can see that the Th atoms are located in the cavity of Rh/Ir-Ge three-dimensional network and form zigzag chains running along the a-axis. As a consequence, the inversion symmetry is absent for all atoms along the c-axis. The lattice parameters determined by the Lebail fitting are plotted as a function of Ir content x in Fig. 1c. With increasing x, the a- and b-axis shrink from 7.2872 Å and 4.3941 Å to 7.2266 Å and 4.3830 Å, respectively. This is somewhat unexpected since the atomic radius of Ir (1.355 Å) is slightly larger than that of Rh (1.342 Å)³⁰. On the contrary, the c-axis increases from 7.6328 Å to 7.7075 Å. Despite this difference, it is noted that all the three axes vary almost linearly, in line with the Vegard’s law. Hence the isovalent substitution of Ir for Rh in β-ThRh_1−xIr_xGe leads to not only the formation of a continuous solid solution but also an anisotropic change in the orthorhombic unit cell.

Fig. 1: X-ray diffraction results and schematic crystal structure of β-ThRh_1−xIr_xGe.

a Room temperature XRD patterns for the series of polycrystalline β-ThRh_1−xIr_xGe samples. The diffraction peak due to the ThRh/ThIr impurity is marked by the asterisk. b Schematic structure of β-ThRh_1−xIr_xGe. The Th, Rh/Ir and Ge atoms are marked by the arrows. c Ir content x dependence of the orthorhombic lattice constants.

Suppression of the structural phase transition

Figure 2a shows the temperature dependence of resistivity (ρ) for the samples with x up to 0.5. For x ≤ 0.4, a ρ bump is observed due to the structural phase transition. With increasing x, this bump shifts to lower temperatures and becomes weakened, as seen more clearly in the inset of Fig. 2a. At x = 0.5, no such ρ anomaly is discernible, suggesting that the transition is either too weak to be detected or disappears completely. This trend is corroborated by the results of magnetic susceptibility (χ) measured under 4 T, as shown in Fig. 2b. Concomitant with the ρ upturn, there exist a drop in χ for x ≤ 0.4, which is attributed to the decrease in the density of states at the Fermi level (E_F). The onsets of these two anomalies agree well and allow us to determine the structural transition temperature T_s = 190, 158, 130, and 100 K for x = 0.1, 0.2, 0.3 and 0.4, respectively. Notably, a thermal hysteresis near T_s is present for x = 0.1 [see the inset of Fig. 2b] but absent at higher x values, signifying that structural transition is smeared out by disorder and becomes crossover like. In the whole x range of 0.1 to 0.5, the χ(T) data exhibit a weak upturn below 50 K, which can be well fitted by the Curie-Weiss law,

$$\chi \,=\,{\chi }_{0}\,+\,\frac{C}{T\,-\,{{\Theta }}},$$

(1)

where χ₀ is the temperature independent term, C is the Curie constant and Θ is the Weiss temperature. The obtained χ₀, C, and Θ fall in the ranges of 1.0 × 10⁻⁴ to 1.4 × 10⁻⁴ emu mol⁻¹, 0.0006 to 0.0022 emu K mol⁻¹, and −10 to −26 K, respectively. These C values correspond to small effective magnetic moments of only 0.07–0.13 μ_B, where μ_B is the Bohr magneton. This implies that the χ(T) upturn is most probably due to the presence of a small amount of paramagnetic impurity. The results of specific-heat (C_p) measurements on the β-ThRh_1−xIr_xGe samples are displayed in Fig. 2c. A C_p anomaly around T_s is detected only for x ≤ 0.3, and it becomes smaller and broader with increasing x [see the inset of Fig. 2c]. Except for these anomalies, the C_p(T) data look rather similar for these samples and their high-temperature limit is close to the Dulong-Petit limit of 3NR = 74.826 J mol⁻¹ K⁻¹, where N = 3 is the number of atoms per unit cell and R = 8.314 J mol⁻¹ K⁻¹ is the gas constant. Overall, these results clearly indicate that the structural transition in β-ThRh_1−xIr_xGe is suppressed by the increase of Ir doping and becomes no longer perceptible for x ≥ 0.5.

Fig. 2: Evolution of physical properties in β-ThRh_1−xIr_xGe with x ≤ 0.5.

a–c Temperature dependencies of resistivity, magnetic susceptibility and specific heat, respectively, for the β-ThRh_1−xIr_xGe samples with x ≤ 0.5. The vertical dashed line indicates the T_s for x = 0.4. In (a), the arrow marks the x increasing direction and the inset shows a zoom of the data near the structural transition. In (b), the solid lines are fits to the data below 50 K by the Curie-Weiss law. The inset shows a zoom of the data for x = 0.1 near the transition and the two arrows mark the temperature changing directions. In (c), the horizontal line corresponds to the Dulong-Petit limit and the inset shows a zoom of the data near the structural transition.

Evolution of superconductivity

Figure 3a shows a zoom of the low-temperature ρ(T) curves for the β-ThRh_1−xIr_xGe samples with x ≤ 0.5. As the increase of x, the resistive transition moves toward higher temperatures, indicating that superconductivity is enhanced in this doping range. It is worth noting that the transition is relatively sharp for x = 0.1 and 0.5 while broadens considerably for the intermediate x values. This is probably attributed to the interplay between structural transition and superconductivity, as will be discussed further below. The bulk nature of superconductivity in these samples is confirmed by the χ and C_p results shown in Fig. 3b, c. Here the χ was measured under 1 mT with a zero-field cooling mode. For each x value, a large shielding fraction exceeding 110% without demagnetization correction and a distinct C_p jump are observed. The onsets of these anomalies coincide with the midpoint of ρ drop for x = 0.1, 0.2 and 0.5 (see the vertical dashed line) and the completion of resistive transition for the other x values. Hence the T_c values are determined to be 4.00, 4.25, 4.63, 5.23, and 6.88 K for x = 0.1, 0.2, 0.3, 0.4, and 0.5, respectively. In the normal state, the C_p(T) data are well described by the Debye model plus electronic contribution,

$${C}_{{{{\rm{p}}}}}/T\,=\,\gamma \,+\,\delta {T}^{2}\,+\,\eta {T}^{4},$$

(2)

where γ and δ(η) are the electronic and phonon specific-heat coefficients, respectively. The best fits yield γ = 8.20, 8.72, 9.48, 9.55, 12.60 mJ mol⁻¹ K⁻², δ = 0.449, 0.660, 0.812, 0.879, 0.924 mJ mol⁻¹ K⁻⁴ for x = 0.1, 0.2, 0.3, 0.4, and 0.5, respectively. Once δ is known, the Debye temperature Θ_D is calculated as

$${{{\Theta }}}_{{{{\rm{D}}}}}\,=\,{(12{\pi }^{4}NR/5\delta )}^{1/3}.$$

(3)

Then the electron-phonon coupling strength λ_ep can be estimated by the inverted McMillan formula³¹,

$${\lambda }_{{{{\rm{ep}}}}}\,=\,\frac{1.04\,+\,{\mu }^{* }\ln \left({{{\Theta }}}_{{{{\rm{D}}}}}/1.45{T}_{{{{\rm{c}}}}}\right)}{\left(1\,-\,0.62{\mu }^{* }\right)\ln \left({{{\Theta }}}_{{{{\rm{D}}}}}/1.45{T}_{{{{\rm{c}}}}}\right)\,-\,1.04},$$

(4)

where μ^* is the Coulomb repulsion pseudopotential and assumed to be 0.13. The resulting Θ_D and λ_ep are listed in Table 1. One can see that the Θ_D decreases from 235 to 185 K, while the λ_ep increases from 0.64 to 0.86 with increasing x up to 0.5. However, the further increase of Ir content x above 0.5 leads to a suppression of the superconductivity in β-ThRh_1−xIr_xGe, which is illustrated in the Fig. 3d–f. Indeed, all of the ρ drop, diamagnetic transition and C_p jumps move towards lower temperatures with increasing x from 0.5 to 1.0. The midpoint of the former one agree well the onset of the latter two, which gives the T_c values of 6.73, 6.46, 5.90, and 5.51 K for x = 0.6, 0.7, 0.8, and 0.9, respectively. Also, the γ, δ, Θ_D and λ_ep are obtained by the analysis of normal-state C_p(T) data. As can be seen from Table 1, while no systematics in γ is found, there is an increase in Θ_D from 185 to 267 K while a decrease in λ_ep from 0.86 to 0.68 with increasing x in the range of 0.5–0.9, which are opposite to the trends at lower x values.

Fig. 3: Evolution of superconductivity in β-ThRh_1−xIr_xGe.

a–c Low-temperature resistivity, magnetic susceptibility and specific heat, respectively, for the β-ThRh_1−xIr_xGe samples with x ≤ 0.5. The vertical dashed line indicates the T_c for x = 0.5, and the solid lines in (c) are fits to the normal-state data by the Debye model. d–f Same set of data for the samples with x ≥ 0.5. The vertical dashed line indicates the T_c for x = 0.9. g–i Normalized electronic specific-heat data plotted as a function of temperature for the samples with x = 0.2, 0.5, and 0.6, respectively. In (a, b), the solid lines are entropy conserving constructions to estimate the size of specific-heat jump. In (c), the solid curve is a fit to the data by the α-model with α = 2.0.

Table 1 Normal-state and superconducting parameters of β-ThRh_1−xIr_xGe.

By subtraction of the phonon contribution, the electronic specific-heat C_el is isolated and plotted as C_el/γT versus T for three representative doping concentrations x = 0.2, 0.5, and 0.6 in Fig. 3g–i. It is pointed out that, for x = 0.2, the monoclinic and orthorhombic phases are expected to coexist below T_s. Hence, only the normalized specific-heat jump ΔC_p/γT is estimated by the entropy conserving construction. This yields ΔC_p/γT = 1.34, close to 1.43 as predicted by the BCS theory³². As x is increased to 0.5, a rather broad C_el/γT jump is observed in spite of its highest T_c. Nevertheless, the entropy conserving construction gives ΔC_p/γT = 1.73, which is almost 30% larger than that at x = 0.2. This result is well reproducible among different sample batches of this doping concentration, and hence is most likely intrinsic. Since T_s disappears around this x value, the associated fluctuation may be responsible for such anomalous behavior. In comparison, the C_el/γT jump is significantly sharper at a slightly higher x = 0.6. To analyze the data, we employed the α-model that was adapted from the single-band BCS theory³³. This model still assumes a fully isotropic superconducting gap while allows for the variation of coupling constant α ≡ Δ(0)/k_BT_c, where Δ(0) is the gap size at 0 K. Note that α = 1.764 for the BCS theory. For x = 0.6, the C_el/γT data can be well described by the α-model with α = 2.0. Given that the T_c and ΔC_p/γT are very similar for x = 0.5 and 0.6, it is reasonable to speculate that, at optimal doping, β-ThRh_1−xIr_xGe behaves as a intermediately coupled, fully-gapped superconductor.

The upper critical fields B_c2 for all the β-ThRh_1−xIr_xGe samples are obtained by magnetoresistivity measurements, and an example for x = 0.5 is shown in Fig. 4a. As expected, the resistive transition gradually shifts toward lower temperatures and becomes broadened with increasing magnetic field. For each field, the T_c is determined using the same criterion as above. The resulting temperature dependencies of B_c2 for all x values are summarized in Fig. 4b. The zero-temperature upper critical field B_c2(0) is derived by extrapolating the B_c2(T) data to 0 K using the Ginzburg–Landau (GL) model³⁴

$${B}_{{{{\rm{c2}}}}}(T)\,=\,{B}_{{{{\rm{c2}}}}}(0)\frac{1\,-\,{t}^{2}}{1\,+\,{t}^{2}},$$

(5)

where t = T/T_c is the reduced temperature. In all cases, the data follow nicely the GL fitting curves. In comparison, the B_c2 data show upward deviation from the Werthamer–Helfand–Hohenberg model³⁵ and the results for selected x = 0.2, 0.5, and 0.6 are displayed in Supplementary Fig. 1. The x dependence of extrapolated B_c2(0) is displayed in Fig. 4c. One can see that the B_c2(0) achieves a maximum of 7.30 T at x = 0.5, which is more than twice those of the end members. As shown in Fig. 4d, the B_c2(0)/T_c ratio remains around 1.05 up to x = 0.7, and decreases rapidly afterwards to a plateau of 0.55 at x ≥ 0.9. It thus appears that the pairing interaction is stronger in the Rh-rich compositions than in the Rh-poor ones. Nonetheless, it is noted that the B_c2(0)/T_c values are far below 1.86 expected for the Pauli paramagnetic limit³⁶, implying that superconductivity in the whole β-ThRh_1−xIr_xGe series is limited by the orbital effect. In addition, the GL coherence length ξ_GL(0) is related to B_c2(0) through the equation

$${\xi }_{{{{\rm{GL}}}}}(0)\,=\,\sqrt{\frac{{{{\Phi }}}_{0}}{2\pi {B}_{{{{\rm{c2}}}}}(0)}},$$

(6)

where Φ₀ = 2.07 × 10⁻¹⁵ Wb is the flux quantum. The calculated ξ_GL(0)s are listed in Table 1 and vary between 6.7 and 10.5 nm.

Fig. 4: Upper critical fields in β-ThRh_1−xIr_xGe.

a Temperature dependence of resistivity under various magnetic fields up to 5.4 T for the β-ThRh_1−xIr_xGe sample with x = 0.5. The dashed line denotes the midpoint of resistive transition and the arrow marks the field increasing direction. b Upper critical field versus temperature phase diagrams for the β-ThRh_1−xIr_xGe samples. The solid lines are fits to the data by GL model. c, d Ir content x dependencies of B_c2(0) and B_c2(0)/T_c, respectively, for β-ThRh_1−xIr_xGe.

Pressure effect in x = 0.2 and 0.5

Given that both the T_s and T_c of β-ThRhGe are sensitive to the application of hydrostatic pressure (P), it is of natural interest to investigate whether this is also the case in the Ir-doped samples. Figure 5a shows the temperature dependence of resistance between 1.8 and 300 K for x = 0.2 under various P up to 2.8 GPa. With increasing P, the resistance curve shifts downwards, indicating enhanced metallicity. Meanwhile, the resistivity bump due to structural transition is gradually suppressed to lower temperatures and no longer visible for P ≥ 1.5 GPa, as seen more clearly in Fig. 5b. On the contrary, one can see from Fig. 5c that the superconducting transition moves towards higher temperatures and becomes sharpened. The overall behavior is very similar to that observed in undoped β-ThRhGe²⁷, and corroborates that superconductivity and structural transition are still competing with each other in lightly Ir-doped samples. For x = 0.5, whose results are displayed in Fig. 5d–f, the increase in P also leads to a decrease in normal-state resistance and an enhancement in superconductivity, although both magnitudes are much smaller compared with those at x = 0.2.

Fig. 5: High-pressure resistance data of β-ThRh_1−xIr_xGe at selected x values.

a Temperature dependence of electrical resistance between 1.8 and 300 K under hydrostatic pressure P = 0, 0.5, 1, 1.5, 2, 2.8 GPa (from top to bottom) for the β-ThRh_1−xIr_xGe sample with x = 0.2. b Zoom of the data near the structural phase transition. c Zoom of the data near the drop to zero resistivity. d–f Same set of data for the sample with x = 0.5.

T-x and T -P phase diagrams

Figure 6a shows the constructed T-x phase diagrams of β-ThRh_1−xIr_xGe. As a consequence of Ir doping, T_s decreases monotonically and disappears at x ~ 0.5. On the other hand, T_c exhibits a dome-like dependence on x with a maximum of 6.88 K at x = 0.5, which is more than twice that (3.36 K) of x = 0. It is worth noting that, while the offset T_c evolves smoothly, the onset T_c shows a step-like upturn above x = 0.1 and then reaches a plateau until x = 0.5. This leads to a broad resistive transition width of 2–3 K for 0.2 ≤ x ≤ 0.4, as already noted above. In this x range, there coexist both the orthorhombic and monoclinic phases below T_s, the latter of which becomes dominant at low temperature. It is thus reasonable to speculate that the bulk superconducting transition with a lower T_c is due to the monoclinic phase, while the orthorhombic one is responsible for the onset of resistive transition with a higher T_c. Indeed, as the monoclinic phase disappears at x = 0.5, the difference between the onset and offset T_c is reduced strongly to ~0.5 K.

Fig. 6: Electronic and temperature-pressure phase diagrams of β-ThRh_1−xIr_xGe.

a T-x electronic phase diagram of β-ThRh_1−xIr_xGe. Here T_s, ${T}_{{{{\rm{c}}}}}^{{{{\rm{onset}}}}}$, ${T}_{{{{\rm{c}}}}}^{{{{\rm{zero}}}}}$ are the structural transition, onset and offset superconducting transition temperatures, respectively. The dashed line is a guide to the eyes. b, c Ir content x dependencies of γ, λ_ep, and Θ_D, respectively, and the vertical dashed line is a guide to the eyes. d, e T-P phase diagrams for β-ThRh_1−xIr_xGe with x = 0.2 and 0.5, respectively. In (d), the dashed line is a guide to the eyes.

To gain insight into the pairing mechanism, we plot the Ir content x dependencies of γ, λ_ep and Θ_D in Fig. 6b, c. Two salient features are noted. First, γ shows a modest increase with initial increasing x, followed by an abrupt jump at x = 0.5, and tends to decrease at higher x values. Second, concomitant with the T_c maximum, a maximum in λ_ep and a minimum in Θ_D are observed. These features are in analogy with those observed in isovalently doped Lu(Pt_1−xPd_x)₂In²⁶, and provides evidence for the existence of a structural QCP at x ≈ 0.5. To further verify this scenario, the low-temperature ρ(T) data are analyzed by the power law

$$\rho \,=\,{\rho }_{0}\,+\,A{T}^{n},$$

(7)

where ρ₀ is the residual resistivity, A is the prefactor and n is the temperature exponent. Since our samples are polycrystalline in nature, the results should be taken with caution and hence presented in Supplementary Fig. 2. In particular, n shows a minimum of n ≈ 1.6 at x = 0.5. This means a non-Fermi liquid behavior due to a strong enhancement in the critical fluctuations and is a standard signature of a QCP. It is pointed out that, in both our case and Lu(Pt_1−xPd_x)₂In²⁶, a minimum in n is observed at the QCP, indicating that they exhibit very similar behavior. Nonetheless, the precise value of n at the QCP is not universal and still the subject of debate. For example, in (Ca, Sr)₃Ir₄Sn₁₃, n ≈ 1 is observed at the QCP¹⁴, which differs from those in both β-ThRh_1−xIr_xGe (n ≈ 1.6) and Lu(Pt_1−xPd_x)₂In (n ≈ 1.8)²⁶.

We then turn the attention to the P-T phase diagrams of x = 0.2 and 0.5, which are shown in Fig. 6d, e. Intriguingly, these two diagrams look very similar with the T-x one for x in the windows of 0.2–0.6 and 0.5–0.6, respectively. In the former case, this points to the presence of a QCP at P ≈ 1.5 GPa, which is corroborated by a minimum n ≈ 1.5 at this pressure obtained from the powder-law analysis of the ρ(T) data under pressure (see Supplementary Fig. 3). In comparison, the same analysis for x = 0.5 indicates a slow increase in n from ~1.6 to ~1.9 up to 2.8 GPa, substantiating that this composition is located almost exactly at a QCP. Obviously, the roles played by isovalent Ir doping and hydrostatic pressure are essentially the same in tuning the structural transition and superconductivity in β-ThRh_1−xIr_xGe.

Theoretical electronic band structure

To investigate the band structure evolution of β-ThRh_1−xIr_xGe, first principles band structure calculations were performed for Ir contents of x = 0.3, 0.5, 0.7, and 0.9. Given that the exact structure of the monoclinic phase remains unclear at present, all the calculations are based on the TiNiSi-type orthorhombic structure. It turns out that, in all cases, the band dispersion without considering spin-orbit coupling exhibits a strong similarity near the E_F, and the results for x = 0.3, 0.5, and 0.7 are shown in Fig. 7a–c, respectively. Only at ~0.5 eV above E_F, a doping dependent band dispersion is discernible near the Γ point, presumably due to the difference between the Rh and Ir states. The total DOS for β-ThRh_1−xIr_xGe in the E − E_F range of −1.5 to 1.5 eV is displayed in Fig. 7d. Irrespective of the x value, the E_F remains very close to a DOS peak associated with a van Hove singularity. The theoretical bare density of states N(0) decreases monotonically from 3.25 to 3.08 states eV⁻¹ f.u.⁻¹ with increasing x from 0.3 to 0.9. These values, together with those of λ_ep, give the estimated γ = 13.41, 13.94, 13.00, and 12.20 mJ mol⁻¹ K⁻² for x = 0.3, 0.5, 0.7, and 0.9, respectively, which are in reasonably good agreement with the experimental values. The overall results support that the enhancement of superconductivity should be closely related to the phonon properties of β-ThRh_1−xIr_xGe, whose evolution as a function of Ir doping is certainly of interest for future studies.

Fig. 7: Calculated electronic band structure of β-ThRh_1−xIr_xGe.

a–c Electronic band structure without SOC for β-ThRh_1−xIr_xGe with x = 0.3, 0.5, and 0.7, respectively. d Total density of states plotted as a function of energy for x = 0.3, 0.5, 0.7, and 0.9. The vertical dashed line indicates the position of Fermi level.

In summary, we have studied systematically the effect of isovalent Ir doping on the structural and superconductivity of β-ThRh_1−xIr_xGe. The undoped β-ThRhGe displays an incomplete structural transition at T_s = 244 K and a superconducting transition at T_c = 3.36 K²⁷. With increasing Ir content x, the structural transition is gradually smeared out and disappears at x = 0.5, where T_c exhibits a maximum of 6.88 K. This maximum is accompanied by a small jump in γ, a maximum in λ_ep, a minimum in Θ_D and a resistivity temperature exponent n ≈ 1.6. These features together unveil a structural QCP located at x ≈ 0.5, which is corroborated by high-pressure resistivity measurements. This is supported by theoretical calculations, which indicate that the Ir doping has little effect on the electronic band dispersion near the Fermi level. Our results suggest that β-ThRh_1−xIr_xGe not only offers an excellent platform to study the interplay between superconductivity and structural instability, but also provides a fresh perspective to understand the structural quantum criticality in actinide-containing materials.

Methods

Sample synthesis and characterization

Polycrystalline samples of β-ThRh_1−xIr_xGe were prepared by the two-step method. Stoichiometric amounts of high-purity Th (99.5%), Rh (99.9%), Ir (99.9%), and Ge (99.99%) powders were mixed thoroughly and pressed into pellets in an argon filled glove-box. The pellets were then melted several times in an arc furnace, followed by rapid cooling on a water-chilled copper plate. The as-cast ingots were annealed in evacuated quartz tubes at 1000 °C for 7 days, followed by quenching to room temperature. The phase purity of resulting samples was checked by powder X-ray diffraction (XRD) at room temperature using a Bruker D8 Advance X-ray diffractometer with Cu Kα radiation. The lattice constants were determined by the Lebail fitting method with the JANA2006 program³⁷.

Physical property measurements

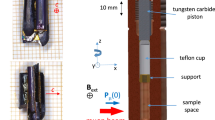
Electrical resistivity and specific-heat measurements were performed on regular-shaped samples in a Quantum Design Physical Property Measurement System (PPMS-9 Dynacool). The electrical resistivity was measured using a standard four-probe method and the data under hydrostatic pressure were taken in a piston-cylinder clamp-type cell using Daphne oil as the pressure transmitting medium and lead as the pressure gauge. The dc magnetization measurements were done in a Quantum Design Magnetic Property Measurement System (MPMS3).

Theoretical calculations

The first principles band structure calculations were carried out within the density functional formalism, as implemented in the Vienna Ab-initio Simulation Package (VASP)³⁸. The Perdew-Burke-Ernzerhof (PBE)³⁹ exchange correlation functional was used. For structural optimization, the convergence threshold of Hellmann-Feynman force and energy convergence criterion were set to 0.01 eV/Å and 10⁻⁶ eV, respectively. The wavefunction cutoff energy was fixed to 450 eV and the Γ-centered k mesh was set to 5 × 8 × 4 in both structural optimization and self-consistent calculations. A virtual crystal approximation has been adopted to elucidate the change in the band dispersion and density of states (DOS) induced by Ir doping using WANNIERTOOLS package⁴⁰. For this purpose, two tight-binding Hamiltonians with maximally localized Wannier functions were constructed through WANNIER90⁴¹ for both ThRhGe and ThIrGe.