Introduction

The heavy fermion (HF) state is one of the most important subjects in strongly correlated systems research and is often accompanied by exotic states such as superconductivity, quantum criticality and magnetism1. In early studies, HF behaviour was mostly found in f-electron systems in which strongly localised f- and itinerant spd- hybridised orbitals coexist and pair to form Kondo-singlets2. Recently, unexpected HF states have been discovered in moderately localised 3d-electron systems such as CaCu3Ir4O12, AFe2As2 (A = K, Rb, Cs), and Fe3GeTe23,4,5, providing a strong impetus to search for possible Kondo-pairing even in less localised 4d/5d-electron systems.

Ca2-xSrxRuO4 (CSRO), a 4d transition metal oxide (TMO), has been reported to exhibit strong HF behaviour near x = 0.56,7,8, which triggered intensive theoretical/experimental investigations9,10,11,12,13,14,15,16 on the existence of an orbital-selective Mott phase (OSMP) for decades. This led to several angle-resolved photo-emission spectroscopy (ARPES) studies that aimed to obtain direct evidence for the OSMP in CSRO14,15,16. However, controversy still remains even regarding the very existence of the OSMP, and the origin of HF behaviour is still unclear. Part of the reason for these problems may arise from the fact that previous studies were performed with limited points in the parameter space, such as substitution (x) and temperature (T).

In this article, we report our systematic x- (0.2 ≤ x ≤ 0.5) and T-dependent ARPES results on CSRO. With variation in x and T, a gradual orbital-selective opening of a soft gap17,18 is observed in the γ (4dxy)-band with spectral weight transfer from low- to high-binding energy (BE), suggesting the emergence of the OSMP. We also observe unexpected spectral weight suppression in the β-band (4dxz/yz) (but not in the α-band (4dxz/yz)). Considering the results of previous studies4,5,6,7,8,12,19,20,21,22, this is indicative of Kondo-hybridisation (KH) between the localised γ- and itinerant β-bands. Our results show a coincidence between the emergence of the OSMP (and KH) and octahedral tilting distortion, implying that the tilting is the key parameter that triggers the OSMP as well as KH. Our results not only provide direct evidence for the OSMP but also constitute the demonstration of possible KH in 4d-orbitals.

Results

Experimental evidence for orbital-selective Mott phase

CSRO may take two types of RuO2 octahedral distortions: an octahedral rotation (Φ, in-plane rotation about the c-axis) and a tilting (Θ, out-of-plane polar rotation about the b-axis). Thus, there are three crystalline forms in terms of the distortions23: (I) neither rotation nor tilting (1.5 ≤ x ≤ 2, I4/mmm, Fig. 1a), (II) finite rotation without tilting (0.5 ≤ x < 1.5, I41/acd, Fig. 1b), and (III) finite rotation and tilting (0 ≤ x < 0.5, Pbca, Fig. 1c). The Fermi surface (FS) topology varies significantly depending on the distortion type (Fig. 1d–f). In Sr2RuO4 (I), four electrons (4d4) in the t2g orbitals make up three FS pockets (Fig. 1d). When octahedral rotation occurs (II), the FS becomes zone-folded due to the reduced BZ (Fig. 1e). Finally, in III with octahedral tilting, the β- and γ-FS pockets are selectively suppressed compared to that of x = 0.5 as marked with black arrows near the S-point, while the α-pocket remains robust as seen in Fig. 1f. This behaviour is reminiscent of the OSMP.

Fig. 1: Crystal structures and Fermi surfaces of Ca2-xSrxRuO4 (CSRO).
figure 1

Top and side view of the CSRO crystal structure a without distortion (\(1.5 \le x \le 2.0\)), b with rotation (\(\Phi ,\;0.5 \le x\, < \,1.5\)) and c with both rotation and tilting (\(\Theta ,\;0.0 \le x\, <\, 0.5\)). Fermi surfaces (FSs, integrated over the Fermi level (EF) ± 20 meV) of x = d 2.0, e 0.5, f 0.2 measured at T = 10 K. Colour-coded dots indicate the Lorentzian-fitted peak positions of α (green), β (brown) and γ (red) FS pockets obtained from the momentum distribution curves (MDCs). The black dashed lines in d–f indicate the reduced Brillouin zone (BZ) induced by octahedral distortions. High-symmetry points in the corresponding symmetry are marked for each substitution (x). The right lower part of each panel shows a 2D-curvature plot50 of the FS map. All the data were measured with π-polarised light (hv = 70 eV, Supplementary Fig. 2).

Full size image

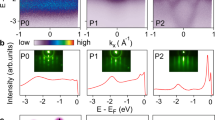
To scrutinise this OSMP-like phenomenon, we performed systematic ARPES studies as a function of x and T. Our x-dependent results (0.2 ≤ x ≤ 0.5) at T = 10 K are presented in Fig. 2a–d. As x decreases from x = 0.5 to 0.2, gradual suppression of the spectral weight is observed near the Fermi level (EF), generating a soft gap17,18 (Supplementary Fig. 3). Interestingly, the soft gap opens only for β- and γ-bands while α-band remains intact as x varies. It can be seen in the momentum distribution curves (MDCs) at EF (Fig. 2j) that the β- and γ-bands are selectively suppressed (among the three t2g-bands) as a function of x. The relative change in the Lorentzian-fitted peak area of each band is plotted in Fig. 2k, which shows clear suppression only for β- and γ-bands. Selective suppressions of β- and γ-bands are consistently observed in all our data (Supplementary Fig. 2) regardless of the photon energy, polarisation and experimental geometry. We thus conclude that it is not due to an extrinsic cause such as the matrix element effect but an intrinsic effect. A similar trend is also observed in the T-dependence (Fig. 2d–h). In Fig. 2l, we plot T-dependent EF spectral weight change relative to that at T = 45 K for x = 0.2. The spectral weight of the β- and γ-bands is suppressed at T = 10 K in a similar fashion to that observed for the x-variation.

Fig. 2: Substitution- (x) and temperature- (T) dependent band-selective suppression at EF.
figure 2

ARPES images along S-Γ1-S for x = a 0.5, b 0.4, c 0.3, and d 0.2 measured at T = 10 K. ARPES images of x = 0.2 along S-Γ1-S measured at T = e 45, f 30, g 20, and d 10 K. h Magnified images of x = 0.2 obtained from region #2 (black rectangles) in d–g measured at T = 45, 30, 20, 10 K; a different colour scale is used to make the T-dependence clearer. Note the soft gap17,18 opening in the β- and γ-bands. i Schematic Fermi surfaces of α- (green), β- (brown), and γ- (red) bands of x = 0.5. Momentum region for ARPES data in this figure is marked with a blue box along Γ1-S. j x-dependent normalised MDCs at EF (integrated over EF ± 10 meV) along Γ1-S from the data in a–d. The colour-coded curves are the data and corresponding Lorentzian fits (black: MDC data, green: α, brown: β, red: γ, blue: sum of fits). k The x-dependent changes in Lorentzian fit areas relative to those of x = 0.5, obtained from j. l T-dependent near EF spectral weight changes relative to that at T = 45 K for x = 0.2 (for the raw data, see Supplementary Fig. 4). All the data were measured with π-polarised light (hv = 70 eV, Supplementary Fig. 2).

Full size image

It is important to note that the γ-band shows gradual development of a soft gap17,18 with T, as can be seen in the energy distribution curves (EDCs) of x = 0.2 in Fig. 3b; as T decreases from 40 K, the spectral weight at 0 ≤ BE (eV) ≤ 0.2 is gradually suppressed while it increases at 0.2 ≤ BE(eV) ≤ 0.8. From the 40 K data subtracted EDCs shown in Fig. 3c, ‘dip’ and ‘hump’ can also be identified. On the other hand, this behaviour is not observed for x = 0.5 (Fig. 3a and Supplementary Fig. 5). The ‘dip’ and ‘hump’ areas for x = 0.2 are found to be almost identical in size but opposite in sign, satisfying the sum rule at all T (Fig. 3d). Hence, we conclude that the spectral weight transfers from the low- to high-BE regions at low T, which has to be understood in terms of Mott localisation rather than a simple downward shift of a band to higher BE. Moreover, the electronic structure of x = 0.2 upon surface electron doping (~0.02e per Ru atom) (Fig. 3e–h and Supplementary Fig. 8) shows a collapse of the soft gap with an emergence of a clear quasiparticle peak, which has been consistently observed in several charge carrier doping studies on Mott insulators24,25,26. In brief, both ‘signature of spectral weight transfer’ and ‘breakdown of Mott localisation (appearance of quasiparticle peak) with charge carrier doping’, prominent criteria for Mott states27,28,29, are present. Thus, we conclude that the spectral weight suppression near EF for the γ-band originates from Mott-localisation.

Fig. 3: Spectral weight transfer and breakdown of the orbital-selective Mott phase (OSMP) upon K deposition.
figure 3

Normalised T-dependent energy distribution curves (EDCs) (top), symmetrised EDCs (middle) and after subtraction of the 40 K data (bottom) for x = a 0.5 and b 0.2. The EDCs are extracted from a region near the S-point, integrated over 0.6 ≤ kx ≤ 0.8 (for the raw data, see Supplementary Fig. 2). c The symmetrised EDCs of T = 6, 40 K in b (top) and their difference (bottom). The ‘dip’ and ‘hump’ are defined as the area in 0 ≤ BE(eV) ≤ 0.2 and 0.2 ≤ BE(eV) ≤ 0.8 regions, respectively. d T-dependent areas of the ‘dip’ and ‘hump’. e–g ARPES images (right) and corresponding 2D curvature plots50 (left) along S-Γ1-S for x = e 0.5, f 0.2, and g x = 0.2 with an electron doping value of 0.02 measured at T = 10 K using σ-polarised light. Solid white/black/red guidelines indicate the dispersions of α-/β-/γ-bands, respectively (Supplementary Fig. 7). For g, 0.2 monolayer of K coverage was deposited in situ on the surface of Ca2-xSrxRuO4 (x = 0.2) to achieve electron doping effect lightly (about 0.02 electrons, Supplementary Fig. 8) h Schematic illustration of alkali metal (potassium K) deposition on the surface of a Ca2-xSrxRuO4 (x = 0.2) single crystal.

Full size image

Role of octahedral tilting

Our observations (orbital-selective suppression and spectral weight transfer in the γ-band) are not inconsistent with the previously proposed OSMP scenario15,30,31. However, there are still questions to be answered, e.g., what triggers OSMP and why the β-band is suppressed when Mott localisation exists only in the γ-band. It was suggested in previous experimental and theoretical studies that octahedral rotation is responsible for the OSMP15,30,31; a study suggests that the rotation sufficiently reduces the γ-bandwidth for Mott localisation30 while others discuss the importance of √2 × √2 × 2 unit cell doubling due to the rotation15,31. In both scenarios, octahedral rotation plays a significant role in the OSMP. Therefore, a larger rotation angle may lead to a stronger OSMP effect. However, the OSMP occurs after the octahedral rotation angle saturates to the maximum value at x = 0.5. Our results show that the OSMP and octahedral tilting distortion appear coincidently and that the strength of the OSMP (spectral weight suppression of the γ-band) is roughly proportional to the tilting angle23,32. Therefore, even though the octahedral rotation significantly reduces the bandwidth of the γ-band, it is the octahedral tilting that triggers the OSMP in CSRO, not the rotation.

The mechanism with which octahedral tilting triggers the OSMP can be understood by considering the effect of the octahedral distortions (rotation/tilting) on bandwidths (Fig. 4). The key aspect of octahedral distortions is that they lead to narrower d-orbital bandwidths. The detailed explanation is as follows. Without octahedral rotation/tilting (I), 4d orbitals (three t2g and two eg) of Sr2RuO4 possess a wide bandwidth (Fig. 4a). Once octahedral rotation sets in (II), the dxy and dx2-y2 orbitals become hybridised, which leads to a bandwidth reduction in the γ- (d*xy) band30 while the dyz/zx orbitals remain almost unchanged (Fig. 4b). On top of that, octahedral tilting (III) leads to hybridisation between dxy (γ-band) and dyz/zx orbitals (α-, β-bands) as shown in Fig. 4c. There are several energy regions (highlighted with yellow shaded area) in which both dxy and dyz/zx have high DOS. This coexistence suggests that dxy (γ-band) and dyz/zx (α-, β-bands) are mixed and hybridised with each other. The hybridisation from the tilting distortion results in formation of fragmented bands with narrower bandwidths (Fig. 4c), which is similar to how octahedral rotation narrows the bandwidth of dxy30. In other words, the octahedral tilting serves as a ‘scissor’ that cuts t2g bands into pieces of narrower bands via hybridisation. The resulting narrow bands provide a sufficient condition for the generation of the OSMP.

Fig. 4: Effect of octahedral distortions on the electronic structure of CSRO.
figure 4

Orbital-dependent (4d) density of states (DOS) at x = a 2.0, b 0.5, and c 0.2 from DFT calculations. Yellow shaded regions in c indicate the BE regions in which dxy and dyz/zx have a coincident DOS peak. Insets in a–c illustrate schematic electronic structure of octahedron distortion types (I–III).

Full size image

Signature of possible Kondo-hybridisation

With the understanding of the bandwidth reduction mechanism described above, the question ‘why is the β-band suppressed simultaneously with the OSMP (while Mott localisation exists only in the γ-band)?’ can be answered. One may consider the possibility that a Mott-localisation may also occur in the β-band in a similar fashion to the OSMP in the γ-band. However, while the γ-band occupation (nγ ~ 1.5) is appropriate for Mott localisation in the doubled unit cell scenario15,31 (Supplementary Fig. 9), the electron numbers of the α- (nα ~ 1.8) and β- (nβ ~ 0.7) bands are inappropriate for Mott localisation14,15. Furthermore, T-dependent EDCs of the β-band do not show a spectral weight transfer behaviour (Fig. 5a and b), unlike the γ-band case. Therefore, a mechanism other than Mott localisation is required to explain the suppression of the β-band. We can gain insight into the origin of β-band suppression from previous studies4,6,7,8,21,22. Some experimental results on 3d iron-based superconductors (IBS) suggest that the emergence of OSMP leads to KH between itinerant (dyz/dzx) and localised (dxy) bands4,21,22. Interestingly, CSRO (0.2 ≤ x < 0.5) exhibits OSMP (similar to IBS) as well as HF-like behaviour6,7,8. Therefore, it is reasonable to consider the KH mechanism for the β-band suppression.

Fig. 5: Determination of Kondo-hybridisation (KH) temperature (TKH) and evolution of KH with OSMP among the 4d t2g orbitals.
figure 5

T-dependent EDCs (a) and their symmetrized form (b) of x = 0.2 integrated over the 0.4 ≤ kx ≤ 0.5 region (around the β-band, region #2 in Supplementary Fig. 2e). The raw ARPES data are also shown in Supplementary Fig. 2e. c Near EF spectral weight (ΔE = ± 20 meV) of the symmetrized EDCs in b as a function of T. TKH is determined to be 45 (±8) K. Schematics of the spin structure and corresponding electronic structure of the β- and γ-bands in three different cases: d without OSMP and KH, e with OSMP but without KH and f with both OSMP and KH.

Full size image

The T-dependent β-band spectral weight at EF may point to an important implication. As seen in Fig. 5c, the EF spectral weight of the β-band decreases linearly in T, then the slope changes at around 45 K. Assuming that the slope change is due to KH, let us define KH temperature (TKH) to be 45 K. Considering the logarithmic T-dependence of Kondo effects, this TKH is of a similar order to the incoherent-to-coherent crossover temperature T* (14 K for x = 0.2) of the resistivity6,8,33 and the peak temperature Tp (12 K for x = 0.2) of the magnetic susceptibility8,33 (Supplementary Fig. 6). Moreover, theoretically estimated Kondo temperature TK is found to be in agreement with our experimentally obtained value in Fig. 5c. HF systems exhibit scaling behaviour with respect to TK which is given as5

$$\gamma _{{{\mathrm{S}}}} \approx \frac{{Rlog2}}{{T_{{{\mathrm{K}}}}}} \approx \frac{{10,000}}{{T_{{{\mathrm{K}}}}}}[mJ/(K^2 \cdot mol)]$$
(1)

where γS and R are the Sommerfeld coefficient and gas constant, respectively. With a reported γS value of about 200–250 \(mJ/(K \cdot mol)\) for CSRO (0.2 ≤ x ≤ 0.5)8, the theoretical TK can be estimated to be 40–50 K, which is consistent with our experimental value of TKH = 45 K. Therefore, based on the consistency in TKH, T*, TP and TK values obtained from ARPES, transport, magnetic susceptibility and theory, we propose a KH scenario at x = 0.2. Then, the electronic structure of x = 0.2 in Figs. 1–3 can be explained within OSMP and KH scenario as schematically illustrated in Fig. 5d–f. The OSMP-driven γ-band works as the localised band in KH while β-band provides itinerant electrons (Fig. 5e). As KH gets stronger, β-/γ-bands renormalise each other (Fig. 5f) and the β-band becomes suppressed as a result of incoherent-to-coherent crossover34,35. Since the γ-band in OSMP serves as a localised bands, which is an essential ingredient for KH, the x-/T-dependences of OSMP lead to a similar x-/T-dependences for KH. It must be noted that the signature of KH in CSRO (T-dependent suppression of β-band) is different from that of an ordinary KH1,2 in f-orbital systems. In cases of ordinary KH in f-orbital, Kondo resonance peak is enhanced with the formation of Kondo coherence as T decreases below T*1,2. On the contrary, the enhancement of Kondo resonance peak is not clearly observed in CSRO, but the spectral weight of β-band around EF is suppressed with the KH in CSRO. We suspect that the difference comes from the types of localised state to form KH. The bandwidth of Hubbard state in OSMP (few hundreds of meV) is much broader than that of f-orbitals (few tens of meV), hence Kondo resonance peak is not clearly resolved in CSRO compared to the case of ordinary KH.

The next question is why only the β-band is involved in KH, while the α-band remains unaffected. This phenomenon can be understood by reference to momentum-dependent-interaction theory, which is essential for explaining ferromagnetic-Kondo systems33,36,37,38,39. In that theory, the proximity of two bands in momentum space is a key factor leading to interactions between them. As can be seen in Figs. 1–3, the β- and γ- bands are located close to each other in the momentum space. Therefore, γ-band forms KH preferentially with the β-band than the α-band.

Discussion

CSRO was the first material for which OSMP was proposed9. Yet, even the very existence of the OSMP in CSRO is still in controversy15,16,40. The critical reason for the controversy may arise from the fact that the OSMP gap appears as a soft gap rather than a hard gap17,18. As can be seen in Figs. 2, 3 and Supplementary Fig. 1, T-dependence shows a gradual spectral weight transfer from low to high-BE regions, rather than a sudden opening of a hard gap. In other words, suppressed spectral weight (Fig. 3b, Supplementary Figs. 1–5) as well as remnant quasiparticle peak intensity at T < 10 K (Supplementary Fig. 1d) are coincidentally observed in the OSMP of CSRO, which explains both previous observations of suppressed spectral weight15 and the remnant γ-band at EF16,40 (Supplementary Fig. 1). Moreover, investigation of the soft gap requires quantitative analysis with a reference point where the gap is closed (x = 0.5). Therefore, we speculate that the absence of the reference point (x = 0.5) data as well as the use of different normalisation methods (Supplementary Fig. 1) may have led previous studies to the conflicting interpretations15,16,40. Our systematic x- and T-dependent studies not only settle down this issue by demonstrating the gradual evolution of the OSMP but also provide critical clues to the microscopic mechanism of the OSMP by demonstrating the coincidence between octahedral tilting and OSMP.

Furthermore, our work on the OSMP advances the understanding of the overall multi-orbital Mott transition from a three-band metallic phase (0.5 ≤ x) to a Mott insulator (x < 0.2) through the comparison of the OSMP and electronic phase of the L-Pbca structure23,41,42,43,44,45 (assumed to be L-phase). However, their connection is poorly understood due to insufficient experimental data over the relevant x range. Our results on the electronic structure evolution of OSMP can shed light on this issue.

Finally, our work also has important implications regarding Kondo physics as well. Even though there have been several reports of HF behaviour in CSRO (0.2 ≤ x ≤ 0.5)6,7,8, absence of quantitative and comprehensive electronic structure studies has hindered to observe a signature of KH. Our systematic electronic structure studies on CSRO not only reveal the signature of KH in a 4d-orbital system, but also suggest that the OSMP may enable KH to appear in other itinerant 4d systems. Therefore, our work advances understanding of the OSMP and Kondo physics in 4d TMOs, and suggests a key role of octahedral tilting in layered perovskite as a control parameter of physical properties.

Methods

Crystal growth and characterisation

High quality Ca2-xSrxRuO4 (x = 0.2, 0.3, 0.4, 0.5, 1.0, 2.0) were grown using the optical floating zone method. Sample quality and stoichiometry were characterised using a physical property measurement system, a magnetic property measurement system, scanning electron microscopy with energy dispersive X-ray analysis, and X-ray diffractometry.

Angle-resolved photoemission spectroscopy (ARPES)

ARPES measurements were performed at Seoul National University (SNU) using an unpolarised He-Iα photon source (hv = 21.2 eV) and at the MERLIN beamline (BL) 4.0.3 of the Advanced Light Source, Lawrence Berkeley National Laboratory using both horizontally (π) and vertically (σ) polarised light (hv = 70 eV) (for detailed information, see Supplementary Fig. 2). Spectra were acquired using DA30 (SNU) and R8000 (BL 4.0.3) electron analysers with energy resolutions of 10 and 15 meV, respectively. For systematic analysis of x- and T-dependent results, the data were normalised and symmetrised as presented in Supplementary Fig. 1 and a reference46, respectively. Sample cleavage and alkali metal deposition were performed (Supplementary Fig. 8) in situ and measurements were performed in an ultrahigh vacuum better than 5 × 10−11 Torr.

First-principles density functional theory (DFT) calculation

To obtain the density of states (DOS), we performed first-principles DFT calculations using the Perdew–Burke–Ernzerhof functional as implemented in the VASP47,48. We used a 400 eV plane wave cut-off energy and 12 × 12 × 8 k-points for all calculations and the projector augmented wave method. For the given x, the structural parameters and lattice constants are employed from a reference23. It was confirmed that the DOS calculated using only Ca-atom is not qualitatively different from that of the calculation considering Sr substitution through virtual crystal approximation49.