Introduction

Current responses provide an experimentally accessible window into the Berry curvature properties of electronic bands1,2. In particular, the quantum Hall effect and the anomalous Hall effect serve as powerful tools across material families3,4,5,6,7,8,9,10. The latter has been conceptualized as an expansion in moments of the Berry curvature distribution over the Brillouin zone—the nth moment yields a response at the (n+1)th order in the applied electric field11. A monopole component (n = 0), which can only exist when time reversal (TR) symmetry is broken, yields a linear response2,6,12. A dipole moment (n = 1) gives rise to a non-linear second-order response13, which has been measured in WTe214,15,16 and other materials17,18,19,20. Recent studies have probed the quadrupole moment (n = 2) and its third-order response21,22,23,24,25,26,27. This has been measured in FeSn, as a transverse voltage generated at three times the frequency of the applied field28. Here, we show that the same physics can yield a dc response when a dc applied field is combined with light.

The Berry curvature and its moments are strongly constrained by the symmetries of the material. We focus on materials that break time reversal (TR) symmetry K and a fourfold rotational symmetry C4, while preserving their combination C4K. In this case, the Berry curvature monopole and dipole moments must vanish, so that the leading contribution comes from a quadrupole moment. C4K symmetry is realized in altermagnets29,30,31 as well as in magnetically ordered materials belonging to certain magnetic point groups26. Electronic bands in such materials may be spin-polarized, a feature allowed by broken time-reversal symmetry. We demonstrate that the Hall response will also be generically spin-polarized. Intriguingly, the very same symmetry requirements are also invoked in chiral higher-order topological crystalline insulators32. Here, we restrict our attention to metallic systems where the Hall response appears as a Fermi-surface property33,34.

Our results provide a counterpoint to the photovoltaic Hall effect. In semiconductor geometries, absorption of circularly polarized light on a biased sample was seen to give rise to spin currents35,36,37. More recently, studies on semi-metallic graphene used a combination of a dc electric field and circularly polarized light to induce a transverse dc current38,39,40. Circular polarization can be viewed as a TR symmetry-breaking field, akin to the magnetic field in the usual Hall effect. Here, we present a logical progression of these ideas to metals with inherent time-reversal breaking such as altermagnets. A charge Hall current is produced by linearly or elliptically polarized light, but not when the polarization is circular. Moreover, spin Hall current appears regardless of the polarization.

Results

Framework

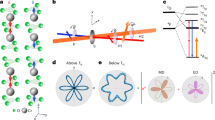
We consider a metal with a single band crossing the Fermi level. We use semiclassical wavepacket dynamics2 to describe transport, denoting wavepacket position as r and momentum as k. Following the well-known semiclassical prescription, its velocity is given by \(\dot{{\boldsymbol{r}}}={\boldsymbol{v}}-\dot{{\boldsymbol{k}}}\times {\mathbf{\Omega }}\), where v is the group velocity (we use units in which ℏ = 1). An anomalous velocity contribution arises from the Berry curvature Ω2,6,12. Neglecting external magnetic fields, momentum evolves according to \(\dot{{\boldsymbol{k}}}=-e[{\boldsymbol{E}}+{{\boldsymbol{E}}}_{{\rm{ac}}}(t)]\), where the total applied electric field is a combination of a static field E and a light-induced field Eac, as shown in Fig. 1. The latter is given by \({{\boldsymbol{E}}}_{{\rm{ac}}}(t)={\rm{Re}}({\boldsymbol{{\mathcal{E}}}}{e}^{-i\omega t})\), where \({\boldsymbol{{\mathcal{E}}}}\) is a complex vector amplitude.

Fig. 1: Proposed configuration for the light-induced Hall effect.
figure 1

The sample is assumed to be in the xy plane with a fourfold axis along z. A static electric field is imposed along y. Light, linear or elliptically polarized, impinges from the z axis. The dc current is measured along x.

Full size image

Following the Boltzmann transport paradigm, we define a distribution function f(k, t) (see Methods). Treating the applied electric fields as perturbations, we expand this function in powers of the fields up to third order: f = f0 + f1 + f2 + f3, where f0 is the equilibrium Fermi-Dirac distribution function. We further divide the distribution into static and time-dependent parts. Keeping only the leading harmonic, we have

$${f}_{a}={f}_{a}^{(0)}+{f}_{a}^{(\omega )}{e}^{-i\omega t}+{f}_{a}^{(\omega ),* }{e}^{i\omega t}\quad (a=1,2,3).$$
(1)

At first order, \({f}_{1}^{(0)}\propto E\) and \({f}_{1}^{(\omega )}\propto {\mathcal{E}}\). Second-order terms can be written as \({f}_{2}^{(0)}\propto {\mathcal{E}}{{\mathcal{E}}}^{* }\) and \({f}_{2}^{(\omega )}\propto E{\mathcal{E}}\). At third order, we have \({f}_{3}^{(0)}\propto E{\mathcal{E}}{{\mathcal{E}}}^{* }\) and \({f}_{3}^{(\omega )}\propto {\mathcal{E}}{\mathcal{E}}{{\mathcal{E}}}^{* }\). Other contributions, such as \({f}_{2}^{(0)}\propto EE\), do not affect the Hall currents discussed below. Details of the calculations are given in Supplementary Material41.

The electric charge (denoted by subscript c) current density is given by \({{\boldsymbol{j}}}_{c}=-e{\int}_{{\boldsymbol{k}}}\dot{{\boldsymbol{r}}}\,f({\boldsymbol{k}})\). Focusing on the dc current, we have

$$\begin{array}{lll}{j}_{c,i}=\,-e{\int}_{{\boldsymbol{k}}}\mathop{\sum }\limits_{a=1}^{3}{v}_{i}\,{f}_{a}^{(0)}+{e}^{2}{\int}_{{\boldsymbol{k}}}\mathop{\sum }\limits_{a=1}^{3}{\Omega }_{ij}{E}_{j}\,{f}_{a}^{(0)}\\\qquad +\,{e}^{2}{\int}_{{\boldsymbol{k}}}\mathop{\sum }\limits_{a=1}^{3}{\Omega }_{ij}[{{\mathcal{E}}}_{j}\,{f}_{a}^{(\omega ),* }+c.c.],\end{array}$$
(2)

where i, j = x, y. We consider the setup in Fig. 1, with a static electric field applied along y and Hall current measured along x. As argued in the supplement41, only one component of the Berry curvature, Ωxy(k), contributes to this current. Henceforth, we disregard other components and denote Ωxy as simply Ω.

We consider the possibility that this current may carry spin polarization. In materials that break time-reversal symmetry, Bloch states may have unequal weights in the two spin components29,42. To incorporate this effect, we introduce a spin-polarization function, s(k), that represents the expectation value of the z component of spin in the Bloch state at momentum k. Here, the z direction represents the C4K axis. Due to C4K symmetry, s(k) must switch sign under a four-fold rotation. The spin-polarized (s) component of charge current is given by \({{\boldsymbol{j}}}_{s}=-e{\int}_{{\boldsymbol{k}}}\dot{{\boldsymbol{r}}}s({\boldsymbol{k}})f({\boldsymbol{k}})\). Henceforth, we refer to this simply as “spin current”. It can be expressed in terms of the Fermi-Dirac distribution as in Eq. (2), by simply including a factor of s(k) in the integrands.

Symmetry considerations

We consider a material that breaks C4 and K, but preserves C4K. Note that we will also have C2 symmetry, by applying C4K twice. We consider the geometry shown in Fig. 1 and calculate the dc Hall current to third order in applied electric fields. Assuming ωτ is small, we obtain

$${j}_{c,x}={j}_{c,x}^{Q}+{j}_{c,x}^{D},$$
(3)

where

$${j}_{c,x}^{Q}={e}^{4}{\tau }^{2}\left({\int}_{{\!\!\boldsymbol{k}}}{f}_{0}\,{\partial }_{i}{\partial }_{j}\Omega \right){E}_{y}{{\mathcal{E}}}_{i}{{\mathcal{E}}}_{j}^{* }$$
(4)

represents the contribution from the Berry curvature quadrupole, defined as \({{\mathcal{Q}}}_{ij}^{c}={\int}_{{\boldsymbol{k}}}\,{f}_{0}{\partial }_{i}{\partial }_{j}\Omega\), a Fermi-surface property33,34. The second term in Eq. (3),

$${j}_{c,x}^{D}=-{e}^{4}{\tau }^{3}\left({\int}_{{\!\!\boldsymbol{k}}}{v}_{x}{\partial }_{i}{\partial }_{j}{\partial }_{y}{f}_{0}\right){E}_{y}{{\mathcal{E}}}_{i}{{\mathcal{E}}}_{j}^{* },$$
(5)

is a Drude-like contribution.

Expressions for the current responses crucially depend on the symmetries of the system. In particular, a Berry monopole contribution is ruled out by the C4K symmetry, whereas the linear Drude and Berry dipole contributions vanish due to the C2 symmetry26. Therefore, the leading contributions are given by Eqs. (4) and (5). Any further contribution is either at a higher order in electric fields or is scaled down by factors of ωτ.

The light-induced Hall current generically carries spin. As with the charge Hall current, the spin Hall current contains two contributions,

$${j}_{s,x}={j}_{s,x}^{Q}+{j}_{s,x}^{D},$$
(6)

where \({j}_{s,x}^{Q}\) and \({j}_{s,x}^{D}\) are the Berry-curvature-driven and Drude-like contributions respectively. These contributions are generically nonzero.

Role of polarization

We assume normal incidence of light on the sample with a spot size much larger than the electronic mean free path. We treat light as a spatially uniform oscillating electric field. Allowing for an arbitrary polarization, the electric field of light of amplitude \({{\mathcal{E}}}_{{\rm{ac}}}\) is described by

$${{\mathcal{E}}}_{x}={{\mathcal{E}}}_{{\rm{ac}}}\cos \theta ,\quad {{\mathcal{E}}}_{y}={{\mathcal{E}}}_{{\rm{ac}}}{e}^{i\phi }\sin \theta .$$
(7)

Linear polarization corresponds to ϕ = 0 or π. Linear polarization along x (y) corresponds to θ = 0 or π (π/2 or 3π/2) with an arbitrary value of ϕ. When \(| {{\mathcal{E}}}_{x}| =| {{\mathcal{E}}}_{y}|\) and ϕ = ±π/2, the light is circularly polarized. For generic values of θ and ϕ, we have elliptical polarization.

With the ac electric field given by Eq. (7), we now calculate each contribution to the current using the C4K symmetry. The Berry quadrupole contribution to the charge Hall current takes the form,

$${j}_{c,x}^{Q}=2{e}^{4}{\tau }^{2}{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}\left({{\mathcal{Q}}}_{xx}^{c}\cos 2\theta +{{\mathcal{Q}}}_{xy}^{c}\sin 2\theta \cos \phi \right).$$
(8)

Here, \({{\mathcal{Q}}}_{ij}^{c}\) is the same as the Berry quadrupole density defined earlier. The Berry quadrupole contribution to the spin Hall current is given by

$${j}_{s,x}^{Q}=2{e}^{4}{\tau }^{2}{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}{{\mathcal{Q}}}_{xx}^{s},$$
(9)

where we have defined the spin-polarized Berry quadrupole density as \({{\mathcal{Q}}}_{ij}^{s}={\int}_{{\boldsymbol{k}}}\,s({\boldsymbol{k}})\,\Omega {\partial }_{i}{\partial }_{j}{f}_{0}\). For the charge current arising from third-order Drude contributions, we obtain

$${j}_{c,x}^{D}=-4{e}^{4}{\tau }^{3}{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}\left[{{\mathcal{M}}}_{xxy}^{c}\cos 2\theta +{{\mathcal{M}}}_{xyy}^{c}\sin 2\theta \cos \phi \right],$$
(10)

where \({{\mathcal{M}}}_{ijk}^{c}={\int}_{{\boldsymbol{k}}}{v}_{x}{\partial }_{i}{\partial }_{j}{\partial }_{k}\,{f}_{0}\). The Drude spin current is given by

$${j}_{s,x}^{D}=-4{e}^{4}{\tau }^{3}{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}{{\mathcal{M}}}_{xxy}^{s},$$
(11)

where \({{\mathcal{M}}}_{ijk}^{s}={\int}_{{\boldsymbol{k}}}{v}_{x}s({\boldsymbol{k}}){\partial }_{i}{\partial }_{j}{\partial }_{k}\,{f}_{0}\). Expressions (8), (9), (10) and (11) have been derived using the constraints placed by the C4K symmetry on the response integrals. This symmetry ensures that \({{\mathcal{Q}}}_{xx}^{c}=-{{\mathcal{Q}}}_{yy}^{c}\), \({{\mathcal{Q}}}_{xx}^{s}={{\mathcal{Q}}}_{yy}^{s}\), \({Q}_{xy}^{s}=0\), \({{\mathcal{M}}}_{xxy}^{c}=-{{\mathcal{M}}}_{yyy}^{c}\), \({{\mathcal{M}}}_{xxy}^{s}={{\mathcal{M}}}_{yyy}^{s}\), and finally \({{\mathcal{M}}}_{xyy}^{s}=0\) (Sec. S4 B in Supplemental Material41).

Remarkably, as seen from Eqs. (8) and (10), both contributions to charge current vanish for circular polarization (e.g., when θ = π/4 and ϕ = π/2). The spin current contributions in Eqs. (9) and (11) are independent of θ and ϕ. They do not change as the polarization of light is varied.

Model and Hamiltonian; C 4 K symmetry

As a concrete demonstration, we build a minimal model with the required symmetries. We consider a 2D system with two bands arising from electron spin. We begin with a long-wavelength description, followed by a tight-binding model.

At momenta that are invariant under C4K, the two bands must necessarily be degenerate, giving rise to Dirac points. In the vicinity of each Dirac point, we may write the two-level Hamiltonian as \(\hat{H}({\boldsymbol{k}})={d}_{0}({\boldsymbol{k}}){\hat{\sigma }}_{0}+{\boldsymbol{d}}({\boldsymbol{k}})\cdot \hat{{\boldsymbol{\sigma }}}\), where \(\hat{{\boldsymbol{\sigma }}}\) is a vector of Pauli matrices that act on the spin degree of freedom, k is measured from the Dirac point, and the coefficients di(k) are real functions of k. With the symmetry group generated by the antiunitary operation C4K, at small k we have41

$$\begin{array}{lll}{d}_{0}({\boldsymbol{k}})\,=\,{a}_{0}+{a}_{1}({k}_{x}^{2}+{k}_{y}^{2}),\\ {d}_{1}({\boldsymbol{k}})\,=\,{b}_{1}{k}_{x}+{b}_{2}{k}_{y},\\ {d}_{2}({\boldsymbol{k}})\,=\,-{b}_{2}{k}_{x}+{b}_{1}{k}_{y},\\ {d}_{3}({\boldsymbol{k}})\,=\,{m}_{1}({k}_{x}^{2}-{k}_{y}^{2})+2{m}_{2}{k}_{x}{k}_{y}.\end{array}$$
(12)

We have used the lowest-order polynomial expressions for the components of d. Similar expressions have previously been used as toy models for altermagnets43. The Berry curvature can be immediately computed using \(\Omega ={\epsilon }^{ijk}{d}_{i}({\partial }_{{k}_{x}}{d}_{j}{\partial }_{{k}_{y}}{d}_{k})/2| {\boldsymbol{d}}{| }^{3}\), where \(| {\boldsymbol{d}}| =\sqrt{{d}_{1}^{2}+{d}_{2}^{2}+{d}_{3}^{2}}\). This results in a quadrupole-like distribution of Ω around k = 041. In the neighborhood of each Dirac point, we will have a long-wavelength Hamiltonian of the form given in Eq. (12).

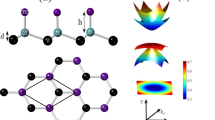
To better understand the origin of various terms in the Hamiltonian, we construct a tight-binding model that reproduces Eq. (12). We start with a 2D square lattice as shown in Fig. 2, with the lattice constant set to unity. We expect to find Dirac points at two C4K-invariant momenta: k = (0, 0) and (π, π), corresponding to Γ and M points in the Brillouin zone respectively. Apart from the usual hopping processes, we have spin-dependent hopping between nearest neighbors, which could arise from the Rashba spin-orbit coupling. We introduce “altermagnetic order parameters” J1 and J2, which encode preferential hopping of each spin along nearest and next-nearest neighbor bonds. Crucially, the J1 and J2 processes break C4 and K, but preserve C4K. We arrive at the following Hamiltonian in momentum space:

$$\begin{array}{ll}\hat{H}({\boldsymbol{k}})=-t\left(\cos {k}_{x}+\cos {k}_{y}\right){\hat{\sigma }}_{0}\\\qquad\quad +\,\displaystyle\frac{\lambda }{2}\left[\sin \left({k}_{x}+{k}_{y}\right){\hat{\sigma }}_{x}+\sin \left({k}_{y}-{k}_{x}\right){\hat{\sigma }}_{y}\right]\\\qquad\quad +\,\left[{J}_{1}(\cos {k}_{x}-\cos {k}_{y})+{J}_{2}\sin {k}_{x}\sin {k}_{y}\right]{\hat{\sigma }}_{z},\end{array}$$
(13)

where t is the usual hopping parameter and λ corresponds to the Rashba spin–orbit coupling.

Fig. 2: Proposed tight-binding model for a generic C4K material.
figure 2

We have standard hopping processes between nearest neighbors. Along diagonals we have Rashba-like hopping shown as blue dotted lines. Altermagnetic order is captured in two spin-dependent hopping processes: J1 between nearest neighbors (red dashed lines) and J2 between next nearest neighbors (black dashed lines).

Full size image

The resulting band structure is plotted in Fig. 3, for a certain choice of model parameters. Changing the chemical potential affects the shape of the Fermi pockets (Supplemental Material, Figs. S1 and S241). To proceed analytically, we examine the behavior of the system near the Dirac nodes. Near the Γ point, we recover the long-wavelength form of Eq. (12) with a0 = −2t, a1 = t/2, b1 = b2 = λ/2, m1 = −J1/2, m2 = J2/2. Near the M point, we recover the same form, but with a0 = 2t, a1 = t/2, b1 = b2 = λ/2, m1 = J1/2, and m2 = J2/2.

Fig. 3: An example of band structure and Fermi surface pockets.
figure 3

a Band structure and b Fermi pockets for λ = 0.4, μ = −0.15, J1 = J2 = 1, and t = 0.02 in arbitrary units of energy.

Full size image

At each Dirac node, we have an upper band and a lower band. Their Berry curvatures are given by

$${\Omega }_{\pm }^{\eta }=\pm \eta \frac{[{J}_{1}({k}_{x}^{2}-{k}_{y}^{2})-2\eta {J}_{2}{k}_{x}{k}_{y}]{\lambda }^{2}}{{\left({[{J}_{1}({k}_{x}^{2}-{k}_{y}^{2})-2\eta {J}_{2}{k}_{x}{k}_{y}]}^{2}+2{\lambda }^{2}{k}^{2}\right)}^{3/2}},$$
(14)

where η = +1 around Γ and −1 around M. The upper (lower) sign applies for the upper (lower) band. Using these expressions, we may evaluate the quadrupole densities, \({{\mathcal{Q}}}_{ij}^{c,s}\), which appear in the charge and spin Hall currents, see Eqs. (8) and (9). Notably, the J1 and J2 order parameters produce distinct quadrupole patterns. The former can be viewed as creating a \({d}_{{x}^{2}-{y}^{2}}\)-wave altermagnet, whereas the latter yields a dxy-wave altermagnet (Fig. S3 in the Supplementary Material41).

On examining the Bloch states of each band, we find them to be generically spin-polarized. The entries in each eigenspinor have unequal amplitudes. This allows us to define the spin-polarization function

$${s}_{\pm }^{\eta }({\boldsymbol{k}})=\mp \eta \frac{{J}_{1}({k}_{x}^{2}-{k}_{y}^{2})-2\eta {J}_{2}{k}_{x}{k}_{y}}{\sqrt{{[{J}_{1}({k}_{x}^{2}-{k}_{y}^{2})-2\eta {J}_{2}{k}_{x}{k}_{y}]}^{2}+2{\lambda }^{2}{k}^{2}}},$$
(15)

which enters the spin Hall current expressions in Eqs. (6), (9) and (11).

Light-induced Hall currents

As an explicit demonstration, we calculate light-induced Hall current with the following simplifying assumptions. The Fermi energy is taken to be close to both Dirac points, resulting in two small Fermi pockets. We further assume weak altermagnetic order with J1, J2 ≪ λ. This results in nearly circular Fermi surfaces (Supplementary Material41). Below, we calculate current contributions to leading order in J1,2/λ. For concreteness, we suppose that the Fermi energy crosses the lower band at each pocket. Neglecting inter-pocket scattering, the charge and spin currents acquire contributions from each pocket separately.

The charge current induced by the Berry curvature quadrupole is obtained from Eq. (8), including contributions from both Fermi pockets:

$$\begin{array}{rcl}{j}_{c,x}^{Q}=&&\frac{{e}^{4}{\tau }^{2}}{16\pi }{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}\left[{J}_{1}\left(\frac{1}{| {\epsilon }_{\Gamma }-\mu | }-\frac{1}{| {\epsilon }_{M}-\mu | }\right)\cos 2\theta \right.\\ &&\left.+{J}_{2}\left(\frac{1}{| {\epsilon }_{\Gamma }-\mu | }-\frac{1}{| {\epsilon }_{M}-\mu | }\right)\sin 2\theta \cos \phi \right],\end{array}$$
(16)

where ϵΓ and ϵM are the energies of the degenerate bands at the Γ and M points, respectively. μ is the chemical potential. The quadrupole-induced spin current of Eq. (9) takes the form

$${j}_{s,x}^{Q}=\frac{{e}^{4}{\tau }^{2}}{64\pi }\frac{{({J}_{1}^{2}+{J}_{2}^{2})}^{2}}{{\lambda }^{4}}{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}\left[\frac{| {\epsilon }_{\Gamma }-\mu {| }^{2}}{{\lambda }^{2}}+\frac{| {\epsilon }_{M}-\mu {| }^{2}}{{\lambda }^{2}}\right].$$
(17)

These expressions show that the quadrupole-induced Hall currents arise from altermagnetic order parameters, J1 and J2. If these order parameters were to vanish, so would the Berry-curvature quadrupole and its contribution to the dc Hall current.

We next calculate the Drude current by including contributions from the two Fermi pockets. The Drude charge current of Eq. (10) comes out to be

$$\begin{array}{rcl}{j}_{c,x}^{D}=&&\frac{{e}^{4}{\tau }^{3}{\lambda }^{2}}{8\pi }{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}\left[\left(\frac{1}{| {\epsilon }_{\Gamma }-\mu | }+\frac{1}{| {\epsilon }_{M}-\mu | }\right)\sin 2\theta \cos \phi \right.\\ &&\left.+\frac{3}{2}\frac{{J}_{1}{J}_{2}}{{\lambda }^{4}}\left(| {\epsilon }_{\Gamma }-\mu | +| {\epsilon }_{M}-\mu | \right)\cos 2\theta \right],\end{array}$$
(18)

whereas the Drude spin current of Eq. (11) yields

$${j}_{s,x}^{D}=\frac{{e}^{4}{\tau }^{3}{J}_{2}}{2\pi }{E}_{y}{{\mathcal{E}}}_{{\rm{ac}}}^{2}.$$
(19)

The Supplementary Material provides estimates of these current magnitudes for realistic parameters41.

Discussion

We have demonstrated a light-induced Hall current in materials with C4K symmetry. This current carries a spin polarization that can be tuned by varying the polarization of light. This result, expressed in Eqs. (3)–(11), arises purely from C4K symmetry and is applicable to both 2D as well as 3D materials, e.g., to thick films where light can penetrate uniformly. We emphasize two features: (i) the charge Hall current vanishes when light is circularly polarized, and (ii) the spin current does not vary with polarization. As an explicit demonstration, we have discussed a 2D toy model where analytic forms are derived. Our analysis is based on the assumption that frequency is lower than the inverse relaxation time (ωτ ≪ 1). With relaxation times typically ranging from femtoseconds to picoseconds in metals, infrared or microwave radiation may be used to see the predicted phenomena.

Our results can be readily tested by shining light on altermagnetic materials such as RuO2, MnO2, and MnF229,30. Light-induced currents complement various other transport properties known in altermagnets44,45,46,47,48. They may provide a simpler signature of C4K symmetry, with a dc charge response that does not require a spin-sensitive apparatus. Our results can also apply to other systems with Berry curvature quadrupoles such as metals with ferro-octupolar order49. In any such material, light can be used as a switch to generate currents on demand. This approach can complement other architectures for switchable spin currents50,51,52.

Methods

The distribution function f (k, t) satisfies the Boltzmann kinetic equation

$$\frac{\partial f}{\partial t}+\dot{{\boldsymbol{k}}}\,\cdot \frac{\partial f}{\partial {\boldsymbol{k}}}=-\frac{f-{f}_{0}}{\tau }.$$
(20)

The relaxation time τ is assumed to be a constant for simplicity. We use the semi-classical equations for \(\dot{{\boldsymbol{k}}}\) and \(\dot{{\boldsymbol{r}}}\) and solve for f(k, t) as a series expansion in the electric fields to calculate currents.