Introduction

The exactly solvable Kitaev model3 has catalyzed a surge of experimental effort to realize a ground-state Kitaev-like spin liquid (KSL). Based on S = 1/2 spins on a honeycomb lattice with bond-dependent Ising exchange, the KSL features emergent anyonic Z2 gauge fluxes and Majorana fermion excitations. Based on the work of Jackeli and Khaliullin4, several candidate magnetic materials with strong spin-orbit interactions were identified wherein Kitaev interactions play a significant role. These include A2IrO3 (A=Li,Na)5,6,7,8,9,10 and α-RuCl311,12,13,14. However these, and most other KSL candidate materials, develop long-range magnetic order at low T likely due to the presence of non-Kitaev interactions that are allowed by symmetry15. The KSL can survive the presence of Heisenberg, Ising, and bond-dependent off-diagonal exchange that must be present in real materials, but only in a narrow window of parameter space16,17,18,19,20, making its materialization challenging.

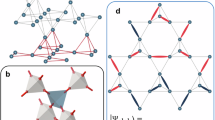
H3LiIr2O6 is a rare example of a putative Kitaev material without long range magnetic order. In contrast to the X-Li2IrO3 (X = α, β, γ) family of compounds, where the Kitaev interaction favors a three-dimensional long range ordered non-collinear spin structures5,9,21,22,23,24, the interlayer Li+ ions in α − Li2IrO3 are replaced by H+25 in H3LiIr2O6, as shown in Fig. 1. Thus the LiIr2O6 honeycomb plane is preserved but with reduced and disordered inter-layer exchange interactions due to positional disorder of the H+ ions. Despite a Curie-Weiss temperature of ΘCW = −105 K, H3LiIr2O6 has no magnetic phase transition down to temperatures as low as T = 50 mK, and zero-field specific heat capacity data C(T)/T ∝ T−1/2 indicates a large density of low energy excited states26.

Fig. 1: Crystal structure of H3LiIr2O6 viewed along the \({\hat{c}}\)-axis (a) and the \({\hat{b}}\)-axis (b).
figure 1

In (a), the dashed red, green, and blue lines denote the putative bond-anisotropic Kitaev interaction. The presence of interlayer H introduces intrinsic disorder between two energetically equivalent (H,D) sites, denoted by the arrows in (b) and described in detail in ref. 27.

Full size image

NMR evidence that these low energy excitations are magnetic26 is, however, inconsistent with a pure KSL26. Quantum paraelectric behavior as measured by dielectric spectroscopy27,28 indicates that H+-induced exchange disorder may play an important role in suppressing magnetic order observed in related honeycomb iridates29,30. Disorder is observed in both the cases of H and 2D, where the interlayer ions hop between sites of equivalent free energies, as depicted in Fig. 1b. The intrinsic local randomness of H+ may perturb the Ir-O-Ir superexchange between the edge-sharing IrO6 octrahedra, promoting a bond-disordered spin liquid2 or, under a specific stacking-fault pattern, a gapless spin liquid31. A random singlet state might be able to account for the low-lying magnetic excitation, where Jeff = 1/2 moments form singlets over a distribution of length scales prescribed by the quenched disorder32,33.

At much higher energies, Raman spectroscopy shows a dome-shaped continuum of magnetic excitations with maximum intensity at 33 meV34. These data are consistent with the anticipated two-spinon process in a KSL35. A recent resonant inelastic x-ray scattering (RIXS) measurement documented a temperature-dependent, momentum-independent excitation continuum with a spectral weight maximum near 25 meV36. This is consistent with Raman spectroscopy and recent μSR measurements37, which together were interpreted as evidence for a potential bond-disordered KSL in H3LiIr2O6. Raman and non spin flip RIXS are sensitive only to pairs of Majorana excitations, meaning that the excitation energy scale is shifted to higher energies than the low energy bare Majorana band structure, which has yet to be measured35,38.

In this work, we examine the scalar momentum ∣Q∣ − resolved spectrum of magnetic excitations in a powder sample of D3LiIr2O6 in the ℏω < 10 meV energy range using inelastic magnetic neutron scattering. We document magnetic spectra that account for the expected magnetic spectral weight of the Jeff = 1/2 states of Ir4+ with no dispersion apparent in the powder averaged continuum. The equal time correlation function can be described by nearest-neighbor correlations only, and the broad spectral maximum at ℏω = 2.5(5) meV is consistent with ferromagnetic Kitaev interactions2,38,39,40,41.

Results

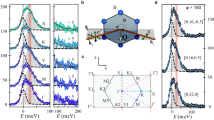
We present the background corrected magnetic neutron scattering intensity measured on SEQUOIA42 in Fig. 2. While no sharp peaks in either Q or ℏω were resolved down to the lowest accessible values of Q = 0.5 Å−1 and ℏω = 1.8 meV, as constrained by kinematics and contamination from elastic scattering, a buildup of intensity is apparent at low-Q and low-E. The wave vector dependence of the intensity I(Q) integrated over ℏω ∈ [2, 10] meV is shown in Fig. 2b. Upon cooling from 100 K to 4 K there is an increase in I(Q) for Q < 1.5 Å−1. While contrary to any nuclear scattering cross-section for a solid, this is consistent with expectations for an anisotropic quantum magnet dominated by dynamic spin correlations.

Fig. 2: Magnetic spectrum of D3LiIr2O6 measured on SEQUOIA after subtracting the non-magnetic background.
figure 2

a Normalized scattering intensity I(Q, ω) of D3LiIr2O6 measured at T = 4.5(1) K. Spectrum within the elastic line of the experimental condition, i.e. ℏω < 1.8 meV, is not presented. b Comparison of integrated scattering intensity I(Q) = ∫ I(Q, ω)dω in the range of ℏω = 2−10 meV at T = 4.5(1) K (black) and T = 100.0(1) K (red). Error bars represent one standard deviation.

Full size image

Data from MACS43 covering ℏω ∈ [0.5, 10] meV is presented in Fig. 3a, b. In the overlapping regimes of (Q, ω), the SEQUOIA (Fig. 2a) and MACS data (Fig. 3a, b) are consistent, which provides an important check on the methods used to isolate magnetic scattering for the different spectrometers and sample configurations. In the regime down to ℏω = 0.5 meV that is uniquely revealed by MACS, there is a flattening of spectral weight for ℏω < 2 meV that will be examined in greater detail below. For a separate model independent determination of the magnetic scattering cross-section in D3LiIr2O6, we performed a fully polarized neutron scattering experiment on HYSPEC42. For an isotropic sample such as a powder, the total magnetic scattering component is given by \({{\sigma }_{\rm{mag}}}=2({\sigma }_{x}^{{\rm{SF}}}+{\sigma }_{y}^{{\rm{SF}}}-2{\sigma }_{z}^{{\rm{SF}}})\)44. Here x, y, z label three perpendicular directions of the guide field for measurement of the spin flip (SF) and non-spin flip (NSF) part of the scattering cross-section, z being perpendicular to the scattering plane in our case.

Fig. 3: Magnetic inelastic scattering at T = 1.8(1) K obtained on MACS.
figure 3

Scattering from the Ef = 5.0 meV is shown in (a) and the Ef = 3.7 meV configuration in (b). The extracted magnetic scattering is strongest within the cyan box. The intensity scale is consistent with Fig. 2a, and a direct comparison of the signal to background is shown in Supplementary Fig. 15.

Full size image

After measuring the \(({\sigma }_{x}^{{\rm{SF}}},{\sigma }_{y}^{{\rm{SF}}},{\sigma }_{z}^{{\rm{SF}}})\) cross-sections and their non spin-flip counterparts, the total spin-flip scattering is shown in Fig. 4. The σmag cross-section can be obtained by averaging over (Q, ω) in coarse-grained cuts along Q (ℏω) direction while integrating over the entire range of ℏω (Q). Such data are presented in Fig. 5a, b and show a magnetic contribution to the scattering cross-section that is quantitatively consistent with the higher statistics unpolarized data. A full color plot of I(Q, ℏω) for σmag is shown in the SI, but the counting statistics are too low for any meaningful conclusions to be drawn from this. The scattering in Fig. 4 is the total spin-flip cross-section, \(({\sigma }_{x}^{{\rm{SF}}}+{\sigma }_{y}^{{\rm{SF}}}+{\sigma }_{z}^{{\rm{SF}}})/2={\sigma }_{{\rm{mag}}}+\frac{3}{2}{\sigma }_{{\rm{N}}}^{{\rm{inc}}}\)44,45. As the incoherent inelastic nuclear scattering cross-section \({\sigma }_{{\rm{N}}}^{{\rm{inc}}}\) has no Q−dependence beyond the Debye-Waller factor \(\exp (-{Q}^{2}\langle {u}^{2}\rangle ){Q}^{2}\), and spin-incoherent phonon scattering goes as ∝ Q2, the resemblance of the low-Q part of \({\sigma }_{{\rm{mag}}}+\frac{3}{2}{\sigma }_{{\rm{N}}}^{{\rm{inc}}}\) (Fig. 4b) with I(Q, ω) presented in Figs. 2 and 3 affirms the magnetic origin of the low-Q scattering for ℏω < 5 meV and Q < 1 Å−1. In all measurements, the overall normalization was cross-checked against the vanadium standard of the SEQUOIA measurement using the integrated intensity of the elastic scattering.

Fig. 4: Polarized neutron scattering spectrum measured at T = 4.0(1) K on HYSPEC using Ei = 20 meV neutrons.
figure 4

The scattering shown is the sum of the x, y, and z spin-flip cross-sections, which is then divided by two such that the magnetic intensity may be compared to Figs. 2a and 3.

Full size image
Fig. 5: Energy and momentum-dependence of magnetic excitation spectrum of D3LiIr2O6.
figure 5

In panels (a) and (b) the blue points are extracted from the MACS Ef = 5 meV measurement, cyan from the MACS Ef = 3.7 meV measurement, black from the SEQUOIA measurement, green points are the σmag contribution from the polarized HYSPEC experiment, and orange points are the \({\sigma }_{x+y+z}^{SF}/2-a-b{Q}^{2}\) contribution from the HYSPEC experiment, where −a − bQ2 is an approximation of the nonmagnetic background. a Momentum-dependence of the spectra \({\mathcal{S}}(Q)\) factorized from the neutron spectrum. The red line is a fit to the nearest-neighbor correlation function described in the text. The dashed magenta line is the Ir4+ squared magnetic form factor, and the dashed red line is a model assuming a nearest-neighbor Heisenberg interaction using Eq. (3). b Energy-dependent spectra G(ω) obtained from the same factorization analysis. Each individual factorization has been normalized following the practice described in the main texts. c THz spectroscopy taken at T = 3 K for two samples, referenced to T = 20 K data. The temperature-dependence is presented in Supplementary Fig. 21. All error bars represent one standard deviation.

Full size image

Discussion

We now seek a quantitative comparison of the three different measurements of the magnetic scattering cross-section. For improved statistical accuracy and to avoid systematic errors associated with the coverage of Q − ω space dictated by the kinematics of the scattering process, we project the data onto the Q and ω–axes. For the unpolarized data we obtain values of I(Q), of length NQ, and G(ω), of length Nω, through a least-squared fit to the data under the assumption of a factorizable cross-section: I(Q, ω) = I(Q)G(ω). Here G(ω) is unity normalized ∫ G(ω)ℏdω ≡ 1 over the inclusive energy range [0.5, 10] meV covered by the overlapping data sets. This projects data from ≲ NQ × Nω pixels in I(Q, ω) to NQ + Nω pixels in I(Q) and G(ω). Due to the lower counting statistics of the polarized data it was more effective to directly integrate the data accommodating the kinematic limits as follows: G(ω) was obtained as the average of I(Q, ω) over Q ∈ [0.2, 1.6] Å−1 scaled by a factor f to enforce its unity normalization. I(Q) was obtained as the average of I(Q, ω) over ℏω ∈ [2, 10] meV scaled by a factor 1/f so that I(Q, ω) ≈ I(Q)G(ω). For a direct comparison of I(Q) from \(\frac{1}{2}{\sigma }_{x+y+z}^{SF}\) to the other measurements in Fig. 5a, a background of the form Ibkg(Q) = a + bQ2 was subtracted to account for nuclear spin-incoherent scattering. Superior statistics also allow for a finer binning than σmag in Fig. 5. Though acquired on different instruments, subjected to different background subtractions, and normalized to different reference cross-sections, the data sets for I(Q) and G(ω) displayed in Fig. 5a, b provide statistically consistent measures of the magnetic scattering cross-ection in D3LiIr2O6. From the total moment sum rule we have \({\mu }_{{\rm{eff}}}^{2}=(6/{r}_{0}^{2})\int\,I(Q)/| F(Q){| }^{2}dQ\)45. Integrating over available data in the ranges Q ∈ [0.5, 1.7] Å−1 and ℏω ∈ [1.8, 10] meV yields a total moment of μeff = 1.8(4) μB for the unpolarized experiments and μeff = 1.6(8) μB for the polarized data, with error bars dominated by the uncertainty in normalization. These values are close to the effective moment inferred from high-temperature magnetic susceptibility data μeff = 1.60 μB26 and consistent with \(g\sqrt{{J}_{{\rm{eff}}}({J}_{{\rm{eff}}}+1)}{\mu }_{B}\) with g ≈ 2 and Jeff = 1/2 for Ir4+. This does not conflict with the higher energy excitations observed in optical measurements34,36, in which the cross-section is dominated by higher order excitations.

Inaccessible through neutron scattering, we obtain the Q = 0 magnetic excitation spectrum through time-domain THz spectroscopy. Figure 5c presents χ″(ω), which reveals low-energy excitation with energy scales similar to neutron scattering spectra (Supplementary Fig. 21) reports the T−dependence of χ″). This critically reveals that the low Q continuum observed in the INS experiments extend from low-Q limit to the Γ-point. With excellent consistency across multiple distinct experiments, our data demonstrate a buildup of magnetic excitations for Q < 1.5 Å−1 and ℏω < 5 meV, with maximal spectral weight near 2 meV energy transfer. The significant spectral weight near Q = 0 simultaneously documented by neutron scattering and THz spectroscopy in the absence of an applied field indicates anisotropic ferromagnetic interactions, as evidenced by a first moment sum rule analysis.

For a system of interacting spins, the first moment sum rule is given by ref. 46

$${\int_{-\infty }^{\infty }}{S}^{\alpha \alpha }({\boldsymbol{Q}},\omega )d\omega =\frac{-1}{N}\left\langle {S}_{{\boldsymbol{Q}}}^{\beta }\left[{\mathcal{H}},{S}_{{\boldsymbol{-Q}}}^{\beta }\right]\right\rangle .$$
(1)

Here, Sαα(Q, ω) is the dynamical spin structure factor, the Cartesian spin axes are denoted by (α, β), and the spin exchange Hamiltonian is defined by \({\mathcal{H}}\). In the case of a Heisenberg magnet with no off-diagonal terms in \({\mathcal{H}}\), this expression may be used to relate the bond exchange energies Jd for bond d to the scattering by

$${\int_{-\infty }^{\infty }}\omega {S}^{\alpha \beta }({\boldsymbol{Q}},\omega )d\omega =-\sum _{{\boldsymbol{d}},\beta }(1-{\delta }_{\alpha \beta }){J}_{d}\left(1-\cos ({\boldsymbol{Q}}\cdot {{\boldsymbol{d}}}_{n})\right)\left\langle \left\langle {S}_{{\boldsymbol{r}}}^{\beta }{S}_{{\boldsymbol{r}}+{{\boldsymbol{d}}}_{n}}^{\beta }\right\rangle \right\rangle .$$
(2)

In this expression dn denotes the nth bond vector, and \(\langle \langle {S}_{{\boldsymbol{r}}}^{\beta }{S}_{{\boldsymbol{r}}+{{\boldsymbol{d}}}_{n}}^{\beta }\rangle \rangle\) is the equal-time two point spin correlator. Thus, after performing a powder average, a correlated spin system with Heisenberg-like exchange interactions may be described by

$${\int_{-\infty }^{\infty }}\omega {S}^{\alpha \alpha }({\boldsymbol{Q}},\omega )d\omega =\sum _{{\bf{d}},\beta }(1-{\delta }_{\alpha \beta }){J}_{{\bf{d}}}\langle {{\bf{S}}}_{{\bf{r}}}\cdot {{\bf{S}}}_{{\bf{r}}+{\bf{d}}}\rangle \left[1-\frac{\sin (Qd)}{Qd}\right].$$
(3)

In the pure Kitaev spin liquid, spin correlations beyond nearest neighbors vanish, approximating the dynamic correlation function as

$${\mathcal{S}}({\bf{Q}},\omega )=2(G(\omega )-\,{\text{sgn}}\,(K)\frac{1}{3}\sum _{i}\cos ({\bf{Q}}\cdot {{\bf{d}}}_{i})G(\omega )),$$
(4)

where di are the three vectors separating nearest neighbors38 and sgn(K) is the sign of the Kitaev interaction. It should be noted that this model is not unique to the Kitaev spin-liquid, and is precisely the same as what one would expect from a random-singlet state.

We find that the powder averaged form

$${\mathcal{S}}(Q,\omega )=2(G(\omega )-\,{\text{sgn}}\,(K)G(\omega )\sin (Qd)/(Qd))$$
(5)

provides an excellent account of I(Q) (solid line in Fig. 5a) with K < 0 corresponding to ferromagnetic Kitaev interactions. Here, we have assumed that the full energy-dependent response can be captured by a single function G(ω), as extracted from the INS measurement in Fig. 2a. This may be contrasted with a Heisenberg model with nearest neighbor ferromagnetic correlated spins, shown by the dashed red line in Fig. 5a, and the Ir4+ magnetic form factor shown by the dotted magenta line, which would correspond to an uncorrelated quantum paramagnet. Both alternative descriptions are qualitatively incompatible with the experimentally observed scattering. The possibility of a Heisenberg-like interaction with an anisotropic contribution from Kitaev K and off-diagonal \(\Gamma ,{\Gamma }^{{\prime} }\) terms must also be considered. The momentum averaged scattering from such a model could be approximated as a linear combination of the dashed and solid red lines in Fig. 5a. Allowing this possibility did not improve the quality of the fit to \({\mathcal{S}}(Q)\).

Our measurements cannot uniquely determine the origin of the observed peak in G(ω). As the scattering is distinctly different from the Ir4+ magnetic form factor shown by the purple dashed line in Fig. 5a, simple single-ion type anistropy can be excluded. As the nearest-neighbor \(JK\Gamma {\Gamma }^{{\prime} }\) model captures all symmetry-allowed interactions17, the exchange anisotropy must be of the Kitaev or off-diagonal \(\Gamma /{\Gamma }^{{\prime} }\) type, which cannot be distinguished in this measurement.

Consistent with this, studies of (α, β)-Li2IrO3, which have similar super-exchange paths to D3LiIr2O6, indicate the nearest-neighbor Kitaev interaction is ferromagnetic even though the Curie-Weiss temperature is negative, implying further antialigning interactions, such as possible antiferromagnetic Heisenberg interactions26,47,48,49. The ideal KSL has a gapful excitation continuum with spectral weight peaked at ∣K∣/538,50. This value is certainly highly modified due to the presence of disorder and non-Kitaev interactions in the current system2, but if one assumes pure KSL physics we estimate K = −13(5) meV from the broad maximum in G(ω) near ℏω = 2.5(5) meV (Fig. 5b). This must only an order of magnitude estimate, as the energetics in this system are significantly modified by disorder. However, it may also be compared to related RIXS and Raman spectroscopy results, which suggest a ferromagnetic Kitaev interaction with ∣K∣ = 25 meV as inferred from the pure Kitaev model35,51. Considering the significant disorder intrinsic in D3LiIr2O6, these results are generally compatible.

It is interesting to compare the present results to our recent neutron scattering experiments on β − Li2IrO324. This material forms a 3D hyper-honeycomb lattice with similar coordination between nearest-neighbor IrO6 octahedra within the honeycomb plane, and thus one might expect similar nearest-neighbor exchange interactions to D3LiIr2O6. However, it develops incommensurate long range magnetic order for TN = 38 K and in this ordered state the inelastic neutron scattering spectrum is radically different from that of D3LiIr2O6. Although the experiments were both conducted on isotopically enriched powder samples under very similar experimental conditions, β − Li2IrO3 develops a well-defined peak in the magnetic excitation spectrum at 12 meV with a 2.1 meV gap to excitations.

In that case, there is also pronounced Q−dependence with low energy magnetic scattering emerging near the incommensurate magnetic wave vector. While diffuse scattering associated with the interlayer H/D copmlicates the interpretation of the experiments presented in this work, the comparison to β − Li2IrO3 makes it clear that we have sensitivity to detect coherent spin wave like excitations and that magnetic excitations in D3LiIr2O6 take a very different form. Spin wave theory using the JKΓ model does provide a good account of the data for β − Li2IrO3 with a Heisenberg term J = 0.40(2) meV, Kitaev term K = −24(3) meV, and off-diagonal term Γ = −9.3(1) meV24. Given the similar local coordination environment for the edge sharing IrO6 nearest neighbor tetrahedra, we expect qualitatitvely similar nearest-neighbor exchange parameters for D3LiIr2O6 with local modification due to H/D disorder and modifications in the specific values of J, K, and Γ from the different crystal structures. It is impossible to say how exactly the H/D disorder will affect the exchange, but previous theoretical studies have treated this as a random perturbation or vacancy leading to a bond-disordered KSL2,52,53.

We have shown that the magnetic neutron scattering cross-section for a powder sample of D3LiIr2O6 is consistent with a Kitaev spin-liquid where the flux excitation gap is closed by disorder and interactions beyond the pure model. The increased spacing between Kitaev layers and the disordered nature of D/Li in the intervening layer leads to weak and disordered interlayer interactions that surely play a role in suppressing long range order and thereby relatively favoring a dynamic spin-liquid-like state. However, compounded by powder averaging, the featureless nature of the magnetic scattering precludes distinguishing between the various scenarios proposed for this material, such as a pure KSL phase, a random-singlet state, and a bond-disordered spin-liquid phase1,2,31,52,54. It is also entirely possible that the true nature of the magnetism in this material is described by none of these scenarios, as disordered quantum magnets tend to have similar featureless excitation spectra to our powder measurements. Inelastic neutron scattering on single crystals will be needed for this purpose, but their availability is still limited to the micrometer length scale23,34.

Methods

The powder sample was prepared by previously published solid-state synthesis methods26 using 2H = D, 193Ir, and 7Li to mitigate absorption and incoherent scattering that is associated with the natural isotope distribution. The powder was held in an annular can with thickness 0.5 mm and outer diameter 20 mm resulting in a calculated 95% neutron transmission for 25 meV neutrons. Three inelastic neutron scattering experiments were performed. We used the SEQUOIA instrument at Oak Ridge National Laboratory (ORNL)42 to measure the spectrum down to 1.8 meV for temperatures T = 4.0(1) K, 100.0(1) K, and 200.0(1) K (Fig. 2 and Supplementary Fig. 3). Lower energy measurements were performed on the MACS spectrometer at the NIST Center for Neutron Research55, with sample temperatures T = 1.7(1) K and T = 55.0(1) K using the Ef = 3.7 meV and Ef = 5 meV configurations (Fig. 3). Scattering angle and energy dependent absorption corrections were applied to all data. Nonmagnetic contributions to the scattering from H/D incoherent scattering and low-energy acoustic phonons were subtracted using analytical methods as described in the Supplementary Information56, which are verified by an McStas Monte-Carlo simulation including all scattering processes57,58. The extracted signal is weak compared to the large background from incoherent scattering, with the signal-to-noise ratios at the peak intensity position of Q = 0.5 Å−1 being approximately 1:4 for SEQUOIA, 1:2 for MACS using Ef = 5.0 meV, 2:3 for MACS using Ef = 3.7 meV, and 1:2 for the spin-flip intensity on HYSPEC. In all cases, the available detectors with the lowest scattering angle were masked to exclude spurious beam effects.

Absolute normalization of the scattering data was achieved by comparing the measured count rates to those for a vanadium standard (SEQUOIA) and through the Q−integrated nuclear Bragg peak intensity (MACS). We used polarized neutrons on the HYSPEC instrument at ORNL42 for an independent determination of the magnetic scattering cross-section. Using three perpendicular guide field directions in succession, six cross-sections (the x, y, z, spin-flip and non-spin-flip channels) were measured at T = 2.0(1) K resulting in a model independent, albeit low statistics, measure of the magnetic scattering cross-section (Fig. 4). Time domain Terahertz spectroscopy was performed on a custom-built spectrometer with a frequency range 0.2 THz to 2 THz59 at zero magnetic field. Details of the data analysis provided in the supplementary information.