Introduction

To date, due to the subtle balance between intrinsic ferroelectric property and external mechanical and electrical conditions1,2,3,4,5,6, polar topologies in the nanoscale are mostly found in mechanical-clamped heterostructures7,8,9,10,11,12,13,14,15,16,17,18 and confined size systems19,20,21,22,23,24,25,26, hindering the manipulation and application of such polar topologies.

Recent advances in moiré systems constructed from two-dimensional (2D) layered materials—including van der Waals heterostructures such as graphene, hexagonal boron nitride, and transition metal dichalcogenides—have established a versatile platform for designing nanoscale strain patterns through stacking and twist engineering. These systems have emerged as a fertile field for investigating novel quantum phenomena, including tunable correlated electronic states27, Chern insulator phases28, enhanced nonlinear optical responses29, unconventional superconductivity30, and emergent ferroic order mechanisms31.

Similar to 2D atomic layers, freestanding perovskite oxide bilayer membranes have recently been shown to form moiré superlattices32,33,34. The groundbreaking discovery of polar vortex arrays in twisted perovskite bilayers has opened new avenues for creating exotic polar topologies through engineered strain patterns, independent of the material’s intrinsic ferroelectric properties35,36,37,38. However, constrained by current experimental and computational limitations, existing studies have primarily focused on characterizing the 2D topological features of these vortices. The three-dimensional (3D) topology remains unresolved, which fundamentally hinders the exploration of emergent physical phenomena and potential device applications.

Herein, within the framework of elastic theory, we established an analytical strain model for a freestanding membrane. Using this framework, we employed phase-field modeling to determine the corresponding polar topology of the vortex patterns. Our results reveal that the moiré vortex patterns are intrinsically linked to the periodic distribution of displacement vorticity induced by moiré stacking. The formation of these patterns is driven by the intricate interplay among elastic, flexoelectric, and gradient energy contributions. In three dimensions, the polar vortices exhibit in-plane (IP) divergence and out-of-plane (OP) polarity, giving rise to a divergent (or convergent) chiral vortex state. Notably, the chirality of the vortices can be controlled by switching their polarity through the application of OP electric fields. Additionally, by tuning the flexoelectric components, the chirality and divergence of the vortices can be quantitatively modulated. These findings not only provide a comprehensive understanding of the 3D topological structure but also offer a practical approach for manipulating the details of moiré vortex patterns.

Results

Structure and mechanical origin of moiré vortex patterns

To initiate our discussion on vortex patterns in twisted ferroelectric bilayers, it is essential to focus on their mechanical origins within the layers, as this provides a foundational understanding of the nanoscale topology. We begin our analysis in two dimensions. Based on prior experimental observations and density functional theory calculations, vortices in 2D systems emerge due to flexoelectric polarization, which is driven by IP shear strain gradients generated during the stacking process39,40. Such shear strain exhibits clear periodicity along the [100] and \([010]\) diagonals in SrTiO3. Take the top layer, for example, we assume that the IP shear strain can be represented by a 2D trigonometric function:

$${\varepsilon }_{xy}=\frac{1}{2}({u}_{,y}+{v}_{,x})=\frac{{\varepsilon }_{xy}^{Max}}{2}(\cos \frac{2\sqrt{2}\pi }{{l}_{0}}x+\,\cos \frac{2\sqrt{2}\pi }{{l}_{0}}y)$$
(1)

where the x and y axes of the 2D Cartesian coordinate system defined here are consistent with the \([1\bar{1}0]\) and [110] diagonals in SrTiO3, respectively, and the origin of the coordinate system matches the center of the clockwise vortex, as shown in the moiré superlattice of Fig. 1a. u and v represent the IP displacement components along the x and y axes, \({\varepsilon }_{{xy}}^{{Max}}\) the mean amplitude of shear strain probed by the ptychography, l0, the shear strain period along a or b axis in cubic SrTiO3, which depends on stacking angle θt. The relationship can be written as41:

$${l}_{0}=\sqrt{2}{\lambda }_{a}=\sqrt{2}{\lambda }_{b}=\frac{\sqrt{2}a_{0}}{\sqrt{(1-\,\cos {\theta }_{t})}}$$
(2)

where \({\lambda }_{a}\) and \({\lambda }_{b}\) represent the moiré pattern wavelength along the a and b axes in cubic phase42. Under assumed shear strain, vortices emerge at the saddle points of the shear strain surface, as depicted in Fig. 1a.

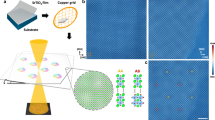
Fig. 1: IP strain model and the strain state of evolved moiré vortex pattern.
figure 1

a Schematic image of moiré vortex patterns and corresponding strain distribution. Where the valleys (peaks) of εxy surface are located at clockwise (counter-clockwise) anti-vortices, as marked by blue (red) circles. b Detailed profile of normal strain components (εxx and εyy) with rotation along lines marked in (a) in experiments. c–e Strain states with the influence of eigen-strain induced by winding polar texture. The scale bar represents 2 nm.

Full size image

Then we further investigate the normal strain components created in twisted bilayers in 2D with θt = 10.43° and l0 = 4.4 nm. As shown in Fig. 1b, the distribution of normal strain (both εxx and εyy) obtained along x and y axes via multi-slice electron ptychography43 exhibits concurrent changes in the sign of IP lattice rotation angle (ωyx). This also indicates that the vorticity and normal strain components of the moiré polar vortex vary synchronously within the (001) plane. The relationship between εxx (εyy) and ωyx displays translational symmetry along the [110] (\([1\bar{1}0]\)) diagonal, which resembles previous experimental observations39. Combined with the symmetry of the moiré pattern, IP normal strain components are simplified as a periodic single-valued wave function here for ease of analysis [Fig. 1a]. Therefore, IP displacement and strain of moiré superlattice can be expressed as follows [Detailed analysis is listed in Note S1 of Supplementary Material]:

$$u=\frac{\sqrt{2}{l}_{0}{\varepsilon }_{xy}^{Max}}{4\pi }\left(\alpha \,\sin \frac{2\sqrt{2}\pi }{{l}_{0}}x+\,\sin \frac{2\sqrt{2}\pi }{{l}_{0}}y\right)$$
(3)
$$v=\frac{\sqrt{2}{l}_{0}{\varepsilon }_{xy}^{Max}}{4\pi }\left(\sin \frac{2\sqrt{2}\pi }{{l}_{0}}x-\alpha \,\sin \frac{2\sqrt{2}\pi }{{l}_{0}}y\right)$$
(4)
$${\varepsilon }_{xx}=\frac{\partial u}{\partial x}=\alpha \cdot {\varepsilon }_{xy}^{Max}\,\cos \frac{2\sqrt{2}\pi }{{l}_{0}}x$$
(5)
$${\varepsilon }_{yy}=\frac{\partial v}{\partial y}=-\alpha \cdot {\varepsilon }_{xy}^{Max}\,\cos \frac{2\sqrt{2}\pi }{{l}_{0}}y$$
(6)

where α is the ratio of normal and shear strain (α is set to 0.5 for ease of analysis).

To validate the reliability of our strain model, we conducted phase-field simulations of the strain state near evolved vortex patterns in the top layer of twisted SrTiO3 bilayers within the framework of Landau-Ginzburg-Devonshire theory, as shown in Fig. 1c–e. The results show periodic moiré vortex patterns created by our assumed strain model. It also reveals that, due to the presence of eigen-strain near highly periodic vortices, the normal strain components εxx and εyy [Fig. 1d, e] lose their translational symmetry along [110] and \([1\bar{1}0]\) diagonals and transform into an interconnected droplet-like pattern, which aligns with the results in centrosymmetric PbS bilayers41. This eigen-strain mainly results from reverse flexoelectricity rather than electrostriction, which is also consistent with the strain profiles previously observed in twisted BaTiO3 bilayers39.

To gain insight into the formation mechanisms of moiré vortex patterns, we analyzed their displacement fields and the associated energy landscape. Figure 2a, b presents the comparison between IP lattice displacement u = (u, v) and polar texture arrangement P = (Px, Py), where f11, f12, and f44 were set as 0 V, −3 V, and −3 V to align with first-principle results40. As shown, the displacement field u closely matches with polarization field P of moiré vortex patterns, highlighting the strong coupling between winding polar texture and the continuous lattice rotation. Correspondingly, displacement vorticity (\(\nabla \cdot \vec{{\bf{u}}}\)) exhibits the same distribution pattern with calculated polarization vorticity (\(\nabla \cdot \vec{{\bf{P}}}\)). The detailed relationship between vorticity and rotation angle along [010] is displayed in Fig. 2c.

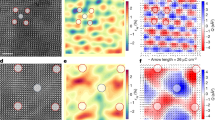
Fig. 2: Elastic and energetic view of the origin of IP vortex patterns with θt = 10.43°.
figure 2

Polar texture (a) and displacement field (b) obtained from phase-field modeling, where color depicts polarization vorticity (\(\nabla \cdot \overrightarrow{{\bf{P}}}\)) and displacement vorticity (\(\nabla \cdot \vec{{\bf{u}}}\)) respectively. c Profile of polarization and displacement vorticity across the line in (a, b). Elastic (d), flexoelectric (e), and gradient (f) energy landscapes, which mainly drive the formation of vortex patterns. The scale bar represents 2 nm.

Full size image

Figure 2d–f displays elastic, flexoelectric, and gradient energy landscapes of vortex patterns, respectively. The elastic energy, originating from lattice rotation, is dominant in the (001) plane and is at least one order-of-parameter larger than the other two energy contributions. Notably, electrostatic energy is relatively negligible. These observations indicate that the delicate balance among elastic, flexoelectric, and gradient energy governs the formation of the moiré vortex pattern in twisted bilayers. This mechanism differs significantly from the origin of the polar vortex in PbTiO3/SrTiO3 superlattices1,2,5,8,44, where interplay among elastic, electrostatic, and gradient energy plays a critical role.

The formation mechanism can be understood as follows: the periodic strain and its gradients induce IP twirling polarization with interleaved vorticity, while the gradient energy decreases to ensure smooth rotation of the vortices, ultimately stabilizing the vortex structures.

3D topology and modulation of moiré vortex patterns

Next, we investigated the 3D polar topology of the moiré vortex pattern. Given the strong coupling between polarization and displacement discussed earlier, we first analyzed the 3D strain distribution induced by twisted stacking. Based on previous studies40, the winding direction of the vortex along the c-axis reverses as the depth increases. This switching behavior can be attributed to the fact that, with increasing depth, the IP polarization decreases monotonically until it reverses and increases back to its original amplitude. Consequently, we assume that the 3D displacement exhibits similar characteristics to the polarization.

In this analysis, we focus on the finite thickness region h1, within which the vortex reverses its rotational direction, as illustrated in Fig. 3a. By solving the Lamé-Navier equations within the framework of continuum theory45,46, the 3D displacement u = (u, v, w) is derived as follows (a detailed analysis is provided in Note S2 of the Supplementary Material):

$$u=\frac{\sqrt{2}{l}_{0}{\varepsilon }_{xy}^{Max}}{4\pi }\left(\alpha \,\sin \frac{2\sqrt{2}\pi }{{l}_{0}}x+\,\sin \frac{2\sqrt{2}\pi }{{l}_{0}}y\right)\cdot \left({\beta }_{1}{e}^{\frac{2\sqrt{2}\pi }{{l}_{0}}z}+{\beta }_{2}{e}^{-\frac{2\sqrt{2}\pi }{{l}_{0}}z}\right)$$
(7)
$$v=\frac{\sqrt{2}{l}_{0}{\varepsilon }_{xy}^{Max}}{4\pi }\left(\sin \frac{2\sqrt{2}\pi }{{l}_{0}}x-\alpha \,\sin \frac{2\sqrt{2}\pi }{{l}_{0}}y\right)\cdot \left({\beta }_{1}{e}^{\frac{2\sqrt{2}\pi }{{l}_{0}}z}+{\beta }_{2}{e}^{-\frac{2\sqrt{2}\pi }{{l}_{0}}z}\right)$$
(8)
$$w=-\frac{\sqrt{2}{l}_{0}{\varepsilon }_{xy}^{Max}}{4\pi }\cdot \alpha \left(\cos \frac{2\sqrt{2}\pi }{{l}_{0}}x-\,\cos \frac{2\sqrt{2}\pi }{{l}_{0}}y\right)\cdot \left({\beta }_{1}{e}^{\frac{2\sqrt{2}\pi }{{l}_{0}}z}-{\beta }_{2}{e}^{-\frac{2\sqrt{2}\pi }{{l}_{0}}z}\right)$$
(9)

where the coefficient vector β = [β1, β2] T =\({[\frac{1}{1-{e}^{2\sqrt{2}\pi }},\frac{{e}^{2\sqrt{2}\pi }}{{e}^{2\sqrt{2}\pi }-1}]}^{T}\).

Fig. 3: 3D topology of moiré vortex patterns.
figure 3

a Schematic image of IP polar texture dependent on depth in the top layer. b Simulated vortex patterns in the top layer with θt = 10.43°, with colored tubes representing their IP vorticity. c Zoomed-in figure of one selected vortex period in (b). d The double-well potential of free energy in the absence (I) and presence (II) of flexoelectric energy. e The cross-sectional view in (010) and (\(\bar{1}\)10) respectively in (b), where color indicates the IP vorticity. The scale bar represents 1 nm. Schematic image of the topology of a chiral vortex in the lower-half layer at position B (f), which can be recognized as the combination of curling and divergent polar textures (g). Color in (f, g) depicts the IP polarization rotation and OP orientation, respectively.

Full size image

The 3D polar texture of the polar vortex can be further elucidated through phase-field simulations. For ease of analysis, only the contribution of shear flexoelectricity is considered (where f11 = f12 = 0 V and f44 = −3 V). Figure 3b, c illustrates a portion of the simulated 3D polarization distribution for a selected unit region. Similar to the strain distribution, the shear flexoelectricity induces a polar vortex that extends across the entire thickness. The vorticity gradually diminishes with increasing depth and subsequently reverses direction, eventually recovering its original amplitude. The variation of vorticity follows a hyperbolic sine functional distribution, as shown in Fig. 3c. Meanwhile, the OP polarization emerges at the vortex core and permeates the entire film at both positions A and B, leading to a chiral vortex pair along the c-axis. Above the central layer in Fig. 3c, all vortices exhibit consistent left-handed chirality, while below the central layer, they display right-handed chirality. This observation aligns with previous first-principles calculations38.

The origin of the OP chirality can be understood by examining the energy landscape depicted in Fig. 3d. In paraelectric SrTiO3, OP electrostriction creates double-well potentials (I) while tensile strain exists32,47. When flexoelectricity is incorporated into the free energy (II), the potential profile tilts under the OP flexoelectric field Ez, causing the OP polarization to align parallel with the flexoelectric field Ez to achieve a stable energy state. Such a flexoelectric field Ez can be expressed as:

$$\begin{array}{l}{E}_{z}=-2\cdot \frac{\partial {f}_{flexo}}{\partial {P}_{z}}={f}_{ijkz}{\varepsilon }_{ij,k}={f}_{11}{\varepsilon }_{zz,z}+{f}_{12}\left({\varepsilon }_{xx,z}+{\varepsilon }_{yy,z}\right)+{f}_{44}\left({\varepsilon }_{xz,x}+{\varepsilon }_{yz,y}\right)\\ =\frac{\sqrt{2}\pi \alpha ({f}_{12}-{f}_{11}+{f}_{44}){\varepsilon }_{xy}^{Max}}{{l}_{0}}\cdot \left(\cos \frac{2\sqrt{2}\pi }{{l}_{0}}x-\,\cos \frac{2\sqrt{2}\pi }{{l}_{0}}y\right)\cdot \left({\beta }_{1}{e}^{\frac{2\sqrt{2}\pi }{{l}_{0}}z}-{\beta }_{2}{e}^{-\frac{2\sqrt{2}\pi }{{l}_{0}}z}\right)\\ =\frac{2\sqrt{2}\pi \alpha ({f}_{12}-{f}_{11}+{f}_{44})}{{l}_{0}}\cdot \frac{{\beta }_{1}{e}^{\frac{2\sqrt{2}\pi }{{l}_{0}}z}-{\beta }_{2}{e}^{-\frac{2\sqrt{2}\pi }{{l}_{0}}z}}{{\beta }_{1}{e}^{\frac{2\sqrt{2}\pi }{{l}_{0}}z}+{\beta }_{2}{e}^{-\frac{2\sqrt{2}\pi }{{l}_{0}}z}}\cdot {\omega }_{yx}\end{array}$$
(10)

It can be observed that Ez is overlapped to the position of IP lattice rotation\({\omega }_{yx}\), and the sign of Ez remains consistent along the c-axis within the same stacking configuration. In the absence of the net effect of longitudinal and transversal flexoelectricity (f11−f12 = 0 V), the OP chirality is primarily driven by OP shear strain gradients. Consequently, the polar vortices on either side of the central layer exhibit opposite chirality. By applying and subsequently removing an external OP electric field Eex = 400 kV/cm, the chirality of the vortices can be effectively switched and fully recovered. Importantly, the IP vortex structure remains intact throughout the application and removal of Eex. These results are illustrated in Supplementary Fig. 1.

Figure 3e provides IP information in the (010) and (1\(\bar{1}\)0) planes. A distinct Néel-type transition is observed between two adjacent vortices in the cross-sectional view. This reveals that the 3D topology of the polar vortex is a superposition of an IP vortex (curling) and meron-like polar textures (divergent)48,49, as illustrated in Fig. 3f. The combination of these two polarization fields finally forms a divergent chiral vortex created by moiré patterns [Fig. 3g].

To quantificationally detect the influence of flexoelectric effects on moiré vortex patterns, we performed the simulation under the modulation from longitudinal (f11), transversal (f12), and shear (f44) flexoelectric coupling by tuning the following coefficients independently.

Shear flexoelectricity is found to be the key factor of IP vorticity and OP polarity. Figure 3a, b gives the dependence of the IP vorticity and OP polarity on shear flexoelectric coefficients f44 at positions A and B in Fig. 2c. As f44 increases, both OP polarization components and IP vorticity exhibit a monotonic enhancement at both stacking configurations, confirming the shear flexoelectric origin of the moiré vortex patterns. Notably, the OP polarization along the c-axis is asymmetric. This is primarily due to the diverse strain state of εzz near the top and bottom surface, where local tension is energy-favorable for higher OP polarizations rather than compression.

Figure 4c–g illustrates the IP vortex state at the bottom surface under modulation of longitudinal (f11) and transversal (f12) flexoelectricity. As f11 increased from −3 to 3 V, the divergence of the IP vortex gradually decreased to zero and then reversed its direction. When the longitudinal and transversal coefficients are equal [Fig. 4h], the resulting vortex exhibits a polar state where the divergence and vorticity match those observed in the absence of longitudinal and transversal coupling [Fig. 4e]. This behavior stems from the symmetric profile of normal strain and its gradients in the (001) plane, consistent with previous studies50,51,52. A similar symmetry is observed along the c-axis, as shown in Fig. 4i, j. Furthermore, as the net effect of longitudinal and transversal flexoelectricity (f11−f12) increases, the divergence and OP polarization show the monotonic increasing and mainly emerge at the two OP interfaces.

Fig. 4: The effect of flexoelectricity on topological details of moiré vortex patterns.
figure 4

IP vorticity (a) and OP polarity (b) at positions A and B, dependent on shear flexoelectric coefficients, vary from 1 to 3 V. c–j IP divergence under the modulation of longitudinal flexoelectric coefficients of bottom surface vortex, where f44 was set as 3 V. The size of a single vortex is 2 nm. h IP divergence under the equal effect of longitudinal and transversal flexoelectricity. i, j IP divergence and OP polarity as a function of the net value of longitudinal and transversal flexoelectric coefficients f11−f12. varies from −6 to 6 V.

Full size image

Discussion

In short, we analytically derived the 2D and 3D strain states in twisted SrTiO3 bilayers by integrating experimental strain with elastic theory. The topological structure of the moiré polar vortex was further investigated through phase-field simulations. Our simulations reveal that the moiré vortex pattern primarily arises from shear flexoelectric polarization induced by lattice rotation, with its energetic origin attributed to the delicate balance among elastic, flexoelectric, and gradient energy contributions. The 3D simulations demonstrate that the vortex exhibits OP chirality, forming chiral vortex pairs along the c-axis at each stacking site. This chirality is also tunable by OP external electric stimuli. By modulating the shear flexoelectricity, the polarity and vorticity of the chiral vortices can be effectively tuned. The net effect of longitudinal and transversal flexoelectricity predominantly governs the divergence of the vortex patterns across the entire layer. Our work not only gives a brief outline to the 3D topology of the moiré polar vortex but also provides a theoretical guideline to manipulating its topological state for promising applications.

Methods

Phase-field modeling

The 3D time-dependent Ginzburg–Landau equation was established to solve the temporal evolution of ferroelectric polarization vector P = (Px, Py, Pz):

$$\frac{\partial {P}_{{\rm{i}}}({\boldsymbol{r}},t)}{\partial t}=-L\frac{\delta F}{\delta {P}_{{\rm{i}}}({\boldsymbol{r}},t)}(i=x,y,z)$$

where L denotes the kinetic coefficient, F the total free energy functional, r the spatial coordinate, and t the evolutionary time. Total free energy functional F includes contributions of Landau energy, gradient energy, electric energy, flexoelectric energy, elastic energy, and electrostrictive energy, respectively:

$$F={\int\!\!\int\!\!\int} ({f}_{Landau}+{f}_{Gradient}+{f}_{Electric}+{f}_{Flexo}+{f}_{Elastic}+{f}_{Es})dV$$

each energy term can be expressed as:

$${f}_{Landau}={\alpha }_{ij}{P}_{i}{P}_{j}+{\alpha }_{ijkl}{P}_{i}{P}_{j}{P}_{k}{P}_{l}$$
$${f}_{Gradient}=\frac{1}{2}{G}_{ijkl}{P}_{i,j}{P}_{k,l}$$
$${f}_{Electric}=-\frac{1}{2}{\kappa }_{0}{E}_{i}{E}_{i}-{P}_{i}{E}_{i}$$
$${f}_{Flesxo}=-\frac{1}{2}{f}_{ijkl}({\varepsilon }_{ij,l}{P}_{k}-{\varepsilon }_{ij}{P}_{k,l})$$
$${f}_{Elastic}=\frac{1}{2}{C}_{ijkl}{\varepsilon }_{ij}{\varepsilon }_{kl}$$
$${f}_{Es}=-{q}_{ijkl}{\varepsilon }_{ij}{P}_{k}{P}_{l}$$

where \({\alpha }_{ij}\) and \({\alpha }_{ijkl}\) are Landau coefficients, \({G}_{ijkl}\) gradient coefficient, \({f}_{ijkl}\) flexoelectric coefficient, \({C}_{ijkl}\) electrostrictive coefficient, \({q}_{ijkl}\) elastic constant, and \({\kappa }_{0}\) dielectric permittivity. \({\varepsilon }_{ij}\) denotes strain component and Ei the electric field component derived from Ei = \({\varphi }_{,i}\), where φ is the electric potential. Each energy expression and corresponding parameters can be found in previous studies53. In addition, the mechanical (\({\sigma }_{ij,j}=0\)) and electric (\({D}_{i,i}=0\)) equilibrium conditions must be satisfied for the body-force-free and body-charge-free system. A finite-element method was employed to solve the above equations to obtain the spatio-temporal evolution of polarization, stress, and electric field.

For simplicity, a set of 120Δx × 120Δx × 11Δx uniform mesh was applied, where Δx represents 0.4 nm. Periodic boundary conditions are set up along IP directions ([100] and [010]). A closed-circuit electric boundary condition was applied on the top and bottom surfaces to simulate the interior environment of one stacked SrTiO3 layer. A fixed displacement boundary condition was employed on the bottom of the film, while the stress on the top surface was free. The amplitude of the initial random noise of P was set as 0.001 C/m−2 for our polarization evolution.