Quantum geometry in quantum materials

Abstract

Quantum geometry, characterized by the quantum geometric tensor, plays a central role in diverse physical phenomena in quantum materials. This pedagogical review introduces the concept and highlights its implications across multiple domains, including optical responses, Landau levels, fractional Chern insulators, superfluid weight, spin stiffness, exciton condensates, and electron-phonon coupling. By integrating these topics, we emphasize the broad significance of quantum geometry in understanding emergent behaviors in quantum systems and conclude with an outlook on open questions and future directions.

Introduction

Quantum materials can be loosely defined as materials for which quantum mechanical effects manifest on a macroscopic scale. Two classes of quantum materials are paradigmatic: superconductors, and quantum Hall systems. For superconductors, electron-electron interaction is the key ingredient that leads to a macroscopic manifestation of quantum mechanics: such interaction causes the electrons to form phase-coherent Cooper pairs and this results in the Meissner effect and the dissipationless transport of charge current. For a two-dimensional (2D) electron gas in the integer quantum Hall regime, the perfect quantization of the Hall conductivity can be understood without explicitly taking any effects of electron-electron interactions into account. The integer quantum Hall effect (QHE) can be attributed to the unique topology of the free-electrons’ ground state¹. Such topology is encoded by the Chern number, C, given by the integral over the Brillouin zone of the Berry curvature that measures the change of the eigenstate’s phase as the momentum k is varied. The Berry curvature is part of the quantum geometry of a material. The QHE is the archetypical demonstration that quantum geometry is one of the key quantities that make a material a quantum material. As we will discuss in the remainder of the review, the Berry curvature turns out to be the anti-symmetric part of a tensor Q, the quantum geometric tensor (QGT)². In recent years it has become apparent that the symmetric part of this tensor, the quantum metric, g, also plays a key role in making a material, quantum. In a loose sense, the quantum metric appears to be the key quantity to understand the properties of materials in which both interactions and quantum geometry lead to macroscopic manifestations of quantum mechanics.

Quantum geometry is the geometric structure that naturally arises in the space of quantum states when such states depend on continuous parameters. One classic example of quantum geometry is the geometric phase of a quantum state under adiabatic evolution, in which case the continuous parameter is time. Within condensed matter physics, the continuous parameters are the components of the crystal momentum k, and quantum geometry refers to the geometric properties of the Bloch states, more precisely, the periodic part of the Bloch states $\left\vert {u}_{{\boldsymbol{k}}}\right\rangle$, which is the focus of this review. In this context, quantum geometry is also called band geometry, which includes long-known concepts such as the spread of the possible Wannier basis and the parallel transport of the electronic states.

The QGT (also called the Fubini-Study metric^3,4) has components:

$${Q}_{ij}({\boldsymbol{k}})=\langle {\partial }_{{k}_{i}}{u}_{{\boldsymbol{k}}}\vert [{\mathbb{1}}-\vert {u}_{{\boldsymbol{k}}}\rangle \langle {u}_{{\boldsymbol{k}}}\vert ]\vert {\partial }_{{k}_{j}}{u}_{{\boldsymbol{k}}}\rangle ,$$

(1)

where k_i is the ith component of the Bloch momentum k. For simplicity in writing Eq. (1) we have considered the case of a well-isolated band. The antisymmetric part of Q_ij(k) is iB_ij(k) = [Q_ij(k) − Q_ji(k)]/2 is related to the well known Berry curvature^5,6,7 F_ij(k) as B_ij(k) = −F_ij(k)/2, and the symmetric part g_ij(k) = [Q_ij(k) + Q_ji(k)]/2 is the quantum metric g given that corresponds to the metric for infinitesimal distances of the Hilbert-Schmidt quantum distance ${d}_{{\rm{HS}}}({\boldsymbol{k}},{{\boldsymbol{k}}}^{{\prime} })\equiv \sqrt{1-{\left\vert \langle {u}_{{\boldsymbol{k}}}| {u}_{{{\boldsymbol{k}}}^{{\prime} }}\rangle \right\vert }^{2}}$: ds² = ∑_i,jg_ij(k)dk_idk_j.

In two dimensions (2D) the integral over the Brillouin Zone (BZ) of B_xy(k)/π for the states of an occupied band is quantized and equal to the Chern number C. Conversely, the integral of g_ij(k) over the BZ is in general not quantized. However, in 2D, the positive semidefinite nature of Q (combined with inequality between trace and determinant) implies the following inequalities⁸

$${\rm{Tr}}g({\boldsymbol{k}})\ge 2\sqrt{\det g({\boldsymbol{k}})}\ge 2| {B}_{xy}({\boldsymbol{k}})|$$

(2)

We can introduce the tensor M ≡ (1/π)∫_BZd^dkQ(k). Because M is a sum of positive semidefinite tensors, it is itself positive semidefinite, and so $\det M\ge 0$. In 2D this leads to the inequality $\det ({\rm{Re}}(M))\ge \det ({\rm{Im}}(M))$, that can be seen as the integral equivalent of Eq. (2), and can be written as

$$\det \left[\frac{1}{\pi }\int\,{d}^{2}k\,g({\boldsymbol{k}})\right]\ge \det \left[\frac{1}{\pi }\int\,{d}^{2}k\,B({\boldsymbol{k}})\right]={C}^{2}.$$

(3)

Eq. (3) is a classic example of topology bounding quantum geometry from below⁹. The generalization of Eq. (3) leads to the lower bound of quantum geometry due to the Euler number^10,11,12,13 (the generalization is most natural in the Chern gauge for the Euler bands), and the lower bound has also been derived for obstructed atomic limits¹⁴ and chiral winding number¹⁵. Recently, the lower bound of quantum geometry has also been derived¹⁶ for the time-reversal protected Z₂ topology^17,18,19,20. These topological bounds allow us to put a lower bound to the geometric contribution to quantities such as the superfluid weight, as discussed in section “Superconductivity and superfluidity”.

The quantization in 2D of the integral of B_ij(k)/(2π) over the BZ, and its direct relation to the off-diagonal conductivity σ_xy¹ made the study of the physical consequences of the anti-symmetric part of Q(k) one of the most active areas of research in condensed matter physics for the past 20 years. It has led to several discoveries, such as topological insulators (TIs) and superconductors^21,22,23, Weyl and Dirac semimetals (SMs)^24,25,26, and, more recently, higher order topological materials^{27,28,29,30,31,32}. Conversely, the study of the symmetric part of Q(k) has received much less attention largely due to the fact until recently g(k) had only been shown to contribute to quantities that are challenging to measure experimentally, like the Hall viscosity^{33,34,35,36,37,38,39,40,41}, and the ‘Drude weight”, D, of the electrical conductivity of clean systems at zero temperature^{42,43,44,45,46}. Theoretical and experimental developments in the last few years have profoundly changed the situation. First, it was shown that g is related to nonlinear responses^{47,48,49,50,51,52,53,54,55,56,57}. It was further pointed out that g contributes to the superfluid weight (same as superfluid stiffness) ${\left[{D}_{{\rm{s}}}\right]}_{ij}$ of a superconductor^{10,58,59,60,61,62,63,64,65,66}, and that such contribution is significant when the bandwidth of the bands crossing the Fermi energy is smaller than the superconducting gap. Both nonlinear responses and ${\left[{D}_{{\rm{s}}}\right]}_{ij}$ could in principle be measured in realistic experimental conditions. In addition, the realization of magic-angle twisted bilayer graphene (TBG)^{67,68,69,70,71,72,73,74,75,76,77,78,79,80} and other twisted materials^81,82,83 introduced experimentally accessible systems with extremely flat bands exhibiting superconductivity and Fractional Chern Insulator/Ferromagnetism for which the quantum metric contribution to the superconducting ${\left[{D}_{{\rm{s}}}\right]}_{ij}$ or to the magnon stiffness can be large. These developments have motivated a huge interest in understanding the role of g_ij in quantum materials.

We now discuss more in detail how the quantum metric affects the properties of condensed matter systems. However, it is worth emphasizing that, besides condensed matter physics, the quantum metric plays a role in many other areas of physics, such as metrology, via the closely related concept of quantum Fisher information⁸⁴, non-equilibrium dynamics⁵⁰, and quantum information science^85,86.

Simple two-bands model

To gain some intuition about quantum geometry, it is useful to consider a simple two-band model described by the following Hamiltonian h(θ, φ) = d(θ, φ) ⋅ σ where σ = (σ_x, σ_y, σ_z) is the vector formed by the 2 × 2 Pauli matrices and

$${\boldsymbol{d}}=(\sin ({J}_{\theta }\theta )\cos ({J}_{\varphi }\varphi ),\sin ({J}_{\theta }\theta )\sin ({J}_{\varphi }\varphi ),\cos ({J}_{\theta }\theta )).$$

(4)

with J_θ, J_φ, two integers. The energy eigenvalues are ϵ_± = ±∣d(θ, φ)∣ = ±1. The eigenvalues ϵ_± do not depend on the variables θ and φ that parametrize h and therefore describe two flat bands. The variables θ and φ only affect the energy eigenstates: ${v}_{-}={(\sin ({J}_{\theta }\theta /2){e}^{-{\rm{i}}{J}_{\varphi }\varphi },-\cos ({J}_{\theta }\theta /2))}^{T}$, ${v}_{+}={(\cos ({J}_{\theta }\theta /2){e}^{-{\rm{i}}{J}_{\varphi }\varphi },\sin ({J}_{\theta }\theta /2))}^{T}$.

In the limit J_θ = J_ϕ = 0 also the eigenstates do not depend on θ and φ a and therefore the QGT is identically zero; the Hamiltonian describes a system with no quantum geometry. If we associate the degree of freedom described by the Pauli matrices to a sublattice degree of freedom, this case can be visualized as the situation in which in each energy eigenstate the electrons are completely localized on one of the two “sublattices” (entries of the spinor wavefunction), as shown schematically in Fig. 1a, c.

Fig. 1: Schematic spectra and states hybridization for a simple two-level model in which the two-fold degree of freedom is mapped to a sublattice, {A, B}.

a, b Energy eigenvalues as a function of θ for the case when J_θ = J_ϕ = 0 and J_θ = J_ϕ = 1, respectively. The colors show the occupation probability of sublattice A, P_A. c, d Representation of the lowest energy eigenstate distribution, as function of θ and φ, between sublattice A, represented by circles, and sublattice B, represented by squares, and the color showing the probability occupation of each sublattice, for J_θ = J_ϕ = 0 and J_θ = J_ϕ = 1, respectively. For the probabilities, P_A, P_B, on each sublattice we use the same color scheme used for P_A in (a, b).

When J_θ = J_ϕ = 1 the eigenstates depend on θ and φ and therefore the two bands possess a non-trivial quantum geometry. Using the expression above for v₋, and the definition Eq. (1) of the QGT (with k_i (i = 1, 2) running over the labels (φ, θ)) for the lowest band we find

$${Q}_{ij}(\varphi ,\theta )=\left(\begin{array}{ll}\frac{{\sin }^{2}\theta }{4}&{\rm{i}}\frac{\sin \theta }{4}\\ -{\rm{i}}\frac{\sin \theta }{4}&\frac{1}{4}\end{array}\right)$$

(5)

As expected the anti-symmetric part of the QGT is equal to −1/2 the Berry curvature⁸⁷. It is straightforward to verify that the inequalities in Eq. (2) are satisfied. Figure 1b, d illustrate the dependence of the eigenstates on the variables that parametrize the Hamiltonian: the dependence on θ and φ of the hybridization of the two degrees of freedom is responsible for a nonzero QGT. In the case of a sublattice, this can be visualized as a dependence on θ of the relative weight of the electron wave function between the sublattices, Fig. 1d.

For the case in which H describes electrons with a two-fold degree of freedom (sublattice, spin, or a generic orbital degree of freedom) a nonzero anti-symmetric part of Q_ij can result in a contribution to off-diagonal (transverse) transport coefficients. For instance, for J_θ = J_ϕ = 1 our simple model exhibits a Chern number C = 1⁸⁷ that can be associated with a non-zero and quantized Hall conductivity, and therefore the presence of delocalized electronic states. Similarly, the real part of Q_ij(k) can result in a contribution to diagonal (longitudinal) transport coefficients. For instance, in this example, in the metallic regime, when the band is not completely filled, one would expect the Drude weight D to be zero given that the band is completely flat and D ~ n/m*, with n the electron’s density and m* the electron’s effective mass, i.e., the curvature of the bands. However, the fact that g_ij(k) is nonzero results in a nonzero Drude weight^43,44, current noise⁸⁸, and a quantum geometric dipole⁸⁹, signaling that even if the band is completely flat, the system can respond, in the ideal case, to an external d.c. electric field. This is an indication that some states in this band are not completely on-site localized.

It is interesting to consider the limit J_φ = 0, J_θ = 1. In this case, h is parametrized by only one variable, θ, and therefore the Berry curvature, and so the anti-symmetric part of Q_ij(k), are identically zero. Nevertheless, the quantum metric is still not zero: g_θθ = 1/4. This simple example is an extreme case of the important fact that the quantum metric can be nonzero even if the Berry curvature is zero. As Eq. (2) shows, the quantum metric is only bounded from below by the Berry curvature.

Localization tensor

The QGT tensor is not limited to the single-band case—it can be defined for an isolated set of any number of bands. Of common interest is the set of occupied bands of a band insulator, for which the QGT reads

$${\left[{Q}_{ij}({\boldsymbol{k}})\right]}_{mn}=\left\langle {\partial }_{{k}_{i}}{u}_{m{\boldsymbol{k}}}\right\vert [{\mathbb{1}}-{P}_{{\boldsymbol{k}}}]\left\vert {\partial }_{{k}_{j}}{u}_{n{\boldsymbol{k}}}\right\rangle \,,$$

(6)

where ${P}_{{\boldsymbol{k}}}={\sum }_{n\in \text{occ.}}\vert {u}_{n{\boldsymbol{k}}}\rangle \langle {u}_{n{\boldsymbol{k}}}\vert$. (Throughout the review, we will focus on the case of fully-filled bands unless specified otherwise.) There is a very physical connection between the QGT in Eq. (6) and the localization of the electronic wavefunctions. This connection is imprinted in the linear response of materials when subjected to applied electric or magnetic fields; it follows naturally from the fact that the QGT defined in Eq. (6), when integrated over the Brillouin zone and traced over all occupied bands,

$${{\mathcal{Q}}}_{ij}=\sum _{n\in \,\text{occ.}}{\int}_{{\rm{BZ}}}\frac{{d}^{d}k}{{(2\pi )}^{d}}{\left[{Q}_{ij}({\boldsymbol{k}})\right]}_{nn}\,,$$

(7)

with d the spatial dimension. ${{\mathcal{Q}}}_{ij}$ can be recast as the ground state dipole-dipole correlator

$${{\mathcal{Q}}}_{ij}=\langle {r}_{i}(1-P){r}_{j}\rangle =\frac{1}{{\mathcal{V}}}{\rm{Tr}}[P{r}_{i}(1-P){r}_{j}P]$$

(8)

where $P={\sum }_{{\boldsymbol{k}}\in \text{BZ}}{\sum }_{n\in {\rm{occ}}.}\vert {\psi }_{n{\boldsymbol{k}}} \rangle \,\langle {\psi }_{n{\boldsymbol{k}}}\vert$ is the projector in the occupied subspace. Here $\langle {\boldsymbol{r}}\vert {\psi }_{n,{\boldsymbol{k}}}\rangle ={e}^{{\rm{i}}{\boldsymbol{k}}\cdot {\boldsymbol{r}}}\langle {\boldsymbol{r}}\vert {u}_{n,{\boldsymbol{k}}}\rangle$ is the Bloch state for the nth band, and henceforth, we choose the unit system in which

$$\hslash =1,$$

(9)

unless specified otherwise The position matrix elements are defined for Bloch states⁹⁰

$$\left\langle {u}_{n{\boldsymbol{k}}}\right\vert {r}_{i}\left\vert {u}_{m{{\boldsymbol{k}}}^{{\prime} }}\right\rangle ={\delta }_{{\boldsymbol{k}},{{\boldsymbol{k}}}^{{\prime} }}{\left[{A}_{i}({\boldsymbol{k}})\right]}_{mn}+i{\delta }_{mn}{\partial }_{{k}_{i}}{\delta }_{{\boldsymbol{k}},{{\boldsymbol{k}}}^{{\prime} }}\,,$$

(10)

where ${\delta }_{{\boldsymbol{k}},{{\boldsymbol{k}}}^{{\prime} }}={(2\pi )}^{d}\delta ({\boldsymbol{k}}-{{\boldsymbol{k}}}^{{\prime} })/{\mathcal{V}}$, ${\mathcal{V}}$ the total volume, and ${\left[{A}_{i}({\boldsymbol{k}})\right]}_{nm}=i\left\langle {u}_{n{\boldsymbol{k}}}\right\vert {\partial }_{{k}_{i}}\left\vert {u}_{m{\boldsymbol{k}}}\right\rangle$. The projector 1—P guarantees that Eq. (8) is gauge independent, by removing the diagonal contributions of the position operator. The integrated geometric tensor ${{\mathcal{Q}}}_{ij}$, whose symmetric part and anti-symmetric parts contain the integrated quantum metric and the Chern number of the ground state, can be interpreted as a localization tensor originating in the uncertainty of the position operator in the ground state⁴². First discussed by Kohn⁹¹, a divergent ${{\mathcal{Q}}}_{ij}$ would correspond to an infinite sensitivity of the ground state to a shift in momentum or a twist in boundary conditions. Among other definitions based on a spectral gap, this definition based on spatial delocalization of the wavefunction is one of the most suited ways to discriminate between a metal and an insulator. Its geometrical interpretation was then put forward by Resta⁹², and Souza, Wilkens, and Martin⁹³.

The localization tensor has deep consequences in both the constraints on the basis functions that can be used to describe a given band subspace. To understand the spatial extent of electronic bands, it is useful to adopt Wannier states, localized in real space to describe Bloch bands⁹⁴. They are defined as

$$\left\vert {w}_{n{\boldsymbol{R}}}\right\rangle =\frac{1}{\sqrt{N}}\mathop{\sum }\limits_{{\boldsymbol{k}}\in {\rm{BZ}}}{e}^{-i{\boldsymbol{k}}\cdot {\boldsymbol{R}}+\varphi ({\boldsymbol{k}})}\left\vert {\psi }_{n{\boldsymbol{k}}}\right\rangle$$

where N is the number of lattice sites, and φ_n(k) is a momentum-dependent phase redundancy, which can be tuned to optimize the localization of the Wannier states $\left\vert {w}_{n{\boldsymbol{R}}}\right\rangle$. This localization is characterized by the localization functional $\Omega ={\sum }_{n}[\langle {w}_{n{\bf{0}}}\vert {r}^{2}\vert {w}_{n{\bf{0}}}\rangle -\langle {w}_{n{\bf{0}}}\vert {\boldsymbol{r}}{\vert {w}_{n{\bf{0}}}\rangle }^{2}]$⁹⁵. While not gauge independent, Ω can be separated into a gauge independent part that coincides with the trace over spatial indices of the integrated quantum metric, often referred to as ${\Omega }_{I}=({\mathcal{V}}/N){\rm{Re}}({\rm{Tr}}{\mathcal{Q}})$, and a gauge dependent part $\tilde{\Omega }$ (see Supplementary Information A). The gauge-dependent part $\tilde{\Omega }$ diverges in the absence of exponentially localized Wannier functions. This happens for metals, or in the presence of a nonzero Chern number⁹⁶. An extended review of these results is presented in Supplementary Information A.

Quantum geometry and correlated states

Superconductivity and superfluidity

Superconductivity is fundamentally influenced by the spread of the Wannier states and hence by quantum geometry: the superfluid weight (superfluid stiffness) D_s has a contribution that arises from quantum geometry, D_s,geom, in addition to the conventional one D_s,conv given by band dispersion⁵⁸:

$${D}_{s}={D}_{{\rm{s,conv}}}+{D}_{{\rm{s,geom}}}\,.$$

(11)

The superfluid weight relates the DC, long-wavelength supercurrent J to the static, long-wavelength, transverse vector potential ${\boldsymbol{{\mathcal{A}}}}$:

$${J}_{i}=-\sum _{j}{\left[{D}_{{\rm{s}}}\right]}_{ij}{{\mathcal{A}}}_{j}$$

(12)

and needs to be positive-definite for supercurrent to exist. Moreover, in the simplest picture, large ${{\mathcal{D}}}_{{\rm{s}}}={\rm{Tr}}[{D}_{{\rm{s}}}]/d$ means a large critical current of superconductivity, ${j}_{{\rm{c}}}\propto {{\mathcal{D}}}_{{\rm{s}}}/\xi$, where ξ is the coherence length of the superconductor. In two dimensions, D_s also determines the critical temperature of superconductivity since the Berezinskii-Kosterlitz-Thouless (BKT) temperature T_BKT depends on ${{\mathcal{D}}}_{{\rm{s}}}$. In 3D the penetration depth λ is directly proportional to $1/\sqrt{{{\mathcal{D}}}_{{\rm{s}}}}$. A finite value of λ is crucial for the Meissner effect. Given that ${{\mathcal{D}}}_{{\rm{s}}}$ is the proportionality constant entering the London equation Eq. (12), the equation responsible for the Meissner effect, and its relation to T_BKT in 2D and to λ in 3D, it is a fundamental defining quantity of superconductivity. Interestingly, D_s has an intrinsic connection to quantum geometry.

The quantum geometric contribution of superconductivity becomes dramatic in a flat Bloch band. The conventional contribution of superfluid weight D_s,conv is inversely proportional to the effective mass of the band and vanishes in a flat band. Superconductivity in a flat band is thus completely based on quantum geometric effects. Such effects arise since D_s is defined via the current-current correlator⁹⁷, and the current operator of a multiband system has two parts (m,n are band indices and i = x, y, z):

$$\left\langle {u}_{m{\boldsymbol{k}}}\vert {J}_{i}\vert {u}_{n{\boldsymbol{k}}}\right\rangle ={\delta }_{mn}{\partial }_{{k}_{i}}{\epsilon }_{n{\boldsymbol{k}}}+({\epsilon }_{m{\boldsymbol{k}}}-{\epsilon }_{n{\boldsymbol{k}}})\left\langle {\partial }_{{k}_{i}}{u}_{m{\boldsymbol{k}}}\vert {u}_{n{\boldsymbol{k}}}\right\rangle ,$$

(13)

Here k is the momentum and ϵ_nk gives the dispersion for the nth band. The last term, which contains a derivative of the Bloch function, connects D_s to the quantum geometric quantities defined in the introduction.

Full formulas of D_s = D_s,conv + D_s,geom are available in the literature^58,60,98. The result is the following in the limit of N_f completely flat degenerate bands, isolated from other bands by large gaps compared to the attractive interaction energy scale ∣U∣, assuming zero temperature and time-reversal symmetry, and under so-called uniform pairing condition where pairing is the same in all the flat band orbitals:

$${[{D}_{s}]}_{ij}=\frac{4{e}^{2}{N}_{{\rm{f}}}}{{(2\pi )}^{d-1}{N}_{{\rm{orb}}}}| U| f(1-f){{\mathcal{M}}}_{ij}^{\min },$$

(14)

$${{\mathcal{M}}}_{ij}^{\min }=\frac{1}{2\pi }{\left[\int{{\rm{d}}}^{d}{\boldsymbol{k}}{g}_{ij}({\boldsymbol{k}})\right]}_{\min }.$$

(15)

Here, f ∈ [0, 1] is the filling fraction of the isolated flat band, N_orb is the number of orbitals where the flat band states have a nonzero amplitude, − e is the electron charge, d is the space dimension, and g_ij(k) is the quantum metric defined in the introduction. The label “min” refers to the integrated quantum metric whose trace is minimal under variation of the orbital positions while keeping all other parameters, e.g., hoppings, the same. (Equivalently, it is minimal under the change of Fourier transformation convention of the atomic basis, which is equivalent to the embedding choice.) This result is in striking contrast with the simple Bardeen-Cooper-Schrieffer (BCS) formula for a single band, ${{\mathcal{D}}}_{{\rm{s}}}={e}^{2}{n}_{{\rm{s}}}/{m}^{* }$, where n_s is the density of Cooper pairs (superfluid density) and m* the effective mass. The result (14)–(15) was essentially derived in ref. ⁵⁸, but in ref. ⁹⁸ it was noted that the ${{\mathcal{M}}}_{ij}$ of the original work⁵⁸ has to be replaced by ${{\mathcal{M}}}_{ij}^{\min }$ because the quantum metric is an embedding (or, basis) dependent quantity⁹⁹ while D_s and ${{\mathcal{M}}}_{ij}^{\min }$ are embedding-independent^98,100. These results are derived within multiband mean-field theory, but the general idea has been confirmed by exact, perturbative and beyond-mean-field numerical calculations^{15,59,60,101,102,103,104} of some carefully chosen attractive interacting flat band models (see the reviews^63,64,105 for more examples). We note that in most of the beyond-mean-field numerical calculations, what one directly calculates is the stiffness of a SU(2) pseudo-spin ferromagnet, which after adding additional terms becomes a superconductor. In refs. ^106,107, it has been shown that many of the analytical results presented in^58,98 can be extended to several cases of non-uniform pairing and the results remain essentially similar. The effect of closing the gap between the flat band and other bands has been studied as well, see ref. ¹⁰⁸ and references therein.

How should one physically understand the role of the quantum metric in flat-band superconductivity? One way to gain intuition is to consider the two-body problem, the Cooper problem¹⁰⁹, in a flat band. In this case there is a massive degeneracy which, however, is lifted by the interaction between the two particles: the bound pair becomes dispersive, with an inverse effective mass given by the quantum metric¹¹⁰! Similar to the Fermi surface Cooper problem, the two-body problem in the flat band gives essentially the same answer as the mean-field approach. Further insight into why quantum geometry may be critical for pair mobility is provided by its connection to the localization of Wannier functions, as discussed in the introduction⁹⁴. Indeed, by projecting the interacting multiband model to a flat band¹⁵ one can show that interactions induce pair hopping that is linearly proportional to the interaction U—and overlap integrals of Wannier functions at neighboring sites. In 2D this relates nicely to the lower bound of superconductivity derived in ref. ⁵⁸: ${{\mathcal{D}}}_{{\rm{s}}}\ge | C|$ (in appropriate units), where C is the spin Chern number of a time-reversal symmetric system; as Wannier functions cannot be exponentially localized in a topological band⁹⁶, their overlaps guarantee interaction-induced motion and eventually superconductivity. The role of Wannier functions in superconductivity offers routes for deriving upper bounds too. For example, the optical spectral weight of a superconductor and superfluid weight were considered in refs. ^111,112, where quantum geometric quantities appeared as key quantities. For further information and discussion of the large literature on this topic, we refer to existing review articles^63,64,105. Here we would like to mention only a few interesting developments published after these review articles.

In refs. ^113,114,115, a Ginsburg-Landau theory was developed for multiband systems, with quantum geometry in focus. According to these works, in the isolated flat band limit and with uniform pairing, the coherence length of the superconductor is determined by the minimal quantum metric. For non-isolated flat bands, the coherence length can be smaller than the quantum geometry length¹¹⁶. Furthermore, for strong interactions the Cooper pair size and the coherence length may be distinct, resembling the BEC-end of the BEC-BCS crossover¹¹⁷. In ref. ¹¹⁸ a definition of the coherence length based on the exponential decay length of the anomalous Green’s function was used, leading to a result that differs from the minimal quantum metric. The decay of the pair correlation function or the anomalous Green’s function can be non-trivial in flat bands. For example, they may completely vanish beyond a few lattice sites, instead of exhibiting a continuous decay^118,119. This happens in flat bands that host compactly localized Wannier functions (such as obstructed atomic limits¹²⁰).

The apparent discrepancy between the coherence length results can be explained through the subtlety of the definition of this concept in flat bands. The mean-field anomalous Green’s function and the pair correlation function may decay rapidly in length scales different from the minimal quantum metric, however, when one includes fluctuations of the order parameter and calculates the spread of the pair correlation function, a coherence length given by the minimal quantum metric is obtained. Fluctuations are included in the Ginzburg-Landau formalism like in the calculation of the superfluid weight (stiffness), so, naturally, dependence on quantum geometry emerges from both. Reference¹¹⁹ studied a superconductor-normal-superconductor (SNS) Josephson junction where the normal part is a flat band system longer than the coherence length. It was found that supercurrent over the junction was only possible by contributions from nearby dispersive bands or by interaction-mediated transport.

One might worry that disorder would kill flat band superconductivity. However, D_s for a flat band, s-wave, superconductor with non-trivial quantum metric appears as robust against non-magnetic disorder as D_s for a superconductor with dispersive bands and trivial quantum metric¹²¹. Interestingly, the dispersive band superfluid weight acquires a geometric contribution in the presence of disorder that at low disorder strengths compensates the suppression of the conventional contribution; this is intuitive as disorder hinders conventional ballistic transport given by the band dispersion. Quantum geometry has been shown to be relevant for correlations in disordered systems also in other contexts than superconductivity^122,123. Another salient feature of flat band superconductors is that quasiparticles seem to be localized¹²⁴. Finally, it is important to keep in mind that although the quantum geometry of the band guarantees superconductivity to be possible, sometimes another competing order, e.g., a charge density wave or phase separation, can win¹²⁵ even with attractive interactions. Quantum geometry can also lead to pair-density wave order instead of superconductivity, signified by a negative superfluid weight^126,127. Quantum geometry may also affect the Kohn-Luttinger mechanism of superconductivity because the form factor in the polarization function responsible for screening depends on the geometric properties of the wave functions^128,129; remarkable enhancements of the critical temperature were found in these works for certain model systems.

Spin-wave stiffness

The close analogy between superconductivity and the XY model^130,131 suggests the connections shown in the previous section between quantum geometry and the properties of superconductors should be relevant for ferromagnetic states in which the ground state is characterized by an order parameter M that breaks a continuous spin, or pseudospin, symmetry. In the continuum limit, this can be seen by considering the effective Ginzburg-Landau action of a ferromagnet

$$S={S}_{0}({\boldsymbol{M}})+\beta \frac{1}{2}\int\,d{\boldsymbol{r}}{{\mathcal{D}}}_{s}^{(s)}[| \nabla {M}_{x}{| }^{2}+| \nabla {M}_{y}{| }^{2}+| \nabla {M}_{z}{| }^{2}]$$

(16)

where M is the magnetization and S₀ is the part of the action that does not depend on the gradient of M. In Eq. (16), we have assumed the spin stiffness tensor to be diagonal and isotropic: ${[{D}_{s}^{(s)}]}_{ij}={{\mathcal{D}}}_{s}^{(s)}{\delta }_{ij}$.

Similar to superconductivity, the spin-stiffness ${[{D}_{s}^{(s)}]}_{ij}$ can be obtained within linear response theory by calculating the spin susceptibility, ${\chi }_{ij}^{(s)}({\boldsymbol{q}},\omega )$, and then taking the limit ω = 0, q → 0: ${[{D}_{s}^{(s)}]}_{ij}=\mathop{\lim }\nolimits_{{\boldsymbol{q}}\to 0}{\chi }_{ij}^{(s)}({\boldsymbol{q}},\omega =0)$. Starting from a microscopic model, it is straightforward to see that the expression of χ^(s)(q, ω = 0) up to order q², involves the first and second derivatives of the Hamiltonian with respect to the momentum k. For single-band systems, such derivatives lead only to the appearance of derivatives with respect to k of the energy eigenvalues, similarly to the first term of Eq. (13). However, for multi-band systems, the second term in Eq. (13) appears, involving the quantum geometry of the Bloch states.

In superconductors, the superfluid stiffness is directly proportional to the superfluid weight and so it can be directly probed by measuring the current response to an external vector field. For ferromagnetic states, the most straightforward way to probe QGT’s effects is by probing the dispersion of the low-energy spin-waves, i.e., the Goldstone modes associated to the continuous symmetry spontaneously broken by the ground state, something that is not straightforward to do for superconductors¹³² also due to the Anderson-Higgs mechanism. For 2D XY ferromagnets, the effect of the quantum geometry can potentially also be inferred indirectly by measuring T_BKT, as discussed in the case of superconductors.

So far the role of quantum geometry in ferromagnetic systems—and especially in realistic experimental systems has not received much attention. Recent works have investigated the connection between ${[{D}_{s}^{(s)}]}_{ij}$ for specific systems^{133,134,135,136,137}. One can obtain an exact solution of the ferromagnetic ground state and its excitations of a flat band subject to a repulsive interaction in the condition that makes the projected orbital occupation the same¹³⁸ (analogous to the uniform pairing condition for superconductors). In this case, the single particle charge excitations are flat. However, the spin wave spectrum can be solved exactly and it can be shown, in this class of models, that the spin stiffness is the same as the integrated minimal quantum metric¹³⁸. In moiré systems, projected Hamiltonians^139,140 do not satisfy the uniform pairing condition, and as such even the single-particle dispersion on top of the ferromagnetic state at integer fillings involves the quantum distance¹³⁴. To exemplify the effect of the quantum metric in ferromagnets in Supplementary Information B we describe the key results for 2D moiré systems^133,134 and saturated ferromagnetism¹³⁷.

Bose-Einstein condensation

Superconductivity is closely related to the physics of Bose-Einstein condensation (BEC) of electron pairs, highlighted by the smooth BCS-BEC crossover and a common mean-field ground state for both regimes. Nevertheless, when it comes to the role of quantum geometry, the BEC limit may show quite a different phenomenology from that of superconductors. Quantum geometry describes how the properties of quantum states vary throughout the Brillouin zone. This raises the question: Does quantum geometry have any impact on a (BEC) that occupies a single quantum state? For a non-interacting BEC at equilibrium, quantum geometry is indeed irrelevant. However, when interactions are introduced and excitations are considered, quantum geometry begins to play a significant role. Another natural question is: what is the bosonic counterpart of superconductivity in a flat band? Specifically, where would bosons condense in a flat band where all energies are degenerate? Once again, interactions change the scenario. Due to Hartree-type renormalization of the bands, certain momenta can acquire slightly lower energies, making them favorable sites for condensation^141,142. This leads to an important question: under what general conditions are such condensates stable? Given that the energies are essentially degenerate, even minimal interactions might excite particles to arbitrary momenta, potentially destabilizing the condensate.

Quantum geometry also plays a crucial role in Bose-Einstein Condensates (BECs). In a weakly interacting BEC within a flat band, the speed of sound-which must be positive to ensure superfluidity-is proportional to the interaction energy U and the square root of a generalized quantum metric^143,144. Note again the linear dependence on the interaction energy U, typical for flat band phenomena: this is an immediate consequence of the existence of only one energy scale. This should be contrasted to the case of a usual dispersive band where the speed of sound is proportional to $\sqrt{U}$. The stability of a BEC can be also determined by calculating the fraction of excitations, due to weak interactions, that result in a finite particle density outside the condensate state, n_ex(k). This is also called the quantum depletion and was found¹⁴³ to be given by the condensate quantum distance${\tilde{d}}_{c}({\boldsymbol{q}})$ (similar to the Hilbert-Schmidt quantum distance d_HS defined in the introduction), and, in the limit of vanishing interaction, is related to n_ex(k) via the equation

$${\rm{lim}}_{U\to 0}{n}_{ex}({\boldsymbol{k}})=\frac{1-{\tilde{d}}_{c}({\boldsymbol{q}})}{2{\tilde{d}}_{c}({\boldsymbol{q}})},$$

(17)

where q = k − k_c and ${\tilde{d}}_{c}({\boldsymbol{q}})$ includes overlaps of the Bloch state at the condensate momentum k_c with states at other momenta. The physical intuition is that depletion of the condensate to excitations is limited not by energetic reasons as in dispersive bands, but by a finite quantum distance between the initial (ground) and the excited state. The result (17) also implies that quantum excitations on top of the mean-field condensate do not vanish in the limit of small interactions; flat bands are thus an ideal platform for studying the beyond-mean-field physics of condensates. The quantum distance appears instead of the quantum metric because the quantum depletion includes finite momentum excitations. The quantum metric on the other hand is an infinitesimal measure and corresponds to long-wavelength limit quantities such as the speed of sound, and supercurrent in the case of superconductors. Quantum geometry manifests also in the superfluid weight of BEC^{144,145,146,147}.

Exciton condensates

An exciton is a bosonic quasiparticle formed by an electron (e), bound to a hole (h). At low temperatures, a gas of excitons can form an exciton condensate (EC)^148,149. Due to the effective interaction among excitons, resulting from the Coulomb interaction, an EC will exhibit superfluidity. An EC can be regarded as superfluid BEC, see section “Bose-Einstein condensation”. However, it is also analogous to a superconducting state, or a ferromagnetic state, as we discuss in this section.

Shortly after the proposal that electron-hole pairs could form an exciton condensate (EC), it was suggested that spatially separating the electrons and holes would enhance the stability of the EC by reducing the rate of electron-hole recombination¹⁵⁰. This can be realized in 2D systems formed by an e-doped 2D layer and h-doped 2D layer separated by a high-quality, thin, dielectric film^150,151. In these double-layer structures, when the doping is sufficiently low, and gates sufficiently far away, so that screening effects are minimized^152,153, an EC can form when the carriers’ intralayer distance $\approx \sqrt{1/n}$ is comparable to the interlayer distance d. In such conditions, the layer degree of freedom can be treated as a pseudospin degree of freedom, or as the particle-hole degree of freedom of a superconductor. In the first case the EC can be regarded as an easy-plane ferromagnet (see section “Spin-wave stiffness”) in the second case as a “charge neutral superconductor”.

We can define the superfluid weight of an EC, in analogy to the definition introduced for a superconductor, as the long-wavelength, zero-frequency, response of the system to a transverse vector field having opposite directions for electrons and holes. For an EC formed in a 2D double-layer this corresponds to having a vector field ${\boldsymbol{{\mathcal{A}}}}$ in the top layer and a vector field $-{\boldsymbol{{\mathcal{A}}}}$ in the bottom layer. It is then straightforward to derive the expression of ${\left[{D}_{s}\right]}_{ij}$ as done for the superconducting case, (roughly speaking) by reinterpreting the particle-hole index^58,60,98, as the layer index^63,154. In this analogy, the superconducting order parameter Δ corresponds to the mean-field order parameter describing the EC, ${\Delta }_{\alpha {\alpha }^{{\prime} },{\boldsymbol{r}}{{\boldsymbol{r}}}^{{\prime} }}^{{\rm{EC}}}\equiv \langle {c}_{\alpha {\boldsymbol{r}}T}^{\dagger }{V}_{{\rm{TB}}}({\boldsymbol{r}}-{{\boldsymbol{r}}}^{{\prime} },d){c}_{{\alpha }^{{\prime} }{{\boldsymbol{r}}}^{{\prime} }B}\rangle$, where α (${\alpha }^{{\prime} }$) is a general orbital degree of freedom, T, B are the indices denoting the top and bottom layer, respectively, and ${V}_{{\rm{TB}}}({\boldsymbol{r}}-{{\boldsymbol{r}}}^{{\prime} },d)$ is the effective interlayer Coulomb interaction with d the distance between the layers.

Similar to superconductors, the critical temperature T_c for forming an exciton condensate (EC) is enhanced in flat-band systems. As the bands become flatter, the conventional contribution to the EC’s superfluid weight and stiffness is suppressed, reducing the neutral superfluid current and making the EC unstable to thermal and quantum fluctuations despite a high T_c. This changes when flat bands have nontrivial geometry: a geometric contribution to the superfluid weight ${\left[{D}_{{\rm{s}}}\right]}_{ij}$ emerges, strengthening the stability of the EC^154,155.

This situation is most apparent in the proposal for an EC formed in a double layer formed by TMDs¹⁵⁵, or by an e-doped TBG and h-doped TBG separated by a thin dielectric layer¹⁵⁴, as schematically shown in Fig. 2a. In this case, for certain twist angles, the conventional contribution to ${\left[{D}_{{\rm{s}}}\right]}_{ij}$ can even be negative, as shown in Fig. 2b. However, for the same twist angle, the geometric contribution is positive and very large guaranteeing the stability of the EC, Fig. 2b–d. We see that for an EC the effect of the quantum geometry of the bands can be even more significant than for superconductors.

Fig. 2

Geometric contributions to the superfluid weight. a Schematics of a double layer formed by two TBGs in which an EC state is expected to form when the chemical potential in the top layer μ_T is equal and opposite to the chemical potential in the bottom layer μ_B. b Dependence on twist angle of the conventional and geometric contributions to the superfluid weight D_s of an EC formed in a double TBG, for fixed chemical potential μ ≡ μ_T = −μ_B = 0.2 mev. c, d Dependence on μ, for different twist angles, of conventional and geometric contributions, respectively, to D_s. Adapted from ref. ¹⁵⁴.

Electron-phonon coupling

One main interaction in solids is the electron-phonon coupling (EPC), which is crucial for various quantum phases, and in particular for superconductivity^156,157,158. It is conceptually intriguing to ask if the EPC has any clear relation to quantum geometry, in particular in the generic case where the electrons have a Fermi surface - characteristic of the great majority of known superconductors. Uncovering this relationship could be crucial for identifying new superconductors, considering the vast array of topological materials^{159,160,161,162,163,164,165,166}.

Recently, ref. ¹⁶⁷ revealed a direct connection between electron band geometry/topology and the bulk electron-phonon coupling (EPC). The study introduces a “Gaussian approximation” where this connection becomes explicit. Within this approximation, a quantum geometric contribution to the electron-phonon coupling constant λ can be naturally distinguished from an energetic contribution. The EPC is the sum of the two (up to a cross-term). (See Supplementary Information C for more details). Explicitly, the geometric contribution is supported by the quantum metric or an extended orbital-selective version of the quantum metric^110,167, and is bounded from below by the topological contributions over the electronic Fermi surface.

The Gaussian approximation can naturally be applied to graphene, where the short-range hopping and the symmetries make it exact, and its generalized version can naturally describe another well-known superconductor, MgB₂. Combined with the ab initio calculation, ref. ¹⁶⁷ finds that the quantum geometric (topological) contribution to λ accounts for roughly 50% (50%) and 90% (43%) of the total EPC constant λ in graphene and MgB₂, respectively. The large contributions from quantum geometry to EPC can be intuitively understood: the quantum geometry affects the real-space localization of the electron Wannier functions, and then affects how the electron hopping changes under the motions of ions. This is an important part of the electron-phonon coupling (and in many cases—such as graphene and MgB₂— is the largest part of EPC).

The analysis for graphene in ref. ¹⁶⁷ can be tested by measuring the phonon linewidth by Raman spectroscopy as well as measuring phonon frequencies by the inelastic x-ray scattering. Reference ¹⁶⁸ found that the quantum metric modifies the electron-phonon coupling by enhancing small-angle scattering. The formalism in ref. ¹⁶⁷ can in principle also be applied to other systems such as Weyl semimetals. One major future direction is to develop a general framework that relates quantum geometry to the bulk EPC for realistic systems. Such a study may provide new guidance for the future search for superconductors from the perspective of quantum geometry.

Fractional Chern insulators

Fractional Chern insulators (FCIs) are zero-magnetic-field analogs of the fractional quantum Hall effect. By definition, FCIs should exhibit fractionally quantized Hall resistance and vanishing longitudinal resistance under zero external magnetic field. FCIs were first proposed in toy models^169,170,171, where fractionally filled nearly flat Chern bands^172,173 (in zero magnetic field) and repulsive interactions are identified as the essential ingredients.

Recall that the fractional quantum Hall effect requires two ingredients: Landau levels (from an external magnetic field) and repulsive interactions. As the repulsive interaction (e.g., Coulomb interaction) is ubiquitous, the special ingredient for the FQH is the Landau level. Therefore, one of the routes (but not the only one) to realizing FCIs is to mimic Landau levels without external magnetic fields.

In this route, quantum geometry plays an important role in assessing how closely a realistic set of bands approximates the Landau levels. Besides its exact flatness and nonzero Chern numbers, the nth Landau level (n = 0, 1, 2, 3, . . .) is characterized by the following three geometric properties: (i) uniform (in momentum space) quantum metric, (ii) uniform (in momentum space) Berry curvature, and (iii) the trace of the quantum metric equals (2n + 1) times the absolute value of the Berry curvature^58,174. This momentum independence of the LL quantum geometry enabled detailed analytical understanding of the LL physics even in the presence of strong electron-electron interactions¹⁷⁵. Therefore, the best system for FCIs is the one that hosts nearly flat Chern bands that nearly satisfy those three geometric properties of the Landau levels. References ^{176,177,178,179} suggest that a flat Chern band is already favorable to realize FCIs even as long as an integrated version of (iii) is satisfied, even if (i) and (ii) conditions are strongly violated. (See also refs. ^{8,180,181,182,183}). Reference ^176,177 promote a concept called “ideal Chern bands”, which motivate the study of analogy in other topological bands, such as ideal Euler bands¹². However, the claims in refs. ^176,177 are made for special short-range interactions instead of generic repulsive interactions and for continuum rather than tight-binding models. In practice, as long as a realistic model hosts nearly flat Chern bands near the Fermi level, it is reasonable to consider the possibility of realizing FCIs in such a system, as shown in Supplementary Information D. Besides the way of mimicking Landau levels, one may also carefully desire the interaction to realize FCI in bands with zero Chern number¹⁸⁴.

Moiré systems are natural platforms for FCIs, since the quantum interference owing to moiré superlattice can easily lead to nearly flat topological bands. Upon spontaneous magnetizing due to interactions, these bands become nearly flat Chern bands. Remarkably, last year, FCIs were experimentally realized in twisted bilayer MoTe₂ at fillings −2/3 and −3/5, as well as integer Chern insulator at filling −1^{83,185,186,187,188,189,190,191}. Theoretically, the system indeed hosts nearly flat Chern bands that have relatively uniform quantum metric and Berry curvature in each spin subspace^{192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211}. Upon spin polarization (Stoner magnetization), the appearance of FCIs follows heuristically from the connection to a single Landau level^{198,199,200,205}. However, as shown in ref. ²⁰⁵, the understanding of the spin properties requires more bands to be considered, i.e., band mixing is essential.

Following the first discovery of FCIs in twisted bilayer MoTe₂, clear evidence of FCIs was later observed in rhombohedral multi-layer graphene-hexagonal boron nitride superlattice (at fractional electron fillings)^{212,213,214,215}, which has almost-fully-connected conduction bands. The theoretical understanding of experimental observations at fractional fillings in those systems requires careful study of various issues, such as the interaction scheme and the roles of temperature and disorder^{216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232}.

Physical responses

The quantum mechanical uncertainty in the position of electrons in solids, quantified by the QGT Q_ij(k) in Eq. (1) or its integrated version ${{\mathcal{Q}}}_{ij}$ in Eq. (8), leads to physical responses, which will be discussed in this section. For this section, we will resume ℏ explicitly.

Polarization fluctuations

Following fluctuation-dissipation theorems^93,233, the quantum fluctuations of a material’s polarization lead to dissipation in the presence of an external field. The electric polarization in solids is obtained²³⁴ by the expectation value of the position operator ${p}_{i}=e\left\langle {r}_{i}\right\rangle$, which can be reduced using Eq. (10) to the integral over the single band Berry connection ${\left[{A}_{i}({\boldsymbol{k}})\right]}_{nn}$ in the Brillouin zone. The position fluctuations in the ground state captured by the QGT are therefore associated with polarization fluctuations²³⁵. They are also hence associated with dissipation in the presence of perturbations that couple with the dipole operator, i.e., in the presence of an applied electric field ${{\mathcal{E}}}_{i}(t)={{\mathcal{E}}}_{i}{e}^{i\omega t}$, which modifies the polarization of the medium by the polarizability ${p}_{i}(t)={\sum }_{j}{\chi }_{ij}(t){{\mathcal{E}}}_{j}(t)$.

To draw the parallel between electric dipole fluctuations of the ground state and quantum geometry, it is convenient to introduce time-dependence to the integrated QGT Eq. (8): ${{\mathcal{Q}}}_{ij}(t-{t}^{{\prime} })=\langle {r}_{i}(t)(1-P){r}_{i}({t}^{{\prime} })\rangle$^236,237,238. This captures the fact that virtual interband (dipole) transitions leading to a nontrivial ${{\mathcal{Q}}}_{ij}$ are modified in the presence of ${{\mathcal{E}}}_{i}(t)$ by how much time the state populates the virtual bands and how much the position operator has evolved with the static Hamiltonian ${\mathcal{H}}$. At t = 0 it reduces to the integrated QGT (8), but away from the time origin, it has the expression

$$\begin{array}{lll}{{\mathcal{Q}}}_{ij}(t)\;=\;{{\mathcal{D}}}_{ij}(t)+\sum _{mn}{\int}_{{\rm{BZ}}}\frac{{d}^{d}k}{{(2\pi )}^{d}}\,{f}_{n{\boldsymbol{k}}}\left(1-{f}_{m{\boldsymbol{k}}}\right)\\\qquad\qquad\,\; \times \left({\left[{{\mathfrak{g}}}_{ij}({\boldsymbol{k}})\right]}_{nm}+{\rm{i}}{\left[{{\mathfrak{b}}}_{ij}({\boldsymbol{k}})\right]}_{nm}\right){e}^{i{\omega }_{mn{\boldsymbol{k}}}t}\end{array}$$

(18)

with ω_mnk = (ϵ_mk − ϵ_nk), ϵ_nk the dispersion of the nth band, and f_nk the occupation factor of the nth band at k. Here

$$\begin{array}{rcl}&&{\left[{{\mathfrak{g}}}_{ij}({\boldsymbol{k}})\right]}_{nm}=\dfrac{1}{2}{\left[{A}_{i}({\boldsymbol{k}})\right]}_{nm}{\left[{A}_{j}({\boldsymbol{k}})\right]}_{mn}+(i\leftrightarrow j)\\ &&{\left[{{\mathfrak{b}}}_{ij}({\boldsymbol{k}})\right]}_{nm}=\dfrac{1}{2{\rm{i}}}{\left[{A}_{i}({\boldsymbol{k}})\right]}_{nm}{\left[{A}_{j}({\boldsymbol{k}})\right]}_{mn}-(i\leftrightarrow j)\,,\end{array}$$

(19)

are the interband metric and curvature matrix elements. It also contains a Fermi surface contribution, ${{\mathcal{D}}}_{ij}(t)$, from the second term in the position operator of Eq. (10). The Fermi surface contribution is normally single-band and only present for metals ${{\mathcal{D}}}_{ij}(t)={F}_{ij}+it{D}_{ij}$, containing the Drude weight ${D}_{ij}={\int}_{{\rm{BZ}}}\frac{{d}^{d}k}{{(2\pi )}^{d}}{f}_{n{\boldsymbol{k}}}{\partial }_{{k}_{i}}{\partial }_{{k}_{j}}{\epsilon }_{n{\boldsymbol{k}}}$ from the dispersion curvature at the Fermi surface; as well as a divergent piece due to the discontinuity at the Fermi surface ${F}_{ij}={\int}_{{\rm{BZ}}}\frac{{d}^{d}k}{{(2\pi )}^{d}}{({f}_{n{\boldsymbol{k}}}^{{\prime} })}^{2}({\partial }_{{k}_{i}}{\epsilon }_{n{\boldsymbol{k}}})({\partial }_{{k}_{j}}{\epsilon }_{n{\boldsymbol{k}}})$. The latter term appears in the real and symmetric part of the geometric tensor, and explains the divergence of the metric for metals, even in single-band metals²³⁹. The singularities coming from the Fermi surface get regularized by the introduction of a scattering time τ. Finally we note that ${{\mathcal{Q}}}_{ij}(t)$ in Eq. (18) has Hermitian and anti-Hermitian components, ${{\mathcal{Q}}}_{ij}(t)={{\mathcal{Q}}}_{ij}^{s}(t)+i{{\mathcal{Q}}}_{ij}^{as}(t)$, which can in principle be independently measured²⁴⁰.

Nondissipative geometric response

The relationship between ${{\mathcal{Q}}}_{ij}$ and response functions such as the electric susceptibility χ_ij(ω) or the electric conductivity σ_ij(ω) follows naturally in the geometric picture. Namely, the antisymmetric (in both ij and ± t) ${{\mathcal{Q}}}_{ij}^{{\rm{as}}}(t)=({{\mathcal{Q}}}_{ij}(t)-{{\mathcal{Q}}}_{ji}(-t))/({\rm{i}})$ is directly related to the polarizability, $\chi (t)=(\pi {e}^{2})\Theta (t){{\mathcal{Q}}}^{as}(t)$^233,240. Noticing that J_i(t) = ∂_tp_i(t), it follows that the conductivity can be written compactly as²⁴¹

$$\begin{array}{rc}{\sigma }_{ij}(t)&=\frac{\pi {e}^{2}}{\hslash }\Theta (t){\partial }_{t}{{\mathcal{Q}}}_{ij}^{{\rm{as}}}(t).\end{array}$$

(20)

which fully reproduces the Kubo formula²³⁶. We introduce back ℏ explicitly. The two response functions are simply related in the frequency domain by σ_ij(ω) = −iωχ_ij(ω). It becomes particularly apparent that for insulators without a Fermi surface, D_ij = 0, the response at frequencies below the gap, and therefore non-dissipative, is strictly geometric, containing both longitudinal contributions with origin in the interband quantum metric matrix elements, g_ij, and Hall contributions from B_ij. To make it more apparent, we can expand Eq. (20) for ingap frequencies,

$$\begin{array}{lll}{\sigma }_{ij}(\omega )\;=\;\displaystyle\frac{{e}^{2}}{i\hslash }{\int}_{{\rm{BZ}}}\displaystyle\frac{{d}^{d}k}{{(2\pi )}^{d}}\mathop{\sum}\limits _{mn}{f}_{mn{\boldsymbol{k}}}\left({\left[{{\mathfrak{g}}}_{ij}({\boldsymbol{k}})\right]}_{nm}+{\rm{i}}{\left[{{\mathfrak{b}}}_{ij}({\boldsymbol{k}})\right]}_{nm}\right)\\\qquad\qquad\;\;\times (1+\omega /{\omega }_{mn{\boldsymbol{k}}}+\cdots \,)\,.\end{array}$$

(21)

Since f_mnk = (f_nk − f_mk) is anti-symmetric in band indices, it is apparent that each order in frequency it selects either the symmetric (quantum metric) or antisymmetric (Berry curvature) geometric matrix elements. Namely, in the DC limit, only the Berry curvature contributes. In two dimensions, we obtain the celebrated Thouless-Kohmoto-Nightingale-Nijs formula σ_ij = ϵ_ije²C/h¹ with ϵ_ij the Levi-Civita symbol. At linear order in ω, the non-dissipative geometric response—the static polarizability, or capacitance of the insulator, χ_ij—emerges from the matrix element of the quantum metric weighted by the inverse energy gaps²³⁶:

$${\sigma }_{ij}(\omega )=\frac{{e}^{2}}{h}\left(C{\epsilon }_{ij}+i\omega {\chi }_{ij}+\cdots \,\right).$$

(22)

Sum rules of dissipative response

In this part, we discuss several sum rule for band insulators. First note that, integrating the conductivity tensor σ_ij(ω) over all frequencies (up to ω dependent factors) can realize the instantaneous, t = 0, response. This realization leads to a sum rule that relates the integrated quantum metric

$${{\mathcal{G}}}_{ij}={\int}_{{\rm{BZ}}}\frac{{d}^{d}k}{{(2\pi )}^{d}}{g}_{ij}({\boldsymbol{k}})=\frac{1}{2}\left[{{\mathcal{Q}}}_{ij}+{{\mathcal{Q}}}_{ji}\right]$$

(23)

to the integrated real part of the longitudinal conductivity as

$${\rm{Tr}}\left[{\mathcal{G}}\right]=\frac{\hslash }{\pi {e}^{2}}\mathop{\int}\nolimits_{0}^{\infty }d\omega \sum _{i}\frac{{\rm{Re}}\left[{\sigma }_{ii}(\omega )\right]}{\omega }\,,$$

(24)

which is now recogonized as the Souza-Wilkens-Martin (SWM) sum rule⁹³. The quantum geometry can also be found in the static structure factor^233,242,243

$$\begin{array}{r}S({\boldsymbol{q}})=\dfrac{1}{2}\mathop{\sum}\limits_{ij}{q}_{i}{q}_{j}{{\mathcal{G}}}_{ij}+...\end{array}$$

(25)

Importantly, dissipation also occurs from the magnetic dipole moment of the medium, leading to Hall response. The simplest example is the Hall counterpart of the SWM sum rule, which is exactly the Kramers-Krönig counterpart of the DC Hall conductivity²⁴⁴ or the dichroic sum rule²⁴⁵ which captures the orbital magnetic moment of bound electrons permitted by the Berry curvature^246,247. Here ${\sigma }_{ij}^{H}(\omega )=[{\sigma }_{ij}(\omega )-{\sigma }_{ji}(\omega )]/2$.

Let us here present the generalization of these results by utilizing Eq. (20) in ref. ²³⁷. Different sum rules can be constructed by weighting different powers η of frequency. Each η captures an instantaneous property of the medium characterizing a given moment of the zero point motion of the ground state, or the various time derivatives of ${{\mathcal{Q}}}_{ij}(t)$,

$${{\mathcal{S}}}_{ij}^{\eta }=\mathop{\int}\nolimits_{0}^{\infty }d\omega \ \frac{{\sigma }_{ij}^{{\rm{abs}}}(\omega )}{{\omega }^{1-\eta }}=\frac{\pi {e}^{2}}{\hslash }{\left.{(-i{\partial }_{t})}^{\eta }{{\mathcal{Q}}}_{ij}(t)\right\vert }_{t = 0}.$$

(26)

The absorptive (or Hermitian) part of the conductivity ${\sigma }_{ij}^{{\rm{abs}}}={\rm{Re}}{\sigma }_{ij}^{L}(\omega )+i{\rm{Im}}{\sigma }_{ij}^{H}(\omega )$ (with ${\sigma }_{ij}^{L}(\omega )=[{\sigma }_{ij}(\omega )+{\sigma }_{ji}(\omega )]/2$) contains a symmetric and real part due to coupling of ${{\mathcal{E}}}_{i}$ aligned with the dipole moment of the dielectric medium, but also a Hall contribution from the coupling with the magnetic dipole, perpendicular to the field. Importantly in the sum rules ${{\mathcal{S}}}^{\eta }$, the entire ${{\mathcal{Q}}}_{ij}$ tensor Eq. (18) appears, not only ${{\mathcal{Q}}}_{ij}^{{\rm{as}}}$, and therefore, sum rules are sensitive to geometric quantities absent in nondissipative linear response, such as the integrated quantum metric⁹³.

Sum rules naturally divide into longitudinal and Hall contributions, where each η-time moment of ${{\mathcal{Q}}}_{ij}$ corresponds to a convolution with ${\omega }_{mn{\boldsymbol{k}}}^{\eta }$. In insulators, all moments are given exclusively in terms of geometric matrix elements and explicitly given by

$${{\mathcal{S}}}_{L,ij}^{\eta }=\frac{\pi {e}^{2}}{\hslash }\sum _{nm}{\int}_{{\rm{BZ}}}\frac{{d}^{d}k}{{(2\pi )}^{d}}{f}_{n{\boldsymbol{k}}}(1-{f}_{m{\boldsymbol{k}}}){\left[{{\mathfrak{g}}}_{ij}({\boldsymbol{k}})\right]}_{nm}{\omega }_{mn{\boldsymbol{k}}}^{\eta }$$

(27)

and

$${{\mathcal{S}}}_{H,ij}^{\eta }=\frac{\pi {e}^{2}}{\hslash }\sum _{nm}{\int}_{{\rm{BZ}}}\frac{{d}^{d}k}{{(2\pi )}^{d}}{f}_{n{\boldsymbol{k}}}(1-{f}_{m{\boldsymbol{k}}}){\left[{{\mathfrak{b}}}_{ij}({\boldsymbol{k}})\right]}_{nm}{\omega }_{mn{\boldsymbol{k}}}^{\eta }\,.$$

(28)

These fluctuation moments reflect various instantaneous properties of bound electrons in periodic lattices²⁴¹ and have been dubbed quantum weights in ref. ²⁴⁸. Let us now focus on 2D (d = 2), where ${{\mathcal{G}}}_{ij}$ has no units. Starting with the zeroth moment of longitudinal fluctuations ${{\mathcal{S}}}_{L,ij}^{0}=\pi {e}^{2}/\hslash {{\mathcal{G}}}_{ij}$, it captures exactly the integrated quantum metric, which is exactly the SWM sum rule⁹³. In Chern insulators or Landau levels, where projected of the position operators in orthogonal directions do not commute, the zeroth moment of Hall fluctuations is nonzero ${{\mathcal{S}}}_{H,ij}^{0}=-(\pi {e}^{2}/2h)C{\epsilon }^{ij}$. At η = 1, quantifying the speed of the polarization fluctuations is the f-sum rule, defining the total spectral weight, ${{\mathcal{S}}}_{L}^{1}=\pi {e}^{2}n/2m$; and the dichroic sum rule²⁴⁵, defining the orbital magnetic moment ${{\mathcal{S}}}_{H}^{1}={\mu }_{M}$, measured in ref. ²⁴⁹. Shot noise, that is zero temperature current fluctuations appear in the second fluctuation moment ${{\mathcal{S}}}_{L}^{2}$ and ${{\mathcal{S}}}_{H}^{2}$⁸⁸. Intriguingly, and also noticed early on²⁵⁰, metals and insulators don’t show remarkably different behavior in current fluctuations ${{\mathcal{S}}}^{\eta }$ with η > 0. However, ${{\mathcal{S}}}_{L}^{0}$, proportional to the integrated quantum metric, can qualitatively distinguish the two, completing the effort of Kohn to unambiguously distinguish a metal from an insulator⁹¹.

Spectral transfer and optical bounds

In metals not all ${{\mathcal{S}}}^{\eta }$ are well defined, but we can focus on the well-behaved first moment of the longitudinal response, the f-sum rule ${{\mathcal{S}}}_{L}^{1}$. This sum rule relates to nondissipative response by expanding the conductivity Eq. (20) to frequencies far above optical transitions, ${\sigma }_{ij}(\omega ) \sim i{\omega }_{p}^{2}/\omega$. Here ${\omega }_{p}^{2}=4\pi n{e}^{2}/m$^250,251, containing the electron density n and optical mass m. The optical mass is defined by ${{\mathcal{S}}}_{L}^{1}$, which has a Fermi surface contribution given by the Drude weight D_ij, the linear in t part of the ${{\mathcal{Q}}}_{ij}(t)$ Eq. (18), and a geometric component from the oscillations in ${{\mathcal{Q}}}_{ij}(t)$. Therefore, it is natural to separate the spectral weight into the charge stiffness n/m* obtained by the dispersion curvature at the Fermi level $\pi {e}^{2}n/{m}_{ij}^{* }={D}_{ij}$ and a geometric contribution from interband optical transitions, $\pi {e}^{2}n/2{m}_{ij}^{g}\equiv {\sum }^{{\prime} }{\omega }_{mn{\boldsymbol{k}}}{[{{\mathfrak{g}}}_{ij}({\boldsymbol{k}})]}_{nm}$^42,252,253 where ${\sum }^{{\prime} }$ is a shorthand for the sum and prefactor of Eq.(27). Therefore, we have that the optical mass of electrons, defined by the sum rule and therefore indicating the instantaneous mass of electrons (usually the bare electron mass²⁵⁴) relates to the Fermi surface electron mass and the geometric mass by

$$\begin{array}{r}\dfrac{1}{{m}_{ij}}=\dfrac{1}{{m}_{ij}^{* }}+\dfrac{1}{{m}_{ij}^{g}}\end{array}$$

(29)

The geometric contribution generally makes the electrons lighter at short time scales²⁵⁵. In the extreme example of flat bands with nontrivial quantum geometry, in which quantum interference creates a band with m* = ∞, the mass is purely geometric. This means that although semiclassical transport would be dictated by infinitely heavy electrons that do not conduct, at short time scales the electrons behave as if they have their original mass before the quenching of the band dispersion. A consequence, as discussed extensively above, is that electrons may still form a superconducting or excitonic condensate.

The transfer of weight from the Fermi surface mass m* to the geometric mass m^g can be best appreciated in Fig. 3 where we consider a square lattice tight-binding model and show the evolution of the total spectral weight and optical mass ${{\mathcal{S}}}_{L}^{1}$. The hoppings are tuned such that the bands evolve smoothly into a Lieb lattice. In this process, the Drude peak gets progressively reduced while the geometric mass is built up to the point that exactly in the Lieb limit, the band is perfectly flat and contributes only to the geometric weight.

Fig. 3: Transfer of optical spectral weight ${\rm{Re}}\,{\sigma }_{xx}(\omega )$ from the Fermi surface (Drude weight) to high frequencies from destructive interference in a frustrated hopping lattice (Lieb).

After cutting the hopping t_p, the resulting Hamiltonian has a flat band with no Drude weight, which was distributed to higher energies in the form of dipolar transitions between the flat and dispersive bands.

By looking at the different geometric responses within a unified framework, some identities become apparent. First, an insulator has a spectral gap E_g, which means the energy differences are bounded by ω_mnk > E_g/ℏ. It follows that for η > 0, ${S}_{L,ij}^{\eta }={\sum }^{{\prime} }{\omega }_{mn{\boldsymbol{k}}}^{\eta }{[{{\mathfrak{g}}}_{ij}({\boldsymbol{k}})]}_{nm}\ge (\pi {e}^{2}/{\hslash }^{2}V){E}_{g}^{\eta }{{\mathcal{G}}}_{ij}$. Similarly ${S}_{H}^{\eta }\ge (4{\pi }^{2}{e}^{2}/{\hslash }^{2}){E}_{g}^{\eta }C$. The signs are reversed for the negative powers of η. Focusing on the f − sum rule η = 1, we have $\pi {e}^{2}nd/m\ge (\pi {e}^{2}/{\hslash }^{2}){\rm{Tr}}{\mathcal{G}}{E}_{g}$, which gives ${\hslash }^{2}nd/m\ge {\rm{Tr}}{\mathcal{G}}{E}_{g}$, where d is the spacial dimension. This fact was pointed out by Kivelson in 1982²⁵⁶ for 1D insulators.

Combining these results with the trace condition Eq. (2) it can be observed that in the presence of a Chern number, it also holds that the energy gap is bounded by the inverse Chern number E_g≤ 2πn/(m∣C∣)²⁴⁴. More optical weight upper and lower bounds have been discussed since focusing on their geometric and topological origins^{257,93,235,241,248,258,259,252}.

Let us conclude this discussion with the example of free electrons in two dimensions under a magnetic field. From Kohn’s theorem²⁶⁰, Galilean invariance requires that all optical transitions happen exclusively across consecutive Landau levels separated by the cyclotron frequency ω_c. In this case, all sum rules become saturated²⁵⁸. In fact, they can be compactly expressed by ${{\mathcal{S}}}_{ij}^{\eta }=\frac{\pi {e}^{2}}{\hslash }C{\omega }_{c}^{\eta }({\delta }_{ij}+2\pi {\epsilon }_{ij})$ with δ_ij the Kronecker delta and ε_ij the Levi-Civita symbol, which saturates all the bounds²³⁷. In this case, all responses are quantized, including DC conductivity, capacitance, or magnetic moment. The quantum geometric effect on the optical response was also studied in the presence of correlations^261,262 and various other systems^{51,263,264,265,266,267}.

Landau levels

Semiclassical quantization of electronic states into Landau levels (LLs) under a magnetic field can be described by the generalized Onsager’s rule:

$$\begin{array}{r}{S}_{0}(\epsilon )=2\pi eB\left(n+\frac{1}{2}-\frac{{\gamma }_{\epsilon ,B}}{2\pi }\right),\end{array}$$

(30)

where S₀(ϵ) is the momentum space area of the closed semiclassical orbit at the energy ϵ, B is magnetic field,—e is the electron charge, n is a nonnegative integer, and γ_ϵ,B is the quantum correction due to Berry phase, magnetic susceptibility, and other band properties^{268,269,270,271,272}. The semiclassical approach can successfully describe the band energy and the geometric properties of Bloch states in metallic systems with energy dispersion. This includes free electron gas with parabolic dispersion and Dirac electrons with linear dispersion^5,273. However, when applied to dispersionless flat bands, the implication of Eq. (30) is subtle since semiclassical orbits are ill-defined. Naively, one may expect vanishing LL spacings due to the infinite effective mass, and thus no response of flat bands to the magnetic field.

However, when a flat band exists in multi-band systems with sizable interband coupling, this naive expectation completely breaks down. Here, the presence of a finite interband coupling indicates that the flat band is not from the decoupled atomic states. In this section, we will first review how the LLs are affected by interband coupling²⁷⁴. In particular, we discuss the role of interband Berry connection and symmetry of the system at zero magnetic field on the LL spectra. After that, we discuss the anomalous magnetic responses of singular flat bands in which the flat band has a quadratic band crossing with another parabolic band at which the Bloch wave function becomes singular²⁷⁵. The geometric idea to describe the LL of singular flat bands can be further generalized to describe the LL spectra of generic quadratic band crossing²⁷⁶. We will discuss the complication when the flat band is made to be weakly dispersive and explain how the geometric effect can be extracted. Based on it, we revisit the magnetic responses of the Bernal stacked bilayer graphene²⁷⁷.

Isolated flat bands

The Landau level spread of isolated single flat bands can be described by using the modified semiclassical approach developed by M.-C. Chang and Q. Niu²⁷⁸. Contrary to Onsager’s approach, where the band structure at zero magnetic field ϵ_nk is used to define the closed semiclassical orbits and the corresponding area S₀(ϵ), the modified semiclassical approach²⁷⁸ employs the modified band structure given by

$${E}_{n,B}({\boldsymbol{k}})={\epsilon }_{n{\boldsymbol{k}}}+{\mu }_{n}({\boldsymbol{k}})B,$$

(31)

where ${\boldsymbol{B}}=B\hat{z}$ is the magnetic field, n is the band index, and μ_n(k) is the orbital magnetic moment of the n-th magnetic band in the z-direction whose explicit form is

$${\mu }_{n}({\boldsymbol{k}})=e\,{\rm{Im}}\left\langle {\partial }_{x}{u}_{n}({\boldsymbol{k}})\vert \left[{\epsilon }_{n{\boldsymbol{k}}}-H({\boldsymbol{k}})\right]\vert {\partial }_{y}{u}_{n}({\boldsymbol{k}})\right\rangle ,$$

(32)

where H(k) is the matrix Hamiltonian in momentum space. Hence, the second term on the right-hand side of Eq. (31) indicates the leading energy correction from the orbital magnetic moment coupled to the magnetic field. In usual dispersive bands, the B-linear quantum correction is negligibly small in weak magnetic field limit compared to the zero-field bandwidth.

In the case of a flat band with zero bandwidth, on the other hand, the B-linear quantum correction always dominates the modified band structure E_n,B(k) in Eq. (31) even in weak magnetic field limit. Moreover, the modified band dispersion of an isolated flat band is generally dispersive so that the relevant semiclassical orbits can be defined unambiguously. As a result, one can obtain the LL spreading of the isolated flat band in the adjacent gapped regions by applying the semiclassical quantization rule to E_n,B(k), which naturally explains the LL spread of the isolated flat band. Especially, around the band edges of E_n,B(k), one can define the effective mass m*, which is inversely proportional to B, from which Onsager’s scheme predicts Landau levels with a spacing eB/m* ∝ B². The resulting LL spectrum is bounded by the upper and lower band edges of E_n,B(k), and thus the total magnitude Δ of the LL spread is given by $\Delta =\max {E}_{n,B}({\boldsymbol{k}})-\min {E}_{n,B}({\boldsymbol{k}})$. This result is valid as long as the band gap E_gap between the isolated flat band and its neighboring band at zero magnetic field is large enough, i.e., ${E}_{{\rm{gap}}}\,\gg\, \max | {E}_{n,B}({\boldsymbol{k}})|$. The generic behavior of an isolated flat band under a magnetic field is schematically described in Fig. 4 where one can clearly observe that the LL spread of the isolated flat band start filling the gaps at zero-field above and below the isolated flat band.

Fig. 4: Landau level spread of an isolated flat band.

a The band structure of a 2D system in the absence of a magnetic field. The second band with the energy ε₂ = 0 corresponds to the isolated flat band. The inter-band coupling ${\varepsilon }_{m}{\chi }_{xy}^{m2}$ of the isolated flat band with the other dispersive band of the energy ε_m (m = 1, 3, 4) is indicated by a dashed vertical arrow. b The modified band dispersion E_m,B (m = 1, …, 4) in the presence of the magnetic field. The corresponding Landau levels are shown by red solid lines. The LL spread of the isolated flat band is represented by the green arrow. [Adapted from ref. ²⁷⁴].

Interestingly, the LL spreading of isolated flat bands is a manifestation of the non-trivial wave function geometry of the flat band arising from inter-band couplings²⁷⁴. One can show that the modified band dispersion of the isolated flat band is given by

$${E}_{n,B}({\boldsymbol{k}})=-2\pi \frac{\phi }{{\phi }_{0}}\frac{1}{{A}_{0}}{\rm{Im}}\,\sum _{m\ne n}{\epsilon }_{m{\boldsymbol{k}}}\,{\chi }_{xy}^{nm}({\boldsymbol{k}}),$$

(33)

in which

$$\begin{array}{lll}{\chi }_{ij}^{nm}({\boldsymbol{k}})\;=\;\langle {\partial }_{i}{u}_{n}({\boldsymbol{k}})| {u}_{m}({\boldsymbol{k}})\rangle \langle {u}_{m}({\boldsymbol{k}})| {\partial }_{j}{u}_{n}({\boldsymbol{k}})\rangle \\\qquad\quad\;\;\, =\,{[{A}_{i}({\boldsymbol{k}})]}_{mn}^{* }{[{A}_{j}({\boldsymbol{k}})]}_{mn},\end{array}$$

(34)

where ϕ₀ = h/e, ϕ = BA₀ is the magnetic flux per unit cell, and A₀ is the unit cell area assumed to be A₀ = 1. Here, we assume that the n-th band is the isolated flat band at zero energy without loss of generality so that ϵ_mk in Eq. (33) should be interpreted as the energy of the m-th band with respect to the flat band energy. We note that ${\left[{A}_{i}({\boldsymbol{k}})\right]}_{nm}={\rm{i}}\langle {u}_{m}({\boldsymbol{k}})| {\partial }_{i}{u}_{n}({\boldsymbol{k}})\rangle$ indicates the cross-gap Berry connection between the n-th and m-th bands (n ≠ m), and ${\chi }_{ij}^{nm}({\boldsymbol{k}})$ is the corresponding fidelity tensor that describes the transition amplitude between the n-th and m-th bands. We note that ${\left[{A}_{i}({\boldsymbol{k}})\right]}_{nm}$ is gauge-covariant while ${\chi }_{ij}^{nm}({\boldsymbol{k}})$ is gauge-invariant, thus directly related to physical observables. Hence, Eq. (33) indicates that the modified band dispersion of the isolated flat band is given by the summation of the transition amplitudes ${\chi }_{xy}^{nm}({\boldsymbol{k}})$ between the isolated flat band and the m-th band weighted by the energy ϵ_mk of the m-th band as illustrated in Fig. 4. This means that the immobile carriers with infinite effective mass in an isolated flat band can respond to the external magnetic field through the inter-band coupling, characterized by the cross-gap Berry connection, to dispersive bands.

The LL spread of an isolated flat band is strongly constrained by the symmetry group of the system²⁷⁴. The B-linear correction to the modified band dispersion E_n,B(k) vanishes when the system respects the chiral C or space-time-inversion I_ST symmetries in the zero magnetic flux. The LL spreading is proportional to B² for a flat-band system with I_ST symmetry in the zero magnetic field, while the LL spreading is forbidden in the presence of chiral symmetry. Interestingly, although I_ST symmetry would be broken as the magnetic field is turned on, the LL spreading is strongly constrained by I_ST symmetry. We further find that $\max {E}_{n,B}({\boldsymbol{k}})=-\min {E}_{n,B}({\boldsymbol{k}})$ when the system respects time-reversal T or reflection R symmetry, at the zero magnetic field, thus the minimum and maximum values of the LL spreading have the same magnitude but with the opposite signs.

Singular flat band with quadratic touching

Next, let us consider the LL spectrum of singular flat bands in which a flat band has a band crossing with other dispersive bands at a momentum where the flat band wave function develops a singularity^279,280,281. As a minimal model of a singular flat band, we consider a two-band model describing a flat band crossing quadratically with a parabolic band. Explicitly, we consider the most general form of two-band continuum quadratic Hamiltonian given by

$${{\mathcal{H}}}_{Q}({\bf{k}})\equiv {f}_{0}({\bf{k}}){\sigma }_{0}+\sum _{\alpha =x,y,z}{f}_{\alpha }({\bf{k}}){\sigma }_{\alpha },$$

(35)

where σ_α’s are Pauli matrices and σ₀ is the 2 × 2 identity matrix. The quadratic functions f_α=0,x,y,z(k) take the form of ${f}_{\alpha }({\bf{k}})={a}_{\alpha }{k}_{x}^{2}+{b}_{\alpha }{k}_{x}{k}_{y}+{c}_{\alpha }{k}_{y}^{2}$ with real coefficients {a_α, b_α, c_α}. A flat band touching with another parabolic band can be obtained by imposing the band flatness condition $\det \left[{{\mathcal{H}}}_{Q}({\bf{k}})\right]=0$. If the resulting flat band wave function develops discontinuity at the band crossing point, we obtain a singular flat band. Otherwise, we have a non-singular flat band.

The singular band crossing point can be characterized by the canting structure of the pseudospin ${\bf{s}}({\bf{k}})\equiv {\sum }_{\alpha = x,y,z}{f}_{\alpha }({\bf{k}})/\sqrt{{f}_{x}{({\bf{k}})}^{2}+{f}_{y}{({\bf{k}})}^{2}+{f}_{z}{({\bf{k}})}^{2}}\hat{\alpha }$ around the band crossing point. The canting structure arises due to the singularity at the band crossing point where the pseudospin direction cannot be uniquely determined. The strength of the singularity can be characterized by the maximum canting angle $\Delta {\theta }_{\max }$ of the pseudospin around the band crossing point. Interestingly, the canting angle between two pseudospins at the momenta ${\bf{k}},{{\bf{k}}}^{{\prime} }$ is related to the Hilbert-Schmidt quantum distance ${d}_{{\rm{HS}}}({\bf{k}},{{\bf{k}}}^{{\prime} })\equiv \sqrt{1-{\vert \langle {u}_{{\boldsymbol{k}}}| {u}_{{{\boldsymbol{k}}}^{{\prime} }}\rangle \vert }^{2}}$ of the perodic parts of the relevant Bloch states $\left\vert {u}_{{\boldsymbol{k}}}\right\rangle ,\,\left\vert {u}_{{{\boldsymbol{k}}}^{{\prime} }}\right\rangle$ as $\Delta \theta ({\bf{k}},{{\bf{k}}}^{{\prime} })=2{\sin }^{-1}\left({d}_{{\rm{HS}}}({\bf{k}},{{\bf{k}}}^{{\prime} })\right)$. Denoting the maximum value of d_HS as ${d}_{\max }$ gives $\Delta {\theta }_{\max }=2{\sin }^{-1}\left({d}_{\max }\right)$. So, either $\Delta {\theta }_{\max }$ or ${d}_{\max }$ can equivalently measure the strength of the singularity²⁷⁵. In the perspective of the quantum distance, the singularity at the band crossing point prevents Bloch wave functions from getting close to each other even in the limit k → 0 yielding nonzero ${d}_{\max }$.

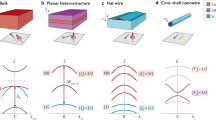
A singular flat band under a magnetic field develops an anomalous LL structure, which directly manifests the quantum geometry of the wave function associated with the singularity at the band crossing point^275,276,277. Figure 5b, c show the generic LL spectra of a non-singular flat band and a singular flat band, obtained by solving Eq. (35) under magnetic field. One can see that the non-singular flat band does not respond to the magnetic field, and all of its LL states are located at the same energy (that of the zero field flat band) without any spread. On the other hand, the singular flat band develops its LL spreading in the empty region (i.e., with energy below that of the flat band). In both cases, the parabolic band develops a conventional LL structure with equal energy spacing ω_c.

Fig. 5: Landau level spectrum of a singular flat band.

a The band structure of a flat band with a quadratic band-crossing. Here m₁ and m₂ are the maximum and minimum effective masses of the dispersive band. b and c show the LL spreading for a non-singular flat band (NSFB) and singular flat band (SFB), respectively. d LL spreading of various flat band models (denoted by the labeling [pm] with an integer m in the inset) as functions of the LL index n. Inset shows their 1/n dependences for n ≫ 1. e The universal relationship between Δ/ω_c and ${d}_{\max }$. Numerical data (diamond symbols) are from the 50 flat band models. [Adapted from ref. ²⁷⁵].

One can define the total LL spread Δ of the singular flat band as the difference between the energy of the singular flat band and that of the lowest LL (E₀) assuming that the flat band has lower energy than the parabolic band. One striking observation²⁷⁵ is that there is a universal relationship between Δ/ω_c and ${d}_{\max }$, independent of model parameters used to define the quadratic Hamiltonian in Eq. (35), given by

$$\begin{array}{r}\frac{\Delta }{{\omega }_{c}}=\xi \left({d}_{\max }^{2}\right),\end{array}$$

(36)

where ξ(x) is a monotonically increasing curve shown in Fig. 5e. The existence of the universal function ξ(x) can be proved analytically as well as numerically. Therefore, measuring Δ/ω_c, ${d}_{\max }$ of the singular flat band can be experimentally extracted. Eq. (36) implies that Δ/ω_c is determined solely by ${d}_{\max }$, and the LL spreading of singular flat bands is characterized by two distinct energy scales Δ and ω_c, contrary to the case of non-singular flat band with just one energy scale ω_c. Describing the LL generation of singular flat bands in the empty region is completely beyond the scope of semiclassical analysis, arising from the level repulsion between the LL spreading from the singular flat band and those from the parabolic band, which is encoded in the maximum quantum distance.

Quadratic band crossing and bilayer graphene

Now we relax the flat band condition and consider the LL spectrum of a general two-band quadratic band crossing Hamiltonian ${{\mathcal{H}}}_{Q}({\bf{k}})$ in Eq. (35) with ${f}_{\alpha = 0,x,y,z}({\bf{k}})={a}_{\alpha }{k}_{x}^{2}+{b}_{\alpha }{k}_{x}{k}_{y}+{c}_{\alpha }{k}_{y}^{2}$. After a series of unitary transformations, the Hamiltonian can be transformed to

$$\begin{array}{lll}{H}_{Q}({\boldsymbol{k}})\;=[{q}_{1}({k}_{x}^{2}+{k}_{y}^{2})+{q}_{2}({k}_{x}^{2}-{k}_{y}^{2})+{q}_{3}(2{k}_{x}{k}_{y})]{\sigma }_{0}\\\qquad\quad\;\;+\,[{b}_{2}({k}_{x}^{2}-{k}_{y}^{2})+{b}_{3}(2{k}_{x}{k}_{y})]{\sigma }_{1}+[{c}_{3}(2{k}_{x}{k}_{y})]{\sigma }_{2}\\\qquad\quad\;\;+\,[{a}_{1}({k}_{x}^{2}+{k}_{y}^{2})+{a}_{2}({k}_{x}^{2}-{k}_{y}^{2})+{a}_{3}(2{k}_{x}{k}_{y})]{\sigma }_{3},\end{array}$$

(37)

thus, the number of the Hamiltonian parameters reduced from twelve to nine²⁷⁹. Interestingly, among the nine parameters, six correspond to the mass tensors of the two dispersive quadratic bands, while the other three describe the interband coupling²⁷⁵, meaning that the two parabolic bands are from decoupled atomic states in the absence of the interband coupling. In particular, considering that the wave function geometry of ${{\mathcal{H}}}_{Q}({\bf{k}})$ appears in the form of an elliptic shape on the Bloch sphere, the three interband coupling parameters determine the major d₁ and minor d₂ diameters of the elliptic curve and the orientation of the ellipse represented by an angular variable ϕ^276,282. When the flat band condition is additionally imposed in a way that one of the two bands becomes flat since it generates five constraint equations among the nine parameters, only four of them become independent and correspond to the three mass tensors of the parabolic band and one interband coupling parameter, which is nothing but the maximum quantum distance²⁷⁵.

Moreover, one can show that the flat band condition is nothing but the condition that the energy eigenvalues of the two-band Hamiltonian have a quadratic analytic form²⁷⁶. Under such quadratic form condition, the generic two-band Hamiltonian has only one interband coupling parameter, which is equivalent to the maximum quantum distance, and the corresponding wave function trajectory on the Bloch sphere is a circle whose diameter is equal to the maximum quantum distance^276,282.

The LL spectrum of generic two-band quadratic band crossing Hamiltonians is also significantly influenced by the three interband coupling parameters. One can reveal the role of the interband coupling in the LL spectrum by comparing two quadratic bands with identical mass tensors but different interband couplings²⁷⁶. To demonstrate the role of the interband coupling in the LL spectrum of quadratic band crossing Hamiltonian, let us consider the following model Hamiltonian²⁷⁷,

$$\begin{array}{l}{{\mathcal{H}}}_{0}({\boldsymbol{k}})=\mathop{\sum}\limits_{\alpha =0,x,y,z}{f}_{\alpha }({\boldsymbol{k}}){\sigma }_{\alpha },\end{array}$$

(38)

where ${f}_{z}({\boldsymbol{k}})=-d\sqrt{1-{d}^{2}}{k}_{y}^{2},\,{f}_{y}({\boldsymbol{k}})=d\,{k}_{x}{k}_{y},\,{f}_{x}({\boldsymbol{k}})={k}_{x}^{2}/2+(1-2{d}^{2}){k}_{y}^{2}/2$, and f₀(k) = 0. Here, the parameter d is defined as $d=\xi {d}_{\max }$ in which ξ = ±1, and ${d}_{\max }$ is the maximum quantum distance. The energy eigenvalues of ${{\mathcal{H}}}_{0}({\boldsymbol{k}})$ remain fixed to be ${\epsilon }_{\pm ,{\boldsymbol{k}}}=\pm \frac{1}{2}({k}_{x}^{2}+{k}_{y}^{2})$ regardless of the value of d within the range −1 ≤ d ≤ 1. When ${d}_{\max }=1$, the Hamiltonian in Eq. (38) corresponds to the low energy Hamiltonian of the Bernal stacked bilayer graphene, and ξ = ±1 denotes the valley index.

In Fig. 6, the ${d}_{\max }$-dependence of LLs is depicted²⁷⁷. When ${d}_{\max }=0$, the LLs ${E}_{N}^{LL}$ are equivalent to those of the conventional parabolic bands ${\epsilon }_{N}^{{\rm{conv}}}=\pm \omega (N+\frac{1}{2})$ with the cyclotron frequency ω = eB/m but start to deviate from ${\epsilon }_{N}^{{\rm{conv}}}$ as ${d}_{\max }$ increases. When ${d}_{\max }$ reaches one, they become ${\epsilon }_{N}^{{\rm{bilayer}}}=\pm \omega \sqrt{N(N-1)}$, the LL of the bilayer graphene. The degeneracy of LLs between ${E}_{0}^{LL}({d}_{\max }=1)$ and ${E}_{1}^{LL}({d}_{\max }=1)$ leads to the absence of a zero energy plateau in the quantum Hall effect. Since such degeneracy of LLs occurs only when ${d}_{\max }=1$, the zero energy plateau is absent only when ${d}_{\max }=1$ while it exists in other cases with ${d}_{\max }\,\ne\, 1$²⁷⁷.

Fig. 6

Effect of quantum distance on Landau levels. The evolution of the Landau levels ${E}_{N}^{LL}$ of a quadratic band crossing Hamiltonian in Eq. (38) as a function of the maximum quantum distance ${d}_{\max }$ for a ξ = +1 and b ξ = −1, respectively, with ω = 1. Here, ξ = ±1 is related to the valley index of graphene. [Adapted from ref. ²⁷⁷].

One can verify that the degeneracy at ${d}_{\max }=1$ exists for both ξ = ±1. However, depending on ξ, the origin of zero LLs is different²⁷⁷. For ξ = +1, the two zero energy levels come from the upper band, while for ξ = −1, the two zero energy levels come from the lower band. Furthermore, when ${d}_{\max }=1$ or ${d}_{\max }=0$, the LLs are symmetric with respect to E = 0, as shown in Fig. 6a, b. This result arises from chiral symmetry, represented by the operator σ_z, which satisfies σ_zH₀(k)σ_z = −H₀(k), exclusively when ${d}_{\max }=1$ or ${d}_{\max }=0$. This symmetry holds even in the presence of a magnetic field. In fact, the chiral symmetry is crucial for the degeneracy observed at ${d}_{\max }=1$. Thus, the presence of the zero energy plateau necessitates chiral symmetry as well as ${d}_{\max }=1$. It is worth noting that although chiral symmetry is not crystalline but approximate symmetry²⁸³, it is an excellent symmetry of bilayer graphene, and thus the absence of the zero energy plateau can be experimentally demonstrated²⁸⁴.

Outlook

The exploration of quantum geometry in condensed matter physics is in its early stages, with many avenues for further research (see ref. ⁶⁵). While the equilibrium behavior of quantum geometric superconductivity under assumed attractive interactions is fairly well understood, simple analytical results are mainly confined to the isolated flat band limit. A significant challenge is that interactions in real materials are predominantly repulsive due to Coulomb forces, making ferromagnetism the primary instability in flat bands with quantum geometry. This is evident in kagome metals²⁸⁵, where most systems become ferromagnetic despite the presence of flat bands at the Fermi level, with only one known low-temperature superconductor.

Further research is needed to identify conditions (if any) where flat-band superconductivity is favored over flat-band ferromagnetism, extending beyond current models. Numerical studies show that superconductivity with purely attractive interactions is enhanced by nearby bands adjacent to flat bands^{59,98,108,286}. Analytical insights into non-isolated flat bands and especially repulsive interactions would be highly beneficial. Additionally, understanding how flat bands and quantum geometry affect various superconducting phenomena—such as critical currents, coherence lengths, vortex properties, Josephson junctions, Andreev reflections, and non-equilibrium responses—is crucial. While research in these areas is still emerging^{113,114,115,117,118,119,287}, early indications suggest that flat-band quantum geometric superconductivity could offer new functionalities like devices with suppressed quasiparticle currents¹²⁴. However, definitive experiments and proposals are still lacking, and most current evidence remains circumstantial.

The exploration of quantum geometry in non-equilibrium phenomena should extend beyond superconductivity to include non-Hermitian systems. Collaborations between condensed matter physics and photonic or artificial quantum systems are particularly promising^{288,289,290,291}. Several experimental observations of the QGT have been reported in the latter systems^{292,293,294,295,296}. Connecting current knowledge on quantum geometric effects in superconductivity and Bose-Einstein condensates via BCS-BEC crossover studies¹¹⁶ would be valuable. To fully grasp the significance of quantum geometry on correlated states, additional experiments and thorough theoretical analyses using realistic models are necessary. Notably, recent experiments have begun exploring quantum geometric effects in TBG superconductivity^66,297, although the extent to which flat band quantum geometry or other, renormalized bands contribute to the physics is unknown. Exploring the effect of quantum geometry in unconventional magentism is also a worthy direction²⁹⁸. In fractional Chern insulators^{83,185,186,187,188,189,190,191,212,213,214,215}, it is expected that both the Berry curvature and quantum geometry will lead to new effects, but a clear theoretical demonstration of this and an experimental observation are missing. Additionally, the first direct observations of quantum geometric quantities in solid-state systems are emerging^299,300,301 (albeit²⁹⁹ in an ionic system).

To expand the impact of quantum geometry in materials research, a key challenge is to define, extract, and apply quantum geometric concepts in ab initio calculations and machine learning methods. These concepts are already utilized in the Wannier approach to electronic structures, serving as indicators for Wannier spread. However, dealing with entangled bands requires addressing issues like divergences in the QGT due to band touchings and extracting QGT from numerical Green’s functions. Expanding the range of quantum geometric tools beyond the QGT—such as incorporating quantum distance or the real-space-local quantum metric^45,110,167-may be necessary.

It is important to note that the QGT is a embedding-dependent quantity⁹⁹; in the case of Bloch states, it depends on Fourier transformation conventions. While some physical observables are embedding-dependent and can be proportional to the QGT, others are embedding-independent and cannot. For instance, the superfluid weight is proportional to the minimal quantum metric⁹⁸, which resolves this issue. Embedding-independent measures like quantum distance and the real-space-local quantum metric^45,110,167 suggest that new, physically relevant quantum geometric quantities remain to be discovered. Furthermore, we would like to mention that the geometric properties of Bloch states are not completely captured by the QGT. In general, all gauge-invariant properties of the Bloch states fall under the concept of quantum geometry. Therefore, finding new quantities that can capture physically-relevant geometric information beyond QGT, such as the orbital-selective quantum metric in^110,167, is one interesting and important future direction.

This review highlighted the role of the single-particle QGT in condensed matter physics, focusing on the geometric properties of the Bloch states. Remarkably, properties of many-body systems—even those that are strongly interacting—can often be described approximately, and sometimes exactly^{59,98,104,302,303}, using the easily computed single-particle QGT. Looking forward, it is promising to explore the physical significance of many-body quantum geometry. For example, the many-body QGT has been predicted to provide a bound on the Drude weight in gapped systems³⁰⁴ and to characterize many-body localization³⁰⁵. Recent works demonstrate the relation between many-body quantum geometry and entanglement^306,307, which means many-body QGT could become valuable in characterizing highly correlated quantum materials where mean-field approaches fail, where the many-body QGT is calculated for many-body states by reinterprating k in Eq. (6) as the phase of the twisted boundary condition. In this context, calculating the many-body QGT and other quantum geometric quantities using current and future quantum computers^308,309 is important. In summary, quantum geometry has garnered significant attention^{310,311,312,313,314,315}, and its study is expected to yield more interesting results within and beyond condensed matter physics in the future.