Introduction

Cellular networks are inherently characterised by tremendous complexity, including numerous interacting molecules, i.e., nodes, and intricate regulations, i.e., edges, between them1,2,3. Furthermore, these nodes and edges intertwine to form diverse paths and feedback loops4,5,6. Together, these nodes, edges, paths, and feedback loops constitute local structures of cellular networks, commonly referred to as local topologies7,8,9. Ultimately, it is the interplay of all these local topologies that determines the global network dynamics, e.g., the stability of equilibria and the occurrence of bifurcations10,11,12.

Most biological processes associated with cellular networks are intricately regulated by an array of exogenous and endogenous stimuli such as ligands, inhibitors, growth factors, and even drugs13,14,15,16, and these processes often exhibit multiple states. Slight variations in these exogenous or endogenous molecules may significantly influence the network dynamics, such as input-output relations and qualitative fate transitions induced by various bifurcations17,18,19. Furthermore, the critical state, as well as the critical transition can be effectively identified20,21,22. It is crucial to achieve insight into how biological processes react to perturbations and how such perturbations propagate within networks, ultimately resulting in cell fate transitions23,24. Fundamentally, an accurate understanding of the effects of these perturbations on cellular networks is crucial for predicting alterations in cell fates and achieving intentional control over these processes, ultimately contributing to the elucidation of network dynamics.

To achieve meaningful insights into the dynamics of a cellular network, relying solely on isolated information regarding individual local structures is insufficient. Actually, network dynamics arise not just from individual nodes but are also intricately intertwined with complex dynamical regulations between them25,26,27,28. Specifically, information on individual nodes or edges is excessively local and insufficient, while the dynamics of a cellular network is global and complex29,30. There exists a notable gap between local topologies and network dynamics.

In addition, for small perturbations to a cellular network, the quantitative variation in an equilibrium can be approximately captured by the linear stability approach31,32,33. However, the linearized approach is invalid for large perturbations. Therefore, how to approximately calculate the quantitative equilibrium variations under large perturbations is less clear and needs to be further investigated. Especially, when a bifurcation occurs, a slight perturbation may cause a large equilibrium variation, inducing qualitative differences in cell states, i.e., cell fate transitions.

Local topologies determine global network dynamics in cellular networks34,35, however, the intricate mechanisms of how local topologies such as paths and feedback loops function are still in need of further exploration. Especially, when perturbations arise, it is worth studying how the perturbations propagate within the networks, how local topologies such as paths and feedback loops operate and determine network dynamics, and ultimately, how local topologies collectively contribute to the emergence of bifurcations under perturbations36. Therefore, the relationship between local topologies and network dynamics remains a fundamental yet unresolved problem in cellular networks.

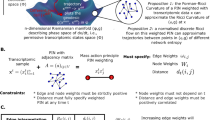
In this study, based on perturbation analysis and network decomposition, we propose a theoretical approach, termed the cumulative linearized approximation (CLA) algorithm, which allows us to investigate the intricate relationship between local network topologies, global network dynamics, and the emergence of bifurcations in cellular networks. To elucidate the general relationship between local network topologies34, global network dynamics35, and occurrence of bifurcations36 in cellular networks, we propose a theoretical approach, which integrates perturbation analysis and network decomposition. More exactly, the network dynamics can be determined by integrating information related to local topologies under perturbations. The methodology facilitates the identification of how paths affect quantitative equilibrium variations and how feedback loops determine the occurrence of bifurcations. We have confirmed the feasibility of the approach in a three-variable model of early T cell development, as well as in a more intricate epithelial-mesenchymal transition (EMT) network. In both models, the CLA algorithm successfully determines the variations in equilibrium under perturbations and accurately identifies the crucial roles played by local topologies, specifically the dominant pathways and feedback loops, in shaping network dynamics. This framework provides valuable insights into the analysis of critical local topologies for cell fate transitions in cellular networks and guide the selection of effective systematic perturbation strategies.

Results

Here, we use the three-variable model in early T cell development and EMT network as illustrative examples to demonstrate the feasibility of the CLA algorithm. Using the CLA algorithm, which integrates linear stability analysis with perturbation iteration, we are able to quantitatively assess the equilibrium variations in a system subjected to a large perturbation. Furthermore, this approach allows us to determine the specific contributions of different pathways to the overall equilibrium variations. For more details on the CLA algorithm, see section “Methods.” The detailed information about all ordinary differential equations (ODEs) and parameters employed, and related information on all paths and feedback loops in the two examples are presented in Supplementary Materials.

Three-variable model in early T cell development

The first example is the three-variable model related to early T cell development37. T cells, which are white blood cells with disease-fighting capabilities, originate from hematopoietic stem cells and undergo a complex and intricate development process within the thymus. During this process, multipotent progenitor cells of T cells differentiate and ultimately mature into functional T cells38,39,40. The development and differentiation of T cells, which involves multiple cellular states, are tightly regulated by a diverse array of transcription factors and environmental signals41,42.

In our example, the network composed of three nodes TCF-1 (T), PU.1 (P), and GATA3 (G) is shown in Fig. 1. Here, the perturbation is imposed on TCF-1, and the output node is PU.1. We use the basal production rate of TCF-1, denoted as k0T, to signify the perturbation to TCF-1. There exist two paths from TCF-1 to PU.1. One is the direct path from TCF-1 to PU.1. The other is the indirect path from TCF-1 to PU.1 through GATA3, which includes two regulation edges: the regulation from TCF-1 to GATA3 and the regulation from GATA3 to PU.1.

Fig. 1: The network composed of TCF-1, PU.1, and GATA3.
figure 1

Arrows represent activations and short bars represent inhibitions.

Full size image

With the perturbation to k0T, the bifurcation diagrams for the three-variable model, derived from ODEs and the CLA algorithm, are depicted in Fig. 2. Obviously, there are two stable equilibrium (SE) curves: C1 and C2. Fate transitions between the two cell states occur through two saddle-node bifurcation: SN1 and SN2. The equilibrium curves obtained using the two approaches exhibit a near-perfect overlap, with minimal deviations only observed in the vicinity of the bifurcation points, thus demonstrating good approximation capabilities of the CLA algorithm.

Fig. 2: Bifurcation diagrams of the three-variable model.
figure 2

The expression levels of TCF-1 A, PU.1 B, and GATA3 C as functions of k0T. The solid and circled equilibrium curves are derived from the ordinary differential equations (ODEs) and cumulative linearized approximation (CLA) algorithm, respectively. Purple and blue (dark or light) curves denote stable and unstable equilibria, respectively.

Full size image

When the bifurcation parameter k0T approaches the bifurcation points, the CLA algorithm encounters difficulties due to the presence of sufficiently small Jacobian determinants in Eq. (13) or Eq. (15), resulting in its inability to accurately compute the equilibria. The total equilibrium variation in PU.1 is induced by two paths. The variation induced by the indirect path from TCF-1 to PU.1 through GATA3 takes the form

$$\Delta {P}_{1}=-\frac{\Delta {k}_{0T}}{\det (J)}\frac{\partial {f_{T}}}{\partial {k}_{0T}}\frac{\partial {f_{G}}}{\partial T}\frac{\partial {f_{P}}}{\partial G}.$$
(1)

While the variation induced by the direct path from TCF-1 to PU.1 is

$$\Delta {P}_{2}=\frac{\Delta {k}_{0T}}{\det (J)}\frac{\partial {f_{T}}}{\partial {k}_{0T}}\frac{\partial {f_{P}}}{\partial T}\frac{\partial {f_{G}}}{\partial G}.$$
(2)

The total equilibrium variation in PU.1 is

$$\Delta \,{\text{PU}}.1\,=\Delta {P}_{1}+\Delta {P}_{2}.$$
(3)

The equilibrium variation in PU.1 induced by the perturbation imposed on TCF-1 through two paths defined by Eqs. (1)-(2) is shown in Figs. 3A and 4A. When the perturbed parameter, i.e., \({k}_{0T}={\bar{k}}_{0T}+\Delta {k}_{0T}\), is smaller than the saddle-node bifurcation, i.e., \({k}_{0T,S{N}_{1}}\) at the C1 branch, the equilibrium variations in PU.1 are mainly induced by the indirect path from TCF-1 to PU.1 through GATA3. Here, \({\bar{k}}_{0T}\) is the basal parameter value and Δk0T is the perturbation to it. The contribution degrees of the two paths are shown in Fig. 3B. The perturbation to TCF-1 leads to the equilibrium variations in PU.1, which are mainly attributed to the indirect path, i.e., the perturbation is mainly transmitted from TCF-1 to PU.1 via GATA3.

Fig. 3: The perturbation effects of two paths on the C1 branch in Fig. 2B at \({\bar{k}}_{0T}=0.3\).
figure 3

A The equilibrium variations defined by Eqs. (1)-(3)). B The contribution degree of each path defined by Eq. (20).

Full size image
Fig. 4: The perturbation effects of two paths on the C2 branch in Fig. 2B at \({\bar{k}}_{0T}=1.5\).
figure 4

A The equilibrium variations defined by Eqs. (1)-(3)). B The contribution degree of each path defined by Eq. (20).

Full size image

Conversely to the perturbation effect on the C1 branch, when the perturbed parameter k0T is larger than the left saddle-node bifurcation, i.e., \({k}_{0T,S{N}_{2}}\) at the C2 branch, the equilibrium variations in PU.1 are mainly induced by the direct path from TCF-1 to PU.1, as shown in Fig. 4A. The contribution degrees of the two paths are shown in Fig. 4B. These results suggest that the same path may play distinct roles in different cell states.

Feedback loops determine stability

It has been shown that each determinant composes a feedback loop or several independent feedback loops43. More exactly, for a given matrix M, the matrix determinant takes the form

$$\det (M)=\sum\limits_{i}\det ({M}_{i}),$$
(4)

where Mis are all sub-matrices.

Still considering the three-variable model. Its Jacobian matrix takes the form

$$J=\left(\begin{array}{ccc}{J}_{11}&{J}_{12}&0\\ {J}_{21}&{J}_{22}&{J}_{23}\\ {J}_{31}&0&{J}_{33}\end{array}\right),$$
(5)

where Jij = ∂fi/∂xj at \({\bf{x}}=\bar{{\bf{x}}}\) with xi (i = 1, 2, 3) representing TCF-1, PU.1, and GATA3, respectively.

The network shown in Fig. 1 can be decomposed into three sub-networks, as shown in Fig. 5. Each sub-network corresponds to a feedback loop and is related sub-matrix. Three feedback loops are the self-activation feedback loop of TCF-1, the feedback loop between TCF-1 and PU.1, and the feedback loop connecting TCF-1, PU.1, and GATA3, as shown in Fig. 5. Denote the sub-matrices which represent these three feedback loops as J1, J2, and J3, respectively. For example, the sub-matrix corresponding to the largest feedback loop is

$${J}_{3}=\left(\begin{array}{ccc}0&{J}_{12}&0\\ 0&0&{J}_{23}\\ {J}_{31}&0&0\end{array}\right).$$
(6)
Fig. 5: The decomposition of the network shown in Fig. 1.
figure 5

Three sub-networks correspond to three feedback loops. Note that all degradations are not shown.

Full size image

It is easy to know that the determinant of matrix J takes the form

$$\det (J)=\mathop{\sum }\limits_{i=1}^{3}\det ({J}_{i}).$$
(7)

Actually, these three matrices exactly correspond to the three feedback loops shown in Figs. 1 and 5. Decomposing a network into distinct feedback loops, i.e., decomposing the Jacobian matrix of a nonlinear dynamical system into all its sub-matrices, can be used to determine the role of each feedback loop in determining the stability of equilibria and the occurrence of local bifurcations. When a local bifurcation with at least one zero eigenvalue occurs, the determinant of the Jacobian matrix J is also zero. Therefore, the emergence of a local bifurcation under a perturbation can be determined by analyzing the alterations in the determinants of the sub-matrices, which correspond to respective feedback loops.

The bifurcation diagram with k0T as a control parameter and the determinants of the Jacobian matrix and all sub-matrices are shown in Fig. 6. With continuous increase in k0T, SE curve C1 with higher PU.1 jumps to SE curve C2 with lower PU.1 through a saddle-node bifurcation SN1. As k0T increases, the equilibrium and therefore the determinant of the Jacobian matrix vary. At saddle-node bifurcation SN1, Jacobian matrix has a zero eigenvalue and therefore \(\det (J)=0\). The occurrence of the bifurcation SN1 is mainly induced by the feedback loop connecting all the three nodes corresponding to the sub-matrix J3. As k0T approaches \({k}_{0T,S{N}_{1}}\), \(\det (J)\) approaches zero quickly, which is mainly induced by the steep variation in \(\det ({J}_{3})\) because the changes in \(\det ({J}_{1})\) and \(\det ({J}_{2})\) are quite gradual, as shown in Fig. 6A. Similarly, the occurrence of the bifurcation SN2 is also mainly induced by the same feedback loop, corresponding to the sub-matrix J3, as shown in Fig. 6B.

Fig. 6: The bifurcation diagram and determinants of the Jacobian matrix and all sub-matrices.
figure 6

The left and right Y-axes represent the determinants and the value of PU.1 at stable equilibrium, respectively. A The C1 process. B The C2 process.

Full size image

EMT network

To assess the suitability of our approach for more intricate biological networks, we applied the CLA algorithm to the EMT network44. EMT plays critical roles in various biological processes, including tissue repair and pathological conditions such as normal embryonic development, wound healing, and cancer metastasis45,46,47. EMT is a biological process where cells undergo a morphological transformation from epithelial (E) to mesenchymal (M) phenotypes, with a hybrid (H) phenotype that exhibits characteristics of both E and M present during this transition. During EMT, epithelial cells can lose their polarity and adhesion, transforming into mesenchymal cells with enhanced motility and invasive capabilities48,49,50.

The core EMT network is shown in Fig. 7. In the network, there are nine molecules: a main inducer transforming growth factor-β (TGF-β), two cell fate microRNA regulators miR34 and miR200, two core transcription factors SNAIL1 and ZEB, two mRNA snail1 and zeb, and the epithelial state maker E-cadherin as well as the mesenchymal state maker N-cadherin. The perturbation is imposed on TGF-β, i.e., k0T, and the output node selected is E-cadherin or N-cadherin. The transition between different cell states occurs as the parameter k0T varies. There are three distinct states characterized by different levels of E-cadherin and N-cadherin expression: (i) high E-cadherin and low N-cadherin, representing the epithelial (E) cell state; (ii) low E-cadherin and high N-cadherin, representing the mesenchymal (M) cell state; and (iii) medium levels of both E-cadherin and N-cadherin, representing the hybrid (H) cell state. For a more intuitive analysis of state transitions between E, H, and M states, the equilibrium curves of E-cadherin and N-cadherin in response to k0T derived from ODEs and the CLA algorithm, are shown in Fig. 8. The equilibrium curves derived from both approaches demonstrate a nearly perfect overlap, exhibiting only negligible deviations in the proximity of the bifurcation points.

Fig. 7: The EMT regulatory network.
figure 7

Arrows represent activations and short bars represent inhibitions.

Full size image
Fig. 8: The bifurcation diagrams.
figure 8

The expression levels of E-cadherin A and N-cadherin B as functions of k0T. The solid and circled equilibrium curves are derived by the ordinary differential equations (ODEs) and cumulative linearized approximation (CLA) algorithm, respectively. Purple and blue (dark or light) curves denote stable and unstable equilibria, respectively.

Full size image

The bifurcation diagrams illustrate that there exist transitions between three cell states. Four saddle-node bifurcations occur when k0T varies, i.e., SN1, SN2, SN3, and SN4. The system stays in the monostable E state when k0T is small. As k0T gradually increases, forward transitions from E to H through SN1 and then from H to M through SN3 occur. Conversely, backward transition from M to E through SN4 for cells at M state or from H to E through SN2 for cells at H state occurs as k0T decreases. More exactly, with the change of k0T, the system may undergo EMT, i.e., E to M indirectly through H or mesenchymal-epithelial transition (MET), i.e., M to E directly. While if k0T decreases before it goes up to SN3, backward transition from H to E via SN2 occurs. Therefore, four different types of fate transitions, i.e., E to H, H to M, H to E, and M to E, may occur.

Next, we analyze how different paths affect equilibrium variations in the cell fate makers E-cadherin and N-cadherin. The variations in E-cadherin are affected by the perturbation to \({\bar{k}}_{0T}\) via four distinct paths. However, among these paths, only the path TGF-β → snail1 → SNAIL1 ⊣ E-cadherin, i.e., ΔPE,2, exerts a significant influence on the variations, as shown in Figs. 9A-B. Therefore, with the perturbation increase, the decrease in E-cadherin preceding the cell fate transition from E to H is primarily induced by this path, which contributes almost entirely to the variations observed in E-cadherin, as shown in Fig. 9A. As the perturbation decreases, the same path also plays a significant role in the accumulation of E-cadherin prior to the fate transition from H to E, as shown in Fig. 9B.

Fig. 9: Equilibrium variations in the cell fate makers E-cadherin (A and B) and N-cadherin (C and D) during cell fate transitions.
figure 9

A E → H at \({\bar{k}}_{0T}=0\). B H → E at \({\bar{k}}_{0T}=0.8\). C M → E at \({\bar{k}}_{0T}=2\). D H → M at \({\bar{k}}_{0T}=0.8\).

Full size image

The equilibrium variations in N-cadherin are also influenced by the perturbation to \({\bar{k}}_{0T}\) through four distinct paths. Among these paths, the path TGF-β → snail1 → SNAIL1 → zeb → ZEB → N-cadherin, i.e., ΔPN,4, exerts the most significant impact on the fate transition from M to E, as shown in Fig. 9C. While the path TGF-β → snail1 → SNAIL1 → N-cadherin, i.e., ΔPN,2, plays the most significant role in the accumulation of N-cadherin and thus the fate transition from H to M, as shown in Fig. 9D.

With a continuous increase in k0T, cell fate transition from E to H occurs through the saddle-node bifurcation SN1, as shown in Fig. 8. As k0T increases, the equilibrium and, consequently, the determinant of the Jacobian matrix vary. At the saddle-node bifurcation SN1, the Jacobian matrix possesses a zero eigenvalue, resulting in a zero determinant, namely \(\det (J)=0\). Based on the decomposition of Jacobian matrix, the occurrence of the saddle-node bifurcation SN1 is primarily induced by the feedback loop between SNAIL1 and miR34, which corresponds to the sub-matrix J3, as shown in Fig. 10A. The determinant \(\det (J)\) tends to zero as k0T approaches the bifurcation SN1, during which only \(\det ({J}_{3})\) increases significantly, while the determinants of all other sub-matrices remain nearly constant.

Fig. 10: The determinants of the Jacobian matrix and all sub-matrices vary with the parameter k0T.
figure 10

The left and right Y-axes represent the determinants and the values of two makers at stable equilibria, respectively. A E → H. B H → E. C M → E. D H → M.

Full size image

Conversely, as k0T continuously decreases, the cell fate transition from H to E occurs through SN2, as shown in Fig. 8. The emergence of bifurcation SN2 is still primarily attributed to the feedback loop between SNAIL1 and miR34, corresponding to the sub-matrix J3, as shown in Fig. 10B. Therefore, the cell fate transition between E and H is mainly driven by the feedback loop between SNAIL1 and miR34.

The cell fate transition from M to E via the saddle-node bifurcation SN4 or the transition from H to M through SN3 is mainly induced by the feedback loop between ZEB and miR200, which corresponds to the sub-matrix J2, as shown in Figs. 10C-D. In addition, the feedback loop TGF-β → snail1 → SNAIL1 → zeb → ZEB ⊣ miR200 ⊣ TGF-β, corresponding to the sub-matrix J7, also plays a crucial role in the fate transition from M to E via the saddle-node bifurcation SN4, as shown in Fig. 10C.

Discussion

As modern biomedical science advances rapidly, the threat to human health has gradually shifted from diseases caused by isolated pathogenic factors to complex diseases. Diseases often originate from intricate regulations among numerous molecules and their surrounding environments, making it highly challenging to analyze them from isolated factors. A perturbation to a single molecule can trigger a cascading series of downstream effects via intricate regulatory networks. Consequently, focusing solely on the individual pathogenic effects of disease-causing genes is inadequate to accurately uncover the emergence of complex diseases. Instead, our research emphasizes a thorough exploration of the intricate interplay among the components within the cellular networks.

To achieve a profound understanding of intricate regulatory mechanisms of cellular networks, it is necessary to investigate the correlations between local network topologies, global network dynamics, and the occurrence of bifurcations. This exploration encompasses multiple dimensions, including the analysis of individual nodes, edges, paths, and feedback loops. Through this research, we can comprehensively and precisely illuminate the underlying causes of various dynamics, thereby offering novel insights and methodologies for dynamics control and therapeutic interventions.

Theoretical analysis and numerical simulations have already validated the feasibility of this approach, for instance, in the context of early T cell development and EMT networks. The network-based approach integrates perturbation analysis and network decomposition. It offers a theoretical framework to reveal how perturbations determine equilibrium variations by integrating distinct regulatory paths. In addition, the crucial roles of feedback loops in determining the stability of equilibrium and the occurrence of bifurcations can be identified. The relationship between local topologies and network dynamics uncovers the significance of nodes, edges, paths, and feedback loops in response to perturbations.

Although the focus is on perturbations to scalar parameters, the synergistic effects of combinatorial perturbations can also be extensively examined. The network decomposition approach introduced offers a comprehensive framework for conducting network dynamics and perturbation analysis in both mathematical and biological sciences. This framework not only aids in discovering crucial relationships between network components, but also has the potential to be applied to various other regulatory systems, such as embryonic stem cell differentiation51, cancer metastasis52, the developmental process of B cell18, and other networks related to cell fate transition53,54. This approach offers an efficient protocol for clinical treatment of certain diseases through the use of specific medications. However, a limitation of our methodology lies in its inability to analyze global bifurcations, restricting its application solely to local bifurcations with zero eigenvalues. Furthermore, the selection of the perturbation step size can significantly impact the accuracy of our calculations, particularly when the perturbation is in proximity to bifurcation points. Therefore, our future research will focus on identifying the essential information associated with both local critical states and global bifurcations.

Methods

By integrating network decomposition with perturbation analysis, we introduce the CLA algorithm under large perturbations. This approach enables us to ascertain how such perturbations influence variations in equilibria and ultimately result in the occurrence of bifurcations.

Consider a dynamical system

$$\frac{d{\bf{x}}}{dt}={\bf{f}}({\bf{x}};{\bf{p}}).$$
(8)

The vector \({\bf{x}}\in {{\mathbb{R}}}^{n}\) denotes the state of a cellular network at time t, \({\bf{p}}\in {{\mathbb{R}}}^{m}\) denotes the vector parameter, and the vector function f(x; p) represents the constraints, which determine the dynamics of the network.

Equilibrium variations under a small perturbation

For simplicity, we consider the case of scalar parameter. The case of vector parameter can be similarly investigated. At the basal parameter value \(\bar{p}\), the equilibrium \(\bar{{\bf{x}}}\) satisfies

$${\bf{f}}(\bar{{\bf{x}}};\bar{p})={\bf{0}}.$$
(9)

In response to a small perturbation to the parameter: \(\bar{p}\to \bar{p}+\Delta p\), the equilibrium varies from \(\bar{{\bf{x}}}\) to \(\bar{{\bf{x}}}+\Delta {\bf{x}}\).

Suppose that the perturbation is imposed on the node k, i.e., fk contains the perturbed parameter. Expanding Eq. (9) at the equilibrium \(\bar{{\bf{x}}}\), the linearized equation takes the form:

$$\frac{d\Delta {\bf{x}}}{dt}=J\Delta {\bf{x}}+\Delta {E}_{p},$$
(10)

where J is the Jacobian matrix at the equilibrium \(\bar{{\bf{x}}}\) and

$$\Delta {E}_{p}=\left(\begin{array}{c}0\\ \vdots \\ \frac{\partial {f}_{k}}{\partial p}\\ \vdots \\ 0\end{array}\right)\Delta p.$$
(11)

Suppose that the Jacobian matrix J is reversible. The equilibrium of Eq. (10) satisfies

$$\Delta \bar{{\bf{x}}}=-{J}^{-1}\Delta {E}_{p}.$$
(12)

For each node xj, the variation deviating from its original position \({\bar{x}}_{j}\), i.e., \(\Delta {\bar{x}}_{j}\), takes the form

$$\frac{\Delta {\bar{x}}_{j}}{\Delta p}=-\frac{\partial {f_{k}}}{\partial p}\frac{{C}_{kj}}{\det (J)},$$
(13)

where Ckj is the algebraic cofactor of element (k, j) in the Jacobian matrix J and \(\det (J)\) is the Jacobian determinant.

For each path Pi from the perturbed node k to the output node j, its contribution to the equilibrium variation is defined as

$$\begin{array}{l}\Delta {P}_{i}={K}_{1}\cdot {K}_{2}\cdot \prod\limits^{{E}_{p}}{J}_{pq},\end{array}$$
(14)

where

$${K}_{1}=-\frac{{(-1)}^{k+j}}{\det (J)}\left(\frac{\partial {f}_{k}}{\partial p}\Delta p\right),$$
(15)
$${K}_{2}={(-1)}^{\tau ({r}_{1},\cdots ,{r}_{j-1},{r}_{j+1},\cdots ,{r}_{n})},$$
(16)

and τ(r1, ⋯ , rj−1, rj+1, ⋯ , rn) is the minimum number of pairwise exchanges to recover order 1, ⋯ , j − 1, j + 1, ⋯ , n. EP is the number of nodes minus one, i.e., the edges in the path Pi from the perturbed node k to the output node j and the edges of the loops, which are not connected to it, and Jpq represents the intensity of the edge from q to p in the path Pi, i.e.,

$${J}_{pq}=\left.\frac{\partial {f_{p}}}{\partial {x}_{q}}\right|_{{\bf{x}} = \bar{{\bf{x}}}}.$$
(17)

Therefore, the total equilibrium variation in node j induced by the perturbation to node k over all paths takes the form

$$\Delta {\bar{x}}_{j}=\mathop{\sum}\limits_{i = 1}^{{N}_{P}}\Delta {P}_{i},$$
(18)

where NP is total number of paths from node k to node j.

Similar to the tree diagram of chain rule, combining Eq. (14) and Eq. (18), we obtain

$$\Delta {\bar{x}}_{j}=\mathop{\sum }\limits_{i=1}^{{N}_{p}}\left({K}_{1}\cdot {K}_{2}\cdot \prod\limits^{{E}_{p}}{J}_{pq}\right),$$
(19)

which means that we need multiply all the derivatives along each path and then add the products over all paths.

Due to the fact that the contribution of each path can be positive or negative, the contribution degree of each path Pi to the equilibrium variation in xj is defined as

$${D}_{{P}_{i}}=\frac{| \Delta {P}_{i}| }{\mathop{\sum }\nolimits_{i=1}^{{N}_{P}}| \Delta {P}_{i}| }.$$
(20)

Thus, we have

$$\mathop{\sum}\limits_{i = 1}^{{N}_{P}}{D}_{{P}_{i}}=1.$$
(21)

The equilibrium variation of xj attributed to each Pi is defined by Eq. (14). While the total equilibrium variation induced by all the paths, i.e., \(\Delta {\bar{x}}_{j}\), can be obtained by Eq. (19). The contribution degree of each path Pi to the total equilibrium variation in xj is defined by Eq. (20).

Equilibrium variations under a large perturbation

Under a small perturbation, the linearized Eq. (10) is used to calculate equilibrium variations. The linearized approach is invalid for large perturbations. For node xj, under a large perturbation Δp, we divide the interval \([\bar{p}\,\bar{p}+\Delta p]\) into s − 1 subintervals with equal width Δstep = Δp/(s − 1), and then compute each approximate \(\Delta {\bar{x}}_{j}\) under each small perturbation by

$${\bar{x}}_{j}(\bar{p}+h* {\Delta }_{{\rm{step}}})={\bar{x}}_{j}(\bar{p}+(h-1)* {\Delta }_{{\rm{step}}})+\Delta {\bar{x}}_{j,h},$$
(22)

where h = 1, ⋯ , s − 1 and j = 1, ⋯ , n. Each \(\Delta {\bar{x}}_{j,h}\) can be calculated using the linearized approximation defined by Eq. (18), specifically for the case of small perturbations.

The vector form can be expressed as follows

$$\bar{{\bf{x}}}(\bar{p}+h* {\Delta }_{{\rm{step}}})=\bar{{\bf{x}}}(\bar{p}+(h-1)* {\Delta }_{{\rm{step}}})+\Delta {\bar{{\bf{x}}}}_{h}.$$
(23)

Then, under a large perturbation, the equilibrium variation can be approximately calculated as follows

$$\bar{{\bf{x}}}(\bar{p}+\Delta p)=\bar{{\bf{x}}}(\bar{p})+\mathop{\sum}\limits_{h = 1}^{s-1}\Delta {\bar{{\bf{x}}}}_{h},$$
(24)

which includes the equilibrium \(\bar{{\bf{x}}}(\bar{p})\) and the equilibrium variation induced by the perturbation Δp, i.e., \(\mathop{\sum }\nolimits_{h = 1}^{s-1}\Delta {\bar{{\bf{x}}}}_{h}\). Therefore, we develop the CLA algorithm, i.e., Eq. (24), to explore the equilibrium variations of cellular network under large perturbations. Note that during the perturbation, if a local bifurcation occurs, the CLA algorithm may encounter difficulties due to the presence of a zero determinant for Jacobian J in Eq. (15).