Abstract
Perikinetic and orthokinetic flocculation are the first steps in drinking water treatment plant (DWTP) and affect all subsequent processes. Leveraging multi-stage water quality parameters, we developed a machine learning (ML) framework for coagulation control that incorporates knowledge embedding (KE) through hyper-parametric constraints on threshold water quality, energy consumption, and economic costs. Random forest (RF) has the best performance among the eight methods with a percentage error of 2.53% and a coefficient of determination of 0.9922. The results of the interpretability analysis show that the model can accurately identify the coagulation demand and balance the removal effect with the energy consumption and economic cost. Through real experimental validation and simulation extrapolation, the RF-KE model can reduce turbidity by 16.36% and dosing cost by 9.64%. This framework reduces economic costs while optimizing water quality through KE and interpretability analyses, providing evidence for the safe and reliable application of future models.
Similar content being viewed by others
Introduction
Drinking water treatment plants (DWTPs) are the core of drinking water processing1,2,3,4. Among various water treatment processes, coagulation and flocculation are key steps in removing suspended solids, colloids, organic matter, and pathogenic microorganisms from water5,6. Insufficient dosing of chemicals can lead to incomplete coagulation, affecting the safety of drinking water7. Excessive dosing can lead to an increase in by-products, costs8,9,10. Traditional dosing calculations depend on empirical parameters11,12, and flocculation tank designs use fixed parameter designs that are difficult to adapt to variable regulation13. Machine learning (ML) can learn the complex nonlinear relationship between raw water quality, dosing rate and treatment effect from historical data, providing new ideas for intelligent dosing control14,15,16.
Multiple ML algorithms with different decision mechanisms also demonstrate better accuracy17,18,19,20. Controls, modeling tools have also become diversified21. However, the internal decision mechanisms of the models proposed in these studies are difficult to interpret, and there is a lack of analysis of multiple interpretable methods to understand the model decision mechanisms22,23. At the same time, most studies have only considered water quality risks, and the economic and integrative benefits are equally worthy of attention24,25. This study aims to develop a knowledge-embedded ML method for flocculant dosing regulation, which systematically considers the water quality characteristics across different treatment stages, as well as economic and energy efficiency. The proposed method is designed to respond to typical water quality fluctuations with strong interpretability, and has been validated under real operational conditions, demonstrating its practical applicability in engineering contexts.
Results
Algorithmic and scenario outlook
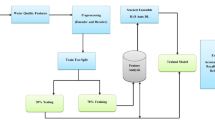
Based on flocculation kinetics, the data required for dosage control via ML needs to include water quality indicators for different parts of the whole process (Text S1, Text S2). In contrast to traditional scoring systems and dosing heuristics that rely on limited end-point indicators, the proposed metrics incorporate multi-stage water quality information across the entire treatment process, enhancing both comprehensiveness and foresight in system monitoring (Fig. 1a). By integrating energy and chemical consumption per pollutant load, the framework enables joint optimization of compliance and operational cost. In practice, this approach effectively identifies critical risk factors, improving system stability and resource efficiency, particularly under complex and dynamic operating conditions.
a Independent variables and dependent variables selected in the dosing machine learning model building process, and constraints used for parameter limitations. b Schematic diagram of the main process sections of the drinking water treatment plant, feature collection locations, and control thresholds of key features. Principles of different algorithms: c Ridge Regression; d Support Vector Regression; e Random Forest; f XGBoosting; g Deep Neural Network; h Recurrent Neural Network; i Long Short-Term Memory; j Transformer. Loss model loss function, RMSE root mean square error, T temperature, Q flow, TUR turbidity, AN ammonia nitrogen, NP network pressure, WVC variation coefficient of water withdrawal, PE Photovoltaic electricity, WE electricity to obtain water, SE electricity for sludge, TE total electricity, EC electricity cost, CC chemical cost, TC total cost. The subscripts indicate different stages of wastewater treatment. \({X}_{R}:\) raw water. \({X}_{{IN}}:\) influent water. \({X}_{P}:\) pre-chlorination water. \({X}_{S}:\) sedimentation tank. \({X}_{D}:\) disinfection contact tank. \({X}_{{EFF}}:\) effluent water.
The water plant uses polybasic aluminum chloride (PAC, Text S3) as the main agent and collects 38 water quality indicators (Table S1) through sensors (Table S2). The sample timeframe was January 1, 2024 to October 31, 2024, with a total of 7320 samples with 1 h intervals. In order to ensure the feasibility of ML methods, eight ML algorithms were selected for comparison in this study (Text S4, Fig. 1c–j). Mean Absolute Percentage Error (MAPE) was used as the primary model performance metric, and Mean Squared Error (MSE), Root Mean Square Error (RMSE), Mean Absolute Error (MAE) and Coefficient of Determination (R-square, R2) were used as auxiliary metrics for model screening (Text S5). The study also provides a modeling environment for model replication (Text S6).
The overall data nulls are missing, and the average of the values before and after the filled-in nulls is used directly (Fig. 2a). The results of the missing value treatment show that the distributional trends of the different indicators vary considerably (Fig. 2b). The data distributions before and after imputation remain largely consistent (Fig. S1), indicating that mean imputation did not significantly alter the original data characteristics, and the introduced error is acceptable. As a whole, the seven raw water characteristics had more extreme cases, such as raw water turbidity mostly below 100 NTU, with turbidity exceeding 400 NTU in extreme cases. water quality was generally smooth during pre-chlorination, sedimentation tank indicators and disinfection. It is worth noting that the distribution of the four change value indicators varies widely and should be focused on in the subsequent modeling process.
a Missing pattern of raw data. The red color blocks represent missing values, the blue color blocks represent normal values. b Distribution of raw data after preprocessing,including 7 raw water indicators, 5 influent water indicators, 4 pre-chlorination indicators, 3 sedimentation tank indicators, 3 disinfection indicators, 4 effluent water indicators, 4 electricity indicators and 3 economic indicators recorded by central server, 4 change value indicators by independently designing and calculating. T temperature, Q flow. TUR turbidity, AN ammonia nitrogen, NP network pressure, WVC variation coefficient of water withdrawal, PE Photovoltaic electricity, WE electricity to obtain water, SE electricity for sludge, TE total electricity, EC electricity cost, CC chemical cost, TC total cost. The subscripts indicate different stages of wastewater treatment.
Model performance comparison
This study explores in detail the training process of each model and its core parameters and the different algorithms during training then show significant variability (Fig. S2). The trained model was used for test set validation and the model fit was good except for RIDGE (Fig. S3). Overall, there are large performance differences between different classical ML models and insignificant performance differences between different deep learning models (Fig. 3, Table S3). RIDGE, though achieving R2 = 0.9387, had the highest MAPE (12.30%) and was used as the baseline. SVR performed moderately (MAPE = 8.49%). Tree-based models outperformed others, with RF achieving the best performance (MAPE = 2.53%, R2 = 0.9922), likely due to its robustness and ensemble diversity. Deep learning models showed MAPE around 5%, with temporal models (RNN, LSTM, TF) outperforming DNN. TF performed best (MAPE = 4.63%), benefiting from its ability to capture long-range dependencies via self-attention.
The results of fitting the dosage to the 8 different algorithms, showing the histogram distribution of the true values on the top and the histogram distribution of the predicted values on the right: a Ridge Regression; b Support Vector Regression; c Random Forest; d XGBoosting; e Deep Neural Network; f Recurrent Neural Network; g Long Short-Term Memory; h Transformer. The regression coefficients are shown in the upper left corner of each subplot. i MAPE, MAE, RMSE of the model of 8 different different algorithms. MAPE mean absolute.
Model Interpretability analysis
In order to study the mechanism of the black box model, the RF model with the smallest MAPE value was chosen for interpretability analysis (Fig. 3i). The heatmap of the correlation between the input characteristics and the predicted targets showed generally weak correlations between most of the variables, but the correlation between the dosage and the turbidity of influent water (TURIN), turbidity change value of pre-chlorination and influent water (TURIN-P) and temperature of pre-chlorination (TP) as very significant (Fig. 4a). All of these correlations were below 0.75, so multicollinearity was not considered in this study.
a Correlation grid plots of cast predicted values and input features, with the thickness and color of each line proportional to the correlation coefficient. b Global interpretation of significance results of model prediction results based on the SHAP approach. c SHAP percentage plot fan charts for the three features with the largest share and other features. d Supervised clustering of the test set distinguishing eigenvalues, with the horizontal axis being the test set sample percentage. e Modes of influence of the main characterizing variable. f Number and average depth of subtrees for the RF model. T temperature, Q flow, TUR turbidity, AN ammonia nitrogen, NP network pressure, WVC variation coefficient of water withdrawal, PE Photovoltaic electricity, WE electricity to obtain water, SE electricity for sludge. TE total electricity, EC electricity cost, CC chemical cost, TC total cost. The subscripts indicate different stages of wastewater treatment. \({X}_{R}:\) raw water. \({X}_{{IN}}:\) influent water. \({X}_{P}:\) pre-chlorination water. \({X}_{S}:\) sedimentation tank. \({X}_{D}:\) disinfection contact tank. \({X}_{{EFF}}:\) effluent water.
The feature importance heatmap reflects the feature contributions of multiple samples and provides a view of global and local interpretations (Table S4, Fig. 4b). The three features with the largest percentage of feature importance are TURIN-P, TP and turbidity of pre-chlorination (TURP), TURIN with high correlations did not have high feature importance, indicating large differences in data distribution and decision-making patterns and the need for in-depth comparisons of decision-making patterns. The distribution of the first ranked feature TURIN-P is such that low true values correspond to high SHAP values and high true values correspond to low SHAP values. This decision pattern refers to the fact that models with small TURIN-P values tend to overestimate. In real water plants, when the disinfection pretreatment process is less effective, the coagulation process requires more dosage.
The distributions of TP, TURP for the second and third ranked features are similar, with low true values corresponding not only to high SHAP values but also to low SHAP values, and high true values corresponding mainly to low SHAP values. This decision pattern indicates two scenarios. The first is lower turbidity and temperature, some times the reaction is incomplete requiring more dosing, and some times there is too much dosing to react. The second is that most of the water plants are in extreme situations such as high temperatures and high turbidity, where the dosage is already excessive, which is directly related to the drawbacks of applying empirical formulas alone in water plants. Percentage importance of the top 3 features were 33.92%, 28.95% and 17.21% and total of 9 features had an importance percentage greater than 1% (Table S4, Fig. S4). The combination of these three characteristics reached 80.08%, indicating that the subsequent application of this dosing model can cut some of the variables to realize the reduction of parameters and data collection difficulties (Fig. 4c).
Supervised clustering and heatmaps reveal the substructure of the test dataset (Fig. 4d). The color blocks for each feature are not homogeneous, suggesting a variety of model decision-making styles. The f(x) function corresponding to the SHAP values also fluctuates above and below 0 and adapts to the different test set conditions, demonstrating robustness. Scatter plots of the SHAP values versus the true values of the TURIN-P show that the effect of the TURIN-P initially attenuates the negative impacts and then transitions to a positive one that deepens with increasing values as the true values increase (Fig. 4e). Then comes the negative impact, which begins to diminish after reaching another trough value. This suggests that the effects of pre-chlorination on the flocculation process are diverse, showing a pattern of increasing, then decreasing and then increasing. Subtree situations and average depths were 1.82, 2.24, and 2.32 for TURIN-P, TP and TURP, respectively (Fig. 4f). The average depth is less than 2.5, and extreme sample depths greater than 5 are rare, suggesting that this RF model has a lower risk of overfitting, better generalization, and is more robust to noise and outliers.
Validation experiments and TEA
In this study, the proposed model is deployed through a cloud-based architecture to enable centralized reasoning and management, and to facilitate remote updating and maintenance. Four dosing scenarios were designed: Scenario 1 (TURS-Lab) applied the conventional dosing method of the DWTP under laboratory conditions, while Scenario 2 (TURS-LabML) adopted an ML-based strategy in the same setting. Scenario 3 (TURS) applied the conventional method under real-world conditions. Based on the comparison between Scenarios 1 and 2, Scenario 4 (TURS-ML) extended the ML-based approach to the actual operation of the DWTP. The water quality of the plant fluctuated greatly during the experimental validation period (Fig. 5a). Since scenario- 1 and scenario-2 involve only part of the day, the corresponding times are shown in light gray on the graphs. The increase in water turbidity was concentrated in the morning of each day due to the effect of cooler winter temperatures. TURIN showed fluctuations compared to the turbidity of raw water (TURR) due to the influence of the flow of recycled water (QRE), especially on days 2, 3, 7 and 10 when the fluctuations were significant and turbidity reached 70.0. This may be due to the fact that the water plant’s response to the low winter turbidity was primarily to overdose, far exceeding the demand and creating a dampening effect through the flowback water.
a Real incoming and outgoing water and stage turbidity of the water plant during the experimental validation.The moments corresponding to the dark gray background do not have laboratory validation, and the moments corresponding to the light gray background have laboratory validation.b Schematic diagram of a scaled-down flocculation tank.c Changes in turbidity under the lab using the original method of dosing at the water plant, and dosing using the ML method.d Turbidity during the actual operation of the water plant, and simulation of the turbidity in the application of ML.e Change in total daily PAC dosing. f Change in total treatment cost per unit volume of wastewater. g Change in percentage of total cost for multiple chemicals. h For each feature, 10% of the values are randomly selected and set to 0, and 100 Monte Carlo simulations are performed. i For key features, randomly select 10%, 20%, 30%, 40%, and 50% of the values and set them to 0, then perform 100 Monte Carlo simulations. TUR: turbidity. PAC: polybasic aluminum chloride.
A scaled-down version of the flocculation tank was designed (Fig. 5b).The flocculation cell was 3D printed using polymethyl methacrylate material (Fig. S5). Turbidity was reduced in 82.5% of cases and all anomalies above the threshold of 0.8 NTU were avoided. Average turbidity of TURS-Lab is 0.49 NTU and average turbidity of TURS-LabML is 0.43 NTU, turbidity was significantly reduced using ML and turbidity exceeding the threshold was significantly avoided (Fig. 5c). Turbidity was reduced in 100% of cases and all anomalies above the threshold of 0.8 NTU were avoided. Average turbidity of TURS-Lab is 0.48 NTU and average turbidity of TURS-LabML is 0.43 NTU, turbidity was significantly reduced using ML and turbidity exceeding the threshold was significantly avoided (Fig. 5d). The average turbidity was 0.55 NTU for TURS and 0.46 NTU for TURS-ML, a 16.36% reduction in average turbidity. All the anomalies above the 0.8 NTU threshold were avoided.
For the most part, the total daily dosing was decreasing when using ML dosing, except for the second day, which may have been identified by the model as having too much turbidity in the influent on the second day (Fig. 5e). This demonstrates that the model does not reduce dosing alone, but rather balances effluent quality and economic costs by accurately identifying dosing and controlling stage effluent close to thresholds. Average cost of PAC used to treat 1,000 tons of wastewater reduced from 10.07 Yuan to 7.45 Yuan (Fig. 5f). Excluding changes in other agents, the average total cost decreased from 27.17 Yuan to 24.55 Yuan, a decrease of 9.64%. Similarly, the cost of the second single day of PAC dosing is higher (Fig. S6). With ML, the PAC pharmacy cost share was reduced by 29.91% from 37.12% (Fig. 5g), and the daily percentage was also significantly reduced (Fig. S7, Fig. S8).
Given that not all regions or facilities in the real world are equipped with comprehensive high-frequency monitoring systems and sensor networks, this study introduces an analytical method to simulate missing monitoring data in order to further assess the adaptability and robustness of the proposed framework under incomplete data scenarios. Specifically, we randomly selected 10% of the values for each input feature and set them to 0, repeating this process 100 times in a Monte Carlo simulation (Fig. S9) to simulate real-world scenarios such as sensor errors, communication packet loss, or missing devices. The results showed that the overall prediction error of the model changed little, with an average MAPE of 5.02% (Fig. 5h), indicating that it exhibits strong stability in the face of a certain degree of feature missingness. Furthermore, we set a higher proportion of zero-setting interference (10%, 20%, 30%, 40%, 50%) for the most important key features in Fig. 4f to assess the model’s sensitivity to missing critical information (Fig. S10). The results show that although the error gradually increases with the proportion of missing data, the overall trend is relatively flat, with an average MAPE of 6.93% (Fig. 5i), indicating that the model retains a certain predictive capability even when some core monitoring data is limited. This analysis suggests that although the framework relies on the fusion of multi-source high-quality data, it still possesses a certain degree of universality and applicability under data-constrained conditions.
The model performance is substantially enhanced compared to the domain’s most classical ML approach to dosing control26. Compared to other ML model building strategies, the present study method reduces the amount of more dosage27. Compared to ML methods with similar performance, such as the modeling method of graph attention multivariate time series forecasting, this study performed validation and TEA on real scenarios28.
Discussion
The research on dosing control of water supply plant based on ML has a broad development prospect. With the continuous progress of artificial intelligence technology, advanced methods such as deep learning and reinforcement learning can further optimize the prediction accuracy and adaptive ability of the dosing model. At the same time, the combination of Internet of Things technology and big data analysis to build a smart water system can realize the comprehensive intelligence of water quality monitoring, dosing control and equipment management. In addition, the method proposed in this study carries out multi-objective optimization, which comprehensively considers various factors such as economy, operational efficiency and environmental impact, and significantly reduces the cost of pharmaceuticals and energy consumption by optimizing the dosing strategy, as well as reduces the negative impact on the environment, reflecting a significant comprehensive benefit. In conclusion, the method proposed in this study realizes the total sum benefit of water quality and economy by approaching the threshold of dosing control stage, which has important theoretical value and practical significance.
Although the model demonstrated robust performance in both laboratory and real-world settings, the current cloud-based deployment still faces limitations in terms of network dependency, latency control, and data security. Programmable logic controller (PLC) integration offers fast response and is suitable for real-time control, but it lacks sufficient computational power to support complex models. Edge computing provides a trade-off between latency and computational capacity, enabling local inference, but involves higher deployment costs and greater maintenance complexity. Future work should explore hybrid architectures combining cloud, edge, and PLC systems to systematically evaluate latency, computational load, reliability, and maintainability under different conditions, thereby enhancing deployment flexibility and practicality. Alternatively, life cycle assessment can be used to provide a more in-depth assessment of economic benefits and long-term environmental impacts. In addition to water supply plants, wastewater plants are another major core component of the water system and require similar dosing of exogenous substances, such as the dosing of external carbon sources, which can be considered as a scenario for the migration of the ML methodology.
Methods
Flocculation dynamics and knowledge embedding
There is a quantitative relationship between flocculants and granules, In flocculation dynamics, the forces driving particle collisions come from two sources: (1) particle collision and aggregation caused by Brownian motion is called perikinetic flocculation (Text S1); (2) particle collision and aggregation caused by fluid motion from hydraulic or mechanical agitation is called orthokinetic flocculation (Text S2). The detailed process is described in Text S1, Text S2. Although perikinetic flocculation itself is not affected by particle size, as particle size increases, the effect of Brownian motion diminishes. To further promote collision and aggregation of larger particles, orthokinetic flocculation is also required. For real water bodies, where perikinetic flocculant and orthokinetic flocculant coexist, the ratio of different collision types is uncertain. In addition, the particle size (d) and collision efficiency (\(\eta\)) also vary with changes in water quality (Text S1, Text S2). Therefore, the accurate dosing amount cannot be described by a quantitative formula, but is more suitable for learning the nonlinear relationship through ML and the types of data collected need to include water quality indicators for different sections of the full process.
How to embed environmental knowledge into the model and thus increase the interpretability of the model is key to the research. The study also considered the economic benefits and energy expenditure. The logical chain of the flocculation process is, addition of flocculant ➝ change in kinetic characteristics ➝ particle flocculation ➝ change in water quality of the flocculation section ➝ change in subsequent water quality ➝ change in water quality of the effluent, and the related economic indicators. Thus, 7 economically relevant indicators (4 electricity indicators and 3 economic indicators recorded by the central server were used as constraints rather than independent variables to optimize the model parameters for use in the training phase, while in the inference and application phases these indicators have been embedded as knowledge in the model (Eq.1, Fig. 1a). Similarly, the metrics before the flocculation segment at timen and after the flocculation segment at timen-1 are used as independent variables, and the metrics after the flocculation segment at timen are used as constraints. The change value features are calculated in real time by the central server along with the results of online monitoring.
\({ML}\) is different machine learning models
\({MLP}\) is different machine learning model parameters
\({WIBC}\) is water quality indicators before coagulation
\({WTIAC}\) is water quality threshold indicators after coagulation
\({PTIAC}\) is power threshold indicators after coagulation
\({ETIAC}\) is economic threshold indicators after coagulation
With the distinction between independent variables and constraints, and then the knowledge of environmental science embedded in the model training process, it is possible to clearly set the problem framework, optimize the calculation process, and improve the efficiency and accuracy of the model. As for the threshold control after the flocculation section, after the disinfection section, and before leaving the plant, the evaluation standard is the closer to the threshold, the better, rather than the lower and lower water quality, the better. Because of the need for water quality, economic costs, and environmental benefits of a comprehensive balance. Finally, an interpretable analysis of the constructed model is performed along with application validation.
Treatment process and data collection
The DWTP from which the data was obtained is located in Guangzhou, China. The design water supply capacity is 800,000 tons per day, the actual water supply capacity is 450,000 tons per day, and the total construction land area is about 180,000 m2. The plant adopts the chlorine disinfection process of pre-chlorination, 3 sodium hypochlorite at the water intake, the disinfection contact pool, and the water delivery pumping station before (Fig. 1a, b). Coagulation chemicals used PAC (Polymerized Aluminum Chloride), the main parameters of PAC are shown in Text S3. China’s current water quality standards for water leaving the plant is GB5749-2022, the water plant to implement more stringent control standards, specifically after the sedimentation tank controls turbidity less than 0.8NTU, after the disinfection tank controls turbidity less than 0.5NTU, the residual chlorine is greater than 0.3 mg/L, the effluent control turbidity is less than 0.3NTU, the residual chlorine is greater than 0.8 mg/L.
To improve the feasibility of the subsequent design, the study selected 38 indicators that can be measured online at most water plants (Fig. 1a). These included 7 raw water indicators,5 influent water indicators, 4 pre-chlorination indicators, 3 sedimentation tank indicators, 3 disinfection indicators, 4 effluent water indicators, 4 electricity indicators and 3 economic indicators recorded by central server, 4 change value indicators by independently designing and calculating, as well as the dosage of PAC (Table S1). The study provided instrument conFig.urations, installation locations, quantities and categories (Table S2). The dataset is divided with a ratio of 8 to 2 between the training set and the test set.
ML principles
For the feasibility of the ML approach, eight ML algorithms were selected for the study29,30,31 (Text S4). It includes Ridge Regression (RIDGE), Support Vector Regression (SVR), Random Forest (RF), Extreme Gradient Boosting (XG), Deep Neural Networks (DNN), Recurrent Neural Networks (RNN), Long Short-Term Memory Networks (LSTM), and Transformer (TF). RIDGE is the baseline model.
RIDGE is a method to improve the stability and predictive power of linear regression by regularizing the penalty term (Fig. 1c). SVR fits linear and nonlinear data via support vector machines (Fig. 1d)32,33. RF is an ensemble learning based on bagging, the subtrees are independent and do not affect each other (Fig. 1e)34,35,36. XG is also an ensemble learning, but it’s based on boosting and the subtrees are dependent on each other (Fig. 1f)37,38,39. DNN consists of multiple layers of neurons and are the simplest deep learning networks (Fig. 1g)40,41,42. RNN captures time dependence in temporal data through cyclic connectivity, but may face gradient vanishing during training (Fig. 1h)43. LSTM controls the flow of information by introducing a gating mechanism that allows the network to selectively retain important information and forget irrelevant information (Fig. 1i)44,45,46. TF captures global information through a self-attention mechanism that allows each input element to be computed in association with all other elements in the sequence (Fig. 1j)47,48,49.
Model interpretability
Shapley Additive Explanations (SHAP) is an explanatory method based on game theory for measuring the contribution of each feature to the prediction results of a ML model50,51. It draws on the concept of Shapley value to derive the contribution value of each feature by calculating the marginal contribution of the features to the prediction in different combinations52,53.The advantage of SHAP is that it provides transparency in model prediction, reveals the specific impact of features on the results, and helps to understand the decision-making process of complex models40,54. During model development, SHAP can help developers identify potential errors or unfair factors and avoid model bias.SHAP is used to understand and validate the ML dosing model in this study.
Subtree depths in Random Forest (RF) can increase the interpretation and understanding of the model. Subtree depth directly affects model complexity, generalization ability, and computational efficiency: trees with greater depth may capture complex patterns but are prone to overfitting, while trees with less depth are simpler and easier to interpret. By adjusting the depth, model performance and interpretability can be balanced to help diagnose overfitting or underfitting problems. In addition, subtree depth affects feature importance analysis and the transparency of decision paths, making the model decision process easier to understand and communicate.
Application feasibility verification
DWTP adopts folded plate flocculation tanks, and the flocculation area is divided into 2 blocks, a total of 8 groups, the length, width and height of each group are 13.75 m, 14.40 m and 7.1 m respectively. Each group of flocculation tank is divided into 3 rows, 2 columns and 6 areas, and the total number of folded plates is 38 blocks. The model constructed during the validation was scaled down 25 times, and the length, width and height of one group were 55 cm, 57.6 cm and 28.4 cm respectively. The designed hydraulic retention time of the flocculation area was 15.1 min, and the designed hydraulic retention time of the sedimentation area was 102 min.
The validation will take place from February 4, 2025 to February 13, 2025, a total of 10 days. There were four sampling time points, 10:00, 12:00, 14:00, and 16:00 daily.The validation was done by directly taking the water before coagulation, calculating the dosing scheme for the original logic of the water plant and the ML-driven dosing scheme, respectively, and mixing the water and the pharmaceuticals through the pump. The water was then fed into two identical downsized flocculation reactors and the coagulated water was left to stand for 102 min to test the indicators. Considering the differences between the reactors and the real water plant, the indicators of the real water plant during the reactor validation were also collected online and used for comparison. All tanks appear in pairs, so separate controls are performed to verify the migratability of the method.
Technical economic analysis (TEA) assesses the economic feasibility, benefits and risks of technologies through quantitative and qualitative analyses, thus providing a scientific basis for decision-making. This study mainly considers the cost of chemical consumption, which mainly includes flocculant (PAC), disinfectant (sodium hypochlorite) and other agents. Other chemicals mainly refer to hydrochloric acid and sodium hydroxide used in backwashing to adjust the pH.
Monte Carlo simulation is an effective numerical method for addressing uncertainty issues, offering advantages such as simplicity of implementation, strong reproducibility, and applicability to perturbation analysis of complex systems. This study introduces this method to assess the robustness of the model under data missing conditions. Specifically, for each specified missing proportion, a corresponding proportion of feature values are randomly selected from the original input data and set to 0 to simulate real-world monitoring anomalies such as sensor failures, communication interruptions, or missing data records. Subsequently, the model is run 100 times based on the disturbed data, and the error from each simulation is recorded. Through statistical analysis of the results from multiple simulations, the performance fluctuations and stability of the model under different missing data ratios can be quantified.
Data availability
The data is at https://github.com/jsdsg666/KERF/blob/main/KERFdatademo.
Code availability
The code is at https://github.com/jsdsg666/KERF/blob/main/KERF.
References
Yamada, Y. et al. Variation in human water turnover associated with environmental and lifestyle factors. Science 378, 909–914 (2022).
Jones, E. R. et al. Sub-Saharan Africa will increasingly become the dominant hotspot of surface water pollution. Nat. Water 1, 602–613 (2023).
Ferraro, P. J. & Prasse, C. Reimagining safe drinking water on the basis of twenty-first-century science. Nat. Sustain 4, 1032–1037 (2021).
Michalak, A. M. The frontiers of water and sanitation. Nat. Water 10–18 https://doi.org/10.1038/s44221-022-00020-1 (2023).
Cherukumilli, K. Evaluating the hidden costs of drinking water treatment technologies. Nat. Water 1, 319–327 (2023).
Chung, M. G., Frank, K. A., Pokhrel, Y., Dietz, T. & Liu, J. Natural infrastructure in sustaining global urban freshwater ecosystem services. Nat. Sustain 4, 1068–1075 (2021).
Turner, S. W. D. et al. Comparison of potential drinking water source contamination across one hundred US cities. Nat. Commun. 12, 7254 (2021).
Nadimpalli, M. L. et al. Drinking water chlorination has minor effects on the intestinal flora and resistomes of Bangladeshi children. Nat. Microbiol. 7, 620 (2022).
Zheng, H. et al. Characterization and Evaluation of Dewatering Properties of PADB, a Highly Efficient Cationic Flocculant. Ind. Eng. Chem. Res. 53, 2572–2582 (2014).
Bazrafshan, E., Mostafapour, F. K., Ahmadabadi, M. & Mahvi, A. H. Turbidity removal from aqueous environments by Pistacia atlantica (Baneh) seed extract as a natural organic coagulant aid. Desalination Water Treat. 56, 977–983 (2015).
Teh, C. Y., Budiman, P. M., Shak, K. P. Y. & Wu, T. Y. Recent Advancement of Coagulation–Flocculation and Its Application in Wastewater Treatment. Ind. Eng. Chem. Res. 55, 4363–4389 (2016).
Ismail, I. M., Fawzy, A. S., Abdel-Monem, N. M., Mahmoud, M. H. & El-Halwany, M. A. Combined coagulation flocculation pre treatment unit for municipal wastewater. J. Adv. Res. 3, 331–336 (2012).
Zhou, Z. Reliable assessment and prediction of moderate preoxidation of sodium hypochlorite for algae-laden water treatment. Water Res. https://doi.org/10.1016/j.watres.2024.122398 (2024).
Yokoyama, H., Yamashita, T., Kojima, Y. & Nakamura, K. Deep learning-based flocculation sensor for automatic control of flocculant dose in sludge dewatering processes during wastewater treatment. Water Res. 121890 https://doi.org/10.1016/j.watres.2024.121890 (2024).
Bankole, A. O. et al. Machine learning framework for modeling flocculation kinetics using non-intrusive dynamic image analysis. Sci. Total Environ. 908, 168452 (2024).
Yamamura, H. et al. Dosage optimization of polyaluminum chloride by the application of convolutional neural network to the floc images captured in jar tests. Sep. Purif. Technol. 237, 116467 (2020).
Wang, Y.-Q. et al. Machine learning framework for intelligent aeration control in wastewater treatment plants: Automatic feature engineering based on variation sliding layer. Water Res. 246, 120676 (2023).
Arab, M. et al. A soft-sensor for sustainable operation of coagulation and flocculation units. Eng. Appl. Artif. Intell. 115, 105315 (2022).
Sela, L., Sowby, R. B., Salomons, E. & Housh, M. Making waves: The potential of generative AI in water utility operations. Water Res. 272, 122935 (2025).
Wang, Y.-Q. et al. Federated Machine Learning Enables Risk Management and Privacy Protection in Water Quality. Environ. Sci. Technol. 59, 10310–10322 (2025).
Wang, D., Wu, J., Deng, L., Li, Z. & Wang, Y. A real-time optimization control method for coagulation process during drinking water treatment. Nonlinear Dyn. 105, 3271–3283 (2021).
Lundberg, S. M. et al. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2, 56–67 (2020).
Wang, Y.-Q. et al. Machine Learning-Driven Dynamic Measurement of Environmental Indicators in Multiple Scenes and Multiple Disturbances. Environ. Sci. Technol. https://doi.org/10.1021/acs.est.5c06126 (2025).
Yu, Y. et al. Revisit the environmental impact of artificial intelligence: the overlooked carbon emission source? Front. Environ. Sci. Eng. 18, 158 (2024).
Tian, W., Fu, G., Xin, K., Zhang, Z. & Liao, Z. Improving the interpretability of deep reinforcement learning in urban drainage system operation. Water Res. 249, 120912 (2024).
Gagnon, C., Grandjean, B. P. A. & Thibault, J. Modelling of coagulant dosage in a water treatment plant. Artif. Intell. Eng. 11, 401–404 (1997).
Wang, Y.-Q. et al. Machine learning strategy secures urban smart drinking water treatment plant through incremental advances. Water Res. 123541 https://doi.org/10.1016/j.watres.2025.123541 (2025).
Lin, S., Kim, J., Hua, C., Park, M.-H. & Kang, S. Coagulant dosage determination using deep learning-based graph attention multivariate time series forecasting model. Water Res. 232, 119665 (2023).
Sun, Y. et al. Application of remote sensing technology in water quality monitoring: From traditional approaches to artificial intelligence. Water Res. 267, 122546 (2024).
Liu, W., Chen, J., Wang, H. & Fu, Z. Perspectives on Advancing Multimodal Learning in Environmental Science and Engineering Studies. Environ. Sci. Technol. 58, 16690–16703 (2024).
Bibri, S. E., Huang, J., Jagatheesaperumal, S. K. & Krogstie, J. The synergistic interplay of artificial intelligence and digital twin in environmentally planning sustainable smart cities: A comprehensive systematic review. Environ. Sci. Ecotechnology 20, 100433 (2024).
Xia, Y. et al. Understanding the Disparities of PM2.5 Air Pollution in Urban Areas via Deep Support Vector Regression. Environ. Sci. Technol. 58, 8404–8416 (2024).
Dai, Y. et al. Prediction of water quality based on SVR by fluorescence excitation-emission matrix and UV–Vis absorption spectrum. Spectrochim. Acta Part A 273, 121059 (2022).
Tesoriero, A. J., Wherry, S. A., Dupuy, D. I. & Johnson, T. D. Predicting Redox Conditions in Groundwater at a National Scale Using Random Forest Classification. Environ. Sci. Technol. acs.est.3c07576 https://doi.org/10.1021/acs.est.3c07576 (2024).
Song, M. J. et al. Identification of primary effecters of N2O emissions from full-scale biological nitrogen removal systems using random forest approach. Water Res. 184, (2020).
Hu, X. et al. Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach. Environ. Sci. Technol. 51, 6936–6944 (2017).
Villanueva, P. et al. One-Week-Ahead Prediction of Cyanobacterial Harmful Algal Blooms in Iowa Lakes. Environ. Sci. Technol. https://doi.org/10.1021/acs.est.3c07764 (2023).
Pan, Y. et al. Machine Learning-Assisted Optimization of Mixed Carbon Source Compositions for High-Performance Denitrification. Environ. Sci. Technol. 58, 12498–12508 (2024).
Li, L. et al. Interpretable tree-based ensemble model for predicting beach water quality. Water Res. 211, 118078 (2022).
Li, X. et al. Accurately Predicting Spatiotemporal Variations of Near-Surface Nitrous Acid (HONO) Based on a Deep Learning Approach. Environ. Sci. Technol. 58, 13035–13046 (2024).
Ma, P. et al. Early Detection of Pipeline Natural Gas Leakage from Hyperspectral Imaging by Vegetation Indicators and Deep Neural Networks. Environ. Sci. Technol. 58, 12018–12027 (2024).
Zhang, D. et al. An optical mechanism-based deep learning approach for deriving water trophic state of China’s lakes from Landsat images. Water Res. 252, 121181 (2024).
Yu, Y., Si, X., Hu, C. & Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 31, 1235–1270 (2019).
Nasser, A. A., Rashad, M. Z. & Hussein, S. E. A Two-Layer Water Demand Prediction System in Urban Areas Based on Micro-Services and LSTM Neural Networks. IEEE Access 8, 147647–147661 (2020).
Liu, R., Zayed, T. & Xiao, R. Advanced acoustic leak detection in water distribution networks using integrated generative model. Water Res. 254, 121434 (2024).
Xie, Y. A hybrid deep learning approach to improve real-time effluent quality prediction in wastewater treatment plant. Water Res. https://doi.org/10.1016/j.watres.2023.121092 (2024).
Baid, G. et al. DeepConsensus improves the accuracy of sequences with a gap-aware sequence transformer. Nat. Biotechnol. 41, 232–238 (2022).
Stebliankin, V. et al. Evaluating protein binding interfaces with transformer networks. Nat. Mach. Intell. 5, 1042–1053 (2023).
Kang, Y., Park, H., Smit, B. & Kim, J. A multi-modal pre-training transformer for universal transfer learning in metal–organic frameworks. Nat. Mach. Intell. 5, 309–318 (2023).
Loh, H. W. et al. Application of explainable artificial intelligence for healthcare: A systematic review of the last decade (2011–2022). Computer Methods Prog. Biomedicine 226, 107161 (2022).
Luo, Z.-N. et al. Enhanced iodinated disinfection byproducts formation in iodide/iodate-containing water undergoing UV-chloramine sequential disinfection: machine learning-aided identification of reaction mechanisms. Water Res. 122975 https://doi.org/10.1016/j.watres.2024.122975 (2024).
Hu, L. et al. Informing Risk Hotspots and Critical Mitigations for Rainstorms Using Machine Learning: Evidence from 268 Chinese Cities. Environ. Sci. Technol. 59, 1619–1630 (2025).
Wang, Y. et al. Predictions of the Optical Properties of Brown Carbon Aerosol by Machine Learning with Typical Chromophores. Environ. Sci. Technol. 58, 20588–20597 (2024).
Lundberg, S. M. & Lee, S.-I. A Unified Approach to Interpreting Model Predictions. NIPS 2017. 30, 4766–4777 (2017).
Acknowledgements
We gratefully acknowledge the financial support by the Fundamental Research Funds for the Central Universities (HIT.DZJJ.2025045), the Shenzhen Science and Technology Program (Grant No. JCYJ20241202123900001), and the POWERCHINA Core Technology Research Project: Research and Development of the Key Technologies and Equipment for Constructing Urban Smart Drainage Systems (No. DJ-HXGG-2022-09).
Author information
Authors and Affiliations
Contributions
Yu-Qi Wang: Conceptualization, Methodology, Data Acquisitions and Analysis, Visualization, Writing the Original Draft. Wenchong Tian: Data Acquisitions and Analysis, Visualization, Writing - Review and Editing. Hao-Lin Yang: Writing - Review and Editing. Yun-Peng Song: Conceptualizatio. Jia-Ji Chen: Methodology.Qiong-Ying Xu: Methodology, Supervision. Wan-Xin Yin: Methodology. Le-Qi Ding: Writing - Review and Editing.Han-Tao Wang: Writing - Review and Editing.Ai-Jie Wang: Writing - Review and Editing, Funding Acquisition.Hong-Cheng Wang: Conceptualization, Methodology, Supervision, Funding Acquisition, Writing - Review and Editing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, YQ., Tian, W., Yang, HL. et al. Knowledge embedding and interpretable machine learning optimize comprehensive benefits for water treatment. npj Clean Water 8, 81 (2025). https://doi.org/10.1038/s41545-025-00510-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41545-025-00510-1