Main

In recent years, a class of objects known as pebbles has received increasing attention in the study of planet formation. Unlike in geology, the precise size of a pebble remains elusive within the field. It is often associated with a Stokes number of St ≈ 1, which indicates a particle that couples to the gas of a protoplanetary disk in a single orbit. For compact particles, this size range extends from several centimetres to a decimetre within the inner few astronomical units of a disk1.

Pebbles play a crucial role, as they serve as a reservoir of particles available for accretion throughout the lifespan of protoplanetary disks. Pebble accretion is proposed as an efficient way to grow terrestrial planets and super-Earths2,3,4. In the earlier stages of evolution, streaming instabilities may gather pebbles into dense clumps that could eventually collapse into planetesimals5,6,7. It is conceivable that such pebbles persist over extended periods, given that collisional growth faces bouncing or fragmentation barriers8,9,10,11,12. However, the precise limiting size remains uncertain.

From a numerical or theoretical standpoint, certain Stokes numbers are deemed necessary owing to the hydrodynamic behaviour, independent of the mechanical properties and collisional outcomes. Generally, centimetre-sized particles might be required13,14. However, from an experimental perspective, millimetres are typically the largest size achievable through hit-and-stick in a standard manner, after which the aggregates encounter a bouncing limit9,15,16,17. Also, recent numerical simulations of collisions converge on the picture that aggregates at the bouncing barrier are rather small18.

Various conditions can locally increase the aggregate size under stickier conditions, such as elevated temperatures that result in water loss or the presence of magnetic fields for particles rich in metallic iron19,20,21. One of the most promising approaches, though, involves the clustering of tribocharged aggregates. This suggests that there is another growth phase beyond the bouncing barrier. As particles collide, bounce off each other and become charged, they can assemble into larger clusters of aggregates, which, eventually, are strongly bound by electrostatic forces. Recent studies indicate the potential of this mechanism for the formation of large clusters22,23,24,25,26. Despite their differing morphology compared to large, compact, dust aggregates, hydrodynamic interactions perceive these clusters as large particles, regardless of composition.

A lingering question pertains to the maximum size attainable by clusters under disk conditions until they encounter the next growth barrier, whether it is cluster bouncing, cluster fragmentation or cluster erosion. These limits remain elusive. Here, we focus on the erosion limit. Erosion is defined as the gradual removal of surface material from a larger body, in our case, through impacts of individual (sub)millimetre grains on a larger cluster of these grains.

We aim to determine the maximum size of a particle cluster capable of withstanding such bombardment in protoplanetary disks. As there will be some transitional range, the core query revolves around the impact speed at which individual grains induce cluster erosion. Upon reaching this limit, more particles are liberated, which become further projectiles that impact aggregates and perpetuate the erosion until the aggregates diminish in size sufficiently for the collision velocities to fall below the erosion threshold.

Suborbital experiment

To study this experimentally, grains need to be charged, clusters of these grains need to be built and these clusters have to be subjected to impacts by individual grains at various speeds. Microgravity is imperative for studying free collisions. Moreover, charged clusters cannot form undisturbed on the ground. The entire process requires minutes to execute. Thus, we conducted a suborbital experiment. A sketch of the experimental set-up is shown in Supplementary Fig. 1. The sample studied essentially comprises identical, monodispersed, basalt beads with a diameter of 0.5 mm. Details of the experimental procedures can be found in Methods.

Upon entering microgravity, the particle reservoir was opened and the particles were gently released through moderate shaking. Through this process, the particles gently collided with each other and gradually assembled into one big aggregate, as depicted in Fig. 1. This is the starting point of our investigations described herein.

Fig. 1: Pebble-sized particle clusters.
figure 1

a, Largest cluster formed in the experiment. It was about 3 cm in length. Unfocused grains are particles at the front window. For reference, individual grains are 0.5 mm. b,c, Numerical simulations of impacts at 0.5 m s−1. The impactor and ejected grains are marked in red. c, With a weak charge, some grains were ejected. b, With a strong charge, no particles were ejected and only the impactor is seen.

Full size image

Results

The experimental chamber was shaken to various degrees. As the granular gas heated up, collisions with a large cluster became fast enough to initiate surface erosion, causing grains to detach from its outer surface. Figure 2 presents a time series of images of an eroding cluster. The shrinking of the cluster was, thus, measured, and its area is marked on the images. Moreover, the erosion was particularly evident for a smaller cluster that was initially present. Owing to its smaller size, the volume reduction was more efficient, leading to its complete disappearance within a few seconds.

Fig. 2: Time series of images of eroded basalt clusters.
figure 2

The clusters shrink as they are eroded by impacts of individual grains. The arrows indicate a smaller cluster that vanished completely over a few seconds. The cross-sectional area A of the large cluster decreased with time.

Full size image

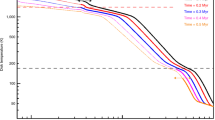
Erosion alters the average brightness of the images27. In our case, the onset of erosion was clearly identifiable by changes in brightness. As the aggregates disintegrated and individual grains became more abundant, the images progressively became more opaque, as depicted in Fig. 3.

Fig. 3: Average pixel brightness of the images over time.
figure 3

a, The range is 0 (black) to 255 (white). Vibrations were started at about 2 to 3 s and were stopped at about 6 s. The times indicated are when the velocity distributions in b–d were taken. Velocities v are 2d projections indicated as index in the y-axis label. b, Velocities at the onset of erosion (t = 4.2 s). c, Velocities at the end of vibrations (t = 6.2 s). Erosion is no longer the dominant process. Therefore, only the largest velocities in a and b are indicative of the erosion threshold. d, Velocities when the dominant collisions are no longer erosive but small aggregates reform (t = 6.5 s).

Full size image

The erosion threshold is defined as the minimum speed at which erosion occurs. We determined this threshold by measuring the velocity of individual particles during erosion. Specifically, we derived the speed from the track lengths of free particles over the exposure time. We analysed the velocity distributions at two distinct stages: when erosion was well underway and when it was about to cease. These distributions are also depicted in Fig. 3. The times at which these velocities were measured are marked by lines and letters (b–d) in the brightness plot in Fig. 3. At t = 6.2 s, the brightness started to increase again, which implies that erosion was no longer dominant. This implies that the highest velocities are indicative of the threshold erosion velocity.

To establish the lower limit, we collected additional velocity data at the point when erosion transitioned back into aggregation. Once the chamber motion had ceased and relaxation slowed the particles down, the brightness increased again and small clusters began to reform (not shown). The remains of the larger cluster then started to collect grains again and regrew. The velocity distribution at this time is also represented as the histogram in Fig. 3d. In comparison to erosion, we found that no particles had a speed higher than 0.3 m s−1.

The collisional outcomes suggest that erosion did not occur below 0.4 m s−1 and that erosion did occur at least at 0.6 m s−1. Thus, the erosion threshold ve = 0.5 ± 0.1 m s−1. All velocities analysed were higher than 0.1 m s−1 at the onset of re-aggregation. This implies that the threshold between sticking and bouncing is larger than this and that 0.1 m s−1 is a lower limit. Importantly, the threshold may depend on the experimental conditions.

Numerical simulations

The cluster observed was surrounded by a cloud of particles and each impact liberated a number of grains locally near the impact point. To supplement our observations, we numerically simulated impacts under conditions closely resembling those of the experiments. Details are given in Methods. To replicate the experimental conditions, we employed an impact velocity of 0.5 m s−1 and observed erosion with weakly charged particles, which ejected a handful of grains. Conversely, strongly charged clusters remained intact at the same velocities and even at velocities exceeding 2.5 m s−1. Figure 1c shows a snapshot of a collision with a weakly charged cluster and Fig. 1b with a strongly charged cluster.

Although the numerical simulations did not precisely replicate the experimental conditions, they provide valuable insights into the role of charge in erosion dynamics. Also note that the charge is usually not distributed homogeneously on the surface, as, for example, seen in measured dipole moments28,29. So, even overall neutral grains can provide strong binding if two spots of opposite polarity on two grains are close to each other. This also supports sticking in cluster–cluster collisions. This mechanism is beyond the scope of this paper. In summary, the numerical simulations, which used similar parameter values as the experiments, found that few or no particles were liberated at certain velocities and charges, which supports the idea that the erosion threshold of a cluster depends on the charges on its constituents.

Discussion

The measured erosion threshold has to be viewed in the context of planet formation. It corresponds to collisions with a cluster several centimetres in size30. That means that the cluster shown in Fig. 1 is actually close to what was expected. Some meteorites largely consist of submillimetre-sized chondrules. Current research suggests that these chondrules gather in particle traps31. In this case, our experiments with solid, monolithic grains are directly applicable. The clusters in our experiments and simulations had an average porosity of between 50% and 60%. Outside chondrule regions, clusters in disks initially consist of dust aggregates rather than monolithic grains, and the sizes and material compositions may be somewhat variable. From recent drop-tower experiments, we know that dust aggregates can become charged to the same order of magnitude and that this charge can also promote cluster growth at speeds beyond regular bouncing (Onyeagusi et al., manuscript in preparation).

The detailed influence of parameter values is, at present, somewhat speculative, but some trends can be identified. Smaller constituents tend to form more ruggedized, charged clusters, as found in test measurements performed before the experiments reported here. These used 0.2 mm basalt particles instead of 0.5 mm. Moreover, centimetre-sized aggregates were incredibly hard to shatter, although we did not quantify this further. As there may be further variations due to material or temperature, we cannot yet give the final cluster size limit for every location within a disk.

Erosion as a limiting factor has also been studied numerically, for example by ref. 32 and ref. 33, and experimentally in ref. 34. These simulations were of very small projectiles at a dust grain level. They found that erosion thresholds were more of the order of 10 m s−1. This is way beyond the phase we considered here but is relevant for collisions in later phases of planetesimal and disk evolution.

Charging versus discharging

The application to protoplanetary disks requires that electric charges can persist on dust aggregates. This cannot be taken for granted. This is not a dominating topic for laboratory experiments, as the collisional timescales in a laboratory or suborbital flight are only minutes and very different from collisional timescales in protoplanetary disks. In disks, collisions could regularly occur on a timescale of years or less35. Trapping, for example, in pressure maxima or vortices, which leads to higher particle densities, could reduce this timescale to months, weeks or less. In any case, this is a long time. If the dust aggregates are conductive enough—and low conductivity should do—then the different polarities may eventually cancel out over these timescales. This would leave behind a neutral aggregate or cluster. The latter may not even have formed, though. Also, particles in a (weakly) ionized disk could be charged and discharged by electrons and ions, which could prevent growth at the surface of protoplanetary disks36,37. We do not consider this to be important in the midplane. To quantify this, we also measured internal and external discharges38. We found that charges could feasibly stay on particles for weeks or years. Dust aggregates should, therefore, be capable of holding on to their charges for long enough.

Conclusion

From the current suborbital experiment, we obtained an initial estimate for the size limit of a cluster grown from charged particles, which probably ranges from centimetres to a decimetre. Therefore, the cluster depicted in Fig. 1 could serve as a close representation of the largest clusters in protoplanetary disks. Erosion occurred at approximately 0.5 m s−1 for our sample. Interestingly, this is not substantially different from the lower limit sometimes assumed as a size-independent value for the fragmentation of large dust aggregates11,12. Although collisions between aggregates with the same size could yield different results, fragmentation speeds may not necessarily be much lower.

The high destructive threshold speeds measured here are for centimetre-sized particles. It is crucial to highlight that growth solely from uncharged dust would not permit the formation of such large entities, as clusters would be dismantled by particles moving at speeds of millimetres per second15. Charge aggregation presents a feasible explanation for the previously assumed large fragmentation speeds, although the presence of charge may introduce further complexity into the collisional growth dynamics.

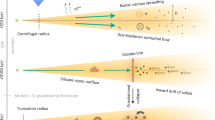
Within an erosion limit, particles have the potential to bounce, acquire charge and cluster into sizes susceptible to capture by streaming instabilities, eventually leading to gravitational collapse into planetesimals. This view is schematically visualized in Fig. 4.

Fig. 4: Bypassing the bouncing barrier.
figure 4

In protoplanetary disks, dust particles can grow up to a millimetre by hit-and-stick. Bouncing prevails at this size. Decimetre-sized particles could further evolve into planetesimals. This leaves a size gap. The stability of tribocharged clusters can overcome this size gap in planetesimal formation.

Full size image

Methods

Experiments

The experiment described here flew as a European Space Agency payload on MASER 15 in November 2022 from Kiruna in northern Sweden. It was engineered by the Swedish Space Corporation. The experimental set-up is shown in Supplementary Fig. 1. Before the launch, the experimental chamber was evacuated to 10−4 mbar. The temperature of the experiment was between 274 and 301 K during the whole procedure.

The entire chamber can be shaken in a single direction. This was carried out for about 30 min before the launch. The experiment commenced within minutes after the cessation of shaking. The particles remained charged for the duration of the experiment38. The entire duration of microgravity could be used to study particle evolution. The sample particles were confined in a dedicated compartment during shaking, and its walls were coated with the same particles. The shaking induced collisions between grains, leading to tribocharging. Due to the identical natures of the particles, there was no predictable preference for the charging, resulting in random net charges with positive or negative polarity and multipole charge patterns on their surfaces22,28,29,39,40.

The wall coating mitigated any net charge bias due to the different materials (basalt, metal or glass) and sizes (curvature of the wall and the curvature of the spherical particles), thus ensuring that the particle cloud was neutral overall, as observed in previous experiments22. These and similar experiments with monodisperse glass and basalt particles of comparable size revealed in more detail the exponential distribution of the net charges on the grains, which typically ranged between 106 and 108 elementary charges22,41,42,43. These values served as benchmarks for weakly and strongly charged clusters in our simulations.

The experimental chamber underwent shaking with a large amplitude of 2.5 mm and a frequency of 20 Hz for several seconds. This accelerated along the direction of shaking some leftover particles that were initially near the walls. These grains transferred momentum to others away from the walls, heating them akin to a granular gas and ultimately randomizing the particle motion.

Numerical simulations

We used the open source DEM package LIGGGHTS v.3.8. We employed a dissipative Hertzian contact model (gran model hertz in the LIGGGHTS implementation), as described in ref. 44 with linearized Johnson–Kendall–Roberts cohesion (skrj2). We generated a cluster of particles with the following properties. The particle diameter was set to 0.5 mm. The surface energy density in this model was set to 7 × 104 ergs cm−3, equivalent to a surface energy of ~0.9 mJ m−2 in the full Johnson–Kendall–Roberts contact. This value is on the lower end of reference values to accentuate the effect of charge on the granular dynamics. Charges were assumed to be homogeneously distributed on each grain. They were drawn from normal distributions with two different standard deviations: σw = 106e for the weakly charged cases and σs = 108e for the strongly charged cases.

To generate a compact cluster like that in the experiment but within a manageable simulation time, particles were dropped into a conical mesh with a flattened ground at 0.1g of gravity. The mesh was vibrated to allow the particles to reposition according to their charge. After settling, gravity was set to zero and the mesh was removed. Further simulation parameters were a Young’s modulus of 5 × 107 Pa, a Poisson ratio of 0.2, a coefficient of restitution of 0.95 and a coefficient of friction of 0.15. Increasing the cohesion energy density to 105 erg cm−3, corresponding to a surface energy of ~10 mJ m−2, raised the limit for ejecta production above 0.5 m s−1 impactor velocities as well. A visual inspection revealed structural differences between weakly and strongly charged clusters, with the latter resembling the experimental conditions more closely.