Main

In the cold, dense molecular clouds where stars form, carbon and oxygen atoms are carried predominantly on icy grains by H2O and CO, which are the second and third most abundant molecules after H2. A third ice species, CO2, is expected to carry a substantial amount of carbon as well, although the final abundance of CO2 depends on whether it formed early within H2O-rich ice or later within CO-rich ice1. The fundamental vibrational modes of all three ice species have proven to be powerful tracers of the complex physics and chemistry in star-forming molecular clouds2,3,4, where they are typically seen in absorption against infrared continuum sources1. Despite the importance of these ices, few studies have obtained measurements of all three species within the quiescent regions of molecular clouds where they first form, as the two main vibrational absorption features of CO2 (4.27 and 15.2 μm (refs. 5,6)) and the blue wing of the H2O stretching mode vibration at ~3 μm are blocked by Earth’s atmosphere. Only space infrared telescopes, such as ISO and AKARI, can simultaneously observe these two ice species along with the stretching absorption mode of CO at 4.67 μm (refs. 6,7,8,9,10).

Previous generations of infrared space telescopes have been able to detect thermally processed ices towards several hundred lines of sight probing protostellar envelopes1,8,11, where star formation has already begun. However, the background stars that provide the infrared continuum needed to detect pristine ices absorbing in prestellar environments, such as foreground molecular clouds, were typically too faint for those observatories. Therefore space observations of ices in dense clouds were biased towards the brightest individual lines of sight sampled from individual clouds, for a total of 23 background star spectra in which all three main ice species were detected8,10,12,13,14,15,16,17,18,19,20,21,22,23. So far, no studies have observed large numbers of background stars towards a single molecular cloud on spatial scales comparable to the size of protostellar cores, which limits astrochemists’ ability to compare the primary solid-state carriers of carbon and oxygen across different physical conditions.

To overcome the limitations of extrapolating observations of multiple clouds and to determine spatially resolved abundances across a given cloud, spatially resolved ice mapping is necessary. Within the same cloud, ice mapping can determine whether common formation conditions give rise to a common chemistry or whether local variations can be observed. The first ice map collated individual ground-based observations (from the PASP2 spectrophotometer on the Wyoming Infrared Observatory and the Mount Lemmon Observing Facility) of a single ice species, H2O, towards 61 lines of sight through a 1.58-square-degree region of the Taurus molecular cloud complex16. More recent efforts have mapped the abundances of the three major ice species H2O, CO2 and CO towards several embedded protostars in the Ophiuchus-F star-forming core with a spatial resolution of ~5,000 AU (ref. 24) or multiple lines of sight across four cores with spatial resolutions as high as ~2,200 AU (ref. 25). Both studies showed that CO2 formation occurs in both the H2O-rich and CO-rich phases of ice formation and, importantly, that there is chemical variation within individual clouds that can be revealed only by comparing multiple lines of sight. The latter study also demonstrated the improved efficiency gained by mapping ices towards multiple lines of sight concurrently using slitless spectroscopy.

The new infrared space facility, the James Webb Space Telescope (JWST), has the spatial resolution, sensitivity and wavelength coverage to make superlative ice observations and small maps of heavily extincted single sources26,27,28,29,30. It has two undemonstrated observing modes capable of mapping ices on spatial scales of a molecular cloud: NIRSpec’s micro-shutter assembly multi-object spectroscopy (MSA MOS) mode31 and NIRCam’s wide-field slitless spectroscopy (WFSS)32 mode. Here, we demonstrate the power of NIRCam WFSS by tripling the total number of detections of all three main ice species towards background stars. These measurements, made simultaneously towards a single molecular cloud core, allow us to test whether we detect a dramatic increase in CO2 ice predicted by the onset of CO ice freeze-out. We present ice maps of H2O, CO and CO2 constructed from observations of 44 lines of sight towards the Chamaeleon I (Cha I) molecular cloud with a median spatial resolution of ~2,000 AU and probing resolutions as high as 250 AU. Our sample size is similar to that in the H2O map of ref. 16, but over only 0.0017 square degrees, that is, with an improvement of three orders of magnitude in spatial sampling and covering multiple ice bands simultaneously.

Results

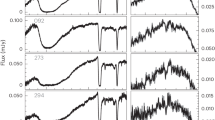
Observations of Cha I were made with the NIRCam WFSS spectral mode using two different filters to cover the 2.5–5 μm spectral region. Each observational set-up had a different footprint (Methods and Extended Data Fig. 1). Within the overlapping region in the densest part of Cha I, 44 spectra were extracted containing absorption features of all three major ice species: H2O (3.0 μm), CO2 (4.27 μm) and CO (4.67 μm). Figure 1 shows five representative 2.5–5 μm spectra extracted from NIRCam WFSS spectral frames as detailed in the Methods. Objects are ordered from top to bottom in decreasing flux density, spanning values from ~0.5 mJy down to ~0.01 mJy at 4.1 μm. The spectra exhibit deep absorption features corresponding to H2O, CO2 and CO ices, while less intense ice absorption features including the so-called dangling OH features33 (~2.7 μm), OCN− (4.59 μm) and the 13C isotopologues (4.38 and 4.78 μm)27 as well as grain scattering signatures34 can also be observed, most easily in the highest-flux sources.

Fig. 1: The 2.5–5 μm spectra along five lines of sight towards background stars behind the Cha I molecular cloud.
figure 1

Objects #077 (NIR38), #268, #273 (J110621), #265 and #267 are ordered from top to bottom in decreasing flux at 4.1 μm and are representative of the dataset, spanning flux values from ~0.6 mJy down to ~10 μJy. All spectra include absorption features corresponding to H2O (3.0 μm, blue), CO2 (4.27 μm, purple) and CO (4.67 μm, green) ices. Sources NIR38 (object #077, top panel) and J110621 (object #273, third panel), whose spectra were recently published27,33,34, were the two background stars with known coordinates in the observed field of view before these JWST measurements. Pixel-to-pixel variation results in occasional large error bars (blue-grey); see Methods for details of the strategy developed in-house to extract several tens of spectra from a single spectral frame.

Full size image

The brightest source in our sample is NIR38 (object #077, F4.1μm ≈ 0.5 mJy)27, a background star of spectral type K7V34 that is fainter than the faintest background star sources extracted from slitless spectroscopy measurements with AKARI, that is, the next-most sensitive infrared telescope with a sensitivity limit of ~1 mJy (ref. 10), and orders of magnitude lower in flux than background stars observed with Spitzer (fluxes ~100 mJy (ref. 35)) or ISO (fluxes ~10 Jy (ref. 15)). At this flux density, signal to noise (S/N) is high in the JWST spectra (for NIR38, S/N of 140 at 3.97 μm; see ref. 27 for the equivalent NIRSpec Fixed Slit value), and any apparent variability in the baseline (for example, between 2.5 μm and 2.7 μm or around 4.5 μm) can be attributed instead to gas-phase absorption features in the stellar photosphere of the background star36. Upon visual inspection, absorption bands of H2O and CO2 can be seen to be saturated (zero flux and flat) for the brightest spectra in Fig. 1. At lower flux densities, the inherent noise level in the spectrum becomes comparable in intensity with stellar photospheric features and with some very weak solid-phase absorption features such as 13CO (ref. 37), 13CO2 (ref. 5) or dangling OH (ref. 33), but the pixel-to-pixel variations begin to dominate the extraction only at fluxes approaching the sensitivity limit of the JWST (~μJy). The extraction limit set for these observations is 2 μJy, corresponding to the limit beyond which errors in background correction or spectral extraction dominate the extracted flux (see Methods for technical details). Owing to the high S/N of spectra down to fluxes of approximately a few microjanskies, column densities of H2O, CO2 and CO could be derived for tens of lines of sight from a single set of NIRCam observations in the region where spectral coverage of all three species was achieved.

Figure 2 shows the H2O, CO2 and CO ice column density distributions, on the left-hand side plotted on a log scale as a function of right ascension (RA) and declination (dec.) position in a ~6.2 arcmin2 field around the most extincted star-forming core of the cloud. This area corresponds to the region within which 44 spectra were observed for objects in which all three molecular species were detected (see Extended Data Fig. 1 for the spatial coverage of H2O, CO2 and CO across the wider cloud and Extended Data Fig. 2 for the object positions). These ice maps cover the densest region, including the deeply embedded Cha MMS1 class 0 protostar38 (which was not detected at all in these JWST observations), and the two lines of sight towards the background sources NIR38 and J110621, whose spectra were previously reported27,33,34. All eight spectra presented in ref. 33 are included in these maps. Column density derivation and map construction are described in the Methods and illustrated in Extended Data Fig. 3. Column density values are provided in Table 1 and are presented as a function of H2 column density on the right of Fig. 2. This is the first time that such a large dataset of this kind has been assembled for a single molecular cloud. The combined dataset of background star spectra collected by previous space missions (ISO, Spitzer and AKARI) and ground-based telescopes numbers in the few tens, does not always cover the same spectral range and is spread over multiple molecular clouds1.

Fig. 2: Cospatial ice maps and correlations of ice column densities with H2 column density in Cha I.
figure 2

Left, cospatial ice maps of H2O (blue), CO2 (purple) and CO (green) column densities across the 44 sources where all three ices were detected towards Cha I. The positions of the 44 individual background sources are indicated by circles with a symbol size reflecting the object’s flux density at 4.1 μm, with the background stars NIR38 (NE) and J110621 (SW)27,33,34 labelled in white. The positions of the deeply embedded class 0 YSO Cha MMS1 and a possible prestellar core identified by ref. 38 are indicated by a yellow star and a white cross, respectively. The log-scale H2 column density contours derived from Herschel far-infrared observations39,40,41 are overplotted. For details of the ice map construction, see Methods. Right, correlation plots for H2O (blue), CO2 (purple) and CO (green) column densities against H2 column density. Open symbols denote sources for which there was partial wavelength coverage of the H2O absorption band. Ice column densities are presented as mean values with error bars of 95% confidence intervals, except for open symbols where the extremes of the fitted templates were used (see Methods for full details).

Full size image
Table 1 Ice column densities for lines of sight towards Cha I
Full size table

In the cospatial ice maps in Fig. 2, the observed column densities of the three species can be easily compared. We observe that H2O is the most abundant of the three species across the mapped region, with column densities typically around double that of the other two species combined. The maximum column densities of H2O ice (9.6 × 1018 cm−2), CO2 ice (4.0 × 1018 cm−2) and CO ice (3.7 × 1018 cm−2) are indicative of the absolute ice column densities, which remain large across the region probed, representing the most extincted part of Cha I, where the visual extinction may reach values in excess of 100 mag (ref. 38). In Elias 16, the only background star towards which ice was extensively probed with ISO, the column densities of H2O, CO2 and CO were 2.5 × 1018 cm−2, 4.6 × 1017 cm−2 and 6.5 × 1017 cm−2, respectively8. These values measured towards the Taurus molecular cloud lie on the lower end of the columns probed in our study. In Cha I, most CO ice column densities exceed 1018 cm−2 but are typically lower than this along lines of sight towards quiescent regions1. Generally speaking, the ice column density broadly follows the H2 contours (that is, the dust density)39,40,41 with the darkest regions of the ice maps (highest ice column densities) coinciding with the highest-density regions towards Cha MMS1. This is as expected given that, if there is more dust present along a line of sight, there will be more ice1,11,23. However, the ice maps and correlation plots also clearly illustrate that the relationship is nonlinear, and one would not be able to precisely predict the ice column density just by knowing N(H2) (Extended Data Fig. 4). It should be noted that the density of background sources decreases as we move to the densest part of the cloud, coherent with the high gradient in N(H2) rapidly obscuring the lines of sight at the highest column.

Discussion

Differences in the relative abundances of H2O, CO and CO2 are key to unravelling which chemical pathways are active in the darkest regions of molecular clouds. In Fig. 3 (left), we present novel maps of the ratios between column densities of CO, CO2 and H2O ices that highlight spatial variation in these species across the observed field of view. More traditional correlation plots are shown in the right-hand panels, while in Extended Data Fig. 4 we compare the ice column densities at high extinction in Cha I with those observed at lower columns from available data across multiple clouds in the literature. Overall, the correlations observed previously at lower extinctions globally hold for column densities an order of magnitude higher, that is, total ice column densities greater than 1019 cm−2 for these three major ices. Despite the increase in cloud depth probed by these observations of Cha I, the correlations between all three ice species are broadly constant across the cloud, probably because the field of view is restricted to the densest regions of the Cha I cloud. However, there are small but consequential spatial variations in the ice abundances that can be seen in the ice ratio maps (Fig. 3). In addition, by following the trends in the ice ratios as a function of variation in the Herschel-derived H2 column density contours, we can trace the dependence of ice ratios on density. For example, it can be seen that, where the dust column densities are lowest, the CO2/H2O ratio exhibits its lowest values (~0.15), while this ratio increases steadily to ~0.4 towards the densest observed region of the Cha I cloud. The ratio map of CO and H2O shows that the CO abundance is greatest in the same dense regions where the CO2 abundance peaks.

Fig. 3: Correlations between the three main ice species, H2O, CO and CO2, in Cha I.
figure 3

Left, maps of the ice ratios CO2 to H2O, CO to H2O and CO2 to CO. These maps are obtained by dividing one ice species' column density map (Fig. 2) by another. Right, correlation plots between CO2 and H2O, CO and H2O, and CO2 and CO measured towards background stars. Ice column densities and errors are presented as those in Fig. 2. Our data for Cha I are compared with literature values from studies on all three main ice species in Extended Data Fig. 4. The two representations of the same ice column density correlations allow visualization of the distribution as a function of spatial position (left) or total column density (right).

Full size image

We can interpret these results in terms of the chemical pathways by which the different ice species form. Whereas H2O is known to form on the grains in molecular clouds, CO is already present in the gas phase and freezes out—either trapped within the H2O layer as the ice is forming, owing to temporary sticking and entrapment, or predominantly during the catastrophic freeze-out that accompanies core collapse42,43. CO2 has been observed to form either early, in a water-dominated ice, or later in a CO-dominated ice1,6,10,17,44. These maps suggest that we not only see the formation of CO2 in H2O ice but also probe the onset of the CO2 formation within the CO ice at higher densities. Because this region of Cha I is denser compared with previously observed targets at lower extinction, more CO should be frozen out, subsequently enabling more CO2 ice production on the grains. The amount of CO ice on the grains suggests that CO freeze-out is well underway, although gas-phase data are needed to determine how complete the freeze-out is. Consistent with increased CO freeze-out, the CO/H2O ratio increases towards the densest region of the map, where Cha MMS1 is located. We see two additional regions with high CO/H2O, at around 5,000 and 10,000 AU southwest of the position of this class 0 object. Both appear along a dense dust ridge, with the second clump being in approximately the same location as (around 2,000 AU southeast of) a potential prestellar core identified in the Herschel dust maps38. The greater sensitivity of JWST allows access to such lines of sight in a cloud.

To see whether there are substantial differences in composition between our results for the three major ices in a single molecular cloud with literature results from a melange of different clouds, we plot the Cha I data against the existing literature in Fig. 4. The ternary plot presented on the left clearly illustrates that our single observational dataset with 44 new objects has tripled the total number of molecular cloud H2O–CO2–CO ice abundance values derived from background stars. In the plot, most Cha I data points fall within the preexisting spread, although overall tending towards higher CO2 and CO contributions than the datasets in Fig. 4. This is not unexpected; the Cha I dataset probes higher extinctions than previous molecular cloud studies, and thus we expect higher CO abundances due to probing more advanced stages of freeze-out. This can be seen on the right of Fig. 4 where the mean and median values of our whole sample are plotted against the ensemble of background star sources from the ternary plot. The median values in Cha I are 29.3% for CO2/H2O and 33.8% for CO/H2O compared with 16.9% and 27.0%, respectively, in the literature values. The lower panel shows data for the five individual lines of sight in Fig. 1. It is immediately apparent that there are considerable variations in relative ice abundances of the three major ice species. CO2 is one of the more difficult of the major ice species to quantify and compare between different observational campaigns, as it can be observed only from non-ground-based observatories, often by only one of its two fundamental modes (at 4.27 or 15.2 μm), and may be quantified using different band strengths. Our values for Cha I are narrowly clustered at 15–25% of the total ice mixture and near the upper end of CO2/H2O ratios previously probed across a range of different molecular cloud environments in H2O, CO2 and CO.

Fig. 4: Comparison of ice column densities in Cha I with other clouds.
figure 4

Left, the total ice column densities presented as a ternary plot, showing the sum of the fractional column densities for the three ice species, that is, [H2O] + [CO2] + [CO] = 1 for each object. Marker size corresponds to the total ice column density \({N_{{{\rm{H}}_{2}}{\rm{O}}}}\) +  \({N_{{{\rm{CO}}_{2}}}}\) + NCO. The 44 Cha I lines of sight are marked in black. Literature data points for other cloud background stars are shown in coloured symbols: red from ref. 8, orange from ref. 20 including data from refs. 12,13,14,16,19, pink from ref. 22 including data from refs. 12,13,14,16,17,18,21,23, and cyan from ref. 10. Note that the axis ranges are truncated for all three species, but the range sampled in each case is 0.55 (for CO and CO2 we plot 0–0.55, while for H2O we plot 0.45–1). Right, the relative column densities of CO and CO2 to H2O for the five representative spectra shown in Fig. 1 are plotted as bars in the bottom panel, with \({N_{{\rm{CO}}}}/{N_{{{\rm{H}}_{2}}{\rm{O}}}}\) in green and \({N_{{{\rm{CO}}_{2}}}}/{N_{{{\rm{H}}_{2}}{\rm{O}}}}\) in purple. The error bars on the ratios are the propagated column density errors. \({N_{{{\rm{H}}_{2}}{\rm{O}}}}/{N_{{{\rm{H}}_{2}}{\rm{O}}}}\) = 100% is marked as a dashed blue line. Median and mean values for the 44 objects in this study and the 23 background stars for which all three ices have been measured in the literature are shown in the top panel for reference. In each case, the median abundance of CO and CO2 ice (relative to H2O ice) is indicated by the orange line on the bar and the mean is shown as a solid black line. The coloured bar (green for CO and purple for CO2) displays the range lying between the first and third quartiles of the data (interquartile range). The dashed black lines show the first quartile minus 1.5 times the interquartile range and the third quartile plus 1.5 times the interquartile range. Data points outside of this range (outliers) are shown as black crosses.

Full size image

In dense clouds, a large fraction of atomic oxygen is locked into dust components, with roughly 16–24% in refractory silicates45. At the high densities probed here in Cha I, the observed H2O, CO2 and CO ices are abundant species that also contain a large fraction of the available oxygen. Cosmic O abundances are debated, but studies typically find a value in the 450–575 ppm range46,47,48. When we compare the O component from our derived ice column densities with the H2 column density estimated from far-infrared emission39,40,41, we observe high levels of O depletion of 255 ± 113ppm (the error is given as two times the standard deviation on the mean, 2σ) over the range of sampled H2O ice column densities spanning an order of magnitude. Although we include the major species, this total O-bearing ice column remains a lower limit because we do not include less abundant species (such as CH3OH, OCN− or complex organic molecules). Their inclusion will moderately increase this estimate at the H2 densities considered here. Although the H2 column density was taken from dust emission studies39,40,41 and intrinsically has uncertainty in the absolute value, the O/H numbers derived here make H2O, CO2 and CO ices the major O-containing species at the high densities probed in the central region of Cha I, effectively locking up in the ices about half of the oxygen, that is therefore not available for gas-phase chemistry. This calculation is consistent with most of the CO being frozen out. Previous estimates of CO freeze-out towards NIR38 and J110621 found that the carbon-rich ices could account for at most ~40% of the expected CO gas column, based on preliminary extinction estimates27. However, updated extinction values 50% lower were recently found by ref. 34, effectively doubling the expected CO freeze-out to 85%.

In this study, we have focused on mapping ices across the core of the Cha I molecular cloud, where the sensitivity of JWST allowed us to probe ice column densities an order of magnitude higher than previous studies along lines of sight towards background stars. The ice ratio maps in Fig. 3 demonstrate the power of observing several tens of objects in one observation. In particular, compared with the traditional correlation plots, the spatial distribution information reveals lines of sight deviating from the broad trends across the cloud. The power of this type of large-scale survey is that the statistical significance and causes of these deviations can now start to be investigated. This was previously not possible, when lines of sight through an individual cloud or core measured by a single observational campaign were limited to a few objects1, sometimes targeting particular spectral bands17,19. This ice mapping approach could be applied to lower-density cloud regions, including for Cha I using data being acquired with the JWST, complementing the dynamic range of densities that can be probed in a single cloud and extending the investigation to the ice onset at cloud edges. Sampling ice in this way also opens the path to comparing solid-phase with gas-phase maps on a similar spatial scale. Cospatial mapping of the entire molecular inventory, both gas and solid phase, would provide the key to tackling open questions around gas–grain exchange phenomena, such as the CO freeze-out accompanying the transition to higher densities and the impact of such an extreme chemistry switch. Ultimately, placing constraints on the oxygen budget in the ice is decisive for setting the initial elemental budget for subsequent star and planet formation chemistry.

Methods

Outline of the observations

The observing programme from which these results are derived was briefly described elsewhere27,33. The observations and the data reduction method are summarized here and described in detail in Smith et al. (manuscript in preparation). JWST/NIRCam WFSS observations of a region of the Cha I molecular cloud were taken across seven observing periods on 3 July, 11 August and 12 August 2022, as part of the Director’s Discretionary Early Release Science (ERS) programme, IceAge (PID 1309, principal investigator McClure49). Spectral observations covered both Grism C and Grism R dispersion directions, with both the F322W2 and F444W filters, with three primary (set to the INTRAMODULEBOX primary dither pattern) and four subpixel dithers, in a mosaic of one row by two columns or two rows by one column, resulting in up to 48 spectral frames per filter per detected background source, with a total exposure time of 15.5 h. The set-up resulted in full or partial spectral coverage (λ = 2.413 μm to 5.084 μm) for many hundreds of detected background sources behind the most extincted central core region of Cha I, encompassing spectral features from material within the extincted cloud region including the H2O, CO2 and CO ice features (see Extended Data Fig. 1 for filter footprints). A subset (44) of these spectra from the central core region feature in this Article. Eight of these spectra were presented in a recent study where the dangling OH stretching mode absorption features of H2O at ~2.7 μm were detected for the first time33. Two of those eight NIRCam spectra correspond to the background stars NIR38 (11:06:25.39-77:23:15.70, J2000; object #077) and J110621 (SSTSL2J110621.63-772354.1, 11:06:21.70-77:23:53.50, J2000; object #273), which were also observed in pointed observations with NIRSpec Integral Field Unit and Mid-Infrared Instrument (MIRI) Low Resolution Spectroscopy spectrometers by the JWST ERS programme Ice Age27,34,49. The lines of sight towards NIR38 and J110621 have been extensively analysed to determine the chemical composition of the ice27 and the extent to which icy grains have grown relative to the diffuse ISM grain distribution34. Short-wavelength imaging was obtained concurrently with the spectral frames, in F150W (with F322W2) and F200W (with F444W). To generate the source catalogue and photometry and subsequently extract the dispersed spectral data, these short-wavelength imaging frames as well as additional direct imaging, using F182M and F430M (with the F444W filter) and F140M and F410M (with the F322W2 filter), were used.

Data reduction and spectral extraction

The data reduction pathway and spectral extraction from the crowded fields in our NIRCam WFSS data are briefly outlined in ref. 33. Data reduction starts with image processing, which follows that in ref. 50, combining the outputs up to and including stage 2 of the JWST/NIRCam direct imaging operational pipeline with custom treatment of NIRCam direct images by members of the NIRCam calibration team51,52. Direct imaging frames (F150W, F200W, F410M and F430M) were cleaned, astrometry corrected with Gaia data, cross-matched and mosaicked. Individual source catalogues for each filter were derived from the mosaicked image in a three-step approach. First, photutils was run to derive an initial catalogue, optimized to identify point sources. Manual corrections were performed to remove the small number of false positives, such as hot pixels, and to add in extra sources of extended geometries, such as galaxies or jets. Finally, the peak_finder function from photutils was used to ensure that the manually added positions were accurately centred on their sources. The final source catalogue was made by combining the source catalogues from the individual filters.

The standard JWST WFSS spectral pipeline products fail to produce accurate spectra in confused fields such as Cha I. The custom spectral extraction programme developed by the IceAge ERS team is briefly outlined here. To obtain the final spectral data, we first reduced each individual grism spectroscopic image frame with the standard JWST calibration pipeline v1.6.2 up to and including stage 2a, using the default Calibration Reference Data System (CRDS) set-up with JWST’s operational pipeline, OPS, and no modifications (CRDS context 0953), as reported previously27. Following this, flat-field correction was applied using the imaging flat data obtained with the same filter, then two-dimensional sky-background subtraction was performed using sigma-clipped median images that were constructed from our spectral frames.

Beyond JWST pipeline stage 2a, an in-house 1D point spread function (PSF) fitting method (as illustrated in Extended Data Fig. 2) was used to extract spectra of each observable source from every individual dispersed frame in the WFSS observations. These individual dispersed frame spectra are then recombined to produce the final spectrum for each source. We were limited to extracting spectral data from sources with flux densities of down to 2 μJy. To extract the flux values at every spectral element of each source’s spectral trace, the 1D PSF fitting is applied to a one-pixel wide, cross-dispersion direction cut-out of the dispersed image, where all the source’s traces that are present are fitted concurrently to correctly attribute flux to the appropriate source in the confused field. χ2 minimization is performed with the iminuit53 Python fitting package to optimize the 1D PSF fit, and WebbPSF (https://www.stsci.edu/jwst/science-planning/proposal-planning-toolbox/psf-simulation-tool) is used to account for positional changes in the PSF on the detector. This provides a wavelength–flux (with flux errors) data point for each source, from each grism spectral frame in which each source appears. This results in up to 48 individually extracted spectra per source, per filter. Because the central region of Cha I is slightly larger than the size of a single dispersed image, some sources near the outer edges of this region are observed in a subset of the 48 dispersed image frames that are analysed here. These individual dispersed frame spectra are all regridded onto a common wavelength grid with 1.006-nm wavelength steps using the SpectRes54 Python package. Once regridded, they are recombined using the weighted median values of each spectral data point from all the individual dispersed frame spectra. The process is repeated for each filter separately. This spectral regridding results in trace lengths of 1,638 for the F322W2 filter (equivalent to ground-based L-band coverage). This is almost equivalent to the preflight-measured F322W2 trace lengths of 1,670. For the F444W filter (equivalent to the ground-based M-band coverage), the trace length is 1,209, again almost equivalent to the preflight-measured F444W trace lengths of 1,249. This means that our spectra have R values very close to those measured preflight for F322W2 and F444W. The preflight R values can be derived for each wavelength using the formula given in ref. 32, and thus, for the reference wavelength of our two spectral filters, we derive R of 1,441 at λref = 3.231976 and 1,654 at λref = 4.404315 μm.

Wavelength and flux calibrations were performed using the in-flight measurements obtained with JWST Commissioning Program #1076 (corrected by CRDS context 1090 in late January 2023 for the flux calibration, and by using the S6 sensitivity curves (private communication Dr Nor Pirzkal) for the wavelength calibration). These updates account for the minor flux and wavelength differences between NIRCam spectral data presented in refs. 27,34 for NIR38, and the spectral data of the same object in this Article and in ref. 33. In some cases, a slight oversubtraction of the local background near the spectral trace during the grism image correction processing stage of the extraction can lead to the PSF fitting returning real spectral shape profiles but (unphysical) negative flux. To account for this oversubtraction in the F444W spectra (where the F410M photometry lies within the filter wavelength range), spectra were shifted up to match the photometric points, a commonplace approach in ice spectral data processing10,11,23,35. Aperture photometry was performed on the F410M mosaicked images, applying a circular aperture with a radius of 4 pixels centred on each source position to determine the source flux, and correcting for the background flux measured within a 10-pixel-wide annulus from 15 to 25 pixels. The sources to which this shift was applied had to match two conditions. First, the photometric flux had to be higher than the average flux of the continuum of a rolling-median-smoothed F444W fully combined spectrum between 4.03 μm and 4.17 μm. Second, the average flux in the peak of the CO2 feature of a rolling-median-smoothed F444W fully combined spectrum, between 4.259 μm and 4.277 μm, had to be negative. The shift applied was the difference between the average continuum 4.03–4.17 μm flux value and the F410M photometric point. The maximum shift applied to a F444W spectrum was 10 μJy. For the F322W2 spectra, there is no photometric point within the filter wavelength range to shift the spectrum to. Therefore to account for the oversubtraction in F322W2 spectra, the average flux in the peak of the H2O feature of a rolling-median-smoothed F322W2 fully combined spectrum between 2.98 μm and 3.1 μm was calculated. If this was negative, a shift equivalent to this value was added to the F322W2 spectrum. The maximum shift applied to a F322W2 spectrum was 2 μJy, that is, the same as the spectral extraction limit. Although, strictly speaking, the oversubtraction of the local background may not be constant along the spectral trace for a given source, the pixel-to-pixel variations in this densest region of the cloud will be extremely low owing to the lack of extraneous light sources.

The total number of detected sources in the imaging frames within the central region of Cha I was 372. After discounting objects below the flux limit for spectral extraction 2 μJy at 4.1 μm and those where the S/N was too low to allow clear detections of all three absorption features for H2O, CO2 and CO ices, 44 lines of sight remain from which to construct ice maps of the central region of Cha I. All objects are identified using their source catalogue IDs. JWST is so sensitive that we now observe lines of sight towards galaxies behind the cloud in addition to the lines of sight that have traditionally been used to probe molecular cloud ices, that is, towards background (field) stars and towards embedded young stellar objects (YSOs). In this case, we can distinguish galaxies from background stars in the direct imaging frames because they are extended sources and not point sources like the background stars. However, we choose not to include the two lines of sight towards galaxies observed in the Cha I central region as (1) there may be issues with undersampling of the flux in these extended sources that are wider than the PSF, and (2) their spectra may intrinsically contain ice absorption features that would confuse the determination of cloud ices.

Spectral analysis and ice map construction

Extracted spectra were analysed to determine ice column densities. The process of spectral analysis is illustrated in Extended Data Fig. 3a. In brief, local baselines were fitted to the continuum around each absorption band using a Gaussian process regression implementation provided by the scikit-learn Python package55. The Gaussian process regression models the baseline as the mean vector of a multidimensional Gaussian probability density function and are fitted to a rolling-median-smoothed version of the spectrum based upon conditioning data points that tether the fit to the continuum at two to three points on each side of each band. The H2O baseline Gaussian process regression model is tethered to flux values at wavelengths 2.55, 2.67, 2.72, 3.86 and 3.91 μm; CO2 at 3.97, 4.1, 4.365, 4.47 and 4.51 μm; and CO at 4.47, 4.53, 4.76, 4.82 and 4.86 μm. The uncertainty at each wavelength in the model is the standard deviation of the Gaussian process along the dimension corresponding to that wavelength, and the best-fitting model minimizes the overall variance, ensuring the statistically most likely baseline.

Optical depth spectra τ(λ) were derived using

$$\tau (\lambda )=-\ln \left(\frac{{F}_{{{\rm{obs}}}}(\lambda )}{{F}_{{{\rm{cont}}}}(\lambda )}\right),$$
(1)

where Fobs(λ) is the observed flux density and Fcont(λ) is the continuum baseline model. In this type of slitless spectroscopy study, where tens or hundreds of spectra are extracted simultaneously, the spectrum-specific approach of deriving column densities by determining the spectral energy distribution of the background source to fit the continuum and correct for photospheric absorption features, then fitting each individual absorption feature with grain shape- and size-corrected laboratory spectra of pure and mixed ices, is very labour intensive. Following a strategy similar to those in studies such as refs. 56,57, the column densities of CO and H2O were determined by integrating the optical depth spectra between two wavelength limits, and dividing by the band strength58. The values are as follows: H2O integrated between 2.716 μm and 3.35 μm, band strength 2 × 10−16 cm per molecule; CO integrated between 4.65 μm and 4.705 μm, band strength 1.1 × 10−17 cm per molecule58. Errors on the derived column densities are computed by applying a toy Monte Carlo approach, based on 1,000 baselines produced from the Gaussian process regression model described above. The column density is calculated for each of the 1,000 baselines, and the final error estimates are determined from the 95% confidence interval (2σ in flux space) on the distribution of derived column densities.

Among the 44 sources analysed here, 11 have truncated or partial spectra across the 3 μm H2O absorption feature due to their proximity to the filter edge. Column densities are estimated for these sources through fitting of a set of nine unsaturated template H2O features measured in mapped regions outside the central region presented here (see F322W2 footprint in Extended Data Fig. 1). This is completed in two stages, illustrated in Extended Data Fig. 3b. First, the template spectra and partial spectrum are shifted in flux space by calculating and subtracting the average continuum flux value of a smoothed (rolling median) spectrum between 3.82 μm and 3.92 μm. The shifted templates are then fitted (rescaled with a limited local y shift) to the shifted partial spectrum to the data points in the range 3.17–3.29 μm, where the best fit is found through χ2 minimization (Extended Data Fig. 3b(i)). The same shift and scale is then applied to the baseline of the best-fit template spectrum, which is used to produce an optical depth spectrum of the truncated source. In optical depth space, the template source’s optical depth spectrum is then fitted by scaling to the partial optical depth spectrum, following ref. 57 (Extended Data Fig. 3b(ii)). The column density of H2O is then derived from the area under the scaled template spectrum, as described above. Column density errors are derived from the extremes of fitted scaled template spectra.

To estimate CO2 column densities, the area under the peak integration method was not used, as illustrated in Extended Data Fig. 3c. After visual inspection of the spectra, it was determined that the CO2 absorption feature was saturated along almost all observed lines of sight (zero flux, with a flat base). Thus, instead of integrating the area under the whole band, the area under the spectral wings of CO2—defined to be between 4.24 μm and 4.249 μm and between 4.281 μm and 4.29 μm (red areas under optical depth spectrum of CO2 feature in Extended Data Fig. 3c)—is first calculated. These wing limits were chosen primarily to avoid the saturated region of the band but also to avoid the edges of the feature where radiative transfer and scattering effects may affect the band profile. The CO2 column densities for saturated bands were derived using NCO2 = α × NCO2,wings, where α is the ratio between the total area under the CO2 band and the area under the wings. This constant was derived from eight unsaturated bands taken from less dense regions of the full cloud area observed (Extended Data Fig. 1) and has a value of 7.62 ± 0.96. CO2 column densities were derived using the band strength 7.6 × 10−17 cm per molecule as reported in ref. 58 based on the original data of ref. 59. Errors on the CO2 column densities are found by calculating the errors on the column density of the CO2 wing regions and applying the same mean ratio scale factor as to the column density itself.

This method for determination of column density via the band wings could not be applied to saturated H2O or CO features within our dataset. As is well known in the field, the derivation of column densities from ice absorption features is complicated by many factors, including but not limited to correct determination of the continuum, overlapping of absorption features from different molecules (functional groups) and scattering due to grain size and shape effects. In particular, for H2O, the broad 3-μm feature’s red wing overlaps with other functional group absorption features from molecules such as CH3OH, CH4 and NH3 and includes a scattering contribution due to the grain size and shape distributions along the line of sight, while the blue wing includes both radiative transfer and extinction effects. For CO, the absorption cross section area is far lower than CO2. In addition to this, CO has a narrower band profile, and so this means only a few spectral elements would be available to define wings from. Within these few spectral elements, noise, potential photospheric lines and radiative transfer and scattering effects cause too much variation in the area under these wings to produce a reliable ratio of wings to total area. Various approaches have been implemented in previous studies to try to mitigate these effects. A few examples include deconvolving spectral contributions from different molecules using laboratory spectra (with or without grain correction)6,10,27, modelling the grain scattering effects2,34 and component fitting across different spectra60. Other studies have taken a more direct approach to estimating the contribution of molecular absorption, using the optical depth as a tracer16, or integrating the area under the peak56,57. As stated above, we adopt a methodology similar to refs. 56,57, and overall, despite the difference in analytical approach, for all three molecules studied here, the column densities derived here agree with those derived by ref. 27 towards the sources NIR38 and J110621. Thus, column densities for all CO and H2O features were derived by integrating the area under the band in optical depth space, as described above.

The derived column densities of H2O, CO2 and CO ice for 44 lines of sight are reported in Table 1. The H2O column densities presented here have been slightly revised compared with those originally presented for objects #077, #085, #089, #092, #268, #273, #282 and #294 in ref. 33, but all values lie within the uncertainties given in Table 1 and this impacts neither the values derived nor the conclusions drawn in ref. 33. For objects #077 and #273, prior quantification of the column densities of H2O, CO2 and CO was derived by two spectral fitting approaches in refs. 27,34. The values derived here for H2O and CO agree with those in ref. 27 within the error bars. It should be noted that, in ref. 27, a band strength of 1.1 × 10−16 cm per molecule was used for CO2, as reported in ref. 61 based on the original data of refs. 58,59. Here, we choose to use the value 7.6 × 10−17 cm per molecule to be consistent when comparing our observations to the CO2 values derived from the 4.27-μm band in literature data from previous studies using ISO and AKARI. For objects #077 and #273, we derive CO2 values of \(1.4{0}_{-0.03}^{+0.03}\) and \(2.7{4}_{-0.04}^{+0.03}\times 1{0}^{18}\) cm−2, respectively, if using the band strength 1.1 × 10−16 cm per molecule. The column densities derived for H2O, CO2 and CO can be converted to total O-in-ice column by: NO = NH2O + 2 × NCO2 + NCO. The O/H ratio for the three ice components is derived by NO/2 × NH2. Our derived O abundance can be compared with the cosmic O abundance to determine the fraction in the ice, corresponding to the O depleted from the gas phase.

To construct ice maps, the discrete natural neighbour interpolation method was implemented for the column density values between each source within the maps. The naturalneighbor Python package (https://github.com/innolitics/natural-neighbor-interpolation) was used to perform this task, the methods of which are outlined in ref. 62. Ice maps were regridded on the same pixel grid as the Herschel high-resolution NH2 maps39,40,41. The interpolated map contains values of column density at all locations within the field of view, regardless of the sparsity (or density) of nearby column density measurements. To avoid including potentially misleading column density values within the interpolated ice maps, regions of the map for which the projected offset from any background source is greater than 4,000 AU are removed (assuming that the distance to Cha I is 192 pc)63. Finally, the boundaries of the ice map were spatially clipped to exclude any region outside a convex hull connecting the outermost mapped sources. This produces a map footprint with primarily straight boundaries and avoids misleading sections at the map boundaries where the interpolated column density value is dominated by the measurement from a single spectrum.