Main

Binaries comprising at least one white dwarf are the progenitors of type Ia supernovae1,2. Type Ia supernovae show an absence of hydrogen in their spectra and are caused by the thermonuclear explosion of a carbon–oxygen white dwarf. Nuclear fusion transforms a substantial amount of, or the entire, white dwarf into heavier elements and ejects them into the interstellar medium. However, the stellar type of the companion to the white dwarf in type Ia progenitors remains largely unclear (see, for example, refs. 3,4,5).

The substantial population size of double white dwarf binaries has naturally led to them being one of the leading progenitor candidates to explain the abundance of type Ia supernovae6,7. These systems form on compact orbits with an orbital period on the timescale of hours to days8 (orbital separations of hundredths to tenths of astronomical units) following a series of mass transfer events9. The gradual loss of orbital angular momentum through gravitational wave radiation draws the two stars closer until the orbital period of massive double white dwarfs is a couple of minutes, initiating unstable mass transfer and leading to the demise of the system10.

Although many compact double white dwarfs have been discovered on the brink of coalescence (see, for example, refs. 11,12,13), we have had no direct evidence that these systems exist in nearby, volume-complete populations14,15,16, which casts doubt on whether double white dwarfs can account for a large percentage of the observed type Ia supernova rates. Current synthetic models of the population indicate that super-Chandrasekhar mass limit double white dwarfs are indeed suspected to be scarce17,18,19. However, based on the models of ref. 17 we expect about 150 compact double white dwarf binaries to have total masses that exceed 1.5 M⊙ within 100 pc, about one quarter of which merge in under a Hubble time. There has been only one super-Chandrasekhar mass double white dwarf binary discovered (NLTT 12758) (ref. 20), but its 1.15 d period means that the two stars will come into contact in about 10 Hubble times. There are a handful of other candidate subluminous type Ia progenitors that are double white dwarfs that have total masses smaller than the Chandrasekhar mass limit (see, for example, refs. 21,22,23,24,25,26), two white dwarf+hot subdwarf systems that exceed 1.4 M⊙ and have an impending supernova fate27,28, and one other white dwarf+hot subdwarf that is also a strong candidate29,30.

Growing observational evidence supports hot subdwarfs as some of the products of binary evolution31, but, although more super-Chandrasekhar mass systems have been discovered, the binaries much less densely populate the Galaxy32. The observed rate of type Ia supernovae initiated from the white dwarf+hot subdwarf channel is expected to be at least (1.5–7) × 10−5 yr−1 (ref. 27), whereas the rate of type Ia supernovae in the Galaxy from all progenitors is about 2.8 ± 0.6 × 10−3 yr−1 (refs. 4,19,33,34) as inferred through observations of explosions in other galaxies of similar redshift. Multiple other evolutionary scenarios have been suggested as causes for normal and peculiar type Ia supernovae4 having different companion compositions, but the extent to which they contribute towards the missing fraction of type Ia supernovae is unclear. This ambiguity on the nature of type Ia progenitors is cosmologically problematic. A primary reason is that, until we confirm the leading progenitors of a type Ia, supernova, systematic errors in the distances derived to other galaxies could lead to inaccurate measurements, which is particularly troublesome for galaxies at high redshifts34,35. In addition, the details of the ejecta velocity and its constituents are important for star formation36 and the dynamics of gas in galaxies37. Not only does the discovery of a local, compact, super-Chandrasekhar mass double white dwarf have the ability to resolve the dearth of systems in the observed sample, but a sample of such systems has the power to reduce the uncertainty of this cosmologically fundamental event.

Results and discussion

Physical and orbital properties of WDJ181058.67+311940.94

WDJ181058.67+311940.94 was first discovered as part of the DBL survey26 which searches for double-lined double white dwarfs using medium-resolution spectra (R ≈ 8,000–9,000). Fits to these identification spectra indicated the source to be a double white dwarf binary with a high total mass. Afterwards, we launched an observational campaign to acquire time-series spectroscopy of the source to confirm the masses derived through the atmospheric parameters and resolve the orbital period. We obtained phase-resolved radial velocities of WDJ181058.67+311940.94 with the following instruments and telescopes: the Intermediate-dispersion Spectrograph and Imaging System (ISIS) on the 4.2 m William Herschel Telescope (WHT); the Intermediate Dispersion Spectrograph (IDS) on the 2.5 m Isaac Newton Telescope; the Fibre-fed Echelle Spectrograph (FIES) and Alhambra Faint Object Spectrograph and Camera (ALFOSC) on the 2.56 m Nordic Optical Telescope (NOT); and a continuous observing window of 4.5 h using the UV-Visual Echelle Spectrograph (UVES) on the 8.2 m Very Large Telescope (VLT).

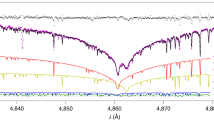
The UVES data was used for an improved accuracy of the atmospherically derived masses from spectral fits because of its full visible coverage. Precise radial velocity measurements of the target were simultaneously obtained and with this an unambiguous determination of the orbital period. As a further test for consistency of the atmospheric solution with a unique dataset, we also fitted a two-star solution to a previously published Hubble Space Telescope (HST) Cosmic Origins Spectrograph (COS) spectrum38. The resultant stellar parameters found by fitting each dataset are quoted in Table 1 and spectral fits to the optical and ultraviolet data are plotted in Fig. 1. Considering the measurements from all datasets, we find stellar parameters of \({T}_{{\rm{eff}},1}=17,26{0}_{-880}^{+1380}\) K, log g1\(=8.35{0}_{-0.052}^{+0.066}\) dex, M1 = 0.834 ± 0.039 M⊙ for the primary (more massive) star and Teff,2 = \(20,00{0}_{-2000}^{+400}\) K, log g2 =\(8.16{4}_{-0.030}^{+0.027}\) dex, M2 = 0.721 ± 0.020 M⊙ for the secondary (less massive) star, leading to a total system mass of MT = 1.555 ± 0.044 M⊙. Teff, log g and M refer to the effective temperature, the surface gravity and the mass of each component, respectively.

Table 1 The atmospheric parameters for each spectroscopic dataset
Full size table
Fig. 1: Atmospheric fits to the photometric and spectroscopic datasets.
figure 1

Left, the HST/COS ultraviolet spectrum with the synthetic spectrum from the hybrid HST/COS with Pan-STARRS photometry fit for a two-star model overlaid in red. The corresponding atmospheric parameters of the DA white dwarfs are Teff,1 = 18,630 K, log g1 = 8.307 dex, Teff,2 = 18,010 K, log g2 = 8.178 dex. Middle, a single UVES spectrum from Hα to H8 with the synthetic spectral model for atmospheric parameters Teff,1 = 17,230 K, log g1 = 8.408 dex, Teff,2 = 20,190 K, log g2 = 8.151 dex, overplotted in red. We remind the reader that all Balmer lines up to H11 were fitted but are omitted from the plot for clarity. Right, the observed fluxes in Pan-STARRS (black circles) and the synthetic photometry in each filter for the same atmospheric parameters (orange crosses). The percentage flux residual between the data and the combined flux is found below. The fluxes contributed from the more massive (red) and less massive (green) stars are included for the ultraviolet (dashed) and optical (solid line) fits. The Gaia parallax measurement with a Gaussian prior was an independent variable to scale the observations from an Eddington to an absolute flux perceived in the Solar System.

Full size image

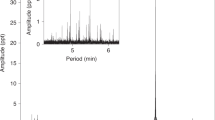
All other data was used exclusively for radial velocity measurements at Hα to precisely quantify the motion of the stars across all orbital phases and to improve the precision of the period. A Lomb–Scargle periodogram of all radial velocity measurements, which was optimized for physical limits of the system, revealed one clear peak representing the orbital period. The binary parameters are quoted in Table 2 and our phase-folded radial velocity (RV) curve with the best-fit orbital solution is depicted in Fig. 2. The best-fitting orbital parameters were orbital period P = 14.23557 ± 0.00002 h, semi-amplitudes K1 = 93.9 ± 2.0 km s−1 and K2 = 95.7 ± 2.1 km s−1, and velocity offsets γ1 = 50.0 ± 1.5 km s−1 and γ2 = 53.5 ± 1.6 km s−1. Being double lined, the mass ratio was independently solvable without knowledge of the orbital inclination using q = M2/M1 = K1/K2, such that the orbitally derived value was q = 0.98 ± 0.03. This result is in best agreement with the star masses derived from the HST/COS spectrum, which was q = 0.90 ± 0.02. Our derived masses from the VLT/UVES spectra yielded a lower q = 0.82 ± 0.02, with the mass of the less massive star being near identical to the ultraviolet, and the adopted value, taking into account all measurements, indicated a mass ratio of q = 0.86 ± 0.04. The surface gravity of the hotter, less massive star was nearly identical across fits to all datasets. This is unsurprising given that it contributes more flux than the cooler white dwarf, whereas its temperature difference between the ultraviolet and optical datasets primarily arises from the fitting of the slope of the spectral energy distribution across the ultraviolet. Forcing the orbitally derived q = 0.98 ± 0.03 in the atmospheric fit led to an increase in the surface gravity of the secondary and a decrease in the surface gravity of the primary, to fit the broadness of the Balmer line profiles well. The secondary would thus be more massive, and the primary less massive, and as such, including a mass ratio of approximately one, all evidence points towards WDJ181058.67+311940.94 being a super-Chandrasekhar mass double white dwarf.

Table 2 Positional, atmospheric and orbital parameters for WDJ181058.67+311940.94
Full size table
Fig. 2: The best-fit orbital solution phase-folded on the orbital period.
figure 2

The hotter star (black) and the cooler star (red). The RV curves are plotted showing the velocity of the two stars across a full orbit, binned into 80 evenly spaced phase bins. In faded colours and with crossed markers are the RVs that were masked in searching for an orbital solution, which are also listed in Supplementary Table 1. One-sigma error bars are given as the standard deviation of 1,000 bootstrapping iterations.

Full size image

The critical time at which the two stars reach closest approach can be calculated using39

$${T}_{\rm{c}}({a}_{0})=\frac{5}{256}\frac{{a}_{0}^{4}{c}^{5}}{{G}^{3}{M}_{1}{M}_{2}({M}_{1}+{M}_{2})}$$
(1)

where a0 is the semimajor axis of the binary at the present day and, for WDJ181058.67+311940.94, a0 = 0.01601 ± 0.00015 A.U. This indicates that the stars will come into contact in 22.6 ± 1.0 Gyr, whereas the less massive component will begin Roche lobe overflow and initiate mass transfer approximately 100 yr before the demise of binary.

Modelling the fate of the binary system

To understand the fate of the binary system, we simulated its interaction when it was just about to merge using the star masses obtained through spectral fits to the VLT/UVES data. Videos of this simulation are presented in the Supplementary Information (Supplementary Videos 1 and 2). The spectral fits indicate that carbon–oxygen cores are appropriate for both white dwarfs, so we consider it highly unlikely that an accretion induced collapse will occur. This would require the more massive white dwarf to have a mass higher than 1.2 M⊙ with an oxygen–neon core to avoid dynamical ignition before or during the merger. We used the moving-mesh code AREPO40,41,42 in a similar set-up to previous work43. The stars were given realistic composition profiles and placed in corotation before applying an accelerated inspiral term that removed angular momentum in the same way as gravitational waves. We switched on a live nuclear reaction network with 55 isotopes43,44 at an orbital period of 39 s as the temperature of the accretion stream at the impact spot approached that required for a thermonuclear runaway. We show an overview of the dynamic evolution of the binary system in Fig. 3. The interaction of the accretion stream with the surface of the primary white dwarf ignites a helium detonation close to the point of interaction (second column of Fig. 3). The helium detonation then wraps around the primary white dwarf and sends a shock wave into its core that converges at a single point. This ignites a second detonation that completely destroys the primary white dwarf. When the shock wave of its explosion hits the secondary white dwarf, the double detonation mechanism repeats itself. The shock wave from the detonation of the primary ignites a helium detonation near the surface of the secondary which drives a shock wave into its core. It is sufficient to ignite the core detonation, destroying the secondary white dwarf as well.

Fig. 3: Time evolution in slices of the binary systems close to merger.
figure 3

The first column shows the time when we stop the accelerated inspiral and continue to evolve the binary system self-consistently. The second and third columns show the time when the helium detonation ignites on the surface of the primary white dwarf, and the time when the shock wave that is driven into the core of the primary by the helium detonation converges in a single point. The fourth column shows the same shock convergence in the core of the secondary white dwarf. The top row shows slices of density in the plane of rotation and the three below are zoomed insets at the point of interest. Top to bottom, density, temperature and kinetic energy density. The shock convergence points in both white dwarfs occur at densities high enough to be very likely to ignite a carbon detonation and destroy the white dwarf.

Full size image

There is no bound remnant and the ejecta of the explosion contain the total mass of the initial binary, having a total explosion energy of 1.2 × 1051 erg. We show the structure and composition of the ejecta in Fig. 4. The outermost layers of ejecta are the ashes of the helium detonation of the primary white dwarf. They consist mostly of intermediate mass elements, dominated by silicon, sulfur and argon. Below them sit the ashes of the carbon–oxygen core of the primary white dwarf. Again they consist mostly of intermediate mass elements, but also contain 0.13 M⊙ of iron group elements, in particular, 0.10 M⊙ of radioactive 56Ni that will power the light curve. The resulting supernova has a maximum brightness in the B band of MB = −16.4 (mB = −14.7) and a maximum brightness in the V band of MV = −17.8 (mV = −16.1), and is most likely to appear as a subluminous type Ia supernova.

Fig. 4: Ejecta profiles after the explosion of both stars.
figure 4

Slices of density (left column) and mean atomic weight (right column) of the supernova ejecta in homologous expansion for a time (texp) 100 s after ignition of the first helium detonation. The top row shows slices in the original plane of rotation and the bottom row shows slices perpendicular to it. The outer layers are close to spherically symmetrical, although significant deviations from spherical symmetry exist in the plane of rotation. The iron group elements (including 56Ni) are essentially all produced in the explosion of the primary white dwarf and form a half-sphere around the ejecta of the secondary white dwarf.

Full size image

Galactic rates of super-Chandrasekhar mass double white dwarfs

We can use WDJ181058.67+311940.94 to observationally predict the number of super-Chandrasekhar mass double white dwarfs in the Milky Way. We start by assuming that WDJ181058.67+311940.94 and NLTT 12758 are the only two within 49 pc and make the rudimentary assumption that double white dwarfs are evenly scattered around the Milky Way having a cylindrical disk with radius Rmax = 15 kpc and scale height hz = 300 pc. The white dwarf birth rate is estimated to be approximately 1.4 × 10−12 pc−3 yr−1 (ref. 45). There are 1,076 white dwarfs within the volume-complete 40 pc Gaia sample16 and extrapolated to 49 pc we would have 1,978 white dwarfs. This means that the birth rate of super-Chandrasekhar mass double white dwarfs in the Galaxy becomes greater than approximately 6.0 × 10−4 yr−1.

Moreover, we can also calculate an observed rate of type Ia supernovae arising from super-Chandrasekhar mass double white dwarfs using WDJ181058.67+311940.94 (Tc = 22.6 ± 1.0 Gyr) and NLTT 12758 (Tc = 139 ± 9 Gyr). The frequency of the two events combined imply a supernova rate of about once every 19 Gyr within 49 pc or (1.04 ± 0.04) × 10−16 yr−1 pc−3. When fully extrapolated with the cylindrical disk approximation, the observed rate of type Ia supernovae from super-Chandrasekhar mass double white dwarfs in the Milky Way hence becomes at least (4.4 ± 0.2) × 10−5 yr−1, although the quoted uncertainty does not account for uncertainties on the Galactic model. This result serves as a minimum based on the 49 pc population as it remains possible that other systems exist within the same radius.

Evidently, the magnitude of super-Chandrasekhar mass systems approaches the (2.8 ± 0.6) × 10−3 yr−1 rate predicted for all evolutionary channels leading to a type Ia (refs. 4,33,34), but we must recall that these two systems are set to come together in more than a Hubble time and consider that the present observed supernova rate from these systems is about sixty times smaller. As such, the rates from Milky Way progenitors through the hot subdwarf binary channel and the double white dwarf channel are about the same, together accounting for about 3% of the Galactic rate. Synthetic populations suspect that around 60% of the Galactic birth rate of type Ia progenitors comes from the double degenerate channel46,47, as is the case for WDJ181058.67+311940.94. The large missing fraction is especially mysterious given the high completion rate of the 40 pc sample of white dwarfs16. Contribution to the double white dwarf type Ia rate from sub-Chandrasekhar mass limits detonation could at least be a partial solution to make up for the deficit, where a mass–period distribution of double white dwarfs in a volume/magnitude limited sample serves as a means to put this to the test26. To date, there have been no sub-Chandrasekhar mass type Ia progenitor candidates inside a 50 pc radius, so ongoing efforts are crucial to properly quantify the number of massive double white dwarf binaries in our local neighbourhood and the Milky Way.

Conclusion

We have presented a compact, super-Chandrasekhar mass double white dwarf binary which will merge in close to a Hubble time, having an orbital period of 14.24 h. With a total mass of 1.555 ± 0.044 M⊙, WDJ181058.67+311940.94 is the most massive double white dwarf binary confirmed to date. We predict it to explode as a quadruple detonation and be destroyed completely. With all the mass ejected and a total explosion energy of 1.2 × 1051 erg, but only 0.1 M⊙ of 56Ni in the ejecta, it will appear as a subluminous type Ia supernova with a peak apparent magnitude of approximately mB = −14.7 and mV = −16.1.

The lack of observational evidence of compact and massive double white dwarf binaries has long troubled the theory that double white dwarfs are the dominating evolutionary channel of type Ia detonations3. WDJ181058.67+311940.94 provides tentative observational evidence that super-Chandrasekhar mass systems with short merger times do exist in the Milky Way, and when combined with the close proximity of 49 pc the rate of super-Chandrasekhar mass double white dwarfs born in the Milky Way is at least 6.0 × 10−4 yr−1. This draws closer the disparity between the observed and predicted birth rates of super-Chandrasekhar mass systems, although the observed rate is still approximately two times smaller. However, there remains a large deficit in the rate of type Ia supernovae from the progenitor systems. A small fraction of the Milky Way rate is accounted for, now with an equal contribution from double white dwarf and white dwarf+hot subdwarf binaries.

Being discovered through a medium-resolution search of overluminous double white dwarfs26, which up to a magnitude limit of G < 17 mag is approximately 20% complete, it is entirely plausible that more super-Chandrasekhar mass double white dwarfs reside in our Galactic neighbourhood and that we have the spectroscopic ability to resolve the formation channel of type Ia supernovae. Deeper completeness through photometric and spectroscopic surveys in the coming years, as well the inauguration of space-based gravitational wave detectors in the next decade, will be pivotal in detecting ultracompact binaries on the cusp of detonation48,49. Combined efforts surveying type Ia progenitors across the full range of orbital periods will be the ultimate means to accurately quantify the contribution of double white dwarfs to type Ia supernovae.

Methods

Observations

WDJ181058.67+311940.94 was first discovered as part of the DBL survey26 using medium-resolution spectra (R = 8,800) on the 4.2 m WHT with the ISIS. Two other ISIS exposures were taken on the nights 13 and 14 April 2019 using the R600B and R1200R gratings with a 1.2″ slit resulting in a spectral resolution of R = 3,000 at Hα and these spectra are included in the full orbital analysis of the double white dwarf. The blue and red set-ups had a wavelength calibration accuracy of approximately 3 km s−1 and 2 km s−1, respectively.

We conducted a continued observational campaign to derive phase-resolved RVs of the double white dwarf binary. We utilized the 2.5 m Isaac Newton Telescope (INT) with the IDS over the nights 4–7 September 2019 (11 exposures, 1,800 s each) and 24 September 2019 (4 exposures, 900 s each) with the Red+2 detector and a 1. 2″ slit width, resulting in a spectral resolution of R = 6,300. Further phase-resolved spectra were taken with the INT on the nights 25 and 26 August 2024 with the H1800V grating at a resolution of R = 9,400 (20 exposures, 1,500 s each). An arc lamp exposure was taken every 45 min of observing time and the science images were wavelength calibrated by interpolation of the nearest two arcs. The wavelength calibration accuracy per frame was approximately 2 km s−1.

Bias, flat field and spectrophotometric flux standard star images were taken on all nights and applied in the reduction. All data from the WHT and the INT were reduced using the MOLLY suite50 using an optimal extraction algorithm51.

These data were supplemented with 18 exposures of length 1,500 s on the 2.56 m NOT using the FIES in low-resolution mode (R = 25,000), having a wavelength calibration accuracy of approximately ±150 m s−1. Observations were obtained through a staff queue at random times, typically being two consecutive exposures, and through a NOT fast-track proposal. All FIES data were reduced using its automated data reduction pipeline, FIEStool52. We also obtained five exposures with the NOT ALFOSC with a 0.5″ slit width, producing spectra at R = 10,000 with wavelength range 6,330–6,870 Å on 1 and 2 June 2024. The data were reduced with the PYPEIT Python package53.

A continuous observing window of 4.5 h was obtained through directors discretionary time on the 8.2 m VLT with the UVES. Each exposure lasted for 730 s with a readout time between exposures of 45 s, totalling 20 exposures. We employed an observing set-up of the dichroic 1 mode with central wavelengths of 3,900 Å and 5,640 Å for the blue and red arms, giving a wavelength range that covered the full visible spectrum apart from gaps of 80 Å at 4,580 Å and 5,640 Å. A slit width of 1.0” and a 2 × 2 binning granted a spectral resolution R = 20,000 and the wavelength calibration accuracy was approximately 200 m s−1 (refs. 54,55).

In deriving final RV errors for these data (Supplementary Table 1), the wavelength calibration error was added in quadrature to the statistical error.

Atmospheric fitting of optical data

We used the package WD-BASS56 to fit atmospheric parameters to the spectra from VLT/UVES. For synthetic spectra, we utilized the 3D-NLTE model grid introduced in ref. 26, which was constructed using the 3D-LTE models of ref. 57 with a further NLTE correction factor applied using the NLTE and LTE synthetic spectra described in ref. 58. The two stars were scaled using temperature–log g–radius relationships with the evolutionary track models of ref. 59 when M ≤ 0.393 M⊙, of ref. 60 when 0.393 < M < 0.45 M⊙, and the hydrogen-rich envelope evolutionary sequences of ref. 61 otherwise. These boundaries come from the expectation that a white dwarf with a mass below 0.45 M⊙ has a helium core and those larger have a carbon–oxygen core. The model spectra were converted from an Eddington flux to that observed at Earth and reddened with an extinction coefficient A(V) = 0.0312 mag (ref. 62) and colour excess E(B − V) = A(V)/3.1 using the reddening curves of ref. 63.

We applied an atmospheric fitting technique that is very similar to that described in ref. 26 by linearly normalizing and fitting the Balmer spectral lines of the UVES data using a Markov Chain Monte Carlo algorithm, maximizing the likelihood for a best-fit solution. We also utilized Pan-STARRS photometry64 to perform a hybrid fit using both datasets simultaneously. With high signal-to-noise ratio data, we were able to fit all Balmer lines from Hα to H11. Furthermore, to give the photometric and spectroscopic data a similar weight, we applied an extra weighting (×1,000) to the photometric fit. Without this weighting, the spectra would have overdominated the best-fit solution. Only spectra taken at the times where a distinct double-line splitting was evident at Hα were modelled to avoid fitting degeneracies between the two stars, of which there were 10 each (a total of 20). In deriving errors, we individually fitted each red-arm spectrum that revealed a double-lined Hα split along with the nearest-in-time blue-arm spectrum while weighting the photometry by ×100. Then we took the standard deviation of all measurements to be the error in the star’s surface gravity and temperature. The new best-fit atmospheric parameters are stated in Table 1, which are entirely consistent with previous values26.

Atmospheric fitting of ultraviolet data

We performed an independent spectroscopic fit using a previously published HST spectrum38. WDJ181058.67+311940.94 was observed for a single 1,000 s exposure using the COS on 19 February 2022. The observation had a central wavelength of 1,291 Å with the G130M grating, giving a resolution of R = 12,000–16,000 and a wavelength range of 1,130–1,430 Å with a gap at 1,278–1,288 Å due to the positioning of the two detector segments. Given the vastly different methods and the fact that WDJ181058.67+311940.94 is not double lined at Lyman-α in the ultraviolet data, no RVs were extracted, but the predicted RVs of the two stars at the centre of exposure (−37.8 km s−1 for the more massive and 139.6 km s−1 for the less massive star, respectively) were fixed in the fitting procedure.

Our spectral fitting method was identical to that presented in ref. 38 with the only exceptions being that a second hydrogen-rich atmosphere white dwarf is included in the model, in which we adopt A(V) = 0.0312 mag and in which the mid-exposure RV of the two stars is considered. A hybrid (spectroscopic and photometric) fit was performed with no extra error weighting applied using the HST/COS spectrum and photometry from Pan-STARRS g, r, i, z, y (ref. 64), fixing the distance to Gaia DR3 parallax. Updated model atmospheres65 with a white dwarf mass–radius relationship61 were used to fit the absolute fluxes. In addition, strong absorption lines affecting the continuum were masked in the COS spectrum38. To address the inconsistencies reported between ultraviolet and optical parameters38, a systematic offset of 1% in Teff and 0.1 dex in log g were added to the ultraviolet values of both stars in the hybrid fitting, whereas trial values in the optical were unchanged. The best-fit model to the spectra are shown in Fig. 1, and the results of our atmospheric fitting are given in Table 1 and compared with the optical solution. We found a total mass of 1.537 ± 0.018 M⊙ through this analysis, which again is consistent with previous values26.

To provide a final adopted value from the atmospheric fitting inclusive of the results from the optical and the ultraviolet datasets, we concatenated the distributions obtained for each parameter to then quote the median and 68% confidence interval on the Teff and log g and interpolated these parameters to obtain masses. The adopted values are quoted in Tables 1 and 2.

RVs and orbital parameters

WD-BASS56 was again used to obtain RVs for all of the optical spectra. The best-fit synthetic spectrum agrees with the data extremely well (Fig. 1), but even with the correction of NLTE effects to the model gridline cores, the synthetic model flux is overpredicted in the line cores of Hα. To obtain the most accurate template for RV extraction possible, we fitted a Gaussian model to the Hα line cores of both stars combined with a four-term polynomial to model the broader wings of Hα, all within 10 Å of the Hα centre. The centre of a Hα absorption was isolated as the splitting of the two stars is most apparent around the non-thermal equilibrium line cores and hence the stars are most easily disentanglable. This method best modelled the shape of the spectral area around the line cores for the high signal-to-noise ratio and high resolution UVES spectra, but not for all other data sources. Instead, we took the result of the best-fit synthetic spectrum and added an extra Gaussian component at the line cores of Hα for both stars (following the method described in Section 4.4 of ref. 26), which improved the line-core shape significantly. The Gaussians were fitted to all relevant spectra simultaneously and this final template spectrum was then used for RV extraction in WD-BASS. We started by fitting the RV of both stars to each spectrum by taking the median of 1,000 bootstrapping iterations and taking errors as the standard deviation of this bootstrapped posterior distribution.

With the full set of 82 RV measurements (Supplementary Table 1), we then searched for an orbital period, P, by minimizing the χ2 of equation (2) for trial semi-amplitudes (K1, K2) and velocity offsets (γ1, γ2) of each star using a least squares algorithm, where

$$P{K}_{1,2}^{3}=\frac{2\uppi G{M}_{2,1}^{3}\sin {(i)}^{3}}{{({M}_{1,2}+{M}_{2,1})}^{2}}$$
(2)

Upper bounds on the semi-amplitudes Kmax,1 and Kmax,2 were set for a trial period by applying an edge-on (i = 90∘) inclination for a 1.4 M⊙ + 0.15 M⊙ double white dwarf in a Keplerian orbit (the maximum and observed minimum mass of a white dwarf, respectively). There is no indication of eccentricity from the RVs, so the orbit was assumed to be circularized (e = 0). In the process, we noticed a deviation from Keplerian motion around conjunction which is caused by degeneracy in the fitted RVs as the stars spectrally overlap. This is unsurprising as the velocity resolution of the ALFOSC, ISIS and IDS data was around 30–40 km s−1, whereas in the higher resolution FIES spectra a lower signal-to-noise ratio led to the same degeneracies. We decided to ignore these RVs when fitting the orbital motion by masking measurements that were within 15 km s−1 of the RV of each star at conjunction. All RVs from the UVES spectra within this range were utilized as its high signal-to-noise combined with twice the velocity resolution did not cause any noticeable deviation. With the final periodogram, two prominent peaks appeared at very similar solutions; we adopted the solution with a 14.2356 h period and another at 14.2308 h, but the second one could be rejected owing to a gravitational redshift difference that would be a strong outlier from that expected in the atmospheric solution.

Returning to equation (2) with the final orbital solution and taking into account all combinations of masses from the atmospheric analysis, we conclude that WDJ181058.67+311940.94 has an inclination i ≈ 35–45 deg. We analysed the TESS66 light curve of WDJ181058.67+311940.94 in all cadences to search for any photometric signature of photometric variability with Lomb–Scargle67,68 and boxed-least-squares periodograms but found no variation on the orbital period. For an eclipse to be witnessed in this system, the inclination would have to be above 89.64 deg and photometric variability from ellipsoidal modulation or irradiation is minute for a system with 14.24 h orbital period. The Doppler beaming from the two stars is nullified by their opposing motion of near-identical RV amplitudes and a similar flux contribution69, and hence non-eclipsing forms of variability are not expected.

Modelling the fate of the binary system

We created two white dwarfs from the premain sequence phase using the stellar evolution code MESA70,71,72,73,74,75, evolving them to carbon–oxygen white dwarfs of 0.87 M⊙ and 0.71 M⊙. These masses align with observations from VLT/UVES spectra fitting. Compared with previous merger simulations, using self-consistent models evolved in MESA allowed us to start from realistic composition profiles. In particular, the two white dwarfs have a helium shell of 8 × 10−3 M⊙ (for the 0.71 M⊙ white dwarf) and 3 × 10−3 M⊙ (for the 0.87 M⊙ white dwarf).

We then created two three-dimensional white dwarfs in hydrostatic equilibrium with the same masses and abundance profiles in AREPO. We resolved the white dwarfs with cells with a roughly constant mass of 10−7 M⊙ and used a passive scalar to resolve the helium shells of both white dwarfs even better with a mass resolution of 10−8 M⊙. We relaxed both white dwarfs in isolation for ten dynamical timescales, actively dampening any gas velocities for the first half of this time. The density and composition profiles of the relaxed white dwarfs, in particular close to the surface, well resembled the initial one-dimensional profiles obtained from MESA.

We put both white dwarfs into a binary system in corotation with an initial period of 73 s. At this period, the separation is about 1.5 times larger than the separation where the secondary white dwarf will fill its Roche lobe. We applied an accelerated inspiral term that removes angular momentum in the same way as gravitational waves, but on a much faster timescale. In this way, we obtained a binary system in equilibrium when mass transfer started on a scale that we could resolve in the simulation. At this time, the physical system would have transferred mass at a low rate for possibly hundreds of years, but the total mass transferred is likely to be negligible. The secondary white dwarf eventually started filling and then overfilling its Roche lobe, and we stopped the accelerated inspiral when the density at the inner Lagrange point between the white dwarfs reached 2 × 104 g cm−3. Only then did the density in the accretion stream become large enough to dynamically affect the surface of the primary white dwarf43,76,77.

The binary system had now shrunk to a separation of 0.03 R⊙ and an orbital period of 39 s. We then continued to evolve the binary system conservatively and switched on a live nuclear reaction network with 55 isotopes43,44. After evolving the binary system conservatively for 55 s, the interaction of the accretion stream with the surface of the primary white dwarf ignited a helium detonation close to the point of interaction (second column of Fig. 3), which is consistent with previous simulations of more massive white dwarf binaries77,78,79. As in the classic double detonation scenario where the helium detonation is caused by instabilities in a massive helium shell80,81, the helium detonation wraps around the primary white dwarf. It sends a shock wave into the core of the white dwarf, that converges in a single point at a density of 9.6 × 106 g cm−3. Because of a lack of numerical resolution, the simulation does not self-consistently ignite a carbon detonation there, but resolved ignition simulations indicated that, at this density, we expect a detonation to form at the convergence point82,83. To model the ignition of the detonation when the shock converges in the simulation, we set the temperature of 178 cells that contained 1.8 × 10−5 M⊙ around the convergence point to 5 × 109 K. This injected 4.8 × 1046 erg (which is negligible compared with the energy release of the whole simulation) and ignited the detonation. The detonation completely destroyed the primary white dwarf. When the shock wave of its explosion hit the secondary white dwarf, the double detonation mechanism repeated itself. The shock wave ignited a helium detonation that drove a shock wave into the core and converged at a density of 8.5 × 106 g cm−3. In this case, carbon burning started at the convergence point, but not strongly enough to start a detonation. We again ignited a detonation at the convergence point by setting the temperature of 708 cells that contained 6.9 × 10−5 M⊙ to 6 × 109 K, which injected 8.2 × 1047 erg and was sufficient to ignite the detonation that then destroyed the secondary white dwarf as well.

The total explosion energy was 1.2 × 1051 erg. The core of the secondary white dwarf ignited 4.2 s after the core of the primary white dwarf. At this time, the ashes of the primary white dwarf had already expanded far beyond the secondary white dwarf. So when the latter exploded as well, its ejecta expanded into and remained in the centre of the ejecta of the primary white dwarf43. The outermost layers of ejecta were the ashes of the helium detonation of the primary white dwarf. The centre of the ejecta consisted of the ashes of the secondary white dwarf, which contained 0.25 M⊙ of oxygen, 0.4 M⊙ of intermediate mass elements and only 0.01 M⊙ of iron group elements, with a roughly equal fraction of 56Ni and 54Fe.

We obtained preliminary synthetic light curves from spherically averaging the ejecta and computing light curves with the Monte Carlo radiation transport code ARTIS84,85. The resulting supernova had a maximum brightness in the B band of MB = −16.4 (mB = −14.7) and a maximum brightness in the V band of MV = −17.8 (mV = −16.1), which is consistent with traditional double detonation models of single white dwarfs with a similar mass to our primary white dwarf, because the secondary white dwarf does not produce any significant amount of radioactive 56Ni (refs. 86,87,88). That said, our explosion is likely to have avoided the imprint of thick helium shells on light curves and spectra88,89,90. It most likely appeared as a subluminous type Ia supernova. However, the obvious large-scale asymmetries visible in Fig. 4 indicate that three-dimensional synthetic observables will be needed to make any reliable statement about the expected display of this supernova79,88. These will be presented and discussed as part of a larger sample of merger simulations in the future. This new simulation also supports previous work which suggests that both stars will explode in massive double white dwarf binaries that are about to merge43,91,92.