Main

Molecular hydrogen (H2) is the most abundant molecule in the universe and a key ingredient in all known star and planet formation. The stellar nurseries nearest to the Sun lie along the surface of a structure known as the Local Bubble1, in which our Solar System currently resides. Spanning a few hundred parsecs in diameter, the Local Bubble is a superbubble probably formed by multiple supernovae that created a hot evacuated interior cavity surrounded by a shell of swept-up gas and dust1,2.

All recent studies of the Local Bubble’s star-forming molecular clouds and, indeed, all molecular clouds identified in the Milky Way Galaxy have relied on three-dimensional (3D) and two-dimensional observations of dust in emission and/or extinction3,4, and molecular spectral-line observations of CO5,6,7,8,9 or gamma rays8,9. CO, in particular, is important because it can be used as a tracer of the total mass of H2 in star-forming clouds, rather than observing the much fainter H2 line emission directly. Observing H2 is challenging because it is a homonuclear molecule and hence has no rotational dipole transitions. The first excited state of H2 capable of emission occurs at a temperature of T = 511 K, in stark contrast with the average T ≈ 10 K in dense regions of molecular clouds. Thus, much of the molecular cloud cannot be directly observed in H2, and other molecules, such as the relatively abundant CO molecule, whose lowest energy level is situated at 5.5 K, and OH10, are often used. Nevertheless, it is possible to directly observe H2 in emission in the infrared and far-ultraviolet (FUV), where it emits primarily along the boundaries of clouds or in warm shock-excited regions.

Here we identify a new Local Bubble diffuse molecular cloud that we name the Eos cloud using the FUV fluorescent emission capabilities of H2 molecules directly. FUV fluorescent emission of H2 stems from the ability of H2 to absorb FUV photons in the Lyman–Werner band (photons with energy between 11.2 eV and 13.6 eV), which sends the molecules into excited electronic states11,12. The relaxation back into the electronic ground state gives rise to fluorescent emission lines ranging between 912 and 1,700 Å.

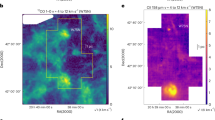
To reveal the Eos molecular cloud we use the FUV fluorescent survey Far-Ultraviolet Imaging Spectrograph (FIMS). Figure 1 shows the all-sky map of FUV fluorescent H2 emission from FIMS13. FIMS, also known as Spectroscopy of Plasma Evolution from Astrophysical Radiation (SPEAR), hereafter referred to as FIMS/SPEAR, was an FUV spectrograph that operated from November 2003 to May 2005 as an instrument on the Korean satellite STSAT-113,14. FIMS/SPEAR observed over 70% of the sky at moderate spatial (5 arcmin) and low spectral resolution (R = λ/δλ ≈ 550).

Fig. 1: FIMS/SPEAR all-sky data.
figure 1

Top: FIMS/SPEAR FUV H2 fluorescence emission map13. Bottom: map of the ratio of H2 intensity to total FUV intensity. In both the top and bottom panels, the location of the Eos cloud is outlined and appears as a bright fluorescent feature that is not present in the FUV continuum. We determine the on-sky boundary for the Eos cloud on the basis of the magenta contours in the bottom panel, which outline the 10% ratio of H2 intensity.

Full size image

In the top two panels, we show the FUV H2 fluorescence emission map, in log line units (LU: photons cm−2 sr−1 s−1). In the bottom panels, we show a map of the ratio of H2 intensity to total FUV intensity, in percentage points (%). In both the top and bottom panels, the location of the Eos cloud, the feature of interest in this work, is highlighted, and appears as a bright fluorescent feature. The cloud line intensity is 20,000 LU on average and spans l = 25–45° and b = 40–63°. The cloud is not present in Hα emission nor is it seen in the FUV continuum data (not shown here, but see Figs. 3b and 4c from ref. 13), indicating a lack of massive stars and pointing to its being a gaseous molecular structure. It can therefore be seen very distinctly when viewing the ratio of H2 fluorescent intensity to total FUV intensity, as seen in the bottom panels of Fig. 1.

The insets in Fig. 1 show Cartesian close-ups of the cloud. The cloud has a characteristic crescent shape, which can be used to determine its correspondence to other gas tracers. For example, the Galactic Arecibo L-Band Feed Array H i (GALFA-H i) Survey is a comprehensive project aimed at mapping the neutral hydrogen in the Milky Way at a spatial resolution of 4 arcmin and a spectral resolution of 0.18 km s−1 (ref. 15). The top right panel of Fig. 2 shows the contours of the Eos cloud overlaid on the 21-cm GALFA Survey map. H i is expected to be observed in and around molecular clouds as it is required for shielding molecules from dissociation from background UV photons16,17,18. In deeper regions of the cloud, the H2 can self-shield against dissociating UV radiation, but the outer layers will still have substantial amounts of H i due to ongoing photodissociation19,20. The fluorescent FUV emission traces the atomic-to-molecular cloud boundary (that is, the H2 to H i transition), and an excellent agreement is indeed observed between the 21-cm map and the FIMS/SPEAR contours. Using a high-latitude CO map6, we can search for CO emission that might be associated with the Eos cloud. In Fig. 2, bottom right, we show the Eos cloud CO data from ref. 6. A small CO cloud is present in the vicinity of the Eos cloud, which is identified as cloud 32 in ref. 6, with l = 37.75° and b = 44.75°, and is coincident with the location of MBM 4021,22. We discuss the implications for star formation given the possible association with this CO feature in Methods.

Fig. 2: The Eos cloud seen in tracers other than H2 fluorescence.
figure 2

The magenta contours in all images represent the H2 emission contour from the fluorescent emission in Fig. 1. Top left: total extinction derived by integrating the Dustribution density along the line of sight. Top middle: column density (NH) map of the Eos cloud derived from Planck 545 GHz data26 assuming T = 10 K, (Planck dust emissivity coefficient) κν = 4.73 cm2 g−1 and a distance of 100 pc. Top right: GALFA-H i column density map15. Bottom left and middle: ROSAT 0.25-keV (left) and 1-keV (middle) maps from ref. 34. The Eos cloud shows a prominent outline absorbing the soft-X-ray flux and creating a bright X-ray halo towards lower Galactic longitude. The interaction region provides a nearby example of a hot–cold gas interface. Bottom right: CO data from ref. 6; the small CO-bright region (known as MBM 40) within the on-sky cloud boundary is shown by the white arrow.

Full size image

We compute the distance of the cloud using 3D dust mapping techniques, estimate its mass and describe its connection to the Local Bubble. The dust-based total column density maps are shown in Fig. 2. Total extinction, derived by integrating the 3D dust mapping technique Dustribution23,24,25, is displayed in the top left panel. We further describe the Dustribution algorithm in Methods. The top middle panel in Fig. 2 shows the column density map of the Eos cloud derived from the Planck mission at 545 GHz (ref. 26).

Using Dustribution, we compute a 3D dust map of the solar neighbourhood out to a distance of 350 pc. Figure 3 shows the reconstructed map, focusing on the region of the Eos cloud as a function of distance. We see a single, distinct cloud that corresponds to the H2 emission stretching from 94 to 130 pc; no other clouds are visible along the same lines of sight in Fig. 3. This establishes the cloud as among the closest to our Solar System, on the near side of the Sco–Cen OB association1 and consistent with some reported distances to the high-latitude portion of the North Polar Spur known as Loop I from refs. 27,28.

Fig. 3: 3D dust density structure of the Eos cloud.
figure 3

Top: two-dimensional slices of the cloud at different distances. The colour bar indicates both the total dust extinction density and the total mass density, assuming dust properties from ref. 29 and a gas-to-dust mass ratio of 124. As in Fig. 1, the magenta contour shows the region with high H2/FUV ratio. Bottom left: Dustribution density for b = 55°. The two red lines indicate the minimum and maximum extents of the magenta contour in Fig. 2, and the cyan and green dashed lines indicate the extent of the Local Bubble at this latitude (from refs. 58 and 59 respectively). Bottom right: projected view of the Eos cloud isosurface and surroundings relative to Local Bubble models. There is no indication of other clouds in the same direction. The 3D dust density of the solar neighbourhood highlighting the Eos cloud and the Local Bubble models can be viewed at links provided in the Data availability section.

Full size image

Smaller condensations are visible inside the cloud, and it seems that the cloud has a distance gradient, with the parts further from the Galactic plane being closer to us, and vice versa. A projected view of the Eos cloud isosurface and surroundings relative to Local Bubble models is shown in the bottom right of Fig. 3. There is no indication of other clouds in the same direction. Integrating the dust density on the basis of dust properties and a gas-to-dust mass ratio of 124 from ref. 29 results in a total dust mass for the cloud of 44 M⊙ and a total mass of 5.5 × 103 M⊙ within the magenta contour in Fig. 1. If we instead include all the dust in the range 20° < l < 50°, 38° < b < 70° and 90 pc < d (distance) < 140 pc, we find a total mass of 8.5 × 103 M⊙. We use Astrodendro to estimate the 3D boundaries of the cloud30,31. From these boundaries, we calculate the effective radius of an equivolume sphere as 25.5 pc. This gives an average mass density of 7.9 × 10−2 M⊙ pc−3. To derive the H i mass of the cloud we convert the H i column density observed within the Eos cloud region assuming an area of 15° × 20° and 〈N(H i)〉 = 3 × 1020, where 〈N(H i)〉 is the column density of H i. In this way we derive an H i mass of 2.0 × 103 M⊙ taking up 36% of the total cloud mass within the contour.

Interestingly, this molecular cloud is located in the vicinity of a region of the sky with significant emission at radio and X-ray wavelengths known as the North Polar Spur (NPS). The NPS is probably composed of a superposition of emitting layers from as far away as the Galactic centre to as close as the Local Bubble1,2. The nearby high-Galactic-latitude portion of the NPS, referred to as Loop I (hereafter NPS/Loop I), is probably at a distance of 105–135 pc (refs. 27,28), although this nearby distance is debated32,33. The 3D dust map from Dustribution as seen in Fig. 3 (bottom panels) agrees well with the nearby literature distances, showing a corresponding arc-like structure at ~100 pc. The proximity of the two structures to each other, on sky and along the line of sight, may suggest they are directly interacting with one another or that the Eos cloud is a foreground object. In Figs. 2 (bottom left and middle panels) and 3 (bottom panels) we show the position of the NPS/Loop I in relation to Eos. The 0.25-keV soft-X-ray map (bottom left panel of Fig. 2) probes hot gas in the local interstellar medium (ISM). The ROSAT 0.25-keV map has been crucial in studying the Local Hot Bubble, showing its extent and structure. Ref. 34 presented a model for the 0.25-keV soft-X-ray diffuse background in which the observed flux is dominated by a ~106 K thermal plasma located in a 100–300-pc-diameter bubble surrounding the Sun but has significant contributions from a very patchy Galactic halo and charge exchange in the heliosphere35. The Eos cloud’s characteristic crescent shape outlines the soft-X-ray emission. The fact that the Eos cloud shape impacts the soft X-rays detected by ROSAT may have significant implications for the distance of the cloud and its column density. The absorption of soft X-rays suggests the nearby nature of the Eos cloud and indicates that the cloud acts as a barrier that prevents the soft X-rays from penetrating34. The bottom middle panel of Fig. 2 shows the higher-energy 1-keV map. Interestingly, the Eos cloud contours appear to absorb the 1-keV X-rays of the NPS/Loop I at b = 40–60°, which is similar to what happens in the 0.25-keV X-ray image. This may suggest that the cloud is interacting with the X-rays from the NPS/Loop I.

The shape of the NPS/Loop I emission at these high latitudes is clearly modulated by the presence of the Eos cloud. In addition to the ROSAT soft-X-ray data, the Eos cloud can be seen as a potential foreground shadow to other hot gas tracers such as O vi (Fig. 4, top panel). The structural similarities seen in Fig. 4 between the soft-X-ray and [O vi] emission, which both intensify at the cloud boundary, are suggestive of an X-ray ‘halo’. This is due to the high ionization potential of O v (113.9 eV, equivalent to λionization ≈ 110 Å) meaning that the generation of O vi ions in the ISM is dominated by collisional ionization and thus requires an interaction of the cloud and hot gas. While earlier studies36, on the basis of [O vi] absorption towards stars with known distances, have shown that such X-ray halos can be physically associated with neutral clouds embedded in hot gas, our [O vi] emission maps are more ambiguous as to the distance to the emitting medium. The geometric similarities and the need for high-energy gas to cause O vi ionization argue for an association of the cloud with the NPS/Loop I material, whether as solely an X-ray foreground shadow or a true X-ray halo. In Methods, we demonstrate that the fluorescent emission of the cloud is probably generated both by the background ISM FUV radiation field and by the X-ray emission from the NPS/Loop I.

Fig. 4: All-sky maps of Galactic gas tracers used in this study.
figure 4

Top row: FIMS/SPEAR O vi data, modified from ref. 52. The Eos cloud shows a distinctive absorption of hot gas traced by O vi. Second row: CO data from ref. 6 highlighting the Eos cloud. The small CO-bright region within the on-sky cloud boundary is shown by the white arrow. Bottom two rows: ROSAT 0.25-keV (third row) and 1-keV (bottom row) all-sky maps from ref. 34. The Eos cloud shows a prominent outline absorbing the soft-X-ray flux and creating a bright X-ray halo towards lower Galactic longitude. The interaction region provides a nearby example of a hot–cold gas interface. Magenta contours are overlaid, showing the location of strong H2 fluorescence from Fig. 1. The Eos cloud is outlined and a cut-out zooming in on the region is provided.

Full size image

The fate of the Eos cloud

Will the cloud be photodissociated by the NPS/Loop I X-rays and ISM FUV background photons before star formation can take place? Regarding the gravitational collapse of the region, we can estimate the thermal Jeans mass of the cloud, assuming a radius of 25.5 pc (estimated using the dust-based distance to the cloud and size on the sky). Masses larger than the Jeans mass are unstable to gravitational contraction, which occurs when the gravitational free-fall timescale is faster than the sound-speed-crossing timescale. Given a range of uncertain temperatures and masses for the cloud, we find that it is marginally stable against gravitational collapse for temperatures typical of warm H2, as described in Methods. Including the effects of turbulence and magnetic fields in this analysis would only increase stability against collapse. More precise temperature measurements could be made in the near future with higher-spectral-resolution FUV instruments (see, for example, ref. 37).

Regarding dissociation, given the average total fluorescent intensity of the Eos cloud and the average 21-cm H i column density, we can compute the dissociation and formation rates of H2 using the framework of ref. 38. Since the process of H2 photo-excitation results in both line emission and H2 dissociation, the H2 dissociation rate is proportional to the total intensity of the H2 emission lines. We estimate the observed H2 dissociation rate to be \({\dot{\varSigma }}_{\mathrm{D}}^{({\rm{obs}})}=0.32\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1}\). Similarly, equation 12 of ref. 38 provides an estimate of the formation rate (\({\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}\)), which we estimate to be \({\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}=0.02\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1}\).

On the basis of the fact that \({\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})} < {\dot{\varSigma }}_{\mathrm{D}}^{({\rm{obs}})}\) and the fact that the cloud is quasi-Jeans supported, we conclude that the cloud is dissociating. Given \({\dot{\varSigma }}_{\mathrm{D}}^{({\rm{obs}})}\), a radius of 25 pc and H2 mass of 3,400 M⊙, the cloud will be destroyed on a timescale of ~5.7 Myr and is being photodissociated at a rate of ~600 M⊙ Myr−1.

It is of interest to connect these numbers to average conditions at the solar circle. The star-formation surface density in the disk local to the Sun is ~0.005 M⊙ yr−1 kpc2 (ref. 39). If the area of disk being surveyed is roughly 200 × 200 pc2, then the average star formation rate is around 200 M⊙ Myr−1 in this region. This calculation suggests that the photodissociation rate (and implied gas cycling rate in equilibrium) is about three times the star-formation rate, which is consistent with typical star-formation inefficiencies when combined with dynamical processes such as interstellar turbulence and stellar jets and winds as predicted in the numerical simulations of ref. 40. In this respect, dissociating clouds such as the one discovered here may be a common component of the feedback cycle that regulates star formation in galaxies.

Methods

FIMS/SPEAR data

We briefly review the data collection and identification of the H2 lines. For this investigation, we have used data from the FIMS/SPEAR long-wavelength channel (L-channel; 1,350–1,710 Å), which includes several key transitions of molecular hydrogen fluorescence. While the spectral resolution of the data is too low for individual line identification, the collected data provides low-resolution H2 bumps within the L-channel spectrum that can be used to detect H2 fluorescence. The H2 fluorescence features are dominant in two bands, from 1,450 to 1,525 Å and from 1,560 to 1,630 Å. Reference 13 used data from the FIMS/SPEAR mission to construct a nearly all-sky map of diffuse molecular hydrogen fluorescence in emission, as well as an FUV continuum map.

The FIMS/SPEAR all-sky diffuse-background FUV spectrum, weighted by exposure time and with direct stellar photons excluded, consists of multiple components: dust-scattered stellar continuum, hydrogen two-photon continuum, extragalactic background continuum, atomic emission lines and H2 fluorescence emission lines. The spectrum includes atomic emission lines such as Si iv λ1403, Si ii* λ1533, C iv λλ1548, 1551, He ii λ1640 and Al ii λ1671, along with several quasi-bandlike features of H2 fluorescence emission lines. The H2 fluorescence features are most prominent in the wavelength ranges 1,450–1,525 Å and 1,560–1,630 Å. To improve the signal-to-noise ratio, the original data cube, with stellar photons removed, was rebinned to the larger wavelength bin size of 3 Å. As a result, the seven H2 fluorescence emission lines with significant peaks consist of many narrow lines and appear as broad lines in the coarse-grained spectrum. An example spectrum can be seen in Fig. 1 of ref. 13. The data are public on the NASA Mikulski Archive for Space Telescopes (MAST) archive.

To extract only the H2 fluorescence emission, ref. 13 removed all continuum background components and atomic emission lines. The H2 fluorescence emission map was constructed using a pixel size of approximately 0.92° (ref. 41). The spectrum for each pixel was obtained by smoothing the spectra of neighbouring pixels with weights proportional to the exposure time. The radius of the smoothing circle for each pixel was adaptively increased from 2° to 15° in steps of 1° until the signal-to-noise ratio per spectral bin was greater than 15. The Eos cloud is a robust feature of the data regardless of whether adaptive smoothing is utilized or not (Supplementary Fig. 1).

The origins of the H2 line emission

Modelling the limited sensitivity of FIMS/SPEAR

The Eos cloud was discovered through H2 fluorescence lines, which were observed by FIMS/SPEAR during its all-sky survey. A variety of factors limited the instrument’s ability to capture all of the H2 fluorescence lines. The primary limitation is the instrument’s bandpass, which is unable to capture H2 lines below 1,350 Å. The spectral resolution and sensitivity of the instrument impose further limitations for the remaining in-band emission lines. From the H2 emission map and corresponding exposure time maps developed in ref. 13, the average exposure time per pixel is ~2,200 s for the Eos cloud. Due to contamination during launch operations, the L-channel sensitivity suffered a loss of ~74% (refs. 42,43). Given the relatively low exposure time, significant loss in sensitivity and low R ≈ 550, only a small fraction of the total intensity emitted in the H2 lines is detected. We define this fraction to be

$$\eta =\frac{\langle {{\mathcal{I}}}_{\det }\rangle }{{{\mathcal{I}}}_{{\rm{tot}}}}$$
(1)

where \({{\mathcal{I}}}_{{\rm{tot}}}\) is the total H2 line intensity emitted by the Eos cloud and \(\langle {{\mathcal{I}}}_{\det }\rangle\) is the H2 line intensity detected by FIMS/SPEAR, both in LU.

To determine the fraction η for the Eos cloud, we utilize the H2Spec model developed in ref. 44 to generate synthetic H2 spectra. H2Spec requires as inputs the column density of H2, the gas temperature of H2 and a source spectrum. We assume that the observed H2 is pumped by the Draine UV interstellar radiation field (ISRF)45, which is parameterized by the Draine field strength:

$$\chi =\frac{u}{{u}_{0}}$$
(2)

where u is the FUV energy density within a wavelength range of 912–2,480 Å and u0 is the FUV energy density of the Draine ISRF. A value of χ = 1 corresponds to a unit Draine field (which is equivalent to G0 = 1.7, where G0 is the field strength in units of the Habing field46). We use χ = 1 as the first model input, representative of the typical UV background for the solar neighbourhood45, along with an H2 gas temperature of T = 100 K. We also explored T = 500 K but found that this did not strongly affect the line amplitudes. We generate synthetic fluorescence spectra with H2Spec, where the H2 column density of the emitting layer is the sole variable. The value of \({{\mathcal{I}}}_{{\rm{tot}}}\) is then calculated for each synthetic spectrum.

To estimate \(\langle {{\mathcal{I}}}_{\det }\rangle\), we model the instrument’s response to the synthetic H2 fluorescence spectrum. We first convolve the synthetic spectrum with a line spread function consistent with a fully illuminated instrument slit. We then calculate the noise floor of a single FIMS/SPEAR observation of the Eos cloud by utilizing the 3σ instrument sensitivity curve as a function of wavelength, found in Fig. 1 of ref. 47. These sensitivities were calculated before FIMS/SPEAR was launched, and account for the ~74% loss in sensitivity in the instrument response model. We adjust the sensitivity curve to be consistent with the exposure time reported in the H2 exposure time map. Finally, the observed spectrum is interpolated onto the FIMS/SPEAR L-channel bandpass.

We combine the H2Spec model and the instrument response model to determine the value of η for the FIMS/SPEAR cloud. We fit the H2 column density to the observed range of \(\langle {{\mathcal{I}}}_{\det }\rangle\) values in the Eos cloud, \(\langle {{\mathcal{I}}}_{\det }\rangle =(1.29\pm 0.29)\times 1{0}^{4}\) LU. The best fit results in \({{\mathcal{I}}}_{{\rm{tot}}}=(1.44\pm 0.10)\times 1{0}^{5}\) LU. Therefore, the Eos cloud is observed to have η = (8.96 ± 2.11) × 10−2. For reference, the value obtained for the model assuming T = 500 K was η = (7.77 ± 1.11) × 10−2.

In the following sections, we compare the value of \({{\mathcal{I}}}_{{\rm{tot}}}\) with model predictions, first considering an analytic photodissociation region model that assumes chemical steady state and then considering an out-of-equilibrium model.

Chemical steady-state theoretical model

Following ref. 48, the total H2 line intensity in a steady-state photodissociation region is given by

$${{\mathcal{I}}}_{{\rm{tot}}}=\frac{Rn}{4\uppi {\sigma }_{\mathrm{g}}}\frac{1-{p}_{{\rm{diss}}}}{{p}_{{\rm{diss}}}}\ln \left(1+\frac{3\chi }{n/[10\,{{\rm{cm}}}^{-3}]}\right)\beta$$
(3)
$$=3.5\times 1{0}^{4}\,\left(\frac{n}{10\,{{\rm{cm}}}^{-3}}\right)\ln \left(1+\frac{3\chi }{n/[10\,{{\rm{cm}}}^{-3}]}\right)\,{\rm{LU}},$$
(4)

where \({{\mathcal{I}}}_{{\rm{tot}}}\) (LU) is the total line FUV intensity, R (cm3 s−1) is the H2 formation-rate coefficient on dust grains, n (cm−3) is the hydrogen nucleus number density (including H and H2), σg (cm2) is the dust absorption cross-section in the Lyman–Werner band per hydrogen nucleus, pdiss is the photodissociation probability per H2 photo-excitation, χ is the illuminating FUV radiation field intensity in units of the Draine field and β is a dimensionless factor accounting for the attenuation of H2 emission lines by dust (Appendix A in ref. 38).

This model assumes chemical steady state between H2 formation on dust grains and H2 photodissociation by Lyman–Werner radiation within an optically thick, uniform-density one-dimensional slab, externally irradiated by Lyman–Werner radiation normal to the slab surface. For a full derivation, see ref. 48 and Appendix A in ref. 38. We express Sternberg’s dimensionless parameter αG (characterizing the H2 dissociation-to-formation-rate ratio) in terms of the radiation-intensity-to-density ratio χ/n, assuming αG = 59χ/n cm3 for standard solar metallicity gas (see equation 22 in ref. 49).

In equation (4), we evaluate the expression assuming standard parameter values: pdiss = 0.15, R = 3 × 10−17 cm3 s−1, σg = 1.9 × 10−21 cm2 and β = 0.5 (ref. 38). Notably, \({{\mathcal{I}}}_{{\rm{tot}}}\) is only weakly sensitive to metallicity and dust-to-gas ratio variations, as both R and σg are proportional to the effective area of dust grains, causing their effects to largely cancel out in equation (4).

Supplementary Fig. 2 presents the theoretical prediction of \({{\mathcal{I}}}_{{\rm{tot}}}\) as a function of χ (blue curve) for n = 10 cm−3, as given by equation (4). The surrounding shaded region corresponds to models with densities varying from n = 1 cm−3 (lower envelope) to n = 100 cm−3 (upper envelope). The vertical magenta-shaded zone encloses expected values of χ = 0.5–1, representing a parameter space around the standard ISRF value χ = 1. The horizontal orange strip above the theoretical models represents the total H2 line intensity emitted by the Eos cloud found in the previous section.

Our analysis reveals that the chemical steady-state model predictions are below the observed total H2 line intensity emitted by the Eos cloud considering a typical UV ISRF. This discrepancy could be attributed to a combination of factors, including the impact of additional excitation sources, such as energetic photoelectrons produced by X-ray absorption, and the invalidity of the chemical steady-state assumption for the Eos cloud. Both factors are likely contributors, given the cloud’s proximity to the NPS/Loop I and its shape imprinted on the NPS/Loop I.

Non-steady-state model

Regarding out-of-equilibrium H2: as described in equation 9 of ref. 38, the observed H2 dissociation rate is given by

$${\dot{\varSigma }}_{\mathrm{D}}^{({\rm{obs}})}=0.3\,{{\mathcal{I}}}_{5}\left(\frac{{N}_{21}}{1-{{\rm{e}}}^{-1.9{N}_{21}}}\right)\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1},$$
(5)

where \({{\mathcal{I}}}_{{\rm{tot}}}\) is the total photon intensity summed over all the FUV emission lines (photons cm−2 s−1 sr−1) and \({{\mathcal{I}}}_{{\rm{5}}}\equiv {{\mathcal{I}}}_{{\rm{tot}}}/1{0}^{5}\,({\rm{photons}}\,{{\rm{cm}}}^{-2}\,{{\rm{s}}}^{-1}\,{{\rm{sr}}}^{-1})\), and N21 ≡ N/1021 (cm−2) is the average column density of atomic neutral hydrogen. With the estimated averaged \({{\mathcal{I}}}_{{\rm{tot}}}=1.4\times 1{0}^{5}\) LU from FIMS/SPEAR line modelling and average N21 ≈ 0.4 from GALFA, we obtain \({\dot{\varSigma }}_{\mathrm{D}}^{({\rm{obs}})}=0.32\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1}\).

Similarly, equation 12 of ref. 38 provides an estimate of the formation rate (\({\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}\)), with this power-law relation:

$${\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}=0.14\,{f}_{{\rm{H}}}{N}_{21}^{1+\alpha }\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1},$$
(6)

where α = 1.3 and fH ≡ N(H)/N. The power-law relation with N21 arises from calibration using numerical simulations50,51 to approximate the product of the formation-rate coefficient of H2 on dust grains and the ISM density. More discussion on the derivation of equation (6) can be found in ref. 38. For the Eos cloud, the estimated formation rate using fH = 1 and the average N21 ≈ 0.4 from GALFA is \({\dot{\varSigma }}_{\mathrm{F}}^{({\rm{obs}})}=0.02\,M_{\odot }\,{{\rm{pc}}}^{-2}\,{{\rm{Myr}}}^{-1}\).

These calculations suggest that photodissociation (from X-rays and UV) dominates H2 formation for this cloud. Future studies using spectral resolution higher than that of FIMS/SPEAR could directly test how far the cloud is from chemical equilibrium37.

All-sky maps of O vi, CO and X-ray data

All-sky maps showing the O vi, CO and X-ray data are provided in Fig. 4 to give context to the location of the cloud on the sky in various tracers. In particular, in addition to the ROSAT soft-X-ray data, the Eos cloud can be seen as a foreground shadow to other hot gas tracers. In the top panel of Fig. 4, we show the cloud contours overlaid on an all-sky map of five-times ionized oxygen (O vi) published in ref. 52. O vi traces hot, ionized regions probably produced by supernova remnants in the ISM with temperatures around a million degrees Kelvin. The cloud discussed herein produces a characteristic absorption in the O vi emission map, similar to what is shown by the soft-X-ray data, indicating that it is a cooler, denser foreground object. We note that the exact shape of the structures in these emission maps depends on where the hot gas causing the O vi ions originates and can include geometric effects of the line of sight and magnetic field. O vi absorption to stars with known distances will be of great value in understanding the relation between the hot gas and the Eos cloud. On the basis of the spatial correspondence between the X-ray data, O vi emission map and Eos cloud, it is very likely that this interaction between the molecular complex and hot gas provides the nearest example of a hot–cold ISM gas interface, which is also thought to be responsible for the O vi absorption observed through many sight lines throughout the Galaxy.

Jeans stability

Given the presence of even a small mass of cold CO-bright gas, it is natural to enquire about the fate of this diffuse high-latitude molecular cloud. Is it on its way to being actively star forming, as is the case of present-day, more massive molecular clouds in the Local Bubble vicinity? Or will the cloud photodissociate before star formation can take place? Using a range of cloud masses and temperatures, we can estimate the Jeans mass of the cloud, assuming a radius of 25.54 pc (estimated using the dust-based distance to the cloud and size on the sky). Masses larger than the Jeans mass are unstable to gravitational contraction, which occurs when the gravitational free-fall timescale is shorter than the sound-crossing timescale.

Supplementary Fig. 3 shows the ratio of the cloud mass to the Jeans mass, considering only thermal support. For a range of estimated masses from 3D dust maps (Supplementary Fig. 4) and over a range of reasonable temperatures for the H2 gas, the cloud is marginally stable against gravitational collapse for temperatures above 100 K. This reflects the very low densities of the diffuse gas of ρ = 0.08 M⊙ pc−3. We note that our calculations make simplistic assumptions about spherical geometry and lack estimations for turbulence and magnetic fields. However, adding these terms would only strengthen the support of the cloud against collapse. Future work will examine the role of turbulence and magnetic fields in the Eos cloud with additional analysis of 21-cm emission maps and Planck polarization data.

Building the 3D dust density map

We compute a 3D dust map of the solar neighbourhood out to a distance of 350 pc using the 3D dust mapping algorithm Dustribution23,24,25 modified with a variational nearest-neighbour Gaussian process53. Variational nearest-neighbour Gaussian processes can scale to almost unlimited numbers of voxels in the map in linear, rather than cubic, time; these modifications will be described in more detail in a forthcoming paper. This volume is divided into voxels such that (nl, nb, nd) = (360, 180, 117) with equal spacing in l and d and in sin b, giving us a grid resolution of l, b, d = 1°, 1°, 3 pc.

Dustribution takes in any catalogue of 3D dust extinction and distances and computes its 3D dust density and extinction within the given region. For the purposes of this Article, we utilize the catalogue of ref. 54, which derives stellar parameters from Gaia Data Release 3 BP/RP spectra, BP/RP and G photometry and parallaxes, 2MASS and Wide-field Infrared Survey Explorer photometry and LAMOST spectra using a data-driven approach.

To derive the 3D isocontour from Astrodendro requires several input parameters: the minimum density above which cells may be included in structures, the minimum difference at which substructures may be identified and the minimum number of pixels in a structure, which we set to 4 × 10−5 mag pc−1, 0.15 dex and 8 pixels, respectively, on the basis of the final mean Dustribution model parameters.

For validation, we compare the Eos cloud line-of-sight width and masses with those of ref. 55. Applying the above methods to determine distance and mass, we derive a line-of-sight distance of 90–140 pc and a mass of 1.6 × 103 M⊙. While the line-of-sight width is in excellent agreement with our results from Dustribution, there is a difference of approximately a factor of 3 in the recovered masses. This mass discrepancy could be a result of the differences in the implementation and the resolutions of the two 3D dust density maps.

CO mass

Several large and well-known molecular complexes in the Local Bubble vicinity are actively star forming, including Taurus, Ophiuchus, Lupus, Chamaeleon and Corona Australis1. These clouds are all observed in dense and cold gas tracers such as CO. In Fig. 4, second row, we show the CO data from ref. 6. As previously mentioned, a small CO cloud (MBM 40) is present at l = 37.75° and b = 44.75°.

While the distance to MBM 40 is not well constrained, if it is associated with the Eos cloud we can compute its mass, given the known distance to Eos. Adopting a CO-to-H2 conversion factor of 2 × 1020 cm−2 (K km s−1)−1 (ref. 56) and including a factor of 1.36 for heavy elements, we can compute the cloud mass from the CO luminosity:

$$M\,({M}_{\odot })=0.0013{L}_{\mathrm{CO}}\,\left({\mathrm{K}}\,{\mathrm{km}}\,{\mathrm{s}}^{-1}\,{\text{deg}}^{2}\right)\,[d\,{(\text{pc})}]^{2}.$$
(7)

Using LCO = 1.53 K km s−1 deg2 from ref. 6 and d = 100 pc, the mass of the Eos cloud predicted by the CO emission is estimated to be M = 19.9 M⊙. Variations of a factor of a few in mass may be expected due to uncertainties in the CO-to-H2 conversion factor at high Galactic latitudes22,57. The CO luminosity estimates a cloud mass that is two to three orders of magnitude off of the mass estimated from dust and traces a much smaller volume than the more diffuse H2 gas. This highlights the importance of tracking CO-dark gas when estimating cloud masses and extents.