A little red dot at z = 7.3 within a large galaxy overdensity

Abstract

The nature of ‘little red dots’ and their relation to other forms of accreting supermassive black holes remain an open question. Here we report the discovery of a little red dot at z = 7.3. It is attenuated by moderate amounts of dust, A_V = 2.79 mag, and has an intrinsic bolometric luminosity of 10^46.6 erg s⁻¹ and a supermassive black hole mass of 5 × 10⁸ M_⊙. Most notably, this object is embedded in an overdensity of eight nearby galaxies, allowing us to calculate a spectroscopic estimate of the clustering of galaxies around little red dots. We find a little red dot versus galaxy cross-correlation length of r₀ = 8 ± 2 h⁻¹ cMpc, comparable to that of z ≈ 6 ultraviolet-luminous quasars. The resulting estimate of their minimum dark matter halo mass $\log_{10}({M}_{{\rm{halo}},\min }/{{{M}}}_{\odot })=12.{0}_{-1.0}^{+0.8}$ indicates that nearly all haloes above this mass must host actively accreting supermassive black holes at z ≈ 7, in strong contrast with the far smaller duty cycle of luminous quasars (<1%). Our results, taken at face value, motivate a picture in which supermassive black holes in little red dot phases could serve as the obscured precursors of ultraviolet-luminous quasars, which provides a natural explanation for the short ultraviolet-luminous lifetimes inferred from both quasar clustering and quasar proximity zones.

Main

James Webb Space Telescope (JWST) spectroscopy has confirmed dozens of (type-1) active galactic nuclei (AGNs) by detecting a broad (full-width at half-maximum, FWHM > 1,000 km s⁻¹) emission-line component to the Hα (or Hβ) line^{1,2,3,4,5,6,7,8}, characteristic of gas motion in the gravitational field of a supermassive black hole (SMBH). A particularly intriguing subclass of these broad-line AGNs appear as compact, red sources in imaging by the near-infrared camera (NIRCam) onboard JWST (F277W − F444W > 1)^1,6,7. Broad-line AGNs photometrically selected with similar criteria have become known as ‘little red dots’⁷ (LRDs). Assuming a power law (f_λ ∝ λ^α, with flux density f_λ, wavelength λ and slope α) to describe parts of their spectrum, it can be characterized by a red rest-frame optical slope (α ≥ 0), often observed in combination with a blue rest-frame ultraviolet (UV) slope (α_UV ≲ −1), resulting in V-shaped continua^6,7 with a minimum around ~3,500 Å. These have been interpreted as moderately obscured (A_V = 1–4) AGNs^1,6,7 superimposed on a galaxy stellar component or a fraction of unattenuated scattered AGN light. Alternatively, the spectral features could be explained by a star-forming galaxy that hosts an AGN encased in a cloud of extremely dense gas^9,10. To date the underlying physical processes that produce the characteristic LRD spectra are not yet fully understood and are highly debated^{11,12,13,14,15}. Although their intrinsic bolometric luminosities and SMBH masses can rival those of quasars, their number densities^6,7,16,17 (10³–10⁴ Gpc⁻³) place them factors of 10–100 above the faint-end extrapolations of the z > 5 quasar luminosity functions^18,19.

The existence of z ≳ 6 quasars²⁰ with M_BH > 10⁹ M_⊙ SMBHs, where M_BH is the black hole mass, challenges models of SMBH formation. In the canonical picture, SMBH growth is bounded by the Eddington limit and black holes grow exponentially with the Salpeter timescale²¹. With an average radiative efficiency of ~0.1, this e-folding timescale is ~50 Myr. To assemble the massive SMBHs of luminous z ≈ 6 quasars, continuous accretion at the Eddington limit comparable to the Hubble time t_H(z) is necessary. Hence, the quasar duty cycle, the fraction of cosmic time a galaxy shines as a luminous quasar, f_duty = t_Q/t_H(z) is expected to be around unity. However, clustering measurements place quasars in massive dark matter haloes^22,23,24 ($\log_{10}({M}_{{\rm{halo}}}/{M}_{\odot })\approx 12.30$) and motivate small UV-luminous duty cycles of f_duty ≈ 0.1% with phases of active growth of t_Q ≈ 10⁶–10⁷ years, thus exacerbating the challenge of growing their SMBHs from stellar seeds to M_BH > 10⁹ M_⊙ by z ≈ 6. Radiatively inefficient accretion, which directly results in much faster SMBH growth, or UV-obscured, dust-enshrouded growth phases for the bulk of the SMBH population and thus a much larger intrinsic duty cycle are two proposed solutions to this problem^{23,25,26,27,28,29}. If LRDs with intrinsic quasar-like properties are found in similarly massive dark matter haloes to quasars, they could belong to the same population and would be appealing candidates for obscured phases of quasar growth, because their expected duty cycles would have to approach unity³⁰. In this Article, we present the first spectroscopic LRD–galaxy clustering measurement to determine how LRDs are embedded in the evolving cosmic web of dark matter haloes, enabling a direct comparison with high-z UV-luminous quasars.

The JWST programme GO 2073 is building the foundation for mapping the morphology of the ionized intergalactic medium around two z ≳ 7 quasars with stringent constraints on SMBH growth. The immediate goals are to identify galaxies at and beyond the redshift of the quasars to study quasar galaxy clustering and to provide targets for subsequent deep spectroscopic observations to map the quasar ‘light echoes’. Based on JWST NIRCam pre-imaging in four filter bands (F090W, F115W, F277W and F444W) and ground-based photometry by the large binocular camera (LBC) at the Large Binocular Telescope (LBT; Methods), we selected galaxy candidates for a spectroscopic follow-up in the same cycle with the micro-shutter assembly (MSA) of the near-infrared spectrograph (NIRSpec) onboard JWST. Among the followed-up galaxy candidates, we identified one broad-line AGN at z = 7.26, J1007_AGN, and eight nearby galaxies at similar redshifts (z = 7.2–7.3) in the field of quasar J1007+2115 (z = 7.51)³¹.

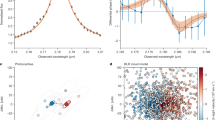
Figure 1 displays the photometric and spectroscopic discovery observations of J1007_AGN. It appears as a compact source with a red rest-frame optical colour (F277W − F444W = 1.65 mag; Extended Data Fig. 1). The NIRSpec/MSA PRISM spectrum of J1007_AGN (Fig. 1, bottom) has a clearly detected continuum, featuring a plethora of strong emission lines. The most prominent feature is the [O iii] λλ4959, 5007 doublet, from which we derive the source redshift z = 7.2583 ± 0.0006 (Methods). As shown in Fig. 2 (left), we decompose the spectrum with a multi-component fit (Methods) and find a broad Hβ linewidth of ${\rm{FWHM}}=\text{3,370}_{-648}^{\text{+1156}}\,{\rm{km}}\,{{\rm{s}}}^{-1}$ (nominal resolution R ≈ 180 ≈ 1,650 km s⁻¹ at Hβ), allowing us to unambiguously classify this source as a type-1 AGN. The source also exhibits weak Hδ (signal-to-noise ratio, SNR ≈ 3) and Hγ (blended with [O iii] λ4364) Balmer lines as well as several high-ionization emission lines (for example, [Ne iii] λ3869.85; SNR ≈ 6) typical for an AGN. We detect high-ionization rest-frame UV lines, notably N iv λ1486 and C iv λλ1548.2, 1550.8 emission (see Methods for details). Its photometric and spectroscopic properties place this source firmly among the population of LRDs^6,7.

Fig. 1: Photometry and discovery spectroscopy of J1007_AGN at z ≈ 7.3.

Top: image cut-outs (2 arcsec × 2 arcsec) covering the six filters from ground-based LBT/LBC r- and i-band images and JWST/NIRCam F090W, F115W, F277W and F444W. By design, the source is not detected in the bluest three bands and appears as a red object (F115W − F444W = 1.94 mag) with compact morphology in F115W, F277W and F444W. Referenced apparent magnitudes are calculated from aperture photometry at the source location. Middle: the co-added 2D NIRSpec/MSA spectrum of the three AB-subtracted dither positions as a function of observed wavelength. The 2D spectrum is displayed in pixel coordinates, resulting in a nonlinear observed wavelength axis. The bright trace is the positive co-added spectrum, whereas the dark traces show the four negative traces of the individual AB dithers. Bottom: the one-dimensional optimally extracted co-added spectrum as a function of rest-frame wavelength. Positions of spectral features, including typical line emission observed in AGNs, are indicated with blue dotted lines. Orange data points show the fluxes measured from the NIRCam photometry. Error bars on the photometry denote the 3σ flux error and the wavelength range of the filter in which the transmission is above 50% of its peak value. The blue data points show the synthetic photometry calculated from the MSA spectrum. 2D, two-dimensional.

Fig. 2: Spectral modelling and physical properties of J1007_AGN.

Left: posterior median of our model fit (bright red) compared with the J1007_AGN spectrum (black). Individual fitting components are highlighted with blue and green lines. Light coloured regions depict fit uncertainties (16th to 84th posterior percentile range). Insets: decomposition of the Hγ and Hβ emission lines (continuum model added to line components). Right: J1007_AGN (bright red diamonds) in comparison with z > 6 AGN^1,6 (blue and green squares) and high-redshift quasars from the literature²⁰ (grey points, systematic 1σ uncertainty in black) in the black hole mass versus bolometric luminosity plane. Error bars on the coloured data denote statistical 1σ uncertainties (or 16th to 84th percentiles of the posterior). We differentiate between the observed (filled diamond) and dereddened (${A}_\mathrm{V}={2.79}_{-0.25}^{+0.25}\,{\rm{mag}}$; open diamond) measurements. Uncertainties on A_V are consistently propagated and included in both bolometric luminosity and black hole mass. For display, we adopted the fiducial bolometric luminosity L_bol,Hβ and the SMBH mass estimate M_BH,GH05,LHβ of Extended Data Tables 1 and 2, which are based on the Hβ emission-line properties (Methods).

We measure an absolute magnitude at rest-frame 1,450 Å of ${M}_{\text{1,450}}=-19.7{6}_{-0.45}^{+0.77}\,{\rm{mag}}$ from the spectrum. In comparison with large samples of LRDs¹⁶, J1007_AGN stands out as a particularly luminous source. For the time being, we follow the literature^2,6 in interpreting the spectral continuum as a combination of a dust-reddened AGN component, which dominates the rest-frame optical, and scattered AGN light, which produces the observed rest-frame UV emission. Fitting an appropriate continuum model to the data (Methods and Extended Data Fig. 2), we find J1007_AGN to be moderately dust obscured with ${A}_\mathrm{V}={2.79}_{-0.25}^{+0.25}\,{\rm{mag}}$.

The standard approach for estimating the black hole masses of LRDs uses scaling relations³² between the linewidth and the line luminosity of the broad Hβ line component. We carefully decompose the rest-frame optical emission with a parametric model (Methods) as shown in Fig. 2 (left) and measure the properties of the individual components, as summarized in Extended Data Table 1. Using the measured Hβ line properties, we derive a black hole mass of ${M}_{{\rm{BH}},{\rm{GH05}},{\rm{LH}}\upbeta }=11.5{2}_{-4.63}^{+10.11}\times 1{0}^{7}\,{{{M}}}_{\odot }$ (where the subscript GH05 refers to the Greene and Ho³² scaling relation that is used to derive the BH mass). The bolometric luminosity is typically estimated from the rest-frame UV continuum emission. However, in LRDs this emission is not fully understood. Therefore, we convert the Hβ line luminosity (L_Hβ) to a continuum luminosity (L₅₁₀₀) using a relation derived from low-z AGNs³² and then adopt a bolometric correction³³ L_bol = 9.26 × L₅₁₀₀. We estimate the bolometric luminosity of $\log_{10}({L}_{{\rm{bol}},{\rm{H}}\upbeta }\,({\rm{erg}}\,{{\rm{s}}}^{-1}))=45.5{2}_{-0.06}^{+0.08}$. With an Eddington luminosity ratio of ${\lambda }_{{\rm{Edd}},{\rm{GH05}},{\rm{LH}}\upbeta }=0.2{0}_{-0.09}^{+0.13}$, J1007_AGN is rapidly accreting mass. These measurements were derived based on the observed spectrum. However, our continuum model indicates that the AGN emission that dominates at the Hβ wavelength is attenuated by dust. Correcting the spectral model for dust attenuation of ${A}_\mathrm{V}={2.79}_{-0.25}^{+0.25}\,{\rm{mag}}$, we derive notably larger values for the SMBH mass M_BH,GH05,LHβ = 4.51 × 10⁸ M_⊙, bolometric luminosity $\log_{10}({L}_{{\rm{bol}},{\rm{H}}\upbeta }\,({\rm{erg}}\,{{\rm{s}}}^{-1}))=46.64$ and Eddington luminosity ratio ${\lambda }_{{\rm{Edd}},{\rm{GH05}},{\rm{LH}}\upbeta }=0.5{8}_{-0.31}^{+0.62}$ (Extended Data Table 2). Figure 2 (right) places these results in the context of quasars²⁰ and other z > 6 AGNs^1,6, using equivalent assumptions to derive bolometric luminosities and black hole masses. Based on its observed bolometric luminosity and black hole mass, J1007_AGN straddles the boundary region between the more luminous LRDs and the faint high-z quasar population³⁴. Taking into account the dust attenuation, it could intrinsically be as luminous (L_bol ≈ 10⁴⁶ erg s⁻¹) and massive (M_BH ≳ 10^8.5 M_⊙) as a typical UV-luminous quasar.

Correcting for our selection function, we estimate a number density for LRDs n_LRD ≈ 2.67 × 10⁴ Gpc⁻³ based on our serendipitous discovery (see Methods for a detailed description). Figure 3 compares this number density (orange diamond) with luminosity function measurements for broad-line AGNs and LRDs (coloured squares) and quasars (grey filled symbols and lines), as a function of UV magnitude (left) and bolometric luminosity (right). The figure underlines that our discovery is consistent with the expectation from z > 6 LRDs but >100 times above the best constraints of the z ≳ 6 quasar luminosity functions^19,35.

Fig. 3: Volume densities of z > 6 broad-line AGN and quasars.

Left: binned UV luminosity function estimates of spectroscopically confirmed JWST (red) AGNs^1,6 (blue and green squares) and photometrically selected LRDs¹⁶ (dark blue squares) in comparison with galaxies^92,93 and quasars¹⁹ at z ≈ 7. Our estimate based on J1007_AGN (bright red) agrees well with the other measurements for faint JWST AGNs but falls orders of magnitude above the faint-end extrapolation of the z ≈ 7 quasar luminosity function¹⁹ (grey solid line). Right: measurements of the bolometric luminosity function for red AGNs spectroscopically confirmed with JWST⁶ (green squares) and photometrically selected LRDs¹⁷ (blue circles) compared with our estimate (bright red) and two bolometric model fits of a quasar luminosity function³⁵ at z ≈ 6 (grey). Model A (solid grey line) has a flexible faint-end slope evolution, whereas the faint-end slope is restricted to evolve monotonically in model B (dashed grey line). Dereddening J1007_AGN by ${A}_\mathrm{V}={2.79}_{-0.25}^{+0.25}\,{\rm{mag}}$ increases the bolometric luminosity by a factor of ~10 (open bright red diamond), pushing the source well into the quasar regime, L_bol ≳ 10⁴⁶ erg s⁻¹. Vertical error bars on the literature measurements reflect the 1σ statistical uncertainties. For our luminosity function estimate (bright red), the error bars indicate the 1σ confidence interval for a N = 1 Poisson distribution⁸³. Error bars in the luminosity direction indicate the luminosity bin width. LF, luminosity function; QLF, quasar luminosity function.

With the preceding analysis, we established that J1007_AGN is a bright z = 7.26 LRD. Exploiting the discovery of eight galaxies in the vicinity of J1007_AGN, we conduct a clustering analysis to constrain the environment of a z ≈ 7.3 LRD for the first time. Details of the galaxies can be found in Methods (Extended Data Figs. 3 and 4 and Extended Data Tables 3 and 4). We restricted our fiducial analysis to the six nearest galaxies out of the eight, which are within |Δv_LOS| < 1,500 km s⁻¹, where |Δv_LOS| is the line-of-sight velocity difference. However, the results do not strongly depend on this assumption (Methods). Taking our survey selection function and targeting completeness into account, we calculate the volume-averaged LRD–galaxy cross-correlation function χ in three radial bins (Methods and Extended Data Table 5). We find an excess of galaxies within the innermost bin, resulting in an overdensity of δ ≈ 30 (Extended Data Fig. 5). Assuming a real-space LRD–galaxy two-point correlation function of the form²³ ${\xi }_{{\rm{LG}}}={(r/{r}_{0}^{{\rm{LG}}})}^{-\gamma }$, where $R_0^\mathrm{LG}$ is the cross-correlation length and γ = 2.0, we calculate a best-fitting cross-correlation length ${r}_{0,{\rm{corr}}}^{{\rm{LG}}}\approx 8.1{7}_{-2.38}^{+2.42}\,{{\rm{h}}}^{-1}\,{\rm{cMpc}}$ (Methods). Our result for ${r}_{0}^{{\rm{LG}}}$ is lower than but still comparable with the recent quasar clustering measurement²³ at 〈z〉 = 6.25 with a cross-correlation length ${r}_{0}^{{\rm{QG}}}\approx 9.{1}_{-0.6}^{+0.5}\,{{\rm{h}}}^{-1}\,{\rm{cMpc}}$.

Assuming that galaxies and LRDs trace the same underlying dark matter overdensities³⁶, we adopt the recent estimate of the galaxy auto-correlation length²³ ${r}_{0}^{{\rm{GG}}}\approx 4.1\,{{\rm{h}}}^{-1}\,{\rm{cMpc}}$ to estimate the LRD auto-correlation length ${r}_{0}^\mathrm{LL}$ and the minimum mass of dark matter haloes hosting z ≈ 7.3 LRDs: $\log_{10}({M}_{{\rm{halo}},\min }/{{{M}}}_{\odot })=12.0{2}_{-1.00}^{+0.82}$ (Methods). Our result is broadly consistent with similar minimum halo mass estimates for (luminous) quasars^22,23, log₁₀(M_halo,min/M_☉) ≈ 12.3–12.7 at z ≳ 6, which would imply that quasars and LRDs are, indeed, hosted by comparable mass dark matter haloes traced by similar overdensities of galaxies and, thus, drawn from the same underlying population. However, we note that the uncertainties also encompass dark matter halo masses of log₁₀(M_halo,min/M_☉) ≈ 11.5, akin to recent measurements³⁷ of broad-line AGNs at z ≈ 5.4. To constrain the duty cycle of LRDs, the fraction of cosmic time a galaxy spends in an LRD phase, we assume that they temporarily subsample their hosts, and so their number density can be expressed as n_LRD ≈ t_LRD/t_H(z)n_halo,min = f_dutyn_halo,min, where n_halo,min is the number density of dark matter haloes with M > M_halo,min and t_LRD is the LRD lifetime. Adopting the LRD abundance¹⁷ at z ≈ 7.5 (log₁₀(n_LRD (cMpc⁻³)) = −5.58 ± 0.44), we calculate the duty cycle $\log_{10}({f}_{{\rm{duty}}})\approx 3.6{6}_{-3.90}^{+5.89}$. Taken at face value, the median duty cycle implied by our measurement is unphysical given the constraints of our cosmological model; LRDs vastly outnumber dark matter haloes with the median dark matter halo mass. This scenario was discussed in a recent paper³⁰, leading the authors to conclude that LRDs and comparably luminous quasars cannot only be hosted in dark matter haloes with similar masses. Given (1) our small sample size of a single LRD, (2) that we have probably underestimated our error bars by neglecting cosmic variance and (3) potential systematics associated with assuming a power-law correlation function²⁴, we do not believe our results imply a departure from the standard cosmology. Instead, we consider it more probable that most LRDs are hosted in less massive haloes than our median result indicates. At z ≈ 7.3, dark matter haloes with log₁₀(M_halo,min/M_☉) ≲ 11.6, well within our uncertainties, would result in physical duty cycles f_duty ≲ 100%. However, the clustering of J1007_AGN underlines that LRDs can also be found in more massive dark matter haloes.

In Fig. 4 we place our clustering results in context with the redshift evolution of auto-correlation lengths, minimum host dark matter halo masses and duty cycles for UV-luminous quasars and JWST broad-line AGNs³⁷. Our LRD auto-correlation length and dark matter halo mass measurements are generally consistent with both UV-luminous quasars at z ≈ 6 and JWST broad-line AGNs at z ≈ 5.5. The high duty cycle indicated by our analysis is in stark contrast with the far lower duty cycle inferred for UV-luminous quasars (<1% at z ≳ 6) from both quasar–galaxy clustering^23,24 and their Lyα forest proximity zones^27,38. It is also slightly larger than the duty cycle implied by the clustering of galaxies around a z ≈ 5.4 broad-line AGN³⁷ (recalculated, see Methods).

Fig. 4: Auto-correlation length, minimum dark matter halo mass and duty cycle for accreting SMBHs as a function of redshift.

Top, middle: comparison of the auto-correlation length (top) and minimum dark matter halo mass (middle) of our results (orange diamond) for LRDs with clustering measurements of quasars^{22,23,24,84,85,91,94} and broad-line AGNs³⁷. Bottom: summary of literature results on the duty cycle for accreting SMBHs. Also included are measurements from quasar proximity zones⁹⁰ (grey cross) and Lyα damping wings^27,38 (filled circles). The green square marks our recalculation of the duty cycle estimate for a broad-line AGN³⁷ (Methods). The duty cycle f_duty should be interpreted as the fraction of cosmic time a galaxy spends in an LRD or quasar phase and is related to the active lifetime by t_Q = f_dutyt_H(z), indicated as grey dashed lines in the bottom panel. Vertical error bars denote the 1σ statistical uncertainty on the measurement, whereas horizontal error bars denote the redshift range of the underlying data sample.

In this work we have introduced the z = 7.3 LRD J1007_AGN. It is one of the most luminous LRDs, and if attenuated by dust, its intrinsic properties would be akin to UV-luminous quasars. Our spectroscopic LRD–galaxy clustering analysis places this source in an ~10¹² M_⊙ dark matter halo, indicating that it could be drawn from the same underlying population as UV-luminous quasars. Generalizing our clustering measurement to the LRD population, we argue that LRDs populate the massive end of the dark matter halo distribution (≳10^11.5 M_⊙), resulting in high duty cycles of f_duty ≈ 100%, in contrast to UV-luminous quasars (f_duty ≈ 1%). Hence, we propose that the bulk of massive SMBH growth at high redshift occurs in long-lived phases wherein the SMBHs appear as LRDs, and that they appear as UV-luminous quasars just a short fraction (f_duty ≈ 1%) of cosmic time. In this picture, the factor of ~100 luminous LRD to quasar abundance ratio naturally results from the fraction of time SMBHs spend in each phase^23,27,28,39, which alleviates the tension between the short, inferred lifetimes of UV-luminous quasars relative to the time required to grow their 10⁹ M_⊙ SMBHs in less than 1 Gyr after the Big Bang⁴⁰. Although highly suggestive, an important caveat is that the UV-luminous quasars we compare with in Fig. 4 have L_bol 5 to 20 times brighter than that of J1007_AGN, which is itself uncertain due to the reddening correction, and there is probably a dependence of clustering, halo mass and duty cycle on L_bol (ref. ³⁰). Furthermore, our analysis, which is based on a handful of galaxies in a single LRD field, has large statistical errors, which are probably underestimated owing to cosmic variance and the simplicity of our modelling. Nevertheless, our study presents highly suggestive evidence for strong LRD clustering and high duty cycles, which provides a compelling motivation to further pursue precise LRD clustering measurements to unravel the nature of this puzzling population and its connection to quasars and SMBH growth.

Methods

Data and data reduction

The data presented in this work were taken as part of the JWST programme GO 2073 ‘Towards Tomographic Mapping of Reionization Epoch Quasar Light-Echoes with JWST’. The goal of the programme is to understand the timescales on which z ≳ 7 quasars grow by tomographically mapping the extended structure of the ionized region around those quasars, their ‘light echoes’⁴¹. For this purpose, one measures the transmission of flux in the spectra of background galaxies, which serve as line-of-sight tracers for the ionized region. The programme GO 2073 was primarily designed to identify galaxies at the redshift and in the background of two high-redshift quasars. We, therefore, first collected JWST/NIRCam photometry in the two quasar fields to select galaxy candidates and then spectroscopically followed up the candidates with the NIRSpec/MSA in the same cycle. J1007_AGN was originally selected as a priority 1 galaxy candidate in the field of quasar J1007+2115 and serendipitously discovered during the spectroscopic follow-up campaign. For all cosmological calculations, we adopt a concordance cosmology⁴² with Hubble constant H₀ = 70 km s⁻¹ Mpc⁻¹, dark energy density parameter Ω_Λ = 0.7 and matter density parameter Ω_M = 0.3.

Photometric data

The source J1007_AGN was discovered in an ~5′ × 6′ field centred on the redshift z = 7.51 quasar J1007+2115 (ref. ³¹). The JWST/NIRCam observations cover the F090W, F115W, F277W and F444W filter bands to enable galaxy dropout selection. The mosaic was built from two pointings employing a FULLBOX 6 dither pattern using the MEDIUM 8 read-out pattern. With 3,736.4 s of exposure time per pointing and the SW/LW filter pair, the NIRCam imaging was charged a total science time of 14,952 s. We downloaded the data using the jwst_mast_query Python package. Our image data reduction was carried out using version 1.6.3 of the JWST Science calibration pipeline (CALWEBB; Calibration Reference Data System (CRDS) context jwst_1046.pmap).

During the reduction, we executed a range of other steps. After CALWEBB stage 1, we performed 1/f-noise subtraction on a row-by-row and column-by-column basis for each amplifier⁴³. We continued by running stage 2 of the pipeline on these 1/f-noise-subtracted images. Detector-dependent noise features were apparent in the stage 2 outputs. To remove them, we constructed master background images for each filter and detector combination by median filtering all available exposures in our programme. Scaled master backgrounds were then subtracted from our stage 2 outputs. Properly aligning the individual detector images proved challenging due to the low number of point sources in reference catalogues. Therefore, we devised a multistage alignment process. We began by running CALWEBB stage 3 on the F444W dither groups with the largest overlap. This resulted in four F444W submosaics corresponding to combined images for each detector and each of our two pointings. These four submosaics were then aligned to the positions of known Gaia stars in the field using tweakwcs. Choosing one tile as a reference, we iteratively aligned the other three tiles using the Gaia star catalogue and point sources from the reference tile. The aligned F444W submosaics were resampled into one mosaic with a pixel scale of 0.03″. As a final step, the full mosaic was then aligned to the full set of Gaia reference stars in the field. With the F444W full mosaic as a reference image, we aligned the CALWEBB stage 2 output files to a common reference frame, (including the F444W images). Then we created association files for the aligned images of each filter and ran CALWEBB stage 3 (with tweakregstep disabled) to create mosaics with a pixel scale of 0.03″ for each filter band. The mean alignment accuracies measured from the full mosaics and the Gaia reference star catalogue were 0.024″, 0.018″, 0.018″ and 0.011″ for the F090W, F115W, F277W and F444W bands, respectively. We estimated that our full mosaics cover a field of view of ~29 arcmin².

To calculate the source photometry, we began by resampling the mosaics to a common world coordinate system grid. Then we convolved the resampled F090W, F115W and F277W mosaics to the lower resolution of the F444W filter. The convolution kernels of the point-spread function were generated empirically from point sources in the field. To extract the photometry, we used the software SExtractor⁴⁴. Source detection was performed on an inverse variance weighted signal-to-noise image stack of the four mosaics. We calculated Kron⁴⁵ aperture photometry on all detected sources using a Kron parameter of 1.2. The fluxes measured in these small apertures were then aperture-corrected in two steps, equivalent to common procedures⁴⁶. The correction for the wings of the point-spread function used empirically generated point-spread functions based on point sources in the field.

To improve our high-redshift galaxy selection, we obtained deep r-band and i-band dropout images with LBT/LBC⁴⁷. The observations were performed in binocular mode, with individual exposures for all images set to ~180 s to minimize the effects from cosmic rays and the saturation of bright stars in the field. In total, the on-source time was 9.5 h for both bands. We processed the LBC data using a custom data-reduction pipeline named PyPhot. The pipeline implements standard imaging data-reduction processes including bias subtraction, flat fielding and sky background subtraction. The master bias and flat frames were constructed using the sigma-clipped median on a series of bias and sky flats, respectively. For the i-band, we corrected for fringing by subtracting a master fringe frame constructed from our science exposures. The sky background was estimated using SExtractor⁴⁴ after masking out bright objects in the images. In addition, we masked cosmic rays using the Laplacian edge-detection algorithm⁴⁸. Finally, we aligned all individual images to Gaia Data Release 3 and calibrated the zero points with well-detected point sources in the Pan-STARRS⁴⁹ photometric catalogues. After image processing, we created the final mosaics for each band using SCAMP⁵⁰ and Swarp⁵¹. The pixel scales of the final mosaics were 0.224″ px⁻¹ for the LBC images.

Selecting galaxy candidates

Based on the JWST/NIRCam and ground-based photometry, we devised a photometric process for selecting galaxy candidates, targeting galaxies in the field of quasar J1007+2115 and in the background. The target redshift interval for this quasar field was 7.43 < z < 9.09. The maximum redshift was chosen so that the foreground quasar was still within the Lyβ forest of the background galaxy. The minimum redshift was chosen so that galaxies with −3,000 km s⁻¹ line-of-sight velocity relative to the quasar were included to allow for a quasar–galaxy clustering analysis. Our galaxy selection procedure was largely informed by the properties of high-redshift galaxies as presented in the JAGUAR catalogue⁵². We first required SNR = 2.0 for source detections in the F115W and F277W bands. We cleaned our photometric sample by removing sources with F115W to F277W colours that were outside the range from −1.5 mag to 1.5 mag. This did not affect galaxies in our target redshift range according to the JAGUAR catalogue. We used a probabilistic dropout selection based on the F090W to F115W colour as the main selection criterion. Based on the F090W to F115W colours of JAGUAR mock galaxies, we assigned to each colour value a purity, which is the fraction of mock galaxies with that colour value within the target redshift range compared with all the mock galaxies with that colour value. Each galaxy candidate was then assigned a purity value, and the full candidate list was ordered by decreasing purity. We continued by grouping the first 100 sources in priority class 1 and then proceeded with 100, 100, 700 and 1,000 sources for classes 2, 3, 4 and 5, respectively. All remaining sources were assigned to priority class 6. The broad priority classes were used in our spectroscopic MSA design with the eMPT tool⁵³. We visually inspected our candidates using the JWST NIRCam and ground-based LBT photometry. Additionally, photometric redshifts were calculated with bagpipes⁵⁴ using all photometric information to guide the process. As we did not expect source flux in the NIRCam F090W filter (λ = 0.795–1.005 μm) for high-redshift sources, galaxy candidates with a notable F090W detection were demoted to a lower priority class. This procedure prioritized sources in the targeted redshift range but did not result in a hard lower-redshift cutoff. The resulting candidate list was used as input for the spectroscopic follow-up observations.

Spectroscopic data

Our galaxy candidates were observed in two NIRSpec/MSA pointings with the PRISM/CLEAR disperser filter combination, providing continuous spectra from 0.6 μm to 5.3 μm with a resolving power R ≈ 30–330. The MSA masks were designed using the eMPT tool⁵³ with the goal of maximizing the coverage of priority 1 sources from our candidate list. Before designing the mask, we visually inspected all priority 1 through 5 candidates, removing sources where the photometry was obviously affected by image artefacts. Of all priority 1 (2 and 3) candidates, 78 (64 and 52) passed this step. We assigned MSA slits to 52 of the 124 candidates that were covered by the area of the two final MSA pointings. Of all 56 (35 and 33) priority 1 (2 and 3) targets, 34 (9 and 9) received slits, resulting in a targeting completeness of 61%, 26% and 27%, respectively. Each pointing was observed using the standard 3 shutter slitlet nod pattern with 55 groups per integrations and 2 integrations per exposure and read out using the NRSIRS2RAPID pattern. This resulted in a total exposure time of 4,902 s per pointing.

The raw rate files were downloaded from the Space Telescope Science Institute (STScI) using jwst_mast_query and then reduced with a combination of the CALWEBB pipeline and the PypeIt⁵⁵ Python package. The spectroscopic reduction was carried out using version 1.13.4 of the JWST Science calibration pipeline (CALWEBB; CRDS context jwst_1188.pmap). Only J1007_AGN has been re-reduced recently with the CRDS context jwst_1215.pmap. PypeIt is a semi-automated pipeline for the reduction of astronomical spectroscopic data, and it includes JWST/NIRSpec as a supported spectrograph. The rate files were first processed with the CALWEBB Spec2Pipeline skipping the bkg_subtract, master_background_mos, resample_spec and extract_1d steps, which were then performed using PypeIt. We used difference imaging with PypeIt for background subtraction and then co-added the 2D spectra according to the nod pattern, super-sampled on a finer pixel grid (factor 0.8). The final one-dimensional spectra for all sources were optimally extracted from their 2D co-added spectra. To ensure that the physical properties determined for J1007_AGN were accurate, we additionally applied an absolute flux correction to the J1007_AGN spectrum. By calculating the synthetic NIRCam F115W, F277W and F444W band fluxes from the final J1007_AGN spectrum, we determined an empirical flux correction factor of 1.21. Figure 1 (bottom) shows the resulting excellent agreement of the photometry with the spectrum in the three detection bands.

Analysis

Galaxy discoveries

The goal of the Cycle 1 programme GO 2073 was to discover bright galaxies at the redshifts of two high-redshift quasars and beyond. We followed up galaxy candidates spectroscopically using the NIRSpec/MSA with the PRISM disperser. Here, we report only on the galaxy discoveries related to the environmental analysis of J1007_AGN. The full sample will be presented in a future publication on this Cycle 1 programme.

Among the 52 galaxy candidates that were followed up in the J1007 field, we discovered 8 galaxies within a line-of-sight velocity difference |Δv_LOS| = 2,500 km s⁻¹ relative to J1007_AGN. These were spectroscopically identified by their [O iii] λλ4960.30, 5008.24 emission-line doublet. It is important to note that these galaxies were not specifically targeted to study the environment of J1007_AGN. Their redshifts were determined by fitting for the redshift of the [O iii] λλ4960.30, 5008.24 doublet in the galaxy spectra. The spectra were modelled using a power-law continuum component and one Gaussian component for each of the doublet emission lines, whose redshift and FWHM were coupled. Extended Data Table 3 provides the galaxy coordinates, their z_OIII redshift and their NIRCam fluxes. For each galaxy, we calculated the line-of-sight velocity distance Δv_LOS, the angular separation (both in arcseconds and in proper kiloparsecs) and their absolute UV magnitudes M_UV, approximated by the absolute magnitude of the F115W filter band. These properties are summarized in Extended Data Table 4 and were used in our analysis of the LRD–galaxy cross-correlation measurement. Note that the faintest galaxy that we could identify in our spectroscopic sample has a UV magnitude of M_UV ≈ −18.9, which we adopted as our spectroscopic UV detection limit for galaxies in the following clustering analysis.

Spectroscopic analysis of J1007_AGN

In many LRDs, rest-frame UV lines (for example, Si iv, C iv, C iii] and Mg ii) are uncharacteristically weak for type-1 AGNs, fully absent or more consistent with photoionization from massive stars⁸. By contrast, the J1007_AGN spectrum shows evidence for rest-frame UV lines, including a weak detection of N iv λ1486 and C IV emission (SNR_peak ≈ 3) and a possible detection of the Mg ii line (SNR_peak ≈ 2). Although N iv λ1486 emission is rarely detected from AGNs or quasars⁵⁶, recent observations have reported nitrogen-enriched gas in a range of z ≳ 6 galaxies^57,58,59 and LRDs^60,61. Curiously, we also observed a downturn of the continuum flux blueward of C iv in combination with the absence of strong Lyα emission, which might indicate the presence of a strong broad absorption line system. However, the low resolution of our present data in this wavelength range precludes further interpretation.

We used the SCULPTOR⁶² Python package to model the J1007_AGN rest-frame optical spectrum in the wavelength range 31,000 Å to 43,000 Å (3,754 Å to 5,207 Å rest-frame) with a combination of a power law for the continuum and Gaussian profiles for the emission lines. The wavelength range was set to not include too much flux redward of the [O iii] lines, where the power-law slope of the continuum was expected to change⁶³. The [O iii] λ4960.30, [O iii] λ5008.24, [O iii] λ4364.44, He ii λ4687.02 and [Ne iii] λ3869.85 lines were modelled with one Gaussian component each. We approximated the Hβ λ4862.68 line and Hγ λ4341.68 lines with two Gaussian components each, whereas the Hδ λ4102.89 line was modelled with a single (narrow) component. Owing to the low SNR of the [Ne iii] λ3968.58 emission line, we decided against including it in the model and accordingly masked out its contribution.

Modelling the rest-frame optical continuum was complicated by contributions from a multitude of atomic and ionic iron emission lines blending into a pseudo-continuum^64,65. Adding an iron pseudo-continuum to the model produced the same results, because the amplitude was effectively set to zero. This indicates that the low resolution and modest SNR of our spectrum cannot constrain the iron pseudo-continuum at present, and hence, we did not include it in our fitting.

We expected the widths and redshifts of some of the narrow or broad emission lines to be correlated. To better decompose these line components, we coupled the redshift and FWHM of the Hβ, Hγ and Hδ narrow line components to the [O iii] λ4960.30, [O iii] λ5008.24 and [O iii] λ4364.44 lines. Additionally, the redshift and FWHM of the Hβ and Hγ broad-line components were also coupled together. To constrain the model of the low signal-to-noise detection of the He ii line, we coupled its redshift to the redshift of the narrow emission lines.

AGNs and type-1 quasars excite both Hγ and [O iii] λ4364.44 emission⁶³, which are usually blended due to the broad nature of the lines. Unfortunately, the quality of our spectrum did not allow us to uniquely decompose the individual line contributions without coupling the redshifts and widths as described above (Fig. 1).

We sampled the full parameter space of the model fitting using emcee⁶⁶. As results, we quote the median value of the fitting parameter and report the 68th-percentile range of the fitting posterior as our 1σ uncertainty. Our model fits account for the low resolution of the PRISM observations by convolving the model spectrum with the wavelength-dependent dispersion curve provided by STScI. As a consequence, all fitted linewidths are intrinsic and did not require a resolution correction. At the wavelength of the narrow [O iii] λ5008.24, this dispersion curve predicted a resolution R ≈ 193 (FWHM ≈ 1,550 km s⁻¹). Without accounting for the line spread function, we measured an FWHM of ~1,150 km s⁻¹ for the [O iii] λ5008.24 line. Hence, the actual spectral resolution is better than the nominal spectral resolution of the MSA PRISM. This was not surprising, as the nominal resolution assumed flat illumination of the MSA slits, whereas our target only partially filled the slit (Fig. 1). For our fitting procedure, we assumed a spectral resolution of R ≈ 273 (≈ 1,100 km s⁻¹) at [O iii] λ5008.24 and scaled the dispersion curve accordingly. We tested the fitting results against various assumptions on the adopted spectral resolution at [O iii] λ5008.24 (R ≈ 268 ≈ 1,120 km s⁻¹ and R ≈ 278 ≈ 1,080 km s⁻¹). Across the three adopted resolutions, the median fitting results all agree well within their 16th to 84th percentile ranges.

Extended Data Table 1 summarizes the main source properties of J1007_AGN calculated from the fitting in addition to the source redshift, which was determined from a separate line fit to the [O iii] λ4960.30 and [O iii] λ5008.24 lines. The absolute magnitude at 1,450 Å, M₁₄₅₀, was directly calculated from the average spectral flux in a 50-Å window around rest-frame 1,450 Å. We note that fluxes and linewidths of the Hβ and Hγ emission-line components face considerable uncertainties. Although our model fitting treated coupled narrow and broad emission linewidths consistently, the low resolution still resulted in a large degeneracy between the narrow and broad components. These uncertainties limited the use of the Balmer decrement to constrain dust attenuation for J1007_AGN and were carried over to the derived properties (for example, the SMBH mass).

Nature of the continuum emission

The width of the Hβ broad-line component, FWHM_Hβ,broad/(km s⁻¹) > 3,000, left little doubt that our source is a bona fide type-1 AGN. However, rest-frame UV emission lines (C iv, Si iv, Mg ii and C iii]), which are expected to be strong in type-1 AGNs, appear weak and the continuum beyond ~3,500 Å has an unusually red slope (α_OPT = 0.28 in ${f}_{\lambda }\propto {\lambda }^{{\alpha }_{{\rm{OPT}}}}$). The resulting red rest-frame optical colour (F277 − F444W ≳ 1.5) and the compact nature of the source (Extended Data Fig. 1) mark this source as belonging to the population of LRDs^6,7,67. These are compact, red (rest-frame optical) sources discovered in JWST imaging data. Spectroscopic surveys have identified broad Hα or Hβ line components in photometrically selected compact, red sources, indicating that a notable fraction are (type-1) AGNs (~60%)⁶. However, their lack of strong rest-frame UV emission lines typical for AGNs and their unusual V-shaped continuum (blue rest-frame UV and red rest-frame optical) make it challenging to classify them in the AGN unification paradigm. One hypothesis is that the continuum emission is the superposition of a dust-attenuated AGN continuum and much weaker scattered intrinsic AGN emission, which is responsible for the blue rest-frame UV slope^6,67, like lower-redshift dust-reddened quasars⁶⁸. Alternatively, the spectrum could be explained with dust-attenuated AGN emission in combination with unattenuated⁶⁹ stellar light dominating the rest-frame UV emission^6,67. It has also been proposed⁹ that dense gas is responsible for the Balmer break and absorption features often observed in LRDs^13,14,70.

Here we consider scenarios that attribute the shape of the LRD continuum emission to some level of dust attenuation between the observer and the broad-line region (BLR) of the AGN. In this scenario, our measurements of the bolometric luminosity, black hole mass and Eddington luminosity ratio derived from the rest-frame optical spectrum will be biased low. To estimate the level of dust attenuation, we first measured the Balmer decrement from the narrow Hβ and Hγ lines (see tabulated values⁷¹ for temperature T = 10⁴ K and electron density n_e = 10⁶ cm⁻³). From the flux ratio of these Balmer lines, we estimated the dust attenuation ${A}_\mathrm{V}={5.67}_{-6.49}^{+6.07}\,{\rm{mag}}$. Different assumptions on the spectral resolution led to similarly high results (for R ≈ 268, ${A}_\mathrm{V}={4.58}_{-6.63}^{+5.15}\,{\rm{mag}}$, and for R ≈ 278, ${A}_\mathrm{V}={6.61}_{-5.90}^{+6.73}\,{\rm{mag}}$).

The large uncertainties are due to the degeneracy with the broad Balmer lines in our fitting. We note that we did not derive a Balmer decrement from the broad-line components. Their flux ratios are known to deviate from theoretical expectations due to the changing conditions and high densities of the BLR⁷². Using the Hδ line for the Balmer decrement led to negative and, hence, unphysical dust-attenuation values. We modelled the marginally resolved (3–4 px) and detected line (SNR ≲ 4) with only one narrow component. A non-negligible broad-line component may explain this inconsistency. However, given the already large uncertainties on the components of the other Balmer lines, we do not believe that a two-component fit for Hδ will lead to meaningful results.

Alternatively, we modelled the spectrum of J1007_AGN in line-free windows with two continuum models. First, we modelled the continuum emission with a combination of an attenuated power-law model f(f₂₅₀₀, α_λ, A_v) and a scattered-light power law g(f₂₅₀₀, α_λ, f_sc). Both power laws were defined by the same intrinsic flux at 2,500 Å, f₂₅₀₀, and the same slope, α_λ. The former model was then attenuated by A_V using a standard attenuation curve⁷³, and the latter was multiplied by a scattered-light fraction f_sc. With these models, we performed a Markov chain Monte Carlo likelihood fit using emcee⁶⁶. We introduced a Gaussian prior on the power-law slope with a mean of −1.5 and a standard deviation of σ = 0.3, because a uniform prior fit always preferred extremely steep (α_λ < −3), physically unmotivated, power-law slopes. All other parameters received uniform priors. Our results indicate that the underlying continuum emission originated from a steep power law (${\alpha }_{\lambda }={-1.98}_{-0.27}^{+0.23}$ and ${f}_{\text{2500}}={21.61}_{-6.58}^{+9.44}$) that has been attenuated (${A}_\mathrm{V}={2.79}_{-0.25}^{+0.25}\,{\rm{mag}}$). We found the scattered-light fraction $\log_{10}(\;{f}_\mathrm{sc})={-1.74}_{-0.21}^{+0.19}$. Figure 2 displays the median model along with the 68th-percentile posterior range in orange. The model can reasonably well approximate the continuum emission within the flux uncertainties. However, the rest-frame ≲3,000 Å region seems slightly underpredicted, whereas the rest-frame ~3,000–4,000 Å region is slightly overpredicted by this fit.

We also fitted a superposition of a galaxy model with a power-law slope to the data. The power-law model is equivalent to the model described above without the scattered-light component. We also imposed the same prior on the power-law slope. We generated the galaxy model using bagpipes⁵⁴ and its default stellar population synthesis models. We adopted a delayed-τ star formation history, with a uniform prior on the galaxy age (10–735 Myr) and timescale of decrease τ (0.1–4.0 Gyr). Stellar masses were allowed within the range 10⁸ to 10¹² M_⊙, and the galaxy model has its own dust-attenuation parameter uniformly sampled within A_V,gal = 0.01–6 mag. The same dust-attenuation law⁷³ was applied consistently for both components. First tests of the galaxy plus power-law model showed that the stellar metallicity cannot be constrained by the fit, and so we fixed it to a value of 0.5 consistent with the gas-phase metallicity of high-redshift, massive galaxies (M ≈ 10¹⁰ M_⊙). The blue solid line in Extended Data Fig. 2 shows the median fit of this model to the spectrum with separate contributions from the galaxy and the power-law component highlighted with different line styles. The galaxy component dominates the continuum in the rest-frame optical with a clear Balmer break. The nominal results for the stellar mass, stellar age and the τ parameter are $\log ({M}_{* }/{M}_{\odot })={9.83}_{-0.22}^{+0.50}$, $t={0.45}_{-0.19}^{+0.17}\,{\rm{Gyr}}$ and $\tau ={2.22}_{-1.30}^{+1.21}\,{\rm{Gyr}}$. We note that the posteriors show strong degeneracies between the stellar age and the τ parameter and that both parameters effectively remain unconstrained. The galaxy component was attenuated by ${A}_\mathrm{V,{{gal}}}={0.93}_{-0.18}^{+2.27}\,{\rm{mag}}$. The AGN, modelled as a power law, was similarly steep as in the scattered-light model (${\alpha }_{\lambda }={-1.72}_{-0.85}^{+0.38}$) with an amplitude ${f}_{\text{2500}}={29.00}_{-25.91}^{+38.45}$. The dust attenuation for the AGN was largely unconstrained, with a nominal median value ${A}_\mathrm{V}={4.47}_{-3.37}^{+1.16}\,{\rm{mag}}$.

Scaling relations between the Hβ broad-line flux and 5,100 Å continuum luminosity³² imply similar levels of dust attenuation for the AGN continuum and broad-line components. The line fitted to the J1007_AGN spectrum (Fig. 2) resulted in a value L_Hβ = 3.89 × 10⁴² erg s⁻¹, which would correspond to an accretion disk continuum flux of L₅₁₀₀ ≈ 4.76 × 10⁴⁰ erg s⁻¹ Å⁻¹, according to the scaling relation. We measured a value L₅₁₀₀ ≈ 2.69 × 10⁴⁰ erg s⁻¹ Å⁻¹ for the continuum component in our spectral fit, close to the value estimated from the scaling relation. For the continuum fits, the scattered-light model found a similar continuum luminosity (L₅₁₀₀ ≈ 1.69 × 10⁴⁰ erg s⁻¹ Å⁻¹), whereas the model with the galaxy component predicted a much lower luminosity L₅₁₀₀ ≈ 5.35 × 10³⁹ erg s⁻¹ Å⁻¹), about a factor of 9 lower than inferred from the Hβ line luminosity. It is notable that the J1007_AGN spectrum almost obeys the established AGN scaling relations between the line luminosity and the continuum luminosity. Any contribution from a stellar component to the continuum would decrease the AGN continuum luminosity, essentially breaking with these scaling relations. In light of this, we prefer the interpretation of the scattered-light model and adopted its posterior attenuation value (A_V = 2.79 mag) for further analysis, a conservative choice in comparison with the results from the Balmer decrement.

Derivation of the SMBH mass and the Eddington ratio

The AGN nature of LRDs and the association of the observed broad Balmer lines originating in a typical BLR is highly debated in the literature^{12,13,14,15,60,74}. To estimate the SMBH mass and Eddington rate of J1007_AGN, we proceeded by assuming that the broad lines observed in our spectrum originated from BLR gas and that the single-epoch virial estimators calibrated in the local Universe do apply to our source. Assuming that the BLR emitting gas is in virial motion around the SMBH, we used the line-of-sight velocity width, as measured by the FWHM of the line, to trace the gravitational potential of the SMBH mass M_BH:

$${M}_{{\rm{BH}}}\approx f\frac{R\times{\rm{FWHM}}}{G},$$

(1)

where R is the average radius of the line-emitting region, G is the gravitational constant and f encapsulates our ignorance regarding the detailed gas structure, its orientation towards the line of sight and more complex BLR kinematics. Correlations connecting the radius R to the continuum luminosity of broad-line AGNs^75,76 then allowed us to rewrite the expression above in terms of direct observables⁷⁷, that is a virial SMBH mass estimator. Traditionally, these relations estimate the SMBH mass from the FWHM of a line (for example, the Hβ line) and a measure of the continuum luminosity of the source (for example, the luminosity at 5,100 Å, L₅₁₀₀). For quasars that dominate the emission at 5,100 Å, this choice is appropriate. However, it is unclear to what extent the emission in the rest-frame optical is dominated by the AGN or by galaxy light. Therefore, we employed a single-epoch virial estimator³² that uses the total Hβ line luminosity as a proxy for the continuum luminosity for our fiducial SMBH estimate, M_BH,GH05,LHβ. Additionally, we adopted three different single-epoch virial estimators^32,78,79 that use the Hβ FWHM and continuum luminosity L₅₁₀₀ for comparison. We used these to gauge the systematic uncertainty inherent in this form of SMBH mass measurement.

To estimate the bolometric luminosity L_bol, we applied a typical bolometric correction factor³³ (L_bol = 9.26L₅₁₀₀) to estimate the bolometric luminosity from the continuum luminosity at 5,100 Å, L₅₁₀₀. To produce consistent results for our fiducial SMBH mass estimator, we alternatively used the empirical line-to-continuum luminosity relations³² to calculate an approximate L₅₁₀₀ from L_Hβ, and then we converted L₅₁₀₀ to a bolometric luminosity (denoted as L_bol,Hβ). We used the appropriate bolometric luminosities to calculate the Eddington luminosity ratios, λ_Edd = L_bol/(1.26 × 10³⁸ erg s⁻¹ M_☉⁻¹ × M_BH), for the different SMBH mass estimates. All measured spectral properties along with the luminosities, SMBH masses and Eddington luminosity ratios are presented in Extended Data Table 1. Based on the observed spectrum, we found J1007_AGN to host an SMBH with a mass of ${M}_{{\rm{BH}},{\rm{GH05}},{\rm{LH}}\upbeta }=11.5{2}_{-4.63}^{+10.11}\times 1{0}^{7}\,{{{M}}}_{\odot }$ with an Eddington luminosity ratio of ${\lambda }_{{\rm{Edd}},{\rm{GH05}},{\rm{LH}}\upbeta }=0.2{0}_{-0.09}^{+0.13}$. At face value, J1007_AGN hosts a rapidly (λ_Edd > 0.1) accreting, relatively massive SMBH (M_BH ≈ 10⁸ M_⊙), akin to the least luminous quasars²⁰ identified at z > 5.9 (see Fig. 2, right, for a comparison). The SMBH mass estimates based on different single-epoch scaling relations vary within a factor of 2, in agreement with the expected systematic uncertainties⁷⁸ of ±0.43 dex depending on the adopted estimator and model assumptions⁸⁰.

Following our discussion on the nature of the continuum emission, we concluded that the J1007_AGN spectrum probably suffers from dust attenuation. To estimate the attenuation-corrected source properties, we adopted the attenuation value of ${A}_\mathrm{V}={2.79}_{-0.25}^{+0.25}\,{\rm{mag}}$ derived from the continuum fit with the scattered-light model.

We corrected the model fit realizations to the optical J1007_AGN spectrum (Fig. 2) by applying an attenuation correction for an A_V value that was randomly sampled from the posterior of the scattered-light model fit. In this way, we consistently propagated both the uncertainties on the line fit and the dust attenuation.

We measured the properties of the dust-corrected model fits and recalculated the luminosities, SMBH mass and the Eddington luminosity ratio for our fiducial choice of single-epoch virial estimator³² based on the Hβ line luminosity. These results are summarized in Extended Data Table 2. Accounting for the attenuation, J1007_AGN reaches quasar-like bolometric luminosities $\log_{10}({L}_{{\rm{bol}},{\rm{H}}\upbeta }/({\rm{erg}}\,{{\rm{s}}}^{-1}))=46.6{4}_{-0.12}^{+0.13}$ and an SMBH mass ${M}_{{\rm{BH}},{\rm{GH05}},{\rm{LH}}\upbeta }=4.5{1}_{-2.32}^{+5.22}\times 1{0}^{8}\,{{{M}}}_{\odot }$, now fully overlapping with the quasar distribution²⁰ at z > 5.9, as shown in Fig. 2 (right).

Number density estimate

To place our serendipitous discovery of J1007_AGN in context with the population of faint high-redshift AGNs discovered with JWST, we calculated its approximate number density. J1007_AGN was discovered as a priority 1 galaxy candidate during our spectroscopic follow-up campaign. Although the target redshift range for galaxy candidates was approximately z ≈ 7.4–9.1, our permissive selection also selected dropout sources at lower redshifts. To calculate the volume surveyed by our observations, we used an inclusive redshift interval of z = 7.2–9.1. Given our deep NIRSpec PRISM observations, we are confident that we would have detected any similarly bright AGN up to z = 9.1. The discovery of J1007_AGN and many z ≈ 7.2 galaxies motivated the extension of the lower redshift limit below the nominally targeted redshift range for galaxies. The total survey area we adopted is 16.73 arcmin², which is the overlap of our NIRCam photometry and NIRSpec/MSA spectroscopy. We derived a survey volume V = 61,402 Mpc³. This led to an approximate source density n = 1/V ≈ 1.63 × 10⁴ Gpc⁻³, assuming a total selection completeness of 100%. However, we already knew that our targeting selection completeness for priority 1 sources was only 61%. Correcting for this effect, we calculated n_corr ≈ 1.64/V = 2.67 × 10⁴ Gpc⁻³. To compare these number estimates in the context of other samples of faint high-redshift AGNs, we calculated luminosity function estimates based on this one source. This was solely for illustration, and we caution that calculating a statistical property from a single source incurs systematic biases due to the small sample size and cosmic variance. First, we placed J1007_AGN in the context of the high-redshift UV luminosity function. As a proxy for the absolute UV magnitude, we used the absolute magnitude at 1,450 Å as measured from the spectrum, M₁₄₅₀ = −19.29 (Extended Data Table 1) and chose a bin size ΔM₁₄₅₀ = 1. With these assumptions, our corrected luminosity function measurement is $\varPhi =2.6{7}_{-2.21}^{+6.14}\times 1{0}^{4}\,{{\rm{Gpc}}}^{-3}\,{{\rm{mag}}}^{-1}$, where the uncertainties encompass the confidence interval for a Poisson distribution that corresponds to 1σ in Gaussian statistics. We compare our estimate with the UV luminosity functions of faint AGNs^1,6, galaxies and quasars in Fig. 3 (left). Figure 3 (right) shows our luminosity function estimate converted to bolometric luminosity. In correspondence with the literature^6,17, we used the bolometric luminosity estimate derived from the Hβ line luminosity, L_bol,Hβ. These panels show that our luminosity function estimate agrees well with other measurements for faint high-redshift AGNs, indicating that the identification of this source in our surveyed volume was likely to be expected. We note that the bolometric luminosity function of these AGNs remains orders of magnitude above the best constraints on the bolometric quasar luminosity function³⁵.

LRD–galaxy cross-correlation measurement

The LRD–galaxy cross-correlation function χ averaged over an effective volume V_eff can be related to the LRD–galaxy two-point correlation function ξ_LG through

$$\chi ({R}_{\min },{R}_{\max })=\frac{\displaystyle\int\xi_\mathrm{LG}(R,Z)\,\mathrm{d}{V}_{{\rm{eff}}}}{{V}_{{\rm{eff}}}},$$

(2)

which is equivalent to that for luminous quasars^36,81. In this case, we chose a cylindrical geometry with radial coordinate R being the transverse comoving distance and the cylinder height Z the radial comoving distance,

$$Z=\frac{c}{H(z)}\delta z,$$

(3)

where H(z) is the Hubble constant at redshift z, c is the speed of light and δz is a redshift interval. The volume-averaged cross-correlation χ(R_min, R_max) was calculated in radial bins with bin edges R_min and R_max. We effectively calculated χ(R_min, R_max) as

$$\chi ({R}_{\min },{R}_{\max })=\frac{\langle\mathrm{LG}\rangle }{\langle\mathrm{LR}\rangle }-1,$$

(4)

where 〈LG〉 is the number of LRD/galaxy pairs in the enclosed cylindrical volume and 〈LR〉 is the number of random LRD/galaxy pairs in average regions of the Universe. We considered only J1007_AGN for the LRD–galaxy clustering measurement here and, thus, 〈LG〉 is simply the number of associated galaxies in the volume. The random number of galaxies can be expressed in terms of the background volume density of galaxies ρ_gal at redshift z in the cylindrical volume V_eff: 〈LR〉 = ρ_galV_eff. Our survey volume was not large enough to allow us to empirically determine the background volume density of galaxies. Hence, we calculated an estimate of ρ_gal from the galaxy luminosity function⁸². We integrated the luminosity over the magnitude range −30.0 < M_UV ≤ −18.9, where the faint-end limit corresponds to the faintest spectroscopically identified galaxy in our sample. The resulting galaxy background density ρ_gal = 7.12 × 10⁵ Gpc⁻³. The effective volume in cylindrical geometry can be expressed as

$${V}_{{\rm{eff}}}=\int_{{Z}_{\min }}^{{Z}_{\max }}\int_{{R}_{\min }}^{{R}_{\max }}S(R,Z\;)2\uppi R\,{\rm{d}}R\,{\rm{d}}Z,$$

(5)

where S(R, Z) is the galaxy selection function in terms of both R and Z. We decompose S(R, Z) into three components:

$$S(R,Z\;)={S}_{Z}(Z\;){S}_{R}(R){S}_{T}(R),$$

(6)

where S_Z(Z) is the redshift-dependent completeness, S_R(R) the radially dependent coverage completeness and S_T(R) the radially dependent targeting completeness. The coverage completeness S_R(R) accounts for the area in the radial annulus that was not covered by our NIRCam observations and NIRSpec/MSA follow-up, whereas the targeting completeness S_T(R) accounts for the fact that only a subset of galaxy candidates in the covered MSA footprints could be followed up with our MSA observations.

Owing to the limited number of companion galaxies, we chose three radial bins with bin edges 0.1 h⁻¹ cMpc, 0.6 h⁻¹ cMpc, 2.7 h⁻¹ cMpc and 7.6 h⁻¹ cMpc (0.14 cMpc, 0.86 cMpc, 3.71 cMpc and 10.86 cMpc). For these bins, we calculated a radial coverage completeness S_R(R) = 1.0, 0.52 and 0.26, respectively, based on the fractional area covered by our NIRSpec observations. We limited our selection of galaxies for the clustering measurement by restricting the relative line-of-sight velocity to |Δv_LOS| ≤ 1,500 km s⁻¹ and |Δv_LOS| ≤ 2,500 km s⁻¹, selecting six or alternatively all of the eight galaxies listed in Extended Data Table 4. These line-of-sight velocity differences correspond to redshift intervals z = 7.22–7.30 or z = 7.20–7.32, respectively. For simplicity, we conservatively set the redshift-dependent completeness S_Z(Z) to a constant 100% over these narrow redshift intervals, providing us with a lower limit on the cross-correlation measurement.

In addition, our assignment of MSA slits with the eMPT tool introduced a targeting selection function S_T(R) that depends on the priority class of a candidate. For each priority and radial bin, we calculated our targeting completeness C_p,R as the fraction of targeted to photometrically selected galaxy candidates in the MSA area. All our identified galaxies belong to the priority classes p = 1 and 2 (Extended Data Table 4). The relevant completeness values for our three radial bins R = [1, 2, 3] in increasing distance to J1007_AGN are C_1,1 = 1.0, C_1,2 = 0.75, C_1,3 = 0.57 and C_2,3 = 0.22. Based on these values, we calculated the ‘corrected’ number of LRD/galaxy pairs 〈LG〉_r,corr per radial bin as

$${\langle\mathrm{LG}\rangle }_{R,\mathrm{corr}}=\sum _{p}\frac{{\langle\mathrm{LG}\rangle }_{p,R}}{{C}_{p,R}},$$

(7)

where 〈LG〉_p,r is the number of LRD/galaxy pairs per radial bin R and priority p. Finally, the targeting selection function was approximated by the fraction of observed to corrected LRD/galaxy pairs:

$${S}_{T}(R)=\frac{{\langle\mathrm{LG}\rangle }_{{{R}}}}{{\langle\mathrm{LG}\rangle }_{R,\text{corr}}},$$

(8)

with values of 1, 0.75 and 0.32 for the three radial bins in order of increasing distance. We present our binned clustering measurements in Extended Data Table 5 for the two samples with relative line-of-sight velocities |Δv_LOS| ≤ 1,500 km s⁻¹ and |Δv_LOS| ≤ 2,500 km s⁻¹, finding an overdensity in the innermost radial bin with δ = 〈LG〉/〈LR〉 − 1 ≈ 45 or 26, respectively.

We next aimed to constrain the real-space LRD–galaxy two-point correlation function ξ_LG by parameterizing its shape as

$${\xi }_{{\rm{LG}}}={\left(r/{r}_{0}^{{\rm{LG}}}\right)}^{-{\gamma }_{{\rm{LG}}}},$$

(9)

where $r=\sqrt{{R}^{2}+{Z}^{\,2}}$ is the radial coordinate, ${r}_{0}^{{\rm{LG}}}$ is the cross-correlation length and γ_LG is its power-law slope. This form is governed by two parameters. However, our limited statistics did not allow us to uniquely constrain both ${r}_{0}^{{\rm{LG}}}$ and γ_LG. Hence, we assumed the value γ_LG = 2.0 for our analysis, which was chosen to allow for comparison with the quasar literature²³. We performed a fit to the binned data and sampled a Poisson likelihood on a grid. We present the median of the posterior as our results on the cross-correlation length ${r}_{0}^{{\rm{LG}}}$ in Extended Data Table 5. Uncertainties reflect the confidence interval for a Poisson distribution that corresponds to 1σ in Gaussian statistics⁸³. Extended Data Fig. 5 (left) presents our binned LRD–galaxy cross-correlation measurement with |Δv_LOS| ≤ 1,500 km s⁻¹, including the targeting completeness correction. The corresponding best-fitting cross-correlation length is ${r}_{0,{\rm{corr}}}^{{\rm{LG}}}\approx 8.1{7}_{-2.38}^{+2.42}\,{{\rm{h}}}^{-1}\,{\rm{cMpc}}$. Increasing the line-of-sight distance to |Δv_LOS| ≤ 2,500 km s⁻¹ to encompass all discovered nearby galaxies produced a consistent result (Extended Data Table 5).

Assuming that galaxies and LRDs trace the same underlying overdensities³⁶, the LRD–LRD auto-correlation ξ_LL can be expressed in terms of the galaxy–galaxy auto-correlation ξ_GG and the LRD–galaxy cross-correlation ξ_LG according to

$${\xi }_{{\rm{LL}}}={\xi }_{{\rm{LG}}}^{2}/{\xi }_{{\rm{GG}}}.$$

(10)

For our analysis, we fixed the slopes of the auto-correlation functions as in previous work on quasars^23,36,84,85, assuming γ_GG = 2.0 and γ_LL = 2.0. As all of our identified galaxies show prominent [O iii] lines (Extended Data Fig. 3), we adopted the recent measurement of the galaxy auto-correlation length, ${r}_{0}^{{\rm{GG}}}=4.1\,{{\rm{h}}}^{-1}\,{\rm{cMpc}}$, at 〈z〉 = 6.25 based on [O iii] emitters²³. Using our cross-correlation length estimate for |Δv_LOS| ≤ 1,500 km s⁻¹, ${r}_{0,{\rm{corr}}}^{{\rm{LG}}}\approx 8.1{7}_{-2.38}^{+2.42}\,{{\rm{h}}}^{-1}\,{\rm{cMpc}}$, we derived an auto-correlation length ${r}_{0}^{{\rm{LL}}}\approx 19.1{1}_{-8.63}^{+11.49}\,{{\rm{h}}}^{-1}\,{\rm{cMpc}}$. We used predictions of a halo model framework (TheHaloMod)^86,87, to link the auto-correlation length to a minimum dark matter halo mass for LRDs at z ≈ 7.3. Assuming that all LRDs live in dark matter haloes with a minimum mass threshold M_halo,min, we predicted the quasar auto-correlation function using the halo model for different M_halo,min. For each quasar auto-correlation function, we tabulated the auto-correlation length ${r}_{0}^{{\rm{LL}}}$ and the cumulative abundance of haloes n_halo,min with M > M_halo,min. This allowed us to link our estimate ${r}_{0}^{{\rm{LL}}}$ to a minimum halo mass. We calculated a minimum halo mass $\log_{10}({M}_{{\rm{halo}},\min }/{{{M}}}_{\odot })=12.0{2}_{-1.00}^{+0.82}$ with a corresponding abundance of $\log_{10}({n}_{{\rm{halo}},\min }/{{\rm{cGpc}}}^{-3})=-0.2{4}_{-5.86}^{+3.86}$. On comparing this value with the z ≈ 7.5 number density of LRDs¹⁷ (M_UV = −20 and 6.5 < z < 8.5), log₁₀(n_LRD/cGpc⁻³) = 3.42 ± 0.44, it became evident that a large range for the estimated minimum halo mass would be inconsistent with our current cosmology (Extended Data Fig. 5, right). Assuming that the LRDs are a subsample of their host distribution, one can relate their number density n_LRD and the minimum mass host halo abundance n_halo,min to their lifetime t_LRD using the same arguments as for UV-luminous quasars^88,89,

$${n}_{{\rm{LRD}}}\approx\frac{{t}_{{\rm{LRD}}}}{{t}_{{\rm{H}}}(z)}{n}_{{\rm{halo}},\min }.$$

(11)

Here, t_H(z) denotes the Hubble time at redshift z. We emphasize that the LRD lifetime t_LRD is the average time period in which we observed the source as an LRD. In this context, the ratio of LRD lifetime to Hubble time is referred to as the duty cycle f_duty = t_LRD/t_H(z) = n_LRD/n_halo,min. Based on the abundance of LRDs and our inferred cumulative halo abundance n_halo,min, we calculated a duty cycle $\log_{10}(\;{f}_{{\rm{duty}}})\approx 3.6{6}_{-3.90}^{+5.89}$, resulting in a lifetime for z ≈ 7.3 LRDs of $\log_{10}({t}_{{\rm{LRD}}}/{\rm{yr}})\approx 12.5{2}_{-3.9}^{+5.9}$. We accounted for the uncertainties by calculating realizations drawn from our best-fitting posterior for n_halo,min, assuming a log-normal distribution for n_LRD and reporting the 16th to 84th percentiles as uncertainties. We display the redshift evolution of the auto-correlation length, the minimum halo mass and the duty cycle for quasars, broad-line AGNs and our result for LRDs in Fig. 4. The unphysical regime for duty cycles is marked in the grey region in the bottom panel. Furthermore, we recalculated the duty cycle for a broad-line AGN³⁷ (green square, $\log_{10}(\;{f}_{{\rm{duty}}})=-1.0{7}_{-0.41}^{+0.45}$). In the original work, the authors integrated over a large range of halo mass abundances (M_halo = 10¹¹–10¹² M_⊙) well beyond their derived characteristic halo mass of log₁₀(M_halo (h⁻¹ M_☉)) = 11.46. Adopting their result as a median mass, we calculated a corresponding minimum halo mass log₁₀ (M_halo (h⁻¹ M_☉)) = 11.31. Using the same approach as above, we calculated the halo abundance using TheHaloMod at z = 5.4. The bottom panel of Fig. 4 compares the duty cycles of different sources and from different tracers across cosmic time. At z > 5, luminous quasars (M₁₄₅₀ ≲ −26.5 mag) usually have low duty cycles f_duty ≈ 0.1% measured from quasar clustering^22,23,24, quasar proximity zones⁹⁰ and Lyα damping wings^27,38. This is in contrast to z ≈ 4 quasars^84,91 and to z ≈ 5 broad-line AGNs³⁷ with f_duty ≳ 10%. Our analysis resulted in a duty cycle $\log_{10}(\;{f}_{{\rm{duty}}})\approx 3.6{6}_{-3.90}^{+5.89}$. Although the median value lies in the unphysical region (f_duty > 1), our lower 16th percentile tail extends well into the region of physical duty cycles f_duty = 0.3–1. This result is driven by the high number densities of LRDs¹⁷ compared with the number densities of available host dark matter haloes in the mass range we inferred.