Evoking stable and precise tactile sensations via multi-electrode intracortical microstimulation of the somatosensory cortex

Abstract

Tactile feedback from brain-controlled bionic hands can be partially restored via intracortical microstimulation (ICMS) of the primary somatosensory cortex. In ICMS, the location of percepts depends on the electrode’s location and the percept intensity depends on the stimulation frequency and amplitude. Sensors on a bionic hand can thus be linked to somatotopically appropriate electrodes, and the contact force of each sensor can be used to determine the amplitude of a stimulus. Here we report a systematic investigation of the localization and intensity of ICMS-evoked percepts in three participants with cervical spinal cord injury. A retrospective analysis of projected fields showed that they were typically composed of a focal hotspot with diffuse borders, arrayed somatotopically in keeping with their underlying receptive fields and stable throughout the duration of the study. When testing the participants’ ability to rapidly localize a single ICMS presentation, individual electrodes typically evoked only weak sensations, making object localization and discrimination difficult. However, overlapping projected fields from multiple electrodes produced more localizable and intense sensations and allowed for a more precise use of a bionic hand.

Main

Manual interactions with objects rely critically on tactile signals from the hand, as evidenced by the deficits experienced when these signals are lost^1,2,3. Myoelectric prosthetic limbs lacking any form of somatosensory feedback are often abandoned⁴. Consequently, adding intuitive feedback about both the location and force of the contact events may also improve the utility and acceptance of brain-controlled bionic limbs. Efforts are underway by several groups to provide tactile feedback via intracortical microstimulation (ICMS) of somatosensory cortex (S1)^5,6,7, and S1 ICMS has been shown to evoke localizable tactile percepts^5,6 and to improve control of prosthetic hands⁸. Information about object location can be intuitively conveyed by matching force sensors on the bionic hand with somatotopically appropriate electrodes in S1^5,8,9. For example, a force sensor on the tip of the bionic index finger can be used to drive stimulation of electrodes located in the corresponding area of S1. Information about contact force at that location can then be conveyed by modulating ICMS amplitude according to the output of the sensor, as higher amplitudes give rise to more intense touch sensations, such as that of increased force on the skin^5,9,10.

A crucial but poorly understood element of ICMS-based tactile feedback is the stability of these percepts over time. As described above, the force sensors can be mapped to specific electrodes; however, whether this mapping is stable, and thus whether repeated calibration is necessary, is unknown. While one study with an individual participant and few timepoints suggested that S1 ICMS projected fields (PFs) are stable⁵, the resolution of these reports was insufficient for the mapping necessary to support dexterous behaviour and the generalizability of these results to other participants is unknown. Consequently, the reliability of ICMS for localizing object interactions over various time scales remains unclear.

Moving beyond percept location, variation in stimulation parameters is known to influence the percepts evoked at a given location^5,10,11,12, with both amplitude and frequency influencing intensity and, to a lesser extent, quality. Though these effects have been investigated, these findings have only been qualitative^5,6,13 and systematic cross-participant analyses have not been attempted. Additionally, the relationship between stimulus amplitude and intensity was never related to real-world physical units. Thus, it is unclear whether these percepts evoke sensations that span the behaviourally relevant range (that is, useful for discriminating a range of grasp forces) or if they only cover an impoverished range that will limit object interactions.

The objective of the present study was threefold. First, we sought to precisely quantify the spatial extent and distribution of sensations evoked by ICMS of individual electrodes over an extended period of time. Second, we aimed to characterize the range of intensities that each electrode could evoke and compare these ranges with that of natural touch. Finally, we sought to quantify the functional implications of our findings. In three human participants with chronic spinal cord injury (SCI) who have had microelectrode arrays implanted in Brodmann’s area 1 of the somatosensory cortex, we found discrete electrode-specific percepts that were stable over several years of experiments. Then, by leveraging the residual sensation of several participants, we were able to establish that the location of each electrode’s PF matched its receptive field (RF). Furthermore, we found that the size and intensity of each PF could be shaped by the stimulus amplitude or frequency. Remarkably, when electrodes with overlapping PFs were stimulated, the resulting percept resembled a summation of its components, becoming more focal and easier to localize. When examining our participants’ ability to discriminate stimulus intensity via individual electrodes, we found that most produced a range of intensities an order of magnitude less discriminable than natural touch. However, by adjusting the temporal structure of the stimuli to mimic naturally evoked responses (biomimicry), we were able to improve intensity discrimination. Additionally, we found that the multi-electrode evoked percepts had a wider range of intensities and thus conferred more discrete steps. Consequently, we demonstrate that the stable representation of PFs, and the fact that percepts can be combined, enables ICMS to evoke sensations that can be well localized and confer a substantial degree of force information.

Results

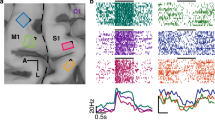
Three participants with cervical SCI were each implanted with four electrode arrays, two in the arm and hand representation of the motor cortex and two in the hand representation in Brodmann’s area 1 of S1, based on pre-operative functional magnetic resonance imaging (fMRI) or magnetoencephalography¹⁴. In all three participants, stimulation through electrodes in S1 evoked sensations experienced on the contralateral hand (Fig. 1 and Extended Data Fig. 1). Several participants had some degree of residual sensation that allowed us to measure S1 responses to peripheral touch on some parts of the hand and to compare them with sensations evoked by ICMS. In the study, we characterized the properties of these ICMS-evoked PF sensations and their dependence on a range of stimulus features. We compared these effects with those achieved by stimulation of multiple electrodes. The latter improved our participants’ ability to localize sensations and to gauge their intensity. Ultimately, better control of perceived location and intensity proved to be critical for mapping force measured on the bionic hand to sensations perceived by the user.

Fig. 1: Array implant locations and percept maps for all participants.

Left: anatomical MRI with (subsequently implanted) arrays superimposed based on intra-operative photos. MC, motor cortex; SC, somatosensory cortex (Brodmann’s area 1). Axes indicate anterior (A) and lateral (L) directions and the central sulcus is indicated by the dashed line. Middle and right: the hand region on which ICMS sensations were experienced along with the electrodes that evoked those sensations. The segment is assigned based on median reported sensation over time. Each row shows data from one participant. Note that S1 arrays were wired in a chequerboard pattern. White sections indicate unwired electrodes. Labels indicate palmar (P) surface of the thumb (P_T), index (P_I), middle (P_M), ring (P_R) and little (P_L) fingers. Coloured electrodes were used for both recording and stimulation.

PFs contain focal hotspots with diffuse borders

The ability to control the size, shape and location of PFs is fundamental to the utility of ICMS as a source of tactile feedback information. As a first step to understanding these properties, we delivered 1-s-long ICMS pulse trains (100 Hz, 60 μA) to each electrode, an intensity reliable enough to elicit a sensation for most electrodes (Extended Data Fig. 2a). Throughout each experiment, the participant was allowed repeated observation of each stimulus and then drew the spatial extent of the PF on a digital representation of their hand, enabled by partial residual motor function. From these drawings, we computed the area and centroid for each PF (Fig. 2a). This task was repeated regularly over several years (Fig. 2b), allowing us to construct an aggregate PF for each electrode by weighting each pixel on the hand drawings by the proportion of times it was included over the duration of the study (Fig. 2c and Methods). This revealed that most PFs comprised a core region within which sensations were reliably evoked, surrounded by a diffuse shell over which sensations were less consistent. With this in mind, we removed pixels reported on fewer than 33% of sessions for each electrode (see Extended Data Fig. 2b–d for the justification of the pixel frequency threshold level). Electrodes for which no pixels met this threshold (25% for participants C1 and P2 and 58% for participant P3) were excluded from further analysis. While the PFs on the excluded electrodes were typically reported on the same digit or region of the hand (Fig. 2b,c, green), we reasoned that they were not sufficiently salient to usefully convey location information. Indeed, these PFs were typically those where the intensity was very low, occasionally peri-detection threshold (Extended Data Fig. 2e).

Fig. 2: PF locations systematically vary in size and location across electrodes and participants but are stable over time.

a, Example PFs from one electrode during one session from each participant. The crosses denote the respective centroids. b, The PFs from the same electrode as in a but across all sessions (n = 8, 43 and 5 for C1, P2 and P3, respectively). c, The pixel frequency computed for the same electrodes as in a and b across all sessions. d, Hand regions over which each participant reported a sensation across all electrodes. The shading indicates whether each pixel’s frequency was above (dark) or below (light) the 33% threshold. e, The area of the hand over which a sensation was evoked (union of PFs across electrodes, after thresholding) for each participant. f, The distribution of individual PF sizes (after thresholding) for each participant (n = 62, 63 and 63, respectively). The box and whiskers show the 5th, 25th, 50th, 75th and 95th percentiles. g, The distance between the centroid of the single-day PF and the aggregate centroid for each electrode, averaged across electrodes. The line denotes the mean, and the shaded area denotes the s.d. h, The area of each percept after thresholding predicts mean distance between single-day PF centroid and aggregate PF centroid for each electrode. The dashed line denotes the best fit. i, The mean centroid distance when reports were collected within a single day compared with that computed across years for a subset of electrodes. The dashed line denotes unity.

Next, to determine the portion of a robotic hand from which we could provide feedback, we examined the spatial distribution of PFs for each participant. While all participants reported a sensation over most of the hand on at least one occasion (Fig. 2d, light shade), participant C1 experienced sensations predominantly on the tips of the digits, participant P2 on the proximal finger pads and thumb and participant P3 on both. When summed over all electrodes, the area over which sensations were evoked above the 33% threshold was 12, 33 and 30 cm² for C1, P2 and P3, respectively (palmar surface of 165 cm², 7%, 20% and 18% of the whole hand, respectively; Fig. 2e). The size of individual PFs varied widely (median of 2.5 cm², 5–95th percentiles 0.3–11.3 cm²) across electrodes and participants (Fig. 2f), with C1 reporting the smallest PFs and P2 the largest. C1 had the most distal PFs and P2 the most proximal ones, suggesting that PFs decrease in size as one progresses distally from the palm to the digit tips.

PFs are stable over time

For ICMS-based tactile feedback to be reliable, the perceived location for a given set of stimulus parameters must be consistent. While previous work found PF locations to be stable over the course of a month for a single participant⁵, stability has not been systematically quantified over longer periods of time. PF stability is of particular importance as it determines how often one would need to remap the relationship between bionic hand sensors and the PFs of implanted electrodes. If PFs change session to session, then interpretations are limited, while if reports are consistent over time, then we can assume that interpretations based on these results are reliable. To fill this gap, we compared the location of the PFs at regular intervals across 2–7 years (for C1/P3 and P2, respectively, 9 surveys for C1/P3 and 48 for P2; Fig. 2b–e). In total, we collected 555, 3,039 and 550 surveys across all electrodes from participant C1, P2 and P3, respectively. First, we computed the degree to which PFs reported for an electrode on any given session matched the first ever reported PF on that electrode. We found that the centroid distance between the initial PF and subsequent ones for a given electrode remained stable, with no significant change over the lifetime of the study for two of the three participants (C1 and P3, r = −0.03 and 0.12, P = 0.99 and 0.34, respectively), and a slight but significant increase in the third participant, who had been implanted the longest (P2, r = 0.23, P < 0.01; Extended Data Fig. 2f, an effect that persisted if we subsampled the first 2 years: r = 0.14, P < 0.01). Next, we computed the slope of the relative distance of each centroid from the first centroid (in millimetres per day). We observed that the slopes tended to be extremely small (mean of 0.006 ± 0.019); however, there was a slight positive tendency for participant P2 (t₍₅₈₎ = 4.35, P < 0.01; Extended Data Fig. 2g). Second, we computed the distance between each single-day centroid and its corresponding aggregate centroid (Fig. 2g) to determine how representative the aggregate PF was of any individual PF for a given electrode. Across all recording sessions, we found that the mean Euclidean distance ranged from 3.5 to 8.7 mm (depending on the participant). Larger PFs tended to yield more variable centroids (r = 0.33, P < 0.01; Fig. 2h), as might be expected. Furthermore, centroid distance with respect to the aggregate centroid was stable over time for one participant (P3, r = −0.1, P = 0.77) and decreased over time for the other two (C1 and P2, r = −0.17 for both, P < 0.01 for both), suggesting that the latter converged onto a more stable reporting of their PFs.

Next, we assessed whether the fluctuations in reported PF reflected true changes in position over time or simply variability in the participants’ reports. To this end, ICMS pulse trains were delivered through a subset of electrodes (n = 8 and 7 for C1 and P2, respectively, chosen to span the range of variabilities) that were randomly interleaved, and the participant reported the PF of each. This procedure was then repeated multiple times throughout the day (six and five times for participants C1 and P2, respectively), each time in a different order to minimize biases. We then assessed the degree to which the centroids of the reported PFs coincided. First, PFs were consistent between repeated reports for the two participants tested (centroid distance: median of 3.5 mm, 25–75th percentiles 1.6–4.8 mm). Second, the within-day versus across-day centroid distances for each electrode were highly correlated (r = 0.68, P < 0.01) and statistically equivalent (paired t-test, t₍₁₅₎ = 0.1, P = 0.93; Fig. 2i). In other words, the change in PF reported within a session was equivalent to the change in PF reported over years of testing. Finally, we examined whether there was any pattern to the variability across sessions and found that centroids consistently moved back and forth along a single axis (for example, the edge of the finger or across a knuckle) instead of being completely random (Extended Data Fig. 2h). Given our participants report that the PFs are not uniform in intensity, this implies that the core of each PF (the areas reported on most trials) is the portion of the PF that is most intense, and the variability is in the reporting of the less intense shell, making the aggregate centroid a reliable estimate of the underlying PF.

PF location varies systematically with cortical location

Having found that the PFs were stable over several years, we sought to determine whether the underlying somatotopy was preserved or whether any cortical reorganization had occurred following injury^15,16. According to the canonical homunculus, the representations of digits and hand segments in S1 proceed along the mediolateral axis, parallel to the central sulcus, with the little finger represented medially and the thumb represented laterally¹⁷. Examination of the PF maps (using the aggregate centroid to determine digit identity; Extended Data Fig. 1) suggests that where the PFs are predominantly located also changes along one axis, consistent with the geometry of the homunculus. To test this quantitatively, we projected the location of each electrode on each array onto a single axis and assessed the degree to which the identity of the digit could be inferred from the electrode’s location along that axis (Fig. 3a). By computing classification accuracy (one-dimensional linear discriminant analysis) across a range of axes (spanning 180°; Fig. 3b), we identified the axis along which the digit/hand segment gradients were most pronounced (Fig. 3c). We found that, for each array, position along the optimal classification axis (one-dimensional) served to classify digit identity as well as the original position (two-dimensional) (Fig. 3d) and that this axis was approximately parallel to the local curvature of the central sulcus for five out of the six arrays, consistent with the canonical homunculus. In the array that did not show this pattern (participant P3’s lateral array), the axis was nearly perpendicular to the S1 curvature, but the PFs were largely confined to a single digit (the index finger), yielding comparable classification at all angles. Next, we examined whether the distance between PFs increased as the distance between electrodes increased, restricting the analysis to pairs of electrodes with PFs on the same digit. We found that, as expected, PF centroid distance increased systematically with cortical distance (Fig. 3e). A 2 mm shift in cortex corresponded to a ~10 mm shift in the PF on the skin, on average. The systematic relationship between cortical location and PF location is thus consistent with the canonical homunculus, in which S1 is characterized by strips that encode individual digits¹⁸.

Fig. 3: Percept location varies along somatotopic axes and is determined by underlying RFs.

a, Example projections of percept centroids in their original position (on array) when projected along either column-wise or row-wise axes. b, Classification performance versus the angle of the projection axis, expressed relative to the local curvature of S1. Each line represents an array for the indicated participant. c, Optimal digit/palmar segment discrimination axis (perpendicular to the projection axis), superimposed on each S1 array (dotted line). The dashed line denotes the local curvature of S1, which, for C1, deviates from the curvature of the central sulcus. d, Digit classification when using either both axes of the array (row and column (2D, two dimensions)) or the best single projected axis (1D, one dimension). e, Within digit, the distance between two PF centroids is significantly correlated with the distance between the electrodes across arrays (Pearson’s correlation, n = 5,892 pairs, r = 0.69, P < 0.0001) and within each array (Pearson’s correlation, r > 0.4, P < 0.0001, Holm–Bonferroni corrected). The dashed lines represent arrays coloured by participant, with the mean and s.d. indicated by the grey line and shaded area, respectively. f, Aggregate PF (red) and RF (blue) for an example electrode from participant P3. g, The size of the RF versus size of the PF for electrodes from participants C1 and P3. The RFs were larger for both participants (two-sided paired t-test, P < 0.0001 and P = 0.0078, respectively). The dashed line indicates unity. h, The proportion of the PF within the RF for all tested electrodes (n = 62 and 25). The median proportion was 1 for both with 25th percentiles of 0.83 and 0.72 for C1 and P3, respectively, suggesting that PFs tended to be completely subsumed by the RF. The box and whiskers show 5th, 25th, 50th, 75th and 95th percentiles. i, The number of regions (digits and palm) encapsulated by each electrode’s RF minus the number of regions encapsulated by its PF for three participants (N = 62, 25 and 21 for participants C1, P3 and R1, respectively). RFs spanned more hand regions than PFs in all three participants (two-sided Wilcoxon rank sum test, P = 0.0035). The bar and whiskers show mean and s.d. *P < 0.0001, **P = 0.0026 and ***P = 0.0035.

Electrode PFs are subsumed by their RFs

To further examine the relationship between the somatotopic homunculus and PF location, we leveraged the residual sensation in two of our participants (C1 and P3; Extended Data Fig. 3) and compared the RF and PF of each electrode. Indeed, C1 has nearly normal sensation over the fingertips and some residual sensation over the rest of the volar surface of his hand. P3 has largely spared sensation on the thumb, some spared sensation on the index and some residual sensation on D3 and D4, but his pinky finger is insensate. To map RFs, we applied gentle touches to the skin and monitored the multi-unit activity through speakers. As for the PFs, RFs were measured over multiple days with the experimenter blinded to electrode identity and the pixel frequency computed. Manual mapping of the RFs for each electrode revealed significant co-localization of the projected and RFs (Fig. 3f). To systematically compare the RF and PF of each electrode, we first compared the areas and found that, across electrodes and participants, the RF was 6.5 times as large as the PF (ratio: median of 6.5, 25–75th percentiles 3.8–14.3; Fig. 3g) and PF size tended to scale with RF size, though this relationship was significant for only one of the two participants (r = 0.15 and 0.76, P = 0.35 and 0.011 for C1 and P3, respectively). Second, PFs were typically subsumed by the RF: on average, 93% of the reported PF fell within the measured RF (Fig. 3h). In both participants, the RF included more hand segments (digits or palmar segments) than did the PF. To verify that this phenomenon was not an artefact of our approach, we repeated this analysis with a participant from an independent clinical trial that involves a partially sensate participant (Extended Data Fig. 3) who had existing data on the size of projected versus RFs at the segment level and found a similar trend (Fig. 3i, Methods and ref. ⁷). We conclude that the PF of an electrode is determined by the RFs of the neurons around the electrode tip.

PF size depends on stimulus parameters

While the previous experiments all used the same stimulus parameters (60 μA, 100 Hz and 1 s duration) to facilitate comparisons across electrodes, the question of how PF features vary as a function of either the amplitude or frequency is also important. Consequently, we examined the degree to which PFs were dependent on ICMS amplitude and frequency by repeating the survey on a subset of electrodes in which the participant drew the PF and gave a magnitude estimate of the sensation. First, we found that the size of the PF increased threefold as amplitude increased from 40 to 80 μA, with ICMS frequency fixed at 100 Hz (median (25–75th percentiles) of 170% (142–330%), two-way analysis of variance (ANOVA), F_(2,11) = 6.26, P < 0.01; Extended Data Fig. 4a). Second, PF size grew systematically as frequency increased from 50 to 200 Hz, with amplitude fixed at 60 μA (median (25–75th percentiles) 129% (121–185%), two-way ANOVA (2,11), F = 7.43, P < 0.01; Extended Data Fig. 4b). Consequently, PF size increased with total charge in both cases; however, amplitude had a greater effect than frequency (three-way ANOVA (2,2,11), F = 42.35 and 19.61, respectively, P < 0.01 for both), implying that the effect cannot be simply explained by total charge. Next, we examined the relationship between the reported size and magnitude estimates on individual trials and found that the size of the reported PF could be accurately predicted from the reported magnitude of the evoked sensation, across ICMS frequencies and amplitudes (r = 0.77, P < 0.01; Extended Data Fig. 4c). The effect of ICMS intensity on PF size is qualitatively consistent with the proposed neural determinants of the PF. Each volume of cortex maps onto a patch of skin; the greater the volume of cortex activated (amplitude modulation^19,20) or the number of activated neurons within that cortical volume (frequency modulation²¹), the greater the corresponding swath of skin.

Overlapping PFs are additive and more localizable

Given that many of the measured PFs overlapped, we next sought to examine the interactions between PFs when observed simultaneously, regardless of whether they overlapped. To this end, we simultaneously delivered ICMS through pairs of electrodes and compared the reported PFs to those when ICMS was delivered through the individual electrodes that formed the pairs (Fig. 4a,b). Single- and multi-electrode trials were interleaved to limit biases in the PF reports. Examination of the single- and multi-electrode PFs suggests that the latter resembled the superposition of the former even when there was substantial difference between them. We computed the pixel-wise correlation between the summed PFs and the multi-electrode PF, and we found that the summed PFs were moderately predictive of the multi-electrode PF (mean r = 0.61; Fig. 4c). We conclude that PFs combine approximately additively when ICMS is delivered through multiple electrodes.

Fig. 4: PFs sum to produce focal and well localizable sensations.

a, Example PFs from two individual electrodes where the PFs broadly overlapped (left and middle) and the PF when both electrodes were stimulated simultaneously (right). b, Another example in which the PFs of the individual electrodes did not overlap (left and middle) along with the combined PF (right). c, The correlation between the additive model and observed PF (observed) versus a null model where two random electrodes were chosen. The additive model significantly outperformed the null model (two-sided, two-sample Kolmogorov–Smirnov test, D = 0.86, P < 0.0001). Data from participant C1. d, The task set-up for the robotic digit localization task. The participant was blindfolded while an experimenter randomly squeezed individual prosthetic digits or pairs of digits. e, Consolidated performance of robotic and open loop localization tasks for single-electrode (n = 128) and multi-electrode (n = 110) localization tasks. Multi-electrode stimulation evokes more localizable sensations (two-sided, two-sample t-test, t₍₂₃₆₎ = 21.6, P < 0.0001). Note that trials where the participant failed to detect stimulation are excluded here to reduce confounding localization performance with detectability. Data from participant C1. The box and whiskers show the 5th, 25th, 50th, 75th and 95th percentiles.

As discussed above, the circumscription and systematic localization of PFs can be exploited to convey information about (bionic) hand locations at which contact with an object is established^5,8. In the surveys used to collect PFs (Fig. 2), participants often requested multiple repetitions of the stimulus so that they could ensure accuracy in their reporting. Thus, while the location of the percept may be stable, it may not be well localizable on individual (one-shot) presentations, that is, users of these brain–computer interfaces (BCIs) will not be able to use this form of feedback to locate sensations on a bionic limb. Given that multi-electrode PFs resemble the summation of the component PFs, we reasoned that multi-electrode stimulation might evoke more focal and thus more easily localizable sensations. To test this possibility, we mapped force sensors on a bionic hand (Ability Hand, Psyonic) to electrodes with matching PFs. For example, sensors on the prosthetic thumb tip drove stimulation through electrodes with PFs on the thumb tip. In some cases, each sensor drove stimulation through a single electrode; in other cases, sensor output drove a quartet of electrodes whose PFs largely overlapped (all stimuli at 60 μA). For these, the overlapping component matched the sensor location. We then randomly touched different bionic digits and had participant C1 (blindfolded) report which finger(s) was (were) touched (Fig. 4d). Touches to single digits were randomly interleaved with touches to two digits. We also repeated the same experiment, except that digit(s) stimulation was software controlled (rather than by physically touching the bionic hand). Results from these two paradigms—one with and one without the bionic hand—were similar and thus combined (Extended Data Fig. 5a). With either single- or multi-electrode ICMS, the participant reported the expected digit(s)—corresponding to the PF of the electrode(s)—on the majority of trials. Compared with multi-electrode ICMS, however, single-electrode stimulation more often failed to elicit a localizable sensation (30% versus 0%) and when it did, participants often incorrectly localized the sensation (42% versus 7%) (Fig. 4e and Extended Data Fig. 5b,c). The difference in performance for single- versus multi-electrode stimulation was more pronounced in blocks in which multiple digits were touched, but in both cases multi-electrode stimulation significantly outperformed single-electrode stimulation (Wilcoxon rank sum test, Z = 8.80, P < 0.01 and Z = 9.02, P < 0.01). Multi-electrode stimulation thus gives rise to more reliably localizable sensations than does its single-electrode counterpart.

Individual electrodes have narrow intensity ranges

The ability to localize sensations in the absence of context is distinct from the ability to use that information once we know how and where to deploy our attention. Indeed, even though individual electrodes appear to be poor in terms of one-shot localization, it is important to understand how this intensive information is processed and interpreted by the user. Our prior analysis on the effect of amplitude and frequency on the perceived size and shape of the PF (Extended Data Fig. 4) did not compare the intensity to a real-world reference and thus precludes intuitive interpretation of the intensity reports or even a direct comparison of intensity between electrodes. Thus, we next sought to contextualize the intensity of the sensations in perceptual space and determine how parameter variation alters this. In natural touch, increases in contact force lead to increases in the firing rate of active neurons and in the recruitment of additional neurons in a somatotopically determined region of S1²², similar to the effect of increases in ICMS amplitude¹⁹, which also increases the perceived magnitude of the evoked sensation^5,6,8. With this in mind, we gauged the consistency of this relationship across participants and electrodes by implementing a magnitude estimation experiment in which the participants freely reported the intensity of each stimulus²³. The ratings were then normalized by the mean rating for each electrode and their relationship with ICMS amplitude was characterized. On every electrode tested, perceived magnitude increased approximately linearly with ICMS amplitude, replicating previous findings⁵ (Fig. 5a). The median correlation between amplitude and intensity rating was 0.97, with all but two correlations (both from participant P3) above 0.9 (range 0.47–0.99).

Fig. 5: Perceived intensity increases linearly with ICMS amplitude.

a, Normalized magnitude ratings following ICMS delivered through single electrodes for three participants. Each line denotes ratings for one electrode. The different colours denote different participants. The black line denotes the mean across electrodes and participants. b, Normalized ratings when ICMS and mechanical stimuli are interleaved for one electrode. Indentations were delivered to the location on the skin corresponding to the PF of that electrode. c, Equal intensity contours for ICMS-evoked and mechanically evoked sensations. Each line represents the contour derived from the ratings from one stimulating electrode. The black line corresponds to the contour of the electrode shown in b. While perceived magnitude increases with amplitude on all electrodes, the range of the evocable intensities varies widely across electrodes. Data from b and c are from participant C1 only. d, Goodness of fit for ICMS or mechanical intensity ratings when using power adjusted versus linear adjusted functions. Power functions provide better fits for intensity ratings of skin indentations but not ICMS.

The limitation of the magnitude estimation approach when used with ICMS, however, is that ratings are (by virtue of the paradigm) specific to both the electrode and the participant^23,24, so they cannot be benchmarked to natural touch. Furthermore, ratings are normalized within each block or session so ratings cannot be compared across sessions. To overcome these limitations, we leveraged the fact that participant C1 has residual tactile sensations on the same part of his hand that ICMS evokes sensations (Fig. 3 and Extended Data Figs. 1 and 3) and that the tactile sensitivity of the contralateral (injured) hand is equal to that of his ipsilateral (uninjured) hand (Extended Data Fig. 6a). Consequently, we had participant C1 judge the magnitude of the sensations evoked by ICMS trains and by skin indentations (delivered to a location matching the PF of the stimulating electrode that evoked sensations similar to those evoked by the mechanical stimulator, as reported by the participant) of varying force, with the two types of stimuli interleaved randomly within each experimental block. We could then directly compare the magnitude of electrically and mechanically evoked sensations (Fig. 5b) because both stimulus types were rated on the same scale. Furthermore, assuming the perceived magnitude of the tactile stimuli remained constant across sessions (Extended Data Fig. 6b), we could also compare the perceived magnitude of ICMS delivered through different electrodes on different sessions. From these combined ICMS and touch sessions, we constructed equal intensity contours for the two stimulus types (Fig. 5c), allowing us to determine the ICMS amplitude required to evoke a sensation whose intensity corresponds to a given force and vice versa. First, we found that perceived magnitude increased approximately linearly with ICMS amplitude but as a power function of mechanical amplitude (decelerating exponent of 0.2 ± 0.08), consistent with existing literature²⁵ (Fig. 5d). Accordingly, the equal intensity contours also followed a power law, reflecting the nonlinearity in the mechanically evoked sensations (Fig. 5b,c). Furthermore, while the magnitude of ICMS-evoked sensations increased with amplitude on all electrodes, the intensity range of the sensations varied widely across electrodes: some electrodes could only evoke weak sensations (<0.25 N, the weight of a USB stick), whereas others could evoke sensations commensurate with moderate forces (~0.5 N, the weight of an egg). Given that contact forces often exceed 1 N during object interactions^26,27, the dynamic range of ICMS-evoked sensations, constrained by the maximum safe stimulation level (100 μA)^5,28, is generally low.

ICMS percept intensities depend on amplitude sensitivity

The ability to localize sensations is critical for object interactions. However, the force exerted during the interaction is also important and the ability of ICMS to convey a time-varying force signal must be understood. Having established that the mapping between ICMS amplitude and perceived contact force was electrode dependent, we then investigated how sensitive participants were to changes in ICMS amplitude. To this end, we had participants discriminate flat ICMS trains that varied in amplitude. On each trial, the participant reported which of two sequentially presented stimuli was more intense. The amplitude of the standard (or reference) stimulus was 60 μA and that of the comparison stimulus varied between 40 and 80 μA. From the behavioural performance (Fig. 6a), we computed, as an index of sensitivity for each electrode, the just noticeable difference (JND), which denotes the change in stimulus amplitude that would yield a criterion level of performance (75% correct). While the median JND was around 13.5 μA (Fig. 6b), consistent with previous results in humans and monkeys^5,6,9,10, JNDs varied widely across electrodes and participants (25–75th percentiles 8.5–22.9 μA).

Fig. 6: Amplitude discriminability is electrode dependent.

a, Example psychometric functions from each participant in which the probability of indicating each comparison stimulus was of higher intensity than the reference stimulus. Note that examples are selected to highlight variability. b, JND computed from psychometric functions for all electrodes across participants (n = 35). The thick grey line denotes median (13.5 μA). Note that values above 40 μA are set to 40 μA for graphical purposes (n = 2, JND = 60 and 106). c, The Weber fraction when the reference amplitude is either 50 μA or 70 μA. d, A diagram showing the estimated discriminable levels plots for the electrodes shown in a. The grey section at the bottom of each bar indicates the subthreshold range for that electrode and the height of each subsequent bar is determined by the JND (following Weber’s law), with the maximum amplitude capped at 100 μA. e, The estimated discriminable levels for tactile stimulation in the same approximate range of forces (0–0.4 N). f, The maximum force or intensity evoked by each electrode compared with the number of discriminable levels computed from the detection threshold and JND. Note that force values are predicted equivalent force at 100 μA based on iso-intensity curves (Fig. 5c) fit on a subset of the amplitude range. g, Example idealized stimulus profiles for linear (stimulus amplitude scales with force) and biomimetic (force transients are emphasized) stimuli. h, JNDs are reduced (sensitivity is enhanced) with biomimetic stimuli versus linear ones. i, The distribution of the number of discriminable levels computed from JNDs with constant (flat) (grey, n = 35), linear (black, n = 22) or biomimetic (blue, n = 22) stimuli. The number of levels is equivalent with constant and linear but higher with biomimetic stimuli. The box and whisker lines in b and i indicate the 5th, 25th, 50th, 75th and 95th percentiles.

To assess whether the discrimination of ICMS amplitude follows Weber’s law—that JNDs increase in proportion to the standard amplitude—we tested amplitude discrimination at two different standards on a subset of electrodes (Extended Data Fig. 6c). We found that, on average, JNDs followed Weber’s law, but the tendency to do so varied widely across electrodes (Fig. 6c). Having measured the detection threshold and the JND for each electrode, we computed the number of discriminable levels (Fig. 6d), defined as the number of discrete, discriminable intensity levels between detection threshold and maximum safe amplitude (100 μA), assuming a constant Weber fraction. We found that the number of discriminable steps ranged from 2 to 14, with a median of 7, implying that the force feedback conveyed by flat ICMS is coarse. As a benchmark, the native touch of participant C1’s (fully sensate) left hand yielded around 45–50 discriminable levels over this range of forces, an order of magnitude more than what could be achieved with single-electrode ICMS within the safe range of amplitudes (Fig. 6e). Natural touch thus confers far greater sensitivity to force variations than does single-electrode linear ICMS.

Given the observed variability in JNDs, we sought to examine whether the sensitivity related to the perceived intensity of ICMS. First, we found that electrodes with lower detection thresholds tended to have higher JNDs (r = −0.496, P = 0.0024; Extended Data Fig. 6d), suggesting that JNDs do not simply reflect overall sensitivity to ICMS. Second, electrodes with more discriminable levels also tended to evoke the most intense sensations (r = 0.97, P = 0.007; Fig. 6f). Together, these imply that the JND for each electrode corresponds to a change in intensity that is approximately consistent across electrodes, a phenomenon that is non-trivial given that magnitude functions are not systematically predictable from JNDs in natural perception^29,30. Furthermore, this demonstrates that approximate intensity matching between electrodes should be possible without a common (that is, mechanical) reference, as the intensity can be expressed in JNDs above threshold, reducing the requirement for extensive magnitude matching.

Electrodes are more sensitive to biomimetic patterning

In the experiments described above, ICMS consisted of pulse trains of constant amplitude (flat trains). Such pulse trains typically evoke an abrupt rise in the activation of neurons around the electrode, followed by a slow decrease³¹. In contrast, interactions with objects evoke phasic responses at the onset and offset of contact and much weaker responses (<10%) during maintained contact, a property inherited from the periphery²². In studies in amputees with electrical stimulation of the peripheral nerves, ‘biomimetic’ tactile feedback that emphasizes contact transients, thereby mimicking natural touch, has been shown to confer greater dexterity to myoelectric bionic hands^32,33,34. With this in mind, we assessed participants’ ability to discriminate biomimetic ICMS trains (Fig. 6g), with the expectation that they might also improve participants’ ability to discriminate intensity and interact with objects. We compared the participants’ performance with biomimetic trains with that with trains designed to track the forces linearly, which largely resembled flat trains with short on- and off-ramps. For this comparison, the biomimetic and linear trains were matched in peak amplitude so the charge delivered in a biomimetic train was less than that in a matched linear one (69 ± 7% on average; Methods). We found that JNDs for biomimetic ICMS were systematically lower than were their linear counterparts (medians of 9.7 and 16.6 μA, 25–75th percentiles 7.7–16.1 μA and 11.5–23.5 μA, respectively, Wilcoxon signed-rank test, n = 22, Z = 3.1, P < 0.01; Fig. 6h). For the set of electrodes tested in this comparison, the median number of discriminable levels increased from 8 to 11 with biomimetic sensory feedback (Wilcoxon rank sum test, Z = 3.21, P < 0.01; Fig. 6i). Biomimetic ICMS trains thus provide higher resolution force feedback, an advantage that holds true when expressed in terms of charge rather than peak amplitude (Wilcoxon signed-rank test, Z = 2.8, P < 0.01; Extended Data Fig. 6e) and does not simply reflect differences in perceived intensity (Extended Data Fig. 6f) nor probably a difference in size (Extended Data Fig. 4).

Multi-electrode ICMS allows for better task performance

Our observation that multi-electrode ICMS improved localization (Fig. 4e) suggested that multi-electrode ICMS might also serve to improve the precision of force discrimination. To test this hypothesis, we selected quartets of electrodes with overlapping or adjacent PFs (as demonstrated in Fig. 4) and used biomimetic encoding. First, we assessed whether multi-electrode stimulation increased the dynamic range of the evoked sensations by comparing magnitude estimates of intensity with single- versus multi-electrode stimulation (three sets of four electrodes in participant C1, all fully interleaved). We found that multi-electrode stimulation evoked systematically more intense sensations than did single-electrode stimulation when equating the current delivered through each electrode individually (so quartet stimulation delivered four times more total current than did its matched single-electrode counterpart; Fig. 7a). Within the safe range of ICMS amplitudes, multi-electrode ICMS allowed for a much wider dynamic range than did any electrode in isolation (more than twice the average electrode; Fig. 7b). Indeed, the peak equivalent force reached 2 N, approximately the weight of a mobile phone. Furthermore, the multi-electrode ICMS amplitude intensity function still followed a linear relationship with amplitude (Extended Data Fig. 7a), implying that the linear relationship is not an artefact of testing a narrow range of intensities²⁹.

Fig. 7: Biomimetic multi-electrode stimulation produces more intense and more discriminable percepts.

a, Normalized magnitude ratings when biomimetic ICMS is delivered through electrodes individually or simultaneously, interleaved with mechanical stimuli for an example quartet. The lines denote the mean and the shaded areas denote the s.d. b, Equal intensity contours for single-electrode and multi-electrode ICMS for an example quartet. Inset: the maximum achievable force for single- or multi-electrode stimulation across all tested quartets, extrapolating fits to 100 μA. c, Psychometric functions for one quartet of electrodes using biomimetic single- or multi-electrode stimulation. The individual performance is in blue and the quartet is in red. Inset: JNDs for all single electrodes and quartets tested (n = 12 and 8, respectively). d, Psychometric functions for one quartet of electrodes using linear or biomimetic multi-electrode stimulation. Inset: JNDs for all quartets tested (n = 5). e, The estimated number of discriminable levels with single-electrode ICMS and biomimetic multi-electrode ICMS (n = 22, 22 and 8 and median of 8, 11 and 19.5, respectively). f, A schematic of the compliance discrimination task using a sensorized bionic hand. g, Compliance discrimination performance with linear single-electrode or biomimetic multi-electrode feedback (2 blocks of 20 trials for each condition). Data in c and e are from participants C1 and P2, and the remaining data are from participant C1. The box and whiskers in c–e show the 5th, 25th, 50th, 75th and 95th percentiles.

To determine whether the increased intensity range also led to improved discriminability, we repeated the amplitude discrimination experiments with multi-electrode biomimetic ICMS trains (n = 8 quartets, 5 from participant C1 and 3 from participant P2). We found that multi-electrode ICMS—with identical stimulation delivered through each electrode of the quartet—yielded substantially lower JNDs than did its single-electrode counterparts when expressed in terms of the amplitude on each electrode (Fig. 7c), mirroring the lower variability in the magnitude estimates of intensity for multi-electrode stimulation compared with its single electrode counterpart (Extended Data Fig. 7b). To determine whether the effect was isolated to biomimetic stimuli, we repeated the amplitude discrimination experiment on a subset of quartets (n = 5 from participant C1) but only compared linear and biomimetic encoding (Fig. 7d) and found that performance was equivalent between the conditions. Next, we computed the number of discriminable levels that multi-electrode stimulation enabled and found that the wider dynamic range increased the number of discriminable levels from 11 to 19.5 (Fig. 7e). Thus, biomimetic (and probably linear) multi-electrode force feedback can deliver a wider dynamic range than standard force feedback through a single electrode with more discrete levels. Indeed, while JNDs expressed in terms of charge were equivalent or higher for multi-electrode than single-electrode stimulation (Extended Data Fig. 7c), the bottleneck in ICMS-based feedback is the charge delivered on any given electrode, which has been identified as the primary determinant of stimulation-induced neuronal damage³⁵. Multi-electrode ICMS circumvents this limitation by distributing the charge, thereby increasing both the range and number of discriminable levels. Additionally, the lower sustained charge profile of biomimetic stimulation increases the effect as a function of charge, further reducing risk of neuronal damage.

Having established that multi-electrode biomimetic feedback leads to improved sensitivity in passive discrimination experiments, we implemented this stimulation paradigm in a bionic hand (Ability Hand, Psyonic) and had participant C1 use it to perform compliance discrimination, a closed-loop task that required force perception. In brief, we trained a long short-term memory (LSTM) network to decode hand aperture from neural signals recorded in M1. Real-time feedback from the sensors on the hand about the forces exerted on the object was conveyed via multi-electrode feedback using linear or biomimetic encoding, with different feedback conditions tested in separate experimental blocks (Extended Data Fig. 8). For linear feedback, ICMS amplitude was proportional to time-varying sensor output while for biomimetic feedback, ICMS amplitude was proportional to sensor output and its derivative. We only tested multi-electrode biomimetic feedback and not multi-electrode linear feedback as other testing has shown that biomimetic stimulation supports improved motor decoding³⁶. On each trial, the (blinded) participant grasped two objects—foam pucks of compliance 3 lb ft⁻³ and 8 lb ft⁻³ (FlexFoam, SmoothOn), presented in random order—and reported which of the two was firmer (Fig. 7f). Consistent with results from the passive discrimination experiments (Fig. 7c), we found that multi-electrode biomimetic ICMS yielded substantially better compliance discrimination performance than did single-electrode linear feedback (25% versus 7.5% error rates for linear and biomimetic, respectively, binomial test, n = 40, P = 0.009; Fig. 7g).

Discussion

Our results show that the location of PFs evoked by ICMS are stable over years. Unfortunately, we also found that individual electrodes are insufficient to evoke robustly localizable sensations and usually only convey coarse intensity information. Promisingly, however, biomimetic encoding of single electrodes and, to a greater degree, multi-electrode stimulation can improve this. Indeed, stimulation through quartets doubled the dynamic range of the evoked touch sensations and dramatically improved localization. The extended dynamic range confers nearly fivefold more discriminable levels of force than does single-electrode linear feedback without increasing the charge density. Consequently, implementing multi-electrode stimulation for tactile feedback will enable bionic limb usage.

PFs are highly stable over time

PFs remained stable over the testing period, which spanned ~2 years for participants C1 and P3 and ~7 years for participant P2. Indeed, the variability in the PF overlap and centroid distance across repeated tests on the same electrode were equivalent within and across sessions. Additionally, the greatest determinant in whether an electrode was included in the analyses was its detection threshold as those electrodes with high thresholds evoked weak and poorly localizable sensations at our survey amplitude. If the survey amplitude had been adjusted on a per-electrode basis, less-sensitive electrodes may not have been excluded. The fact that the location of the PFs was consistent over the entire study duration indicates that we can assume that the location of evoked percepts for both individual and combinations of electrodes to be stable and reliable for bionic limb tactile feedback.

Given that the PF location largely coincides with RF location, this stability suggests that the somatosensory homunculus is highly stable, consistent with fMRI studies with amputees¹⁴ and people with tetraplegia^15,17. Moreover, the participants varied in the extent of spared sensation, where participant C1 had spared sensation over most of his hand, P3 over all but the little finger and P2 only on the thumb and index. Across participants, the PFs were indistinguishable in their size and relative locations, whether these were on sensate or insensate patches of skin, suggesting that the homunculus remains stable regardless of the degree of residual sensation. Furthermore, recent results with intraneural electrodes implanted in the human nerves suggested that the PF changes observed over time were most likely caused by the foreign body reactions and their impact on the coupling between nerve and electrode¹⁹. Indeed, attempts to modify the PFs of electrodes implanted in the nerves—leveraging both cortical and subcortical plasticity—failed to change the PF location²⁰. The idea of major post-injury cortical reorganization¹⁶ has lost favour recently, with the changes in observed cortical activity being explained by existing lateral connectivity instead^21,22. This work furthers the notion that the underlying somatotopy does not change because of injury, as direct stimulation evokes percepts in the expected locations.

Electrode PFs are subsumed by their RFs

Since the PF of an electrode is determined by its location on the somatosensory homunculus, the spatial extent of the PF is expected to be determined by the spatial extent of activation across the cortical surface. Consistent with this, increases in ICMS amplitude or frequency would lead to increases in the volume of activated neurons and/or density of activated neurons within a volume^23,24,25,26 producing concomitant increases in PF area. Furthermore, the PF of an electrode is, on average, a sixth to a seventh the size of its RF. If we assume that the spatial extent of a PF is determined by the activated cortical area, ICMS at 60 μA activates the somata of neurons over a span of around 1 mm (ref. ²³) (Extended Data Fig. 9a). The RF size is determined by (1) the area over which neurons contribute to the multi-unit activity on a given electrode (~150 μm radius) and (2) the area of cortex that is activated by a touch (Extended Data Fig. 9b). Regarding the latter, a punctate indentation applied to the skin evokes neuronal activity on two spatial scales (Extended Data Fig. 9c). Contact transients evoke responses over a wide swath of cortex (spanning ~15 electrodes on the array) that would typically be associated with multiple digits. Contact maintenance, however, is associated with a much more spatially restricted sustained response (spanning ~2 electrodes), reflecting the hot zone²⁷. Consequently, we believe that a large portion of our result is due to the fundamental difference in cortical activation pattern between ICMS and natural touch. Indeed, if we had performed the RF mapping based on the sustained response to von Frey hairs instead of strokes with a cotton bud, we may have found smaller RFs. Importantly, however, either approach is biased towards slow or fast adapting afferents inputs, respectively, and the comparison of both methods might be best for future mapping.

ICMS discrimination tends to follow Weber’s law

Weber’s law—which states that the JND is proportional to the reference stimulus³⁰—is ubiquitous across sensory modalities. In previous studies with monkeys¹⁰ and humans⁵, we found that the discrimination of amplitude did not follow Weber’s law, a phenomenon we hypothesized might reflect differences in the trial-to-trial variability of natural sensory responses and other ICMS-evoked counterparts¹⁰. In the present study, we find that, on average, JNDs increased in proportion to the standard, consistent with Weber’s law and with natural touch. At the level of single electrodes, however, we saw that Weber’s law was violated in some cases, with some JNDs lower for the higher standard. We attribute this to two possible causes: first, there is a reasonable amount of variation expected even with 60 trials and, second, across the eight electrodes tested, the likelihood of a single false positive is substantial. Overall, this should be tested more robustly in the future, though the narrow range of perceptible and safe ICMS amplitudes may preclude a more systematic investigation of Weber’s law with single-electrode ICMS. Note, however, that the computed number of discriminable levels is similar with and without the assumption of Weber’s law. The large variability across electrodes in their disposition to follow Weber’s law might account for the discrepancy between this and previous studies^5,10 (along with minor differences in the experimental design). Given that multi-electrode ICMS evokes a wider range of responses and has lower JNDs (in terms of microamps), further testing of Weber’s law could be performed with groups of electrodes.

Biomimetic ICMS confers higher resolution force feedback

The rationale behind biomimetic feedback is that it evokes more natural patterns of neural activation, which then gives rise to more easily interpretable sensations^34,35. In experiments with human amputees, biomimetic sensory feedback via peripheral nerve stimulation has been shown to improve the function of myoelectric bionic hands^36,37,38. Our results further support the notion that biomimetic stimulation strategies are a promising avenue for the development of ICMS. The fact that amplitude discrimination performance was better with biomimetic, rather than linear, single-electrode stimulation, but equivalent with multi-electrode stimulation, implies that the models we use to generate biomimetic profiles could be improved to better capture the natural spatiotemporal profile. Nevertheless, the fact that even simple multi-electrode biomimetic stimuli tend to be lower in terms of total charge means that less current is required to evoke the same range of sensations, may improve electrode longevity and reduces the risk of damaging nearby neural tissue³⁹. In conjunction with the reduced disruption of motor decoding⁴⁰ and the improved quality of the evoked sensations⁴¹, biomimetic stimulation should be the preferred approach to delivering tactile feedback with ICMS.

Multi-electrode ICMS confers a wider range of intensities

Multi-electrode ICMS leads to more intense sensations than single-electrode ICMS. This finding is perhaps unsurprising given that multi-electrode stimulation at a fixed amplitude entails more charge delivery than does single-electrode stimulation. In fact, multi-electrode stimulation less efficiently modulates the overall perceived magnitude compared with single-electrode stimulation when expressed as a function of overall charge (Extended Data Fig. 7c). The major bottleneck in ICMS-based sensory feedback, however, is that the amplitude used in human experiments is capped at 100 μA to prevent damage to tissue⁴². Even if this maximum level turns out to be more conservative than it needs to be, evidence suggests that charge per phase is the main determinant of ICMS-induced neuronal damage³⁹. Accordingly, multi-electrode ICMS enables a widening of the dynamic range without increasing the charge per phase on any given electrode. As the PF density varies on a participant-to-participant basis (Fig. 1 and Extended Data Fig. 1) and the discriminability can be well expressed in terms of difference in total charge (Extended Data Fig. 7c), we expect that the exact number of electrodes used can be adapted to each participant, though the extent to which the gains asymptote with greater numbers of electrodes is unclear.

Multi-electrode stimulation improves tactile feedback

Mapping sensors on the bionic hand to somatotopically matched electrodes in S1 yields intuitive feedback about the locations on the bionic hands at which contacts with an object occur. Indeed, contact with the prosthetic thumb tip, for example, leads to a sensation experienced on the thumb tip. Here, we show that this mapping is even more effective if the sensor output drives ICMS through multiple electrodes, whose common PF matches the sensor location. For example, if multiple electrodes have PFs that include the thumb, their aggregate PF will be dominated by the thumb. Multi-electrode ICMS thus results in sensations that not only are more tangible, but also more readily localizable to the hand regions corresponding to the PF overlap. While the same outcome might be achieved by increasing the amplitude of ICMS delivered through a single electrode, resulting in a more salient PF core despite the concomitant increase in PF area, multi-electrode ICMS enables improved localizability within the safety limits of ICMS⁴². In addition to the improvement in localization, multi-electrode ICMS also leads to an improvement in force feedback compared with its single-electrode counterpart, as evidenced by a greater number of discriminable levels of force within the safe and perceptible range of amplitudes. Though it should be considered that as the number of levels corresponds to the maximum perceived intensity (Fig. 5f), the discriminability per force range does not change.

Optimizing the number of electrodes for tactile feedback

Our results imply that increasing the number of electrodes will allow for ever greater intensities to be evoked with ICMS. There are three limitations to this line of reasoning. First, our results do not describe the relationship between the maximum intensity and the number of electrodes. Indeed, our data show that the perceived intensity with quartet stimulation is less than the sum of its components (Fig. 6a). Consequently, it is unclear what the optimal number of electrodes is to evoke the maximum intensity per electrode. Second, all tested quartets involved electrodes with substantial overlap. In cases where electrodes do not overlap, this scaling may differ. Third, unless electrodes overlap perfectly, the usage of more electrodes will also result in the percept occurring over a larger area of the skin, potentially reducing the spatial precision of the feedback. Consequently, any strategy must be adapted to the specific pattern of PFs for each participant and even for each implanted array. Future array technologies should thus have sufficiently high density such that they are able to target nearby regions of cortex, probably with overlapping PFs, while safely distributing charge to minimize damage.

In summary, multi-electrode ICMS robustly evokes somatosensory sensations at much shorter latencies than does single-electrode ICMS^43,44. On the other hand, multi-electrode ICMS of S1 has a stronger deleterious effect on the ability to decode motor intent by evoking more activity in M1 than does single-electrode ICMS⁴⁰. This disruption, however, can be minimized by implementing biomimetic stimulation^35,45. Overall, multi-electrode stimulation leads to more effective tactile feedback for bionic hands.

Methods

Participants

This study was conducted under an investigational device exemption from the US Food and Drug Administration and approved by the institutional review boards at the Universities of Pittsburgh and Chicago. The clinical trial is registered at ClinicalTrials.gov (NCT01894802). Informed consent was obtained before any study procedures were conducted. Participant C1 (male, m), 57 years old at the time of implant, presented with a C4-level American Spinal Injury Association (ASIA) D SCI that occurred 35 years before the implant. Participant P2 (m), 28 years old at the time of implant, presented with a C5 motor/C6 sensory ASIA B SCI that occurred 10 years before the implant. Participant P3 (m), 28 years old at the time of implant, presented with a C6 ASIA B SCI that occurred 12 years before the implant. Participant R1 (m), who performed a subset of experiments, was enrolled under a separate institutional review board and investigational device exemption-approved clinical trial (NCT3898804). R1 presented with a C3/C4 ASIA B SCI that occurred 5 years before the implant, and his cortical implants are described in detail in ref. ⁷.

Participant C1 had retained sensation over the entire volar surface of the hand, with nearly normal detection thresholds (measured with von Frey hairs) on the digit tips and elevated thresholds over the rest of the hand (Extended Data Fig. 3). Participant P2 had retained sensation over the thumb, index finger and underlying palm, albeit with elevated thresholds, but the rest of his hand was insensate. Participant P3 had nearly normal thresholds on the thumb and most of the index finger, higher thresholds on the middle finger, was nearly insensate on the ring finger and completely insensate on the little finger.

Cortical implants

We implanted four microelectrode arrays (Blackrock Neurotech) in each participant (C1, P2 and P3). The two arrays (one medial and one lateral array) in Brodmann’s area 1 of S1 were 2.4 mm × 4 mm with 60 1.5-mm-long electrode shanks wired in a chequerboard pattern such that 32 electrodes could be recorded from or stimulated. The two arrays in motor cortex were 4 mm × 4 mm with 100 1.5-mm-long electrode shanks wired such that 96 (C1 and P3) or 88 (P2) electrodes could be used to monitor neural activity. The inactive shanks were located at the corners of these arrays. Two percutaneous connectors, each connected to one sensory array and one motor array, were fixed to the participant’s skull. We targeted array placement during surgery based on functional neuroimaging (fMRI) or magnetoencephalography of the participants attempting to make movements of the hand and arm (all participants) and imagining feeling sensations on their fingertips (participant P2), within the constraints of anatomical features such as blood vessels and cortical topography (see ref. ⁴⁶ for a full description of the implantation approach). Participant R1 was implanted with two 64 electrode arrays (8 × 8) in Brodmann’s area 1, with PFs primarily on the index and middle fingers (see ref. ⁷ for details).

ICMS

ICMS was delivered via a CereStim 96 (Blackrock Neurotech). Each stimulating pulse consisted of a 200 µs cathodic phase followed by a half-amplitude 400 µs anodic phase (to maintain charge balance), the two phases separated by 100 µs. For multi-electrode stimulation, the same pulse train was delivered to all electrodes simultaneously and synchronously.

Detection thresholds

Detection thresholds for ICMS were measured on each electrode in both sensory arrays on a quarterly basis as described previously⁵. We either used a three up one down transformed staircase or the method of constant stimuli, both in a two-alternative forced choice paradigm targeting 50% detection performance.

Multi-electrode ICMS

We selected groups of four electrodes, referred to as quartets. In most cases, the four electrodes had overlapping PFs (the patch of skin over which the ICMS-evoked sensation is experienced). In one case, one pair of electrodes in the quartet had PFs on one digit and the other pair had PFs on the adjacent digit. When stimulating through a quartet, all electrodes delivered the same ICMS pulse train synchronously. During each experimental block, we randomly interleaved stimulation through each electrode in each quartet with stimulation through the entire quartet.

PF mapping and quantification

To map each PF, ICMS was delivered through one or more electrodes (60 µA, 100 Hz, 1 s unless otherwise specified), and the participant reported whether a sensation was evoked. The participant could request as many repetitions of the stimulus as desired as the goal was to maximize location accuracy. During or after the stimulation, the participants drew the spatial extent of the sensation on a digital representation of the hand using a stylus. The original image was 1,050 × 1,200 pixels (discrete two-dimensional digital visual elements) but was scaled down to the resolution of the tablet.

Periodically (every 1–3 months), this procedure was repeated for every electrode on both sensory arrays, with electrodes interleaved in random order, across a span of approximately 800, 2,750 and 750 days for participants C1, P2 and P3, respectively. From these digital images, we counted the number of pixels subsumed by the PF, computed its area and centroid (centre of mass). To gauge the validity of the computed centre of mass, one participant also marked, on a subset of electrodes in one session, the centre of the PF on the picture of their hand. We found that the estimated centroids matched the reported centroids with submillimetre accuracy (median of 0.71 mm, Q₁, Q₃ = 0.52, 1.33 mm). Each participants retained at least partial control of the proximal muscles. Through a combination of forearm muscle tension (tendonesis grip), participants were able to manipulate a stylus to complete the sensory survey. Participants were right-handed before their injury and continued to use their right hand for these tasks.

In a fourth participant (R1), the PF mapping procedure differed slightly. On each experimental block, a group of five electrodes were randomly selected, and each electrode was stimulated approximately five times (n = 4–7 times, mean of 5.12) in a randomized order within the block. The participant verbally reported the hand segments on which the sensation was experienced (for example, distal and medial finger pads), each segment numbered on a digital representation of the hand⁷. ICMS was identical as that for the other participants, except that pulse amplitude was 80 µA. Skin locations included in the reported PF on at least 60% of trials for a given electrode were included in its PF.

Aggregate PFs

Having established that day-to-day variations in PF location were essentially random and primarily reflected noise in the reports, we constructed an estimate of each PF that weighted skin regions according to the frequency with which these were included in the single-day PF reports. Specifically, we computed the proportion of times a given pixel was included in the single-day PF. We then eliminated pixels that were included on fewer than 33% of single-day reports and normalized the remaining proportions such that they summed to one. For some electrodes, this criterion eliminated all pixels. These electrodes were not included in subsequent analysis and are reported as having no reliable PF. In the computation of the aggregate centroid, each pixel was weighted according to its value (normalized proportion). When aggregate centroids spanned multiple hand segments, the one with the largest summed pixel values was identified as the dominant one. The size of the aggregate field was the total number of pixels that exceeded the threshold.

PF stability

We gauged PF stability in three ways. First, we computed the distance between each single-day PF centroid and the centroid of the first reported PFs. Second, as this measure was susceptible to an anomalous report on the first session, we also computed the distance between the PF centroid on any given session and the centroid of the aggregate PF. Third, we measured the proportion of all unique pixels reported for a given electrode that exceeded each of several thresholds, reasoning that stable PFs would be consistent across a wide range of thresholds.

PF progression over the cortical surface

To test the degree to which PF progressions follow the canonical homunculus, we assessed how well we could identify the dominant hand segment for an electrode given that electrode’s location. In brief, we used the row and column coordinates of the array as the X and Y coordinates in Cartesian space, whose origin was the centre of the array. We then projected the coordinates onto each of 72 axes, spanning the range from 0° to 360° in increments of 5°. For example, for the 0° axis, the coordinate would be identical to the X coordinate (row). For each axis, we then applied a linear discriminant classifier with the projected coordinates as inputs and the dominant hand segments (digit) as output classes (MATLAB’s fitcdiscr). To further test the degree to which PFs progress somatotopically, we computed, for each pair of electrodes, the distance between their respective aggregate centroids and assessed the relationship between PF centroid distance and the physical distance between the electrodes over the cortical surface.

RF mapping

To map the extent of the RFs of the multi-unit around each electrode, we lightly brushed the skin of the hand using cotton swabs or Von Frey hairs while monitoring the multi-unit response using a speaker. One experimenter stimulated the hand while the other experimenter selected the electrode to be mapped (unknown to the first). In the case of participant C1, where three sessions were completed, the electrode order was randomized across sessions. The RF was reported on the same tablet interface used for PFs so that the same analytical protocols could be applied to both types of fields. An aggregate RF was produced for participant C1 with a cut-off of 33% (the pixel must have been present on one-third of observations) using the method described above for PFs. Measured RFs were nearly identical across sessions in the one participant for whom these were measured repeatedly over multiple sessions. For participant R1, a trapezoidal indentation was delivered to the distal finger pad of each digit using a tactile linear actuator (LCA25-025-6MSD6, SMAC) while recording the neuronal activity evoked in S1. Each indentation was presented 60 times at a constant amplitude. As the neuronal signal was weak, we computed spike band power—the root mean square of the filtered signal in 1 ms bins—to quantify the strength of the neural response. The spike band power was normalized within trials by z-scoring the signal during the 2 s stimulus by the 2 s prestimulus interval, then the normalized metric was trial averaged for each indenter location. Electrodes with peak normalized spike band power greater than 1.5 s.d. above baseline were considered responsive to indentation at the specific location. While this RF mapping approach involved a much more controlled and systematic mechanical stimulus than that used in the other three participants (P2, P3 and C1), it suffers from the poor coverage, able only to detect neuronal responses evoked by stimulation of the distal digit tips.

Localization task

To assess the degree to which ICMS conveys information about the location of contact between bionic hand and objects, we implemented a sensory encoding algorithm that linked sensors on the robotic hand (Ability Hand, Psyonic) and somatotopically matched electrodes in S1. For example, the output of a sensor on the index fingertip drove ICMS delivered through one or more electrodes with PFs on the index fingertip. Then, on each trial, the experimenter squeezed one or more digits and the participants’ task was to report which digits were squeezed. Single-digit and two-digit trials were randomly interleaved and the participant was warned that one or two fingers might be squeezed on any given trial. On some experimental blocks, the digit(s) were selected by the experimenter and an automated protocol randomly selected stimulating electrodes corresponding to the selected digits for testing, allowing for greater flexibility to test different electrodes. Sensor output drove ICMS (at 100 Hz) through a single electrode with a PF on the corresponding digit or through multiple electrodes, all with PFs that were predominantly on that digit. The amplitude of the ICMS was proportional to the sensor output and capped at 60 μA. For multi-electrode stimulation, the same ICMS was delivered to all the electrodes simultaneously. For computer-controlled trials, selection of digit triggered a 1 s, 100 Hz, 60 μA ICMS pulse train delivered through one or four electrodes. We could then compare the participant’s performance with single- versus multi-electrode stimulation on the single- versus multi-digit task. The participant reported the location of the sensation (individual digits, combinations of digits or no sensation) at the end of the stimulus. On single-digit trials, the participant received full credit if he correctly identified the digit where the aggregate PF was located and on multi-digit trials, he received half credit for each correctly identified digit.

Magnitude estimation

The objective of this paradigm was to assess the relationship between stimulus amplitude and sensory magnitude. On each trial, the participant was presented with an ICMS or a mechanical stimulus and rated its sensory magnitude on a scale of his choosing. If the stimulus was imperceptible, the participant ascribed to it a rating of zero. If one stimulus was twice as intense as another, it was ascribed a rating that was twice as large. The participant was encouraged to use fractions or decimals. At the beginning of each set, the participant was presented with each of the test stimuli in a random order to familiarize them with the stimulus range, as is typically done. The amplitude of the ICMS stimulus varied between 20 and 80 µA while the mechanical stimuli ranged from 0.05 to 2 mm. In all cases, the mechanical stimulus was delivered to the location of the PF for the given electrode. Both ICMS and mechanical stimuli were interleaved throughout each block, with a 5 s inter-trial interval. For each electrode, each rating was divided by the grand mean of all ratings in the experimental block, then averaged across repeated presentations of each stimulus.

In experimental blocks involving both skin indentations and ICMS, the range of indentation depths was selected in preliminary measurements to match the range of intensities of the electrical stimuli (based on participant ratings) to maximize the overlap and minimize range-related biases^47,48. To this end, we estimated at the start of the session and, with the participants help, the range of mechanical indentations that evoked sensations of comparable intensity as their ICMS counterparts (which varied from electrode to electrode). When multiple electrodes were tested, we selected the weakest and strongest sensations across electrodes. We then evenly sampled intermediate indentation depths between these two extremes. In some cases, the intensity of the multi-electrode ICMS exceeded the maximum indentation that could be delivered with the indenter, precluding comparisons at higher amplitudes.

A minimum of eight blocks were completed for each electrode and condition. Blocks were sometimes distributed across several days to minimize the effects of adaptation⁴⁹ and maintain participant engagement.

Equal intensity contours

We fit a power function to the magnitude mechanical ratings, M_m, of the skin indentations

$${M}_{\mathrm{m}}=\alpha {a}_{\mathrm{m}}^{\gamma },$$

where a_m is the amplitude, and α and γ are fitted parameters. We fit a linear function to the magnitude electrical ratings, M_e, of the ICMS

$${M}_{\mathrm{e}}=\beta {a}_{\mathrm{e}},$$

where a_e is the ICMS amplitude and β is the change in magnitude per unit amplitude. We then derived an equal intensity contour by finding the conditions under which M_m equals M_e

$${a}_{\mathrm{e}}=\frac{\alpha }{\beta }{a}_{\mathrm{m}}^{\gamma }.$$

Force approximation

To convert skin indentations into equivalent forces in the magnitude estimation task, we used the following equation:

$$F=0.06\times d,$$

which was derived from a previous study using a 2 mm radius indenter, where F is the force in newtons and d is the indentation depth in millimetres. As the stimuli for the magnitude estimation experiments used a 5 mm radius, we accounted for the difference in surface area between the tips when computing force. It is worth noting that given the variability in skin stiffness between participants, the absolute force values will vary between participants but the linear relationship between depth and force is consistent across participants.

Psychometric functions

Psychometric functions were fit with a logistic function

$$p=\frac{1}{1+{e}^{c\times{(x-{\upmu})}}},$$

where p is the probability of judging the comparison stimulus as more intense than the standard, x is the amplitude, c is the slope and µ the point of subjective equality. The JND is half the difference between the amplitudes that yield a p of 0.25 and 0.75.

Amplitude and force discrimination

Participants performed an amplitude discrimination task in a two-alternative forced choice paradigm. On each trial, a pair of stimuli, each lasting 1 s, was presented with a 1 s inter-stimulus interval and the participant reported which stimulus was stronger. The standard stimulus, consistent across the experimental block, was paired with a comparison stimulus whose amplitude varied from trial to trial and spanned the standard amplitude. The order of presentation of the standard and comparison stimuli was randomized and counterbalanced to minimize order effects⁵⁰. Data were obtained from each electrode over a minimum of eight experimental blocks, each consisting of two presentations (one for each order) of each stimulus pair. The frequency of the ICMS stimuli was either 50 Hz (Fig. 5) or 100 Hz (all other experiments).

In force discrimination experiments, trapezoidal force traces (1 s in duration, 0.1 s ramps) were converted to ICMS according to a linear or biomimetic mapping. For the linear mapping, the ICMS profile matched that of the force profile, with a peak amplitude proportional to the peak force. For the biomimetic mapping, ICMS consisted of 0.1 s transients during the on- and off-force ramps whose amplitude matched the peak amplitude of the corresponding linear train and a sustained phase, during which the amplitude was either 30 μA less than the peak amplitude or the detection threshold, whichever was highest. The envelope of the resulting biomimetic trains mimics the envelope of the spiking response to an indentation in S1 (ref. ²⁷). On any given experimental block, the standard force was mapped to an ICMS amplitude of 60 µA and comparison forces mapped onto amplitudes that ranged from 40 to 80 µA (Fig. 5a). Note that the JNDs were the same at 50 and 100 Hz, as has been previously found in experiments with monkeys¹⁰.

To test whether ICMS amplitude discrimination was subject to Weber’s law, we selected two standards—either at 50 and 70 μA—and paired them with comparison amplitudes that spanned a range of ±16 µA around the standard (based on previously observed JNDs). Tests for both standards were interleaved and randomized within an experimental block. This design contrasts with that adopted in previous experiments testing Weber’s law, in which the two standards were at the extremes and comparisons fell between the extremes^5,10. The narrow range of the standards was adopted such that none of the comparisons fell below threshold or above the safety limit of 100 μA.

The same behavioural paradigm was used to measure amplitude JNDs with the mechanical indenter as for ICMS. The indentation depths varied between 0.85 and 1.15 mm with a standard amplitude of 1 mm and an onset- and offset-ramp speed of 5 mm s⁻¹.

Discriminable levels

To estimate the number of discriminable levels for ICMS we used the formula

$${{\mathrm{DL}}}=\left\lfloor \frac{\mathrm{ln}\left(\frac{100}{{\mathrm{dt}}_{50}}\right)}{\mathrm{ln}(1+k)}\right\rfloor,$$

where DL is the number of discriminable levels, dt₅₀ is the 50% detection threshold and k is the Weber fraction for that electrode. For touch, we estimated the number of levels based on a computed Weber fraction of 1.083 and dt₅₀ of 0.05 mm.

Decoding of hand aperture

Neural signals from M1 arrays were recorded at 30 kHz using the NeuroPort system (Blackrock Neurotech). The data were high-pass filtered with a first-order Chebychev filter above 750 Hz. Whenever the signal crossed a threshold (−4.5 times root mean square of baseline voltage, set at the start of each recording session), a spiking event was recorded. Spikes were binned in 20 ms bins for decoding, then smoothed with an exponential filter of 440 ms. Only electrodes with firing rates above 0.5 Hz were used.

To decode aperture, we used a recurrent neural network that consisted of one middle layer of 150 LSTM nodes implemented online in participant C1. Network hyperparameters were optimized to achieve the best cross-validated fit. For each session, we first harnessed M1 responses as the participant attempted to grasp an object in virtual reality, following the motion of a virtual hand. During training, contact with the object triggered ICMS (linear single electrode and biomimetic multi-electrode) to expose the decoder to the activity in M1 evoked by ICMS delivered to S1, which would otherwise have disrupted decoder performance when not accounted for⁴⁰. Offline training lasted less than 5 min. An LSTM decoder of hand aperture was constructed based on these data, and the participant proceeded to use the decoder to perform the compliance discrimination task described below.

Compliance discrimination task

On each trial, the participant was instructed to squeeze two foam pucks of differing compliance with the bionic index and thumb. The output of the sensor on the thumb and index finger were summed separately to yield two force signals, one stemming from each digit, which then drove ICMS delivered through electrodes with PFs on the corresponding digit. These sensor signals were converted into ICMS using either a linear or biomimetic algorithm. For the linear algorithm, ICMS amplitude was proportional to (summed) sensor output, F(t) from

$${a}_{\mathrm{e}}\left(t\right)={\alpha }_{\rm{L}}F\left(t-{\Delta{t}}\right),$$

where Δt is the change in time, also known as bin size (20 ms), and α_L (where L is limit) is a parameter, chosen such that the ICMS amplitude spanned the range from 20 to 90 µA based on preliminary measurements of the sensor output ranges in this task.

For the biomimetic algorithm, ICMS amplitude was proportional to both the sensor output and its derivative,

$${a}_{\mathrm{e}}\left(t\right)=\alpha F\left(t-{\Delta{t}}\right)+\beta \frac{{\Delta{f}}(t)}{{\Delta{t}}}$$

where αF and β are the relative weights for force and its derivative for driving stimulation, respectively, and Δf is the absolute change in force between each time bin. For this, α and β were selected such that the resulting ICMS trains peaked at comparable amplitudes as with the linear feedback, based on the aforementioned preliminary testing. For the biomimetic feedback, ICMS was delivered through quartets of electrodes with PFs on the thumb and index, with the same stimulus applied to all four electrodes.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.