Main

The immune composition of the tumour microenvironment (TME) plays a crucial role in determining patient prognosis and response to cancer immunotherapies1,2,3. Immunotherapies that alter the immune composition using transplanted or engineered immune cells (chimeric antigen receptor T-cell therapy) or remove immunosuppressive signalling (checkpoint inhibitors) have shown exciting results in relapsed and refractory tumours in haematological cancers and some solid tumours. However, effective therapeutic strategies for most solid tumours remain limited4,5,6. The TME is a complex mixture of immune cells, including T cells, B cells, natural killer cells and macrophages, as well as stromal cells and tumour cells1. The interactions between these cells can either promote or suppress tumour growth and progression, and ultimately impact patient outcomes. For example, high levels of tumour-infiltrating lymphocytes in the TME are associated with improved prognosis and response to immunotherapy across multiple cancer types7,8. Conversely, an immunosuppressive TME characterized by low levels of tumour-infiltrating lymphocytes is associated with poor prognosis and reduced response to immunotherapy9. Durable, long-term clinical response of T-cell-based immunotherapies is often constrained by a lack of T-cell infiltration into the tumour, as seen in classically ‘cold’ tumours such as triple-negative breast cancer or pancreatic cancer, which have seen little benefit from immunotherapy10,11,12. The precise cellular and molecular factors that limit T-cell infiltration into tumours is an open question.

Spatial omics technologies capture the spatial organization of cells and molecular signals in intact human tumours with unprecedented molecular detail, revealing the relationship between localization of different cell types and tens to thousands of molecular signals13. T-cell infiltration is modulated by a rich array of signals within the TME such as chemokines, adhesion molecules, tumour antigens, immune checkpoints and their cognate receptors14. Recent advances in in situ molecular profiling techniques, including spatial transcriptomic15,16 and proteomic17,18 methods, simultaneously capture the spatial relationship of tens to thousands of molecular signals and T-cell localization in intact human tumours with micrometre-scale resolution. Imaging mass cytometry (IMC) is one such technology that uses metal-labelled antibodies to enable simultaneous detection of up to 40 antigens and transcripts in intact tissue17.

Recent work on computational methods as applied to multiplexed tumour images has primarily focused on predicting patient-level phenotypes such as survival by identifying spatial motifs from TMEs19,20,21,22. These methods have generated valuable insights into how the complex composition of TMEs influences patient prognosis and treatment response, but they fall short of generating concrete, testable hypotheses for therapeutic interventions that may improve patient outcomes. Given the prognostic value of T-cell infiltration into tumours, we need computational tools that can predict immune cell localization from environmental signals and systematically generate specific, feasible tumour perturbations that are predicted to alter the TME to improve patient outcomes.

Counterfactual explanations (CFEs) can provide important insight in image analysis applications23 but have not been applied to multiplexed imaging data. Traditionally, CFEs help clarify machine learning model decisions by exploring hypothetical scenarios, showing how the model’s interpretation would change if a feature in an image were altered slightly24. For instance, slight pixel intensity variations or minor edge alterations in a tumour’s appearance on an X-ray might lead a diagnostic model to classify the scan differently. Numerous CFE algorithms exist to elucidate a model’s decision boundaries and shed light on its sensitivity to specific image features25. In multiplexed tissue images where each pixel captures detailed molecular information, variations in pixel intensity directly correspond to specific molecular interventions. Thus, spatial omics data enable the extension of CFEs from understanding to predicting actionable interventions.

In this work, we introduce Morpheus, an integrated deep-learning framework that first leverages large-scale spatial omics profiles of patient tumours to formulate T-cell infiltration prediction as a self-supervised machine learning problem, and combines this prediction task with counterfactual optimization to propose tumour perturbations that are predicted to boost T-cell infiltration. Specifically, we train a convolutional neural network to predict T-cell infiltration using spatial maps of the TME provided by IMC. We then apply a gradient-based counterfactual generation strategy to the infiltration neural network to compute changes to the signalling molecule levels that increase predicted T-cell abundance. We apply Morpheus to melanoma26 and colorectal cancer (CRC) with liver metastases27 to discover tumour perturbations that are predicted to support T-cell infiltration in tens to hundreds of patients. We provide further validation of machine learning-based T-cell infiltration prediction using an additional breast cancer dataset28. For patients with melanoma, Morpheus predicts that combinatorial perturbation to the CXCL9, CXCL10, CCL22 and CCL18 levels can convert immune-excluded tumours to immune-inflamed in a cohort of 69 patients. For CRC liver metastasis, Morpheus discovered two cohort-dependent therapeutic strategies consisting of blocking different subsets of CXCR4, PD-1, PD-L1 and CYR61 that are predicted to improve T-cell infiltration in a cohort of 30 patients. We experimentally validated Morpheus’ predictions by showing that perturbing these targets substantially enhanced T-cell migration in vitro. Our work provides a paradigm for counterfactual-based prediction and design of cancer therapeutics based on classification of immune system activity in spatial omics data.

Results

Counterfactual optimization for therapeutic prediction

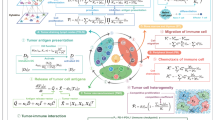
The general logic of Morpheus (Methods and Fig. 1a) is to first train, in a self-supervised manner, a classifier to predict the presence of CD8+ T cells from multiplexed tissue images (Fig. 1b). Then we compute counterfactual instances of the data by performing gradient descent on the input image, allowing us to discover perturbations to the tumour image that increases the classifier’s predicted likelihood of CD8+ T cells being present (Fig. 1c). The altered image represents a perturbation of the TME predicted to improve T-cell infiltration. We mask CD8+ T cells from all images to prevent the classifier from simply memorizing T-cell expression patterns, guiding it instead to learn environmental features indicative of T-cell presence.

Fig. 1: An integrated counterfactual optimization framework for discovering therapeutic strategies predicted to drive CD8+ T-cell infiltration in human tumours.
figure 1

a, Overview of the Morpheus framework, which consists of first training a T cell predictor and then generating perturbations. b, Training a neural network classifier to predict the presence of CD8+ T cells from multiplexed tissue images where cells in the IMC images are pixelated and CD8+ T cells are masked (Methods). c, The trained classifier is then used to compute an optimal perturbation vector δ(i) per patch by jointly minimizing three loss terms (Lpred, Ldist and Lproto). The perturbation δ(i) represents a strategy for altering the level of a small number of signalling molecules in patch \({x}_{0}^{(i)}\) in a way that increases the probability of T-cell presence as predicted by the classifier. The optimization also favours perturbations that shift the image patch to be more similar to its nearest T-cell patches in the training data, shown as Proto. Each perturbation corresponds to adjusting the relative intensity of each imaging channel. Taking the median across all perturbations produces a whole-tumour perturbation strategy, which we assess by perturbing in silico tumour images from a test patient cohort and examining the predicted T-cell distribution after perturbation.

Full size image

We leverage IMC profiles of human tumours to train a model to predict the spatial distribution of CD8+ T cells in a self-supervised manner. We first divide IMC images into patches representing local tissue signalling environments, and then we create a masked copy of each patch by removing all signals originating from CD8+ T cells (Fig. 1b). We train a neural network model to classify whether T cells are present or absent using only the masked copy. Using our trained model, we apply counterfactual optimization to generate tumour perturbations predicted to enhance CD8+ T-cell infiltration (Fig. 1c). For each image patch x0 that does not contain CD8+ T cells, our optimization algorithm searches for a perturbation δ such that our classifier f predicts the perturbed patch xp = x0 + δ as having T cells; hence, xp is referred to as a counterfactual instance. Furthermore, our algorithm favours simple and realistic strategies by minimizing the number of molecules perturbed while also ensuring that the counterfactual instance is not far from image patches in our training data, so we can be more confident of the model’s prediction. We can obtain a perturbation δ with these desired properties by solving a constrained optimization problem (Methods).

Since drug treatments cannot act at the spatial resolution of individual micrometre-scale pixels, we constrain our search space to only perturbations that affect all cells in the image uniformly. Specifically, we only search for perturbations that change the level of any molecule by the same relative amount across all cells in an image.

Taken together, our algorithm obtains an altered image predicted to contain T cells from an original image, which lacks T cells, by minimally perturbing the original image in the direction of the nearest training patch containing T cells until the classifier predicts the perturbed image to contain T cells. Since our strategy may find different perturbations for different tumour patches, we reduce the set of patch-wise perturbations \({\{{\delta }^{(i)}\}}_{i}\) to a whole-tumour perturbation by taking the median across the entire set (Fig. 1c).

Convolutional neural networks predict T-cell distribution

We applied Morpheus to two publicly available IMC datasets of tumours from patients with metastatic melanoma26 and CRC with liver metastases27 (Fig. 2a). We validate the infiltration prediction on an additional breast cancer dataset28. While this breast cancer data focuses on cell-type markers over functional modulators of T-cell infiltration, making it unsuitable for therapeutic prediction, it serves to further validate our machine learning-based prediction of T-cell infiltration.

Fig. 2: U-Net classifiers accurately predict T-cell distribution in IMC images of melanoma, metastatic liver and breast tumour.
figure 2

a, Histograms showing the distribution of tumour cores per patient and CD8+ T-cell fractions per core across all three datasets and data splits. b, Predicted and actual T-cell distribution of tissue sections from test cohorts in melanoma, liver tumour and breast tumour dataset. c, Predicted and true proportion of patches with T cells within a tissue section; each dot corresponds to a tissue section, and the diagonal black line indicates perfect prediction. d, The RMSE (equation (3), Methods) across all (test) tissue sections for three different classes of models.

Full size image

The melanoma dataset26 was obtained by IMC imaging of 159 tumour cores from 69 patients with stage III or IV metastatic melanoma. Each tissue was imaged across 39 molecular channels, consisting of markers for tumour, immune and stromal cells, as well as 11 different chemokines (RNA) (Methods). The CRC dataset27 consists of 209 tissue sections taken from 30 patients imaged across 42 channels, including 60 sections from primary CRC tumours, 89 sections CRC metastases to the liver and 60 ‘healthy’ liver sections obtained away from the metastases (Methods). The breast cancer dataset28 was obtained by IMC imaging of 749 breast tumour cores from 693 patients. The tissues were imaged across 37 channels, consisting of markers for tumour, lymphoid, myeloid and stromal cells (Methods).

For each of the three tumour datasets, we trained a separate U-Net classifier that effectively predicts CD8+ T-cell infiltration level in unseen tumour sections (Methods). The two classifiers trained on melanoma and CRC datasets achieved the best performance (Supplementary Table 4) with an AUROC (area under the receiver operating characteristic curve) of 0.87 and 0.89, respectively, whereas the classifier trained on breast tumours achieved an AUROC of 0.83 (Supplementary Fig. 2). A limited overlap in imaging channel across the three datasets makes it difficult to compare the TME across cancer types or to determine how difference in the TME between the three cancer types affects Morpheus’ ability to predict T-cell presence. Figure 2b shows examples of actual and predicted T-cell distributions in tumour sections, demonstrating that our classifiers accurately predict the general distribution of T cells. For each tissue section of a cancer type, the predictions were obtained by applying the corresponding U-Net classifier to each image patch independently. Comparing the true proportion of T-cell patches in a tissue section against our predicted proportion also shows strong agreement (Fig. 2c). The true proportion of patches with T cells is calculated by dividing the number of patches within a tissue section that contain CD8+ T cells by the total number of patches within that section. We quantify the performance of our U-Nets on the entire test dataset using the root mean square error (RMSE) (equation (3), Methods), which represents the mean difference between our predicted proportion and the true proportion per tumour section (Fig. 2d). Our classifiers perform well on liver tumour and melanoma, achieving an RMSE of only 7% and 8%, respectively, and a relatively poorer performance of 11% on breast tumour. Taken together, these results suggest that our classifier can accurately predict the T-cell infiltration status of multiple tumour types.

To gain insight into the relative importance of nonlinearity and spatial information in the performance of the U-Net on the T-cell classification task, we compared the U-Nets’ performance with a logistic regression model and a multi-layer perceptron (MLP). Both the logistic regression and MLP models are given only mean channel intensities as input, so neither have explicit spatial information. Furthermore, the logistic regression model is a linear model with a threshold, whereas the MLP is a nonlinear model. Figure 2d shows that across all three cancer datasets, the MLP classifier consistently outperforms the logistic regression model, reducing RMSE by 20–40% to suggest that there are considerable nonlinear interactions between different molecular features in terms of their effect on T-cell localization. The importance of spatial features on the T-cell prediction task, however, is less consistent across cancer types. Figure 2d shows that for predicting T cells in breast tumour, the U-Net model offers negligible boost in performance relative to the MLP model (<2% RMSE reduction), whereas for liver tumour, the U-Net model achieved an RMSE 30% lower compared with the MLP model. This result suggests that the spatial organization of signals may have a stronger influence on CD8+ T-cell localization in liver tumour compared with breast tumour.

Applying Morpheus to metastatic melanoma samples

Applying our counterfactual optimization procedure using the U-Net classifier trained on melanoma IMC images, we discovered a combinatorial therapy predicted to be highly effective in improving T-cell infiltration in patients with melanoma. Currently, there are substantial efforts to augment T-cell therapy using chemokines29, which are a family of secreted proteins that are known for their ability to stimulate cell migration30. Since this dataset is unique in its broad coverage of chemokine profiles, we applied Morpheus to systematically search for optimal chemokine therapy by restricting the optimization algorithm to only perturb chemokines. By optimizing over multiple chemokines, Morpheus opens the door to combinatorial chemokine therapeutics that has the potential to more effectively enhance T-cell infiltration into tumours. Figure 3a shows that patients from the training cohort separate into two clusters based on hierarchical clustering of perturbations computed for each patient. Taking median across all patients in cluster 1, the optimized perturbation is to increase the CXCL9 level by 215%, whereas in patient cluster 2, the optimized perturbation consists of increasing CXCL10 level by 88% while decreasing CCL18 and CCL22 levels by 100% and 100%, respectively (Fig. 3a). Both CXCL9 and CXCL10 are well known for playing a role in the recruitment of CD8+ T cells to tumours. However, CCL22 is known to be a key chemokine for recruiting regulatory T cells31 and CCL18 is known to induce an M2-macrophage phenotype32, so their expression likely promotes an immunosuppressive microenvironment inhibitory to T-cell infiltration and function.

Fig. 3: Combinatorial chemokine therapy predicted to drive T-cell infiltration in patients with metastatic melanoma.
figure 3

a, Whole-tumour perturbations optimized across IMC images of patients (row) from the training cohort, with bar graph showing the median relative change in intensity for each molecule. b, Distribution of cancer stages among patients within two clusters; grey indicates unknown stage. c, Volcano plot comparing chemokine level and cell-type abundance from patient clusters 1 and 2, computed using mean values and Wilcoxon rank-sum test with Šidák correction. Grey indicates non-statistical significance. Non-significant chemokines not shown: CXCL12 (fold change = 0.96, P = 1) and CCL8 (fold change = 0.93, P = 0.91). d, Patch-wise chemokine profile (left); one-dimensional heatmap (right): infiltration status (light/dark = from infiltrated/deserted tumour), tumour cell (light/dark = present/absent), CD8+ T cells (light/dark = present/absent). e, Patch-wise correlation between chemokine signals and the presence of CD8+ T cells. f, Top: UMAP projection of tumour patches (chemokine channels) shows a clear separation of masked patches with and without T cells. Bottom: coloured arrows connect UMAP projection of patches without T cells and their corresponding counterfactual (perturbed) patch, where the colours correspond to k-nearest neighbour clusters (i–iv) of the counterfactual patches. Pie charts (i–iv) show the distribution of patients whose original tumour patches are found in the corresponding cluster regions in the UMAP. g, Cell maps computed from a patient’s IMC image, showing the distribution of T cells before and after perturbation. h, Original versus perturbed (predicted) mean infiltration level across all patients (test cohort) with 95% confidence interval (only shown for patients with more than two samples). i, Mean infiltration level across all patients (test cohort) for optimized perturbation strategies of varying sparsity. The error bar represents 95% confidence interval.

Full size image

Figure 3b shows that the choice of which of these two strategies does not appear to be related to a patient’s cancer stage. We do find, however, that nearly all chemokines have higher mean expression in the tumours of patients in cluster 2 compared with cluster 1, while there are no significant differences between the two groups in terms of the cell-type compositions within tumours (Fig. 3c). Since the levels of CCL22 and CCL18 are nearly 25% higher in patients from cluster 2 and both chemokines have been implicated in having an inhibitory effect on T-cell infiltration, it is reasonable that the optimization algorithm suggests inhibiting CCL18 and CCL22 only for patients in cluster 2. However, the switch from boosting CXCL9 to CXCL10 is not as straightforward. A possible explanation is that boosting CXCL10 is important when blocking CCL18 and CCL22 in order for the perturbed patches to stay close to the data manifold, leading to more realistic tissue environments. Interestingly, the single-cell nature of the dataset appears to be necessary for discovering this strategy as counterfactuals generated using pseudobulk data led to different strategies (Extended Data Fig. 2a and Supplementary Note 3).

Morpheus selected perturbations that would make the chemokine composition of a TME more similar to T-cell-rich regions of immune-infiltrated tumours. Figure 3d shows that melanoma tissue patches can be clustered into distinct groups based on their chemokine concentration profile. One cluster (highlighted in blue) contains exactly the patches from immune-infiltrated tumours that contain both tumour and T cells, which likely represents a chemokine signature that is suitable for T-cell infiltration. Alternately, a second cluster (highlighted in red) that contains patches from immune-desert tumours that have tumour cells but no T cells likely represents an unfavourable chemokine signature. Compared with the cluster highlighted in red, Fig. 3d shows that the cluster highlighted in blue contains elevated levels of CXCL9 and CXCL10 and reduced levels of CCL22, which partially agrees with the perturbation strategy (Fig. 3a) discovered by Morpheus. Lastly, Fig. 3e shows that our four selected chemokine targets cannot simply be predicted from correlation of chemokine levels with the presence of CD8+ T cells, as both CCL18 and CCL22 are weakly correlated (<0.2) with CD8+ T cells, even though the optimized perturbations require inhibiting both chemokines, suggesting the presence of notable nonlinear effects not captured by correlations alone.

We can directly observe how Morpheus searches for efficient perturbations by viewing both the original patch and perturbed patches in a dimensionally reduced space. Figure 3f (top) shows a UMAP (Uniform Manifold Approximation and Projection) projection where each point represents the chemokine profile of an IMC patch. T-cell patches (with their CD8+ T cells masked) are well separated from patches without CD8+ T cells. The coloured arrows in the bottom UMAP of Fig. 3f illustrate the perturbation for each patch as computed by Morpheus and demonstrate two key features of our algorithm. First, optimized perturbations push patches without T cells towards the region in UMAP space occupied by T-cell-infiltrated patches. Second, the arrows in Fig. 3c are coloured to show that optimized perturbations seem efficient in that patches are perturbed just far enough to land in the desired region of space. Specifically, red points that start out on the right edge end up closer to the right after perturbation (regions iii and iv), while points that start on the left/bottom edge end up closer to the left/bottom (region i), respectively. We make this observation while noting that UMAP, although designed to preserve the topological structure of the data, is not a strictly distance-preserving transformation33. Furthermore, the pie charts (i–iv) are coloured by the patient of origin to show that the region of space where points are being perturbed to is not occupied by tissue samples from a single patient with highly infiltrated tumour. Rather, these regions consist of tissue samples from multiple patients, suggesting that our optimization procedure can synthesize information from different patients when searching for therapeutic strategies.

After applying the second perturbation strategy from Fig. 3a in silico to IMC images of a tumour, Fig. 3g shows that T-cell infiltration level (defined as the proportion of tumour patches with T cells) is predicted to increase by 20-fold. In this dataset, patients that respond favourably to immunotherapy tend to have significantly higher levels of T cells within tumours before treatment (t-test, P = 0.006; Supplementary Fig. 3). We applied both perturbation strategies on patients in our test cohort in silico and show that this predicted improvement holds across nearly all 14 patients from the test group, boosting T-cell infiltration level from an average of 21% across samples to a predicted 50% post perturbation (Fig. 3h).

The combinatorial nature of our optimized perturbation strategy is crucial to its predicted effectiveness. We systematically explored the importance of combinatorial perturbation by changing parameter β of equation (4), which adjusts the sparsity of the strategy, where a more sparse strategy means that fewer molecules are perturbed. Figure 3i shows that perturbing multiple targets is predicted to be necessary for driving significant T-cell infiltration across multiple patients, with the best perturbation strategy involving one target predicted to achieve 30% less T-cell level compared with the optimal strategy involving four targets. In conclusion, within the scope of the chemokine targets considered, combinatorial perturbation of the TME appears necessary for improving T-cell infiltration in metastatic melanoma.

Applying Morpheus to CRC with liver metastases samples

Applying Morpheus to IMC images from the CRC cohort, we discovered two patient-dependent therapies predicted to be highly effective in improving T-cell infiltration (Fig. 4a). Taking median over patients in the first cluster, the optimized strategy involves inhibiting PD-1, PD-L1 and CXCR4. Meanwhile, for the second group of patients, the optimized strategy involves inhibiting CYR61, PD-1, PD-L1 and CXCR4 (Fig. 4a). Interestingly, all four of the perturbation targets correlated poorly with the presence of CD8+ T cells compared with the other proteins that were not selected as perturbation targets (Fig. 4b), suggesting the presence of substantial spatial and nonlinear effects not captured by correlations alone.

Fig. 4: Blocking subsets of PD-L1, CXCR4, PD-1 and CYR61 predicted to drive T-cell infiltration in CRC cohort.
figure 4

a, Optimized tumour perturbations aggregated to the patient (row) level (train cohort). The bar graph shows the median relative change in intensity for each molecule across all patients within their cluster. b, Patch-wise correlation between the levels of different molecules and the presence of CD8+ T cells. c, Pie charts show the proportion of patients in each cluster that have FLD; P value from the hypergeometric test. d, Volcano plot comparing molecule levels and cell-type abundance between the two patient cluster using tumour tissues, computed using mean values and Wilcoxon rank-sum test with Šidák correction. Cell types include natural killer (NK) cells, myeloid-derived suppressor cells (MDSCs), dendritic cells (DCs) and others. e, Optimized perturbations aggregated to the level of tissue samples (row). f, UMAP projection of IMC patches. Left: UMAP shows T-cell patches coloured by the tissue samples that they are taken from. Right: UMAP shows counterfactual (perturbed) instances (blue) optimized for tumour patches without T cells (red). g, Line plots show the predicted T-cell infiltration level for each tissue section from the test cohort, before and after perturbation. Bar plots show the predicted mean T-cell infiltration level for each test patient. h, Predicted mean infiltration level across all test patients using perturbation strategies of varying sparsity, obtained by varying β in equation (4). The error bar represents 95% confidence interval.

Full size image

All perturbation targets identified by our optimization procedure have been found to play crucial roles in suppressing T-cell function in the TME, and treating patients with inhibitors against subsets of the selected targets has been shown to improve T-cell infiltration in human CRC liver metastases. Tumour-associated lymphatic vessels promote T-cell exit from tumour via the CXCL12/CXCR4 axis34, and the PD-1/PD-L1 pathway inhibits CD8+ T-cell activity and infiltration in tumours. In addition, CYR61 is a chemoattractant and was recently shown to drive M2 tumour-associated macrophage infiltration in patients with CRC liver metastases27. Inhibition of both PD-1 and CXCR4, which were consistently selected by Morpheus as targets, has already been shown to increase CD8+ T-cell infiltration in preclinical mouse models of colon cancer35,36. The single-cell nature of the CRC dataset appears to be necessary for discovering this strategy as counterfactuals generated using pseudobulk data led to different strategies (Extended Data Fig. 2b and Supplementary Note 3).

The emergence of the two distinct perturbation strategies may be explained by variation in liver fat build-up among patients. Patient cluster 1 is made up of significantly more patients with fatty liver disease (FLD) (67%) compared with patient cluster 2 (12%) (Fig. 4c). Furthermore, Fig. 4d shows that both YAP and CYR61 levels are significantly higher in tumours from patient cluster 1 by 50% and 3.5%, respectively. Indeed, CYR61 is known to be associated with non-alcoholic FLD27 and YAP is a transcription coregulator that induces CYR61 expression37. However, despite patients in cluster 1 having higher levels of CYR61, it is only for patients in cluster 2 where the optimal strategy involves blocking CYR61. We postulate that this seemingly paradoxical finding may arise because removing CYR61 from patients in cluster 1 represents a more pronounced perturbation, given their inherently higher concentration. A perturbation of this magnitude would likely shift the tumour profile substantially away from the data manifold, where the classifier’s prediction about the perturbation’s effect becomes less reliable; hence, such a perturbation would be heavily penalized during optimization owing to the Lproto term.

Using only raw image patches, Morpheus discovers tissue-dependent perturbation strategies (Fig. 4e). As depicted in Fig. 4e, by aggregating perturbations at the individual tissue level, we observe that the optimized perturbation for ‘healthy’ liver sections is straightforward, necessitating only the inhibition of CXCR4. Recall ‘healthy’ sections are samples obtained away from sites of metastasis. By contrast, promoting T-cell infiltration into primary colon tumours is anticipated to involve targeting a minimum of three signals. Morpheus finds that liver metastases appear to fall between these two tissue types. Furthermore, direct comparison between perturbations optimized for metastatic tumour and primary tumour samples does not reveal a notable difference in strategy (Supplementary Fig. 1). We can partly understand the discrepancy between tissues by plotting a UMAP projection of all T-cell patches from the three tissue types (Fig. 4f, left). The clear separation between T-cell patches from ‘healthy’ tissue and those from primary tumours underscores that the signalling compositions driving T-cell infiltration likely differ substantially between the two tissue types, prompting Morpheus to identify markedly different perturbation strategies. Furthermore, some patches from metastatic tumours co-localize with ‘healthy’ tissue patches in UMAP space, while other patches co-localize with primary tumour patches. This observation again aligns with our previous result, where optimized perturbation strategies for metastases samples share similarities with strategies for either ‘healthy’ tissue or primary tumour (Fig. 4e).

Despite the CRC dataset comprising a mixture of healthy, tumour and hybrid metastatic samples, Morpheus targets the most pertinent tissue type when optimizing perturbations. During both the model training and counterfactual optimization phases, we did not make specific efforts to segregate the three tissue types. Furthermore, we did not provide tissue type labels or any metadata. Despite these nuances, Fig. 4f shows that the counterfactual instances for tumour patches (dark blue) from primary and metastases samples are mostly perturbed to be near T-cell patches from primary (cyan) and metastatic tumour (gold), instead of being perturbed to be similar to T-cell patches from ‘healthy’ tumours (purple). This result is partly a consequence of our prototypical constraint, which encourages patches to be perturbed towards the closest T-cell patch. For a patch from a metastatic tumour without T cells, the closest (most similar) T-cell patch is likely also from a metastatic tumour than from a ‘healthy’ tissue. However, there are occasional exceptions where T-cell patches from ‘healthy’ tissues can influence the optimization of tumour tissues, as outlined by the dashed ellipse in Fig. 4f, especially if they share similar features as tumour regions.

The two therapeutic strategies that we discovered generalize to patients in our test cohort (Fig. 4g,h). Given that we have two therapeutic strategies, one enriched for patients with FLD and another for patients without FLD, we apply different perturbation strategies in silico across all test patients depending on their FLD status. Aggregated to the patient level, Fig. 4g shows that the CD8+ T-cell infiltration level is predicted to increase for nearly all patients, significantly boosting mean infiltration level from 17% to a predicted 35% post perturbation (Fig. 4h). However, when comparing individual tissue samples, Fig. 4g reveals substantial variation in the predicted response to perturbation among samples from the same patient and tissue types. In patient 7, the two metastatic tumour sample is predicted to see a nearly sevenfold increase in T-cell infiltration after perturbation, yet almost no change is expected for patient 7’s other three primary and one metastatic samples. Similar patterns are observed in patients 14 and 17. This marked variability in response among a substantial portion of test patients underscores the challenges posed by intra-tumour and inter-patient heterogeneity in devising therapies for CRC with liver metastases. This result further implies that, for studying CRC with liver metastases, collecting numerous tumour sections per patient could be as crucial as establishing a large patient cohort.

Lastly, combinatorial perturbation is again predicted to be necessary to drive significant T-cell infiltration in large patient cohorts. By increasing β in equation (4), we generated strategies with between one and five total targets, where perturbing at least four targets is predicted to be necessary to produce a statistically significant boost to T-cell infiltration (Fig. 4h).

Experimental validation of predicted perturbation strategies

Morpheus-derived strategies boost T-cell level in in vitro migration assays using human melanoma and CRC cells. We tested Morpheus’ predictions using a transwell migration assay (Methods), which consists of two chambers separated by a permeable membrane allowing for selective passage of molecules and cells (Fig. 5a). We place human peripheral blood mononuclear cells (PBMCs) initially in the top chamber and human cancer cells in the bottom chamber, where we apply different perturbations proposed by Morpheus and count the number of CD8+ T cells that infiltrate the bottom chamber after 4 h using flow cytometry (Methods). This transwell/co-culture system is a common method for assessing the effect of different perturbations in altering the migratory capacity of T cells towards cancer cells. The PBMC population contains a mixture of immune cell types, including CD8+ T cells. For CRC, perturbations are applied to both chambers as some target molecules are expressed by immune cells (for example, PD-L1 and CXCR4). Similar transwell/co-culture systems are commonly used for assessing the effect of different perturbations in altering the migratory capacity of T cells towards cancer cells38,39,40.

Fig. 5: In vitro experimental validation of Morpheus predictions.
figure 5

a, T-cell transwell migration assay for assessing the effect of Morpheus-derived perturbation strategies on CD8+ T-cell infiltration into an in vitro tumour compartment. Human PBMCs are placed into the top chamber, and a human tumour cell line (A375 for melanoma and HCT116 for CRC) is placed into the bottom chamber. We measure CD8+ T-cell infiltration into the bottom chamber after 4 h in the presence or absence of signalling perturbations predicted by Morpheus. Signalling perturbations include both signalling protein addition and blocking antibodies, which are indicated by α/anti. b, Log fold change in CD8+ T-cell abundance within the lower chamber containing A375 melanoma cells relative to CD8+ T-cell abundance in unperturbed controls. CXCL9 and {CXCL10, αCCL18, αCCL22} are Morpheus predicted infiltration strategies, while the CXCL10 addition alone strategy is shown for comparison to CXCL9 alone. c, Log fold change in CD8+ T-cell abundance within the lower chamber containing HCT116 CRC cells relative to CD8+ T-cell abundance in unperturbed control. {αPD-1, αPD-L1, αCXCR4} and {αPD-1, αPD-L1, αCXCR4, αCYR61} are Morpheus predicted strategies. The αPD-1 and αPD-L1 strategies, blocking PD-1 or PD-L1, are clinical immunotherapy strategies shown for comparison. Each perturbation trial was normalized to its paired control trial. *P < 5 × 10−2 and **P < 1 × 10−2. Two-sided paired t-tests used to assess significance; see Supplementary Tables 6 and 7 for raw data. The error bars represent the mean ± s.e.m. of independent biological replicates and dots indicate individual n = 8 and n = 9 replicate values for b and c, respectively (n = 12 for bars 2–3 in c).

Full size image

We used the human A375 melanoma cell line to test both sets of melanoma perturbations (Fig. 3a). Directly adding either CXCL9 proteins alone or a triple strategy consisting of CXCL10, anti-CCL22 antibody and anti-CCL18 antibody increased the T-cell level in the tumour chamber by 17- and 14-fold, respectively (paired t-test, P = 1 × 10−3 and 1 × 10−4, respectively; Fig. 5b). Although CXCL9 and CXCL10 are often considered to have similar functions as they both bind to the receptor CXCR3 and act as chemoattractants for CD8+ T cells, Morpheus did not predict the addition of CXCL10 alone as an effective perturbation; rather, Morpheus always predicted CXCL10 perturbation as one part of a combinatorial perturbation (Fig. 3a). We found that, in fact, the addition of CXCL10 alone did not lead to any significant increase in the T-cell level compared with the perturbed control (paired t-test, P = 0.09; Fig. 5b).

We used the human HCT116 colorectal cell line to test both sets of CRC perturbations (Fig. 4a), by adding either blocking antibodies against PD-1, PD-L1 and CXCR4 or an additional blocking antibody against CYR61. In close agreement with model predictions (Fig. 4h), Morpheus’ four-target combinatorial perturbation increased T-cell abundance by twofold compared with unperturbed control (paired t-test, P = 2 × 10−3). The Morpheus four-target strategy also significantly outperforms anti-PD-1 and anti-PD-L1 treatment alone in our in vitro assays where we observed a 1.3-fold and 1.4-fold increase in T-cell abundance for anti-PD-1 and anti-PD-L1, respectively. The T-cell abundance change induced by anti-PD-1 and anti-PD-L1, which represent standard immunotherapies, was significantly lower than that induced by Morpheus across replicates as quantified by a paired t-test with P = 0.02 for Morpheus four-target versus PD-1 and P = 0.04 for Morpheus four-target versus PD-L1 (Fig. 5c). Unlike the four-target combination, we did not observe a significant increase in T-cell infiltration with the three-target strategy predicted by Morpheus (inhibition PD-1, PD-L1 and CXCR4) (1.5-fold increase, paired t-test, P = 0.09). We hypothesize that this relatively modest improvement from this three-target strategy is due to the absence of lymphatic endothelial cells in our in vitro assay. It was recently shown that tumour-associated lymphatic vessels control T-cell exit from tumour through the interaction between CXCL12 and CXCR4, and inhibiting CXCR4 boosts the quantity of intratumoural T cells specifically in tumours with lymphatic vessel-derived CXCL1234.

Altogether, we show that experimentally perturbing molecular targets according to Morpheus’ predicted strategy consistently improves the ability of T cells to migrate towards cancer cells in vitro. For cancers for which PD-1/PD-L1 therapy is ineffective, Morpheus suggests new alternatives with promising in vitro results.

Discussion

Our integrated deep-learning framework, Morpheus, combines deep learning with counterfactual optimization to directly predict therapeutic strategies from spatial omics data. One of the major strengths of Morpheus is that it scales efficiently to deal with large diverse sets of patient samples including metachronous tissue from the same patients but different sites, which will be crucial as more spatial transcriptomics and proteomics datasets are quickly becoming available41.

Morpheus identifies fundamentally different strategies to increase T-cell abundance, beyond just enhancing the rate of T-cell entry into the tumour. In the literature, the term ‘infiltration’ is often used as a catch-all term to refer to T-cell abundance. For clarity, while we align with this terminology, our focus is on strategies that boost overall T-cell abundance. For example, Morpheus’ strategy of inhibiting CXCR4 prevents T cells from exiting the tumour via the vasculature, thereby increasing T-cell abundance by reducing outflow. This illustrates Morpheus’ ability to reveal diverse mechanisms for enhancing T-cell presence in tumours.

While the molecular targets identified by Morpheus require experimental validation to confirm their causal role in T-cell infiltration, both the biological context and Morpheus’ counterfactual optimization objective strengthen their potential value. Biologically, many effects of T cells on their microenvironment feed back to influence further T-cell infiltration42,43,44, creating cyclical relationships where effects may become causes. For example, T cells promote tertiary lymphoid structures supporting further infiltration42, release cytokines such as interferon-γ (IFNγ) to both inhibit and facilitate T-cell infiltration by inducing PD-L1 expression and upregulating chemokines43, and enhance vascular permeability to facilitate additional T-cell infiltration44. Morpheus’ counterfactual optimization objective helps to address the association versus causation challenge by focusing on minimal interventions with significant effects. This approach attempts to prioritize direct causal factors, which typically have stronger associations with outcomes than non-causal correlates. While these factors do not guarantee causality, they may increase the likelihood that the identified targets meaningfully influence T-cell infiltration. Nonetheless, further experimental validation remains necessary to confirm any causal relationships.

For future work, we would like to apply Morpheus to spatial transcriptomics datasets with hundreds to thousands of molecular channels. Although spatial transcriptomics can profile substantially more molecules compared with spatial proteomic techniques15,16, the number of spatial transcriptomic profiles of human tumours is currently limited owing to the cost, with most public datasets containing single tissue sections from one to five patients, which is far too small to apply Morpheus. However, spatial transcriptomics is likely to be more standardized compared with proteomics, which use customized panels. As commercial platforms for spatial transcriptomics start to come online45, we will likely be seeing large-scale spatial transcriptomics datasets in the near future, with ~70–90% of the same probes shared between experiments.

A technical extension of Morpheus involves incorporating prior knowledge of gene–gene interactions to model the causal relations between genes. Molecular features in tissue profiles can exhibit strong dependencies; therefore, changing the level of one molecule can affect the expression of others. For example, increased levels of IFNγ in the TME can upregulate the expression of PD-L1 on tumour cells46. To be more realistic and actionable, a counterfactual should maintain these known causal relations. We can apply a regularizer to penalize counterfactuals that are less feasible according to established gene interactions from knowledge graphs, such as Gene Ontology47.

Other extensions of Morpheus include predicting cell-type-specific perturbations, which can be done by directly restricting the perturbation to only alter signals within specific cell types. In addition, although we applied Morpheus to the specific problem of driving T cells to infiltrate solid tumours, we can generalize our framework to predict candidate therapeutics that alter the localization of other cell types. For example, Morpheus can train a classifier model to predict localization of tumour-associated macrophages and compute perturbations predicted to reduce their abundance in the TME.

In this work, we focused on identifying generalized therapies by pooling predictions across multiple patient samples, but we can also apply Morpheus to find personalized therapy for treating individual patients. The variation in the optimized perturbations that we observe among patients in both melanoma and liver datasets suggests that personalized treatments could be substantially more effective compared with generalized therapies (Figs. 3a and 4a). Furthermore, Fig. 4g shows that a therapeutic strategy could have a highly variable effect even across different tissue samples from the same patient. This variability suggests that to generate therapy for an individual patient, it may be necessary to acquire substantial quantities of biopsy data. We can then apply our optimization procedure to a random subset of samples and then test the resulting perturbation strategy on the remaining samples to see how well the strategy is predicted to perform across an entire tumour or other primary and secondary tumours.

Incorporating Morpheus in a closed loop with experimental data collection is another promising direction for future work. Data can be collected from patients or animal models with perturbed/engineered signalling context, and this data can be easily fed back into the classifier model to refine the model’s prediction. The perturbation could be based on what the model predicts to be effective interventions, as is the case with Morpheus. We can also study tissue samples on which the model tends to make the most mistake and train the model specifically using samples from similar sources, such as similar patient strata or disease state.

Methods

Description of IMC datasets

All datasets used in this paper are publicly available. Metastatic melanoma dataset from Hoch et al.26 contains 159 images or cores taken from 69 patients, collected from sites including skin and lymph node. CRC liver metastases dataset from Wang et al.27 contains 209 images or cores taken from 30 patients. Breast tumour dataset from Danenberg et al.28 contains 693 images or cores taken from 693 patients. The RNA and protein panels used for each of the three datasets are listed in Supplementary Table 8.

Data split

For all three IMC datasets, we followed the same data splitting scheme to divide patients into three different groups (training, validation and testing) while ensuring similar class balance across the groups, which in our case means that the proportion of image patches with and without T cells is roughly equal across the three groups for each dataset. Patients are shuffled between the three groups until three criteria are met: (1) the number of patients across the three groups follow a 65/15/20 ratio, (2) the difference in class proportion between any two of the three groups is less than 2%, and (3) the training set contains at least 65% of total patches. The actual data splits used in the paper are described in Supplementary Table 9.

Overview of the Morpheus framework

The Morpheus framework consists of two main steps, the first being self-supervised training of a classifier to predict the presence of CD8+ T cells from multiplexed tissue images (Fig. 1b). Then we compute counterfactual instances of the data by performing gradient descent on the input image, allowing us to discover perturbations to the tumour image that increases the classifier’s predicted likelihood of CD8+ T cells being present (Fig. 1c). The perturbed image corresponds directly to a perturbation of the TME predicted to improve T-cell infiltration. We mask CD8+ T cells from all images to prevent the classifier from simply memorizing T-cell expression patterns, guiding it instead to learn environmental features indicative of T-cell presence. We will describe both model training and counterfactual optimization in detail in the following sections.

Training a classifier to predict T-cell localization

We leverage IMC profiles of human tumours to train a classifier to predict the spatial distribution of CD8+ T cells in a self-supervised manner.

Cell segmentation and phenotyping

Raw IMC images were processed to obtain single-cell masks using the ImcSegmentationPipeline48. The segmentation process began by converting raw data to ome-tiff format, followed by pixel classification in Ilastik49, which segmented images into nuclear, cytoplasmic and background regions. Probability maps generated from Ilastik were further processed in CellProfiler50 to create single-cell masks. To correct for channel spillover, a non-negative least squares method was applied using CATALYST51. For cell phenotyping, we adopted an automated approach complemented by manual curation. Single-cell segmentation masks were overlaid with single-channel tiff images to extract mean marker expression values for each cell, which were then arcsinh transformed using a cofactor of 1 and censored at the 99th percentile. Cell clusters were determined by applying PhenoGraph52 on the single-cell expression vectors using default hyperparameters. Channel gating was used to refine the identification of specific cell populations. Two levels of PhenoGraph clustering were performed: the first level identified major cell types (immune, stromal and tumour) and the second level further classified immune cells into subtypes. For the purpose of Morpheus, only identification of CD8+ T cells and tumour cells was required. Manual curation of cell clusters was guided by specific proteins (Supplementary Table 10) to ensure accurate classification. See Supplementary Table 3 for cell-type distribution.

Cell pixelation of IMC images

The purpose of model training is for the model to learn molecular features of a tissue environment that supports the presence of CD8+ T cells, so it is important for us to remove features of the image that are predictive of CD8+ T-cell presence but are not part of the cell’s environment, such as the expression of the T cell itself. A simple masking strategy of zeroing out all pixels belonging to CD8+ T cells will introduce contiguous regions of zeros to image patches with T cells, which is an artificial feature that is nonetheless highly predictive of T-cell presence and hence will likely be the main feature learned by a model during training. To circumvent this issue, we first apply a cell ‘pixelation’ step to each IMC image, where we reduce each cell to a single pixel positioned at the cell’s centroid. The value of this pixel is the sum of all pixels originally associated with the cell, representing the total signal from each channel within the cell. In this way, we can simply mask this ‘pixelated’ version of the image by zeroing all pixels representing CD8+ T cells. Our strategy is effective at masking T cells without introducing an artificial signal whereby simply removing cells at random will increase the chance that T cells are predicted to be present (Supplementary Note 1, Supplementary Table 1).

Patching and T-cell masking

From the set of ‘pixelated’ IMC images, we obtain a set of image patches {I(i)} by first dividing each image into local patches of tissue and then downsample each patch using a max-pooling operation (3 × 3 kernel, stride = 3, no padding) to reduce the dimensionality of the input with minor information loss (Supplementary Table 2). Thus, \({I}^{(i)}\in {{\mathbb{R}}}^{l\times w\times c}\) is an array with l and w denoting the pixel length and width of the image and c denoting the number of molecular channels in the images (Fig. 1b). Each image patch shows the level of c proteins across all cells within a small region of tissue. We set l = w = 16, corresponding to a 48 μm × 48 μm region (previously each pixel = 1 μm, now each pixel = 3 μm owing to downsampling). We applied spectral analysis to study the effect of using different patch sizes to predict T-cell infiltration and found that our selected patch size remains highly informative of T-cell presence (Extended Data Fig. 1 and Supplementary Note 2).

From a patch I(i), we can obtain a binary label s(i) indicating the presence and absence of CD8+ T cells in the patch and a masked copy x(i) with all signals originating from CD8+ T cells removed (set to zero). The task for the model f is to classify whether T cells are present (s(i) = 1) or absent (s(i) = 0) in image I(i) using only its masked copy x(i). Specifically, f(x(i)) ∈ [0, 1] is the predicted probability of T cells, and then we apply a classification threshold p to convert this probability to a predicted label \({\hat{s}}^{(i)}\in \{0,1\}\). Since we obtain the image label s(i) from the image I(i) itself by unsupervised clustering of individual cell expression vectors, our overall task is inherently self-supervised.

Classifier training objective

Given a set of masked image patches {x(i)} with corresponding CD8+ T-cell label {s(i)}, we train a model f to minimize the following T-cell prediction loss, also known as the binary cross entropy loss:

$$L=-\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}\left[{s}^{(i)}\log \left({\hat{s}}^{(i)}\right)+\left(1-{s}^{(i)}\right)\log \left(1-{\hat{s}}^{(i)}\right)\right],$$
(1)

where

$${\hat{s}}^{(i)}=\left\{\begin{array}{ll}1\quad &{\rm{if}}\;f({x}^{(i)})\ge p\\ 0\quad &{\rm{if}}\;f({x}^{(i)}) < p\end{array}\right.$$
(2)

and p is the classification threshold. We select p by minimizing the following RMSE on a separate set of tissue sections Ω:

$${{\rm{RMSE}}}^{2}=\frac{1}{| \Omega | }\sum _{j\in \Omega }{\left\vert \frac{1}{{N}_{j}}\mathop{\sum }\limits_{i = 1}^{{N}_{j}}{s}^{(i)}-\frac{1}{{N}_{j}}\mathop{\sum }\limits_{i = 1}^{{N}_{j}}{\hat{s}}^{(i)}\right\vert }^{2}.$$
(3)

The RMSE is a measure of the differences between the observed and predicted proportions of T-cell patches in a tissue section averaged across a set of tissues Ω, which we take to be the validation set.

U-Net architecture

To obtain a model that can accurately predict T-cell localization from environmental cues, we trained a fully convolutional neural network with the U-Net architecture to minimize (equation (1)). The U-Net architecture consists of a contracting path and an expansive path, which gives it a U-shaped structure53. The contracting path consists of four repeated blocks, each containing a convolutional layer followed by a rectified linear unit (ReLU) activation and a max pooling layer. The expansive path mirrors the contracting path, where each block contains a transposed convolutional layer. Skip connections concatenates the upsampled features with the corresponding feature maps from the contracting path to include local information. The output of the expansive path is then fed to a fully connected layer with softmax activation to produce a predicted probability.

U-Net training

We train our U-Net classifiers on patches obtained from patients from the training cohort, using stochastic gradient descent with momentum and a learning rate of 10−2 on mini-batches of size 128. Image augmentation was used to prevent overfitting, including random horizontal/vertical flips and rotations, in addition to standard channel-wise normalization. All models presented in this paper were trained with early stopping based on the validation Matthews correlation coefficient, computed using patches from the validation cohort, for a max of 30 epochs. All model performances are reported on patches from the test cohort. All models were trained on an NVIDIA GeForce RTX 3090 Ti GPU using PyTorch v2.0.0 (ref. 54) and PyTorch Lightning v2.2.2 (ref. 55). Implementation code can be found in our GitHub repository along with a tutorial Jupyter notebook illustrating the entire workflow using an example dataset.

We evaluated the performance of various classifiers, including both traditional convolutional neural networks and vision transformers. In all cases, we observed similar performance (Supplementary Table 5). We settled on a U-Net architecture because of ease of extension of the model to multichannel datasets.

Generating counterfactuals using the T-cell prediction model

Our trained model allows us to formulate counterfactual optimization as a constrained optimization problem to generate tumour perturbations predicted to enhance CD8+ T-cell infiltration (Fig. 1c).

Mathematical formulation of optimization problem

Given an image patch \({x}_{0}^{(i)}\) that does not contain CD8+ T cells, our optimization algorithm searches for a perturbation δ(i) such that our classifier f predicts the perturbed patch \({x}_{p}^{(i)}={x}_{0}^{(i)}+{\delta }^{(i)}\) as having T cells; hence, \({x}_{p}^{(i)}\) is referred to as a counterfactual instance. Ideally, we want each perturbation to involve perturbing as few molecules as possible and realistic in that the counterfactual instance is not far from image patches in our training data so we can be more confident of the model’s prediction. We can obtain a perturbation δ(i) with these desired properties by solving the following optimization problem adopted from ref. 56:

$${\delta }^{(i)}=\mathop{\min }\limits_{\delta }{L}_{{\rm{pred}}}\left({x}_{0}^{(i)},\delta\right)+{L}_{{\rm{dist}}}(\delta )+{L}_{{\rm{proto}}}\left({x}_{0}^{(i)},\delta\right),$$
(4)

such that

$$\begin{array}{rcl}{L}_{{\rm{pred}}}\left({x}_{0}^{(i)},\delta\right)&=&c\max\left(1-2f\left({x}_{0}^{(i)}+\delta\right),\,-\kappa\right),\\ {L}_{{\rm{dist}}}(\delta )&=&\beta \parallel \delta {\parallel }_{1}+\parallel \delta {\parallel }_{2}^{2},\\ {L}_{{\rm{proto}}}\left({x}_{0}^{(i)},\delta\right)&=&\theta\,\left|\left|\,{x}_{0}^{(i)}+\delta -{{\rm{proto}}}^{(i)}\right|\right|_{2}^{2}\end{array}$$
(5)

where δ(i) is a three-dimensional tensor that describes perturbation made to each pixel of the patch.

The three loss terms in equation (4) each correspond to a desirable property of the perturbation that we aim to discover. The term Lpred encourages validity, in that the perturbation increases the classifier’s predicted probability of T cells, so the network is more likely to predict the perturbed tissue patch as having T cells when it previously did not contain T cells. Next, the term Ldist encourages sparsity using elastic net regularization, favouring perturbations that do not require making many changes to the TME. Lastly, the term proto(i) in the expression for Lproto refers to the nearest neighbour of \({x}_{0}^{(i)}\) among all patches in the training set that are classified as having T cells. Thus, the term Lproto explicitly guides the perturbed image \({x}_{{\rm{p}}}^{(i)}\) to lie close to the data manifold defined by our training set, making perturbed patches appear similar to what has been observed in TMEs infiltrated by T cells.

Since drug treatments cannot act at the spatial resolution of individual micrometre-scale pixels, we constrain our search space to only perturbations that affect all cells in the image uniformly. Specifically, we only search for perturbations that change the level of any molecule by the same relative amount across all cells in an image. We incorporate this constraint by defining δ(i) in the following way:

$${\delta }^{(i)}={\gamma }^{(i)}\;{\odot }_{3}\,{x}_{0}^{(i)},$$
(6)

where \({\gamma }^{(i)}\in {{\mathbb{R}}}^{c}\) defines a single factor for each channel in the image and the circled dot operator represents channel-wise multiplication, so that within each channel, the scaling factor is constant across the spatial dimensions of the image. In practice, we directly optimize for γ(i), where \({\gamma }_{j}^{(i)}\) can be interpreted as the relative change to the mean intensity of the jth channel. However, given that our classifier does have fine spatial resolution, we can search for targeted therapies such as perturbing only a specific cell type or restricting the perturbation to specific tissue locations by changing equation (6) to match these different types of perturbation.

Taken together, the optimization procedure produces an altered image predicted to contain T cells from an original image that lacks T cells, by minimally perturbing the original image in the direction of the nearest training patch containing T cells until the classifier predicts the perturbed image to contain T cells (Fig. 1c).

Implementation of optimization procedure

We solve for the optimal perturbation δ(i) for each individual patch I(i) from the training cohort that (1) contains tumour cells and (2) does not contain CD8+ T cells (Fig. 1c). Since our strategy may find different perturbations for different tumour patches, we reduce the set of patch-wise perturbations \({\{{\delta }^{(i)}\}}_{i}\) to a whole-tumour perturbation by first taking the median across all patches for each patient and then across all patients. We evaluate the performance of a whole-tumour perturbation by applying the perturbation computationally to patches from the test cohort, before passing the perturbed patches through our trained classifier.

During optimization, the weight c of the loss term Lpred is updated for n iterations, starting at cinit. If we identify a valid counterfactual (predicted to contain T cells) for the present value of c, we will then decrease c in the subsequent optimization cycle to increase the weight of the additional loss terms to help regularize our solution. If, however, we do not identify a counterfactual, c is increased to put more emphasis on increasing the predicted probability of the counterfactual. The parameter \({s}_{\max }\) sets the maximum number of optimization steps for each value of c. The parameter linit sets the initial step size for each optimization step. Our optimization code was implemented in Python and was adapted from the Python library Alibi57, with substantial modifications including PyTorch compatibility and improved speed.

For the purpose of speed, Lproto is defined by first building a k-d tree of training instances classified as having T cells and setting the k-nearest item in the tree (in terms of Euclidean distance to \({x}_{0}^{(i)}\)) as proto. We use k = 1 for all counterfactual optimization. For all other parameters, we list their values in Supplementary Table 11.

Non-spatial models

In addition to the U-Net model, we also trained a single-layer neural network on the average intensity values from each molecular channel to obtain a logistic regression classifier, predicting the probability of CD8+ T-cell presence in the image patch. This model represents a linear model where only the average intensity of each molecule is used for prediction instead of their spatial distribution within a patch. Furthermore, we trained an MLP that also uses averaged intensity as input features for prediction but is capable of learning nonlinear interactions between features. The MLP model consists of two hidden layers (30 and 10 nodes) with ReLU activation.

Primary cell isolation and cell culture

Cryopreserved human PBMCs (Charles River Laboratories or STEMCELL Technologies 70025.1) were thawed in RPMI media supplemented with 100 U ml−1 penicillin and 100 U ml−1 streptomycin (Thermo) and 10% fetal bovine serum (FBS; Thermo). The human melanoma cell line A375 (American Type Culture Collection, CRL-1619) was cultured in DMEM media supplemented with 100 U ml−1 penicillin, 100 U ml−1 streptomycin, 1 mM HEPES, sodium and 10% FBS. The human colon cancer cell line HCT116 (American Type Culture Collection; kindly provided by the Ekihiro Seki lab in Cedars-Sinai Medical Center) was cultured in DMEM media (10569010; Thermo) supplemented with 100 U ml−1 penicillin and 100 U ml−1 streptomycin and 10% FBS in an incubator at 37 °C with 5% CO2.

T-cell migration assay

We used a transwell assay to examine the impact of predicted perturbations on CD8+ T-cell migration. Before the start of the experiment, PBMCs were thawed and rested for 12 h, after which they were pre-treated with combinations of chemokines and antibodies for an additional 12 h or maintained in RPMI. Tumour cells (either A375 or HCT116 cells) were thawed and grown to 80–90% confluence in the bottom chamber of 96-well plates. Cancer cells (and PBMCs for CRC) were incubated overnight in a 37 °C incubator, with supplementation of signalling proteins and antibodies, according to Morpheus’ predictions. A full list of signalling proteins and antibodies used to implement perturbations is in Supplementary Table 12. After incubation, PBMCs were seeded into an HTS 96-well permeable support (CLS3387, Corning), which were then placed inside 96-well plates containing cancer cells. Cells were allowed to migrate for 4 h according to published transwell migration protocols for T cells38.

Flow cytometric counting of CD8+ T cells

To count CD8+ T cells, supernatants from the bottom well of the transwell assay were collected and centrifuged at 500 × g for 5 min. The supernatant was discarded and the cell pellet was used for subsequent staining for CD8+ T cells using a mouse anti-human CD8 monoclonal antibody (CD8 monoclonal antibody 3B5) labelled with either Qdot 800 or fluorescein isothiocyanate (FITC). PBMCs were resuspended in HBSS buffer with 10 mM HEPES and 0.5% BSA. Unstained PBMCs were used as a control to determine gating strategy (Supplementary Fig. 4). Staining was performed according to the manufacturer’s instructions. Flow cytometry was performed using either an MACSQuant Analyzer 10/VYB (Miltenyi Biotec) or a Cytoflex S flow cytometer (Beckman Coulter).

Statistical analysis

We assessed the likelihood of observing a specific number of patients with a particular phenotype in a given cluster (Figs. 3b and 4c) using the hypergeometric test. This statistical test calculates the probability of k successes in n draws from a population of size N containing m successes, where draws are made without replacement. The formula used is

$$P(X=k)=\frac{\left(\begin{array}{c}m\\ k\end{array}\right)\left(\begin{array}{c}N-m\\ n-k\end{array}\right)}{\left(\begin{array}{c}N\\ n\end{array}\right)}.$$

For the melanoma dataset, this test was applied to determine the probability of observing the distribution of patients with stage III and stage IV melanoma among the two clusters. For the CRC dataset, this test was applied to determine the probability of observing the distribution of patients with non-alcoholic fatty liver disease (NAFLD) among the two clusters.

We used the Wilcoxon rank-sum test to compare molecule levels and cell-type abundance between two patient clusters using tumour tissue samples (Figs. 3c and 4d). This non-parametric test evaluates whether there is a significant difference in the distributions of two independent samples. The Wilcoxon rank-sum test statistic W is calculated as

$$W=\mathop{\sum }\limits_{i=1}^{{n}_{1}}R({X}_{i}),$$

where R(Xi) is the rank of the ith observation from the first sample in the combined sample of size n1 + n2. To account for multiple comparisons, P values obtained from the Wilcoxon rank-sum test were adjusted using the Šidák correction. The Šidák-adjusted P value Padj is given by

$${P}_{{\rm{adj}}}=1-{(1-P)}^{m},$$

where P is the original P value and m is the number of tests performed. This method adjusts the P values by calculating the cumulative probability of avoiding type I errors across all tests, providing a rigorous control of the family-wise error rate.

We used Welch’s t-test to assess whether there is a statistically significant difference in T-cell infiltration between responder and non-responders (Supplementary Fig. 3). Welch’s t-test is used to compare the means of two independent samples without assuming equal variance. The t statistic is defined as follows:

$$t=\frac{{\bar{X}}_{1}-{\bar{X}}_{2}}{\sqrt{\frac{{s}_{1}^{2}}{{n}_{1}}+\frac{{s}_{2}^{2}}{{n}_{2}}}},$$

where \({\bar{X}}_{1}\) and \({\bar{X}}_{2}\) are the sample means, \({s}_{1}^{2}\) and \({s}_{2}^{2}\) are the sample variances, and n1 and n2 are the sample sizes.

We used paired t-tests to assess the significance of the perturbation effect across multiple replicates in our transwell assay. The paired t-test is used to compare the means of two related samples, typically before and after a treatment or intervention. The t statistic for paired samples is defined as follows:

$$t=\frac{\bar{d}}{{s}_{d}/\sqrt{n}},$$

where \(\bar{d}\) is the mean difference between paired observations, sd is the standard deviation of the differences and n is the number of pairs.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.